ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4.  Скользящие и приложенные векторные величины.6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме.  4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения. 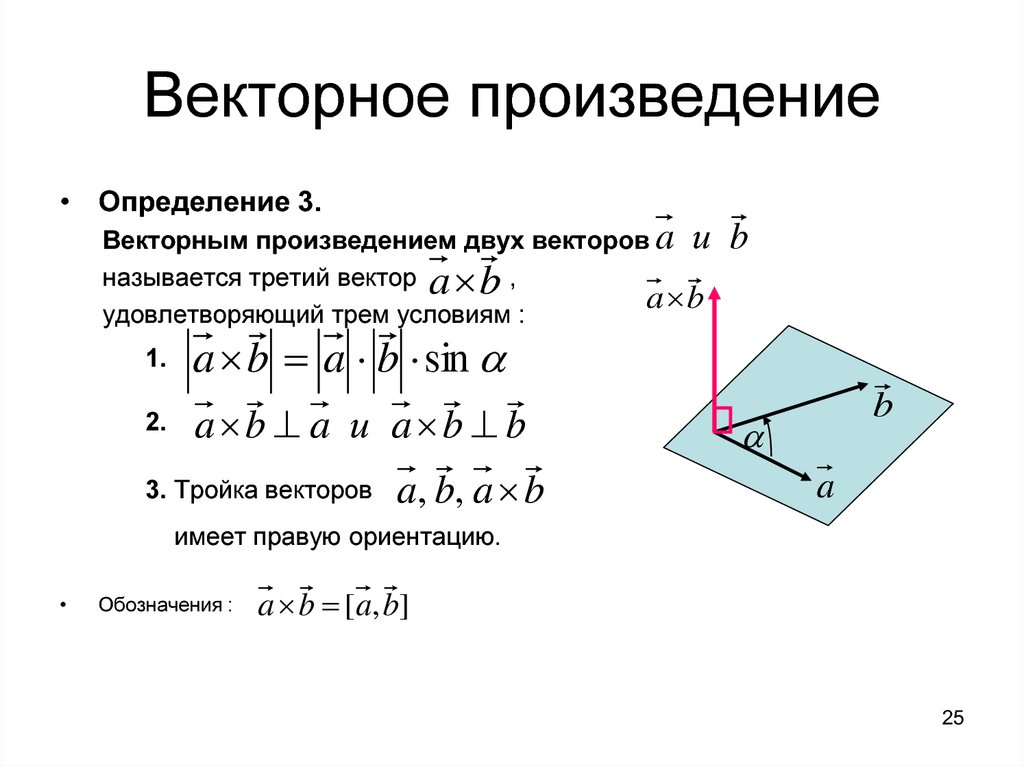 § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов.  4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII.  ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ§ 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3.  § 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности.  5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2.  3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV.  ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ§ 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII.  ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ§ 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах.  § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
вектор на вектор произведение
Вы искали вектор на вектор произведение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и векторного произведения векторов свойства, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вектор на вектор произведение».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вектор на вектор произведение,векторного произведения векторов свойства,векторного произведения векторов формула,векторного произведения формула,векторное,векторное произведение,векторное произведение 2 векторов,векторное произведение в координатах,векторное произведение в координатной форме,векторное произведение векторов,векторное произведение векторов в координатах формула,векторное произведение векторов в координатной форме,векторное произведение векторов и его свойства,векторное произведение векторов как найти,векторное произведение векторов определение,векторное произведение векторов примеры,векторное произведение векторов примеры решения,векторное произведение векторов свойства,векторное произведение векторов трех,векторное произведение векторов формула,векторное произведение векторов формула в координатах,векторное произведение векторов формулы,векторное произведение векторов через координаты,векторное произведение векторов это,векторное произведение двух векторов,векторное произведение двух векторов это вектор который,векторное произведение как найти,векторное произведение на плоскости,векторное произведение определение,векторное произведение по координатам,векторное произведение примеры,векторное произведение свойства,векторное произведение трех векторов,векторное произведение формула,векторное произведение через координаты,векторное произведение через координаты векторов,векторное произведение это,векторные произведения,вычислить векторное произведение векторов,геометрический смысл векторного произведения,как вычислить векторное произведение двух векторов,как найти векторное произведение,как найти векторное произведение векторов,как найти модуль векторного произведения,как найти площадь треугольника через векторное произведение,как найти произведение векторов,координаты векторного произведения,модуль векторного произведения,модуль векторного произведения векторов,модуль векторного произведения как найти,найти векторное произведение,найти модуль векторного произведения,определение векторного произведения,определение векторное произведение,определение векторное произведение векторов,площадь параллелограмма векторное произведение,площадь параллелограмма через векторное произведение,площадь треугольника через векторное произведение,примеры векторное произведение,примеры векторное произведение векторов,произведение вектор на вектор,произведение вектора на вектор,произведение векторов,произведение векторов формула,произведение векторов через координаты,произведения векторов,произведения векторов формула,свойства векторного произведения,свойства векторного произведения векторов,свойства векторное произведение,свойства векторное произведение векторов,свойства векторов векторного произведения,свойство векторного произведения,формула векторного произведения,формула векторного произведения векторов,формула произведения векторов.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор на вектор произведение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, векторного произведения векторов формула).
Решить задачу вектор на вектор произведение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Как применять формулу перекрестного произведения в многомерном исчислении
В векторном исчислении перекрестное произведение двух векторов — это специальная операция, которая дает новый вектор, перпендикулярный обоим исходным векторам.
Перекрестное произведение имеет множество приложений в многомерном исчислении и вычислительной геометрии. В этой обзорной статье мы дадим определение векторному произведению и исследуем его свойства. Вы узнаете, как рассчитать перекрестное произведение, как вывести формулу перекрестного произведения и как использовать формулу перекрестного произведения в различных приложениях.
Перекрестное произведение двух векторов
Для описания векторов в трехмерном пространстве воспользуемся стандартным ортонормированным базисом в правой системе координат, который образован векторами \vec{i} , \vec {j} и \vec{k} . Здесь \vec{i} = (1,0,0) — единичный вектор вдоль оси x, \vec{j} = (0,1,0) — единичный вектор вдоль оси y, а \ vec{k} = (0,0,1) — единичный вектор вдоль оси z. Любой вектор \vec{a} = (a_x, a_y, a_z) в трех измерениях может быть однозначно выражен как линейная комбинация векторов \vec{i} , \vec{j} и \vec{k} следующим образом :
\vec{a} = a_x \vec{i} + a_y \vec{j} + a_z \vec{k}
На следующем рисунке показано разложение вектора \vec{a} на стандартные базисные векторы:
Стандартный базис в правой системе координат.
Источник изображения: Wikimedia Commons Для двух произвольных векторов \vec{a} = (a_x, a_y, a_z) и \vec{b} = (b_x, b_y, b_z) в пространстве векторное произведение \vec{c} = \vec{a} \times \vec{b} — новый вектор, \vec{c} = (c_x, c_y, c_z) , такой, что
\begin{array}{c} c_x = a_y b_z — a_z b_y c_y = a_z b_x — a_x b_z c_z = a_x b_y — a_y b_x \end{array}
Это определение можно запомнить, записав векторное произведение в виде определителя:
\vec{c} = \vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} a_x & a_y & a_z b_x & b_y & b_z \end{массив} \right| = (a_y b_z — a_z b_y) \vec{i} + (a_z b_x — a_x b_z) \vec{j} + (a_x b_y — a_y b_x) \vec{k}
Следующий пример иллюстрирует это определение.
Пример 1
Пусть \vec{a} = (1,-3,1) и \vec{b} = (-1,-1,1) . Перекрестное произведение двух векторов \vec{a} и \vec{b} в этом случае является новым вектором, \vec{c}, который можно вычислить следующим образом:
\vec{c} = \ vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} 1 & -3 & 1 -1 & -1 & 1 \end{массив} \right| = (-3+1) \vec{i} + (-1-1) \vec{j} + (-1-3) \vec{k} = -2 \vec{i} -2 \vec{j } -4 \vec{к}
В компонентной записи имеем \vec{c} = \vec{a} \times \vec{b} = (-2,-2,-4).
Формула перекрестного произведения
Для двух векторов \vec{a} и \vec{b} удобно выбрать такую систему координат, чтобы оба вектора лежали в плоскости x-y, а ось x была параллельна вектор \vec{a} . В этом случае мы имеем \vec{a} = (|\vec{a}|,0,0) и \vec{b} =(|\vec{b}| cos\theta,|\vec{b} |sin\theta,0) , где |\vec{a}| и |\vec{b}| — нормы векторов \vec{a} и \vec{b} соответственно, а \theta — угол между векторами. По определению векторное произведение векторов \vec{a} и \vec{b} в такой системе координат равно
\vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} |\vec{a }| & 0 & 0 |\vec{b}| cos\тета & |\vec{b}| sin\theta & 0 \end{массив} \right| = |\vec{a}|,|\vec{b}| грех\тета,\vec{k}
В компонентной нотации мы можем написать \vec{a} \times \vec{b} =(0,0,|\vec{a}|,|\vec{b}| sin\theta) . Этот результат раскрывает некоторые важные свойства перекрестного произведения:
1. Перекрестное произведение двух векторов, \vec{a} и \vec{b} , есть вектор \vec{a} \times \vec{b} , который перпендикулярен как к \vec{a}, так и к \vec{b}
2.
Перекрестное произведение \vec{a} \times \vec{b} указывает направление, из которого поворот от \vec{a} к \vec{b} (через меньший из двух возможных углов) кажется против часовой стрелки
3. В отличие от скалярного произведения, перекрестное произведение не является коммутативной операцией, и \vec{b} \times \vec{a} = — ,\vec{a} \times \vec{b} . Мы можем легко проверить это свойство прямым вычислением:
\vec{b} \times \vec{a} = \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec {к} |\vec{b}| cos\тета & |\vec{b}| sin\theta & 0 |\vec{a}| & 0 & 0 \end{массив} \right| = — ,|\vec{a}|,|\vec{b}| sin\theta ,\vec{k} = — ,\vec{a} \times \vec{b} 9{\circ} ), векторным произведением является нулевой вектор: \vec{a} \times \vec{b} = \vec{0} = (0,0,0)
5. Величина векторного произведения двух векторов, | \vec{a} \times \vec{b} | , можно задать следующим соотношением:
| \vec{a} \times \vec{b} | = |\vec{a}|,|\vec{b}| грех\тета
Это последнее равенство известно как формула перекрестного произведения.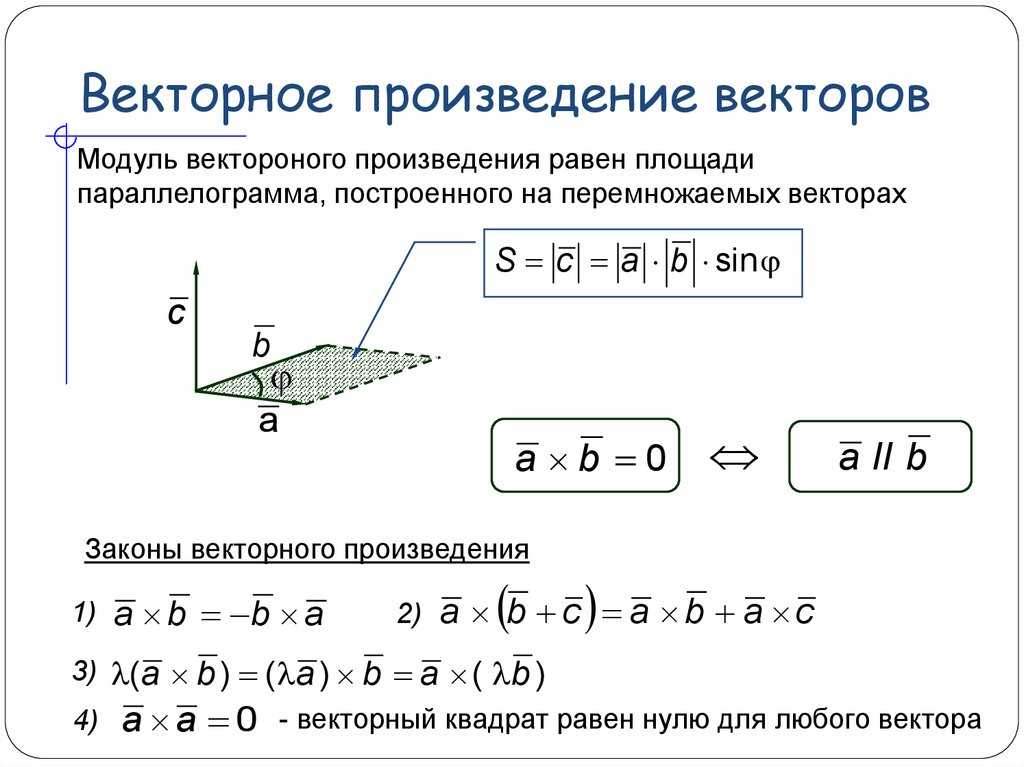
Формула перекрестного произведения подразумевает, что величина перекрестного произведения |\vec{a} \times \vec{b}| равно площади параллелограмма, стороны которого имеют векторы \vec{a} и \vec{b}, как показано на следующем рисунке:
Давайте продемонстрируем, как использовать векторное произведение на примерах.
Пример 2
Найдем вектор \vec{c}, перпендикулярный обоим векторам \vec{a} = (1,1,-1) и \vec{b} = (1,-1, 1) . Из-за свойств перекрестного произведения любой вектор, перпендикулярный как к \vec{a}, так и к \vec{b}, параллелен \vec{a} \times \vec{b} . Другими словами, \vec{c} = \alpha \left[ \vec{a} \times \vec{b} \right] , где \alpha — некоторое действительное число. Для перекрестного произведения двух векторов, \vec{a} и \vec{b}, мы имеем
\vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} 1 & 1 & — 1 1 & -1 & 1 \end{массив} \right| = (1+1) \vec{i} + (-1-1) \vec{j} + (-1-1) \vec{k} = 2 \vec{i} -2 \vec{j} — 2 \vec{k}
В компонентной записи \vec{a} \times \vec{b} = 2(1,-1,-1), и любой вектор, параллельный (1,-1,-1), перпендикулярен обоим \vec {а} и \vec{b} .
{,\prime} : 9{,\простое}| = объявление-BC
Скалярное тройное произведение и объем параллелепипеда
Формула векторного произведения имеет множество применений в вычислительной геометрии. Например, с его помощью можно вычислить объем параллелепипеда. Давайте посмотрим, как это можно сделать. Рассмотрим три вектора, \vec{a} , \vec{b} и \vec{c} , представляющие три ребра параллелепипеда, которые встречаются в одной вершине, как показано на рисунке ниже:
Объем параллелепипеда. Источник изображения: ВикискладОбъем параллелепипеда, V , можно рассчитать следующим образом:
V = S \cdot h
Здесь S — площадь основания, а h — высота этого параллелепипеда. Площадь основания по формуле векторного произведения определяется следующим соотношением:
S = |\vec{b} \times \vec{c}|
Высота параллелепипеда равна проекции вектора \vec{a} на направление \vec{b} \times \vec{c} . Таким образом, мы имеем 9{\ круг} . Теперь мы можем использовать определение скалярного произведения двух векторов:
\vec{m} \cdot \vec{n} = m_x n_x + m_y n_y + m_z n_z = |\vec{m}| |\век{п}| cos\phi
Здесь угол \phi — это угол между векторами \vec{m} и \vec{n} .
Следовательно, мы можем написать
V = S \cdot h = |\vec{b} \times \vec{c}| \cdot |\vec{a}| \кдот | кос\фи | = | (\vec{b} \times \vec{c},)\cdot \vec{a} |
Скалярное произведение вектора на векторное произведение двух других векторов известно как скалярное тройное произведение. Используя определения перекрестного произведения и скалярного произведения, мы можем вывести следующее выражение:
(\vec{b} \times \vec{c},)\cdot \vec{a} = (b_y c_z — b_z c_y) a_x + (b_z c_x — b_x c_z) a_y + (b_x c_y — b_y c_x) a_z = \det \left|\begin{array}{ccc} a_x & a_y & a_z b_x & b_y & b_z c_x & c_y & c_z \end{array} \right|
Из известного свойства определителей следует, что скалярное тройное произведение инвариантно относительно циклических перестановок векторов \vec{a} , \vec{b} и \vec{c} :
(\vec{b} \ раз \vec{c})\cdot \vec{a} = (\vec{c} \times \vec{a})\cdot \vec{b} = (\vec{a} \times \vec{b} )\cdot\vec{с}
Более того, скалярное тройное произведение равно нулю, если любые два вектора \vec{a} , \vec{b} и \vec{c} параллельны.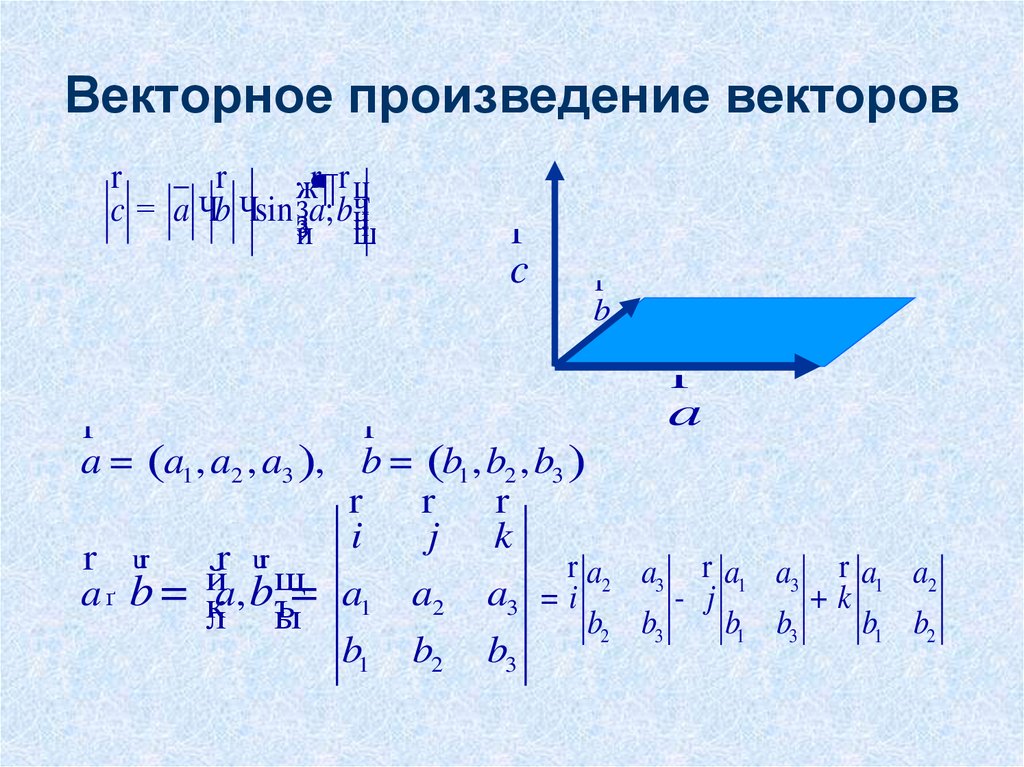
Естественно, объем параллелепипеда в этом случае равен нулю. Отсюда следует, что три вектора линейно зависимы тогда и только тогда, когда их скалярное тройное произведение равно нулю:
(\vec{a} \times \vec{b})\cdot \vec{c} = \det \left|\begin{ array}{ccc} a_x & a_y & a_z b_x & b_y & b_z c_x & c_y & c_z \end{array} \right| = 0
Если (\vec{a} \times \vec{b})\cdot \vec{c} > 0 , три вектора \vec{a} , \vec{b} и \vec{c} образуют правый Основа в космосе. Базис является левым в противоположном случае, когда (\vec{a} \times \vec{b})\cdot \vec{c} < 0 . Типичный правый базис состоит из трех векторов \vec{i} , \vec{j} и \vec{k} . Это можно продемонстрировать прямым вычислением:
\vec{i} \times \vec{j} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec {k} 1 & 0 & 0 0 & 1 & 0 \end{массив} \right| = \vec{k} , \quad (\vec{i} \times \vec{j})\cdot \vec{k} = \vec{k} \cdot \vec{k} = 1
В следующем примере показано, как можно использовать скалярное тройное произведение.
Пример 4
Предположим, что нам даны три вектора: \vec{a} = (1,2,3) , \vec{b} = (4,5,0) и \vec{c} = (3,2,1) . Давайте вычислим скалярное тройное произведение этих трех векторов:
(\vec{a} \times \vec{b},)\cdot \vec{c} = \det \left|\begin{array}{ccc} 1 & 2 & 3 4 & 5 & 0 3 & 2 & 1 \end{массив} \right| = (5-0) + 2(0-4) + 3(8-15) = -,24
Поскольку (\vec{a} \times \vec{b},)\cdot \vec{c} < 0 , три вектора \vec{a} , \vec{b} и \vec{c} равны линейно независимы и образуют левый базис. Объем параллелепипеда, натянутого на векторы \vec{a} , \vec{b} и \vec{c}, определяется следующим выражением:
V = |(\vec{a} \times \vec{ б},)\cdot \vec{c},| = 24
Перекрестное произведение и изгиб векторного поля
Перекрестное произведение играет важную роль в многомерном исчислении. Рассмотрим векторное поле \vec{v}(\vec{r},) = {v_x(x,y,z), v_y(x,y,z), v_z(x,y,z)} . Векторное поле \vec{v}, определенное таким образом, имеет важную дифференциальную характеристику; а именно, завиток \vec{v} , обозначаемый curl \vec{v} .
По определению, ротор \vec{v} — это просто векторное произведение дифференциального оператора {\ парциальное} {\ парциальное г}} :
\text{curl}, \vec{v} = \nabla \times \vec{v} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \ vec{k} \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} v_x & v_y & v_z \end{array} \ правильно|
Отсюда следует, что компоненты \text{curl}, \vec{v} определяются следующим образом:
\begin{array}{c} v_x = \dfrac{\partial v_z}{\partial y} — \dfrac{\partial v_y}{\partial z} v_y = \dfrac{\partial v_x}{\partial z} — \dfrac{\partial v_z}{\partial x} v_z = \dfrac{\partial v_y}{ \partial x} — \dfrac{\partial v_x}{\partial y} \end{массив}
Давайте проиллюстрируем этот метод нахождения ротора векторного поля на простом примере.
Пример 5
Рассмотрим векторное поле \vec{v} = (-y,x,0) . Изгиб \vec{v} можно рассчитать следующим образом:
\text{curl}, \vec{v} = \nabla \times \vec{v} = \det \left|\begin{array} {ccc} \vec{i} & \vec{j} & \vec{k} \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial} {\partial z} -y & x & 0 \end{массив} \right| = \vec{i} \left(-,\dfrac{\partial x}{\partial z}\right) + \vec{j} \left(-,\dfrac{\partial y}{\partial z}\ справа) + \vec{k} \left(\dfrac{\partial x}{\partial x} + ,\dfrac{\partial y}{\partial y}\right) = 2 \vec{k}
Следовательно, в этом случае \text{curl}, \vec{v} является постоянным вектором: \text{curl}, \vec{v} = (0,0,2) .
Завершение перекрестного произведения
В этой обзорной статье мы исследовали перекрестное произведение и его свойства. Теперь вы сможете вычислить векторное произведение двух векторов и ротор вектора. Вы также сможете применить формулу векторного произведения, чтобы найти площадь параллелограмма и объем параллелепипеда. Мы надеемся, что эта статья придаст вам большей уверенности в ваших знаниях о векторном произведении и облегчит изучение многомерного исчисления.
Давайте применим все на практике. Попробуйте этот практический вопрос по многомерному исчислению: Ищете больше упражнений по многомерному исчислению? Вы также можете найти тысячи практических вопросов на Albert.io. Albert.io позволяет вам настроить учебный процесс так, чтобы он ориентировался на практику, в которой вам больше всего нужна помощь. Мы дадим вам сложные практические вопросы, которые помогут вам достичь мастерства в многомерном исчислении.
Начните тренироваться здесь .
Вы учитель или администратор, заинтересованный в повышении успеваемости учащихся по многомерному исчислению?
Узнайте больше о наших школьных лицензиях здесь .
линейная алгебра — Формула для перекрестного произведения
Я связал видео в комментариях выше, но я обобщу идеи из видео в этом ответе. У нас есть 2 вопроса:
- Почему имеет смысл подставлять $\mathbf{i,j,k}$ в определитель? 93 \to \Bbb R$ можно записать в виде
$$
f(\mathbf x) = p_1 x_1 + p_2 x_2 + p_3 x_3.
$$
Вектор $\mathbf p = (p_1,p_2,p_3)$ можно рассматривать как способ «кодирования» функции $f$, поскольку мы имеем $f(\mathbf x) = \mathbf p \cdot \mathbf x$, где $\cdot$ обозначает скалярное произведение. Это приводит к нашему ответу на вопрос 1: когда мы вычисляем определитель с $\mathbf {i,j,k}$ имеет элементы верхней строки, мы получаем вектор $p_1 \mathbf i + p_2 \mathbf j + p_3 \mathbf k$.
Векторы $\mathbf{i,j,k}$ служат заполнителями для наших входных координат $x_1,x_2,x_3$: если мы вычислим $\mathbf p \cdot \mathbf x$, мы получим
$$
р_1 х_1 + р_2 х_2 + р_3 х_3,
$$
это именно то, что мы получили бы, если бы мы вычислили определитель с элементами $\mathbf x$ в качестве нашей верхней строки, т.е. если бы мы вычислили $f_{\mathbf a, \mathbf b}(\mathbf x)$ из определение я дал выше.Что касается вопроса 2, мы можем сделать следующие наблюдения:
- Если $\mathbf x$ равно $\mathbf a$ или $\mathbf b$, то $\mathbf p \cdot \mathbf x = f_{ \mathbf a, \mathbf b}(\mathbf x) = 0$. Таким образом, $\mathbf p$ ортогонален как $\mathbf a$, так и $\mathbf b$.
- Если мы подставим $\mathbf x = \mathbf p/\|\mathbf p\|$, то получим, что $\mathbf p \cdot \mathbf x = \frac{\mathbf p \cdot \mathbf p} {\|\mathbf p\|} = \|\mathbf p\|$. Из положительности определителя мы видим, что направление $\mathbf p$ таково, что $\mathbf p, \mathbf a, \mathbf b$ образуют правую систему.
Векторы $\mathbf{i,j,k}$ служат заполнителями для наших входных координат $x_1,x_2,x_3$: если мы вычислим $\mathbf p \cdot \mathbf x$, мы получим
$$
р_1 х_1 + р_2 х_2 + р_3 х_3,
$$
это именно то, что мы получили бы, если бы мы вычислили определитель с элементами $\mathbf x$ в качестве нашей верхней строки, т.е. если бы мы вычислили $f_{\mathbf a, \mathbf b}(\mathbf x)$ из определение я дал выше.
