Формула — томсон — Большая Энциклопедия Нефти и Газа, статья, страница 3

Cтраница 3

Несмотря на очевидные недостатки, формула Томсона часто используется в прикладных расчетах из-за ее аналитической простоты и физической прозрачности; не прекращаются по — сей день и попытки усовершенствовать эту модель, прежде всего учитывая движение атомного электрона.  [31]

Радиус г8КВ, определяемый по формуле Томсона ( Кельвина), имеет смысл только для капиллярной модели. Если же поры нецилиндрические, радиус Кельвина не соответствует параметру, описывающему реальные поры.  [32]

Дифференциальное сечение рассеяния как функция угла.  [33]

При высоких частотах наступает отклонение от формулы Томсона.  [34]

Ряд задач на электромагнитные колебания решается с применением формулы Томсона, а также формулы емкости плоского конденсатора и формулы связи между длиной волны, скоростью распространения колебаний и периодом.

При этом необходимо учитывать, что формула Томсона справедлива только в том случае, если активным сопротивлением колебательного контура можно пренебречь. В процессах, происходящих в колебательном контуре, выполняется закон сохранения и превращения энергии.  [35]

Если скорость валентного электрона положить равной нулю, то отсюда получаем формулу Томсона.  [36]

Получаемое в них количество электрической энергии больше, чем соответствует расчету по формуле Томсона.  [37]

Сравнивая формулу Томсона с формулой ( 1) задачи 3.22, находим, что формула Томсона является частным случаем, отвечающим ионизации атома электронным ударом в классическом приближении.  [38]

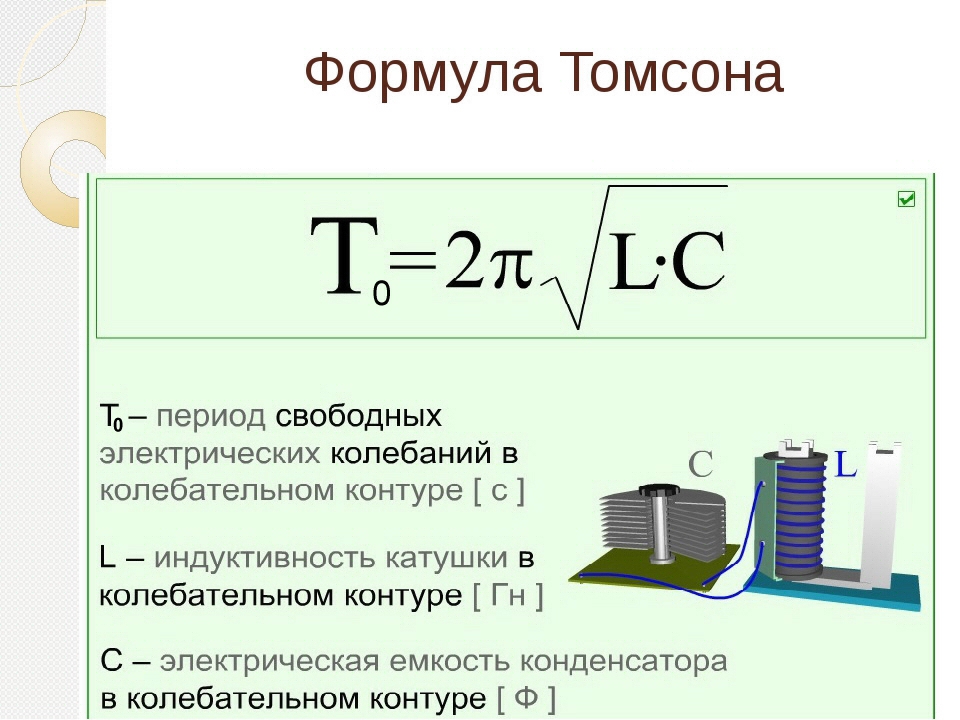
Уравнение (66.6), определяющее значение периода свободных электромагнитных колебаний в электрическом контуре, называется формулой Томсона.  [39]

В пределе малых частот сечение рассеяния фотона на всякой неподвижной заряженной частице стремится к своему классическому значению, даваемому формулой Томсона.  [40]

Теоретическую наименьшую разность потенциалов, ниже которой не может начаться разложение растворов поваренной соли, можно вычислить, например, приближенно по

формуле Томсона, считая, что энергия, необходимая для разложения вещества, эквивалентна тепловому эффекту реакции, протекающей при разложении вещества ( подобное вычисление приближенно, так как в большинстве случаев-тепловой эффект реакции не равен свободной энергии, которую можно превратить в электрическую энергию.  [41]

Интересно отметить, что хотя из-за резонансных явлений при /, ) ионизация может быть в несколько раз больше, чем требуется по формуле Томсона (3.3), при — / т) ( что соответствует осколкам деления в значительной части их пробега) формула Томсона весьма точна.  [42]

Изотерма адсорбции.| Структурная кривая ( а и кривая распределения объема пор по значениям эффективных радиусов ( б для сили-кагеля.  [43]

Умножая величину а на vm ( мольный объем жидкости), находят объем пор v, заполненный жидкостью, а подставляя соответствующую величину p / ps в формулу Томсона ( XIX, 15), получают эффективный радиус гш шаровидного мениска в поре.  [44]

Изотерма адсорбции.| Структурная кривая ( а и кривая распределения объема пор по значениям эффективных радиусов ( б для сили-кагеля.  [45]

Страницы:      1    2    3    4

Электромагнитные колебания. Формула Томсона

Тема: «ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. Формула Томсона». Цель урока: вспомнить понятия : колебания, виды, частоту и период колебаний; изучить понятие «электромагнитные колебания» и познакомится формулой Томсона.Ход урока: I Орг. момент II Устный опрос по: «колебательному движению» — Что такое математический маятник? (Математическим маятником называют материальную точку (тело небольших размеров), подвешенную на тонкой невесомой нерастяжимой нити или на невесомом стержне

. ) — От чего зависит период колебаний математического маятника?( Период математического маятника зависит только:
1) от длины нити, на которой подвешена материальная точка(чем длина этой нити, тем период математического маятника больше и чем 2) от ускорения (чем ускорение, тем T=2*пи*корень квадратный из(L\g)    — Какие колебания называются свободными?( Свободными называют колебания, происходящие под действием внутренних сил в системе выведенной из положения равновесия и предоставленной самой себе.) — Почему колебания затухают?( Затухающие колебания это колебания с постоянной убывающей по времени амплитудой. Свободные колебания реальных систем всегда затухают, потому что в механических системах происходит трение и за счет него идет затухание, а в электромагнитных системах происходит сопротивление

.) — Что такое амплитуда колебаний?( Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. ) III Изучение нового материала: ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. Формула Томсона. 1. Открытие электромагнитных колебаний было неожиданным. После того как изобрели простейший конденсатор и научились сообщать ему большой заряд с помощью электростатической машины, ученые начали наблюдать его электрический заряд. С простейшим конденсатором — лейденской банкой — вы ознакомились в 8 классе.

Конденсатор — это устройство, предназначенное для накопления заряда и энергии электрического поля 

Замыкая обкладки лейденской банки с помощью проволочной катушки, обнаружили, что стальные спицы внутри катушки намагничиваются. В этом ничего странного не было, так как электрический ток и должен намагничивать стальной сердечник катушки. Удивительным было то, что нельзя было предсказать, какой конец намагниченного сердечника катушки окажется северным полюсом, а какой — южным. Опыты, проведенные в одних и тех же условиях, давали различные результаты.

Ученые не сразу поняли, что при разрядке конденсатора через катушку возникают колебания. За время разряда конденсатор успевает несколько раз перезарядиться, и электрический ток тоже меняет направление. Из-за этого сердечник может намагничиваться по-разному, и его полюсы поочередно меняются. Итак, при разрядке конденсатора периодически (или почти периодически) изменяются заряд, ток, напряжение, электрические и магнитные поля. Периодическое изменение этих величия называют электромагнитными колебаниями. Получить электромагнитные колебания почти так же просто, как и заставить тело колебаться, подвесив его на пружине. Но наблюдать электромагнитные колебания уже не так просто. Ведь мы непосредственно не видим ни перезарядки конденсатора, ни тока в катушке. К тому же колебания обычно происходят с очень большой частотой. Для наблюдения и исследования электромагнитных колебаний самым подходящим прибором является электронный осциллограф. Стр.75 Электромагнитные колебания возникают в электрической цепи, состоящей из батареи конденсаторов и катушки индуктивности. Цепь, состоящая из последовательно соединенных конденсатора и катушки и позволяющая получать электромагнитные колебания, называется колебательным контуром. Стр.74 Такие поочередно изменяющиеся в колебательном контуре процессы можно увидеть на экране осциллографа. В идеальных условиях, когда электрическое сопротивление равно или близко к нулю, на экране можно увидеть свободные электромагнитные колебания . А в случае, когда электрическое сопротивление контура будет большим, то на экране осциллографа появляется осциллограмма затухающего колебания. При увеличении электрической емкости конденсатора в установке можно увидеть растягивание осциллограммы в горизонтальном направления. Следовательно, с увеличением емкости колебательного контура период электромагнитного колебания возрастает (частота соответственно уменьшается). Когда емкость уменьшается, период колебания тоже уменьшается, а частота, естественно, возрастает. Такой же результат получается при изменении индуктивности катушки в контуре.

Физические величины — индуктивность и емкость — вам известны из курса физики для 8 классов. При увеличении индуктивности период колебания возрастает, и, наоборот — при уменьшении индуктивности период сокращается. Этот результат аналогичен изменению периода колебания пружинного маятника при изменении массы груза и жесткости пружины. Таким образом, период свободного электромагнитного колебания в колебательном контуре вычисляется через индуктивность контура (L) и емкость (С) по формуле: В честь него это выражение называется формулой Томсона. Для того чтобы получить период (Т) в секундах (с), индуктивность (L) должна быть выражена в генри (Гн), а емкость (С) — в фарадах (Ф).(  Электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.) Явления в колебательном контуре аналогичны явлениям в пружинном маятнике. Действительно, для того чтобы возникли колебания в пружинном маятнике, пружину надо деформировать (сжать), сообщив ей потенциальную энергию. Аналогично, чтобы в колебательном контуре возникли колебания, следует зарядить конденсатор и таким образом сосредоточить в нем энергию электрического поля. Через четверть периода деформация пружины исчезает, а груз с максимальной скоростью проходит положение равновесия. При этом потенциальная энергия пружины превращается в кинетическую энергию груза. Точно так же через четверть периода конденсатор разряжается, и через обмотку катушки течет электрический ток максимальной силы. Энергия электрического поля конденсатора превратилась в энергию магнитного поля катушки. Далее груз, продолжая свое движение, растягивает пружину, и к концу полупериода кинетическая энергия груза вновь превращается в потенциальную энергию пружины. Аналогично электрические заряды за счет энергии магнитного поля начинают накапливаться на обкладках конденсатора, и к концу полупериода энергия магнитного поля катушки превращается в энергию электрического поля конденсатора. Этот процесс вновь повторяется, и к концу периода система возвращается в первоначальное состояние. Таким образом, можно сделать вывод: в цепи, состоящей из конденсатора и катушки индуктивности, при очередной разрядке конденсатора возникают электромагнитные колебания. Решение задач: №1. Для демонстрации медленных электромагнитных колебаний собирается колебательный контур с конденсатором, емкость которого равна 2,5 мкФ. Какова должна быть индуктивность катушки при периоде колебания 0,2 с?

Дано:	СИ:	Решение:
C=2,5 мкФ T=0,2 c	2,5 10-6 Ф	Ответ:
L-?

Работа в парах — решение задач самостоятельно: №2. Какой должна быть длина математического маятника, чтобы период его колебаний был равен 1 с?( 0,25м) №3. Тело массой 200 г, подвешенное на пружине с жесткостью 16 Н/м колеблется с амплитудой 2 см в горизонтальной плоскости. 6 c) №4. Колебательный контур состоит из конденсатора емкостью 250 пФ и катушки индуктивностью 10 мГн. Определите период и частоту свободных колебаний. №5. Необходимо собрать колебательный контур частотой 3 мГц, используя катушку индуктивностью 1,3 мГн. Какова должна быть емкость конденсатора?

V Закрепление: Фронтально отвечают на вопросы: — Что представляет собой колебательный контур? Начертите его схему. — Что необходимо сделать, чтобы в колебательном контуре возникли свободные колебания? — Почему свободные электромагнитные колебания затухают? — Как влияет изменение емкости конденсатора на период свободного колебания в контуре? — Как влияет изменение индуктивности катушки на период свободного колебания в контуре? — Какой формулой выражается период свободных колебаний в колебательном контуре? В каких единицах измеряются величины, входящие в нее? VI Подведение итогов Рефлексия: — что я узнал сегодня на уроке? — что меня удивило? Поразило? — что мне было известно до изучения темы? VII Домашнее задание: § 17-20 стр. 76 №1-3 формулы

Доп.задачи№3-5 громцева стр.159

Статья о Томсоне+формула из The Free Dictionary

Томсон+формула | Статья о формуле Томсона в The Free Dictionary

Томсон+формула | Статья о Томсон+формула из The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.

Возможно, Вы имели в виду:

Пожалуйста, попробуйте слова отдельно:

thomson формула

Некоторые статьи, соответствующие вашему запросу:

Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?

• ▲
• Трасса Гран-при Томсон Роуд
• Томсон Роуд, Гонконг
• Томсон Роуд, Сингапур
• Томсон С.А.
• Томсоновское рассеяние
• Томсоновское рассеяние
• Длина рассеяния Томсона
• Томсон Сайентифик
• Thomson Scientific & Healthcare
• Знак Томсона
• Программные продукты Thomson
• Студенческий медицинский центр Томсона
• Студенческий медицинский центр Томсона при Университете Южной Каролины
• Синдом Томсона
• Синдром Томсона
• Thomson Technology Services Group
• Томсон Тауншип, округ Карлтон, Миннесота
• Томсон Тауншип, Миннесота
• Томсон Трэвел Групп
• ПЛК Thomson Travel Group

• Томсон Вирджил Гарнетт
• Напряжение Томсона
• Томсон Уэст
• Газель Томсона
• Газель Томсона
• Газель Томсона
• Газели Томсона
• Газели Томсона
• Лампа Томсона
• Перевод Томсона
• Томсон+формула
• Томсон, Александр
• Томсон, Бобби
• Томсон, Чарльз
• Томсон, Чарльз Эдвард Пулетт
• Томсон, Чарльз Вайвилл
• Томсон, Элиу
• Томсон, Фредерик Х
• Томсон, Фредерик Х.
• Томсон, Джордж Пэджет
• Томсон, Джордж Пэджет

• Томсон, Джорджия
• Томсон, Иллинойс
• Томсон, Дж. Эдгар
• Томсон, Джеймс
• Томсон, Джеймс
• Томсон, Джеймс
• Томсон, Джозеф
• Томсон, Джозеф Джон
• Томсон, Джозеф Джон
• Томсон, Кит Стюарт
• Томсон, Мэтью Сидни
• Томсон, Миннесота
• Томсон, Мортимер Нил
• Томсон, Питер Уильям
• Томсон, Рой Герберт, первый барон Томсон флота
• Томсон, Рой Герберт, первый барон Томсон флота
• Томсон, Рой Герберт, первый барон Томсон флота
• Томсон, Сэмюэл
• Томсон, Сингапур
• Томсон, сэр Чарльз Вайвилл
• ▼

Сайт: Следовать:

Делиться:

Открыть / Закрыть

 

Томсоновское рассеяние

Томсоновское рассеяние

Next: Теория дырок и заряд Up: Уравнение Дирака Previous: Решение уравнения Дирака Содержимое

Сечение для Томсоновское рассеяние иллюстрирует необходимость наличия состояний с «отрицательной энергией» в наших расчетах . Напомним, что мы получили правильное сечение из нерелятивистского расчета и что Томсон также получил правильный результат от классического E&M.

В теории Дирака у нас есть только один член в гамильтониан взаимодействия ,

Поскольку оно линейно по он может создать фотон или аннигилировать фотон. Следовательно, рассеяние фотонов имеет второй порядок (и пропорционально ). Поле квантованных фотонов

Начальное и конечное состояния — это состояния с определенным импульсом , как и промежуточные состояния электрона. Сначала мы проведем вычисление, предполагая, что электроны из моря «отрицательной энергии» не участвуют , кроме как исключить переходы в эти состояния с «отрицательной энергией». Таким образом, начальное и конечное состояния являются состояниями плоской волны с положительной энергией. за . Промежуточные состояния также должны быть состояниями с положительной энергией, поскольку все состояния с «отрицательной энергией» заполнены.

Вычисление сечения рассеяния следует тем же шагам, что и при разработке уравнения Краммерса-Гейзенберга. формула рассеяния фотонов. Здесь нет поэтому мы просто вычисляем два члена второго порядка .

Как и в предыдущем расчете, фотонные состояния были исключены из уравнения поскольку они дают коэффициент 1, когда фотон в начальном состоянии аннигилирует, а фотон в конечном состоянии создается в каждом сроке.

Теперь давайте посмотрим на один из элементов матрицы . Предположим, что электрон в начальном состоянии покоится и что импульс фотона мал .

За а также , дельта-функция требует, чтобы . Оказывается, что , так что сечение в этом пределе равно нулю.

Эта матрица соединяет только спиноры к spinors из-за его недиагонального характера. Таким образом, расчет дает нуль для поперечного сечения, в отличие от двух других расчетов. На самом деле, поскольку импульс фотона не совсем равен нулю, вклад небольшой, но слишком маленький.

Приведенный выше расчет упускает 90 166 важных членов из-за «моря отрицательной энергии» 90 167 . Есть дополнительные условия, если мы рассматриваем возможность того, что фотон может поднять электрон с «отрицательной энергией» иметь положительную энергию.

Одним словом, фотон в начальном состоянии поглощается электроном с «отрицательной энергией», затем электрон в начальном состоянии заполняет дыру в море «отрицательной энергии», испуская фотон конечного состояния. С другой стороны, еще дальше от массовой оболочки электрон с «отрицательной энергией» излучает фотон конечного состояния и переходит в состояние с положительной энергией, то электрон в начальном состоянии поглощает исходный фотон и заполняет дырку оставленный в море. Эти термины больше, потому что матрица связывает положительную энергию и состояния «отрицательной энергии».

Матричный элемент должен быть взят с начальным электроном в состоянии покоя , , последний электрон (приблизительно) в состоянии покоя и, следовательно, промежуточный электрон в состоянии покоя из-за дельта-функции сохранения импульса получается из пространственного интеграла.