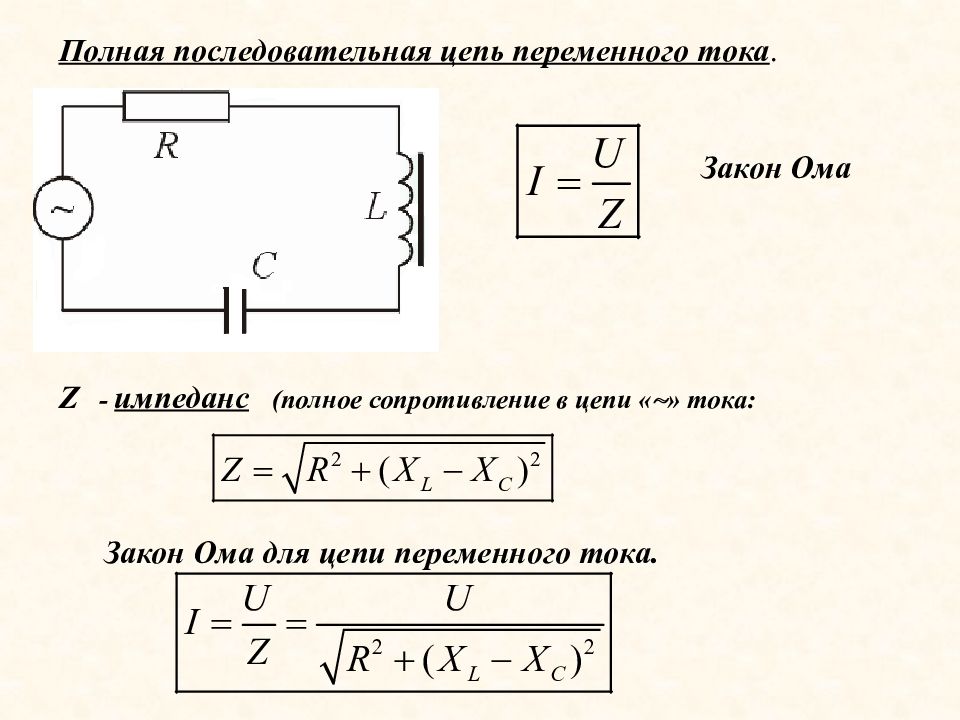
формула формула мощности электрического тока

Электрический ток является физическим процессом. Если говорить упрощенно, то это упорядоченное движение заряженных частиц. Его протекание можно измерить и соответственно выразить в символьном и цифровом виде. Формула электрического тока, представляет собой выражение качественных и количественных параметров через сопротивление проводника, напряжение или разность потенциалов, а также через его силу. Так как любое перемещение чего-либо, подразумевает под собой совершение работы, то дополнительно можно вести разговор об электричестве используя формулу мощности электрического тока.

Основные понятия и формулы характеризующие электрический ток

Количественным параметром электрического тока является его сила, представляющая собой скалярную величину и выражающуюся в отношении заряда (принято обозначать буквой q) к периоду времени (t), за которое он пересекает сечение проводника.

Следовательно, формула электрического тока, а если говорить правильно его сила, будет выглядеть следующим образом — I=q/t. Измеряется данный параметр в амперах. Так как скалярные величины являются действительными числами и определяются только значением, сила тока не может иметь отрицательный знак. С учетом того, что величина заряда не является постоянным параметром для разных электрических цепей, было введено понятие – плотность электрического тока (j), формула которой выглядят так – j=I/S, где S – площадь, пересекаемая зарядами. Следовательно, при увеличении силы тока и уменьшении поперечного сечения проводника плотность тока возрастает и наоборот. Как отмечалось выше, важными параметрами электричества, вернее электрической цепи являются напряжение в ней и сопротивление проводящих ток элементов.

Формула выражения силы электрического тока через сопротивление и напряжение

В отличие от фундаментальных исследований, в основе которых лежат теоретические выкладки данная зависимость была выведена практическим путем. Автором открытия является физик Ом, в честь которого закон и получил свое имя. По результатам своих опытов и экспериментов Ом пришел к выводу что сила тока (I) напрямую зависит от величины напряжения (U)и имеет обратную зависимость от сопротивления (R

) элементов и деталей, включенных в электрическую цепь. Эту связь можно представить в виде – I=U/R. Путем несложных преобразований, формулы сопротивления и напряжения, выраженные через силу тока, будут выглядеть следующим образом – R=U/I и U=IxR, соответственно.

Формула силы электрического тока

Сопротивление электрического тока: формула
Формула напряжения электрического тока

Работа и мощность электрического тока

Формула мощности (Р) электрического тока напрямую зависит от его работы (А). Под работой тока подразумевается преобразование электрической энергии в механический, тепловой, световой или иной ее вид.

Величина данного процесса напрямую зависит от времени его протекания, силы тока и напряжения в сети. Это можно выразить следующей формулой – А=IxUxt. Произведение (IxU) является ничем иным как мощностью. Следовательно, чем выше напряжение или сила тока в сети, тем большую мощность имеет электрический ток и большую работу он может совершить за единицу времени. Формула мощности электрического тока имеет следующий вид – Р=А/t или Р=IxU.

Работа электрического тока формула
Формула мощности электрического тока

Поэтому, если необходимо вычислить, какую работу производит ток, протекая по цепи в течение определенного времени, необходимо умножить мощность на временной промежуток, выраженный в секундах. Рассмотрим применение формул расчета работы и мощности электрического тока на примере электрического двигателя, подключенного к сети 220 В, а сила тока, измеренная амперметром для этого участка, составила 10А.

Р (мощность двигателя) = 10А (сила тока) х 220В (напряжение в сети) = 2200 Вт = 2,2 кВт.

Зная данный показатель, а также реальное или предполагаемое время функционирования электродвигателя можно определить какую работу он совершит за этот отрезок времени или другим словами сколько будет потрачено электроэнергии. Если двигатель был включен, например, 1 час, то можно найти искомое значение.

А (работа, совершенная двигателем) = 2,2 кВт (мощность) х 1 (время работы в часах) = 2,2 кВт ч. Именно этот показатель будет отражен на приборе учета расхода электроэнергии.

Исходя из того, что электрический ток является физическим процессом, то какой-либо его неизвестный параметр можно определить, зная его остальные характеристики. Приведем наиболее распространенные формулы для определения характеристик электрической цепи применяемые в электротехнике.

Напряжение или разность потенциалов

• U = RxI
• U = P/I
• U = (P*R)^1/2

Сила электрического тока

Сопротивление

• R = U / I
• R = U²/ P
• R = P / I²

Мощность

В заключение отметим, что приведенная информация справедлива для цепей с постоянным электрическим током. Формулы, применяемые для расчета характеристик переменного тока, будут отличаться за счет введения дополнительных переменных и характеристик свойственных данному типу электричества.

Закон Ома для участка цепи, формула, определение

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит.

Возьмем замкнутую электрическую цепь (рисунок 1) и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

• I — ток, протекающий по участку цепи.
• R — сопротивление этого участка.
• φ1-φ2 — разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R

Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U₁=I*R₁
• U₂=I*R₂
• Un=I*Rn
• U=I*(R₁+R₂+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U₁+U₂+…+Un или U₁/U₂/…/Un=R₁/R₂/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

ПРАВИЛО ЗНАКОВ ДЛЯ ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной (рис.

3.1). В противном случае — ЭДС считается отрицательной (рис.3.2).

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E₁+E₂+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E₁+E₂-E₃.

При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

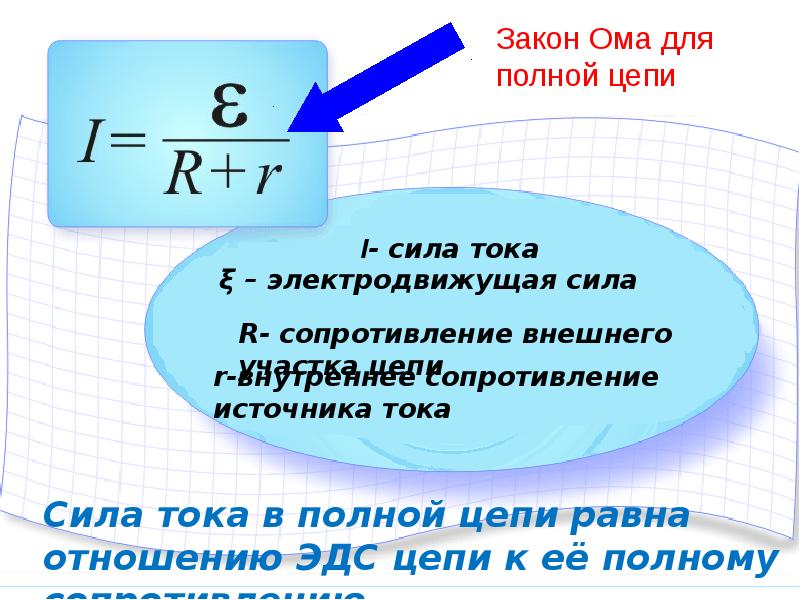
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ

Закон Ома для полной цепи — его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r).

Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС.

Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r — сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной.

Закон Ома рассмотрен здесь достоточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

© 2012-2020 г. Все права защищены.

Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

Закон Ома для участка цепи: формулировка и формула, применение

 

От силы тока в цепи зависит величина воздействия, которое ток может оказывать на проводник, будь то тепловое, химическое или магнитное действие тока. То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток, в свою очередь – это упорядоченное движение частиц под действием электрического поля.

Зависимость силы тока и напряжения

Очевидно, что чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением. Следовательно, мы приходит к выводу, что сила тока зависит от напряжения.

И действительно, опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.

Связь с сопротивлением

Однако любая цепь или участок цепи характеризуются еще одной немаловажной величиной, называемой сопротивлением электрическому току. Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.

Формула закона Ома для участка цепи

Сопоставив две эти зависимости, можно прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 г. Он связал воедино три вышеуказанные физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

I=U/R,

где I – сила тока,
U – напряжение,
R – сопротивление.

Применение закона Ома

Закон Ома – один из основополагающих законов физики. Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».

Из формулы для закона Ома можно рассчитать также величины напряжения и сопротивления участка цепи:

U=IR    и    R=U/I

Правда, следует понимать, что в собранной цепи величина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.

Нужна помощь в учебе?

Предыдущая тема: Сопротивление тока: притяжение ядер, проводники и непроводники
Следующая тема:&nbsp&nbsp&nbspРасчёт сопротивления проводников и реостаты: формулы

Работа и мощность электрического тока в цепи

Определение 1

Во время протекания тока по однородному участку цепи электрическое поле совершает работу. За пройденное время Δt по цепи имеется заряд Δq=IΔt.

Электрическое поле выделенного участка выполняет работу, формулу которой мы запишем так: ΔA=(φ1–φ2) Δq=Δφ12IΔt=UIΔt, где U=Δφ12 – напряжение. Такая величина называется работой электрического тока.

Обе части формулы RI=U выражают закон Ома для однородного участка цепи с сопротивлением R, умноженным на IΔt. В итоге получим соотношение RI2Δt=UIΔt=ΔA, выражающее закон сохранения энергии для однородного участка цепи. Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике. ΔQ=ΔA=RI2Δt.

Закон Джоуля-Ленца

Дж. Джоуль и Э. Ленц установили закон преобразования работы тока в тепло.

Определение 2

Формула мощности электрического тока (измеряется в амперах) записывается в виде отношения изменения работы тока ΔA за определенный промежуток времени Δt:

P=∆A∆t=UI=I2R=U2R.

Работа и мощность электрического тока обратно пропорциональны.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

По таблице СИ понятно, в чем измеряется мощность: в ваттах (ВТ), а работа в Джоулях (Дж).

Перейдем к рассмотрению полной цепи постоянного тока, которая состоит из источника с электродвижущей силой ε и внутренним сопротивлением r на участке R. Запись основного закона Ома для полной цепи имеет вид (R + r)I=ε. При умножении обеих частей на Δq=IΔt получаем, что соотношение для выражения сохранения энергии полной цепи постоянного тока запишется: R I2Δt+r I2Δt=ε IΔt=ΔAст. Из левой части видно, что ΔQ=R I2Δt обозначает выделяющееся тепло на внешнем участке за промежуток времени Δt, а ΔQист=rI2Δt – внутри источника за тот же время.

εIΔt – это обозначение работы сторонних сил ΔAст,_{действующих внутри. Если имеется замкнутая цепь, тогда ΔAстпереходит в тепло, которое выделяется во внешней цепи (ΔQ)и внутри источника (ΔQист).}

ΔQ+ΔQист=ΔAст=εIΔt.

Работа сторонних сил

Работа электрического поля не входит в данное соотношение, так как в замкнутой цепи работа не совершается, следовательно, тепло идет только от внутренних сторонних сил. В данном случае электрическое поле перераспределяет тепло по всем участкам цепи.

Внешняя цепь может иметь не только проводник с R сопротивлением, но и механизм, потребляющий мощность. Такой случай говорит о том, что R эквивалентно сопротивлению нагрузки. Энергия, которая выделяется по внешней цепи, преобразуется в тепло и другие виды энергии.

Определение 3

Работа, совершаемая сторонними силами за единицу времени, равняется Pист=εI=ε2R+r. Внешняя цепь характеризуется мощностью P=RI2=εI-rI2=ε2R(R+r)2.

Коэффициентом полезного источника называют отношение η=PPист, записываемое как η=PPист=1-rεI=RR+r.

Рисунок 1.11.1 показывает зависимость Pист, полезной Р, выделяемой во внешней цепи, кпд η от тока I для источника с ЭДС, равной ε, и внутренним сопротивлением r. Изменение тока в цепи происходит в пределах от I=0( при R=∞) до I=Iкз=εr( при R=0).

Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи Р и КПД источника η от силы тока.

Приведенные графики показывают, что максимальная мощность во внешней цепи может быть достигнута при R=r и запишется Pmax=ε24r. Формула тока в цепи будет иметь вид Imax=12Iкз=ε2r, где КПД источника не превышает 50%. При I→0может достигаться максимальное значение КПД, тогда сопротивление R→∞. При коротком замыкании значение мощности Р=0. Тогда она только выделяется внутри источника, что грозит перегревом, причем КПД обращается в ноль.

Задачи на нахождение силы тока в цепи, напряжения. Как решать задачи на закон Ома.

Задачи на силу тока в основном касаются определения силы тока, напряжения и сопротивления. В данном разделе Вы найдете формулы для решения задач.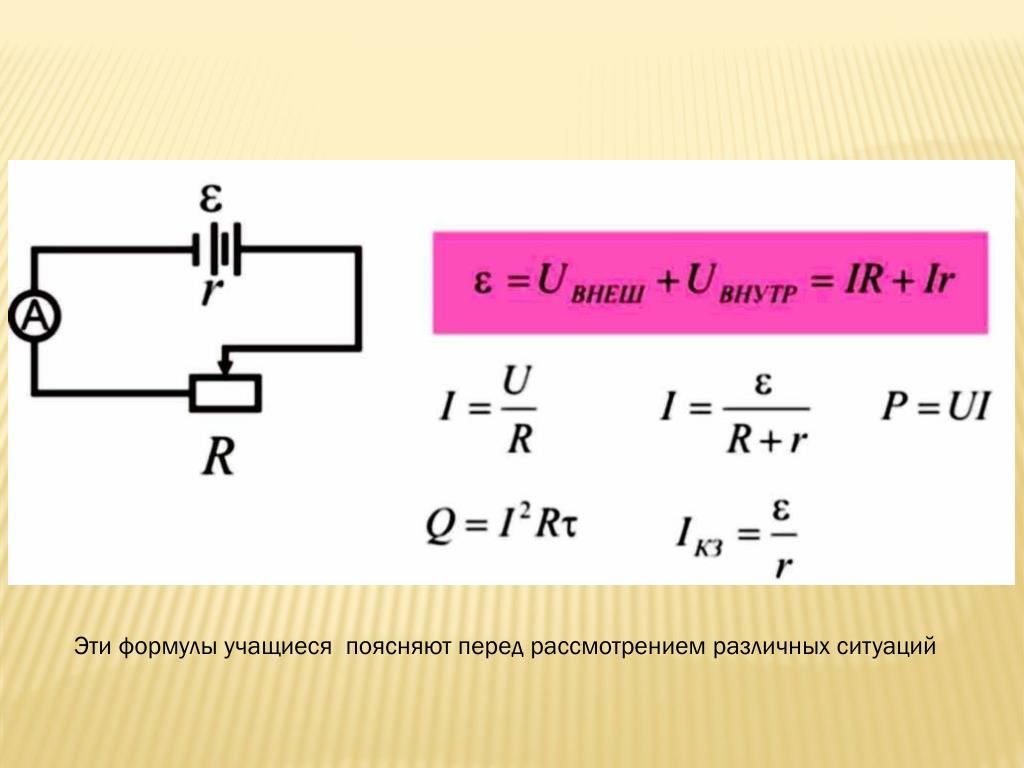 Мы разберем решение типичных элементарных задач, используя закон Ома.

Задача 1. Сила тока

Через нить накаливания лампочки от карманного фонарика за 2 мин проходит электрический заряд, равный 30 Кл. Определите силу тока в этой лампочке.

Дано:	CИ	Решение
q = 30 Кл		Сила тока I определяется по формуле
t = 2 мин	120 с	I= q/t
I – ?		I = 30Кл/120с = 0,25А = 250м А

Сила тока. Решение задач

Ответ: I = 250 мА

Задача 2. Напряжение в цепи

Электродвигатель включен в электрическую цепь с напряжением 24В. Определите заряд, прошедший через электродвигатель, если при этом была  совершена работа, равная 84 кДж

Дано:	CИ	Решение
U = 24 В		Напряжение на электродвигателе определяется по формуле
А = 84 кДж	84000  Дж	U=A/q q= A/U
q – ?		Q = 84000 Дж/24 В = 3500 Кл

Напряжение в цепи. Решение задач

Ответ: q = 3500 Кл

Задача 3. Закон Ома сила тока

Определите силу тока в кипятильнике, включенном в сеть с напряжением 220 В, если сопротивление спирали составляет 55 Ом.

Дано:	CИ	Решение
U = 220 В		Силу тока в кипятильнике можно определить, воспользовавшись законом Ома
R = 55 Ом		І=U/R
І – ?		І = 220 B/55 Ом = 4 А

Сила тока по закону Ома. Решение задач

Ответ: І = 4 А

Задача 4. Закон Ома напряжение

Какое напряжение нужно приложить к концам проводника сопротивлением 5 Ом, тобі по проводнику пошел ток с силой тока, равной 300 мА

Дано:	CИ	Решение
R = 5 Ом		Необходимое напряжение можно определить, воспользовавшись законом Ома
І = 300 мА	0.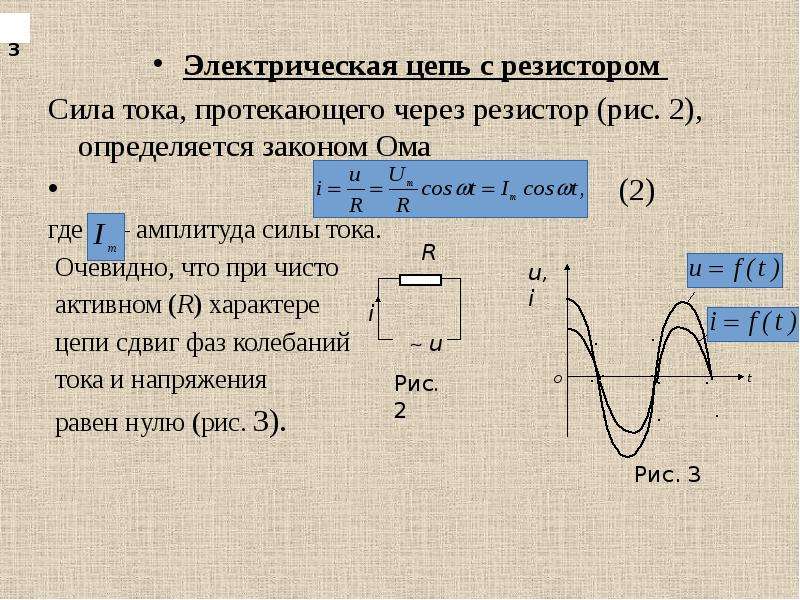 3 A	І=U/R U = IR
U – ?		U = 0,3 А * 5 Ом = 1,5 В

Напряжение в сети. Закон Ома

Ответ: U = 1.5 B

Задача 5. Сопротивление по закону Ома

Определите cопротивление резистора, если за время 10 мин через него проходит заряд 200 Кл. Напряжение на концах резистора равно 6 В.

Дано:	CИ	Решение
t = 10 мин q = 200 Кл U = 6 В	600 с	Сопротивление резистора можно определить, воспользовавшись законом Ома
		І=U/R R=U/I Поскольку значение силы тока I  не задано по условию задачи, его можно определить по формуле I=q/t Подставив формулу силы тока в формулу сопротивления, получим R=Ut/q
R – ?		R = 6 В *600с/200 Кл = 18 Ом

Сопротивление по закону Ома

Ответ: R = 18 Ом

Закон Ома (страница 1)

Применение закона Ома к расчету линейных электрических цепей постоянного тока

1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.

Решение:

Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;

Аналогично определяются токи в схемах б, в, г рисунка 3:

2. Найти напряжение между зажимами нетвей (рисунок 4).

Решение:

Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:

откуда выразим напряжение на зажимах:

Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.

3. Определить неизвестные потенциалы точек участка цени (рисунок 5).

Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:

откуда выразим напряжение на зажимах ветви:

Если представить напряжение как разность потенциалов:

тогда при известных параметрах цепи, токе и потенциале определим потенциал :

Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС , без учета внутреннего сопротивления источника, по величине равно и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):

и тогда, зная потенциал , определим потенциал точки С:

Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:

тогда

Потенциал точки а определяем с учетом направления напряжения на зажимах источника ЭДС . Напряжение направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):

откуда следует, что

или

Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:

откуда следует

Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:

4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением . Определить величину сопротивления резистора .

Решение:
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:

или, согласно закону Ома:

По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:

По закону Ома напряжение на зажимах определится:

тогда величина сопротивления резистивного элемента:

5. Определить показания вольтметров цепи (рисунок 7), если .

Решение:
Ток в цепи определим по закону Ома:

Вольтметр показывает напряжение на источнике ЭДС Е:

Вольтметры показывают величину падения напряжения на резистивных элементах :

Вольтметр , показывает напряжение на участке 2 — 1 , которое определим как алгебраическую сумма напряжений :

6. Ток симметричной цепи (рисунок 8) , внутреннее сопротивлении источника ЭДС . Определить ЭДС Е и мощность источника энергии.

Решение:
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:

Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:

Мощность, развиваемая источником энергии, определится:

ТОК В КОМБИНИРОВАННЫХ ЦЕПЯХ

Комбинированные схемы — это схемы, в которых существуют как последовательные, так и параллельные условия. Как вы знаете, последовательная цепь — это цепь, в которой есть только один путь для прохождения тока. Параллельные цепи имеют несколько путей. Чтобы определить тип цепи, проследите путь тока через компоненты, используя схематический чертеж. Если ток может проходить более чем по одному пути, цепь не является последовательной. Изучая ток в предыдущих главах, вы узнали, что в чисто последовательных цепях все компоненты имеют одинаковую величину тока.В параллельных цепях полный ток равен сумме всех токов ответвления. Полный ток в комбинированной цепи может быть рассчитан после определения тока каждой ветви параллельных цепей и расчета токов последовательных цепей (то есть после того, как станет известно общее эквивалентное сопротивление).

ТОК ПО ПРОСТОЙ КОМБИНИРОВАННОЙ ЦЕПИ

Изучите рисунок 6–2. Чтобы определить полный ток в цепи, сначала определите эквивалентное сопротивление параллельных компонентов, состоящих из R ₂ и R ₃ .Как видите, от точки B до точки C можно добраться несколькими путями. Следовательно, этот участок от B до C представляет собой параллельную цепь. К этой части схемы применяются правила для параллельных цепей. Используйте правила параллельности для параллельных резисторов, чтобы создать эквивалентный одиночный резистор, представляющий комбинацию R ₂ и R ₃ . Простым методом для использования было бы уравнение произведения на сумму:

Теперь цифра с эквивалентным сопротивлением выглядит так, как показано на Рисунке 6–3, где показаны два резистора: R ₁ , соединенные последовательно с комбинированным эквивалентным резистором R _2,3 .Эту эквивалентную схему теперь можно перерисовать или «свести» к схеме, показанной на Рисунке 6–4.

Эта схема объединяет последовательный резистор R ₁ и эквивалентный резистор R _{2, 3} с использованием правил последовательной цепи для последовательного сопротивления, которое составляет:

Имея эту информацию, теперь можно рассчитать полный ток по закону Ома:

Это ток, протекающий от источника питания, и будет ток, измеренный в точке A на Рисунке 6–2. Это по-прежнему часть последовательной цепи комбинированной схемы, и поэтому применяются правила последовательной цепи для тока. Другими словами, весь ток течет через R ₁ к точке B. Теперь у тока есть два пути. Изучив правила для параллельного тока, мы знаем, что ток не будет делиться равномерно. Через меньший резистор будет протекать больший ток. Чтобы быть точным, мы должны рассчитать величину напряжения, доступного между точкой A и точкой B. Поскольку весь ток протекает через резистор R ₁ , мы можем определить, сколько напряжения падает на R ₁ и, следовательно, сколько оно ушел к параллельным веткам.Из закона Ома для R ₁ :

При подключенном источнике 100 В 79 В падает при R ₁ , и правила последовательной цепи для падения напряжения определяют, что оставшееся напряжение составляет:

Напряжение, которое появляется между точками B и C, составляет 21 В. Теперь мы вернемся к правилам параллельной схемы на Рисунке 6–4. Рассматривая только R ₂ и R ₃ и используя напряжение 21 В, мы можем теперь определить ток через каждый резистор следующим образом:

и

Чтобы убедиться, что это правильно, посмотрите на точку C на рисунке 6–2, чтобы определить, суммируются ли теперь два параллельных тока ответвления, чтобы равняться исходному последовательному току, который разделяется в верхней части параллельной цепи (0.21 + 0,105 = 0,315 А). Полный ток, текущий обратно к источнику, должен быть таким же, как ток, текущий от источника. Обратите внимание, что они не совпадают точно во многих вычислениях из-за округления десятичного числа до трех значащих цифр. Мы говорим, что эти цифры достаточно близки, чтобы доказать это. Если бы мы хотели вычислить значения с точностью до многих значащих цифр, ответы были бы точными. Здесь нас больше интересует процесс, чем точные значения. Еще одна проверка для проверки ваших расчетов — использовать эквивалентное сопротивление (R _2,3 ). Это сопротивление оказалось 66,67 Ом. Падение напряжения на этой части схемы было принято равным 21 В. Если использовать закон Ома,

Опять же, это дает полный ток цепи через параллельную эквивалентную ветвь полной цепи.

ПЕРЕКЛЮЧЕНИЕ СЛОЖНОЙ КОМБИНИРОВАННОЙ ЦЕПИ

Процесс, который мы только что использовали для определения тока, протекающего через простую комбинированную схему, называется упрощением.

Рисунок 6–5 представляет собой простую комбинированную схему.Первый шаг в анализе этой схемы — максимально сократить (упростить) схему. Каждая секция, подлежащая уменьшению, будет представлять собой группу из двух или более резисторов, с эквивалентными значениями сопротивления, заменяющими группу. Сначала анализируются параллельные части схемы. Резисторы R ₂ и R ₃ включены параллельно. Сначала найдите эквивалентное сопротивление для R ₂ и R ₃ , используя уравнение произведения на сумму, как описано ранее, или любым подходящим методом для определения эквивалентного сопротивления параллельного участка цепи. С этим результатом перерисуйте схему и замените два параллельных резистора их «эквивалентными» одиночными резисторами, как показано на Рисунке 6–6.

Теперь схема на рис. 6–5 сведена к простой последовательной схеме с двумя последовательно включенными резисторами. В любой комбинированной схеме с несколькими параллельными ветвями и последовательными цепями мы можем упростить схему до одного резистора. Этот процесс может занять много времени. Лучше всего записывать каждое упрощение на промежуточной диаграмме.По мере того, как вы решаете итоги, вы затем перестраиваете схему с простой обратно на сложную. Если вы оставите промежуточные цепи доступными, вы сможете вернуться к исходной схеме. Это первое упрощение было несложным: переход от трех резисторов к двум резисторам к одному резистору. Как вы видели ранее, нам нужно было вернуться от одного (всего R) к двум резисторам и, наконец, вернуться к исходным трем резисторам, чтобы решить всю проблему.

Ток в параллельной цепи

Ток в параллельной цепи

Закон

Ома гласит, что ток в цепи обратно пропорционален сопротивлению цепи. Это верно как для последовательных, так и для параллельных цепей.

Существует единственный путь для тока в последовательной цепи. Величина тока определяется общим сопротивлением цепи и приложенным напряжением. В параллельной цепи ток источника делится между доступными путями.

Поведение тока в параллельных цепях будет показано серией иллюстраций с использованием примеров цепей с разными значениями сопротивления для заданного значения приложенного напряжения.

Часть (A) рисунка 3-40 показывает базовую последовательную схему.Здесь полный ток должен проходить через единственный резистор. Величину тока можно определить.

Рисунок 3-40. — Анализ тока в параллельной цепи.

Дано:

Решение:

На части (B) рисунка 3-40 показан тот же резистор (R ₁ ) со вторым резистором (R ₂ ) равного номинала, подключенным параллельно через напряжение источник. Когда применяется закон Ома, ток, протекающий через каждый резистор, оказывается таким же, как ток через единственный резистор в части (A).

Дано:

Решение:

Очевидно, что если через каждый из двух резисторов проходит ток 5 ампер, то должен быть ОБЩИЙ ТОК 10 ампер от источника.

Общий ток в 10 ампер, как показано на рисунке 3-40 (B оставляет отрицательный вывод батареи и течет в точку a. Поскольку точка a является точкой соединения двух резисторов, она называется СОЕДИНЕНИЕМ. В переходе а общий ток делится на два тока по 5 ампер каждый.Эти два тока протекают через соответствующие резисторы и снова соединяются в переходе b. Затем полный ток течет от перехода b обратно к положительной клемме источника. Источник обеспечивает общий ток 10 ампер, и каждый из двух одинаковых резисторов пропускает половину общего тока.

Каждый отдельный путь тока в цепи на рисунке 3-40 (B) называется ОТВЕТЛЕНИЕМ. Каждая ветвь несет ток, который составляет часть общего тока. Два или более филиала образуют СЕТЬ.

Из предыдущего объяснения характеристики тока в параллельной цепи могут быть выражены в терминах следующего общего уравнения:

I _T = I ₁ + I ₂ +. . . I _n

Сравните часть (A) рисунка 3-41 с частью (B) схемы на рисунке 3-40. Обратите внимание, что удвоение значения резистора второй ветви (R ₂ ) не влияет на ток в первой ветви (I _R1 ), но снижает ток второй ветви (I _R2 ) вдвое. его первоначальная стоимость.Полный ток в цепи падает до значения, равного сумме токов ответвления. Эти факты подтверждаются следующими уравнениями.

Дано:

Решение:

Рисунок 3-41. — Текущее поведение в параллельных цепях.

Величина протекающего в ответвленных цепях тока и общий ток в цепи, показанной на рисунке 3-41 (B), определяются с помощью следующих вычислений.

Дано:

Решение:

Обратите внимание, что сумма омических значений в каждой цепи, показанной на рисунке 3-41, равна (30 Ом), и что приложенное напряжение одинаково (50 вольт) .Однако общий ток в 3-41 (B) (15 ампер) в два раза больше, чем в 3-41 (A) (7,5 ампер). Таким образом, очевидно, что способ подключения резисторов в цепи, а также их фактические омические значения влияют на общий ток.

Разделение тока в параллельной сети происходит по определенной схеме. Этот образец описывается ЗАКОНОМ ТОКОВ Кирхгоффа, который гласит:

«Алгебраическая сумма токов, входящих и выходящих из любого соединения проводников, равна нулю.»

Математически этот закон можно сформулировать следующим образом:

I _a + I _b + … I _n + 0

где: I _a , I _b и т. Д. токи, входящие и выходящие из соединения. Токи, входящие в соединение, считаются ПОЛОЖИТЕЛЬНЫМИ, а токи, выходящие из соединения, считаются ОТРИЦАТЕЛЬНЫМИ. При решении проблемы с использованием закона Кирхгофа, токи должны быть помещены в уравнение СО ЗНАКАМИ НАДЛЕЖАЩЕЙ ПОЛЯРНОСТИ ПРИКРЕПИЛ.

Пример. Найдите значение I ₃ на рисунке 3-42.

Дано:

Решение:

I _a + I _b +. . . I
_a + 0

Рисунок 3-42. — Цепь например проблема.

Токи указаны в уравнении с соответствующими знаками.

I ₃ имеет значение 2 ампера, и отрицательный знак показывает, что это ток, ПОХОДЯЩИЙ из соединения.

Пример.Используя рисунок 3-43, найдите величину и направление I ₃ .

Рисунок 3-43. — Цепь например проблема.

Дано:

Решение:

I ₃ — 2 ампера, и его положительный знак показывает, что это ток, поступающий в переход.

Существует взаимосвязь между общим током и током через отдельные компоненты в цепи. Что это за отношения в последовательной и параллельной цепях?

На что указывает полярность тока при применении закона Кирхгофа?

15.S: Цепи переменного тока (Резюме) — Physics LibreTexts

Ключевые термины

Уравнение

переменный ток	ток, синусоидально колеблющийся во времени с фиксированной частотой
напряжение переменного тока	напряжение, которое синусоидально колеблется во времени с фиксированной частотой
переменный ток (ac)	Поток электрического заряда, который периодически меняет направление
средняя мощность	среднее время мгновенной мощности за один цикл
полоса пропускания	диапазон угловых частот, в которых средняя мощность больше половины максимального значения средней мощности
емкостное реактивное сопротивление	Противодействие конденсатора изменению тока
постоянный ток (dc)	Поток электрического заряда только в одном направлении
сопротивление	переменного тока аналог сопротивления в цепи постоянного тока, который измеряет совокупное влияние сопротивления, емкостного реактивного сопротивления и индуктивного реактивного сопротивления
индуктивное сопротивление	Противодействие катушки индуктивности изменению тока
фазовый угол	величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
Коэффициент мощности	величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
добротность	безразмерная величина, описывающая резкость пика полосы пропускания; высокая добротность — острый или узкий пик резонанса
резонансная частота	частота, при которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения
действующее значение тока	среднеквадратичное значение текущего
действующее напряжение	среднеквадратичное значение напряжения
понижающий трансформатор	трансформатор, понижающий напряжение и увеличивающий ток
повышающий трансформатор	трансформатор, повышающий напряжение и понижающий ток
трансформатор	устройство, которое преобразует напряжения из одного значения в другое с помощью индукции
уравнение трансформатора	, показывающее, что отношение вторичного напряжения к первичному в трансформаторе равно отношению количества витков в их обмотках

Ключевые уравнения

Напряжение переменного тока	\ (\ Displaystyle v = V_0sinωt \)
Переменный ток	\ (\ Displaystyle я = I_0sinωt \)
емкостное реактивное сопротивление	\ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = \ гидроразрыва {1} {ωC} = X_C \)
действующее напряжение	\ (\ Displaystyle V_ {rms} = \ frac {V_0} {\ sqrt {2}} \)
действующее значение тока	\ (\ displaystyle I_ {rms} = \ frac {I_0} {\ sqrt {2}} \)
индуктивное сопротивление	\ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = ωL = X_L \)
Фазовый угол цепи последовательного RLC	\ (\ Displaystyle ϕ = загар ^ {- 1} \ гидроразрыва {X_L − X_C} {R} \)
Вариант закона Ома для переменного тока	\ (\ Displaystyle I_0 = \ гидроразрыва {V_0} {Z} \)
Импеданс цепи серии RLC	\ (\ Displaystyle Z = \ sqrt {R ^ 2 + (X_L − X_C) ^ 2} \)
Средняя мощность, связанная с элементом схемы	\ (\ Displaystyle P_ {ave} = \ frac {1} {2} I_0V_0cosϕ \)
Средняя мощность, рассеиваемая резистором	\ (\ Displaystyle P_ {ave} = \ frac {1} {2} I_0V_0 = I_ {rms} V_ {rms} = I ^ 2_ {rms} R \)
Резонансная угловая частота контура	\ (\ Displaystyle ω_0 = \ sqrt {\ frac {1} {LC}} \)
Добротность контура	\ (\ Displaystyle Q = \ гидроразрыва {ω_0} {Δω} \)
Добротность цепи по параметрам цепи	\ (\ Displaystyle Q = \ гидроразрыва {ω_0L} {R} \)
Уравнение трансформатора с напряжением	\ (\ displaystyle \ frac {V_S} {V_P} = \ frac {N_S} {N_P} \)
Уравнение трансформатора с током	\ (\ Displaystyle I_S = \ frac {N_P} {N_S} I_P \)

Резюме

15.2 источника переменного тока

• Постоянный ток (dc) относится к системам, в которых напряжение источника постоянно.
• Переменный ток (ac) относится к системам, в которых напряжение источника периодически изменяется, особенно синусоидально.
• Источник напряжения системы переменного тока выдает напряжение, которое рассчитывается по времени, пиковому напряжению и угловой частоте.
• В простой схеме ток определяется делением напряжения на сопротивление.Переменный ток рассчитывается с использованием пикового тока (определяемого делением пикового напряжения на сопротивление), угловой частоты и времени.

15.3 Простые цепи переменного тока

• Для резисторов сквозной ток и напряжение совпадают по фазе.
• Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла. Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току, называемую емкостным реактивным сопротивлением, которое измеряется в омах.
• Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на индуктор подается синусоидальное напряжение, оно опережает ток на одну четверть цикла.
• Противодействие катушки индуктивности изменению тока выражается как тип реактивного сопротивления переменного тока. Это индуктивное реактивное сопротивление, измеряемое в омах, зависит от частоты источника переменного тока.

Цепи серии 15,4 RLC с AC

• Последовательная цепь RLC представляет собой последовательную комбинацию резистора, конденсатора и индуктора через источник переменного тока.
• Одинаковый ток течет через каждый элемент последовательной цепи RLC во все моменты времени.
• Сопротивлением в цепи постоянного тока является импеданс, который измеряет комбинированное воздействие резисторов, конденсаторов и катушек индуктивности. Максимальный ток определяется версией закона Ома для переменного тока.
• Импеданс измеряется в омах и определяется как сопротивление, емкостное и индуктивное сопротивление.

15.5 Питание в цепи переменного тока

• Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения.
• Закон Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного значения напряжения на полное сопротивление.
• В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.
• Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
• Коэффициент мощности составляет от –1 до 1.

15.6 Резонанс в цепи переменного тока

• На резонансной частоте индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.
• График зависимости средней мощности от угловой частоты для цепи RLC имеет пик, расположенный на резонансной частоте; резкость или ширина пика называется полосой пропускания.
• Ширина полосы связана с безразмерной величиной, называемой коэффициентом качества.Высокое значение добротности — это острый или узкий пик.

15,7 Трансформаторы

• Электростанции передают высокое напряжение при малых токах для достижения более низких омических потерь на многокилометровых линиях передачи.
Трансформаторы
• используют индукцию для преобразования напряжения из одного значения в другое.
• Для трансформатора напряжения на первичной и вторичной катушках или обмотках связаны уравнением трансформатора.
• Токи в первичной и вторичной обмотках связаны количеством первичных и вторичных петель или витков в обмотках трансформатора.
• Повышающий трансформатор увеличивает напряжение и снижает ток, тогда как понижающий трансформатор снижает напряжение и увеличивает ток.

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Расчет базового тока короткого замыкания | EC&M

Основная электрическая теорема гласит, что величина тока, протекающего через короткое замыкание, зависит от двух переменных величин: напряжения системы и связанного полного сопротивления пути прохождения тока от источника до точки повреждения.

Типичные системные напряжения хорошо знакомы всем нам. Однако связанный полный импеданс пути прохождения тока короткого замыкания требует небольшого пояснения. Этот импеданс обычно включает сопротивление и реактивное сопротивление проводников фидера, любые импедансы трансформаторов (идущие от точки повреждения обратно к источнику энергии) и любое другое оборудование, подключенное на пути прохождения тока.

Рис. 1 представляет собой очень простую однострочную схему со следующим: источником питания, трансформатором и устройством защиты от перегрузки по току (OCPD), имеющим определенный номинальный ток отключения при коротком замыкании.

Давайте сначала поговорим об источнике питания. Во многих примерах расчета тока короткого замыкания вы увидите такие ссылки, как «Предположим, что источник питания имеет бесконечную мощность» или «Источник имеет бесконечную шину». Что это означает, и почему так важен выборочный расчет? Все, что говорится, это то, что напряжение источника не имеет внутреннего сопротивления. В результате выборочный расчет становится очень консервативным. Поскольку предполагается, что источник не имеет собственного импеданса, соответствующий ток короткого замыкания будет в худшем случае.

Теперь посмотрим на трансформатор. Импеданс, определяющий величину тока короткого замыкания на его вторичной обмотке, состоит из двух отдельных импедансов: собственного импеданса плюс импеданса вторичных проводников, идущих к точке повреждения. Собственный импеданс трансформатора — это величина его сопротивления протеканию через него тока короткого замыкания.

Все трансформаторы имеют импеданс, который обычно выражается в процентах напряжения. Это процент от нормального номинального первичного напряжения, которое должно быть приложено к трансформатору, чтобы вызвать протекание номинального тока полной нагрузки по короткозамкнутой вторичной обмотке.Например, если трансформатор 480 В / 120 В имеет импеданс 5%, это означает, что 5% от 480 В или 24 В, приложенных к его первичной обмотке, вызовут ток номинальной нагрузки во вторичной обмотке. Если 5% первичного напряжения вызовут такой ток, то 100% первичного напряжения вызовут 20-кратный (100 деленный на 5) вторичный ток с номинальной полной нагрузкой, который пройдет через твердое короткое замыкание на его вторичных выводах. Очевидно, что чем ниже полное сопротивление трансформатора с заданным номиналом кВА, тем больше ток короткого замыкания он может выдать.

Для пояснения возьмем еще один пример. Предположим, у нас есть два трансформатора, каждый мощностью 500 кВА. Поскольку они имеют одинаковый номинал, каждый имеет одинаковый номинальный вторичный ток нагрузки. Предположим, что у одного из блоков импеданс 10%. Следовательно, он может подавать 10-кратный (100 деленный на 10) номинальный вторичный ток нагрузки для короткого замыкания на своих вторичных выводах. Теперь предположим, что второй блок имеет импеданс 2%. Это устройство может подавать намного больший кратный номинальный ток вторичной нагрузки при коротком замыкании на его клеммах вторичной обмотки: в 50 раз (100 делится на 2) это значение.Сравнивая оба блока, последний трансформатор может обеспечивать в пять раз больше тока короткого замыкания, чем первый блок.

Пример расчета Теперь, когда мы понимаем основные переменные, которые определяют токи короткого замыкания, давайте выполним пример расчета. Как показано на рис. 2, предположим, что у нас есть простая распределительная система с неисправным состоянием. Для ясности и упрощения предположим, что сопротивление линии между вторичной обмоткой трансформатора и местом повреждения пренебрежимо мало.

Шаг 1. Определите вторичный ток полной нагрузки (IsubS). IsubS = 100000 ВА / 240 В = 417 А

Шаг 2. Определите ток короткого замыкания (IsubSC) на клеммах вторичной обмотки трансформатора по его полному сопротивлению. IsubSC * (100% /% ZsubT) x IsubS = (100 / 2,5) * 417 = 16,680A

Следовательно, OCPD должен быть способен безопасно прерывать это количество тока вместе с асимметричным значением тока (обычно это множитель, умноженный на симметричное значение).

По общему признанию, это сильно упрощено. На самом деле при расчете учитываются все импедансы и расстояние до места повреждения относительно трансформатора. Тем не менее, это дает вам представление о том, что входит в анализ тока короткого замыкания.

Простой метод расчета основных токов короткого замыкания

Чтобы глубже изучить простой способ расчета тока короткого замыкания, мы должны сначала разработать нашу базу знаний по основам анализа короткого замыкания.

«Анализ тока короткого замыкания используется для определения величины тока короткого замыкания, который способна производить система, и сравнения величины величины короткого замыкания с отключающей способностью устройств защиты от сверхтоков (OCPD)».

Мы всегда должны помнить, что номинальный ток отключения не совпадает с номинальным током короткого замыкания (SCCR). Если вы хотите узнать об этом больше, расскажите нам в комментариях, и мы обсудим это в другом блоге.

В предыдущем блоге мы кратко познакомили вас с «Анализ короткого замыкания» . Если вы еще не проверяли его, прочтите этот блог, а затем вернитесь к этому!

Основная электрическая теорема гласит, что ток короткого замыкания на самом деле зависит от двух наиболее важных параметров:

1. Общее сопротивление от источника до точки повреждения
2. Номинальное напряжение системы

С помощью основной формулы мы можем легко рассчитать ток короткого замыкания в месте повреждения, и с помощью этих значений мы можем проанализировать систему и установить защитные устройства и защитить объект от любого серьезного повреждения или повреждения.

I_fault = V / Z

Существует множество методов расчета токов короткого замыкания, однако мы дадим вам основное представление о том, как можно рассчитать токи короткого замыкания в простой распределительной системе переменного тока.

Пожалуйста, рассмотрите однолинейную схему (SLD) с электросетью, трансформатором и устройством защиты от перегрузки по току (OCPD), имеющим определенный номинал прерывания тока короткого замыкания.

Давайте сначала поговорим об источнике питания.Обычно мы рассматриваем источник питания или сеть как бесконечную мощность или «Источник имеет бесконечную шину».

Все, что было сказано, это то, что напряжение источника не имеет внутреннего сопротивления. В результате простой расчет становится очень консервативным. Поскольку предполагается, что источник не имеет собственного импеданса, соответствующий ток короткого замыкания будет наихудшим сценарием.

Теперь следующее, что у нас есть на нашей однолинейной схеме, — это трансформатор. Импеданс, определяющий величину тока короткого замыкания на вторичной обмотке трансформатора, состоит из двух отдельных импедансов:

«Собственный импеданс плюс импеданс кабеля, подключенного между электросетью и трансформатором.Собственный импеданс трансформатора — это величина его сопротивления протеканию через него тока короткого замыкания ».

Все трансформаторы имеют импеданс, который обычно выражается в процентах напряжения. Это процент от нормального номинального первичного напряжения, которое должно быть приложено к трансформатору, чтобы вызвать протекание номинального тока полной нагрузки по короткозамкнутой вторичной обмотке.

Что это значит? а почему важен простой расчет?

Мы только что запустили нашу серию видеоблогов Power Systems Engineering Vlog , и в этой серии мы поговорим о всевозможных различных исследованиях и комментариях по инженерной энергетике.Мы рассмотрим различные блоги, написанные AllumiaX. Это весело, весело, по сути, это видеоблог, и мы надеемся, что вы, , присоединитесь к нам, , и получите от этого пользу.

Предположим, что если у нас есть понижающий трансформатор 480 В / 220 В с импедансом 5%, это означает, что 5% от 480 В, т.е. 24 В, приложенные к его первичной стороне, вызовут ток номинальной нагрузки во вторичной обмотке. .

Если 5% первичного напряжения вызовут такой ток, то 100% первичного напряжения вызовут 20-кратное (100 деленное на 5) вторичное напряжение полной нагрузки, протекающее через короткое замыкание на его вторичных выводах.

Очевидно, что чем ниже полное сопротивление трансформатора с заданным номиналом кВА, тем больше ток короткого замыкания он может выдать.

Теперь, когда мы понимаем основные переменные, которые определяют токи короткого замыкания, давайте сделаем простой расчет для той же однолинейной схемы, которая упоминалась выше.

Предположим, у нас есть простая система распределения, состоящая из следующих компонентов:

• Энергосистема, обеспечивающая питание системы
• Понижающий трансформатор для преобразования уровня напряжения
• Трансформатор тока для понижения уровня тока, который затем подается на реле
• Реле для защиты, которое подает сигнал на автоматический выключатель при любом ненормальном состоянии.Ознакомьтесь с курсом Основы защиты энергосистемы Курс, в котором мы кратко обсудили «Типы реле защиты и требования к конструкции».

Считайте, что на главной шине произошло короткое замыкание. Для ясности и упрощения предположим, что сопротивление линии между вторичной обмоткой трансформатора и местом повреждения пренебрежимо мало.

Во время неисправности трансформатор тока определяет величину тока, протекающего через вторичную обмотку трансформатора, в результате чего реле максимального тока (OC Relay) немедленно срабатывает и подает сигнал на подключенный автоматический выключатель, который срабатывает. со временем разомкнуть его контакты и уберечь рабочий персонал от травм.Таким образом будет защищена система, подключенная к выходу этой шины.

Итак, для правильной работы всех этих защитных устройств нам необходимо определить 2 вещи.

1. Определить вторичный ток полной нагрузки (Isec)
2. Определите значение тока короткого замыкания на вторичной стороне трансформатора (Isc)

Для этого мы будем использовать простую формулу. Предположим, сеть имеет номинальную мощность 100 кВА и значение импеданса 2.5%, и мы уже знаем, что 220 вольт доступны на вторичной обмотке трансформатора. Итак,

I_sec = (номинальная мощность источника в кВА) / (напряжение вторичной обмотки трансформатора)

Подставляя значения, мы получим;

I_sec = 100000/220

Теперь мы рассчитаем значение тока короткого замыкания на вторичной обмотке трансформатора, это поможет защитному устройству действовать соответствующим образом.

I_sc = ((100%) / ((Импеданс трансформатора (Z%))) * I_sec

Подставляя значения, мы получим;

I_sc = (100/2.5) * 454,54

I_sc = 18181,6 А

Ор, 18,18 КА. Это означает, что защитное устройство, которое мы будем использовать, должно иметь мощность короткого замыкания более 20 кА. Это поможет устройству защиты от перегрузки по току (OCPD) безопасно прервать это количество тока короткого замыкания.

В этом блоге вы получили общее представление о том, как рассчитать ток короткого замыкания для малой энергосистемы.

В следующем блоге (посвященном короткому замыканию) мы углубимся и объясним каждый аспект расчета токов короткого замыкания в однофазной и трехфазной энергосистеме.

Надеюсь, вам понравится этот блог, и вы также будете рекомендовать его другим. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.

ИСКРЫ: Расчет импеданса

Расчет импеданса

В цепях переменного тока Закон Ома принимает более общая форма: E = I⋅Z , где E — напряжение, а I актуален, как и раньше. Новый член, Z , равен импедансу , комбинация векторов:

• Сопротивление, R (в Ом), при падении напряжения синфазно с электрический ток.
• Индуктивное реактивное сопротивление, X _L (в Ом), с напряжением опускает опережающий ток на 90 °.
• Емкостное реактивное сопротивление, X _C (в Ом) с напряжением падает , отставая от тока на 90 °.

f = 6,4 кГц R = 120 Ом L = 3,6 мГн C = 0,38 мкФ

Рисунок 1. Пример цепи RLC

Рис. 2. Векторная сумма R и X L — X C дает Z

Из формул для X _L и X _C можно видим, что реактивные сопротивления зависят от обоих значений компонентов L и C , а также частота переменного тока, f :

а также

, где f — частота в Герцы (или сек ^-1 ), L — индуктивность по Генри, а C — емкость в фарадах.Потому что X _L и X _C различаются по фазе на 180 °, общее реактивное сопротивление X последовательной цепи составляет X _L — X _C .

Знакомые применения закона Ома, такие как последовательная и параллельная цепь. расчеты, все еще применяются. Однако теперь вы должны рассмотреть конкурирующий вектор. вклады от сопротивлений и реактивных сопротивлений.

Фазовые углы и векторы

Давайте найдем полное сопротивление цепи на Рисунке 1.Используя формулы выше:

Создавая импеданс Z , резистор вносит вклад в горизонтальную составная часть. Вертикальная составляющая — это разница реактивных сопротивлений: X _L — X _C . Тогда Z — это векторная сумма R и X _L — X _C , как показано на рисунке 2.

На рисунке 2 видно, что Z — гипотенуза прямоугольного треугольника, мы можем использовать теорему Пифагора и геометрию прямоугольного треугольника, чтобы вычислить Z .

Итак, в этой схеме мы наблюдаем эффект импеданса 144 Ом, при отставании тока от напряжения питания на фазовый угол 33,5 °.

Как вы могли догадаться из обсуждения выше, вполне возможно, что индуктивное и емкостное сопротивление для точной компенсации при правильных комбинациях из L , C и f значения.Это очень важное условие, известное как резонанс .

расчетов тока повреждения | Графическая продукция

Ток повреждения — это непреднамеренное неконтролируемое протекание большого тока через электрическую систему. Токи повреждения вызваны короткими замыканиями с очень низким импедансом. Это может быть короткое замыкание на массу или между фазами. Возникающий в результате большой ток может привести к перегреву оборудования и проводов, чрезмерным усилиям, а иногда даже к серьезным дугам, взрывам и взрывам.Причины неисправностей включают такие вещи, как удары молнии, животные, грязь и мусор, упавшие инструменты, коррозия и человеческий фактор.

Расчет тока повреждения основан на законе Ома, в котором ток (I) равен напряжению (V), деленному на сопротивление (R). Формула I = V / R. Когда происходит короткое замыкание, сопротивление становится очень маленьким, а это означает, что ток становится очень большим.

Если бы сопротивление было равно нулю, то расчетный ток повреждения увеличился бы до бесконечности.Однако даже медный провод имеет некоторое сопротивление; это не идеальный дирижер. Для определения тока повреждения необходимо знать полное сопротивление от источника питания до места повреждения.

Требуются расчеты тока повреждения

Знание доступного тока короткого замыкания важно при выборе защитных устройств, но это также необходимо для кода. Национальный электрический кодекс (NEC) 110.24 (A) гласит:

«Сервисное оборудование, не являющееся жилищем, должно иметь четкую маркировку в поле с максимальным доступным током короткого замыкания.Маркировка (и) поля должна включать дату выполнения расчета тока короткого замыкания и быть достаточно прочной, чтобы выдерживать воздействие окружающей среды ».

Это означает, что на электрическом оборудовании, таком как служебное входное оборудование, должны быть установлены ярлыки, указывающие доступный ток короткого замыкания. Это позволяет легко сравнивать номинальный ток короткого замыкания (SCCR) оборудования с максимально доступным током короткого замыкания.

Каждый раз при замене оборудования расчет тока короткого замыкания необходимо выполнять заново.Это указано в NEC 110.24 (B):

.

«При внесении изменений в электрическую установку, которые влияют на максимальный доступный ток повреждения в сервисе, максимальный доступный ток повреждения должен быть проверен или пересчитан по мере необходимости, чтобы гарантировать, что номинальные параметры сервисного оборудования достаточны для максимального доступного тока повреждения в линии. терминалы оборудования. Обязательная маркировка поля в 110.24 (A) должна быть скорректирована для отражения нового уровня максимального доступного тока короткого замыкания.”

Типы неисправностей

В электрической системе возможны несколько типов неисправностей:

• Короткое замыкание, в результате которого ток проходит в обход нормальной нагрузки.
• «Замыкание на землю», при котором ток течет в землю.
• В трехфазных системах может быть короткое замыкание между одной или несколькими фазами. Этот тип короткого замыкания обычно создает самые высокие токи замыкания.

Четвертый тип неисправности, неисправность обрыва цепи, не приводит к возникновению тока короткого замыкания. Открытый отказ возникает из-за непреднамеренного прерывания тока.

Защитные системы должны предотвращать повреждение оборудования и защищать людей во всех вышеперечисленных ситуациях. Это означает, что необходимо произвести расчеты тока короткого замыкания, чтобы можно было выбрать соответствующие защитные устройства.

Замыкание на болтах и ​​дуговое замыкание

Электрическая неисправность может быть либо замыканием на болтах, либо дуговым замыканием.

В неисправности с болтовым креплением соединение прочное. Это позволяет току короткого замыкания течь через проводник. Этот тип неисправности может произойти, когда установщик подключает источник питания к земле, а не к точке, где он должен быть подключен. При включении питания немедленно возникает неисправность болтового соединения, которая срабатывает защитное устройство. Поскольку текущий поток был ограничен, ущерб обычно ограничен. Однако замыкание на болтах создает самые высокие токи замыкания.

Дуговое короткое замыкание возникает, когда нет твердого соединения, но проводники подходят достаточно близко, так что ток прыгает через зазор, создавая дугу.Первоначальная дуга ионизирует воздух, создавая плазму, которая позволяет току быстро увеличиваться и поддерживаться, что приводит к вспышке дуги или возникновению дуги. Когда возможна вспышка дуги, необходимо выполнить расчеты тока короткого замыкания, чтобы определить безопасные границы защиты и необходимые средства индивидуальной защиты, а также предоставить информацию, необходимую для этикеток вспышки дуги, которые должны быть установлены в дополнение к требуемым этикеткам тока короткого замыкания NEC 110.24.

Трехфазные неисправности

IEC 60909 «Токи короткого замыкания в трехфазных системах» дает принятый метод расчета токов трехфазного замыкания.

Повреждение в трехфазной системе может быть симметричным (сбалансированным) или несимметричным (несимметричным). При симметричном КЗ все три фазы одинаково затронуты. Однако такое случается редко. Большинство трехфазных КЗ несимметричны, что затрудняет расчет тока КЗ.

Источники содержания

Прежде чем можно будет выполнить расчет тока короткого замыкания, необходимо определить все возможные источники тока. Это может включать некоторые источники тока, которые, возможно, не были учтены.Существует четыре возможных источника тока короткого замыкания:

• Электрогенераторы, устанавливаемые на месте: они расположены близко друг к другу, и ток короткого замыкания ограничен только импедансом самого генератора и электрической цепи.
• Синхронные двигатели: синхронный двигатель — это двигатель переменного тока, в котором скорость двигателя пропорциональна частоте электроэнергии. При отключении питания, как это произойдет при коротком замыкании, инерция механической нагрузки на двигатель будет продолжать вращать двигатель.Затем двигатель будет действовать как генератор, обеспечивающий ток, и это будет способствовать общему току, протекающему в месте повреждения.
Асинхронные двигатели
• : этот тип двигателя также станет генератором в случае короткого замыкания в другом месте системы. Однако ток короткого замыкания, генерируемый асинхронным двигателем, будет длиться всего несколько циклов. Ток будет примерно равен пусковому току двигателя с заторможенным ротором.
• Система электроснабжения: большая часть тока повреждения обычно исходит от электросети.Уровень тока короткого замыкания будет зависеть от:
• номинальное напряжение вторичной обмотки трансформатора и полное сопротивление
• Импеданс генераторов
• сопротивление цепи от трансформатора до короткого замыкания.

Для упрощения расчета тока повреждения предполагается, что все электрические генераторы в системе находятся в фазе и что они работают при номинальном напряжении системы.

Трехфазное соединение на болтах

Проводится исследование короткого замыкания, чтобы можно было рассчитать ток короткого замыкания.Обычно это включает рассмотрение наихудшего сценария, которым является состояние трехфазного короткого замыкания с болтовым креплением. Основываясь на этой ситуации, можно приблизительно определить другое состояние неисправности.

Вклад двигателей в систему по току короткого замыкания очень важен. Во многих случаях электродвигатели могут давать в четыре-шесть раз больший ток нормальной полной нагрузки. Даже если ток непродолжительный, очень важно, чтобы он был включен в расчет тока короткого замыкания.

Когда выполняется исследование вспышки дуги, расчет тока короткого замыкания по-прежнему должен производиться для максимального тока трехфазного короткого замыкания с болтовым соединением.

Маркировка тока повреждения

После того, как ток короткого замыкания был рассчитан, на оборудование должны быть нанесены метки с указанием доступного тока короткого замыкания. Если требуется этикетка для вспышки дуги, ее также следует распечатать и наклеить в соответствующем месте. Для каждой метки требуется специальная информация, полученная при расчете тока короткого замыкания.

Сделайте следующий шаг!

Теперь, когда у вас есть базовое представление о переменных в расчетах вспышки дуги, загрузите наше бесплатное руководство по энергии вспышки дуги, чтобы получить подробные советы о том, как реализовать систему безопасности на вашем предприятии.