Урок 30. закон джоуля-ленца. эдс — Физика — 10 класс
Физика, 10 класс
Урок 30. Закон Джоуля — Ленца. ЭДС
Перечень вопросов, рассматриваемых на уроке:
1) Работа электрического тока;
2) Мощность электрического тока;
3) Закон Джоуля — Ленца;
4) Сторонние силы;
5) Электродвижущая сила.
Глоссарий по теме
Работа тока на участке цепи равна произведению силы тока, напряжения на этом участке и времени, в течении которого совершалась работа.
Мощность тока равна отношению работы тока ко времени прохождения тока.
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока.
Любые силы, действующие на электрически заряженные частицы, за исключением электростатических (кулоновских) сил, называются сторонними силами.
Электродвижущая сила (ЭДС) в замкнутом проводящем контуре равна отношению работы сторонних сил по перемещению заряда вдоль контура к этому заряду.
Основная и дополнительная литература по теме урока:
Обязательная литература:
1. Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 343 – 347.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа,2009.- 68 – 74.
Дополнительная литература.
http://kvant.mccme.ru/1972/10/zakon_dzhoulya-lenca.htm
Основное содержание урока
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу, равную произведению заряда, прошедшего через проводник, и напряжения.

Сила тока равна отношению заряда прошедшего через проводник ко времени прохождения
Выразим заряд из формулы силы тока 
через силу тока и время:

после подстановки в формулу (1) получим

Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого шёл ток.
Из закона Ома для участка цепи выразим напряжение через силу тока и напряжение


и подставив в формулу работы получим:

При последовательном соединении проводников для определения работы тока удобнее пользоваться этой формулой, так как сила тока одинакова во всех проводниках.
При параллельном соединении проводников формулой:

так как напряжение на всех проводниках одинаково.
Работа тока показывает, сколько электроэнергии превратилось в другие виды энергии за конкретный период времени. Для электроэнергии справедлив закон сохранения энергии.
Мощность определяется по формуле:

Мощность тока равна отношению работы тока ко времени прохождения тока.
Так же формулу для мощности можно переписать в нескольких эквивалентных формах:



Если на участке цепи не совершается механическая работа и ток не производит химических действий, то происходит только нагревание проводника.
Электрическое поле действует с силой на свободные электроны, которые начинают упорядоченно двигаться, одновременно участвуя в хаотическом движении, ускоряясь в промежутках между столкновениями с ионами кристаллической решетки. Во время этих столкновений расходуется кинетическая энергия заряженных частиц. Именно эта энергия и становится теплом. Последующие столкновения электронов с другими ионами увеличивают амплитуду их колебаний и соответственно температуру всего проводника.
В неподвижных металлических проводниках вся работа тока идет на увеличение их внутренней энергии:

Количество теплоты, выделяемое проводником, по которому течет ток, равно работе тока.

Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику:


При последовательном соединении большее количество теплоты выделяется в проводнике с большим сопротивлением, а при параллельном соединении – с меньшим.
Измерения, приводящие к закону Джоуля-Ленца, можно выполнить, поместив в калориметр с водой проводник с известным сопротивлением и пропуская через него ток определенной силы в течение известного времени. Количество выделяющейся при этом теплоты определяют, составив уравнение теплового баланса.



Если соединить проводником два металлических шарика, несущих заряды противоположных знаков, под влиянием электрического поля этих зарядов в проводнике возникает кратковременный электрический ток. Заряды быстро нейтрализуют друг друга, и электрическое поле исчезнет.
Чтобы ток был постоянным, надо поддерживать постоянное напряжение между шариками. Для этого необходимо устройство, которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со стороны электрического поля шариков. В таком устройстве на заряды, должны действовать силы неэлектростатического происхождения. Одно лишь электрическое поле заряженных частиц не способно поддерживать постоянный ток в цепи.
Любые силы, действующие на электрически заряженные частицы, за исключением сил электростатического происхождения (то есть кулоновских), называют
Электростатическое поле потенциально. Работа этого поля при перемещении в нем заряженных частиц вдоль замкнутой электрической цепи равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — проводник нагревается. Следовательно, в цепи должен быть какой-то источник энергии, поставляющий ее в цепь. Работа этих сил вдоль замкнутого контура отлична от нуля. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрицательному), а во внешней цепи их приводит в движение электрическое поле.
Действие сторонних сил характеризуется важной физической величиной, называемой электродвижущей силой (сокращенно ЭДС).
Электродвижущая сила источника тока равна отношению работы сторонних сил при перемещении заряда по замкнутому контуру к величине этого заряда:

Электродвижущую силу выражают в вольтах.
Разбор тренировочных заданий
1. Электрочайник со спиралью нагревательного элемента сопротивлением 30 Ом включен в сеть напряжением 220 В. Какое количество теплоты выделится в нагревательном элемента за 5 мин?
1) 7260000 Дж;
2) 2200 Дж;
3) 484000 Дж.
Дано:
R=30Ом
U=220B
t=5мин=300с
Найти Q-?
Решение. Количество теплоты выделяемой нагревательным элементом определяется законом Джоуля – Ленца: 

Правильный ответ 3) 484000 Дж.
2. Определите работу сторонних сил при перемещении по проводнику заряда 10 Кл, если ЭДС равно 9 В. Ответ округлите до десятых.
Дано:
q=10Кл
 =9В
=9В
Найти: Аст
Решение. Из формулы ЭДС  выражаем
выражаем 

Правильный ответ: 90 Дж.
Закон Джоуля — Ленца | энергетик
Закон Джоуля Ленца — физический закон, дающий: количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем.
Закон Джоуля Ленца — количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка:
.
Закон Джоуля Ленца в интегральной форме в тонких проводах:
.
Если сила тока изменяется со временем, проводник неподвижен и химических превращений в нем нет, то в проводнике выделяется тепло.
Закон Джоуля Ленца — Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля:
,
где Q — количество теплоты, q — заряд, A — работа тока, U — напряжение в проводнике, I — сила тока в проводнике, t — время, dt— промежуток времени, R — сопротивление, w — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды.
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах. Тот же эффект в электрических машинах и аппаратах приводит к непроизвольным затратам энергии (потере энергии и снижении КПД). Тепло, вызывая нагрев этих устройств, ограничивает их нагрузку; при перегрузке повышение температуры может вызвать повреждение изоляции или сокращение срока службы установки.
Всем удачи!!!
Теплота и энергия в электрической цепи
Процесс преобразования электрической энергии в тепловую играет большую роль в практическом применении, что широко используется в разных нагревательных приборах в промышленной и бытовой сфере.
В то же время, тепловые потери нежелательны по причине того, что могут сопровождаться непроизводительными расходами энергии. Это может касаться, например, электрических машин, трансформаторов и прочих устройств, что существенно снижает их КПД.
Закон Джоуля-Ленца
Замечание 1
Первым сформулировал зависимость выделения теплоты от силы электрического тока Джеймс Джоуль, что произошло в 1841 году. Позднее это сделал Эмиль Ленц. Так появляется закон Джоуля-Ленца, позволяющий рассчитывать мощность электронагревателей наряду с потерями на тепловыделение в линиях электропередач.
В словесной формулировке, согласно исследованиям этих ученых, закон будет звучать таким образом: количество выделяемой в определенном объеме проводника теплоты в момент протекания электрического тока оказывается прямо пропорциональным произведению величины напряженности электрического поля и плотности электрического тока. Формула записывается так:
Готовые работы на аналогичную тему
$w=\vec{j}\vec{E} = QE^2$, где:
- $w$ представляет мощность выделяемого тепла в единице объема;
- $\vec{j}$ считается плотностью электрического тока;
- $\vec{E}$ — напряженность электрического поля;
- $Q$ -проводимость среды.
Принимая во внимание неизменность со временем силы тока и сопротивления проводника, можно записывать закон Джоуля-Ленца более упрощенно:
$Q = I^2Rt$
Применяя закон Ома в совокупности с алгебраическими преобразованиями, получаем следующие эквивалентные формулы:
$Q = \frac{U^2t}{R} = UIt$
Исследования физиков Джоуля и Ленца относительно тепловыделения от действия электрического тока значительно продвинули научное понимание определенных физических процессов, а выведенные при этом основные формулы, не претерпев изменений, продолжают активно использоваться в различных научно-технических отраслях.
В сфере электротехники выделяют несколько технических задач, где количество теплоты, которая будет выделяться при протекании тока, имеет критически важное значение при расчете таких параметров, как:
- теплопотери в ЛЭП;
- характеристики для проводов сетей электропроводки;
- тепловая мощность электронагревателей;
- температура срабатывания автовыключателей;
- температура плавления плавких предохранителей;
- тепловыделение разных электротехнических аппаратов, а также элементов радиотехники.
Замечание 2
Тепловое действие электротока в проводах ЛЭП является нежелательным из-за весомых потерь электроэнергии на тепловое выделение. Согласно различным данным, в ЛЭП теряется до 40% всей производимой в мировом формате электрической энергии. С целью сокращения потерь в процессе передачи электроэнергии на большие расстояния, напряжение в ЛЭП поднимают (с произведением расчетов на основании производных формул закона Джоуля-Ленца).
Расчеты потерь электроэнергии в линии электропередач
Как пример, гипотетически берется участок ЛЭП от электростанции до трансформаторной подстанции. По причине того, что провода ЛЭП и потребитель электрической энергии (трансформаторная подстанция) соединены последовательным образом, через них будет течь один и тот же ток $I$. Тогда, на основании закона Джоуля – Ленца, количество теплоты $Q_w$, которая выделится на проводах, рассчитывают, согласно формуле:
$Q_w = R_wI^2$
Производимая электротоком мощность $Q_c$ в нагрузке определяется на основании закона Ома:
$Q_с = U_сI$
При условии равенства токов, таким образом, в первую формулу вместо $I$ вставляется выражение $\frac{Q_c}{U_c}$:
$Q_w = \frac{R_wQ_c^2}{U_c^2}$
При условии игнорирования зависимости сопротивления проводников от изменения температуры, $R_w$ можно считать неизменной величиной (константой). При стабильном энергопотреблении потребителя (трансформаторной подстанции), таким образом, выделение тепловой энергии в проводах ЛЭП будет считаться обратно пропорциональным квадрату напряжения в конечной точке линии. Иными словами, чем больше окажется напряжение электропередачи, тем меньшими станут потери электроэнергии.
Энергия в электроцепи
Замечание 3
В источнике электроэнергии, равно как и в нагрузке (в резисторах), мы наблюдаем необратимое преобразование электрической энергии в тепловую
Совершаемая источником электроэнергии за время t работа (направленная на разделение зарядов сторонними силами в источнике) будет определяться формулой:
$w = EQ = EIt$.
В приемнике электроэнергии при напряжении $U$ и токе $I$ расходуется энергия по формуле:
$W_{пр} = UQ = UIt = I^2Rt = \frac{U^2t}{R}$
Мощность $P$ характеризуется интенсивностью преобразования энергии из одного вида в иную за единицу времени. Мощность источника для цепей постоянного тока будет такой:
$P = \frac{w}{t} = E+I$
Мощность приемника тогда определяется по формуле:
$P = \frac{w}{t} = U+I = R + I^2 = \frac{U^2}{R}$
В системе СИ энергия и мощность измеряются в Джоулях (Дж) и Ваттах (Вт) соответственно. Для всех приведенных выше величин применяются кратные и дольные единицы измерения. Энергию часто выражают в киловатт-часах.
Закон Джоуля-Ленца — Студопедия
В случае, когда проводник неподвижен и химических превращений в нем не происходит, то работа тока целиком расходуется на нагревание проводника. Количество теплоты, выделяющееся в проводнике за конечный промежуток времени при прохождении постоянного тока I, рассчитывается по формуле
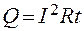 . (2.7)
. (2.7)
Формула (2.7) выражает закон Джоуля-Ленца для участка цепи постоянного тока: количество теплоты, выделяемое постоянным электрическим током на участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.
Так как IR = U, то формулу (2.7) можно переписать в виде
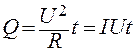 . (2.8)
. (2.8)
Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t, вычисляется по формуле
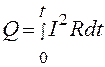 . (2.9)
. (2.9)
Закон Джоуля-Ленца в дифференциальной форме (для данной точки проводника с током) имеет вид
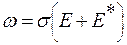 , (2.10)
, (2.10)
где ω − плотность тепловой мощности; σ − удельная электропроводность; Е− напряженность электрического поля в данной точке проводника; Е* − напряженность поля сторонних сил.
Примеры решения задач
Задача 1. За время τ = 20 с при равномерно возраставшей силе тока от нуля до Io в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Найти Io.
| Io – ? | Решение:
Так как ток равномерно возрастает, то зависимость силы тока от времени имеет вид
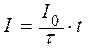 . (1) . (1)
|
| τ = 20 с R = 5 Ом Q = 4 кДж |
По закону Джоуля-Ленца за время dt в проводнике выделится количество тепла
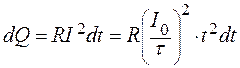 .
.
Полное количество тепла за время от 0 до τ
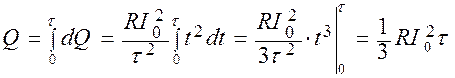 .
.
Отсюда находим
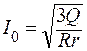 ;
; 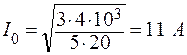 .
.
Ответ: I0 = 11 А.
Задача 2. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление обмотки мотора R = 6 Ом.
| Pп – ? η – ? | Решение:
Полная мощность, потребляемая мотором:
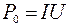 ,
Р0 = 1100 Вт. ,
Р0 = 1100 Вт.
|
| U = 220 В I = 5 А R = 6 Ом |
Мощность, выделяющаяся в виде тепла:
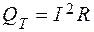 .
.
Полезная мощность (механическая)
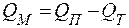 .
.
КПД мотора
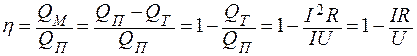 ;
;
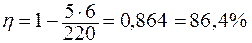 .
.
Ответ: η = 86,4%.
Задача 3. Источник тока с ЭДС замкнут на реостат. При силе тока I1 = 0,2 А и I2 = 2,4 А на реостате выделяется одинаковая мощность. Найти:
1) при какой силе тока на реостате выделяется максимальная мощность?
2) чему равна сила тока короткого замыкания?
| I – ? Iкз – ? | Решение:
При силе тока I1 на реостате выделяется мощность
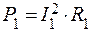 ,
при силе тока I2 ,
при силе тока I2
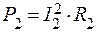 , ,
|
| I1 = 0,2 А | |
| I2 = 2,4 А P1 = P2 |
где R1 и R2 – сопротивления реостата в каждом случае. По условию P1 = P2, поэтому
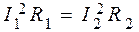 . (1)
. (1)
По закону Ома для полной цепи
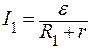 , (2)
, (2)
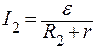 . (3)
. (3)
Из (2) и (3) выражаем R1 и R2:
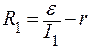 ;
; 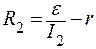 ,
,
подставив их в (1), получаем:
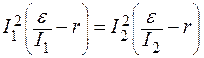 .
.
Отсюда находим отношение 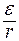 :
:
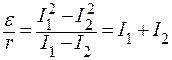 ;
;
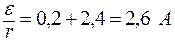 .
.
Максимальная мощность выделяется при условии R = r, при этом ток
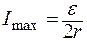 . (4)
. (4)
Ток короткого замыкания
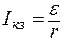 . (5)
. (5)
Произведем вычисления:
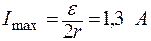 ;
; 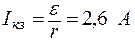 .
.
Ответ:I = 1,3 А; Iкз = 2,6 А.
Задача 4. При изменении внешнего сопротивления с R1 = 6 Ом до R2 = 21 Ом. КПД схемы увеличился вдвое. Чему равно внутреннее сопротивление источника тока r ?
| r − ? | Решение:
При сопротивлении R1 КПД источника тока
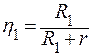 ,
а при сопротивлении R2 ,
а при сопротивлении R2
|
| R1 = 6 Ом R2 = 21 Ом η2 = 2η1 |
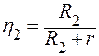 .
.
Так как по условию задачи η2=2η1, то
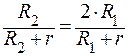 .
.
Отсюда выражаем r:
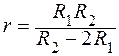 ;
;
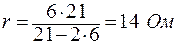 .
.
Ответ: r = 14 Ом.
Задача 5. Две батареи с ЭДС ε1 = 20 В и ε2 = 30 В и внутренними сопротивлениями r1 = 4 Ом и r2 = 60 Ом соединены параллельно и подключены к нагрузке R = 100 Ом. Найти: 1) мощность, которая выделяется в нагрузке; 2) параметры ε и r генератора, которым можно заменить батареи без изменения тока в нагрузке; 3) КПД этого генератора.
| P – ? ε, r – ? η – ? | Решение:
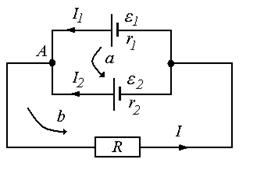 Рис. 52
Рис. 52
|
| ε1 = 20 В ε2 = 30 В r1 = 4 Ом r2 = 60 Ом R = 100 Ом |
Используя правила Кирхгофа, найдем токи I1, I2, I в узле A:
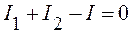 . (1)
. (1)
Для контура a с обходом против часовой стрелки
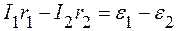 . (2)
. (2)
Для контура b с обходом против часовой стрелки
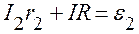 . (3)
. (3)
Решим систему линейных уравнений (1) – (3) относительно I1, I2, I.
Из (1) выразим I
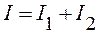 . (4)
. (4)
Подставим в (3)
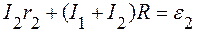
или
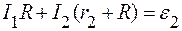 . (5)
. (5)
Умножая уравнение (2) на R, а уравнение (5) – на r1, и складывая их, получаем:
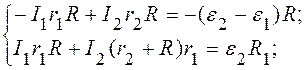
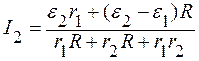 . (6)
. (6)
Подставляя (6) в выражение (2), находим I1:
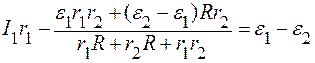 .
.
Отсюда
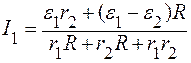 . (7)
. (7)
Подставляя выражения (6) и (7) в (4), находим I:
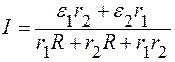 . (8)
. (8)
В нагрузке выделяется мощность:
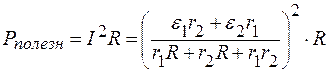 ;
;
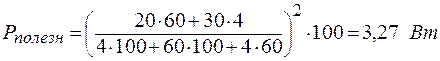 .
.
Находим параметры генератора. Если данные в задаче батареи заменить на одну с ЭДС ε и внутренним сопротивлением r, то через сопротивление R потек бы ток
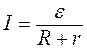 . (9)
. (9)
Преобразуем выражение (8), поделив числитель и знаменатель дроби на (r1+r2), получим
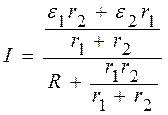 . (10)
. (10)
Для того чтобы эти выражения были одинаковыми, необходимо выполнение условий:
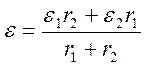 ;
;
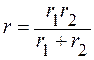 ;
;
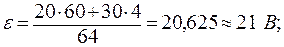
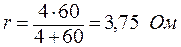 .
.
КПД этого генератора в данной схеме
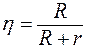 ;
;
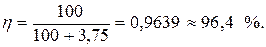
Ответ: η = 96,4 %.
Электрические формулы и их описание
Чтобы работать с электричеством, делать разводку по дому, понимать правила ПУЭ и решать различные задачи, нужно знать основные формулы электричества, физические законы, приведенные известными учеными-физиками. Ниже рассмотрены основные теоремы по электрике, выведенные константы, физические правила, которые следует понимать каждому человеку.
Основные формулы электричества
Изучение основ электродинамики, электрики невозможно без определения электрического поля, точных зарядов, сопротивления и прочих явлений.
 Формулы электричества
Формулы электричестваПоэтому важно рассмотреть все основные формулы электричества и примеры решения задач с их использованием.
Закон Кулона
Согласно короткому описанию, это физический закон, который говорит о взаимодействии между прямо стоящими точечными электрозарядами в зависимости от того, на каком расстоянии они находятся. Согласно полному определению, формулировка обозначает, что между двумя точками в виде электрических зарядов формируется вакуум. Там появляется конкретная сила, которая пропорциональна умножению их модульных частиц, поделенных на квадратный показатель расстояния.
Расстояние — длина, которая соединяет заряды. Сила взаимодействия направлена по отрезку. Кулоновская сила — сила, отталкивающая при зарядах минус-минус и плюс-плюс и притягательная при минус-плюс и плюс-минус.
Обратите внимание! Электрическая сила формула выглядит так: F=k⋅|q1|⋅|q2|/r2, где F — сила заряда, q — величина заряда, r — вектор или расстояние между зарядами, а k — коэффициент пропорциональности. Последний равен c2·10−7 Гн/м.
 Закон Кулона
Закон КулонаРешение задачи с законом Кулона. При наличии заряженных шариков, которые находятся на расстоянии 15 см и отталкиваются с силой 1 Н в поиске начального заряда, выявить неизвестное можно, переведя основные единицы в систему СИ и подставив величины в указанную формулу. Выйдет значение 2 * 5 * 10 (-8) = 10 (-7).
Напряженность поля уединенного точечного заряда
Электрическое поле будучи материей, создаваемой электрическими точечными зарядами, характеризуется разными величинами, в том числе напряженностью. Напряженность выступает векторной величиной или силовой характеристикой поля, которая направлена в сторону электростатического взаимодействия зарядов. Чтобы получить ее, нужно использовать формулу E = k (q / r (2)), где Е — векторное поле.
 Напряженность поля уединенного точечного заряда
Напряженность поля уединенного точечного зарядаСогласно данной формулировке, напряженность поля заряда имеет обратную пропорциональность квадратному значению расстояния от заряда. То есть если промежуток увеличивается в несколько раз, показатель напряжения снижается в четыре.
Применить закон можно для решения задач. Например, неизвестен радиус. Тогда нужно преобразовать константу. Нужно решить уравнение E / r (2) = kq, подставив известные числа.
Потенциал точки в поле точечного заряда
Потенциалом в электростатическом поле называется скалярная величина, которая равна делению потенциального показателя энергии заряда на него. Он не зависит от величины q, которая помещена в область. Так как потенциальный показатель энергии зависит от того, какая выбрана система координат, то потенциал определяется с точностью до постоянной. Он равен работе поле, которое смещает единичный положительный заряд в бесконечность. Выражается через ф = W / q =const.
 Потенциал точки в поле точечного заряда
Потенциал точки в поле точечного зарядаОбратите внимание! В задачах можно преобразовывать константу. Если неизвестно W, то можно поделить q на ф, а если q — то, W на ф.
Потенциальная энергия заряда в электростатическом поле
 Потенциальная энергия заряда в электростатическом поле
Потенциальная энергия заряда в электростатическом полеПоскольку работа электрического поля не зависит от выбранного движения заряженной частицы, а от его начального и конечного положения, есть термин потенциальной энергии. Это скалярная величина в координате пространства, которая показывает, как работает сила, когда частица перемещается по произвольному промежутку из одной в другую точку. Она равна разности значений передвижения частиц в этом промежутке. Выражается в следующем виде: А = П1 — П2, где П1 может быть x, y и z, а П2 — x2, y2 и z2. В задачах по физике нужно рисовать график, подставлять в константу известные значения и решать уравнения.
Потенциальная энергия заряда q1 в поле точечного заряда
Во время перемещения заряженных частиц по полю из одной точки в другую они совершают некую работу за определенный временной промежуток. Потенциальная энергия в этих точках не зависит от того, какой путь держат заряженные частицы. Энергия первого заряда пропорциональна его модулю. Выражается это все в формуле, представленной на картинке ниже. Задачи решать можно, используя представленную константу и вставляя известные значения.
 Потенциальная энергия заряда q1 в поле точечного заряда
Потенциальная энергия заряда q1 в поле точечного зарядаТеорема Гаусса
Основной закон в электродинамике, входящий в уравнения Максвелла. Это следствие из кулоновского умозаключения и принципа суперпозиции. По ней вектор напряжения поля движется сквозь произвольное значение замкнутой поверхности, окруженной зарядами. Он имеет пропорциональность сумме заряженных частиц, которые находятся внутри этого замкнутого пространства. Указанный вектор поделен на е0. Все это выражается формулой, указанной ниже.
 Теорема Гаусса
Теорема ГауссаНапряженность электрического поля вблизи от поверхности проводника
Напряженность суммарного пространства заряженных частиц имеет прямую пропорциональность поверхностному показателю их плотности. Если в задаче требуется найти напряженность, а поверхностная заряженная плотность это сигма, то нужно нарисовать цилиндр и обозначить, что поток сквозь его боковую поверхность равен 0. В таком случае линии напряженности будут параллельны боковой поверхности. Получится, что ф = 2ф, осн =2еs, а 2es =q / 2ε0.
 Напряженность электрического поля вблизи от поверхности проводника
Напряженность электрического поля вблизи от поверхности проводникаЕмкость плоского конденсатора
Емкостью называется проводниковая характеристика, по которой электрический заряд может накапливать энергию. Плоским конденсатором называются несколько противоположно заряженных пластин, разделенных диэлектрическим тонким слоем. Емкостью плоского конденсатора считается его характеристика, способность к накоплению электрической энергии.
Обратите внимание! Это физическая величина, которая равна делению заряда на разность потенциалов его обкладки. Зарядом при этом служит заряженная одна пластина.
Если в задаче требуется узнать емкость конденсатора из двух пластин с площадью в 10(-2) квадратных метров и в них находится 2*10(-3) метровый лист, ε0 электрическая постоянная с 8,85×10-12 фарад на метр и ε=6 — диэлектрическая проницаемость слюды. В таком случае нужно вставить значения в формулу C= ε* ε* S/d.
 Емкость плоского конденсатора
Емкость плоского конденсатораЭнергия плоского конденсатора
Поскольку любая частица конденсатора имеет способность запаса энергии, который сохранен на конденсаторной обкладке, вычислить эту самую Е просто, поскольку чтобы элемент зарядился, ему нужно совершить работу. Работа совершается полем. В результате была выведена следующая формула: Еp = А = qEd, где А является работой, d — расстоянием.
 Энергия
ЭнергияФормулы для постоянного электрического тока
Постоянный электрический ток не изменяется в величине и направлении. Он используется для расчета замкнутой, однородной цепи, мощности и прочих параметров. Поэтому важно знать формулы для него и основные законы, связанные с ним.
 Основной список формул
Основной список формулЗакон Ома для участка однородной цепи
Чтобы электрический ток существовал, нужно поле. Для его образования, нужны потенциалы или разность их, выраженная напряжением. Ток будет направлен на снижение потенциалов, а электроны начнут свое передвижение в обратном направлении. В 1826 г. Г. Ом провел исследование и сделал заключение: чем больше показатель напряжения, тем больше ток, который проходит через участок.
К сведению! Смежные проводники при этом проводят электричество по-разному. То есть каждый элемент имеет свою проводимость, электрическое сопротивление.
В результате, согласно теореме Ома, сила тока для участка однородной цепи будет иметь прямую пропорциональность показателю напряжения на нем и обратную пропорциональность проводниковому сопротивлению.
 Закон Ома
Закон ОмаПо формуле I = U / R, где I считается силой тока, U — напряжением, а R — электрическим сопротивлением, последнее значение можно найти, если p * l / S, где p является удельным проводниковым сопротивлением, l — длиной проводника, а S — площадью поперечного проводникового сечения.
Закон Ома для замкнутой цепи с источником тока
Ом сделал формулу и для замкнутой цепи. По ней ток на этом участке из токового источника, имеющего внутреннее и внешнее нагрузочное сопротивление, равен делению электродвижущей силы источника на сумму внутреннего и внешнего сопротивления. Она выглядит так: I = e / R + r, где I является токовой силой, е — ЭДС, R — сопротивлением, а r — внутренней сопротивляемостью источника напряжения.
Обратите внимание! В физическом смысле по этому закону, чем выше показатель ЭДС, тем выше источник энергии, больше скорость движения зарядов. Чем выше сопротивляемость, тем ниже величина тока.
 Закон Ома для замкнутой цепи
Закон Ома для замкнутой цепиРабота постоянного тока
Энергия, когда проходит через проводник, упорядоченно двигается в носитель. Во время движения она совершает работу. В результате работой постоянного тока называется деятельность поля, направленная на перенос электрических зарядов по проводнику. Она равна умножению I на совершаемое работой напряжение и время.
Закон Джоуля-Ленца
Когда электричество проходит через какой-то проводник с сопротивляемостью, всегда высвобождается теплота. Количество тепла, которое высвободилось за определенный промежуток времени, определяет закон Джоуля-Ленца. По формуле мощность тепла равняется умножению плотности электричества на напряжение — w =j * E = oE(2).
Обратите внимание! В практическом понимании закон имеет значение для снижения потери электроэнергии, выбора проводника для электроцепи, подбора электронагревательного прибора и использования плавкого предохранителя для защиты сети.
 Закон Джоуля-Ленца
Закон Джоуля-ЛенцаПолная мощность, развиваемая источником тока
Мощность — работа, которая совершается за одну секунду времени. Электрическая мощность является физической величиной, которая характеризует скорость передачи с преобразованием электроэнергии.
Работа, которая развивается источником электроэнергии по всей цепи, это полная мощность. Ее можно определить по формуле Р = El, где E считается ЭДС, а I — величиной токовой характеристики.
К сведению! Если есть линейная нагрузка, то полный мощностный показатель равен квадратному корню из квадратов активной и реактивной работы источника. Если есть нелинейная нагрузка, то она равна квадратному корню из квадратов активной и неактивной работы источника.
 Полная мощность
Полная мощностьВ практических измерениях такая работа выражается в киловаттах в час. Используется, чтобы измерять потребление электричества в бытовых и производственных условиях, определять выработанную электрическую энергию в электрическом оборудовании.
Полезная мощность
Максимальная или полезная мощность — та, что выделяется во внешнем промежутке цепи, то есть во время нагрузки резистора. Она может быть применена для выполнения каких-либо задач. Подобное понятие можно применить, чтобы рассчитать, как работает электрический двигатель или трансформатор, который способен на потребление активной и реактивной составляющей.
 Полезная мощность
Полезная мощностьПолезный мощностный показатель можно рассчитать по трем формулам: P = I 2R, P = U2 / r, P = IU, где I является силой тока на определенном участке цепи; U — напряжением на части клемм (зажимов) токового источника, а R — сопротивлением нагрузки или внешней цепью.
Коэффициент полезного действия источника тока
Коэффициентом полезного действия токового источника называется деление полезного мощностного показателя на полный. Если внутреннее сопротивление источника равно внешнему, то половина результатов всей работы будет утеряна в источнике, а другая половина будет выделена на нагрузке. В такой ситуации КПД будет равен 50 %.
Если рассматривать это понятие наиболее полно, то когда электрические заряды перемещаются по замкнутой электрической цепи, источник тока выполняет определенную полезную и полную работу. Совершая первую, он перемещает заряды во внешнюю цепь. Делая вторую работу, заряженные частицы перемещаются по всему участку.
 КПД источника тока
КПД источника токаОбратите внимание! Полезное действие достигается, когда сопротивление внешней электроцепи будет иметь определенное значение, зависящее от источника и нагрузки. Соотношения полезной работы на полную выражают формулой: η = Аполез / Аполн = Рполез / Рполн = U/ε = R / (R + r).
Первое правило Кирхгофа
Согласно первому закону Кирхгофу, токовая сумма в любом участке электрической цепи равняется нулевому значению. Направленный заряд к узлу положительный, а от него — отрицательный. Алгебраическая токовая сумма зарядов, которые направлены к узлу, равна сумме тех, которые направлены от него. Если перевести это правило, то можно получить следующее определение: сколько тока попадает в узел, столько и выходит из него. Это правило вытекает из закона о сохранности заряженных частиц.
Благодаря решению линейных уравнений на основе кирхгофских правил можно отыскать все токовые значения и напряжения на участках постоянного, переменного и квазистационарного электротоков.
Обратите внимание! В электотехнике правило Кирхгофа имеет особое значение, поскольку оно универсально для решения многих поставленных задач в теории электроцепи. С помощью него можно рассчитать сложные электрические цепи. Применяя его, можно получить систему линейных уравнений относительно токам или напряжениям на всех межузловых ветвях цепей.
 Первое правило Кирхгофа
Первое правило КирхгофаВторое правило Кирхгофа
Второе кирхгофское правило вытекает из первого и третьего максвеллского уравнения. По нему алгебраическая сумма напряжений на резистивных элементах замкнутого участка равна сумме ЭДС, которая входит в него. Если на участке нет ЭДС, то суммарный показатель падения напряжения равен нулевому значению. Если еще проще, то во время полного обхода контура потенциал изменяется. Он возвращается на исходное значение.
Частый случай для участка одного контура — это закон Ома. Составляя уравнения напряжений для контура, требуется подобрать его положительный обход. Чтобы это сделать, нужно знать, что при подборе обхода показатель падения напряжения ветви будет положительным, если обходное направление в ветви совпадает с тем, которое было ранее выбрано. Если оно не совпадает, то показатель напряжения ветви будет отрицательным.
Важно! Второе правило Кирхгофа можно использовать в линейной или нелинейной линеаризованной цепи при любом изменении токов и напряжения.
 Второе правило Кирхгофа
Второе правило КирхгофаВ результате, чтобы понять основы физики явлений, электрики, электродинамики и с успехом использовать знания в процессе жизнедеятельности, необходимо знать выведенные теоремы, законы, формулы и правила в области электричества, которые представлены выше. Например, представляя, как выглядит та или иная формула, можно решить любую задачу в учебнике по физике или жизни.
| 1. |
Закон Джоуля—Ленца — формула
Сложность: лёгкое |
1 |
| 2. |
Закон Джоуля—Ленца — определение
Сложность: лёгкое |
1 |
| 3. |
Закон Джоуля—Ленца — физические величины
Сложность: лёгкое |
1 |
| 4. |
Анализ величин, входящих в закон Джоуля—Ленца.
Сложность: среднее |
2 |
| 5. |
Сравнение количества теплоты, выделяемого в последовательно соединённых проводниках
Сложность: среднее |
1 |
| 6. |
Различные схемы соединения резисторов
Сложность: сложное |
2 |
| 7. |
Работа с формулой закона Джоуля—Ленца
Сложность: лёгкое |
4 |
ЭФФЕКТ ОТОПИТЕЛЬНОГО ТОКА
Введение
Когда ток проходит через проводник, тепловая энергия генерируется в проводнике. Нагревательный эффект электрического тока зависит от трех факторов:
- Сопротивление, р проводника. Более высокое сопротивление производит больше тепла.
- Время, за которое течет ток. Чем дольше время, тем больше выделяется тепла
- Количество тока, I. Чем выше ток, тем больше количество выделяемого тепла.
Следовательно, эффект нагрева, создаваемый электрическим током I через проводник сопротивления R в течение времени t, определяется как H = I 2 Rt. Это уравнение называется уравнением электрического нагрева Джоуля.
Электроэнергия и мощность
Работа, проделанная при проталкивании заряда по электрической цепи, определяется как w.d = VIt
.Так что мощность, P = W.D / T = VI
Электрическая мощность, потребляемая электрическим прибором, определяется как P = VI = I 2 R = V 2 / R
Пример
- Электрическая лампочка имеет маркировку 100 Вт, 240 В.Рассчитать:
б) Сопротивление нити накала, используемой в колбе.
Решение
- I = P / V = 100/240 = 0,4167A
- R = P / I 2 = 100 / 0,4167 2 = 576,04Ω или R = V 2 / P = 240 2 /100 = 576Ω
- Найдите энергию, рассеиваемую за 5 минут электрической лампочкой с нитью накала сопротивления 500 Ом, подключенной к источнику питания 240 В.{ отн. 34 560J }
Решение
E = Pt = V2 / R * t = (240 2 * 5 * 60) / 500 = 34 560J
- Погружной нагреватель 2,5 кВт используется для нагрева воды. Рассчитать:
- Рабочее напряжение нагревателя, если его сопротивление составляет 24Ом
- Электрическая энергия превращается в тепловую энергию за 2 часа.
{ ответ. 244,9488 В, 1,8 * 10 7 J }
Решение
- P = VI = I 2 R
I = (2500/24) 1/2 = 10.2062А
В = ИК = 10,2062 * 24 = 244,9488 В
- E = VIt = Pt = 2500 * 2 * 60 * 60 = 1,8 * 10 7 J
ИЛИ E = VIt = 244,9488 * 10,2062 * 2 * 60 * 60 = 1,8 * 10 7 J
Электрическая лампочка имеет маркировку 100 Вт, 240 В. Вычислить:Ток через нить накала
Сопротивление нити накала, используемой в колбе.
Решение
P = VI I = P / V = 100/240 = 0,4167AПо закону Ома V = IR R = V / I = 240 / 0,4167 = 575,95 Ом
Применения эффекта нагрева электрическим током
Таким образом большинство бытовых электроприборов преобразуют электрическую энергию в тепло.К ним относятся лампы накаливания, электрический нагреватель, электрический утюг, электрический чайник и т. Д.
В осветительных приборах
- Лампы накаливания — изготовлены из вольфрамовой проволоки, заключенной в стеклянную колбу, из которой был удален воздух. Это потому, что воздух будет окислять нить накала. Нить нагревается до высокой температуры и становится белым горячим. Вольфрам используется из-за его высокой температуры плавления; 3400 0 Колба заполнена неактивным газом, например, аргон или азот при низком давлении, что уменьшает испарение вольфрамовой проволоки.Однако одним из недостатков инертного газа является то, что он вызывает конвекционные токи, которые охлаждают нить накала. Эта проблема сводится к минимуму за счет наматывания проволоки, чтобы она занимала меньшую площадь, что уменьшает потери тепла в результате конвекции.
- Люминесцентные лампы — эти лампы более эффективны по сравнению с лампами накаливания и служат гораздо дольше. Они содержат пары ртути в стеклянной трубке, которая излучает ультрафиолетовое излучение при включении. Это излучение заставляет порошок в трубке светиться (флуоресцировать), т.е.е. испускает видимый свет Разные порошки дают разные цвета. Обратите внимание, что люминесцентные лампы дороги в установке, но их эксплуатационные расходы намного меньше.
В электрическом отоплении
- Электрические плиты — электрические плиты становятся красными, и вырабатываемая тепловая энергия поглощается кастрюлей через проводимость.
- Электрические обогреватели — излучающие обогреватели становятся красными при температуре около 900 0 C, и излучаемое излучение направляется в комнату полированными отражателями.
- Электрические чайники — нагревательный элемент расположен на дне чайника так, чтобы нагреваемая жидкость покрывала его. Затем тепло поглощается водой и распределяется по всей жидкости путем конвекции.
- Электрические утюги — при прохождении тока через нагревательный элемент вырабатываемая тепловая энергия подводится к основанию из тяжелого металла, повышая его температуру. Эта энергия затем используется для прессования одежды. Температуру электрического утюга можно контролировать с помощью термостата (биметаллическая полоса).
Формула электрической мощности
Электрическая мощность — это скорость, с которой энергия передается в электрическую цепь или из нее. Батарея может передавать энергию, или элемент схемы, такой как резистор, может выделять энергию в виде тепла. Для любого элемента схемы мощность равна разности напряжений на элементе, умноженной на ток. По закону Ома V = IR, и поэтому существуют дополнительные формы формулы электрической мощности для резисторов. Мощность измеряется в единицах Вт (Вт), где Вт равен Джоулю в секунду (1 Вт = 1 Дж / с).
Общая форма:
электрическая мощность = разность напряжений х ток
P = VI
Резисторы:
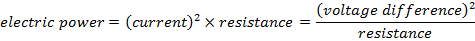
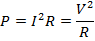
P = электрическая мощность (Вт)
В = разность напряжений (В = J / C)
I = электрический ток (A = C / s)
R = сопротивление (Ом = В / А)
Формула электроэнергии Вопросы:
1) Если аккумулятор сотового телефона работает при напряжении 12,0 В и должен выдавать ток 0.9 Какая мощность требуется во время воспроизведения музыки?
Ответ: Требуемую мощность от батареи можно найти по формуле электрической мощности:
P = VI
P = (12,0 В) (0,9 A)
P = (12,0 Дж / с) (0,9 C / с)
P = 10,8 Дж / с
P = 10,8 Вт
Потребляемая мощность от аккумулятора телефона составляет 10,8 Вт.
2) Резистор с разностью потенциалов 24,0 В излучает тепло. Тепловая энергия генерируется в размере 16.0 Вт. Какое значение сопротивления?
Ответ: Значение сопротивления можно найти, переставив одну из формул формулы электроэнергии. Форма, которая применима, относится к мощности, напряжению и сопротивлению:
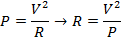
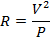
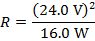
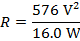
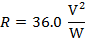
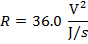
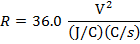
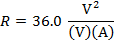
R = 36,0 В / А
R = 36,0 Ом
Значение сопротивления составляет 36,0 Ом.
Электрические формулы с решенными примерами
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса 9
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Учебный курс по бизнес-классу 11000
- Учебная программа по экономическому классу
- Учебная программа по 12 классу
- Учебная программа по 12 классу
- Учебная программа по экономическому классу
- Решения TS Grewal Класс 12 Бухгалтерский учет
- Решения TS Grewal Класс 11 Бухгалтерский учет
- ML Решения Aggarwal Class 10 Maths
- ML Решения Aggarwal Class 9 Математика
- ML Решения Aggarwal Class 8 Maths
- ML Решения Aggarwal Class 7 Математические решения
- ML 6 0004
- ML 6
- Selina Solution для класса 8
- Selina Solutions для класса 10
- Selina Solution для класса 9
Что такое электрическая цепь? (с картинками)
Электрическая цепь — это устройство, которое использует электричество для выполнения такой задачи, как запуск вакуума или включение лампы. Схема представляет собой замкнутый контур, образованный источником питания, проводами, предохранителем, нагрузкой и выключателем. Электричество протекает по цепи и доставляется к объекту, к которому он подключен, например, к вакуумному двигателю или лампочке, после чего электричество отправляется обратно к первоначальному источнику; этот возврат электричества позволяет цепи поддерживать ток электричества.Существуют три типа электрических цепей: последовательная цепь, параллельная цепь и последовательно-параллельная цепь; в зависимости от типа цепи, электричество может продолжать течь, если цепь перестает работать. Два понятия, закон Ома и напряжение источника, могут влиять на количество электричества, протекающего по цепи, и, следовательно, на то, насколько хорошо функционирует электрическая цепь.
 Техник по ремонту электрических цепей.
Техник по ремонту электрических цепей.Как это работает
Большинство устройств, работающих на электричестве, содержат электрическую цепь; при подключении к источнику питания, например при подключении к электрической розетке, электричество может проходить через электрическую цепь внутри устройства, а затем возвращаться к исходному источнику питания, чтобы продолжать поток электроэнергии.Другими словами, когда выключатель питания включен, электрическая цепь замыкается, и ток течет от положительной клеммы источника питания, через провод к нагрузке и, наконец, к отрицательной клемме. Любое устройство, которое потребляет энергию, протекающую по цепи и преобразует эту энергию в работу, называется нагрузкой. Лампочка является одним из примеров нагрузки; он потребляет электричество из цепи и превращает его в работу — тепло и свет.
 Немецкий физик Георг Ом обнаружил, как состав материала, длина и толщина влияют на то, сколько тока будет проходить через него при определенном напряжении.
Немецкий физик Георг Ом обнаружил, как состав материала, длина и толщина влияют на то, сколько тока будет проходить через него при определенном напряжении.Типы схем
Последовательная цепь является самой простой, потому что у нее есть только один возможный путь, по которому может течь электрический ток; если электрическая цепь оборвана, ни одно из нагрузочных устройств не будет работать.Разница с параллельными цепями заключается в том, что они содержат более одного пути для прохождения электричества, поэтому, если один из путей нарушен, другие пути продолжат работать. Последовательно-параллельная схема, однако, представляет собой комбинацию первых двух: она присоединяет некоторые нагрузки к последовательной цепи, а другие — к параллельным цепям. Если последовательная цепь обрывается, ни одна из нагрузок не будет работать, но если одна из параллельных цепей разорвется, эта параллельная цепь и последовательная цепь перестанут работать, в то время как другие параллельные цепи продолжат работать.
 Предохранители в блоке предохранителей.
Предохранители в блоке предохранителей.закон Ома
Многие «законы» применяются к электрическим цепям, но закон Ома, вероятно, самый известный.Закон Ома гласит, что ток электрической цепи прямо пропорционален ее напряжению и обратно пропорционален ее сопротивлению. Так, например, если напряжение увеличивается, ток также увеличивается, а если сопротивление увеличивается, ток уменьшается; Обе ситуации напрямую влияют на эффективность электрических цепей. Чтобы понять закон Ома, важно понимать понятия тока, напряжения и сопротивления: ток — это поток электрического заряда, напряжение — это сила, которая управляет током в одном направлении, а сопротивление — это сопротивление объекта текущий проход через него.Формула для закона Ома E = I x R, где E = напряжение в вольтах, I = ток в амперах и R = сопротивление в омах; Эта формула может быть использована для анализа напряжения, тока и сопротивления электрических цепей.
 Амперы, вольт, ватты и омы измеряют различные аспекты электричества, когда оно проходит через цепь.
Амперы, вольт, ватты и омы измеряют различные аспекты электричества, когда оно проходит через цепь.Источник напряжения
Другая важная концепция в отношении электрических цепей, напряжение источника относится к величине напряжения, которое вырабатывается источником питания и подается на цепь.Другими словами, напряжение источника зависит от того, сколько электроэнергии получит цепь. На напряжение источника влияет величина сопротивления в электрической цепи; это также может повлиять на величину тока, так как на ток обычно влияют как напряжение, так и сопротивление. Однако сопротивление не зависит от напряжения или тока, но может уменьшить количество напряжения и тока в электрических цепях.
 Предохранитель является ключевой частью электрической цепи.
Предохранитель является ключевой частью электрической цепи. Резисторы — это электрические устройства, которые управляют потоком тока через цепь.
,
Резисторы — это электрические устройства, которые управляют потоком тока через цепь.
,
