Связь между напряжением и напряжённостью. Эквипотенциальные поверхности

Урок 48. Физика 10 класс ФГОС

В этом видеоуроке мы дадим определение эквипотенциальным поверхностям и укажем правила их построения. Найдём связь между разностью потенциалов и напряжённостью электростатического поля. А также укажем соответствия между основными величинами электростатического и гравитационного полей.

Конспект урока «Связь между напряжением и напряжённостью. Эквипотенциальные поверхности»

В 1839 году немецкий учёный Карл Фридрих Гаусс предложил изображать электростатические поля с помощью эквипотенциальных поверхностей.

Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков.

Из определения эквипотенциальной поверхности следует, что разность потенциалов между двумя любыми её точками равна нулю.

Давайте с вами вспомним, что разностью потенциалов называют скалярную физическую величину, численно равную отношению работы сил поля по перемещению заряда между данными точками поля к величине этого заряда:

Из этого определения следует, что при переносе заряда вдоль эквипотенциальной поверхности работа полем не совершается (то есть она равна нулю).

Однако мы с вами знаем, что в общем случае работа сил электростатического поля пропорциональна переносимому заряду, модулю напряжённости поля, модулю перемещению и косинусу угла между направлением вектора электрической силы и вектора перемещения:

Но в записанной формуле значения заряда, модуля напряжённости и модуля перемещения всегда отличны от нуля. Поэтому должно равняться нулю значение косинуса угла альфа. А это значит, что угол альфа должен быть равен 90^о

. Отсюда следует, что линии напряжённости электростатического поля всегда перпендикулярны эквипотенциальным поверхностям.

Так, например, эквипотенциальные поверхности однородного электростатического поля представляют собой плоскости, перпендикулярные линиям напряжённости. А эквипотенциальные поверхности точечного заряда — это сферы, в центре которых расположен заряд.

Зная картину эквипотенциальных поверхностей, можно определить напряжённость поля в любой его точке. Например, пусть заряд перемещается с одной эквипотенциальной поверхности на другую, расстояние между которыми по нормали равно

d.

Мы уже знаем, что в этом случае работа, совершаемая электростатическим полем по перемещению заряда прямо пропорциональна величине этого заряда, напряжённости поля и модулю перемещения заряда:

С другой стороны, работа поля по перемещению заряда из одной его точки в другую пропорциональна значению переносимого заряда и разности потенциалов начальной и конечной точек:

Давайте почленно разделим первое уравнение для работы на второе:

А из полученного выражения выразим модуль напряжённости поля:

Полученная нами формула выражает

связь между напряжённостью и разностью потенциалов (или напряжением) однородного электростатического поля. На её основании и вводится единица напряжённости в СИ — вольт на метр (В/м).

1 В/м — это модуль напряжённости такого однородного электростатического поля, в котором напряжение между двумя точками, лежащими на одной силовой линии на расстоянии 1 м, составляет 1 В.

В заключении отметим, что при изучении электростатического поля мы очень часто сравнивали его с гравитационным полем Земли.

В таблице представлены соответствия между механическими и электрическими величинами этих полей. Обсудите их со своим соседом (или соседкой) по парте.

А теперь, для закрепления материала, решим с вами несколько несложных задач. Задача 1. Напряжённость однородного электростатического поля, образованного двумя эквипотенциальными поверхностями, равна 10 кВ/м. Определите расстояние между этими поверхностями, если потенциал одной из них равен 200 В, а второй — – 150 В.

Задача 2. Между двумя разноимённо заряженными параллельными пластинами, находящимися на расстоянии 1 см друг от друга, покоится отрицательно заряженная капелька масла, плотность которого 900 кг/м

3. Определите модуль заряда капельки, если её радиус равен 8 нм, а напряжение между пластинами составляет 650 В.

Предыдущий урок 47 Потенциал электростатического поля. Разность потенциалов

Следующий урок 49 Электроёмкость. Конденсаторы

Получите полный комплект видеоуроков, тестов и презентаций Физика 10 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Связь между напряженностью и напряжением.

Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности

Сначала повторим электростатику. Заряженные тела притягивают или отталкивают друг друга. При перемещении заряженных тел действующие на них силы совершают работу. Из механики известно, что система, способная совершить работу благодаря взаимодействию тел друг с другом, обладает потенциальной энергией. Значит, система заряженных тел обладает потенциальной энергией, называемой  

электростатической  или  электрической

–

+

С точки зрения теории близкодействия на заряд непосредственно действует электрическое поле, созданное другим зарядом.

При перемещении заряда действующая на него со стороны поля сила совершает работу.

Работа при перемещении заряда в однородном электростатическом поле

Однородное поле создают большие металлические пластины, имеющие заряды противоположного знака и поле при перемещении заряда совершает работу А=F s, у нас F=qE, a s=∆d

Это поле действует на заряд q с постоянной силой

подобно тому, как Земля действует с постоянной

силой

на камень вблизи её поверхности.

Потенциальная энергия

Поскольку работа электростатической силы не зависит от формы траектории точки её приложения, сила является консервативной, и её работа равна изменению потенциальной энергии, взятому с противоположным знаком т.е

W p1= qEd 1 W p1 =qEd 2 A= — (qEd 2 — qEd 1)

Потенциальная энергия

Потенциальная энергия заряда меняется и в однородном электростатическом поле равна: Wp 1  = qEd 1 это потенциальная энергия в точке 1,  а Wp 2  = qEd 2 в точке 2 где d 1 — это положение заряда в точке 1, а d 2 – это следующее положение заряда, при движении в электрическом поле.

Работа электрического поля по перемещению заряда не зависит от траектории.

На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю:

A= -ΔW п  = -(W п1  — W п1 ) = 0.

Поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю, называют  потенциальным .

Потенциалом точки электростатического поля  

называют отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.

Потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:

φ=W p /q=qEr/q=Еr=kq/r²·r=q/4πr

Потенциал φ — скаляр, это  энергетическая характеристика поля ; он определяет потенциальную энергию заряда q в данной точке поля. Тогда φ=W p /q=qEd/q=Ed

Потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:

Разность потенциалов

Разность потенциалов называют также  напряжением . φ 1 -φ 2 =U

Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении положительного заряда из начальной точки в конечную к этому заряду.

Единица разности потенциалов

Разность потенциалов или напряжение между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Из формулы U=A/q видно,

1 В = 1 Дж/1 Кл.

Мы знаем, что A= -(W p2 -W p1 )= = — (qEd 2 -qEd 1 ) = qEd 1 -qEd 2 = = q( Ed 1 -Ed 2 ) = q( φ 1 — φ 2 ) = qU A = q U

Из формул работы поля по перемещению заряда

A=qE∆d и A=qU получаем U=E ∆d или

В этой формуле U — разность потенциалов между точками 1 и 2, лежащими на одной силовой линии поля

Формула показывает: чем меньше меняется потенциал на расстоянии Δd, тем меньше напряжённость электростатического поля . Если потенциал не меняется то напряженность поля равна нулю.

  Напряжённость электрического поля направлена в сторону убывания потенциала.

0, т.е. линии напряженности направлены в сторону убывания потенциала. «

При перемещении положительного заряда в направлении напряженности Е электростатического поля, поле совершает положительную работу, а это значит, что (φ1-φ2)0, т.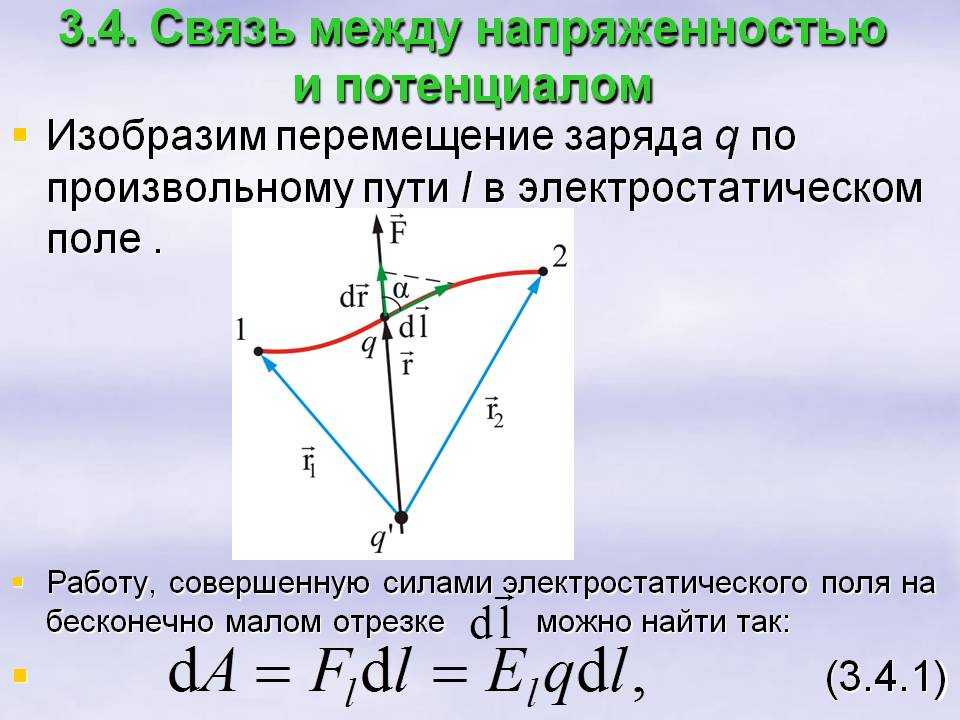 е. линии напряженности направлены в сторону убывания потенциала.

Единица напряжённости электрического поля

Напряжённость электрического поля численно равна единице, если разность потенциалов между двумя точками, лежащими на одной силовой линии, на расстоянии 1 м в однородном поле равна 1 В, и единица измерения напряженности электростатического поля – Вольт на метр — В/м.

Это из формулы Е=U/d

Единица измерения напряженности электростатического поля

Первое определение напряженности поля дает нам формула Е=F/q, мы узнали, что единица измерения напряженности – Н/Кл, а из формулы U=E∆d то, что E=U/∆d — В/м видно, что одна и та же величина измеряется и Н/Кл и В/м величину, и вот почему:

1 В/м = 1 Дж/Кл · 1 1/м = 1 Н · м / Кл · 1 1/м =

= 1 Н/Кл

1 В = 1 Дж / 1 м 1 Дж = 1 Н · м, мы показали ,что

1 В/м = 1 Н/Кл

Эквипотенциальные

поверхности

Запомни!   Поверхности равного потенциала называют  эквипотенциальными .

Важно!   Эквипотенциальной  является поверхность любого проводника в электростатическом поле. Ведь силовые линии перпендикулярны поверхности проводника. Причём не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряжённость поля внутри проводника равна нулю, значит, равна нулю и разность потенциалов между любыми точками проводника.

Эквипотенциальные поверхности однородного поля представляют собой плоскости

Эквипотенциальные поверхности поля точечного заряда представляют собой концентрические сферы

Домашнее задание

Параграф 100,

упр. 17 № 6,7,8

26.2: Напряжение и деформация при растяжении и сжатии

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

28027

• Питер Дурмашкин
• Массачусетский технологический институт через MIT OpenCourseWare

Рассмотрим стержень с площадью поперечного сечения A и длиной \(l_{0}\). Две силы одинаковой величины \(F_{\perp}\) приложены перпендикулярно к двум концам сечения, растягивая стержень на определенную длину \(l\) (рис. \(\PageIndex{1}\)), где балка растянута на положительную величину \(\delta l=l-l_{0}\).

Рисунок \(\PageIndex{1}\): Растягивающее напряжение на стержне

Отношение приложенной перпендикулярной силы к площади поперечного сечения называется растягивающим напряжением ,

\begin{equation}\sigma_{T}=\frac{F_{\perp}}{A}\end{equation}

Отношение величины растяжения секции к первоначальной длине называется деформацией растяжения ,

\begin{equation}\varepsilon_{T}=\frac{\delta l}{l_{0}}\end{equation}

Экспериментально при достаточно малых напряжениях для многих материалов напряжение и деформация линейно пропорциональны,

\[ \frac{F_{\perp}}{A}=Y \frac{\delta l}{l_{0}} \quad(\text {Закон Гука}) \label{26.2.3} \] 9{-2}\), материал перестает быть эластичным.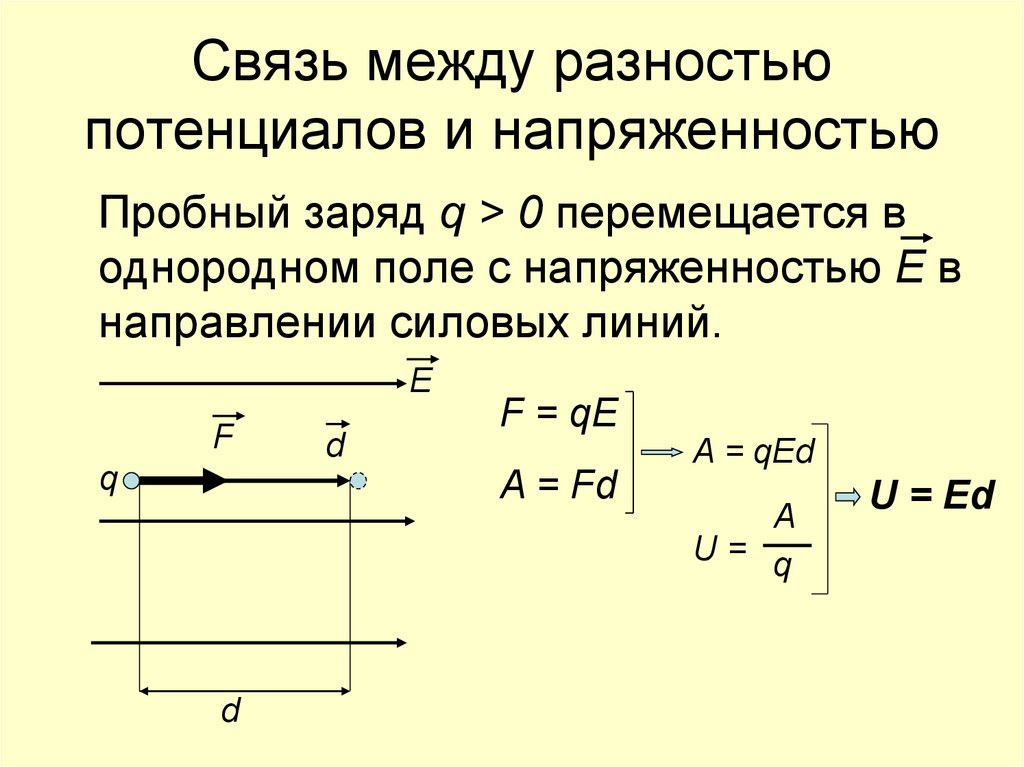 В определенный момент для каждой кости зависимость между напряжением и деформацией останавливается, представляя собой точку перелома.

Таблица 26.1: Модуль Юнга для различных материалов

Рисунок \(\PageIndex{2}\): Зависимость напряжения от деформации для различных костей человека (рисунок из H. Yamada, Strength of Biological Materials)

Когда материал сжимается, силы на концах направлены друг к другу, создавая сжимающее напряжение, приводящее к деформации сжатия (рис. \(\PageIndex{2}\)). Для сжимающих деформаций, если мы определим \(\delta l=l_{0}-l>0\), то уравнение \ref{26.2.3} справедливо для сжимающих напряжений при условии, что сжимающие напряжения не слишком велики. Для многих материалов модуль Юнга одинаков при растяжении и сжатии материала. Есть несколько важных исключений. Бетон и камень могут подвергаться сжимающим напряжениям, но разрушаются при одинаковом растягивающем напряжении. При строительстве из этих материалов важно спроектировать конструкцию таким образом, чтобы камень или бетон никогда не подвергались растягивающим напряжениям. Арки используются как архитектурный конструктивный элемент прежде всего по этой причине.

Рисунок \(\PageIndex{3}\): Compression Stress

---

Эта страница под названием 26.2: Stress and Strain in Tension and Compression распространяется по незаявленной лицензии, ее автором, ремиксом и/или куратором является Питер Доурмашкин (MIT OpenCourseWare ) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Петр Доурмашкин

   Версия лицензии

   4,0

   Программа OER или Publisher

   MIT OpenCourseWare

   Показать оглавление

   нет

2. Теги

   1. Закон Гука
   2. источник@https://ocw. mit.edu/courses/8-01sc-classical-mechanics-fall-2016/
   3. деформация растяжения
   4. растягивающее напряжение
   5. Модуль Юнга

Механика материалов: деформация » Механика гибких конструкций

---

исследование

человек

курсы

блог

---

Штамм

До сих пор мы сосредоточились на напряжении в элементах конструкции. Когда вы прикладываете нагрузку к объекту, он деформируется . Подумайте о резиновой ленте: вы тянете за нее, и она становится длиннее — она растягивается . Деформация — это мера того, насколько сильно растянулся объект, а деформация — это отношение между деформацией и исходной длиной. Думайте о напряжении как  процентное удлинение – насколько больше (или меньше) становится объект при его загрузке.

Как и при напряжении, существует два типа деформаций, которым может подвергаться конструкция: 1. Нормальная деформация и 2. Деформация сдвига . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она создает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.

Рассмотрим стержень, находящийся под одноосным растяжением. Стержень под действием этого напряжения удлиняется на новую длину, и нормальная деформация представляет собой отношение этой небольшой деформации к исходной длине стержня.

Деформация — это безразмерная мера того, насколько объект становится больше или меньше от приложенной нагрузки. Нормальная деформация  происходит, когда удлинение объекта происходит в ответ на нормальное напряжение (т. е. перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует растяжению деформации, а отрицательное сжатию . Деформация сдвига возникает, когда деформация объекта является ответом на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой гамма .

 

Механическое поведение материалов

Очевидно, что стресс и напряжение связаны. Напряжение и деформация связаны конститутивным законом , и мы можем определить их взаимосвязь экспериментально, измерив, какое усилие требуется для растяжения материала. Это измерение может быть выполнено с помощью испытание на растяжение.   В простейшем случае, чем больше вы тянете за объект, тем больше он деформируется, и при малых значениях деформации эта зависимость является линейной. Эта линейная упругая зависимость между напряжением и деформацией известна как закон Гука . Если построить график зависимости напряжения от деформации, то для малых деформаций этот график будет линейным, а наклон линии будет свойством материала, известным как модуль упругости Юнга . Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали. Для большинства технических материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые линейно-упругие (т. е. они следуют закону Гука) и изотропные  (они ведут себя одинаково независимо от того, в каком направлении вы их тянете).

Из закона Гука и наших определений напряжения и деформации мы можем легко получить простое соотношение для деформации материала.

Интуитивно этот экзамен имеет смысл: приложите больше нагрузки, получите большую деформацию; приложите ту же нагрузку к более жесткому или толстому материалу, получите меньшую деформацию. Если конструкция меняет форму или материал или по-разному нагружена в разных точках, мы можем разделить эти множественные нагрузки, используя принцип 9.0034 суперпозиция .

Обобщенный закон Гука

На прошлом уроке мы начали изучать связь между стрессом и напряжением – с помощью закона Гука. Но до этого момента мы рассматривали только очень упрощенную версию закона Гука: мы говорили только о напряжении или напряжении в одном направлении. В этом уроке мы рассмотрим обобщенный закон Гука для однородных, изотропных и упругих материалов, на которые действуют силы более чем по одной оси.

Прежде всего, даже простое вытягивание (или толкание) большинства материалов в одном направлении на самом деле вызывает деформацию во всех трех ортогональных направлениях . Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что вытягивание объекта в осевом направлении вызывает его сжатие в поперечном направлении в поперечном направлении:

Таким образом, потянув за него в направлении x , он сожмется в y  и  z направления. Это свойство материала известно как коэффициент Пуассона и обозначается греческой буквой nu и определяется как:

Или, более математически, используя осевую нагрузку, показанную на изображении выше, мы можем записать это как уравнение:

Поскольку коэффициент Пуассона представляет собой отношение двух деформаций, а деформация безразмерна, коэффициент Пуассона также безразмерен. Коэффициент Пуассона является материальным свойством . Коэффициент Пуассона может варьироваться от -1 до 0,5. Для большинства инженерных материалов, например стали или алюминия, коэффициент Пуассона составляет около 0,3, а для каучуков коэффициент Пуассона составляет около 0,5, которые называются «несжимаемыми». Несжимаемость просто означает, что на любую величину, которую вы сжимаете в одном направлении, она расширится на такую ​​же величину в других направлениях — следовательно, ее объем не изменится.

В последнее десятилетие было проведено очень интересное исследование по созданию структурированных материалов , которые используют геометрию и упругую нестабильность (тема, которую мы кратко рассмотрим в следующей лекции) для создания ауксетических материалов — материалов с отрицательным коэффициентом Пуассона. Физически это означает, что когда вы тянете материал в одном направлении, он расширяется во всех направлениях (и наоборот):

Этот принцип можно применить и в 3D для создания расширяемых/складных оболочек:

Благодаря коэффициенту Пуассона у нас теперь есть уравнение, связывающее деформацию в направлении y или z с деформацией в направлении z. Мы можем, в свою очередь, связать это обратно со стрессом с помощью закона Гука. Это важное замечание: натяжение объекта в одном направлении вызывает напряжение только в этом направлении , а вызывает напряжение во всех трех направлениях . Итак, сигма _y = сигма _z = 0. Выпишем деформации в y и z относительно напряжения в направлении x .

Помните, до этого момента мы рассматривали только одноосную деформацию . В действительности конструкции могут быть одновременно нагружены в нескольких направлениях, вызывая напряжение в этих направлениях. Полезный способ понять это — представить очень крошечный «кубик» материала внутри объекта. Этот куб может иметь напряжений , которые являются нормальными к каждой поверхности , например:

Таким образом, приложение нагрузки в направлении x вызывает нормальное напряжение в этом направлении, и то же самое верно для нормальных напряжений в направлениях y и z . И, как мы теперь знаем, напряжение в одном направлении вызывает напряжение во всех трех направлениях . Итак, теперь мы включим эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как:

Эти уравнения выглядят сложнее, чем они есть на самом деле: деформация в каждом направлении (или каждый компонент деформации) зависит от нормального напряжения в этом направлении, а коэффициент Пуассона умножается на деформацию в двух других направлениях. Теперь у нас есть уравнения того, как объект изменит форму в трех ортогональных направлениях. Что ж, если объект меняет форму во всех трех направлениях, значит, он изменит свои том . Простую меру этого изменения объема можно найти, сложив три нормальных компонента деформации:

Теперь, когда у нас есть уравнение для изменения объема, или расширение , в терминах нормальных деформаций, мы можем переписать его в терминах нормальных напряжений.

Очень распространенный тип стресса, который вызывает дилатацию, известен как гидростатический стресс. Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:

Итак, в случае гидростатического давления мы можем сократить наше окончательное уравнение для расширения до следующего:

Это окончательное соотношение важно, потому что оно определяет, как объем материала изменяется под действием гидростатического давления. Предварительный коэффициент для p можно переписать как объемный модуль материала , K .

Наконец, вернемся к идее «несжимаемых» материалов. Что происходит с K — мерой того, как материал изменяет объем при заданном давлении, — если коэффициент Пуассона для материала равен 0,5?

 

Закон Гука при сдвиге

В предыдущем разделе мы установили связь между нормальным напряжением и нормальной деформацией. Теперь нам нужно поговорить о сдвиге. Вернемся к этому воображаемому кубу материала. В дополнение к внешним силам, вызывающим напряжения, перпендикулярные каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба.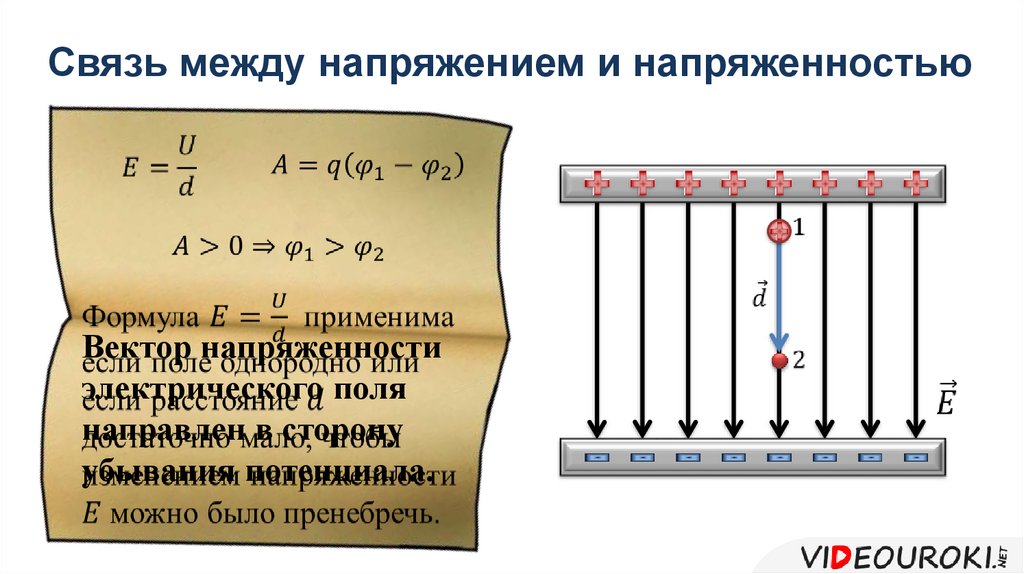 А, как известно, параллельные поперечному сечению напряжения равны касательных напряжений

Теперь этот куб материала выглядит намного сложнее, но на самом деле это не так уж и плохо. На каждой поверхности есть два напряжения сдвига, и нижние индексы говорят вам, в каком направлении они указывают и какой поверхности они параллельны. Например, возьмем правую грань куба. Напряжения, перпендикулярные этой грани, являются нормальными напряжениями в направлении x . Есть два напряжения, параллельных этой поверхности, одно указывает в направлении y (обозначается тау _xy ) и одно указывает в направлении z (обозначается тау _хз ). Чтобы куб находился в равновесии, tau _xy = tau _yx (иначе куб вращался бы). Таким образом, теперь имеется шести напряжений (сигма _x , сигма, сигмаз, тау _xy, тау _yz, тау _xz ), которые характеризуют напряженное состояние в однородном, изотропном, упругом материале.

Итак, как эти напряжения сдвига связаны с деформациями сдвига? Закон Гука при сдвиге очень похож на уравнение, которое мы видели для нормального напряжения и деформации:

В этом уравнении пропорция между напряжением сдвига и деформацией сдвига известна как модуль сдвига материала. Это уравнение в его общей форме, но мы можем переписать его более явно в терминах компонентов x, y и z . Это даст нам обобщенный закон Гука для однородных, изотропных, упругих материалов.

В нашем обобщенном законе Гука у нас есть шесть компонентов напряжения и деформации и три свойства материала. Возникает естественный вопрос: как эти три свойства материала соотносятся друг с другом? Это соотношение задается следующим уравнением:

Сводка

В этой лекции мы ввели понятие напряжения. Деформация – это деформация материала от напряжения. Это просто отношение изменения длины к первоначальной длине. Деформации, прикладываемые перпендикулярно поперечному сечению, представляют собой нормальных деформаций , а деформации, прикладываемые параллельно поперечному сечению, представляют собой деформации сдвига . Для линейных эластичных материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как материальная модуль упругости . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под действием внешней нагрузки.

Кроме того, в этом разделе мы узнали о многоосевой нагрузке . В частности, мы узнали, что напряжение в одном направлении вызывает деформацию в трех направлениях . Это происходит из-за свойства материала, известного как коэффициент Пуассона  – отношение между поперечной и осевой деформациями. Деформации, происходящие в трех ортогональных направлениях, могут дать нам меру прочности материала. 0034 расширение  в ответ на многоосевую нагрузку. В частности, материал обычно может изменять объем в ответ на изменения внешнего давления или гидростатического напряжения . Это привело к определению устойчивости материалов к изменению объема под действием гидростатического напряжения – модуль объемного сжатия . Исследуя воображаемый кубический элемент в произвольном материале, мы смогли представить напряжения, возникающие перпендикулярно и параллельно каждой грани куба. Это дало нам шести напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы соотнесли друг с другом с помощью обобщенного закона Гука для однородных , изотропных и эластичных материалов. Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости Юнга , модулем сдвига и коэффициентом Пуассона .