Сумма, разность векторов, произведение вектора на число. Свойства этих операций.
Линейные операции над векторами.
Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.
b
a+b
a Замечание. Такое правило сложения векторов называют правилом треугольника.
Свойство 1. a + b = b + a.
Свойство 2. (a+b)+c=a+(b+c).
Свойство 3.
Для
любого вектора а существует нулевой вектор О такой, что а+О=а.
Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.
a a—b
b
Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением
Свойство 1. k(a + b) = ka + kb.
Свойство
2. (k
+ m)a = ka +
ma.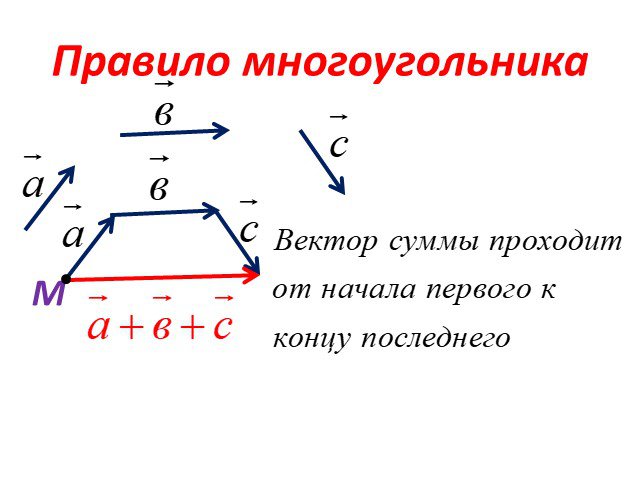
Свойство 3. k(ma) = (km)a.
Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.
Угол между векторами.
Угол между векторами
Вычисление ортогональной проекции.
Найдем ортогональную проекцию х на в предположении, что в задан некоторый ортогональный базис h1,…,hk. Дополним этот базис до ортогонального базиса в пространстве ε, присоединив к нему произвольный ортогональный базис hk+1,…,hn из . Так как сумма и прямая, искомое разложение вектора х единственно, и мы, группируя слагаемые в формуле:
получаем: .
Если k = 1, проекция имеет вид х1 = ((х, h)/|h|2)h, и мы видим, что правая часть формулы – сумма проекций на ортогональные одномерные пространства, натянутые на h1,…,hk. Так же истолковывается формула , а значит, равенство Парсеваля является обобщением теоремы Пифагора.
Из (х1, х2) = 0 следует .
Длина |х2| ортогональной проекции х на обладает следующим свойством минимальности, обобщающую теорему о длине перпендикуляра и наклонной из элементарной геометрии.
Предположение: Пусть х1 – ортогональная проекция х на . Тогда для любого вектора , отличного от х1, выполнено
.
Доказательство. Обозначив х1 – у через z, имеем: .
Но (z, x2) = 0, так как , и, следовательно,
Отсюда
непосредственно вытекает доказываемое
утверждение.
Ортогональная проекция суммы векторов и произведения вектора на число.
Линейная комбинация векторов, линейно независимые вектора. Условия линейной зависимости векторов.
Линейной комбинацией векторов а1, а
Векторы а1, а2,…,аn называются линейно зависимыми, если существует такая линейная комбинация k1a1 + k2a2 +…+ knan = 0. (2),
при
ki не равных нулю одновременно, т.
Если же равенство (2) возможно только при всех ki = 0, векторы называются линейно независимыми.
Замечание 1. Если система векторов содержит нулевой вектор , то она линейно зависима.
Замечание 2. Если среди n векторов какие-либо (n-1) линейно зависимы, то и все n векторов линейно зависимы. (Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.)
Замечание 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Замечание 3. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Замечание
4.
Необходимым и достаточным условием
линейной зависимости трех векторов
является их компланарность.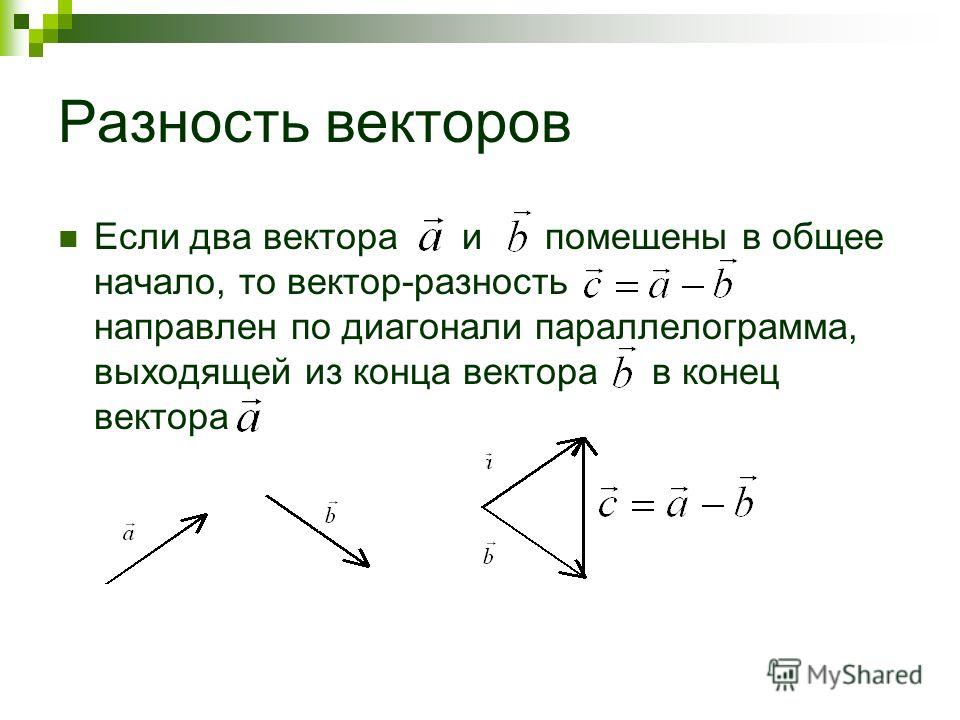
Замечание 5. Любые четыре вектора в трехмерном пространстве линейно зависимы.
Ошибка
Перейти к основному содержанию
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (
Извините, не удалось найти запрашиваемый Вами файл
Подробнее об этой ошибке
Перейти на…
Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы.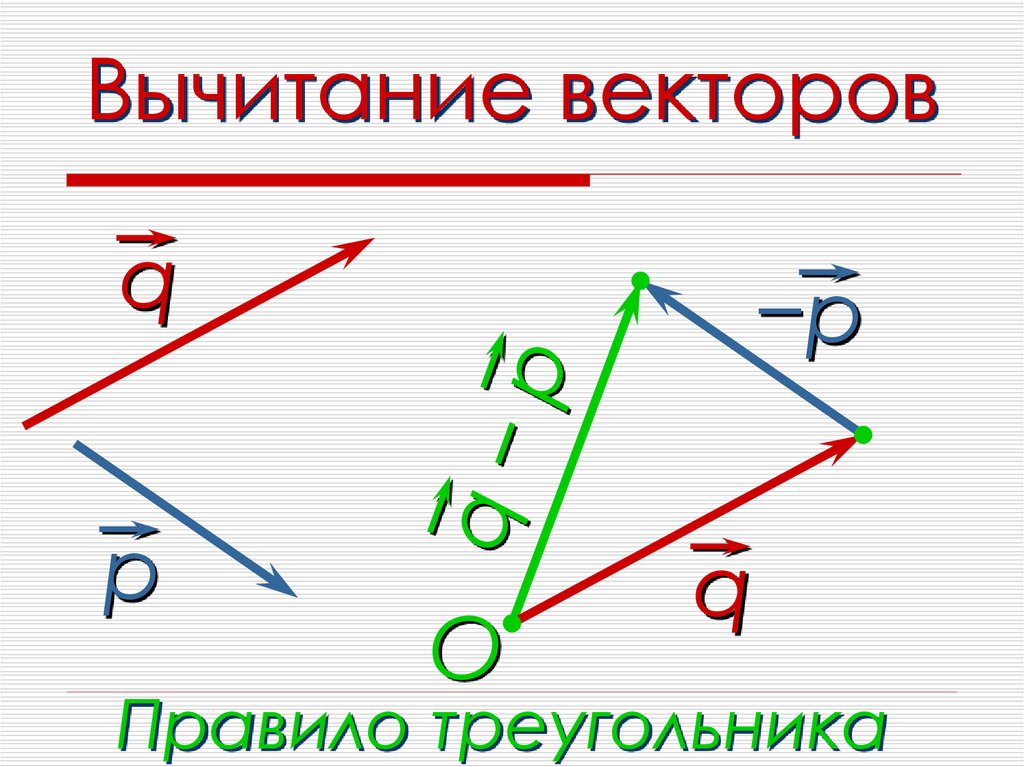

 Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1.
Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.
Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности.
Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности. Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика».
Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.
Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)
Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)Формула результирующего вектора — GeeksforGeeks
В математике мы часто слышали о двух терминах скаляр и вектор. Скаляр — это величина, которая имеет только величину, т.е. скалярная величина описывает расстояние. С другой стороны, Вектор — это величина, которая имеет дело как с величиной, так и с направлением. Векторная величина имеет как величину, так и направление.
Скаляр — это величина, которая имеет только величину, т.е. скалярная величина описывает расстояние. С другой стороны, Вектор — это величина, которая имеет дело как с величиной, так и с направлением. Векторная величина имеет как величину, так и направление.
Формула результирующего вектора дает результирующее значение двух или более векторов. Результат получается путем вычисления векторов с учетом направления каждого вектора по отношению к другим. Эта формула имеет различные приложения в технике и физике. В зависимости от направления вектора относительно других векторов формула результирующего вектора подразделяется на три типа.
Результирующий вектор 1-я формула
Если векторы имеют одинаковое направление, то результирующая вектора может быть вычислена путем сложения векторов, направленных в одном направлении. Пусть « A» и « B» — векторы с таким же направлением, затем результирующий вектор « R» дается-
R ».
а + б
Результирующий вектор 2-я формула
Если векторы разнонаправлены, то результирующий вектора можно вычислить путем вычитания векторов друг из друга. Пусть « B» — вектор, который находится в противоположном направлении по отношению к вектору « A» , затем полученное вектор « R» дается-
.г = а – б
Результирующий вектор 3-я формула
Если какие-либо векторы наклонены друг к другу под некоторым углом, то по этой формуле можно вычислить равнодействующую этих векторов. Пусть «а» и «b» — два вектора, наклоненные друг к другу под углом θ , тогда результирующий вектор «r» равен: + b 2 + 2abcosθ
Здесь a 2 , b 2 представляет модуль вектора a, b.
Представление результирующего вектора
Примеры задач
Вопрос 1. Найдите результирующий вектор для векторов i+2j+3k и 4i+8j+12k
Решение: i+2j+3k и b=4i+8j+12k
Отношения направлений двух векторов равны. Итак, два вектора направлены в одну сторону.
Формула результирующего вектора для заданных векторов:
r = a + b
= (i+2j+3k) + (4i+8j+12k)
= 5i+10j+15k
Результирующий вектор из заданных векторов равен 5i+10j+15k
92:007 Вопрос Найдите результирующий вектор для векторов i-2j+5k и 2i-4j+10k
Решение:
Даны два вектора: a=i-2j+5k и b=2i-4j+10k
отношения направлений двух векторов находятся в равной пропорции. Итак, два вектора направлены в одну сторону.
Результирующая векторная формула для заданных векторов имеет вид-
r = a + b
= (i-2j+5k) + (2i-4j+10k)
= 3i-6j+15k
Результирующий вектор из данных векторов равен 3i-6j+15k
Вопрос 3. Найдите результирующий вектор для векторов 2i-2j+k и 2i+7j+3k
Найдите результирующий вектор для векторов 2i-2j+k и 2i+7j+3k
Решение:
Даны два вектора a=2i-2j+k и b=2i +7j+3k
Отношения направлений двух векторов не равны. Итак, два вектора направлены в противоположные стороны.
Формула результирующего вектора для заданных векторов: Результирующий вектор из данных векторов равен 0i-9j-2k
Вопрос 4. Найдите результирующий вектор для векторов 9i+2j-3k и i-3j+2k
Решение:
0 Дано два вектора: a=9i+2j-3k и b=i-3j+2kОтношения направлений двух векторов не равны. Итак, два вектора направлены в противоположные стороны.
Формула результирующего вектора для заданных векторов:
r = a – b
= (9i+2j-3k) – (i-3j+2k)
= 8i+5j-5k
Результирующий вектор из данных векторов равен 8i+5j-5k
Вопрос 5: Найдите равнодействующую векторов 2i+2j+2k и i+2j+3k, наклоненных друг к другу под углом 30°.
Решение:
Даны два вектора: a=2i+2j+2k и b=i+2j+3k
92}= \ sqrt {1 + 4 + 9}
= √14
B 2 = √14
R = A 2 + B 2 + 2Abcosθ
= 2√3 + + √14 + 2(2√3)(√14)cos30°
= 2√3 + √14 + 4(√3)(√14)(√3/2)
= 29,65
Результирующий вектор из заданных векторов равно 29,65
Вопрос 6: Найдите равнодействующую вектора с величиной 2, 4, наклоненного под углом 45°.
Ответ:
Дано,
Величина вектора a (a 2 )=2
Величина вектора b (b 2 )=4
θ = 45°
Таким образом, результирующий вектор представляет собой формулу для данного вектора определяется как-
r = a 2 + b 2 + 2abcosθ
= 2+4+2(2)(4)cos45°
= 6+16×(1/√2)
= 17.31
Результирующий вектор из заданных векторов: 17.
31
Учебное пособие по сложению векторов
Учебное пособие по сложению векторов Скалярные количества имеют
только величина. (Примерами являются температура и объем).
В этом разделе мы добавим те же векторы математически . Для этого мы сначала должны разложить каждый вектор на его горизонталь и вертикальные компоненты. Y = Вертикальная составляющая = Величина * Sin (θ) (Примечание: на этой диаграмме угол представлен греческим
буква θ
или «тета». В математике и естественных науках углы обычно обозначаются как таковые). Y = 3 * Sin(45°) В этом случае нет горизонтальной составляющей . X = 6 * Cos(90°) Y = 6 * Sin(90°) Y = 5 * Sin(150°) Суммируя вертикальные компоненты (значения Y): Определяем звездную величину результирующий вектор по теореме Пифагора: ArcTangent (результирующего вектора) = Арктангенс (результирующего вектора) = -4,8086237976514 На данный момент мы должны быть будьте осторожны при выборе правильного угла для результирующего вектора .  | ||


 а + б
а + б  31
31 сторону схемы ниже). В этом примере с помощью линейки и транспортира мы можем получить
результирующий вектор величиной около 11 и углом 102 °.
сторону схемы ниже). В этом примере с помощью линейки и транспортира мы можем получить
результирующий вектор величиной около 11 и углом 102 °.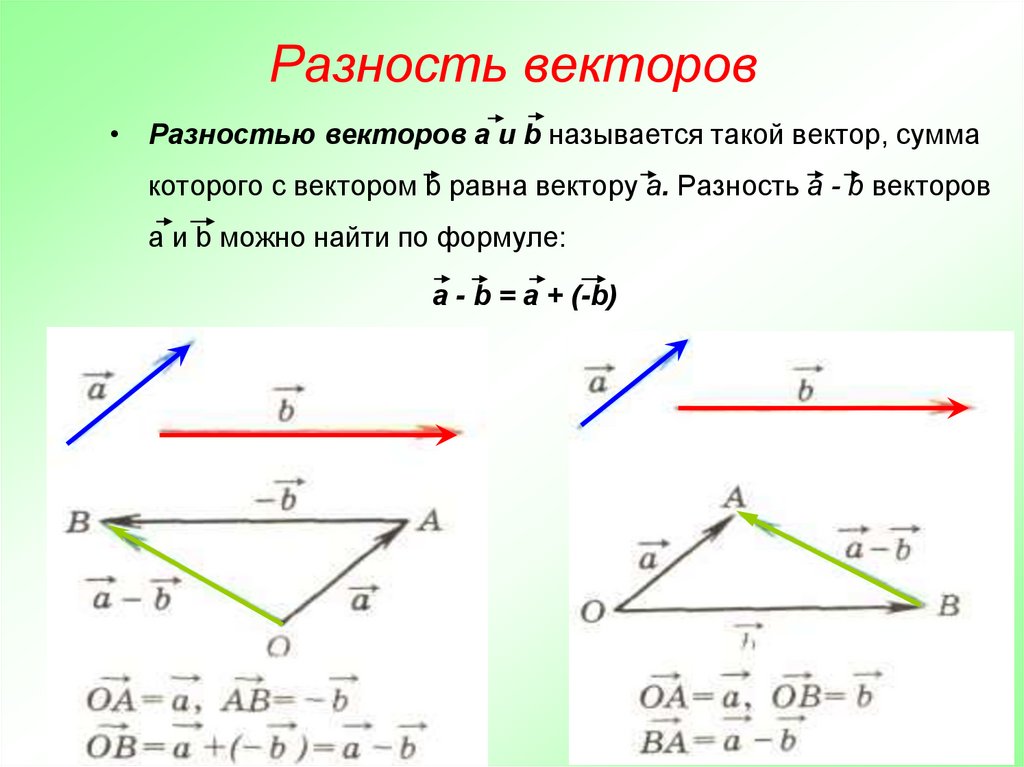
 62132034355964 2
62132034355964 2