формула расчета сопротивления при параллельном соединении резистора
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.

Общий вид
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Типичные подключения
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.

Пример
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.

Смешанная схема
В приведённом выше примере требуется посчитать суммарное значение номиналов цепи, состоящей из трех резисторов.
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
Для элементов из группы 2 значение общего сопротивления находится как сумма R2 и R3:
R (2+3) = R2 + R3.
Для получения окончательного результата приводим схему к виду, получаемому при параллельном соединении двух сопротивлений. После этого суммарное значение для всей схемы в целом вычисляется согласно уже рассмотренной ранее формуле.
В заключение отметим, что для проведения расчётных операций, относящихся к категории сложных соединений, можно воспользоваться теми же методиками. В их основу заложены всё те же закон Ома и правила Кирхгофа, известные ещё со школьной скамьи. Главное – это грамотно распорядиться всеми описанными выше формулами.
Видео
Оцените статью:формула и примеры расчета сопротивления, напряжения, тока и мощности
 При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
 Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать.
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
 Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
 В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
 Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * [1 + a * (t — 20)] * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Объединение резистивных радиокомпонентов
 Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
 При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
Как найти сопротивление резистора. Формула сопротивления резистора. Изображение резисторов на схемах
Среди прочих показателей, характеризующих электрическую цепь, проводник, стоит выделить электрическое сопротивление. Оно определяет способность атомов материала препятствовать направленному прохождению электронов. Помощь в определении данной величины может оказать как специализированный прибор – омметр, так и математические расчеты на основании знаний о взаимосвязях между величинами и физическими свойствами материала. Измерение показателя производится в Омах (Ом), обозначением служит символ R.
Закон Ома – математический подход при определении сопротивления
Соотношение, установленное Георгом Омом, определяет взаимосвязь между напряжением, силой тока, сопротивлением, основанную на математическом взаимоотношении понятий. Справедливость линейной взаимосвязи – R = U/I (отношение напряжения к силе тока) – отмечается не во всех случаях.
Единица измерения [R] = B/A = Ом. 1 Ом – сопротивление материала, по которому идет ток в 1 ампер при напряжении в 1 вольт.
Эмпирическая формула расчета сопротивления
Объективные данные о проводимости материала следуют из его физических характеристик, определяющих как его собственно свойства, так и реакции на внешние влияния. Исходя из этого проводимость зависит от:
- Размера.
- Геометрии.
- Температуры.
Атомы проводящего материала сталкиваются с направленными электронами, препятствуя их дальнейшему продвижению. При высокой концентрации последних атомы не способны им противостоять и проводимость оказывается высокой. Большие значения сопротивления характерны для диэлектриков, которые отличаются практически нулевой проводимостью.
Одной из определяющих характеристик каждого проводника является его удельное сопротивление – ρ. Оно определяет зависимость сопротивления от материала проводника и воздействий извне. Это фиксированная (в пределах одного материала) величина, которая представляет данные проводника следующих размеров – длина 1 м (ℓ), площадь сечения 1 кв.м. Поэтому взаимосвязь между данными величинами выражается соотношением: R = ρ* ℓ/S:
- Проводимость материала падает по мере увеличения его длины.
- Увеличение площади сечения проводника влечет за собой снижение его сопротивления. Такая закономерность обусловлена уменьшением плотности электронов, а, следовательно, и контакт частиц материала с ними становится более редким.
- Рост температуры материала стимулирует рост сопротивления, в то время как падение температуры влечет за собой его снижение.
Расчет площади сечения целесообразно производить согласно формуле S = πd 2 / 4. В определении длины поможет рулетка.
Взаимосвязь c мощностью (P)
Исходя из формулы закона Ома, U = I*R и P = I*U. Следовательно, P = I 2 *R и P = U 2 /R.
Зная величину силы тока и мощность, сопротивление можно определить как: R = P/I 2 .
Зная величину напряжения и мощности, сопротивление легко вычислить по формуле: R = U 2 /P. 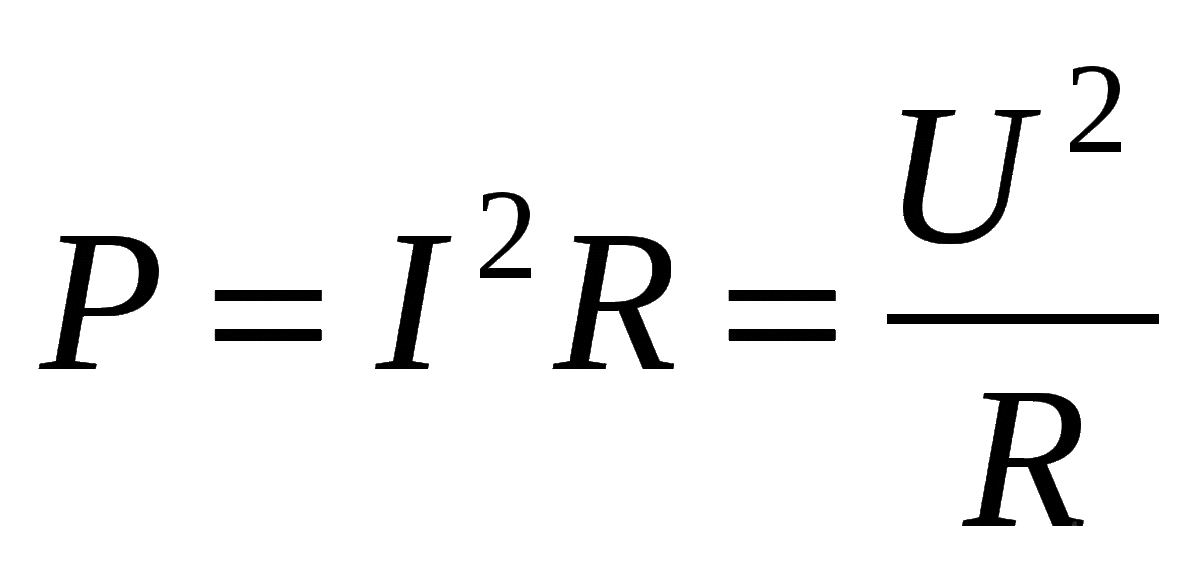
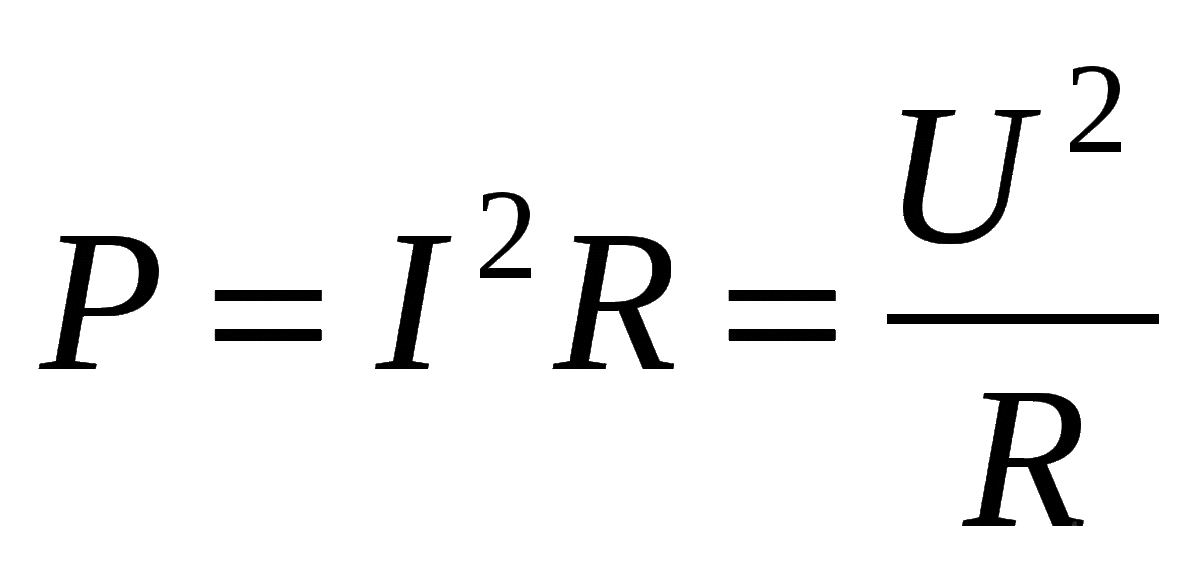
Сопротивление материала и величины других сопутствующих характеристик могут быть получены с применением специальных измерительных приборов или на основании установленных математических закономерностей.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R экв, и вся схема представляется в виде схемы на рис. 1.3, где R=R экв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
|
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U 1 + U 2 + U 3 или IR экв = IR 1 + IR 2 + IR 3 ,
откуда следует
R экв = R 1 + R 2 + R 3 .
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
и по вышеприведенным формулам рассчитывают падение напряжений U 1 , U 2 , U 3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
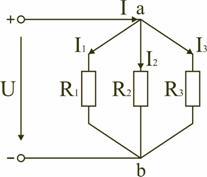
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I
= I 1
+ I 2
+ I 3 ,
т.е. 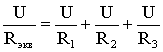 ,
,
откуда следует, что
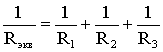 .
.
В том случае, когда параллельно включены два сопротивления R 1 и R 2 , они заменяются одним эквивалентным сопротивлением
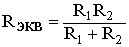 .
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
g экв = g 1 + g 2 + g 3 .
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление R экв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IR экв = I 1 R 1 = I 2 R 2 = I 3 R 3 .
Отсюда следует, что
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
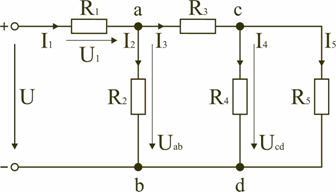
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R. Сопротивления R 4 и R 5 включены параллельно, тогда сопротивление участка цепи cd равно:
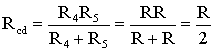 .
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
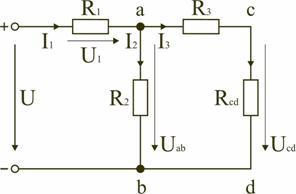
На схеме (рис. 1.8) сопротивление R 3 и R cd соединены последовательно, и тогда сопротивление участка цепи ad равно:
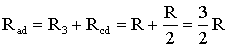 .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис
Формула электрического сопротивления от А до Я
В моей практике много случаев, когда электрик тратит лишнее время на правильный подбор деталей при ремонте оборудования. А решить эту проблему довольно просто: достаточно представлять принцип его работы.
Формула электрического сопротивления, выраженная разными способами для цепей постоянного или переменного тока, позволяет правильно выполнить расчет под исходные данные действующей схемы.
При этом соотношение проходящей через нее мощности, создающей нагрев, должно соответствовать условиям теплоотвода. Выполняя эти требования, вы будете работать быстрее, повысите свой авторитет в глазах окружающих.
Для начинающих электриков я подготовил небольшой теоретический материал про физические процессы, происходящие с электричеством.
Вы же можете сразу перейти к вычислениям, щелкнув по второму подзаголовку из содержания по формулам или третьему через онлайн калькулятор удельного сопротивления.
Содержание статьи
Что надо знать про электрические процессы
Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.
Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.
Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.
Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.
В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.
Приведу для примера картинку из предыдущей моей статьи.
Ее, как и верхнюю, можно представить таким обобщенным видом.
На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.
Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.
Как работает резистор
Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.
Такие столкновения повышают температуру среды, уменьшают силу тока.
За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.
Электрическое сопротивление металла зависит от его структуры и геометрических размеров.
Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.
Какие существуют виды сопротивлений
В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.
Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.
При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.
Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.
Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.
2 Шутки электриков о токах через конденсатор и дроссель
Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.
Шутка №1 о емкости
В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.
Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно. К их серединам подключены провода, нарисованные перпендикулярными линиями.
Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.
Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.
Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.
Шутка №2 о дросселе
Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.
Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.
Что же это за зверь: сверхпроводимость
Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах. Выглядит этот процесс следующим образом.
Со сверхпроводниками домашний мастер не работает. Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление.
При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.
Как просто вычислить сопротивление по закону Ома из электрических величин
Шутки и их разъяснения закончились, хотя они приведены для объяснения поведения токов внутри индуктивностей и емкостей. Пора переходить к расчетам.
Его позволяет выполнить одна из формул, приведенных в шпаргалке электрика. Для этого достаточно знать два из трех электрических параметров: ток I, мощность P или напряжение U.
Если же вам лениво вычислять цифры, то можете спокойно использовать онлайн калькулятор закона Ома. Он избавит вас от сложных арифметических действий.
Формула электрического сопротивления по свойствам среды: научный подход
Электротехника давно использует термин: удельное сопротивление. Он учитывает свойства материала токопроводящей среды с ее размерами: длиной и поперечным сечением, через которое протекает электрический ток.
Все данные для него получены в результате многочисленных исследований и сведены в таблицы. Для бытовых вычислений достаточно следующих сведений.
Таблица характеристик металлов, используемых в быту
| Металл провода | Удельное сопротивление (Ом∙мм.кв/м) |
| Медь техническая | 0,017 |
| Алюминий | 0,028 |
| Стальные сплавы | 0,11 |
| Свинец | 0,21 |
| Сплавы нихрома | 1,11 |
На основе этих данных удобно подбирать провода, детали, вычислять их сопротивление R либо определять другие параметры.
Например, нас интересует сопротивление проволоки нихрома диаметром 1 мм, при температуре 20 градусов.
Определяем площадь поперечного сечения через площадь круга.
S = 3.14 x 1 x 1 / 4 = 0,785 мм кв.
Делаем расчет на основе приведенной формулы.
R = 1,1 х 5 / 0,785 = 7 Ом
Простой онлайн калькулятор сопротивления проводов
Его назначение — облегчить работу с формулами и арифметическими действиями. Он позволяет решать одну из двух часто встречающихся задач:
- Определение сопротивления провода.
- Расчет его длины.
Достаточно заполнить исходные данные в соответствующей размерности и нажать кнопку “Рассчитать”.
Формулы расчета электрического сопротивления для переменного тока простыми словами
Переменное напряжение наводится вращением рамки (ротора генератора) в магнитном поле (создается обмоткой или магнитами статора).
Ток потребителя, подключенного к выводам генератора, по-разному ведет себя на резисторе, индуктивности и конденсаторе.
Формула активного сопротивления
Резисторы изготавливают из металлов с повышенными удельными характеристиками для ограничения силы тока без изменения его направления.
Синусоиды токов и напряжений на резисторе совпадают по времени. В векторном выражении они обладают одинаковым направлением.
Активное сопротивление переменному току вычисляется по закону Ома так же, как и при постоянной форме напряжения.
Формула индуктивного сопротивления
В обмотках катушек электромагнитов, дросселей, трансформаторов наводится электродвижущая сила индукции. Она взаимодействует с приложенным переменным напряжением. В результате происходит сдвиг фазы тока относительно направления вращения электромагнитного поля (ротора генератора).
Формула индуктивного сопротивления XL сильно зависит от частоты тока f и индуктивности L.
Ток в такой цепи сдвигается от напряжения и отстает от него на 90 угловых градусов.
Число ∏ в формуле отображает отношение длины окружности к ее диаметру (3,14).
Формула емкостного сопротивления ХС
Конденсатор состоит из двух токопроводящих пластин, отделенных слоем диэлектрика. При появлении на них напряжения они накапливают электрический заряд.
Его энергия постоянно взаимодействует с приложенным переменным напряжением. Поэтому в цепи создается ток, зависящий от частоты электромагнитного сигнала и емкости конденсатора.
Он сдвигается вперед от вектора напряжения по направлению вращения поля.
Формула полного сопротивления
Электротехника, как и сама жизнь, описывает явления, переплетенные между собой, а не в чистом виде.
Электрическая энергия, поступающая к нам в квартиру по проводам и кабелям от трансформаторной подстанции, преодолевает:
- активное сопротивление токоведущих шин;
- емкость кабельных линий;
- индуктивное противодействие обмоток трансформаторов.
Поэтому для расчетов применяют метод полного сопротивления, выражаемый законом прямоугольного треугольника.
Каждая его сторона отображает определенную характеристику сопротивления:
- гипотенуза — суммарную, полную величину Z:
- прилегающий катет — активную составляющую R;
- противолежащий — реактивную X, представленную геометрической суммой емкостного XL и индуктивного сопротивления XC.
Точно так же каждая сторона этого треугольника создает определенную величину затраченной мощности электрической энергии.
На активном участке создается мощность, совершающая полезную для нас работу, обеспечивающую вращение роторов электродвигателей, свечение осветительных приборов, нагрев обогревателей и другие нужные действия.
Полная мощность, расходуемая всеми видами потребителей, состоит из полезной активной и потерь, создающих индуктивными и емкостными составляющими. Они снижают эффективность работы электрической системы. Поэтому с ними борются.
Запомнить роль реактивной мощности помогает простая и наглядная картинка, естественно, выраженная в шутливой форме.
Однако стоит понимать, что угол φ, образованный между гипотенузой и прилегающим к нему катетом, характеризует величину реактивной части, создающей бесполезные потери энергии. Ее всегда стремятся снизить.
Что такое вольтамперная характеристика
Металлы в обычном состоянии формируют электрический ток строго по прямолинейной характеристике в зависимости от величины приложенного напряжения.
У других сложных веществ и индуктивностей этот принцип не соблюдается. Зависимость выражается кривыми линиями и называется вольтамперной характеристикой.
ВАХ индуктивностей
Характер протекания тока зависит от величины индуктивности. Если в рабочей обмотке возникает пробой изоляции, приводящий к образованию короткозамкнутого витка, то вольтамперная характеристика резко изменяет свой вид: падает.
За счет уменьшения индуктивного сопротивления при меньшем значении величины приложенного напряжения в обмотке начинают протекать бОльшие токи.
Они свидетельствуют о возникновении неисправности, требующей немедленного устранения. Поэтому снятие ВАХ является обязательным элементом проверки исправности обмоток всех видов трансформаторов или дросселей.
Она выполняется различными методами с определением состояния точки перегиба характеристики.
ВАХ полупроводникового прибора
На правой картинке показан один из примеров работы нелинейного элемента — диода.
В первой четверти квадранта проходит прямой участок характеристики, а у третьей — обратный.
На прямом участке повышение напряжения выше точки перегиба ведет к открытию переходного полупроводникового слоя и пропусканию через него тока практически по прямой линейной характеристике.
Такие же действия на обратном участке ведут к потере диодом своих свойств.
Закон Шварцнегера или как надо обеспечивать надежную работу резистора под нагрузкой
Знаменитый на весь мир атлет Арнольд постоянно тренировался по методике нашего советского силача Юрия Власова. Он брал его опыт за основу и даже приезжал в Россию погостить к своему кумиру.
В основе метода постоянных результативных тренировок положен принцип не столько полноценного питания и отдыха, сколько подбор правильных нагрузок, которые должен преодолевать организм.
Все это полностью соответствует законам электротехники, применяется в работе любого электрического сопротивления. Рассмотрим его на примере резистора: так проще для понимания.
Его металл не только пропускает электрический ток, но и нагревается, выделяя тепло. Нагрев увеличивается с повышением тока. При этом температура может снижаться за счет теплоотвода в окружающую среду или увеличиваться в герметичном, не теплопроводящем объеме.
Так работает электропроводка, выполненная одним и тем же кабелем, проложенным открыто по стенам или спрятанным в штробах.
В первом случае от нагревающегося током кабеля тепло отводится в окружающий воздух за счет его естественной циркуляции, а во втором нагрев идет более интенсивно.
Однако повышать температуру жил можно только до определенной величины. За ее рабочим диапазоном вначале происходит разрушение слоя изоляции, а потом — простое перегорание металла, когда проводка сгорает.
На этом примере я попытался показать, что любой резистор обладает запасом тепловой мощности, за который его нельзя переводить.
Для облегчения работы электриков всем видам резисторов введен термин мощности теплового рассеивания. Она указывается в технической документации или прямо на корпусе, измеряется ваттами. Ее же показывают на электрических схемах.
Как выбрать резистор по тепловой нагрузке за 2 шага
Действуют по следующему алгоритму:
- Вначале определяют мощность, которая будет проходить через искомый резистор. Достаточно перемножить величину номинального тока на напряжение, выразить полученное значение в ваттах.
- Под эту величину из всего многообразия элементов подбирают тот, который соответствует по значению сопротивления и обладает мощностью теплового рассеивания не меньшего номинала.
Желательно брать его с небольшим резервом. Он не будет лишним для работы в критических ситуациях электрической схемы, но повлияет на габариты устройства.
Полезные примеры из жизни
Как продлить ресурс лампы накаливания
В пожарном депо Ливермоля (Калифорния) зарегистрирован рекорд рабочего режима осветительной лампы: 117 лет. Она практически непрерывно выполняет свою задачу с 1901 года по настоящее время.
Такой ресурс обеспечен за счет:
- правильного выбора сопротивления, ограничивающего ток через нить накала и создания экономного режима освещения;
- беспрерывной работы, исключающей переходные процессы при включениях/выключениях, сопровождаемые бросками токов;
- надежной конструкции.
Как регулировать токи от 100 ампер в силовой цепи
Этот случай я привожу не для повторения, а с целью расширения кругозора и лучшего уяснения процессов, происходящих в электричестве.
Ни один обычный резистор не способен длительно выдерживать токи такой величины. Он просто сгорит. Однако при наладке промышленных генераторов требуется иметь устройство, справляющееся с подобными мощностями.
Это водяной реостат, состоящий из металлического корпуса — ведра прямоугольной формы, служащего одним из контактов для подключения провода от нагрузки.
Второй контакт составляет металлический нож, подключаемый через изоляторы.
Внутрь ведра наливают воду и засыпают соль: создают электролит, хорошо проводящий большие токи.
Перемещение ножа в электролите меняет сопротивление среды и обеспечивает регулировку высоких токов. Проводимость можно изменять концентрацией соли в растворе.
Напоминаю: подобное устройство нельзя использовать в бытовых цепях: оно не отвечает требованиям безопасности.
Таким образом, под каждый конкретный случай расчета используется своя формула электрического сопротивления, которой следует внимательно пользоваться. Исключить ошибки в расчетах помогает специализированный онлайн калькулятор.
По этой теме рекомендую посмотреть видеоролик Владимира Романова.
Если хотите задать вопрос или дополнить информацию, то воспользуйтесь разделом комментариев.
Расчет сопротивления онлайн по схеме — Moy-Instrument.Ru
Конвертер величин

Калькулятор параллельных сопротивлений

Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.
Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.
Введите величины сопротивлений в поля R1, R2 и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление Req группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.


Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для Req и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:


Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Расчет сопротивления онлайн по схеме
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.
Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Этот круг также, как и треугольник можно назвать магическим.
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:


Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Расчёт сопротивления электрических цепей с использованием законов последовательного и параллельного соединений
Разделы: Физика
Цели:
- Образовательная: систематизировать и закрепить знания учащихся о различных соединениях проводников, сформировать умения применять законы последовательного и параллельного соединений для расчёта электрических цепей, объединить знания, полученные на уроках физики и математики.
- Развивающая: развить мышление учащихся, активизировать познавательную деятельность через решение задач на расчет электрических цепей, развить умение рассчитывать параметры электрических цепей и совершенствовать полученные на уроке навыки.
- Воспитательная: формирование интереса к изучаемому предмету, продолжить формирование коммуникативных умений.
Тип урока: урок проверки и закрепления новых знаний по физике и математике.
Метод проведения урока: практический
Оборудование:
- Громов С.В. Учебник “Физики-9”;
- план урока;
- методика расчета участка электрической цепи постоянного тока;
- карточки-задания.
Сегодня на уроке мы должны применить полученные ранее знания о законах последовательного и параллельного соединений для расчёта участка электрической цепи, а также определить степень усвоения изученного материала с помощью карточек – заданий.
Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:
1) Какие виды соединений бывают и как они изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
4) Какая отличительная особенность параллельного соединения?
Рассмотрим расчёт участка электрической цепи на примере следующих задач:
1. Рассчитайте общее электрическое сопротивление участка цепи?
1) Наиболее удалённые от источника элементы – это резисторы R2 и R3.
2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R2 и R3 подключены параллельно, т.к образуют в соединении два узла, следовательно:
Ом
3) Изображаем получившуюся в результате свёртывания резисторы R2 и R3 электрическую схему:
4) Полученные в результате объединения схему с двумя резисторами группируем во второй участок и рассчитываем их общее сопротивление. Так как резисторы R1 и Rоб.1 соединены последовательно, значит:
Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.
2. Рассчитайте общее электрическое сопротивление участка цепи?
1) Резисторы R1 и R2 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
2) Резисторы R3 и R4 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
3) Полученные в результате объединения схему с двумя резисторами группируем в третий участок и рассчитываем их общее сопротивление. Так как резисторы Rоб.1 и Rоб.2 соединены параллельно, значит:
Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.
3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:
а) Рассчитайте общее электрическое сопротивление участка цепи?
б) Рассчитайте общее электрическое сопротивление участка цепи?
в) Рассчитайте общее электрическое сопротивление участка цепи?
Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.
Онлайн калькулятор для параллельного соединения резисторов
 В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
 Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Видео: Последовательное и параллельное соединение проводников
Параллельное соединение: общая информация
 Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
 В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
- R(общ) – суммарное значение сопротивления;
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
 Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
 Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчёта
 Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
 Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Правильный расчет резистора для светодиода, подбор резистора по цветовой маркировке + онлайн калькулятор
Светоизлучающие диоды, характеризуются рядом эксплуатационных параметров:
- Номинальный (рабочий) ток – Iн;
- падение напряжения при номинальном токе – Uн;
- максимальная рассеиваемая мощность – Pmax;
- максимально допустимое обратное напряжение – Uобр.
Самым важным из перечисленных параметров является рабочий ток.
При протекании через светодиод номинального рабочего тока – номинальный световой поток, рабочее напряжение и номинальная рассеиваемая мощность устанавливаются автоматически. Для того чтобы задать рабочий режим LED, достаточно задать номинальный ток светодиода.
В теории светодиоды нужно подключать к источникам постоянного тока. Однако, на практике, LED подключают к источникам постоянного напряжения: батарейки, трансформаторы с выпрямителями или электронные преобразователи напряжения (драйверы).
Для задания рабочего режима светодиода, применяют простейшее решение – последовательно с LED включают токоограничивающий резистор. Их еще называют гасящими или балластными сопротивлениями.
Рассмотрим, как выполняется расчет сопротивления резистора для светодиода.

Расчет резистора светодиода (по формулам)
При расчете вычисляют две величины:
- Сопротивление (номинал) резистора;
- рассеиваемую им мощность P.
Источники напряжения, питающие LED, имеют разное выходное напряжение. Для того чтобы выполнить подбор резистора для светодиода нужно знать напряжение источника (Uист), рабочее падение напряжения на диоде и его номинальный ток. Формула для расчета выглядит следующим образом:
При вычитании из напряжения источника номинальное падение напряжения на светодиоде – мы получаем падение напряжения на резисторе. Разделив получившееся значение на ток мы, по закону Ома, получаем номинал токоограничивающего резистора. Подставляем напряжение, выраженное в вольтах, ток – в амперах и получаем номинал, выраженный в омах.
Электрическую мощность, рассеиваемую на гасящем сопротивлении, вычисляют по следующей формуле:
P = (Iн) 2 ⋅ R
Исходя из полученного значения, выбирается мощность балластного резистора. Для надежной работы устройства она должна быть выше расчетного значения. Разберем пример расчета.
Пример расчета резистора для светодиода 12 В
Рассчитаем сопротивление для LED, питающегося от источника постоянного напряжения 12В.
Допустим в нашем распоряжении имеется популярный сверхяркий SMD 2835 (2.8мм x 3.5мм) с рабочим током 150мА и падением напряжения 3,2В. SMD 2835 имеет электрическую мощность 0,5 ватта. Подставим исходные значения в формулу.
R = (12 — 3,2) / 0,15 ≈ 60
Получаем, что подойдет гасящий резистор сопротивлением 60 Ом. Ближайшее значение из стандартного ряда Е24 – 62 ома. Таким образом, для выбранного нами светодиода можно применить балласт сопротивлением 62Ом.
Теперь вычислим рассеиваемую мощность на сопротивлении.
P = (0,15) 2 ⋅ 62 ≈ 1,4
На выбранном нами сопротивлении будет рассеиваться почти полтора ватта электрической мощности. Значит, для наших целей можно применить резистор с максимально допустимой рассеиваемой мощностью 2Вт.
Осталось купить резистор с подходящим номиналом. Если же у вас есть старые платы, с которх можно выпаять детали, то по цветовой маркировке можно выполнить подбор резистора. Воспользуйтесь формой ниже.
На заметку! В приведенном выше примере на токоограничительном сопротивлении рассеивается почти в три раза больше энергии, чем на светодиоде. Это означает, что с учетом световой отдачи LED, КПД нашей конструкции меньше 25%.
Чтобы снизить потери энергии лучше применить источник с более низким напряжением. Например, для питания можно применить преобразователь постоянного напряжения AC/AC 12/5 вольт. Даже с учетом КПД преобразователя потери будут значительно меньше.
Параллельное соединение
Довольно часто требуется подключить несколько диодов к одному источнику. Теоретически, для питания нескольких параллельно соединенных LED, можно применить один токоограничивающий резистор. При этом формулы будут иметь следующий вид:
P = (n ⋅ Iн) 2 ⋅ R
Где n – количество параллельно включенных ЛЕДов.
Почему нельзя использовать один резистор для нескольких параллельных диодов
Даже в «китайских» изделиях производители для каждого светодиода устанавливают отдельный токоограничивающий резистор. Дело в том, что в случае общего балласта для нескольких LED многократно возрастает вероятность выхода из строя светоизлучающих диодов.
В случае обрыва одного из полупроводников, его ток перераспределится через оставшиеся LED. Рассеиваемая на них мощность увеличится и они начнут интенсивно нагреваться. Вследствие перегрева следующий диод выйдет из строя и дальше процесс примет лавинообразный характер.
Совет. Если по какой-то причине нужно обойтись одним гасящим сопротивлением, увеличьте его номинал на 20-25%. Это обеспечит большую надежность конструкции.
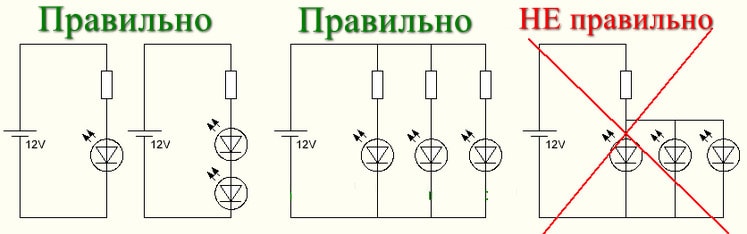 Пример правильного подключения резистора
Пример правильного подключения резистора
Можно ли обойтись без резисторов?
Действительно, в некоторых случаях можно не использовать токоограничивающий резистор. Рассмотренный нами светодиод можно напрямую запитать от двух батареек 1,5В. Так как его рабочее напряжение составляет 3,2В, то протекающий через него ток будет меньше номинального и балласт ему не потребуется. Конечно, при таком питании светодиод не будет выдавать полный световой поток.
Иногда в цепях переменного тока в качестве токоограничивающих элементов вместо резисторов применяют конденсаторы (подробнее про расчет конденсатора). В качестве примера можно привести выключатели с подсветкой, в которых конденсаторы являются «безваттными» сопротивлениями.
Ряды номиналов резисторов: сопротивление номинала Е 24
Номиналы резисторов, конденсаторов и других радиотехнических деталей соответствуют определенным регламентируемым показателям. Диапазон значений определяют e24 ряд, е12 и другие линейки сопротивлений. Чтобы выбрать предпочтительный вариант детали, нужно иметь представление о рядах сопротивлений и том, как определяются характеризующие элемент параметры.

Резисторные детали с маркировкой из цветных полос
Номинальные ряды E6, E12 и E24
Используемые в практике линейки интервалов, в том числе е24 ряд, имеют в названии цифровой код после литеры Е. Он означает количество показателей номиналов в рамках десятичного промежутка. Сама буква Е обозначает соответствие нормативам Electronic Industries Alliance. Несколько различных номинальных серий нужно для того, чтобы охватывать максимально возможное число значений сопротивления, задействованных при изготовлении разного рода электронных компонентов. Стандартизировать данные параметры в табличные блоки стало принято также для того, чтобы добиться унификации кодировки радиодеталей, производящихся в разных странах.
Ряд Е6 включает в себя наименьшее число элементов и имеет наибольшие расстояния между ними. Помимо этого, у этой линии максимальный процент погрешности – 20. Погрешностью называется возможное отклонение значения от номинала в большую или меньшую сторону. Чем больше значение цифры, стоящей вслед за буквой Е в наименовании линейки, тем большее количество элементов она включает и тем выше ее точность.
Число в названии соответствует количеству элементов линейки; самая многочисленная из имеющихся – Е192. Внутри каждый последующий компонент имеет номинал немного более, чем на удвоенную погрешность превышающий таковой у предыдущего. Пользуясь таблицей номиналов резисторов для того или иного ряда, можно определить показатель для конкретной радиодетали. Если сравнить две соседних таблицы, можно увидеть, что систему с меньшим числом элементов можно получить из таковой с большим посредством вычеркивания четных компонентов.
Важно! Линейка Е6 предназначается для использования при работе с резисторами, обладающими переменным сопротивлением. Более точные ряды для таких деталей не применяются и разработаны для изделий с постоянным сопротивлением.
Линейка Е12 включает в два раза большее число элементов, чем предыдущая, и обладает вдвое меньшей погрешностью (10%). Ряд Е24 резисторы и Е48 сохраняют тот же принцип – показатели допустимого отклонения у них равны соответственно 5% и 2,5% в ту и другую стороны. Используются также серии Е96 и Е192, у последней из них отклонение составляет меньше процента. Такие низкие показатели дают возможность отнести детали, нормируемые по двум последним таблицам, в категорию обладающих повышенной точностью.
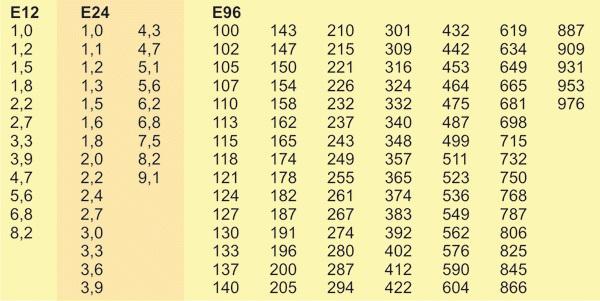
Сравнительная таблица разных серий номиналов
Как образуется
Формирование рядов резисторов производится строго в соответствии с правилами, определяемыми технологией изготовления данных радиодеталей. Поскольку любой изготовленный на производстве резистивный компонент имеет некоторую погрешность своего основного параметра (сопротивления), и значения этих отклонений могут быть разными, простое использование непрерывных рядов становится нерелевантным.
К примеру, у детали с указанным заводом-производителем сопротивлением в 100 Ом и отклонением в 10% реальный показатель может составлять 104 Ом, тогда изготавливать отдельный компонент, обладающий данным номиналом, становится бессмысленно. Следующим в такой линейке может быть использован резистор в 120 Ом, на нижней границе допустимого интервала будет иметься показатель 108 Ом, а на верхней – 132. Дальнейшим элементом можно поставить резистор примерно 150 Ом. Возникает необходимость в системе, в которой учитывались бы как номинал, так и диапазон его возможных изменений.
По подобному принципу может быть сформирован список радиодеталей с выбранной погрешностью. Если она составляет 10%, список полагается делать состоящим из 12 единиц. Если стоит цель добиться более точной категоризации (например, погрешность в 5%), элементы будут более плотно сидящими, без большого разрыва по значениям между соседними, а число их будет вдвое больше. Из этих величин можно формировать табличные сводки. Таблицы для разных серий будут отличаться между собой количеством задействованных символов и разнесенностью номинальных значений.
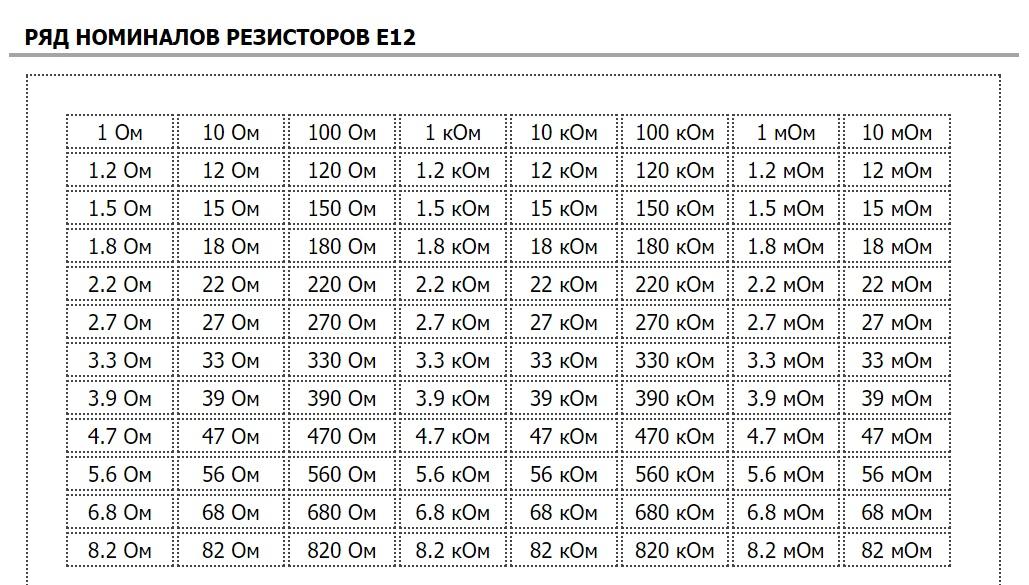
Резисторная серия Е12
Принципы построения рядов
Серию резисторов е24 можно приближенно описать в виде геометрической прогрессии. Входящие в эту линейку компоненты могут поделить интервал [1;10] на равные отрезки, число которых равно наименованию таблицы (24). Серии, включающие меньшее число составляющих, могут быть получены через удаление четных элементов из исходной линейки. Если в прогрессии, описывающей таблицу Е24, будет применяться знаменатель 101/24, то для Е12 его значение будет равно 101/12, а для Е6 – 101/6. Серии, в которых больше 24 чисел, приближаются к прогрессии с почти абсолютной точностью. В знаменателе 101/k число k является утроенной степенью двойки. Помимо этого, линейки могут быть описаны последовательностями десятичных логарифмов. Вычислить номинал резисторного устройства можно, воспользовавшись калькулятором онлайн.
Важно! Подсчитать номинальный показатель для компонента той или иной серии можно, воспользовавшись следующим выражением: V(k)=10k/K=exp((k/K)*ln 10). Здесь К – это номер самой линейки (6, 12, 24 – числа, стоящие вслед за литерой Е), k – порядковый номер номинального значения внутри нее.
Таблицами значений можно пользоваться и следующим образом. Если при расчете необходимых показателей для некоторой цепи выявилось, что необходимо приобрести резистор, к примеру, на 1180 Ом, а доступ имеется только к стандартным деталям (не повышенной точности), можно взять таблицу Е24. В ней есть значения 1,1 и 1,2. Они перемножаются на 10 столько раз, чтобы получились показатели, схожие с необходимыми. В данном случае после троекратного умножения получаются 1100 и 1200. Вторая величина ближе к искомой, соответственно, именно такой компонент целесообразно приобретать.
Номинальные ряды с большим числом элементов
Помимо трех рассмотренных линий номиналов сопротивлений резисторов, существуют значительно более точные: у таблицы Е48 отклонение находится в районе 2% в обе стороны, для Е96 – 1%, у Е192 – около 0,5%. Знаменатели прогрессий у таких серий описываются числом 101/k , где k – цифра, вместе с буквой Е описывающая название линии. Последние две группы принято относить к классификациям, обладающим наивысшей точностью.
Существует и, наоборот, максимально грубая серия – Е3. Ее погрешность составляет целых 50%. Таким образом, у относящихся к ней деталей сопротивление может изменяться до половины своего значения в обе стороны. Здесь тройка умножена на нулевую степень двойки, равную единице. На практике эта линия в настоящее время практически не используется, но при работе со старыми устройствами можно обнаружить радиодетали, соответствующие Е3. Закономерности, справедливые для двух соседних серий элементов, будут распространяться и на Е3, и на Е6.
Особенности стандартного ряда Е24
Свойственное ряду сопротивлений е24 стандартное отклонение составляет 5%. Такая точность считается достаточной для рутинной радиолюбительской деятельности, поэтому данная серия получила широкое распространение.
Важно! Корпуса изделий зачастую снабжаются маркировкой из цветовых полос, позволяющей получить представление об их основных характеристиках. Отдельные фирмы-изготовители пользуются разными системами кодировки, поэтому целесообразно найти таблицу, используемую производителем, и изучить, что обозначают те или иные цвета и их последовательности. Расшифровка маркировки также может быть найдена в прилагаемой к деталям документации или на упаковке. Зная активное сопротивление изделия, можно посчитать его вклад в мощность цепи.

Радиодетали с маркировкой из полосок
Использование рядов упрощает кодировку номинальных показателей резистивных деталей, давая представление и о точности параметра. Из линейки можно получить другую (более или менее точную), если знать законы ее образования. Подобные линии существуют и для индуктивных катушек и конденсаторов.
Видео
Формула расчета реактивного сопротивления проводника: калькулятор расчетов
Реактивное сопротивление относится к числу явлений, наблюдаемых в цепях переменного тока. Тем, кто занимается ремонтом и эксплуатацией таких цепей, будет полезно знать, как определяется эта величина, и каким образом она влияет на процессы, происходящие в электросети.

Соленоид – устройство, обладающее индуктивностью
Понятие реактивного сопротивления
Данная разновидность репрезентирует взаимоотношение электротока и напряжения на определенных типах подключенных в сеть нагрузок (дросселях, конденсаторных компонентах), не сопряженное с объемами электроэнергии, используемыми потребителем. Измерительной единицей, как и для других разновидностей, выступает ом. Рассматриваемое явление обнаруживает себя только при переменном электротоке. В расчетах оно обозначается латинской литерой Х.
Различия между активным и реактивным сопротивлением
Разница между активным и реактивным сопротивлением состоит в том, что при прохождении электротока по компонентам цепи, несущим активную нагрузку, имеют место мощностные потери в виде выделения тепла, которое не может быть снова превращено в электрическую энергию. В качестве наглядного примера можно привести конфорку электроплиты, выделяющую тепловую энергию. Такими свойствами обладают и осветительные устройства, электрические двигатели, различные кабели. Фазы проходящих через такие компоненты напряжения и электротока будут совпадать.
Реактивные нагрузки отличаются наличием емкостных свойств либо способностью к индукции. В первом случае величина рассматриваемого сопротивления зависит от емкости, во втором – от электродвижущей силы самоиндукции.
Важно! Величина, в противоположность активной, может иметь плюсовой и минусовой знаки. Это зависит от того, в какую сторону идет фазовый сдвиг. При опережении электрическим током напряжения будет иметь место отрицательный показатель, в обратном случае – положительный.
Виды и свойства реактивного сопротивления
Данная величина может иметь две формы:
- емкостную – присущую конденсаторным элементам;
- индуктивную – характерную для катушек, соленоидов и обмоток.
Важно! Если к трансформатору подключить активную нагрузку, реактивное сопротивление понизится, так как упадет значение того типа мощности, который его вызывает. В некоторых цепях с несколькими индуктивными или емкостными нагрузками имеет место взаимоуничтожение фазовых сдвигов, приходящихся на разные детали, тогда комплексная величина будет равной нулю.
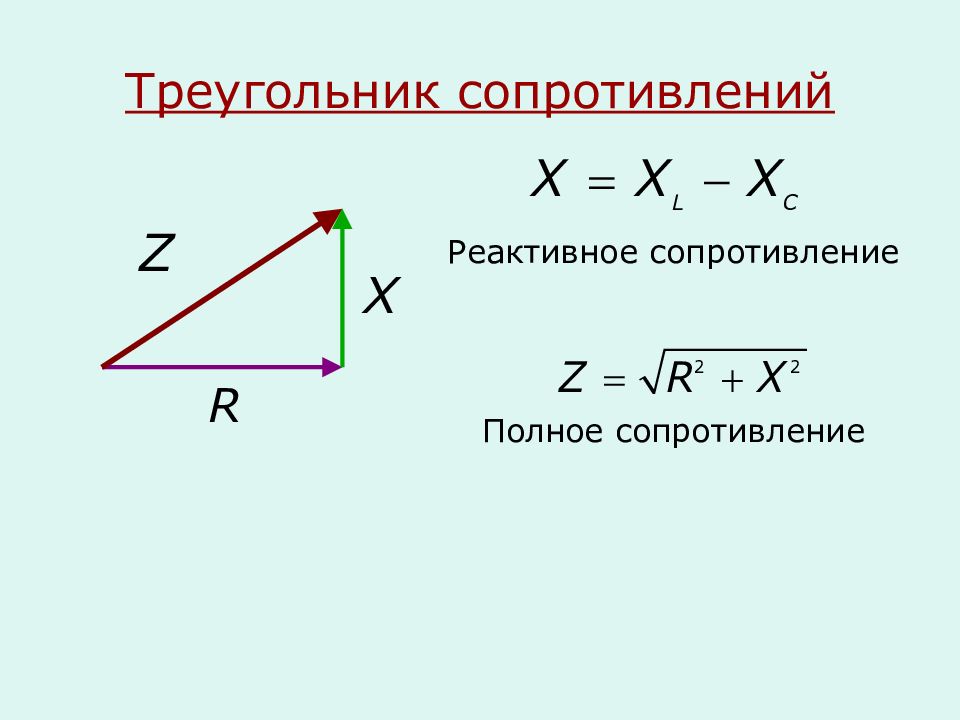
Треугольник сопротивлений
Виды пассивных элементов
Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.
Катушка индуктивности
Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.

Подключение катушки в электрическую цепь
Емкостной элемент
Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.
Подсоединение конденсатора в электроцепь
Конденсатор в цепи переменного тока
Конденсаторные устройства характеризуются неспособностью пропускать константный электроток. Так что если устройство подсоединить последовательно к источнику такого тока, в цепи электроток идти не будет. В переменных цепях дело обстоит иначе. Если цепочка содержит только емкостной компонент, в ней будет проходить ток, обгоняющий по фазе напряжение на 90°.
Важно! Величина электротока определяется его частотой и емкостной характеристикой использованного конденсатора.
Реактивное сопротивление конденсатора
Его можно узнать, воспользовавшись формулой:
Х=1/(C*w).
Здесь С – емкостная величина рассматриваемой детали, а w – угловая частота. При параллельном подключении элементов будет справедлива формула:
1/Хобщ = 1/Х1 + 1/Х2 +…
Если конденсаторы объединены последовательно, для нахождения комплексного показателя системы потребуется сложить значения для всех компонентов:
Хобщ = Х1 + Х2 +…
Катушка индуктивности в цепи переменного тока
В отличие от предыдущего случая, при подключении катушечного элемента идущий по нему электроток будет отставать от напряжения. Однако величина фазового сдвига будет аналогичной – 90°. При этом за препятствование быстрому увеличению тока ответственна ЭДС. Элемент способен играть роль безваттного резистора.
Реактивное сопротивление катушки индуктивности
В его расчете поможет выражение:
X = L*w.
Здесь L – показатель индуктивности подсоединенного элемента. При последовательном включении в сеть серии катушек индуктивная компонента сопротивления такой композиции может быть выражена как сумма таковых для всех деталей. Если применено параллельное соединение, справедливым будет выражение:
1/Хобщ = 1/Х1 + 1/Х2 +…
Как для катушки, так и для конденсаторных деталей будет верной запись закона Ома:
X = U/I, в которой U – величина падения напряжения на элементе.
Почему не сгорает первичная обмотка трансформатора
Иногда при эксплуатации трансформаторов возникает вопрос, почему не происходит сгорание обмотки, если ее сопротивляемость оказывается малой. Обмоточный компонент по своему устройству может быть приравнен к катушке. Соответственно, искомый показатель может быть вычислен с помощью выражения:
X = 2*π*L*F, где L – частота, F – индуктивность.
Поскольку последняя у трансформатора оказывается достаточно большой, таковым будет и итоговое число.
Мощность в цепи с реактивными радиоэлементами
При подключении таких элементов в цепь в четных четвертях периода мощность будет иметь отрицательное значение (в это время компонент направляет накопленную энергию в источник напряжения). В итоге использование энергии элементом за весь цикл оказывается равным нулю. Это означает, что на нем не происходит выделения энергии, так что на электросхемах такие детали изображаются холодными. На деле положение вещей может быть немного иным (это зависит от параметров конкретного элемента), бывает, что небольшие тепловые потери на конденсаторе или соленоиде все-таки имеют место. Но они не будут значительными, измеряющимися в кв.
Компенсация реактивной мощности
При подключении большого числа индуктивных компонентов генерируемая ими реактивная мощность создает избыточную нагрузку на трансформаторы и в целом ведет к бесполезной потере энергии. Чтобы это нивелировать, параллельно можно подсоединить конденсатор. Если правильно подобрать номинал, можно скомпенсировать фазовый сдвиг, что сильно снизит энергетические потери. Емкость этого устройства С равна 1/(2*π*f*X), где Х – параметр сопротивляемости подключенной нагрузки, равный U2/Q (Q – реактивная мощность).
Формула расчета реактивного сопротивления
В общем случае для деталей катушечного типа применяются выражения:
X = L*w = 2* π*f*L.
Для конденсаторов применяют формулы:
X = 1/(w*C)= 1/(2* π*f*C).
Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.
Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.


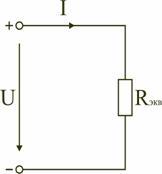 Рис.
1.5
Рис.
1.5