Формула емкостного сопротивления
После замыкания электрической цепи начинается зарядка, после чего конденсатор сразу же становится источником тока и напряжения, в нем возникает электродвижущая сила – ЭДС. Одно из основных свойств конденсатора очень точно отражает формула емкостного сопротивления. Данное явление возникает в результате противодействия ЭДС, направленного против источника тока, используемого для зарядки. Источник тока может преодолеть емкостное сопротивление лишь путем существенных затрат его собственной энергии, которая становится энергией электрического поля конденсатора. При разрядке конденсатор вся энергия возвращается обратно в цепь, превращаясь в энергию электрического тока.
Емкостное сопротивление конденсатора
Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
Емкостное сопротивление можно отнести к реактивному, не вызывающему безвозвратных энергетических потерь. Зарядка конденсатора происходит до того уровня напряжения, которое отдается источником питания.
Существуют качества, присущие только конденсаторам. Например, они совершенно не пропускают через себя постоянный ток, хотя и заряжаются от него. После полной зарядки емкости, течение тока полностью прекращается, а внутреннее сопротивление устройства принимает бесконечно высокое значение.
Совершенно по-другому на конденсатор воздействует переменный ток, вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.
Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
Названия других элементов определяются материалами обычных диэлектриков. Поэтому они относятся к категории бумажных, керамических, стеклянных и т.д. Каждый из них, в соответствии с характеристиками и особенностями, применяется в конкретных электронных схемах, с разными параметрами электротока.
В связи с этим, применение керамических конденсаторов необходимо в тех цепях, где требуется фильтрация высокочастотных помех. Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Емкостное сопротивление в цепи переменного тока
При включении конденсатора в цепь постоянного тока, на протяжении короткого периода времени будет наблюдаться течение по цепи зарядного тока. По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью заряженный конденсатор при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
Более подробное рассмотрение этого процесса указывает на нулевое значение напряжения в конденсаторе в момент его включения. После поступления к нему переменного напряжения сети начнется зарядка. В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q является количеством электричества, протекающим по цепи в течение промежутка времени t. В соответствии с законами электростатики, количество электричества в устройстве составит: q = C x Uc = C x U. В этой формуле С будет емкостью конденсатора, U – напряжением сети, Uc – напряжением на обкладках элемента. В окончательном виде формула тока в цепи будет выглядеть следующим образом: i = C x (∆Uc/∆t) = C x (∆U/∆t).
При наступлении второй четверти периода произойдет уменьшение сетевого напряжения и начнется разрядка конденсатора. Ток в цепи изменит свое направление и будет течь в обратную сторону. В следующей половине периода направление сетевого напряжения изменится, наступит перезарядка элемента, а потом он вновь начнет разряжаться. Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.
В следующей половине периода направление сетевого напряжения изменится, наступит перезарядка элемента, а потом он вновь начнет разряжаться. Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.
Установлено что изменения тока конденсатора происходят со скоростью, находящейся в пропорциональной зависимости с угловой частотой ω. Поэтому в соответствии с уже известной формулой тока в цепи i = C x (∆U/∆t), аналогично получается, что действующее значение тока также будет представлять собой пропорцию между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.
Далее уже совсем несложно установить значение емкостного сопротивления или реактивного сопротивления емкости: xc = 1/2π x f x C = 1/ ω x C. Данный параметр вычисляется, когда конденсаторная емкость включается в цепь переменного тока. Поэтому в соответствии с законом Ома в цепи переменного тока с включенным конденсатором, значение силы тока будет следующим: I = U/xc, а напряжение на обкладках составит: Uc = Ic x xc.
Часть сетевого напряжения, приходящаяся на конденсатор, получила название емкостного падения напряжения. Она известна также, как реактивная слагающая напряжения, обозначаемая символом Uc. Величина емкостного сопротивления хс, так же, как и значение индуктивного сопротивления xi напрямую связана с частотой переменного тока.
Расчёт сопротивления резисторов и ёмкости конденсаторов
Автор: admin, 22 Мар 2013
Расчёт сопротивления резисторов и ёмкости конденсаторов
В этой статье рассмотрим как можно с помощью параллельного и последовательного включения резисторов и конденсаторов подобрать нужный номинал радиодетали, при отсутствии нужного. Расчёт производится по формулам расчёта сопротивления и ёмкости для параллельного и последовательного включения, а также с помощью удобной таблицы подбора ёмкости и сопротивления.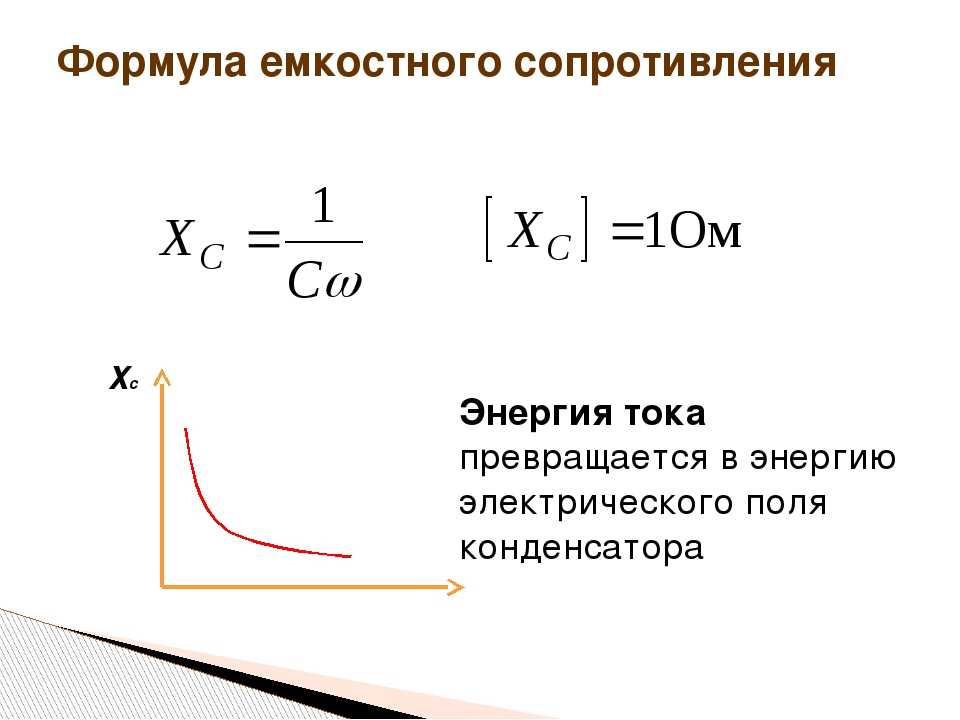
Резисторы
Широко применяются в радиоприёмниках, усилителях сигналов и во многих других схемах. Они служат для ограничения тока, создания падения напряжения, регулирования частоты, громкости и других сигналов. Обозначаются на схемах буквой R. Сопротивление резистора измеряется в Омах. Для больших сопротивлений используют единицы: килоомы (1кОм=1000Ом), мегаомы (1Мом=1000кОм). Кроме сопротивления резисторы характеризуются мощностью рассеяния, это такая наибольшая мощность, которую резистор может выдержать длительное время. Мощность рассеяния измеряется в ваттах (Вт). Ещё один показатель — это наибольшее возможное отклонение действительного сопротивления от номинального, указанного на резисторе, выражается в %. Резисторы бывают постоянные (не изменяют своего сопротивления) и переменные(изменяют сопротивление в зависимости от положения движка резистора).
Иногда, при сборке схемы не оказывается под рукой резистора нужного номинала. В этом случае в большинстве случаев можно заменить резистор на ближайший по номиналу — например вместо 110 Ом можно использовать резистор номиналом 100 или 120 Ом. А если нет и ближайшего по номиналу или требуется точное значение сопротивления, то можно составить нужное сопротивление с помощью последовательного или параллельного соединения нескольких резисторов.
А если нет и ближайшего по номиналу или требуется точное значение сопротивления, то можно составить нужное сопротивление с помощью последовательного или параллельного соединения нескольких резисторов.
Последовательное соединение резисторов:
последовательное соединение резисторов
При последовательном соединении резисторов их общее сопротивление равно их сумме: Rобщ = R1+R2+…+Rn.
Параллельное соединение резисторов:
параллельное соединение резисторов
При параллельном соединении резисторов их общее сопротивление рассчитывается по формуле:
1/Rобщ = 1/R1 + 1/R2 +…+1/Rn или
Rобщ = 1/(1/R1 + 1/R2 +…+1/Rn).
На практике для подбора нужного сопротивления обычно включают параллельно два резистора, в этом случае формула примет вид:
Rобщ = R1*R2/(R1+R2).
Ещё можно отметить, что при включении резисторов одинакового сопротивления, то их общее сопротивление будет равно половине сопротивления каждого их них. Мощность рассеяния, в этом случае, увеличится в 2 раза. Также при параллельном соединении общее сопротивление всегда меньше наименьшего из включенных в параллель резисторов.
Мощность рассеяния, в этом случае, увеличится в 2 раза. Также при параллельном соединении общее сопротивление всегда меньше наименьшего из включенных в параллель резисторов.
Конденсаторы
Конденсаторы, как и резисторы, тоже очень широко применяются. Конденсатор это накопитель энергии, в простейшем виде это две пластины, между которыми находится диэлектрик, в качестве диэлектрика может быть просто воздух. Конденсаторы также бывают постоянной и переменной ёмкости. Единицей ёмкости является фарада(Ф). На практике используют меньшие ёмкости, их выражают в микрофарадах(1Ф=1 000 000 мкФ), нанофарадах(1мкФ = 1 000 нФ), пикофарадах(1нФ=1 000 пФ). Также конденсаторы характеризуются рабочим напряжением, выражаемом в вольтах (В). Превышение на конденсаторе напряжения выше рабочего может привести к «пробою» диэлектрика конденсатора.
Конденсатор не проводит постоянный ток, а переменному току оказывает сопротивление, которое вычисляется по формуле:
Хс = 1/(2πfC), где
- Хс — емкостное сопротивление конденсатора, Ом;
- π
- f — частота переменного тока, Гц;
- С — ёмкость конденсатора, Ф.

Рассмотрим как можно собрать нужную ёмкость из имеющихся под рукой.
Последовательное включение конденсаторов:
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов их общая ёмкость рассчитывается по формуле, очень похожей на формулу для параллельного включения резисторов:
Собщ = 1/(1/С1+1/С2+…+1/Сn).
Но чаще тоже используют два конденсатора, тогда формула упрощается:
Собщ = С1*С2/(С1+С2).
Также, при включении конденсаторов с одинаковой ёмкостью их общая ёмкость будет в два раза меньше ёмкости каждого из них. Рабочее напряжение такого сборного конденсатора увеличится в 2 раза.
Параллельное включение конденсаторов:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов их общая ёмкость будет равна сумме всех емкостей.
Собщ = С1+С2+…+Сn.
При необходимости можно делать даже комбинированные соединения и параллельные и последовательные, в этом случае высчитывается ёмкость(или сопротивление) по одинаковым группам соединений, получают промежуточные значения, например Собщ1, Собщ2.
Но, как правило, более двух деталей для составления нужного номинала не используют, для параллельного соединения конденсаторов и последовательного резисторов всё просто — считаем сумму. А для последовательного соединения конденсаторов и параллельного соединения резисторов нужно считать, поэтому будет удобно пользоваться заранее составленной таблицей, которая подойдёт для обоих радиоэлементов.
Таблица расчёта общего сопротивления (ёмкости) для двух параллельно соединённых резисторов (двух последовательно соединённых конденсаторов)
Таблица расчёта общего сопротивления(ёмкости)
По горизонтали смотрим значения, выделенные зелёным цветом, первого резистора(конденсатора) по вертикали второго. На перекрестии этих двух значений и будет общее сопротивление (ёмкость).
Будет интересно почитать:
Рубрики: Электронные устройства, Электросхемы
Метки: электроника, электросхема
Формула емкостного реактивного сопротивления Известно, что конденсатор определяется как устройство, которое накапливает ток и имеет возможность влиять на величину заряда, которую он может достичь.
 Величина его емкости определяется частотой f проходящего через него электрического сигнала. Это сопротивление элемента цепи изменениям тока или напряжения. Его стандартная единица измерения Ом (Ом). Обозначается символом X c и его размерная формула определяется как [M 1 L 2 T -3 I -2 ]. Его математическая формула равна единице, деленной на удвоенное произведение пи, частоты и емкости конденсатора.
Величина его емкости определяется частотой f проходящего через него электрического сигнала. Это сопротивление элемента цепи изменениям тока или напряжения. Его стандартная единица измерения Ом (Ом). Обозначается символом X c и его размерная формула определяется как [M 1 L 2 T -3 I -2 ]. Его математическая формула равна единице, деленной на удвоенное произведение пи, частоты и емкости конденсатора.Кемковая формула реактивной способности
Примеры задачx C = 1/2πfc
, где,
x C — это неприемлемое реактивное вещество,
π -контейн «Ценность» — это концентрация.0002 f — частота,
c — емкость.
Задача 1. Найдите емкостное сопротивление, если емкость равна 5 Ф при частоте 20 Гц.
Решение:
Мы имеем,
F = 20
C = 5
, используя формулу, мы имеем,
x C = 1/2πfc
= 1,143 C = 1/2πfc 9000 = 1 (2 ° С = 1/2πFC 9000 = 1 (2000 2 x = 1/2πfc 9000 = 10003.× 20 × 5)
= 1/628
= 0,0016 Ом
Задача 2. Найти емкостное сопротивление, если емкость равна 4 Ф для частоты 50 Гц.
Решение:
Мы имеем,
F = 50
C = 4
Используя формулу. × 50 × 4)
= 1/2512
= 0,00039 Ом
Задача 3. Найти емкостное реактивное сопротивление, если емкость равна 0,5 Ф за время 10 с.
Решение:
Мы имеем,
T = 10
C = 0,5
с использованием Formula F = 1/T Get,
F = 1/10
= 0,1 Гц
F = 1/10
= 0,1 Гц
F = 1/10
= 0,1 Гц
. Используя полученную формулу,
X c = 1/2πfc
= 1/(2 × 3,14 × 0,1 × 0,5)
= 1/0,314
= 3,183 Ω
900 Найти задачу. емкостное реактивное сопротивление, если емкость равна 2,5 Ф в течение 16 с.Решение:
.
Мы имеем,
x C = 1/2πfc
= 1/(2 × 3,14 × 0,0625 × 2,5)
= 1/0,98125
= 1,0186 Ом
. емкостное сопротивление 2 Ом для частоты 25 Гц.
Решение:
Мы имеем,
x C = 2
F = 25
Используя формулу, которую мы имеем,
x C = 1/2πfc
=> C = 1/2πx C f
=> c = 1/(2 × 3,14 × 2 × 25)
=> c = 1/314
=> c = 0,003183 F
Задача 6. Найти емкость, если емкостное сопротивление 0,01 Ом для частоты 12 Гц.
Решение:
У нас есть,
x C = 0,01
F = 12
с использованием формулы, которую мы имеем,
x C = 1/2πfc
=> C = 1/2πx C F
=> C = 1/2πx C F
=> C = 1/2πx C F
=> C 1/(2 × 3,14 × 0,01 × 12)
=> c = 1/0,7536
=> c = 1,327 Ф
Задача 7.
Найдите частоту, если емкостное сопротивление равно 0,004 Ом при емкости 2 Ф
Решение:
У нас есть,
X c = 0,004
c = 2
Используя формулу, которую мы имеем,
X c = 1/2πfc
=> f = 1/2πX c = /2 = 1(
>9002 3,14 × 0,004 × 2)=> f = 1/0,05024
=> f = 20 Гц
конденсатор — Расчет сопротивления с учетом емкости и заряда во времени
спросил
Изменено 8 лет, 4 месяца назад 9{-t/RC})\$, будет ли формула сопротивления \$R = \dfrac{-t}{C \cdot log(1-V_t/V_0)}\$?
- конденсатор
- резисторы
- разряд
\$\конечная группа\$
7
\$\начало группы\$
Напряжение конденсатора, изначально при напряжении \$V_0\$ с емкостью \$C\$, разряжающейся через сопротивление \$R\$ в момент времени \$t\$, определяется выражением
\$ V_t = V_0 e^ {-t/(RC)} \$ 9{-t/(RC)} \$
\$ \log_e(V_t/V_0) = \dfrac{-t}{RC} \$
\$ R = \dfrac{-t}{C \cdot \ log_e(V_t/V_0)} \$
Почти то же самое, что и у вас, за исключением бита \$(1-.



 × 20 × 5)
× 20 × 5)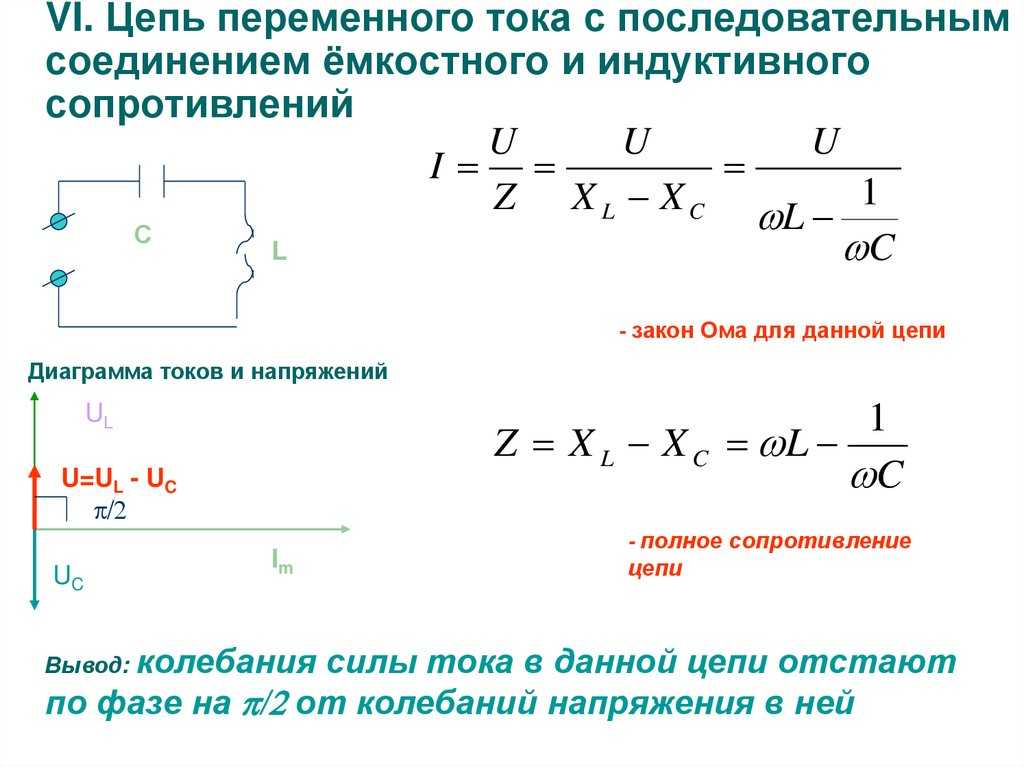 Мы имеем,
Мы имеем, Найдите частоту, если емкостное сопротивление равно 0,004 Ом при емкости 2 Ф
Найдите частоту, если емкостное сопротивление равно 0,004 Ом при емкости 2 Ф 