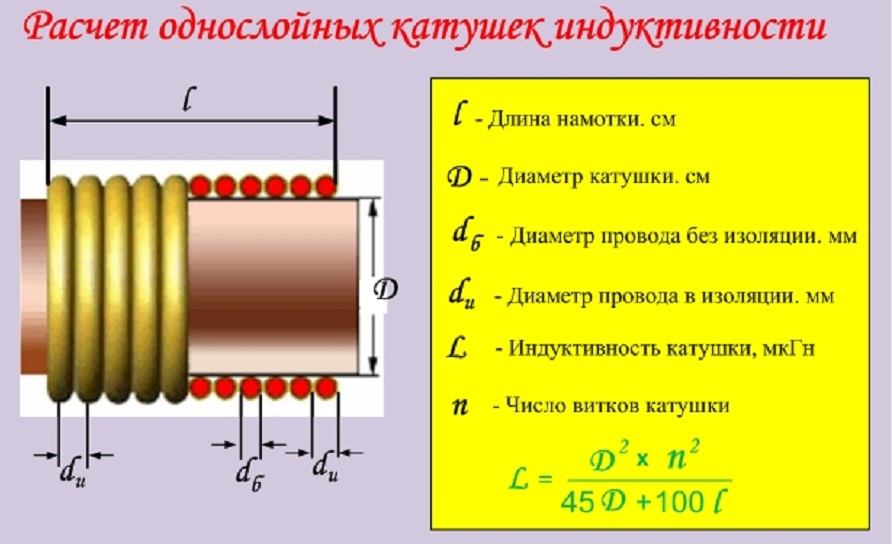
Определение сопротивления кабелей на напряжение 6

В данной статье приводятся таблицы активного и индуктивного сопротивления кабелей на напряжение 6 — 35 кВ взятые из различных справочников по проектированию электрических сетей и руководящих указаний.

Значения активного и индуктивного сопротивления кабелей необходимы при расчете токов короткого замыкания и проверки кабеля на потери напряжения.

Сопротивление кабелей с бумажной, резиновой и поливинилхлоридной изоляцией на напряжение 6 — 35 кВ

1. РД 153-34.0-20.527-98 – Руководящие указания по расчету токов короткого замыкания и выбору электрооборудования. 2002 г. Таблица П.8, страница 145.

2. Проектирование кабельных сетей и проводок. Хромченко Г.Е. 1980 г. Таблица 2-5, страница 48.

3. Справочник по проектированию электроснабжению. Ю.Г. Барыбина. 1990 г. Таблица 2.63, страницы 175-176.

4. Справочная книга электрика. Григорьева В.И. 2004г. Таблицы 3.9.7; 3.9.11; страницы 448-449

Если значения активных и реактивных сопротивлений кабелей, вы не нашли в приведенных таблицах. В этом случае, сопротивление кабеля можно определить по приведенным формулам с подстановкой в них фактических параметров кабелей.

Методика расчета представлена в книге: «Проектирование кабельных сетей и проводок. Хромченко Г.Е. 1980 г, страницы 45-48».

Активное сопротивление кабеля

1. Активное сопротивление однопроволочной жилы, определяется по формуле 2-1, Ом:

где:

• l — длина жилы, м;
• s – поперечное сечение жилы, мм2, определяется по формуле: π*d²/4;
• d – диаметр жилы кабеля;
• α₂₀ – температурный коэффициент сопротивления, равный при 20 °С:
• 0,00393 1/град – для меди;
• 0,00403 1/град – для алюминия;
• ρ₂₀ – удельное сопротивление материала жилы при 20 °С (температура изготовления жилы), можно принять согласно книги «Справочная книга электрика. Григорьева В.И. 2004г.» Таблица 1.14, страница 30.

• tж – допустимая температура нагрева жилы, согласно ПУЭ п.1.3.10 и 1. 3.12.

2. Активное сопротивление многопроволочной жилы определяется также по формуле 2-1, но из-за конструктивных особенностей многопроволочной жилы, вместо значений ρ₂₀ вводиться в формулу ρ_р равное:

• 0,0184 Ом*мм2/м – для медных жил;
• 0,031 Ом*мм2/м – для алюминиевых жил.

3. Удельное активное сопротивление жилы, отнесенное к единице длины линии 1 км, определяется из следующих зависимостей, Ом/км:

Индуктивное сопротивление кабеля

1. Удельное реактивное (индуктивное) сопротивление кабеля определяется по формуле 2-8, Ом/км:

где:

• d – диаметр жилы кабеля.
• lср – среднее геометрическое расстояние между центрами жил кабеля определяется по формуле [Л1.с.19]:

где:

• l_А-В — расстояние между центрами жил фаз А и В;
• l_В-С — расстояние между центрами жил фаз В и С;
• l_С-А — расстояние между центрами жил фаз С и А.

Пример

Определить активное и индуктивное сопротивление кабеля марки АВВГнг(А)-LS 3х120 на напряжение 6 кВ производства «Электрокабель» Кольчугинский завод».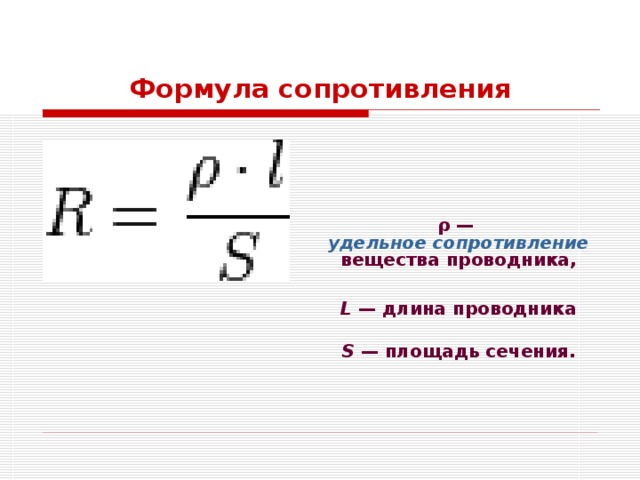 Длина кабельной линии L = 300 м.

Решение

1. Определяем поперечное сечение токопроводящей жилы кабеля имеющую круглую форму:

S = π*d²/4 = 3,14*13,5²/4 = 143 мм²

Расчет поперечного сечение секторной жилы, а также размеры секторных жил на напряжение 0,4 — 10 кВ представлен в статье: «Расчет поперечного сечения секторной жилы кабеля«.

где: d = 13,5 мм – диаметр жилы кабеля (многопроволочные уплотненные жилы), определяется по ГОСТ 22483— 2012 таблица С.3 для кабеля с токопроводящей жилой класса 2. Класс токопроводящей жилы указывается в каталоге завода-изготовителя кабельной продукции.

Ниже представлена классификация жил кабелей, согласно ГОСТ 22483— 2012:

2. Определяем удельное активное сопротивление кабеля марки АВВГнг(А)-LS 3х120, отнесенное к единице длины линии 1 км, Ом/км:

где:

• l = 1000 м – длина жилы, м;
• α₂₀ – температурный коэффициент сопротивления, равный при 20 °С:
• 0, 00393 1/град – для меди;
• 0,00403 1/град – для алюминия;
• ρ_р – удельное сопротивление материала многопроволочной жилы, равное:
• 0,0184 Ом*мм2/м – для медных жил;
• 0,031 Ом*мм2/м – для алюминиевых жил;
• tж = 65 °С — допустимая температура нагрева жилы, для кабеля напряжением 6 кВ, согласно ПУЭ п. 1.3.10.

3. Определяем удельное активное сопротивление кабеля, исходя из длины кабельной трассы:

где: L = 0,3 км – длина кабельной трассы, км;

4. Определяем среднее геометрическое расстояние между центрами жил кабеля, учитывая что жилы кабеля расположены в виде треугольника.

где:

• l_А-В = 20,3 мм — расстояние между центрами жил фаз А и В;
• l_В-С = 20,3 мм — расстояние между центрами жил фаз В и С;
• l_С-А = 20,3 мм — расстояние между центрами жил фаз С и А.

Что бы определить расстояние между центрами жил кабеля, нужно знать диаметр жил кабеля d = 13,5 мм и толщину изоляции жил из поливинилхлоридного пластиката dи.ж = 3,4 мм, согласно ГОСТ 16442-80 таблица 4. Определяем расстояние между центрами жил фаз равное 20,3 мм (см.рис.1).

5. Определяем удельное реактивное (индуктивное) сопротивление кабеля марки АВВГнг(А)-LS 3х120, Ом/км:

где: d = 13,5 мм – диаметр жилы кабеля;

6. Определяем удельное реактивное сопротивление кабеля, исходя из длины кабельной трассы:

Сопротивление кабелей с изоляцией из сшитого полиэтилена на напряжение 6 — 35 кВ

Значения активного и реактивного (индуктивного) сопротивления кабелей с изоляцией из сшитого полиэтилена приводятся в каталогах завода-изготовителя. Для ознакомления приведу лишь некоторых производителей кабельной продукции.

«Электрокабель» Кольчугинский завод» – Каталог кабельной продукции.

В таблице 12 – приводятся значения активного сопротивления кабелей согласно ГОСТ 22483-2012

Компания «Estralin» — Каталог силовые кабели и кабельные системы 6 – 220 кВ.

Компания «Камкабель» — Настольная книга проектировщика. Кабели с изоляцией из сшитого полиэтилена на напряжение 6-35 кВ.

Справочники по проектированию электрических сетей и руководящие указания, которые упомянуты в данной статье, вы сможете найти, скачав архив.

СКАЧАТЬ

Литература:

1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.

Всего наилучшего! До новых встреч на сайте Raschet.info.

Как измерить сопротивление изоляции: формула, физический смысл, прибор

Пример HTML-страницы

Прибор, который используется для определения сопротивления изоляции называется мегомметром, он известен с конца позапрошлого (XIX) века.

На рисунке ниже схематически представлен участок изоляции И, вверху находится корпус машины К, внизу- изолируемый проводник П. Далее представлена схема замещения.

Предположим, что напряжение постоянного тока толчком приложено между проводником и корпусом, и рассмотрим возникающие после этого явления. Вся конструкция в целом (корпус, изоляция, обмотка) представляет собой конденсатор сложной формы. Емкость такого конденсатора определяется размерами поверхности его обкладок, в данном случае — наружной и внутренней поверхностью соприкосновения изоляции с корпусом и обмоткой электрической машины- и свойствами изоляции- ее толщиной и диэлектрической проницаемостью.

При приложении напряжения эта емкость (С~) заряжается. Заряд происходит за очень короткое время, много меньшее периода промышленной частоты. В результате этого на поверхностях корпуса машины и проводников обмотки сосредоточатся положительные и отрицательные заряды, создающие в изоляции электрическое поле, под их действием в толще изоляции возникнут поляризационные явления- электроны и ионы устремятся к полюсам противоположных знаков, дипольные молекулы изоляции начнут поворачиваться так, чтобы их заряды ориентировались по направлениям линий электрического поля; в слоистой изоляции внутренние слои, являющиеся своеобразными последовательно включенными емкостями, станут заряжаться через очень большие сопротивления смежных слоев. Эти процессы сопровождаются накапливанием в слоях изоляции зарядов, вследствие чего от источника постоянного тока через емкости слоев потекут токи.

Описанные физические процессы могут быть отражены схемой замещения на рис. 4. В этой схеме имеются три параллельные цепи.

Одна цепь с емкостью С отражает заряд геометрической емкости и электронную и ионную поляризацию; соответствующие этим явлениям токи протекают одинаково быстро, поэтому обобщены в одну цепь.

Вторая цепь- последовательно включенные емкость С и сопротивление r, эквивалентные емкостям и сопротивлениям последовательно включенных емкостей и сопротивлений по числу слоев.

Третья цепь — сопротивление R соответствует сквозной проводимости.

Через измерительный прибор потечет ток, равный сумме токов трех ветвей:

i, iабс, iпр. Первый ток не отразится на показаниях прибора, т.к. он быстро затухает; ток сквозной проводимости iпр останется постоянным в продолжение всего процесса. Его величина определит установившееся значение показаний прибора. ток поляризации — ток абсорбции iабс является затухающим. Время его затухания зависит от свойств изоляции. Ток абсорбции изменяется по экспоненциальному закону с постоянной времени , т.е. он тем медленнее убывает, чем больше сопротивление тех слоев изоляции, через которые заряжается межслоевая емкость. Сопротивление слоя зависит от его увлажнения – чем суше изоляция, тем медленнее затухает ток абсорбции. На рис. 5 показано изменение токов и сопротивления изоляции во времени. Прибор градуируется в единицах сопротивления.

Чтобы судить о быстроте спада , снимают показания прибора через 15 и 60 с после приложения напряжения и берут их отношение, называемое коэффициентом абсорбции:

При сухой изоляции = 2 — 2.5, при влажной 1 (рис.6).

Коэффициент абсорбции служит для характеристики внутреннего увлажнения изоляции, он не зависит от наружного увлажнения.

Большая зависимость сопротивления изоляции от увлажнения вызывает и не меньшую зависимость сопротивления изоляции от температуры, т.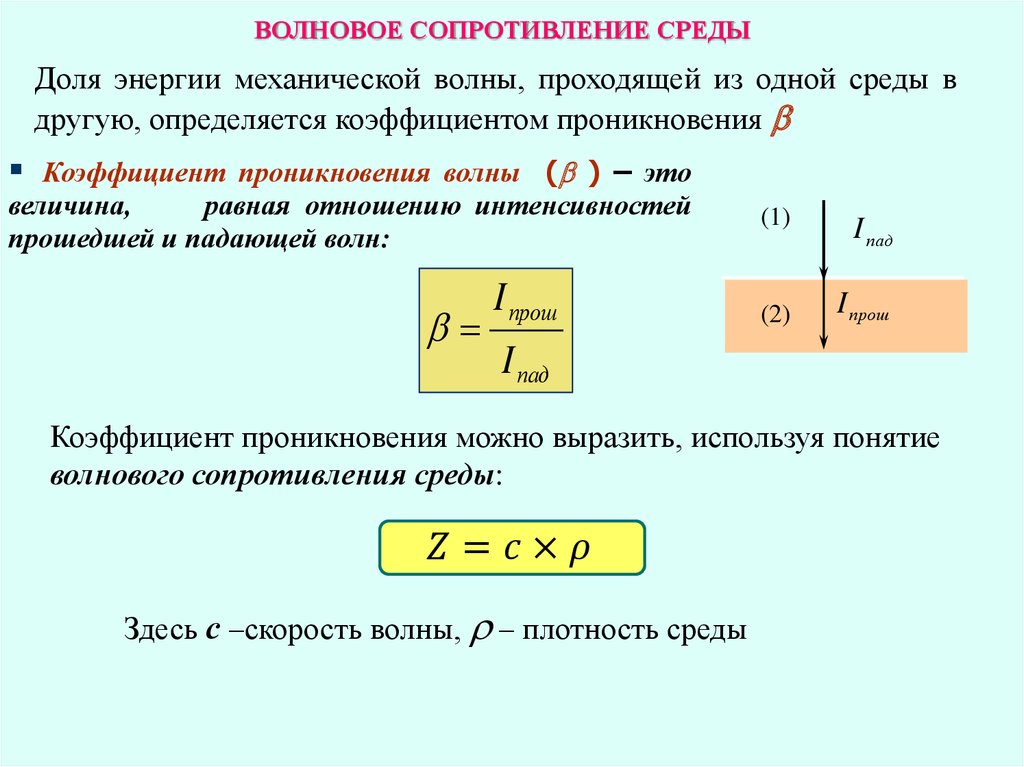 к. при повышении температуры вода и ее пары проникают во внутренние слои изоляции, образуют непрерывные проводящие цепочки и снижают сопротивление изоляции

Можно определить, что

ГОСТ на электрические машины требует, чтобы сопротивление изоляции, МОм, при температуре +75 °С было больше

Здесь Uном -номинальное напряжение машины, В; — номинальная мощность машины, кВт.

Если измерение производится при отличной от 75°С температуре, необходимо воспользоваться формулой пересчета или специальными кривыми. Значение коэффициента абсорбции практически не зависит от температуры.

Как правило, сопротивление изоляции большинства машин выше. Для того, чтобы установить, не произошло ли каких-либо изменений в изоляции, целесообразно сопоставлять результаты вновь производимых измерений с прежними. Значение нормируется ТУ и «Нормами испытания оборудования», как правило, оно должно быть не меньше 1,2 — 1,3.

Формула сопротивления — GeeksforGeeks

Если кто-то хочет контролировать ток, протекающий внутри проводов, то ему нужно знать о сопротивлении. В цепи это противодействие протеканию тока. Измеряется в омах (Ом). Его можно рассчитать по закону Ома. Он определяется как отношение приложенного напряжения к току. Следовательно,

R = V/I

Где

R = сопротивление

I = ток

В = напряжение

Формулу электрического сопротивления можно рассчитать, используя длину и площадь провода. Формула утверждает, что величина сопротивления через провод прямо пропорциональна длине и обратно пропорциональна площади поперечного сечения.

Математически это соотношение часто записывается как

Сопротивление проводника прямо пропорционально его длине,

R α L

Сопротивление проводника обратно пропорционально площади его поперечного сечения,

Удаление пропорциональности и постоянной называется удельным сопротивлением,

Где,

R = сопротивление

ρ = удельное сопротивление проводника

l = длина поперечного проводника

3 A -сечение проводника

Вышеупомянутое уравнение также может быть записано как

Сопротивление зависит от материала, из которого он сделан. Предметы, сделанные из электрических изоляторов, таких как резина, имеют очень высокое сопротивление, в то время как предметы, сделанные из электрических проводников, таких как металлы, имеют очень низкое сопротивление.

Аналогия водопроводной трубы для электрического сопротивления

• Когда длина трубы большая, сопротивление потоку воды будет высоким.
• При большом поперечном сечении трубы сопротивление потоку воды низкое.

Связь электрического сопротивления с мощностью

Электрическая мощность (P) – это произведение тока на напряжение. Единицей мощности в системе СИ является ватт (Вт). Электрическая мощность рассчитывается по закону Ома и по значениям напряжения, силы тока и сопротивления.

P = VI

Где,

P = электрическая мощность

V = напряжение

I = ток

Из закона Ома мы знаем, что

V = IR

3

уравнение, 

P = I ² /R

Когда значения тока и сопротивления заданы, уравнение выглядит следующим образом:

P = V ² /R

Влияние температуры на электрическое сопротивление веществ изменяется при изменении температуры.

Величина изменения зависит от типа материала.

• Металлы

Электрическое сопротивление чистых металлов увеличивается при повышении температуры. Таким образом, металлы имеют положительный температурный коэффициент сопротивления. например, медь, алюминий, серебро и т. д.

• Сплавы

Электрическое сопротивление сплавов увеличивается с повышением температуры, но сплавы имеют низкое значение положительного температурного коэффициента сопротивления. например, нихром и т. д.

• Полупроводники, изоляторы и электролиты

Электрическое сопротивление полупроводников и изоляторов уменьшается с повышением температуры. Уменьшается значение сопротивления. Поэтому эти материалы имеют отрицательный температурный коэффициент сопротивления.

Факторы, влияющие на электрическое сопротивление

• Длина проводника

Чем больше длина провода, тем больше сопротивление провода.

• Площадь поперечного сечения проводника

Сопротивление провода уменьшается по мере увеличения площади поперечного сечения провода.

• Материал проводника.

Различные материалы имеют разное сопротивление. Для металлов предлагаемое сопротивление очень низкое, но для изоляторов предлагаемое сопротивление довольно велико.

• Температура материала

Электрическое сопротивление чистых металлов и сплавов увеличивается при повышении температуры, но для изоляторов электрическое сопротивление уменьшается при повышении температуры.

Удельное сопротивление

Удельное электрическое сопротивление — это свойство материала, которое является фундаментальным по своей природе и измеряет, насколько сильно это свойство сопротивляется электрическому току. Единицей удельного электрического сопротивления в СИ является ом-метр, а символом является строка (ρ).

Для идеальных случаев, когда поперечное сечение и физический состав материала однородны по всему образцу. Удельное сопротивление можно записать как:

Для менее идеальных случаев ток и электрическое поле различаются в разных частях материала. Мы используем общее выражение,

Где,

ρ — электрическое сопротивление металла, Ом.м

E — электрическое поле, В.м ^-1

Дж — плотность тока, А.м-2

3 Образец Задачи

Вопрос 1: Что такое закон Ома?

Ответ: 

 Закон Ома гласит, что ток в проводнике между двумя точками прямо пропорционален напряжению в двух точках.

Вопрос 2: Два провода длиной 50 м и 40 м соответственно имеют одинаковую площадь поперечного сечения и изготовлены из одного и того же материала. Какой провод имеет большее сопротивление?

Ответ: 

Мы знаем, что R α L, провод длиной 50 м будет иметь более высокое сопротивление. Сопротивление тонкого провода мало, а сопротивление длинного провода велико. t

Вопрос 3: Два провода L1 и L2 имеют длину L и 2L соответственно. Площадь поперечного сечения равна 2А и А соответственно. Оба провода изготовлены из одного и того же материала. Найдите отношение сопротивлений в проводе L ₁ и L ₂ ?

Решение:

Итак,

 ⇢ (1)

⇢ (2)

Разделив два уравнения 1, 3 90 90 на уравнение 2 выше 0003

Вопрос 4: Расчет сопротивление медного провода длиной 5 м и площадью поперечного сечения 2×10 ^-6 м². Удельное сопротивление меди 1,7·10 ^-8 Ом·м.

Решение:  9 ^-6 м , 

Итак, подставив значения ρ, l и A в приведенное выше уравнение,

R = 4,25 × 10 ^-2 Ом

Вопрос 5: Что такое сопротивление?

Ответ:

Удельное электрическое сопротивление — это фундаментальное свойство материала, которое показывает, насколько сильно он сопротивляется электрическому току. Единицей удельного электрического сопротивления в системе СИ является ом-метр, а символом является строка (ρ).

Вопрос 6: Объясните связь Силы с Сопротивлением?

Ответ: 

Мощность равна напряжению, умноженному на ток, 

P = VI ⇢ (1)

Из закона Ома, 

В = RI ⇢ (2) 900 значение в уравнении в уравнение (1)

Решение:

Мощность прибора = 1500 Вт

Напряжение питания прибора = 220 В ,

I = 6,81 А

Вопрос 8: Рассчитайте силу тока и сопротивление электрической лампочки мощностью 50 Вт, 100 В.

Решение:

Мощность прибора = 100 Вт

Напряжение = 100 В

Из отношения мощность-ток мы знаем, что

P = VI

Кроме того,

I = 0,5 А

= 9,0002 Итак, ток 2 Из закона Ома

R = 200 Ом

Сопротивление электрической лампочки = 200 Ом

Вопрос 9: Что происходит с сопротивлением изоляторов при повышении температуры?

Ответ:

С повышением температуры сопротивление изоляторов уменьшается. Таким образом, такой материал имеет отрицательный температурный коэффициент сопротивления.

Вопрос 10: Металлическая проволока с удельным сопротивлением 6 × 10 ^-6 Ом·м и длиной 20 м имеет сопротивление 10 Ом. Вычислите его радиус.

Ответ:

Удельное сопротивление провода = 6 × 10 ^-6 Ом·м

Длина провода = 20 м

Сопротивление провода 9 = 10 Ом0003

Приведенное выше уравнение можно переписать как

⇢ (1)

Заменив значения в уравнении (1),

A = 12 × 10 ^-6 м 2

Обычно площадь поперечного сечения провода представляет собой круг. Таким образом, площадь круга равна

A = πr ² ⇢ (3)

r = радиус поперечного сечения провода

Подставляя значение (2) в (3),

πr ² = 12 × 10 ^-6

r = 1,954 × 10 ^-3 м  

Вопрос 11. Первоначально длина провода равна L. Длина провода изменяется от L до 2L, сохраняя площадь поперечного сечения той же . Найдите начальное отношение сопротивления к конечному?

Решение:

Первоначально

Длина провода = Lm

Площадь поперечного сечения провода = Am ²

Окончательно 90,3 Ом = R00,3 9 ²

Сопротивление провода = R2Ом 12 : Что такое единица удельного сопротивления в системе СИ?

Ответ: 

Единицей удельного сопротивления в системе СИ является строка (ρ).

Расчет сопротивления коаксиального кабеля

спросил 2 года 3 месяца назад

Изменено 11 месяцев назад

Просмотрено 3к раз

\$\начало группы\$

Как указано здесь, вывод сопротивления для коаксиальных кабелей

Рассмотрим коаксиальный кабель длиной \$L\$, состоящий из цилиндрического проводника радиуса a, окруженного цилиндрической проводящей оболочкой радиуса \$b\$.

Пространство между проводниками заполнено изоляционным материалом. 9б\frac1rdr$$ Следовательно $$R = \frac{ρ}{2\pi L} \ln\bigg(\frac ba\bigg)$$ Обычно это сопротивление составляет несколько сотен 90 522 Ом/м 90 523, чтобы свести к минимуму «ток утечки», который проходит через изоляционный материал между проводниками.

Дело в том, что я не могу этого понять, но я знаю, что это полностью объясняет. Может быть, кто-то другой, читающий, поймет это. Я просто хочу спросить, может ли кто-нибудь объяснить это более подробно? Например, вы можете полностью использовать те же переменные и вывод, как показано на рисунке, просто объясните это по-другому. Таким образом, я могу оглянуться на источник и понять, что происходит, из более подробных объяснений.

Я знаком с основной формулой сопротивления
$$ R = \frac {ρL}{A} $$ Основываясь на информации, мое номинальное значение представления переменных составляет

• Сопротивление: \$R \rightarrow dR\$
• Удельное сопротивление : \$\rho \rightarrow \rho\$
• Длина: \$L \rightarrow dr\$
• Площадь поперечного сечения: \$A \rightarrow 2\pi rL\$

Что ж, думаю, что-то не так.

Я думаю, что \$dr\$ должен быть связан с площадью поперечного сечения. Поэтому я был бы признателен, если бы можно было объяснить аналоги оригинальной формулы. Я могу взять на себя решение оттуда, так как я знаком с интегральными формулами, и \$dr/r\$ определенно приводит к ответу, имеющему натуральный логарифм. \$a\$ — нижний предел, радиус кабеля, а \$b\$ — верхний предел, который представляет собой радиус кабеля, включая изоляцию.

• сопротивление
• кабели
• проводники
• удельное сопротивление
• коаксиальный кабель

\$\конечная группа\$

2

\$\начало группы\$

Исходя из основной формулы для сопротивления :

R = \$\rho L/A\$ рассмотрим концентрические цилиндрические оболочки и длину кабеля G

Мы хотим рассчитать сопротивление от одной стороны до другой тонкая цилиндрическая оболочка длиной G и толщиной dr (ток проходит радиально через оболочку).

Таким образом, L в данном случае представляет собой бесконечно малое изменение радиуса dr

Мы будем использовать тонкий срез в радиальном направлении, потому что радиус изменяется при движении изнутри наружу, и, таким образом, сопротивление среза той же толщины dr уменьшается когда мы идем наружу, и мы хотим интегрироваться по этому пути, чтобы найти полное сопротивление. Мы интегрируем по пути, по которому ток следует от внутреннего проводника к внешнему проводнику. Предполагается пренебрежимо малое сопротивление вдоль центрального и внешнего проводников. 9b\frac{1}{r}dr\$

Определенный интеграл, который мы знаем, равен ln(b)-ln(a) = ln(b/a), и мы получаем решение с сайта.

\$\конечная группа\$

9

\$\начало группы\$

Утверждение «Как правило, это сопротивление составляет несколько сотен Ом/м для минимизации [утечки]» вводит в заблуждение как минимум по двум причинам.

Во-первых, это проблема юнитов. Единица «Ом/м» означает, что существует сопротивление, которое увеличивается с расстоянием. Однако сопротивление утечки 9{-15}\$См/м будет ближе к сопротивлению утечки типичного коаксиального кабеля.

Как указывалось в комментариях, расчет проводимости/длины по удельному сопротивлению изоляционного материала требует интегрирования по площади, но формула приведена в задаче.

\$\конечная группа\$

2

\$\начало группы\$

Итак, обычная формула для сопротивления, или способ, которым вы ее найдете, состоит в том, чтобы интегрировать по пути, по которому движется ток. Если ток течет в направлении +x, вы интегрируете по x. Каждая секция, которую вы интегрируете, имеет сопротивление rho / A * dx. А — площадь поперечного сечения проводника. ОБЫЧНО в этих задачах A равномерна. Константа.

Это можно вытащить вперед, прежде чем делать интеграл. Так что это вряд ли интеграл, и вы просто умножаете ро на экстент в x и делите на площадь. Так что обычно Rtotal — это просто ро*длина/площадь.

Но в нашем случае сечение неоднородное, поэтому интеграл сложнее. Кроме того, поскольку ток не течет по длине L, мы используем L в другом месте, что также сбивает с толку.

Итак, какие есть аналоги? Вместо dx у нас есть dr, потому что ток течет наружу радиально. Вместо А у нас длина окружности * длина. Итак, A = (2 * pi * r * L).

Теперь наше выражение обретает форму. Это просто:

Rshell = (rho / (2 * pi * r * L)) dr

Вы просто собираетесь интегрировать от r = a до r = b. Все постоянно, кроме dr/r, поэтому rho/(2 * pi * r * L) выдвигается вперед. Если мы предположим, что L равно 1 метру, то он исчезает.

Не уверен, что это имеет для вас смысл. Суть в том, что вы интегрируете по пути тока и делите на площадь поперечного сечения этого пути.

До сих пор я не выучил mathjax.