формула движения, скорость и давление

Сила трения покоя

На тело, лежащее на наклонной плоскости действуют сила тяжести и сила нормальной реакции опоры. Но если бы на него действовали только две эти силы, то тело обязательно соскальзывало бы вниз. Существует сила, которая мешает лежащему на наклонной поверхности телу двигаться, ее называют силой трения.

Когда тело находится в покое на наклонной плоскости, оно удерживается силой трения. Если тело, лежащее на горизонтальной поверхности, пытаться сдвинуть, то сила трения создаст сопротивление этому движению.

Определение 1

Сила трения покоя — сила, возникающая между двумя контактирующими телами и препятствующая относительному движению.

Сила трения покоя возникает при попытке вывести тело из состояния покоя, и приложена к этому телу. Направление силы трения покоя — против того движения, которое должно было бы возникнуть (вдоль поверхности соприкосновения).

Сила трения покоя всегда по модулю равна приложенной внешней силе и увеличивается по мере увеличения этой силы.

Формула 1

На рисунке ниже изображено направление и место приложения силы трения покоя.

Причины возникновения силы трения

Возникновение силы трения связано с двумя причинами.

1. Неровная поверхность соприкасающихся тел. Даже ровные на вид поверхности имеют шероховатости, которыми они цепляются друг за друга, что создает силу, препятствующую движению.
2. Если поверхности тел идеально гладкие и имеют минимум неровностей, то контакт между такими поверхностями очень тесный. При соприкосновении часть молекул располагается настолько близко друг от друга, что становится заметным притяжение между молекулами соприкасающихся тел.

Предельная сила трения покоя

Существует предельная или максимальная величина силы трения покоя, равная величине силы, необходимой, чтобы вывести тело из состояния покоя. Если приложить к телу силу меньше предельной силы трения покоя, то тело не сдвинется. Если приложить силу больше предельной силы трения покоя, то тело придет в движение.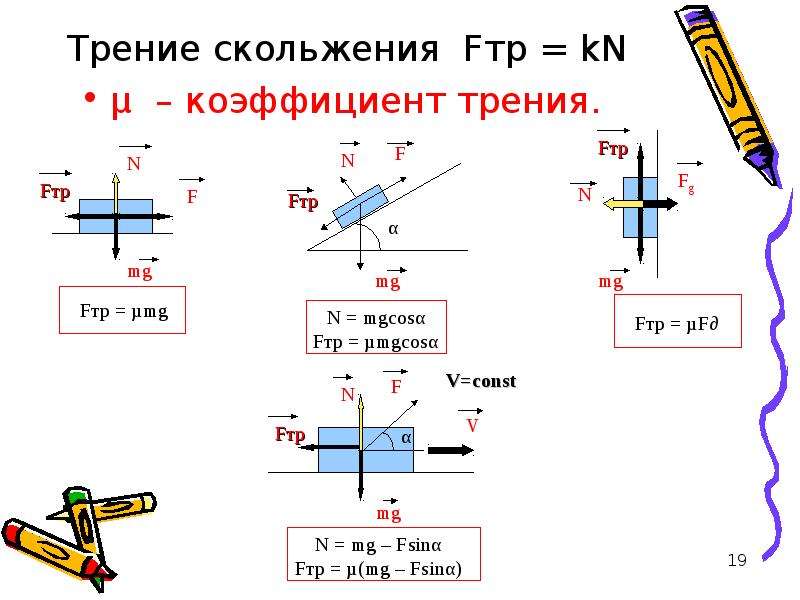

Величина модуля максимальной силы трения покоя прямо пропорциональна модулю силы нормальной реакции опоры. Максимальная сила трения покоя зависит от массы покоящегося тела и характеристик соприкасающихся поверхностей, и не зависит от площади соприкосновения тел.

 

μ — коэффициент пропорциональности или коэффициент трения.

Коэффициент трения покоя μ характеризует две соприкасающиеся поверхности и зависит от материалов, из которых они изготовлены, и качества обработки поверхности. 0<μ<1.

Сила трения скольжения

Если на покоящееся на плоскости тело действует сила, большая чем предельная сила трения покоя, то тело начинает скользить по поверхности, и на него начинает действовать сила трения скольжения.

Определение 2

Сила трения скольжения — сила, возникающая между контактирующими телами, движущимися относительно друг друга.

При равномерном скольжении сила трения скольжения лишь немного меньше предельной силы трения покоя. Приближенно можно считать, что они равны. Также при равномерном прямолинейном скольжении по горизонтальной поверхности модуль силы трения скольжения равен модулю силы, своим действием вызывающей движение тела.

Формула 3

При скольжении на каждое из соприкасающихся тел действует своя сила трения. Сила трения скольжения параллельна плоскости соприкосновения тел и направлена противоположно скорости относительного движения тела.

Сила трения на наклонной плоскости

Уравнение движения тела, находящегося на наклонной плоскости

Формула 4Формула 5

Уравнение движения принимает следующий вид:

Формула 6

Тогда силу трения можно найти по формуле:

Формула 7Формула 8Формула 9

Сила трения на графике

На графике ось абсцисс — приложенная сила, ось ординат — сила трения. На первом этапе с увеличением приложенной силы растет сила трения покоя, в этот период тело еще не движется. Точка максимума — предельное значение силы трения покоя, за которой наступает скольжение.

Если и дальше увеличивать приложенную силу, то на тело будет действовать уже не сила трения покоя, а сила трения скольжения, при этом она будет иметь постоянное значение (горизонталь на графике).

Задачи на силы трения покоя и скольжения с решениями

ЗадачаЗадача 2Задача 3

Динамика — Силы трения. Коэффициент трения

В этом параграфе: Классификация основных видов трения При соприкосновении движущихся (или приходящих в движение) тел с другими телами, а также с частицами вещества окружающей среды возникают силы, препятствующие такому движению. Эти силы называют силами трения. Действие сил трения всегда сопровождается превращением механической энергии во внутреннюю и вызывает нагревание тел и окружающей их среды. Существует внешнее и внутреннее трение (иначе называемое вязкостью). Внешним называют такой вид трения, при котором в местах соприкосновения твердых тел возникают силы, затрудняющие взаимное перемещение тел и направленные по касательной к их поверхностям. Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении. слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению. Внешнее трение подразделяют на трение покоя (статическое трение) и кинематическое трение. Трение покоя возникает между неподвижными твердыми телами, когда какое-либо из них пытаются сдвинуть с места. Кинематическое трение существует между взаимно соприкасающимися движущимися твердыми телами. Кинематическое трение, в свою очередь, подразделяется на трение скольжения и трение качения. В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу. Трение покоя Наблюдения показывают, что сила трения покоя всегда направлена противоположно действующей на тело внешней силе, стремящейся привести это тело в движение. До определенного момента сила трения покоя увеличивается с возрастанием внешней силы, уравновешивая последнюю. Максимальное значение силы трения покоя пропорционально модулю силы F д давления, производимого телом на опору. По третьему закону Ньютона сила Fд давления тела на опору равна по модулю силе N реакции опоры. Поэтому максимальная сила трения покоя пропорциональна силе реакции опоры. Для модулей этих сил справедливо следующее соотношение: Fп=fпN,     (2.19) где fп — безразмерный коэффициент пропорциональности, называемый коэффициентом трения покоя. Значение этого коэффициента зависит от материала и состояния трущихся поверхностей. Определить значение коэффициента трения покоя можно следующим образом. Пусть тело (плоский брусок) лежит на наклонной плоскости АВ (рис. 23). На него действуют три силы: сила тяжести F, сила трения покоя Fп и сила реакции опоры N. Нормальная составляющая Fп силы тяжести представляет собой силу давления Fд, производимого телом на опору, т. е. FН=Fд.    (2.20) Тангенциальная составляющая Fт силы тяжести представляет собой силу, стремящуюся сдвинуть тело вниз по наклонной плоскости. При малых углах наклона a сила F т уравновешивается силой трения покоя Fп и тело на наклонной плоскости покоится (сила N реакции опоры по третьему закону Ньютона равна по модулю и противоположна по направлению силе Fд, т. е. уравновешивает ее). Будем увеличивать угол наклона a до тех пор, пока тело не начнет скользить вниз по наклонной плоскости. В этот момент Fт=Fпmax    (2.21) Подставив в формулу (2.19) выражения (2.20) и (2.21), получим fп=Fт/Fн    (2.22) Из рис. 23 видно, что F т=Fsina = mg sina; Fн=Fcosa = mg cosa. Подставив эти значения Fт И Fн в формулу (2.22), получим fн=sina/cosa=tga.    (2.23) Измерив угол a, при котором начинается скольжение тела, можно по формуле (2.25) вычислить значение коэффициента трения покоя fп. Виды кинематического трения Трение скольжения возникает при скольжении одного твердого тела по поверхности другого. Закон для трения скольжения имеет вид Fc= fcN,     (2.24) где Fc — модуль силы трения скольжения; fc — безразмерный коэффициент трения скольжения; N — модуль силы реакции опоры. Значение f c зависит от того, из каких веществ изготовлены трущиеся поверхности и от качества их обработки. Если сделать поверхности более гладкими, значение fc уменьшится. Однако уменьшать шероховатость поверхностей можно лишь до определенного предела, так как при очень гладких (например, полированных) поверхностях значение fc вновь увеличивается. Происходит это потому, что молекулы тел с гладкими поверхностями близко подходят друг к другу и силы молекулярного притяжения между ними вызывают «прилипание» тел, препятствующее их скольжению. Трение качения возникает при качении (без скольжения) твердых тел круглой формы по поверхности других твердых тел. Причина появления трения качения заключается в следующем. Под действием силы тяжести круглое твердое тело (например, шар или колесо), находящееся на плоской поверхности, деформируется, вследствие чего оно опирается не на одну точку, а на площадку больших или меньших размеров. Это приводит к тому, что, когда тело начинает катиться, точка А приложения реакции опоры смещается немного вперед от вертикали, проходящей через центр тяжести тела, а линия действия силы реакции опоры R отклоняется немного назад от этой вертикали (рис. 24). При этом нормальная составляющая Rн = N реакции опоры компенсирует силу тяжести F (т.е. Rн =-F), а не скомпенсированная тангенциальная составляющая Rт реакции опоры направлена против движения тела и играет роль силы трения качения Fк. Модуль силы трения качения Fк определяют по закону Fк = Kк·N/r     (2.25) где Kк-безразмерный коэффициент трения качения; N=Rн — модуль нормальной составляющей силы реакции опоры; r — радиус катящегося тела. Если мы сравним между собой коэффициенты всех видов внешнего трения для каких-либо двух материалов, из которых изготовлены соприкасающиеся тела, то увидим, что f п>fc>Kk, т. е. при прочих равных условиях наибольшим является трение покоя, а наименьшим — трение качения. Роль смазки С целью уменьшения внешнего трения между соприкасающимися поверхностями твердых тел вводят смазку, т. е. вязкую жидкость, которая прилипает к твердым телам и образует между их поверхностями слой большей или меньшей толщины. При этом трение возникает уже не между твердыми телами, а между слоями смазки, что и приводит к значительному уменьшению силы трения. Внешнее трение называют сухим, если смазка вообще отсутствует, гидродинамическим, если слой смазки толстый, граничным, если слой смазки очень тонкий. Силы сопротивления движению тел в жидкостях и газах Сила сопротивления движению возникает и при движении твердых тел в жидкостях и газах. В данном случае трение покоя вообще отсутствует, так как в жидкости или в газе сколь угодно малая сила может вывести тело из состояния покоя, сообщив ему ускорение. Сила сопротивления, возникающая в жидкости или газе, всегда направлена против движения тела, по касательной к его поверхности и зависит от скорости движения тела. При небольших скоростях движения сила сопротивления F c пропорциональна скорости, а при больших скоростях — Fc пропорциональна квадрату скорости. В газах, из-за их малой плотности, тело может развить большую скорость, поэтому сила сопротивления Fc=-k1v2. В жидкостях плотность вещества велика, тело не может развить большую скорость, а потому Fc=-k2v. В последних формулах коэффициенты пропорциональности k1 и k2 зависят от рода жидкости или газа и их температуры. Наблюдения показывают, что сила сопротивления движению в жидкостях или газах в значительной степени зависит также от формы движущегося тела. Геометрическую форму тела, при которой сила сопротивления движению со стороны среды мала, принято называть обтекаемой. Вопросы для самоконтроля: Какие силы называют силами трения? Какое превращение энергии происходит в результате действия этих сил? Какое трение называют внешним? внутренним? Назовите виды внешнего трения. Когда они возникают? Какие существуют виды кинематического трения? Охарактеризуйте трения покоя. Напишите формулу закона, определяющего модуль силы трения покоя. Что представляет собой коэффициент трения покоя? От чего зависит его значение? Сделав чертеж и расчет, объясните, как на опыте определяют значение коэффициента трения покоя. Охарактеризуйте трение скольжения. Напишите формулу закона, определяющего модуль силы трения скольжения. Что собой представляет коэффициент трения скольжения? От чего зависит его значение? Охарактеризуйте трение качения. Сделав чертеж, объясните природу силы трения качения, т. е. причину возникновения этой силы. Напишите формулу закона, определяющего модуль силы трения качения. Объясните роль смазки. Какое трение называют сухим? гидродинамическим? граничным? Существует ли трение покоя в жидких и газообразных средах? От чего зависит сила сопротивления движению тела в жидкости и газе? Напишите формулы, по которым определяют модули этих сил. Как влияет форма тела на силу сопротивления в жидкости или газе?

Калькулятор коэффициента трения | Универсальные конусы

Сопротивление относительному движению между любыми двумя соприкасающимися поверхностями под нагрузкой обычно возникает в результате механического сцепления острых неровностей на двух сопрягаемых поверхностях и называется трением.

Рис. 1. Коэффициент трения

Сопротивление трению математически определяется для блока, движущегося по плоской поверхности, как отношение силы скольжения (Fs) к контактной силе (Fc)
т. е. μ = Fs ÷ Fc (рис. 1)
(где «μ» называется коэффициентом трения)

Если блок расположен на наклонной поверхности, «μ» также равно тангенсу угла наклона (θ) в точке перехода между относительным скольжением и условия удержания для этих двух материалов (рис. 1)

Например: для коэффициента трения 1,0 этот угол равен 45°

‘μ’ может быть изменен путем изменения контактирующих материалов, их относительной шероховатости поверхности или введения постороннего вещества, такого как в качестве смазки или химического агента между двумя поверхностями.

Две чистые, идеально гладкие и бесконечно твердые поверхности не будут оказывать сопротивления относительному движению (μ = 0).

Две шероховатые соединительные поверхности, соединенные вместе с жидкостью с высоким сдвиговым усилием (такой как патока), могут привести к сопротивлению трения (‘μ’) больше 1, то есть: сила, необходимая для вызывания относительного движения, может быть больше, чем сила контакта сила между ними.

Проблемы трения

Трение всегда будет приводить к износу между двумя движущимися поверхностями, находящимися в контакте и под нагрузкой, например, в подшипниках, и этот износ в конечном итоге приведет к отказу в работе, если между двумя сопрягаемыми поверхностями важна стабильность размеров.

Трение также приводит к повышению температуры и шума, что обычно приводит к потерям мощности и энергии и, следовательно, к снижению эффективности работы.

Преимущества трения

Сопротивление трению полезно в приводных механизмах, предназначенных для проскальзывания при чрезмерных нагрузках, таких как сцепление, или там, где требуется регулируемое сцепление, например тормозные системы.

Самоудерживающиеся конусы

Рис. 2. Самоудерживающиеся конусы

Особым случаем полезного использования трения являются «самоудерживающиеся» конусы (рис. 2) для легкой сборки и разборки компонентов станка/оборудования, таких как сверлильные патроны и принадлежности задней бабки токарного станка.

Самоудерживающийся «конус» представляет собой точно обработанный сужающийся вал и сопрягаемую втулку (оба сухие и чистые), которые соединяются друг с другом за счет коэффициента трения между двумя поверхностями (вала и втулки) и усилия сборки (F ). Если конус обработан правильно, для разделения вала и втулки потребуется одно и то же усилие (F).

Если угол конусности «точно правильный», вал или втулка будут способны приводить в движение другой вал или втулку без дополнительной помощи для легких условий эксплуатации и при этом легко разъединяться без повреждения какой-либо из сопрягаемых поверхностей.

Важно помнить, что простой самоудерживающийся конус способен передавать усилие, достигаемое только за счет «фрикционного» захвата, и, таким образом, его приводная способность ограничена. Для тяжелых условий эксплуатации конус обычно снабжен шпонкой, а фрикционная рукоятка обеспечивает только удерживающую способность.

Конус Морзе

В середине 19-го века Стивен Морс разработал самоудерживающийся конус, основанный на включенном (диаметральном) наклоне 5/8 дюйма для каждого фута контактной длины (≈3°), который стали известны как конус Морзе. Конус Морзе основан на коэффициенте трения между сопрягаемыми поверхностями 0,8 (т. е. чистая, сухая, шлифованная, углеродистая сталь).

Существует 8 калибровочных классов для конуса Морзе (0-7) с использованием стандартных диаметров и сопряженных длин в зависимости от грузоподъемности. Они перечислены следующим образом:

Класс:	0	1	2	3	4	5	6	7
Малый диам. Ø̂	0,252	0,369	0,572	0,778	1,02	1,475	2,116	2,75
Большой диам. №	0,3561	0,475	0,7	0,938	1,231	1,748	2,494	3,27
Длина заглушки (Lᴘ)	2	2,125	2,5625	3,1875	4,0625	5.1875	7,25	10

Размеры в приведенной выше таблице указаны в дюймах
Диаметры, указанные в приведенной выше таблице (Ø̂ и Ø̌), указаны на обоих концах длины плунжера (рис. 2)
Длина плунжера (Lᴘ) — это длина контакта между валом и втулкой.

Но Стивен Морс был не единственным разработчиком самоудерживающихся конусов, и они не должны применяться только к углеродистой стали; они действительно универсальны и могут быть применены к любой комбинации материалов, как показано в Трении.

Конус Ярно

Оскар Джеймс Бил оптимизировал размер конуса Морзе, который настолько умен, что, хотя он имеет практически такой же угол, как конус Морзе (2,8642 ° против 2,981 °), он был индивидуально признан под его псевдонимом как «Ярно Тапер».

Конструкция конуса

Конус Морзе составляет ≈3° не просто так. Оптимальное соотношение между углом конуса, длиной и коэффициентом трения обеспечивает способность самофиксации, для которой предназначен конус. Все это основано на той же нагрузке на извлечение вала, что и при вставке, и коэффициенте трения для углеродистой стали (0,8).

Правила для коэффициента трения

1) Для условий незначительной деформации поверхности коэффициент трения пропорционален контактному поверхностному давлению
2) Трение не зависит от площади контакта с поверхностью
3) В условиях незначительного нагрева поверхности и/или деградации трение не зависит от относительной скорости (между двумя поверхностями).

Калькулятор коэффициента трения – Техническая помощь

Единицы измерения

Вы можете использовать любые единицы измерения, но вы должны быть последовательны.

Угол естественного откоса

Сцепление

Поскольку коэффициент(ы) трения между любыми двумя материалами, скользящими относительно друг друга и под нагрузкой, представляет собой их угол естественного откоса, вы можете точно найти значение «μ» для любого два материала, как описано ниже (рис. 3).

Рис. 3. Измерение сопротивления

1.1) Изготовить регулируемое наклонное основание из одного из материалов с соответствующим состоянием поверхности и отделкой

1.2) Снова изготовьте блок из другого материала с правильным состоянием поверхности и отделкой

1.3) Отрегулируйте наклонное основание до горизонтального уклона

1.4) Поместите блок на наклонное основание

1.5) Поднимите один конец наклонное основание медленно и осторожно, пока блок не начнет скользить

1.6) Повторите 1.5) выше столько раз, сколько необходимо, чтобы обеспечить точное значение «θ»

1.7) Измерьте размеры «x» и «y» (рис. 3 )

1.8) Рассчитайте: μ = y÷x (используя вариант расчета «Фрикционное скольжение»)

Вышеупомянутое «μ» является коэффициентом «трения», иногда называемым коэффициентом «инициации трения».

Трение

Для расчета коэффициента трения для тех же материалов требуется немного больше внимания, но точный результат можно получить следующим образом (рис.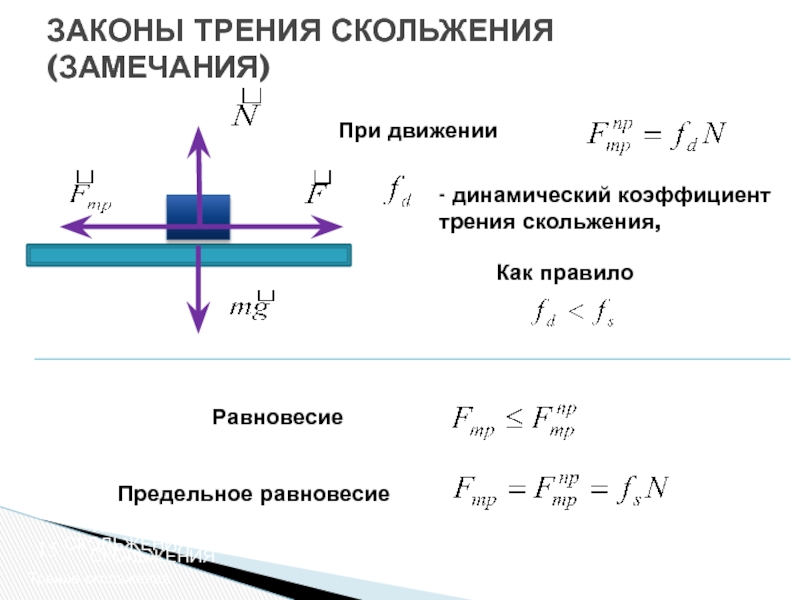 4):

Рис. 4. Измерение трения

2.1) Возьмите указанное выше наклонное основание и заблокируйте

2.2) Поднимите один конец наклонного основания на угол, больший, чем угол наклона (выше)

2.3) Поместите блок на наклонное основание в самой высокой точке (рис. 4) и дайте ему скользить

2.4) Уменьшите угол наклона наклонного основания, пока блок скользит, пока он не остановится «в середине скольжения» на своем собственный

2.5) Повторяйте 2.3) и 2.4) выше, пока вы не сможете начать скольжение и снова остановить его «в середине скольжения», просто отрегулировав угол основания

2.6) Когда вам удалось найти точный угол, под которым блок останавливается в середине салазок, вы измеряете размеры «x» и «y» (рис. 4)

2.7) Рассчитайте: μ = y÷x (используя опцию расчета «Фрикционное скольжение»)

Вышеупомянутое «μ» является коэффициентом «трения».

Коэффициент трения обычно примерно на 10 % больше, чем коэффициент трения, однако это очень сильно зависит от двух материалов и их относительного состояния поверхности.

Чем выше точность измерения указанных выше углов (θ), тем точнее будут ваши коэффициенты.

Фрикционные салазки

После определения значения μ (см. Угол естественного откоса выше) вы можете ввести это значение в параметр расчета «Фрикционное скольжение» вместе с наклоном и расстоянием скольжения, и Трение сообщит вам, как быстро блок достигнет дна вместе с ускорением и кинетической энергией.

Конусы

Хотя конус Морзе изначально был разработан для поверхностей из углеродистой стали (μ = 0,8), калькулятор коэффициента трения может предсказать угол конуса, изготовленного для любого коэффициента трения, т. е. любой комбинации материалов и состояния поверхности, но с одинаковым самоудерживающая способность, как у конуса Морзе того же класса.

Калькулятор коэффициента трения дает вам возможность выбрать рекомендуемый (CalQlata) коэффициент трения с помощью ряда вариантов комбинации материалов, или вы можете ввести свое собственное независимое значение. В то время как Friction будет принимать любое значение для «μ» в соответствии с нашим принципом «GiGo», значения меньше или равные 0 приведут к ошибочным вычислениям или отрицательным углам, а значения для «μ» больше 3, хотя теоретически правильные, будут обычно дают нереальные результаты.

Расчет в этом параметре применяет модифицированный угол конуса (θ) к тому же внутреннему диаметру (Ø̂; рис. 2) и площади контактной поверхности, что и исходный конус Морзе для выбранного сплава («G» см. «Конус Морзе» выше). Другими словами, если вы изготовите конус в соответствии с размерами, указанными калькулятором коэффициента трения для выбранных вами материалов (‘μ’), сборка будет иметь такую ​​же «самоудерживающую» способность, что и конус Морзе из углеродистой стали для той же марки. .

Примечание: включенный угол, используемый в качестве основы для конуса Морзе в калькуляторе коэффициента трения, равен 2,9.745503204919°, так как это оптимальный угол для коэффициента трения 0,8 в его конструкциях.

Дополнительная литература

Дополнительную информацию по этому вопросу можно найти в справочных публикациях ^{(2 и 3)}

Расчет надлежащего сопротивления качению: более безопасное движение при погрузочно-разгрузочных работах

Трение играет важную роль в промышленном мире, и также в повседневной жизни. Трение — это сопротивление скольжению, качению или плавному движению объекта из-за его контакта с другим объектом. Это может быть как полезно (когда мы тормозим машину, чтобы остановиться), так и вредно (когда мы пытаемся ехать одной ногой на педали тормоза). В этой статье основное внимание будет уделено сопротивлению качению, важному аспекту промышленных колес.

Сопротивление качению – это мера тормозящего действия поверхности пола на поверхности контакта колес с протектором. Обычно он выражается в фунтах и ​​является мерой энергии, рассеиваемой на единицу пройденного пути. Рассмотрим шину, катящуюся по ровной поверхности. Шина будет до некоторой степени деформироваться, и эта деформация вызовет некоторое сопротивление движению качения. Плоская поверхность также может деформироваться, особенно если она относительно мягкая. Песок является хорошим примером мягкой, устойчивой к качению поверхности. Ехать на велосипеде по асфальтированной дороге гораздо проще, чем по белому песчаному пляжу. Сопротивление качению измеряет потерю энергии, когда что-то катится на определенное расстояние.

В мире промышленных колес контакт качения в идеале не должен оказывать сопротивления движению (за исключением случаев, когда мы хотим, чтобы что-то оставалось на месте). Но реальность так не работает. Энергия рассеивается:

• Из-за трения на поверхности контакта
• Из-за упругих свойств материалов
• Из-за шероховатости поверхности качения.

Как можно видеть на этом преувеличенном изображении, и колеса, и поверхность подвергаются деформации в степени, определяемой упругими свойствами двух поверхностей.

Трение качения и трение скольжения

Коэффициент трения качения не следует путать с коэффициентом трения скольжения или, как его часто называют, коэффициентом трения. Коэффициент трения (скольжения) — безразмерное число, описывающее отношение силы трения между двумя телами к силе, прижимающей их друг к другу. Коэффициент трения (скольжения) зависит от используемых материалов; например, сталь на льду имеет низкий коэффициент трения, а резина на дорожном покрытии имеет высокий коэффициент трения.

На приведенной ниже диаграмме рассматривается трение скольжения. Представьте себе силу, необходимую для того, чтобы толкнуть тяжелую коробку по полу. Статическое трение требует определенной приложенной силы, чтобы заставить коробку двигаться. После движения динамическое трение требует относительно постоянной силы для поддержания этого движения. В этом примере толкающий человек создает «приложенную силу», а коробка весом «N» и пол создают «силу трения», которая стремится сопротивляться этому движению.

Причина, по которой мы используем колеса для погрузочно-разгрузочных работ, заключается в том, что для перемещения объекта требуется значительно меньшее усилие (сила). Представьте, что вы толкаете холодильник или пианино без колес! Кроме того, подумайте, насколько легче было бы толкать коробку (упомянутую ранее) по полу, если бы она была на колесах.

Сила, необходимая для толкания/тяги колесного оборудования, всегда максимальна в начале, непосредственно перед началом движения. Эргономисты называют эту силу начальной или стартовой силой. К счастью, первоначальные силы обычно действуют лишь короткое время и падают до уровней устойчивых сил, как только начинается ускорение и преодолеваются любые механические помехи в начале движения. При движении с относительно постоянной скоростью требуемая сила обычно ниже. Эта сила называется устойчивой или катящейся силой.

Для облегчения качения

Чтобы уменьшить усилие, необходимое для преодоления сопротивления качению колеса, можно выбрать колесо с более низким коэффициентом сопротивления качению (например, колесо из кованой стали имеет коэффициент сопротивления качению 0,019 дюйма) или использовать колесо большего диаметра. Оптимизируйте, выполнив и то, и другое — используйте колесо самого большого практического диаметра с самым низким коэффициентом сопротивления качению.

Выбор ступичного подшипника с точки зрения сопротивления качению не так важен, как материал и диаметр колеса. Антифрикционные подшипники не так сильно влияют на сопротивление качению, как такие факторы, как материал и диаметр колеса. Однако выбор подшипника может быть очень важен по другим причинам, таким как грузоподъемность, ручное или буксируемое управление, наличие ударных нагрузок или боковых нагрузок, а также необходимость технического обслуживания. Как можно предположить, более мягкий материал протектора колеса обычно приводит к большему сопротивлению качению, чем очень прочный/твердый материал протектора колеса.

Основные факторы сопротивления качению

Наиболее важные факторы, которые следует учитывать: , чистота, уклон и т.д. .).

Факторы, которыми обычно можно пренебречь при расчетах:

• Тип подшипника
• Консистентная смазка или воздействие смазки
• Температура окружающей среды
• Пробуксовка колес.

Рекомендации по эргономике

Общие рекомендации по эргономике для максимальных (ручных) толкающих усилий можно найти в интерактивных таблицах в разделе Liberty Mutual Manual Material Handling на веб-сайте.

Использование калькулятора, представленного на этом веб-сайте, даст результаты, предлагающие процент населения (мужчины или женщины могут быть указаны), которые могут безопасно выполнять задачу толкания или тяги. Переменные включают силу толкания или тяги (которая исходит из расчетов, описанных в этой статье), высоту, на которой прикладывается сила, продолжительность толкания или тяги и частоту.

В целом любой результат, превышающий 75% женского населения, будет приемлемым с точки зрения безопасности. В частности, использование этого в качестве руководства в значительной степени предотвратит травмы поясницы. Конечно, никогда не бывает гарантии предотвращения травм спины.

Общие рекомендации для ручных и механических операций:

• Выберите подходящее колесо/протектор на основе максимальной нагрузки и состояния пола.

• При выборе эластичного протектора, как правило, для защиты пола, необходимо учитывать:

• Диапазон температур
• Ударопрочность
• Влагостойкость и вода
• Устойчивость к свету, химическим веществам
• Отскок.
• Выберите максимально возможный/практичный диаметр колеса.
• Выберите колесо с наименьшим коэффициентом сопротивления качению.
• Рассчитайте сопротивление качению (имейте в виду, что при запуске усилие будет в 2-2,5 раза выше).
• Используйте коэффициент запаса при расчете требуемой мощности для привода.
• Не забудьте учесть любой уклон (a°). Рассчитанное сопротивление качению будет увеличиваться вверх по склону и уменьшаться вниз по склону (F = Fx/cosa). Например, наклон 10° увеличит требуемую силу (F = Fx/cos10° = Fx/0,9848 = 1,015Fx). Если угол наклона увеличить до 30°, требуемая сила значительно возрастет, с 1,015Fx до 1,155Fx (приблизительно 14%).
• Для буксировки с механическим приводом очень важен выбор ступичного подшипника! Обязательно выбирайте подшипники, которые выдержат высокие скорости, боковые нагрузки и непрерывную работу.

Сопротивление качению играет важную роль при обработке материалов. Независимо от того, будут ли грузы буксироваться или толкаться вручную, правильный выбор колес существенно повлияет на результаты. Использование описанных здесь принципов позволит сделать правильный выбор.

Дэйв Липперт — вице-президент по маркетингу, а Джефф Спектор — технический директор компании Hamilton Caster. С ними можно связаться по адресу [email protected] и [email protected].

---

Расчет силы прокатки

Для количественной оценки сопротивления качению промышленных колес используется «коэффициент трения качения». Это число, которое было определено эмпирически для различных материалов и может варьироваться в зависимости от скорости колеса, нагрузки на колесо и материала, с которым колесо соприкасается. На приведенной ниже диаграмме неудивительно, что самый мягкий материал протектора (резина) имеет самый высокий коэффициент трения, а самый твердый материал (кованая сталь) — самый низкий.

*Полиуретан имеет диапазон значений коэффициента в зависимости от выбранного поли материала.

Допущения

Общая нагрузка:

• 1200 фунтов

Материал пола: Сталь 90 003

Скорость колеса: 3 мили в час

Формула

• F = f x W/R

F = сила, необходимая для преодоления трения качения

f = коэффициент трения качения (единицы измерения должны совпадать с R (радиус))

W = нагрузка на колесо

R = радиус колеса. полиуретановые колеса диаметром 85А на ровном стальном полу.

Шаг 1: На основе данной нагрузки мы можем определить нагрузку на колесо «W».

W = 4800 фунтов/4 (колеса) = 1200 фунтов на каждое колесо

Шаг 2: Из предоставленной таблицы найдите коэффициент сопротивления качению «f».

f = 0,047 (дюйма) [Примечание: полиуретан имеет диапазон значений коэффициента в зависимости от выбранного материала. ]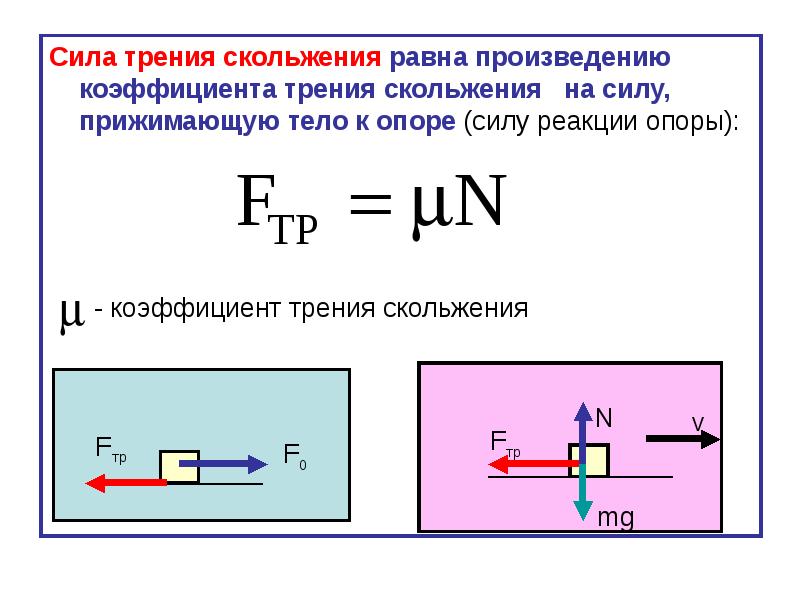

Шаг 3: Мы знаем, что радиус составляет ½ 8 дюймов. диаметр колеса.

R = 4 дюйма

Шаг 4: Рассчитайте силу «F», необходимую для преодоления трения качения колеса.

F = 0,047 x 1200/4 = 14,1 фунта (Примечание: Это для каждого отдельного колеса.)

Шаг 5: Рассчитайте усилие, необходимое для перемещения указанного загруженного грузовика.

Сопротивление на колесо составляет 14,1 фунта. Поскольку у грузовика четыре колеса, общая сила, необходимая для перемещения (продолжительного движения) грузовика, составляет 14,1 х 4 = 56,4 фунта.

Диаметр колеса играет важную роль в силе, необходимой для перемещения груза. В примере выше, используя 16-дюймовый. диаметр колеса (с радиусом 8 дюймов) уменьшил бы требуемую силу вдвое. На самом деле, это закономерность, установленная уравнением. Каждое удвоение диаметра колеса приводит только к половине силы, необходимой для перемещения колеса или поддержания движения.