С использованием Л. с. были объяснены Холла эффект, нормальный Зеемана эффект, диамагнетизм и др. эффекты, связанные с взаимодействием в веществе движущихся зарядов и магнитного поля.
Билет № 1, 4 (вопрос 3). Задача на формулу силы Лоренца
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Билет № 1, 4 (вопрос 3)
Задача на формулу силы Лоренца
q
B
sin
Fл
Fл – сила Лоренца (Н)
— скорость (м/с)
В – магнитная индукция (Тл)
α – угол между скоростью и магнитной индукцией
Билет № 2, 5 (вопрос 3)
Задача на закон Ома для участка цепи
с учетом формулы сопротивления проводника
U
I
R
R
S
I – сила тока (А)
U – напряжение (В)
R –сопротивление (Ом)
ℓ — длина (м)
S – сечение (мм2)
ρ – удельное сопротивление ( ом мм2/м)
Билет № 3, 7(вопрос 3)
Задача на закон Ома для полной цепи
E
I
R r
I –сила тока (А)
Е –ЭДС (В)
r – внутреннее сопротивление (Ом)
R – внешнее сопротивление (Ом)
Билет № 8, 9(вопрос 3)
Задача на расчет цепи с последовательным
и параллельным соединением проводников
I
U
I1 I 2
U 1 U 2
R R R
1
U U U
1
U
I
R
I
1
2
R
2
I1 I 2
1
R
1
1
R
2
Билет № 10, 11 (вопрос 3)
Задача на радиоактивные превращения
1
1
H
1
0
4
2
n
He
0
1
e
масса
протон
заряд
7
3
Li
нейтрон
α -частица
β — частица
7
3
Li H n Be
1
1
1
0
7
4
Билет № 12, 14 (вопрос 3)
Задача на закон Ампера
I
B
sin
FА
Fа – сила Ампера (Н)
ℓ – длина проводника (м)
I — сила тока (А)
В – магнитная индукция (Тл)
α – угол между силой тока и магнитной индукцией
Задача на уравнение Менделеева-Клайперона
m
pV
RT
M
р – давление (Па)
V – объем (м3)
0
0
Т – абсолютная температура (К) T = t + 273
m – масса газа (кг)
М — молярная масса (кг/моль)
R – молярная газовая постоянная
R = 8,31 Дж / К моль
Билет № 15(вопрос 3)
Задача на первый закон термодинамики
U Q A Q U A
Q – количество теплоты (Дж)
U — изменение внутренней энергии (Дж)
А – работа (Дж)
А – работа газа (Дж)
Билет № 16, 19 (вопрос 3)
Задача на формулу Томсона
T 2 LC
1
2 LC
Т — период (с)
— частота (Гц)
С – емкость (Ф)
Билет № 17(вопрос 3)
Задача на закон Кулона
F k
r
1
2
F – сила (Н)
q – заряд (Кл)
r – расстояние между зарядами (м)
ε – диэлектрическая проницаемость
нм
2
k
9 10
9
Кл
2
2
Билет № 18(вопрос 3)
Задача на расчет массы, энергии и импульса фотона
Е h
m
h
c
2
Е – энергия фотона (Дж)
m – масса фотона (Кг)
р – импульс фотона (Кг /м с)
— частота (Гц)
— длина волны (м)
h — постоянная Планка
h h
p mc
c
h
с
34
6,6 10
Дж с
3 10 м
8
с
Билет № 20(вопрос 3)
Задача на уравнение Эйнштейна
h А 2
в
— частота (Гц)
А
— работа выхода (Дж)
в
m
2
2
Е к — кинетическая энергия электрона (Дж)
m
— масса электрона (кг)
— скорость электрона (м/с)
h
— постоянная Планка
2
English Русский Правила
Закон силы Лоренца: определение, уравнение и пример
ЦЕРН — один из самых известных и крупнейших ускорителей частиц в мире.
Эта лаборатория элементарных частиц была основана различными европейскими правительствами и стремится раскрыть больше секретов, скрытых в области физики элементарных частиц и стандартной модели. Большие ускорители частиц в центре работают, используя электрические и магнитные поля, чтобы воздействовать на частицы, разгоняя их до высоких скоростей и сталкивая частицы друг с другом. Это взаимодействие между заряженными частицами и электромагнитными полями называется сила Лоренца, , если вам интересно, как работает сила Лоренца и как она применяется в различных ситуациях, продолжайте читать!
Рис. 1 Невероятно сложное оборудование в центре ЦЕРН создано для использования силы Лоренца.
Определение закона силы Лоренца
Силу Лоренца можно определить следующим образом.
Сила Лоренца — это сила \(\vec{F}\) на заряженную частицу \(\vec{q}\), движущуюся со скоростью \(\vec{v}\) через магнитное поле \ (\vec{B}\) и электрическое поле \(\vec{E}\).
В частности, сила Лоренца учитывает действие и электрических и магнитных полей на заряженные частицы.
Уравнение закона силы Лоренца
Сила Лоренца принимает математическое уравнение
\[ \vec{F} = q\vec{E} + (q \vec{v} \times \vec{B} ),\]
где \(\vec{F}\) — вектор силы, действующей на заряженные частицы, измеренный в ньютонах \(\mathrm{N}\), \(q\) — заряд частиц, измеренный в кулонах \( \mathrm{C}\), \(\vec{v}\) — вектор скорости заряженной частицы, измеренный в \(\mathrm{\frac{m}{s}}\), \(\vec{B }\) — вектор магнитного поля, измеренный в теслах \(\mathrm{T}\), а \(\vec{E}\) — вектор электрического поля, измеренный в \(\mathrm{\frac{V}{m }}\).
Мы видим, что это уравнение состоит из двух компонентов; первый член в правой части представляет собой электрическую силу, тогда как второй член представляет собой магнитную силу.
Чтобы найти величину силы Лоренца, мы берем величину векторных величин, фигурирующих в приведенном выше уравнении.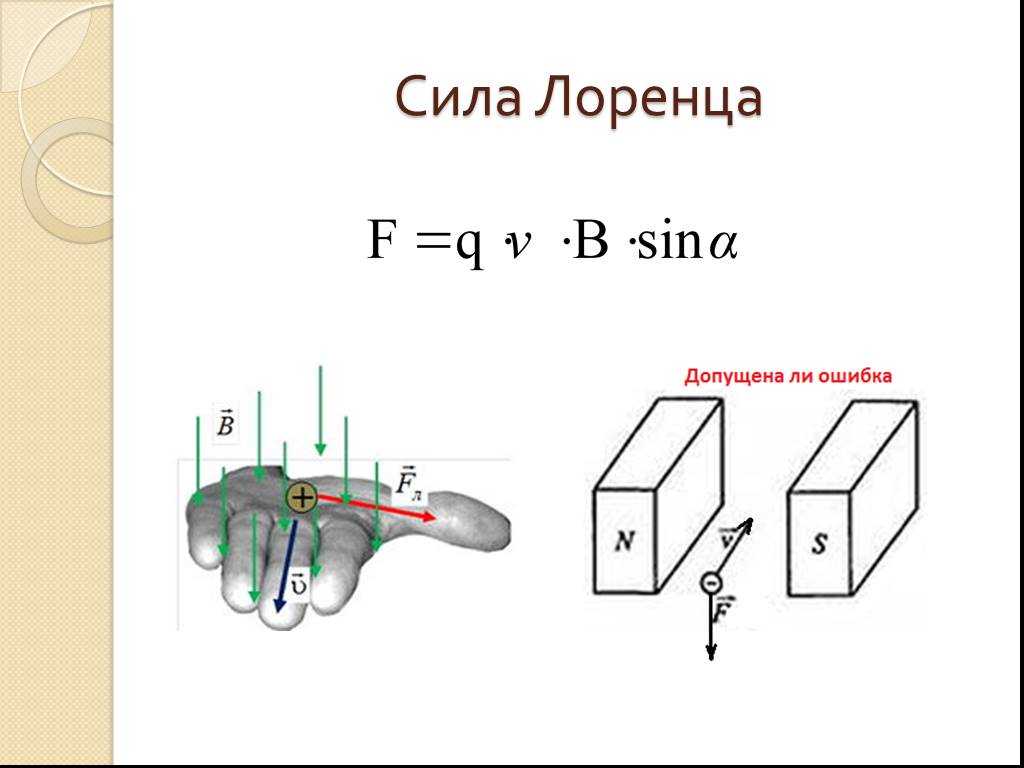
Для термина электрической силы это относительно просто, поскольку нам нужно только взять величину электрического поля \(|\vec{E}|\), умноженную на величину заряда \(q\).
С другой стороны, величина перекрестного произведения немного сложнее. Напомним, что при получении величины векторного произведения мы должны умножить величины двух векторов на синус угла между векторами. Это гарантирует, что мы берем перпендикулярные компоненты обоих векторов. Приходим к уравнению
\[ | \vec{a} \times \vec{b}| = |\vec{a}||\vec{b}| \sin(\theta),\]
где \(|\vec{a}|\) и \(|\vec{b}|\) — величины векторов \(\vec{a}\) и \(\vec{b}\) соответственно, а \(\theta\) — угол между двумя векторами.
Теперь мы можем применить это к нашему уравнению для силы Лоренца, чтобы найти, что величина силы Лоренца определяется выражением
\[ |\vec{F}| = q |\vec{E}|+ q|\vec{v}||\vec{B}|\sin(\theta),\]
, где \(\theta\) — угол между магнитным полем и скорость заряженной частицы, измеренная в радианах \(\mathrm{rad}\).
Поскольку \(q\) является скалярной величиной, нам не нужно ничего с ней делать.
Вывод закона силы Лоренца
Один из выводов, который можно сделать из определения силы Лоренца, — это скорость заряженной частицы при движении в магнитном поле. Если мы предположим, что электрического поля нет, а есть только магнитное поле, мы можем видеть из векторного произведения, что результирующая сила Лоренца, действующая на заряженную частицу, всегда перпендикулярна направлению движения частицы. Следствием этого является кривизна траектории заряженной частицы. С какой силой мы уже встречались ранее, которая также действует в направлении, перпендикулярном движению объекта? 92}{r},\]
где \(F_{\mathrm{cent}}\) — центростремительная сила, измеряемая в ньютонах, \(\mathrm{N}\), \(m\) — масса объекта, измеренная в \(\mathrm{kg}\), \(v\) — скорость объекта, измеренная в \(\mathrm{\frac{m}{s}}\), а \(r\) — радиус вращения измеряется в \(\mathrm{м}\).
Теперь, когда мы знаем, что заряженная частица находится во вращательном движении, мы можем приравнять величину силы Лоренца и центростремительной силы, чтобы найти величину результирующей скорости из-за взаимодействия заряженной частицы с магнитным полем.
Приравнивая и переставляя, находим 9{\bотмена{2}} \\v &= \frac{Bqr\sin(\theta)}{m}. \end{align}\]
При решении задач, связанных с любой из этих величин, мы можем изменить это уравнение, чтобы выделить величину, для которой нас интересует решение. Каково это количество, будет варьироваться от проблемы к проблеме.
Рис. 2. На электрон, движущийся в магнитном поле, действует сила Лоренца, вызывающая круговое движение.
Применение закона силы Лоренца
Во время экспериментов по физике в школе мы часто сталкиваемся с устройством, называемым электронно-лучевая трубка или электронная пушка. Эти устройства позволяют нам увидеть путь электронного луча, отклоняющегося из-за приложения внешнего электрического поля. Металлическая нить нагревается с одного конца, так что электроны в металле получают достаточную кинетическую энергию, чтобы вырваться на свободу. Поскольку электроны заряжены отрицательно, они притягиваются к положительно заряженному аноду на другом конце вакуумной трубки.
Кроме того, вакуумная камера, через которую проходят электроны, облицована флуоресцентным материалом, так что, когда электроны сталкиваются со стенками, они проявляются в виде света, видимого человеческим глазом. Наконец, искривление электронного пучка обусловлено взаимодействием силы Лоренца между заряженными электронами и окружающим электрическим полем. 9{-17} \, \mathrm{N} . \end{align} \]
Закон силы Лоренца – ключевые выводы
Уравнение силы Лоренца задается выражением \(\vec{F} = q\vec{E} + (q \vec{v} \times \vec{B} ) \).
Сила Лоренца учитывает действие как электрического, так и магнитного полей на заряженные частицы.
Величина силы Лоренца определяется выражением \(|\vec{F}| = q |\vec{E}|+ q|\vec{v}||\vec{B}|\sin( \тета)\).
Круговая скорость заряженной частицы, движущейся в магнитном поле, равна \(v = \frac{Bqr\sin(\theta)}{m}\).
Сила Лоренца заставляет электронный пучок в электронно-лучевой пушке искривляться.
Ссылки
- Рис. 1 — ЦЕРН, Wikimedia Commons (https://commons.wikimedia.org/wiki/File:CERN_Large_Hadron_Collider.jpg) org/licenses/by-sa/4.0/)
- Рис. 2 — Круговое движение электрона, StudySmarter Originals.
- Рис. 3 — Электронная пушка, Wikimedia Commons (https://commons.wikimedia.org/wiki/File:Electron_gun_jyu.jpg), лицензия CC BY-SA 3.0 (https://creativecommons.org/licenses/by -са/3.0/)
Калькулятор силы Лоренца в App Store
Описание
Калькулятор силы Лоренца представляет собой физико-математический калькулятор для быстрого и простого определения магнитного поля, заряженных частиц, силы или скорости частиц.
Особенности:
— Мгновенный расчет
— Результат можно скопировать в другое приложение
— Формула включена в качестве ссылки
— Поддержка до 16 знаков после запятой
— Поддержка различных единиц измерения для каждого ввода
В физике (особенно в электромагнетизме) Сила Лоренца представляет собой комбинацию электрической и магнитной сил на точечный заряд из-за электромагнитных полей.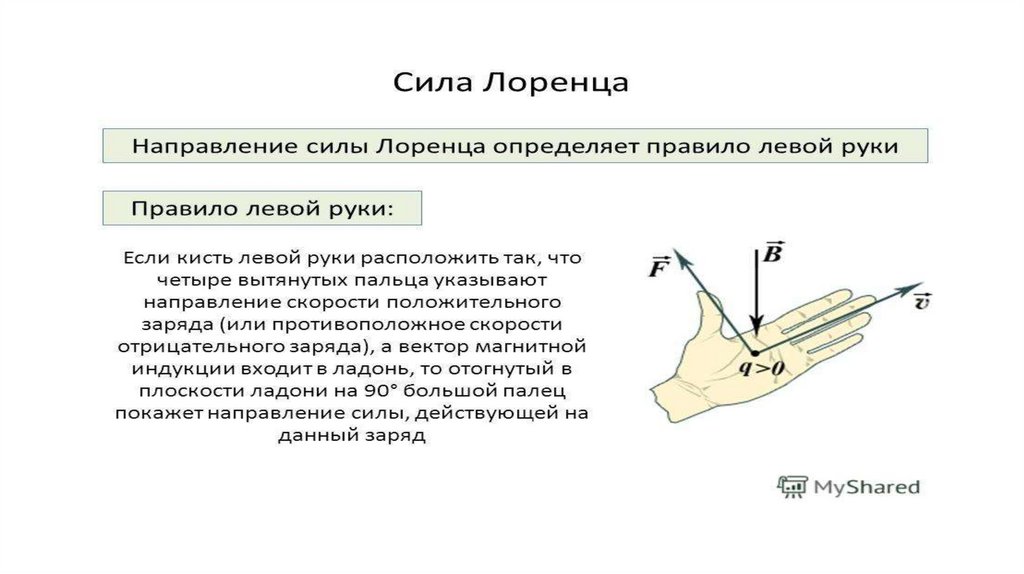
На частицу с зарядом q, движущуюся со скоростью v в присутствии электрического поля E и магнитного поля B, действует сила
Сила Лоренца — это сила, приложенная к заряженной частице, движущейся со скоростью v вертикально в магнитном поле. Положительно заряженная частица будет ускоряться в той же линейной ориентации, что и поле E, но будет искривляться перпендикулярно как к вектору мгновенной скорости v, так и к полю B в соответствии с правилом правой руки.
Уравнение силы Лоренца
F = q v B sin(α)
где:
q — заряд частицы
v — скорость частицы
B — напряженность магнитного поля
α — угол между направлением траектории частицы и направлением магнитного поля
F — результирующая сила
Спасибо за вашу поддержку и посетите nitrio.com для получения дополнительных приложений для ваших устройств iOS.
Версия 1.1
— Обновление для новейших устройств
— Исправлена ошибка
Разработчик, Nitrio, указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные не собираются
Разработчик не собирает никаких данных из этого приложения.
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше
Информация
- Продавец
- Тан Чиа Линг
- Размер
- 8,7 МБ
- Категория
- Утилиты
- Возрастной рейтинг
- 4+
- Авторское право
- © Тан Чиа Лин
- Цена
- 2,99 $
- Сайт разработчика
- Тех.
