Гравитационная постоянная — Википедия

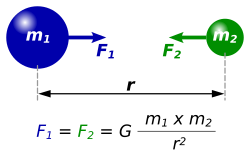Гравитационная постоянная G лежит в основе закона всемирного тяготения.

Гравитацио́нная постоя́нная, постоянная Ньютона (обозначается обычно G, иногда G_N или γ)^[1] — фундаментальная физическая постоянная, константа гравитационного взаимодействия.

Согласно Ньютоновскому закону всемирного тяготения, сила гравитационного притяжения F между двумя материальными точками с массами^[2]m₁ и m₂, находящимися на расстоянии r, равна:

F=Gm1m2r2.{\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}.}

Коэффициент пропорциональности G в этом уравнении называется гравитационной постоянной. Численно она равна модулю силы тяготения, действующей на точечное тело единичной массы со стороны другого такого же тела, находящегося от него на единичном расстоянии.

Точность измерений гравитационной постоянной на несколько порядков ниже точности измерений других физических величин^[3].

В единицах Международной системы единиц (СИ) рекомендованное Комитетом данных для науки и техники (CODATA) на 2018 год значение гравитационной постоянной^[4]:

G = 6,67430(15)·10⁻¹¹ м³·с⁻²·кг⁻¹, или Н·м²·кг⁻².

Гравитационная постоянная является основой для перевода других физических и астрономических величин, таких, например, как массы планет во Вселенной, включая Землю, а также других космических тел, в традиционные единицы измерения, например, килограммы. При этом из-за слабости гравитационного взаимодействия и результирующей малой точности измерений гравитационной постоянной отношения масс космических тел обычно известны намного точнее, чем индивидуальные массы в килограммах.

Гравитационная постоянная является одной из основных единиц измерения в планковской системе единиц.

Гравитационная постоянная фигурирует в современной записи закона всемирного тяготения, однако отсутствовала в явном виде у Ньютона и в работах других ученых вплоть до начала XIX века. Гравитационная постоянная в нынешнем виде впервые была введена в закон всемирного тяготения, по-видимому, только после перехода к единой метрической системе мер. Возможно впервые это было сделано французским физиком Пуассоном в «Трактате по механике» (1809), по крайней мере никаких более ранних работ, в которых фигурировала бы гравитационная постоянная, историками не выявлено

[источник не указан 883 дня].

В 1798 году Генри Кавендиш поставил эксперимент с целью определения средней плотности Земли с помощью крутильных весов, изобретённых Джоном Мичеллом (Philosophical Transactions 1798). Кавендиш сравнивал маятниковые колебания пробного тела под действием тяготения шаров известной массы и под действием тяготения Земли. Численное значение гравитационной постоянной было вычислено позже на основе значения средней плотности Земли. Точность измеренного значения G со времён Кавендиша увеличилась, но и его результат

[5] был уже достаточно близок к современному.

Значение этой постоянной известно гораздо менее точно, чем у всех других фундаментальных физических постоянных, и результаты экспериментов по её уточнению продолжают различаться^[6][7].

В то же время известно, что проблемы не связаны с изменением самой постоянной от места к месту и во времени (неизменность гравитационной постоянной проверена с точностью до ΔG/G ~ 10⁻¹⁷), но вызваны экспериментальными трудностями измерения малых сил с учётом большого числа внешних факторов^[8]. В будущем, если опытным путём будет установлено более точное значение гравитационной постоянной, то оно может быть пересмотрено

[9]^[10].

В 2000 г. было получено значение гравитационной постоянной G=6,67390×10−11{\displaystyle G=6{,}67390\times 10^{-11}} см³ г⁻¹ c⁻², с погрешностью 0,0014 %^[11].

В 2013 г. значение гравитационной постоянной было получено группой ученых, работавших под эгидой Международного бюро мер и весов:

G = 6,67554(16) × 10⁻¹¹ м³·с⁻²·кг⁻¹ (стандартная относительная погрешность 25 ppm (или 0,0025 %), первоначальное опубликованное значение несколько отличалось от окончательного из-за ошибки в расчётах и было позже исправлено авторами)^[12][13].

В июне 2014 года в журнале «Nature» появилась статья итальянских и нидерландских физиков, где были представлены новые результаты измерения G, сделанные при помощи атомных интерферометров^[14]. По их результатам

G = 6,67191(99) × 10⁻¹¹ м³·с⁻²·кг⁻¹ с погрешностью 0,015 % (150 ppm).

Авторы указывают, что поскольку эксперимент с применением атомных интерферометров основан на принципиально других подходах, он помогает выявить некоторые систематические ошибки, не учитывающиеся в других экспериментах.

В августе 2018 года в журнале «Nature» физиками из Китая и России были опубликованы^[15] результаты новых измерений гравитационной постоянной с улучшенной точностью (погрешность 12 ppm, или 0,0012 %). Были использованы два независимых метода — измерение времени качаний торсионного подвеса и измерение углового ускорения, получены значения G, соответственно:

G = 6,674184(78) × 10⁻¹¹ м³·с⁻²·кг⁻¹;

G = 6,674484(78) × 10⁻¹¹ м³·с⁻²·кг⁻¹.

Оба результата в пределах двух стандартных отклонений совпадают с рекомендованным значением CODATA, хотя отличаются друг от друга на ~2,5 стандартных отклонения.

По астрономическим данным постоянная G практически не изменялась за последние сотни миллионов лет, скорость её относительного изменения (dG/dt)/G не превышает нескольких единиц на 10⁻¹¹ в год^[16][17][18].

1. ↑ В общей теории относительности обозначения, использующие букву G, применяются редко, поскольку там эта буква обычно используется для обозначения тензора Эйнштейна.
2. ↑ По определению массы, входящие в это уравнение, — гравитационные массы, однако расхождения между величиной гравитационной и инертной массы какого-либо тела до сих пор не обнаружено экспериментально. Теоретически в рамках современных представлений они вряд ли отличаются. Это в целом было стандартным предположением и со времен Ньютона.
3. ↑ Новые измерения гравитационной постоянной еще сильнее запутывают ситуацию // Элементы.ру, 13.09.2013
4. ↑ CODATA Internationally recommended values of the Fundamental Physical Constants (англ.). Дата обращения 20 мая 2019.
5. ↑ Разные авторы указывают разный результат, от 6,754⋅10⁻¹¹ м²/кг² до (6,60 ± 0,04)⋅10⁻¹¹м³/(кг·с³) — см. Эксперимент Кавендиша#Вычисленное значение.
6. ↑ Gillies G. T. The Newtonian Gravitational Constant // Sevres (France), Bureau Intern. Poids et Mesures, 1983, 135 p.
7. ↑ Ляховец В. Д. Проблемы метрологического обеспечения измерений гравитационной постоянной. // Проблемы теории гравитации и элементарных частиц. Выпуск 17. — М., Энергоатомиздат, 1986. — с. 122-125.
8. ↑ Игорь Иванов. Новые измерения гравитационной постоянной ещё сильнее запутывают ситуацию (неопр.) (13 сентября 2013). Дата обращения 14 сентября 2013.
9. ↑ Так ли постоянна гравитационная постоянная? Архивная копия от 14 июля 2014 на Wayback Machine Новости науки на портале cnews.ru // публикация от 26.09.2002
10. ↑ Brooks, Michael Can Earth’s magnetic field sway gravity? (неопр.). NewScientist (21 September 2002). [Архивная копия на Wayback Machine Архивировано] 8 февраля 2011 года.
11. ↑ Ерошенко Ю. Н. Новости физики в сети Internet (по материалам электронных препринтов), УФН, 2000 г., т. 170, № 6, с. 680
12. ↑ Quinn Terry, Parks Harold, Speake Clive, Davis Richard. Improved Determination of G Using Two Methods (англ.) // Physical Review Letters. — 2013. — 5 September (vol. 111, no. 10). — ISSN 0031-9007. — DOI:10.1103/PhysRevLett.111.101102.
13. ↑ Quinn Terry, Speake Clive, Parks Harold, Davis Richard. Erratum: Improved Determination of G Using Two Methods [Phys. Rev. Lett. 111, 101102 (2013)] (англ.) // Physical Review Letters. — 2014. — 15 July (vol. 113, no. 3). — ISSN 0031-9007. — DOI:10.1103/PhysRevLett.113.039901.
14. ↑ Rosi G., Sorrentino F., Cacciapuoti L., Prevedelli M., Tino G. M. Precision measurement of the Newtonian gravitational constant using cold atoms (англ.) // Nature. — 2014. — June (vol. 510, no. 7506). — P. 518—521. — ISSN 0028-0836. — DOI:10.1038/nature13433.
15. ↑ Li Qing, Xue Chao, Liu Jian-Ping, Wu Jun-Fei, Yang Shan-Qing, Shao Cheng-Gang, Quan Li-Di, Tan Wen-Hai, Tu Liang-Cheng, Liu Qi, Xu Hao, Liu Lin-Xia, Wang Qing-Lan, Hu Zhong-Kun, Zhou Ze-Bing, Luo Peng-Shun, Wu Shu-Chao, Milyukov Vadim, Luo Jun. Measurements of the gravitational constant using two independent methods (англ.) // Nature. — 2018. — August (vol. 560, no. 7720). — P. 582—588. — ISSN 0028-0836. — DOI:10.1038/s41586-018-0431-5.
16. ↑ van Flandern T. C. Is the Gravitational Constant Changing (англ.) // The Astrophysical Journal. — 1981. — September (vol. 248). — P. 813. — DOI:10.1086/159205. — Bibcode: 1981ApJ…248..813V.
    Результат: (dG/dt)/G = (−6,4 ± 2,2)×10⁻¹¹ год⁻¹
17. ↑ Verbiest J. P. W., Bailes M., van Straten W., Hobbs G. B., Edwards R. T., Manchester R. N., Bhat N. D. R., Sarkissian J. M., Jacoby B. A., Kulkarni S. R. Precision Timing of PSR J0437−4715: An Accurate Pulsar Distance, a High Pulsar Mass, and a Limit on the Variation of Newton’s Gravitational Constant (англ.) // The Astrophysical Journal. — 2008. — 20 May (vol. 679, no. 1). — P. 675—680. — ISSN 0004-637X. — DOI:10.1086/529576.
    Результат: |Ġ/G| ≤ 2,3 × 10⁻¹¹ год⁻¹
18. ↑ Взрыв звезд доказал неизменность Ньютоновской гравитации в космическом времени

Гравитационное поле — Википедия

Гравитацио́нное по́ле, или по́ле тяготе́ния, — фундаментальное физическое поле, через которое осуществляется гравитационное взаимодействие между всеми материальными телами^[1].

Гравитационное поле в классической физике[править | править код]

Закон всемирного тяготения Ньютона[править | править код]

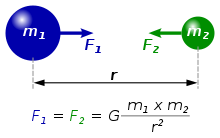Закон тяготения Ньютона

В рамках классической физики гравитационное взаимодействие описывается «законом всемирного тяготения» Ньютона, согласно которому сила гравитационного притяжения между двумя материальными точками с массами m1{\displaystyle m_{1}} и m2{\displaystyle m_{2}} пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними:

F=Gm1m2r2.{\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}.}

Здесь G{\displaystyle G} — гравитационная постоянная, приблизительно равная 6,673⋅10−11{\displaystyle 6{,}673\cdot 10^{-11}} м³/(кг с²), r{\displaystyle r} — расстояние между точками.

Решение задачи динамики в общем случае, когда тяготеющие массы нельзя считать материальными точками, подразделяется на два этапа: вначале рассчитывается гравитационное поле, создаваемое этими массами, а затем определяется его действие на массивные тела в изучаемой системе.

Расчёт гравитационного потенциала[править | править код]

Гравитационное поле является потенциальным. Его потенциал φ(r){\displaystyle \varphi (\mathbf {r} )} удовлетворяет уравнению Пуассона

Δφ(r)=−4πGρ(r){\displaystyle \Delta \varphi (\mathbf {r} )=-4\pi G\rho (\mathbf {r} )},

где Δ{\displaystyle \Delta } — оператор Лапласа. Решение данного уравнения имеет вид:

φ(r)=−G∫V′ρ(r′)dV′|r−r′|{\displaystyle \varphi (\mathbf {r} )=-G\int _{V^{\prime }}{\frac {\rho (\mathbf {r} ^{\prime })dV^{\prime }}{|\mathbf {r} -\mathbf {r} ^{\prime }|}}}.

Здесь r{\displaystyle \mathbf {r} } — радиус-вектор точки, в которой определяется потенциал, r′{\displaystyle \mathbf {r} ^{\prime }} — радиус-вектор элемента объёма dV′{\displaystyle dV^{\prime }} c плотностью вещества ρ(r′){\displaystyle \rho (\mathbf {r} ^{\prime })}, а интегрирование охватывает все такие элементы. На бесконечности φ=0{\displaystyle \varphi =0}.

В частном случае поля, создаваемого расположенной в начале координат точечной массой M{\displaystyle M}, потенциал равен

φ(r)=−GMr{\displaystyle \varphi (\mathbf {r} )=-G{\frac {M}{r}}}.

Этим же выражением описывается потенциал тела со сферически-симметрично распределённой массой M{\displaystyle M}, за его пределами.

В общем случае тела произвольной формы на больших расстояниях от него неплохое приближение для потенциала даёт формула^[2]:

φ(r)=−G(Mr+A+B+C−3I2r3),{\displaystyle \varphi (\mathbf {r} )=-G\left({\frac {M}{r}}+{\frac {A+B+C-3I}{2r^{3}}}\right),}

где за начало координат принят центр масс тела, A,B,C{\displaystyle A,B,C} — главные моменты инерции тела, I{\displaystyle I} — момент инерции относительно оси r{\displaystyle \mathbf {r} }. Эта формула несколько упрощается для астрономических объектов, представляющих собой сплюснутые сфероиды вращения с концентрически однородным распределением масс. У таких тел A=B{\displaystyle A=B} и I=A+(C−A)sin2⁡α,{\displaystyle I=A+(C-A)\sin ^{2}\alpha ,} где α{\displaystyle \alpha } — угол между r{\displaystyle \mathbf {r} } и плоскостью главных осей A{\displaystyle A} и B{\displaystyle B}. В итоге

φ(r)=−G(Mr+C−A2r3(1−3sin2⁡α)).{\displaystyle \varphi (\mathbf {r} )=-G\left({\frac {M}{r}}+{\frac {C-A}{2r^{3}}}(1-3\sin ^{2}\alpha )\right).}

Движение в гравитационном поле[править | править код]

Если потенциал поля определён, то сила притяжения, действующая в гравитационном поле на материальную точку с массой m{\displaystyle m}, находится по формуле:

F(r)=−m∇φ(r)=−Gm∫V′ρ(r′)(r−r′)dV′|r−r′|3{\displaystyle \mathbf {F} (\mathbf {r} )=-m\nabla \varphi (\mathbf {r} )=-Gm\int _{V^{\prime }}{\frac {\rho (\mathbf {r} ^{\prime })(\mathbf {r} -\mathbf {r} ^{\prime })dV^{\prime }}{|\mathbf {r} -\mathbf {r} ^{\prime }|^{3}}}}.

В частном случае поля точечной массы M{\displaystyle M}, расположенной в начале координат (r′=0{\displaystyle \mathbf {r} ^{\prime }=\mathbf {0} }), действующая сила составит

F(r)=−GmMr3r{\displaystyle \mathbf {F} (\mathbf {r} )=-G\,{\frac {mM}{r^{3}}}\,\mathbf {r} }.

Траектория материальной точки в гравитационном поле, создаваемом много большей по массе материальной точкой, подчиняется законам Кеплера. В частности, планеты и кометы в Солнечной системе движутся по эллипсам или гиперболам. Влияние других планет, искажающее эту картину, можно учесть с помощью теории возмущений.

Если исследуемое тело нельзя рассматривать как материальную точку, то его движение в гравитационном поле включает также вращение вокруг оси, проходящей через центр масс^[3]:

dHdt=K.{\displaystyle {\frac {d\mathbf {H} }{dt}}=\mathbf {K} .}

Здесь: H{\displaystyle \mathbf {H} } — угловой момент относительно центра масс, K{\displaystyle \mathbf {K} } — равнодействующая моментов действующих сил относительно центра масс. Более общий случай, когда масса исследуемого тела сравнима с массой источника поля, известен как задача двух тел, и её формулировка сводится к системе двух независимых движений. Исследование движения более чем двух тел («задача трёх тел») разрешимо только в нескольких специальных случаях.

Недостатки ньютоновской модели тяготения[править | править код]

Практика показала, что классический закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Однако ньютоновская теория содержала ряд серьёзных недостатков. Главный из них — необъяснимое дальнодействие: сила притяжения передавалась неизвестно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс: потенциал поля всюду обращается в бесконечность. В конце XIX века обнаружилась ещё одна проблема: заметное расхождение теоретического и наблюдаемого смещения перигелия Меркурия.

На протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году, с созданием общей теории относительности Эйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона оказалась приближением более общей теории, применимым при выполнении двух условий:

1. Гравитационный потенциал в исследуемой системе не слишком велик (много меньше c2{\displaystyle c^{2}}). В Солнечной системе это условие для большинства движений небесных тел можно считать выполненным — даже на поверхности Солнца отношение |φ|/c2{\displaystyle |\varphi |/c^{2}} составляет всего 2,12⋅10−6{\displaystyle 2{,}12\cdot 10^{-6}}. Заметным релятивистским эффектом является только указанное выше смещение перигелия^[4].
2. Скорости движения в этой системе незначительны по сравнению со скоростью света.

Гравитационное поле в общей теории относительности[править | править код]

В общей теории относительности (ОТО) гравитационное поле является не отдельным физическим понятием, а свойством пространства-времени, появляющимся в присутствии материи. Этим свойством является неевклидовость метрики (геометрии) пространства-времени, и материальным носителем тяготения является пространство-время. Тот факт, что гравитацию можно рассматривать как проявление свойств геометрии четырёхмерного неевклидова пространства, без привлечения дополнительных понятий, есть следствие того, что все тела в поле тяготения получают одинаковое ускорение («принцип эквивалентности» Эйнштейна). Пространство-время при таком подходе приобретает физические атрибуты, которые влияют на физические объекты и сами зависят от них.

Пространство-время ОТО представляет собой псевдориманово многообразие с переменной метрикой. Причиной искривления пространства-времени является присутствие материи, и чем больше её энергия, тем искривление сильнее. Для определения метрики пространства-времени при известном распределении материи надо решить уравнения Эйнштейна. Ньютоновская же теория тяготения представляет собой приближение ОТО, которое получается, если учитывать только «искривление времени», то есть изменение временно́й компоненты метрики, g00{\displaystyle g_{00}}^[5] (пространство в этом приближении евклидово). Распространение возмущений гравитации, то есть изменений метрики при движении тяготеющих масс, происходит с конечной скоростью, и дальнодействие в ОТО отсутствует.

Другие существенные отличия гравитационного поля ОТО от ньютоновского: возможность нетривиальной топологии пространства, особых точек, гравитационные волны.

1. ↑ Советский энциклопедический словарь. — 2-е изд. — М.: Советская энциклопедия, 1982. — С. 332.
2. ↑ Основные формулы физики, 1957, с. 574..
3. ↑ Основные формулы физики, 1957, с. 575..
4. ↑ Гинзбург В. Л. Гелиоцентрическая система и общая теория относительности (от Коперника до Эйнштейна) // Эйнштейновский сборник. — М.: Наука, 1973. — С. 63..
5. ↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7., § «Закон Ньютона».

• Дубошин Г. Н. . Небесная механика. Основные задачи и методы. — М.: Наука, 1968. — 800 с.
• Иваненко Д. Д., Сарданашвили Г. А. . Гравитация. — 3-е изд. — М.: УРСС, 2008. — 200 с.
• Мензел Д. (ред.). Основные формулы физики. Глава 29. Небесная механика. — М.: Изд. иностранной литературы, 1957. — 658 с.
• Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977.

• Тюлина И. А. Об основах ньютоновой механики (к трёхсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: МГУ, 1989. — Вып. 36. — С. 184—196..

Всемирный закон тяготения: точная формула силы всемирного притяжения, определение гравитации

Самым главным явлением, постоянно изучаемым физиками, является движение. Электромагнитные явления, законы механики, термодинамические и квантовые процессы – все это широкий спектр изучаемых физикой фрагментов мироздания. И все эти процессы сводятся, так или иначе, к одному – к движению тел….

Все во Вселенной движется. Гравитация – привычное явление для всех людей с самого детства, мы родились в гравитационном поле нашей планеты, это физическое явление воспринимается нами на самом глубоком интуитивном уровне и, казалось бы, даже не требует изучения.

Но, увы, вопрос, почему и каким образом все тела притягиваются друг к другу, остается и на сегодняшний день не до конца раскрытым, хотя и изучен вдоль и поперек.

В этой статье мы рассмотрим, что такое всемирное притяжение по Ньютону – классическую теорию гравитации. Однако прежде чем перейти к формулам и примерам, расскажем о сути проблемы притяжения и дадим ему определение.

Быть может, изучение гравитации стало началом натуральной философии (науки о понимании сути вещей), быть может, натуральная философия породила вопрос о сущности гравитации, но, так или иначе, вопросом тяготения тел заинтересовались еще в Древней Греции.

Движение понималось как суть чувственной характеристики тела, а точнее, тело двигалось, пока наблюдатель это видит. Если мы не можем явление измерить, взвесить, ощутить, значит ли это, что этого явления не существует? Естественно, не значит. И с тех пор, как Аристотель понял это, начались размышления о сути гравитации.

Как оказалось в наши дни, спустя многие десятки веков, гравитация является основой не только земного притяжения и притяжения нашей планеты к Солнцу, но и основой зарождения Вселенной и почти всех имеющихся элементарных частиц.

Задача движения

Проведем мысленный эксперимент. Возьмем в левую руку небольшой шарик. В правую возьмем такой же. Отпустим правый шарик, и он начнет падать вниз. Левый при этом остается в руке, он по-прежнему недвижим.

Остановим мысленно ход времени. Падающий правый шарик зависает в воздухе, левый все также остается в руке. Правый шарик наделен энергией движения, левый – нет. Но в чем глубокая, осмысленная разница между ними?

Где, в какой части падающего шарика прописано, что он должен двигаться? У него такая же масса, такой же объем. Он обладает такими же атомами, и они ничем не отличаются от атомов покоящегося шарика. Шарик обладает потенциальной энергией? Да, это правильный ответ, но откуда шарику известно, что обладает потенциальной энергией, где это зафиксировано в нем?

Именно эту задачу ставили перед собой Аристотель, Ньютон и Альберт Эйнштейн. И все три гениальных мыслителя отчасти решили для себя эту проблему, но на сегодняшний день существует ряд вопросов, требующих разрешения.

Гравитация Ньютона

В 1666 году величайшим английским физиком и механиком И. Ньютоном открыт закон, способный количественно посчитать силу, благодаря которой вся материя во Вселенной стремится друг к другу. Это явление получило название всемирное тяготение. Когда вас просят: Сформулируйте закон всемирного тяготения, ваш ответ должен звучать так:

Сила гравитационного взаимодействия, способствующая притяжению двух тел, находится в прямой пропорциональной связи с массами этих тел и в обратной пропорциональной связи с расстоянием между ними.

Важно! В законе притяжения Ньютона используется термин расстояние. Под этим термином следует понимать не дистанцию между поверхностями тел, а расстояние между их центрами тяжести. К примеру, если два шара радиусами r1 и r2 лежат друг на друге, то дистанция между их поверхностями равна нулю, однако сила притяжения есть. Все дело в том, что расстояние между их центрами r1+r2 отлично от нуля. В космических масштабах это уточнение не суть важно, но для спутника на орбите данная дистанция равна высоте над поверхностью плюс радиус нашей планеты. Расстояние между Землей и Луной также измеряется как расстояние между их центрами, а не поверхностями.

Для закона тяготения формула выглядит следующим образом:

,

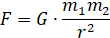где:

• F – сила притяжения,
• – массы,
• r – расстояние,
• G – гравитационная постоянная, равная 6,67·10−11 м³/(кг·с²).

Что же представляет собой вес, если только что мы рассмотрели силу притяжения?

Сила является векторной величиной, однако в законе всемирного тяготения она традиционно записана как скаляр. В векторной картине закон будет выглядеть таким образом:

.

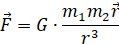Но это не означает, что сила обратно пропорциональна кубу дистанции между центрами. Отношение следует воспринимать как единичный вектор, направленный от одного центра к другому:

.

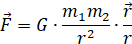Закон гравитационного взаимодействия

Вес и гравитация

Рассмотрев закон гравитации, можно понять, что нет ничего удивительного в том, что лично мы ощущаем притяжение Солнца намного слабее, чем земное. Массивное Солнце хоть и имеет большую массу, однако оно очень далеко от нас. Земля тоже далеко от Солнца, однако она притягивается к нему, так как обладает большой массой. Каким образом найти силу притяжения двух тел, а именно как вычислить силу тяготения Солнца, Земли и нас с вами – с этим вопросом мы разберемся чуть позже.

Насколько нам известно, сила тяжести равна:

P = mg,

где m – наша масса, а g – ускорение свободного падения Земли (9,81 м/с2).

Важно! Не бывает двух, трех, десяти видов сил притяжения. Гравитация – единственная сила, дающая количественную характеристику притяжения. Вес (P = mg) и сила гравитации – одно и то же.

Если m – наша масса, M – масса земного шара, R – его радиус, то гравитационная сила, действующая на нас, равна:

.

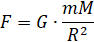Таким образом, поскольку F = mg:

.

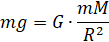Массы m сокращаются, и остается выражение для ускорения свободного падения:

.

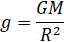Как видим, ускорение свободного падения – действительно постоянная величина, поскольку в ее формулу входят величины постоянные радиус, масса Земли и гравитационная постоянная. Подставив значения этих констант, мы убедимся, что ускорение свободного падения равно 9,81 м/с2.

На разных широтах радиус планеты несколько отличается, поскольку Земля все-таки не идеальный шар. Из-за этого ускорение свободного падения в отдельных точках земного шара разное.

Вернемся к притяжению Земли и Солнца. Постараемся на примере доказать, что земной шар притягивает нас с вами сильнее, чем Солнце.

Примем для удобства массу человека: m = 100 кг. Тогда:

• Расстояние между человеком и земным шаром равно радиусу планеты: R = 6,4∙106 м.
• Масса Земли равна: M ≈ 6∙1024 кг.
• Масса Солнца равна: Mc ≈ 2∙1030 кг.
• Дистанция между нашей планетой и Солнцем (между Солнцем и человеком): r=15∙1010 м.

Гравитационное притяжение между человеком и Землей:

.

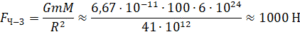Данный результат довольно очевиден из более простого выражения для веса (P = mg).

Сила гравитационного притяжения между человеком и Солнцем:

.

Как видим, наша планета притягивает нас почти в 2000 раз сильнее.

Как найти силу притяжения между Землей и Солнцем? Следующим образом:

.

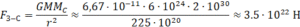Теперь мы видим, что Солнце притягивает нашу планету более чем в миллиард миллиардов раз сильнее, чем планета притягивает нас с вами.

Первая космическая скорость

После того как Исаак Ньютон открыл закон всемирного тяготения, ему стало интересно, с какой скоростью нужно бросить тело, чтобы оно, преодолев гравитационное поле, навсегда покинуло земной шар.

Правда, он представлял себе это несколько иначе, в его понимании была не вертикально стоящая ракета, устремленная в небо, а тело, которое горизонтально совершает прыжок с вершины горы. Это была логичная иллюстрация, поскольку на вершине горы сила притяжения немного меньше.

Так, на вершине Эвереста ускорение свободного падения будет равно не привычные 9,8 м/с2, а почти м/с2. Именно по этой причине там настолько разряженный воздух, частицы воздуха уже не так привязаны к гравитации, как те, которые упали к поверхности.

Постараемся узнать, что такое космическая скорость.

Первая космическая скорость v1 – это такая скорость, при которой тело покинет поверхность Земли (или другой планеты) и перейдет на круговую орбиту.

Постараемся узнать численной значение этой величины для нашей планеты.

Запишем второй закон Ньютона для тела, которое вращается вокруг планеты по круговой орбите:

,

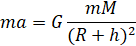где h высота тела над поверхностью, R радиус Земли.

На орбите на тело действует центробежное ускорение 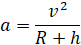, таким образом:

.

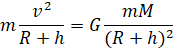Массы сокращаются, получаем:

,

.

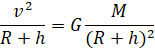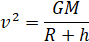Данная скорость называется первой космической скоростью:

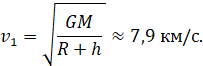
Как можно заметить, космическая скорость абсолютно не зависит от массы тела. Таким образом, любой предмет, разогнанный до скорости 7,9 км/с, покинет нашу планету и перейдет на ее орбиту.

Первая космическая скорость

Вторая космическая скорость

Однако, даже разогнав тело до первой космической скорости, нам не удастся полностью разорвать его гравитационную связь с Землей. Для этого и нужна вторая космическая скорость. При достижении этой скорости тело покидает гравитационное поле планеты и все возможные замкнутые орбиты.

Важно! По ошибке часто считается, что для того чтобы попасть на Луну, космонавтам приходилось достигать второй космической скорости, ведь нужно было сперва разъединиться с гравитационным полем планеты. Это не так: пара Земля Луна находятся в гравитационном поле Земли. Их общий центр тяжести находится внутри земного шара.

Для того чтобы найти эту скорость, поставим задачу немного иначе. Допустим, тело летит из бесконечности на планету. Вопрос: какая скорость будет достигнута на поверхности при приземлении (без учета атмосферы, разумеется)? Именно такая скорость и потребуется телу, чтобы покинуть планету.

Вторая космическая скорость

Запишем закон сохранения энергии:

,

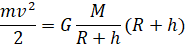где в правой части равенства стоит работа силы тяжести: A = Fs.

Отсюда получаем, что вторая космическая скорость равна:

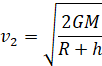
Таким образом, вторая космическая скорость в 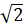  раз больше первой:

.

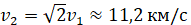Закон всемирного тяготения. Физика 9 класс

Закон Всемирного тяготения.

Вывод

Мы с вами узнали, что хотя гравитация является основной силой во Вселенной, многие причины этого явления до сих пор остались загадкой. Мы узнали, что такое сила всемирного тяготения Ньютона, научились считать ее для различных тел, а также изучили некоторые полезные следствия, которые вытекают из такого явления, как всемирный закон тяготения.

Ускорение свободного падения — Википедия

Ускоре́ние свобо́дного паде́ния на пове́рхности^[1] некоторых небесных тел, м/с² и g

Земля	9,81 м/с2	1,00 g	Солнце	273,1 м/с2	27,85 g
Луна	1,62 м/с2	0,165 g	Меркурий	3,68—3,74 м/с2	0,375—0,381 g
Венера	8,88 м/с2	0,906 g	Марс	3,86 м/с2	0,394 g
Юпитер	23,95 м/с2	2,442 g	Сатурн	10,44 м/с2	1,065 g
Уран	8,86 м/с2	0,903 g	Нептун	11,09 м/с2	1,131 g

Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил. В соответствии с уравнением движения тел в неинерциальных системах отсчёта^[2]ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.

Ускорение свободного падения на поверхности Земли g

(обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах^[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет g = 9,80666 м/с²^[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или, грубо, 10 м/с².

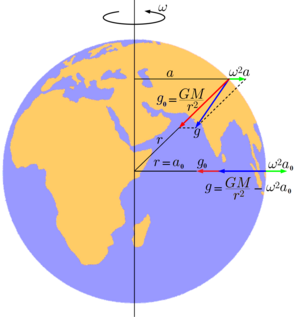Две компоненты ускорения свободного падения на Земле g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна GM/r² и центробежная, равная ω²a, где a — расстояние до земной оси, ω — угловая скорость вращения Земли.

Для определённости будем считать, что речь идёт об ускорении свободного падения на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центростремительного ускорения, связанного с вращением Земли.

Центростремительное ускорение[править | править код]

Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии

a от оси вращения, центростремительное ускорение равно ω²a, где ω — угловая скорость вращения Земли, определяемая выражением ω = 2π/T, в котором Т — время одного оборота вокруг своей оси (звёздные сутки), равное для Земли 86164 секунды. Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с², причем на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.

Гравитационное ускорение[править | править код]

Гравитационное ускорение на различной высоте h над уровнем моря

h, км	g, м/с2	h, км	g, м/с2
0	9,8066	20	9,7452
1	9,8036	50	9,6542
2	9,8005	80	9,5644
3	9,7974	100	9,505
4	9,7943	120	9,447
5	9,7912	500	8,45
6	9,7882	1000	7,36
8	9,7820	10 000	1,50
10	9,7759	50 000	0,125
15	9,7605	400 000	0,0025

В соответствии с законом всемирного тяготения, величина гравитационного ускорения вызванного космическим телом, связано с его массой M следующим соотношением:

g=GMR2{\displaystyle g=G{\frac {M}{R^{2}}}},

где G — гравитационная постоянная (6,67408(31)·10⁻¹¹м³·с⁻²·кг⁻¹)^[6], а R — растояние от центра гравитации. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо наоборот по известной массе и радиусу определить ускорение свободного падения на поверхности.

Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.

Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:

g(h)=GM(r+h)2{\displaystyle g(h)=G{\frac {M}{(r+h)^{2}}}},

где M — масса планеты, а r — её радиус .

Ускорение свободного падения на Земле[править | править код]

Ускорение свободного падения у поверхности Земли зависит от широты, времени суток, атмосферного давления и других факторов. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле^[7][8]:

g=9,780318(1+0,005302sin2⁡φ−0,000006sin2⁡2φ)−0,000003086h,{\displaystyle g=9{,}780318(1+0{,}005302\sin ^{2}\varphi -0{,}000006\sin ^{2}2\varphi )-0{,}000003086h,}

где φ{\displaystyle \varphi } — широта рассматриваемого места,

h{\displaystyle h} — высота над уровнем моря в метрах.

Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли, дополнив её поправками, связанными с вращением Земли, приливными воздействиями и другими факторами.

Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.

Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счет центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от следствий из этой упрощённой модели. Так, самое низкое значение g зафиксировано на горе Уаскаран в Перу (9,7639 м/с²) в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от северного полюса^[9].

Ускорение свободного падения для некоторых городов
Город	Долгота	Широта	Высота над уровнем моря, м	Ускорение свободного падения, м/с2
Алматы	76,85 в.д.	43,22 с.ш.	786	9.78125
Берлин	13,40 в.д.	52,50 с.ш.	40	9,81280
Будапешт	19,06 в.д.	47,48 с.ш.	108	9,80852
Вашингтон	77,01 з.д.	38,89 с.ш.	14	9,80188
Вена	16,36 в.д.	48,21 с.ш.	183	9,80860
Владивосток	131,53 в.д.	43,06 с.ш.	50	9,80424
Гринвич	0,0 в.д.	51,48 с.ш.	48	9,81188
Каир	31,28 в.д.	30,07 с.ш.	30	9,79317
Киев	30,30 в.д.	50,27 с.ш.	179	9,81054
Мадрид	3,69 в.д.	40,41 с.ш.	667	9,79981
Минск	27,55 в.д.	53,92 с.ш.	220	9,81347
Москва	37,61 в.д.	55,75 с.ш.	151	9,8154
Нью-Йорк	73,96 з.д.	40,81 с.ш.	38	9,80247
Одесса	30,73 в.д.	46,47 с.ш.	54	9.80735
Осло	10,72 в.д.	59,91 с.ш.	28	9,81927
Париж	2,34 в.д.	48,84 с.ш.	61	9,80943
Прага	14,39 в.д.	50,09 с.ш.	297	9,81014
Рим	12,99 в.д.	41,54 с.ш.	37	9,80312
Стокгольм	18,06 в.д.	59,34 с.ш.	45	9,81843
Токио	139,80 в.д.	35,71 с.ш.	18	9,79801

Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.

Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.

• Енохович А. С. Краткий справочник по физике. — М.: «Высшая школа», 1976. — 288 с.

Поверхностная гравитация — Википедия

Поверхностная гравитация (англ. surface gravity) — ускорение свободного падения, испытываемое на поверхности астрономического или иного объекта. Поверхностную гравитацию можно рассматривать как ускорение вследствие притяжения, испытываемое гипотетической пробной частицей, находящейся вблизи поверхности объекта и обладающей пренебрежимо малой массой, чтобы не вносить возмущения.

Поверхностная гравитация измеряется в единицах ускорения, которые в системе СИ равны м/с². Иногда её удобно выражать в единицах земного ускорения свободного падения g = 9,80665 м/с².^[1] В астрофизике поверхностную гравитацию иногда выражают в виде lg g, который представляет собой десятичный логарифм от значения ускорения, выраженного в системе единиц СГС, в которой ускорение измеряется в см/с².^[2] Следовательно, поверхностная гравитация Земли в системе СГС равна 980,665 см/с², а десятичный логарифм этой величины равен 2,992.

Гравитация на поверхности белого карлика очень сильна, а для нейтронных звёзд она ещё сильнее. Компактность нейтронной звезды приводит к тому, что для неё поверхностная гравитация составляет около 7·10¹² м/с², типичные значения имеют порядок 10¹² м/с², что в 100 000 000 000 раз превышает значение земной поверхностной гравитации. При этом скорость убегания с поверхности нейтронной звезды имеет порядок 10⁵ км/с (треть скорости света).

Масса, радиус и поверхностная гравитация[править | править код]

Поверхностная гравитация различных тел Солнечной системы^[3]
(1g = 9,81 м/с², ускорение свободного падения на Земле)

Название	Поверхностная гравитация
Солнце	28,02g
Меркурий	0,38g
Венера	0,904g
Земля	1,00g
Луна	0,1654g
Марс	0,376g
Фобос	0,0005814g
Деймос	0,000306g
Церера	0,0275g
Юпитер	2,53g
Ио	0,183g
Европа	0,134g
Ганимед	0,15g
Каллисто	0,126g
Сатурн	1,07g
Титан	0,14g
Энцелад	0,0113g
Уран	0,89g
Нептун	1,14g
Тритон	0,0797g
Плутон	0,067g
Эрида	0,0677g
67P-CG	0,000017g

В теории гравитации Ньютона сила притяжения, создаваемая объектом, пропорциональна его массе: объект с вдвое большей массой создаёт вдвое большую силу. Сила притяжения в теории Ньютона обратно пропорциональна квадрату расстояния, поэтому удалившийся на вдвое большее расстояние объект создаёт в четыре раза меньшую силу. По аналогичному закону изменяется с расстоянием освещённость, создаваемая точечным источником.

Крупный объект, такой как планета или звезда, обычно имеет круглую форму вследствие достижения гидростатического равновесия (все точки на поверхности обладают одинаковой гравитационной потенциальной энергией). На малых масштабах более высокие области подвергаются эрозии, а осыпающееся вещество откладывается на более низких областях. На больших масштабах планета или звезда целиком деформируется до момента достижения равновесия.^[4] Для большинства небесных тел результатом является то, что рассматриваемую планету или звезду можно считать почти идеальной сферой в случае малой скорости вращения. Для молодых массивных звёзд экваториальная скорость вращения может достигать 200 км/с и более, что может приводить к значительной сплюснутости. Примерами таких быстро вращающихся звёзд являются Ахернар, Альтаир, Регул A и Вега.

Тот факт, что многие крупные небесные тела имеют почти шарообразную форму, позволяет относительно несложно вычислять их поверхностную гравитацию. Сила притяжения вне сферически симметричного тела равна силе притяжения точечного тела той же массы, помещённого в центр исходного тела, что было доказано И. Ньютоном.^[5] Следовательно, поверхностная гравитация планеты или звезды данной массы примерно обратно пропорциональна квадрату радиуса, а поверхностная гравитация планеты или звезды с заданной средней плотностью приблизительно пропорциональна радиусу. Например, недавно открытая планета Глизе 581 c превосходит Землю по массе в 5 раз, но маловероятно, что поверхностная гравитация также в 5 раз превосходит земную. Если масса данной планеты превосходит земную не более, чем в 5 раз^[6] и планета является каменистой с крупным железным ядром, то её радиус примерно на 50% больше земного.^[7][8] Гравитация на подобной планете приблизительно в 2,2 раза будет превышать земную. Если же планета ледяная или водная, то радиус вдвое может превышать радиус Земли, вследствие чего гравитация на поверхности превысит земную не более чем в 1,25 раза.^[8]

Указанные выше пропорциональности можно выразить формулой

g=mr2,{\displaystyle g={\frac {m}{r^{2}}},}

где g равно поверхностной гравитации, выраженной в единицах ускорения свободного падения для поверхности Земли, m равно массе объекта в единицах массы Земли (5,976·10²⁴ кг), r равно радиусу объекта, выраженному в единицах среднего радиуса Земли (6371 км).^[9] Например, Марс имеет массу 6,4185·10²³ кг = 0,107 массы Земли и средний радиус 3390 км = 0,532 радиуса Земли.^[10] Тогда поверхностная гравитация Марса равна

0,1070,5322=0,38{\displaystyle {\frac {0,107}{0,532^{2}}}=0,38}

в единицах значения для Земли. Если не использовать Землю в качестве тела отсчёта, то поверхностную гравитацию можно определять напрямую из закона всемирного тяготения:

g=GMr2,{\displaystyle g={\frac {GM}{r^{2}}},}

где M — масса объекта, r — его радиус, G — гравитационная постоянная. Если ρ = M/V показывает среднюю плотность объекта, то выражение можно переписать в виде

g=4π3Gρr,{\displaystyle g={\frac {4\pi }{3}}G\rho r,}

поэтому для фиксированной средней плотности поверхностная гравитация g пропорциональна радиусу r.

Поскольку гравитация обратно пропорциональна квадрату расстояния, то космическая станция на высоте 400 км над поверхностью Земли испытывает почти такую же силу притяжения, как и мы на поверхности Земли. Причина, по которой космическая станция не падает на землю, состоит не в том, что на неё не действует притяжение, а в том, что станция находится на орбите в свободном падении.

Объекты, не являющиеся сферически-симметричными[править | править код]

Большинство астрономических объектов не являются абсолютно сферически-симметричными. Одной из причин является то, что данные объекты обычно вращаются, то есть на их форму оказывают совместное влияние сила притяжения и центробежная сила, вследствие чего звёзды и планеты приобретают сплюснутую форму. На экваторе при этом поверхностная гравитация будет меньше, чем на полюсе. Данное явление использовал Хол Клемент в новелле «Экспедиция „Тяготение“», в которой упоминается массивная быстро вращающаяся планета, на которой гравитация на полюсах значительно превышала гравитацию на экваторе.

Поскольку распределение внутреннего вещества объекта может отклоняться от симметричной модели, то мы можем использовать поверхностную гравитацию для получения сведений о внутреннем строении объекта. В 1915-1916 годах на основе данного вывода по методу Лоранда Этвёша осуществлялся поиск нефти около города Гбелы в Словакии.^{[11], стр. 1663;[12], стр. 223.} В 1924 году аналогичный метод использовался для уточнения положения нефтяных полей Nash Dome в Техасе.^{[12], стр. 223.}

Иногда полезно вычислять поверхностную гравитацию простых гипотетических объектов, которые не встречаются в природе. Поверхностная гравитация бесконечных плоскостей, трубок, тонких оболочек и других нереалистичных фигур может использоваться при построении моделей гравитации реальных объектов.

Поверхностная гравитация чёрной дыры[править | править код]

В теории относительности ньютоновское понятие ускорения перестаёт быть чётко определённым. Для чёрной дыры поверхностную гравитацию нельзя определить как ускорение, испытываемое пробным телом на поверхности объекта, поскольку на горизонте событий ускорение стремится к бесконечности. Обычно используется понятие местного собственного ускорения (стремится к бесконечности вблизи горизонта событий), умноженного на коэффициент, связанный с гравитационным замедлением времени (стремится к нулю вблизи горизонта событий).

При рассмотрении поверхностной гравитации чёрной дыры следует определить понятие, аналогичное случаю ньютоновской поверхностной гравитации. Гравитация на поверхности чёрной дыры в общем случае определяется плохо. Можно определить поверхностную гравитацию для чёрной дыры, горизонт событий которой является горизонтом Киллинга.

Для случая статического горизонта Киллинга поверхностная гравитация κ{\displaystyle \kappa } представляет собой ускорение, необходимое для удержания объекта на горизонте событий. Если ka{\displaystyle k^{a}} представляет нормированный вектор Киллинга, то поверхностная гравитация определяется как

ka∇akb=κkb,{\displaystyle k^{a}\,\nabla _{a}k^{b}=\kappa k^{b},}

уравнение записывается для горизонта. Для статичного и асимптотически плоского пространства-времени нормализацию следует выбирать так, чтобы kaka→−1{\displaystyle k^{a}k_{a}\rightarrow -1} при r→∞{\displaystyle r\rightarrow \infty }, а также κ≥0{\displaystyle \kappa \geq 0}. Для решения Шварцшильда мы принимаем такое ka{\displaystyle k^{a}}, что ka∂a=∂∂t{\displaystyle k^{a}\partial _{a}={\frac {\partial }{\partial t}}}, для решения Керра — Ньюмена мы принимаем ka∂a=∂∂t+Ω∂∂φ{\displaystyle k^{a}\partial _{a}={\frac {\partial }{\partial t}}+\Omega {\frac {\partial }{\partial \varphi }}}, где Ω{\displaystyle \Omega } показывает угловую скорость.

Решение Шварцшильда[править | править код]

Поскольку ka{\displaystyle k^{a}} является вектором Киллинга, то ka∇akb=κkb{\displaystyle k^{a}\,\nabla _{a}k^{b}=\kappa k^{b}} соответствует −ka∇bka=κkb{\displaystyle -k^{a}\,\nabla ^{b}k_{a}=\kappa k^{b}}. В координатах (t,r,θ,φ){\displaystyle (t,r,\theta ,\varphi )} ka=(1,0,0,0){\displaystyle k^{a}=(1,0,0,0)}. Переход к системе координат Эддингтона-Финкельштейна v=t+r+2Mln⁡|r−2M|{\displaystyle v=t+r+2M\ln |r-2M|} приводит к виду метрики

ds2=−(1−2Mr)dv2+2dvdr+r2(dθ2+sin2⁡θdφ2).{\displaystyle ds^{2}=-\left(1-{\frac {2M}{r}}\right)\,dv^{2}+2\,dv\,dr+r^{2}\left(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}\right).}

В общем случае изменения системы координат вектор Киллинга преобразуется как kv=Atvkt{\displaystyle k^{v}=A_{t}^{v}k^{t}}, что даёт вектора s ka′=(1,0,0,0){\displaystyle k^{a’}=(1,0,0,0)} и ka′=(−1+2Mr,1,0,0).{\displaystyle k_{a’}=\left(-1+{\frac {2M}{r}},1,0,0\right).}

Если b = v для ka∇akb=κkb{\displaystyle k^{a}\,\nabla _{a}k^{b}=\kappa k^{b}}, то получаем дифференциальное уравнение −12∂∂r(−1+2Mr)=κ.{\displaystyle -{\frac {1}{2}}{\frac {\partial }{\partial r}}\left(-1+{\frac {2M}{r}}\right)=\kappa .}

Следовательно, поверхностная гравитация для решения Шварцшильда при массе M{\displaystyle M} равна κ=14M.{\displaystyle \kappa ={\frac {1}{4M}}.}^[13]

Решение Керра[править | править код]

Поверхностная гравитация для незаряженной вращающейся чёрной дыры равна

κ=g−k,{\displaystyle \kappa =g-k,}

где g=14M{\displaystyle g={\frac {1}{4M}}} является поверхностной гравитацией решения Шварцшильда, k:=MΩ+2{\displaystyle k:=M\Omega _{+}^{2}}, Ω+{\displaystyle \Omega _{+}} равна угловой скорости у горизонта событий. Данное выражение приводит к температуре Хокинга 2πT=g−k{\displaystyle 2\pi T=g-k}.^[14]

Решение Керра — Ньюмена[править | править код]

Поверхностная гравитация для решения Керра — Ньюмена равна

κ=r+−r−2(r+2+a2)=M2−Q2−J2/M22M2−Q2+2MM2−Q2−J2/M2,{\displaystyle \kappa ={\frac {r_{+}-r_{-}}{2(r_{+}^{2}+a^{2})}}={\frac {\sqrt {M^{2}-Q^{2}-J^{2}/M^{2}}}{2M^{2}-Q^{2}+2M{\sqrt {M^{2}-Q^{2}-J^{2}/M^{2}}}}},}

где Q{\displaystyle Q} — электрический заряд, J{\displaystyle J} — угловой момент, r±:=M±M2−Q2−J2/M2{\displaystyle r_{\pm }:=M\pm {\sqrt {M^{2}-Q^{2}-J^{2}/M^{2}}}} — расположение двух горизонтов, a:=J/M{\displaystyle a:=J/M}.

Динамические чёрные дыры[править | править код]

Поверхностная гравитация для стационарных чёрных дыр определяется, поскольку все стационарные чёрные дыры обладают горизонтом Киллинга.^[15] Недавно были предприняты попытки определения поверхностной гравитации динамических чёрных дыр, чьё пространство-время не является полем Киллинга.^[16] На протяжении нескольких лет различными авторами предлагались разные варианты определения. На настоящий момент нет окончательного решения о справедливости каких-либо из определений.^[17]

1. ↑ p. 29, The International System of Units (SI), ed. Barry N. Taylor, NIST Special Publication 330, 2001.
2. ↑ Smalley, B. The Determination of Teff and log g for B to G stars (неопр.). Keele University (13 июля 2006). Дата обращения 31 мая 2007.
3. ↑ Isaac Asimov. The Collapsing Universe (неопр.). — Corgi, 1978. — С. 44. — ISBN 0-552-10884-7.
4. ↑ Why is the Earth round?, at Ask A Scientist, accessed online May 27, 2007.
5. ↑ Book I, §XII, pp. 218–226, Newton’s Principia: The Mathematical Principles of Natural Philosophy, Sir Isaac Newton, tr. Andrew Motte, ed. N. W. Chittenden. New York: Daniel Adee, 1848. First American edition.
6. ↑ Astronomers Find First Earth-like Planet in Habitable Zone Архивировано 17 июня 2009 года., ESO 22/07, press release from the European Southern Observatory, April 25, 2007
7. ↑ The HARPS search for southern extra-solar planets XI. Super-Earths (5 & 8 M_Earth) in a 3-planet system, S. Udry, X. Bonfils), X. Delfosse, T. Forveille, M. Mayor, C. Perrier, F. Bouchy, C. Lovis, F. Pepe, D. Queloz, and J.-L. Bertaux. arXiv:astro-ph/0704.3841.
8. ↑ ^{1 2} Detailed Models of super-Earths: How well can we infer bulk properties?, Diana Valencia, Dimitar D. Sasselov, and Richard J. O’Connell, arXiv:astro-ph/0704.3454.
9. ↑ 2.7.4 Physical properties of the Earth Архивная копия от 28 марта 2015 на Wayback Machine, web page, accessed on line May 27, 2007.
10. ↑ Mars Fact Sheet, web page at NASA NSSDC, accessed May 27, 2007.
11. ↑ Ellipsoid, geoid, gravity, geodesy, and geophysics Архивировано 28 августа 2003 года., Xiong Li and Hans-Jürgen Götze, Geophysics, 66, #6 (November–December 2001), pp. 1660–1668. DOI 10.1190/1.1487109.
12. ↑ ^{1 2} Prediction by Eötvös’ torsion balance data in Hungary Архивировано 28 ноября 2007 года., Gyula Tóth, Periodica Polytechnica Ser. Civ. Eng. 46, #2 (2002), pp. 221–229.
13. ↑ Raine, Derek J.; Thomas, Edwin George. Black Holes: An Introduction (неопр.). — illustrated. — Imperial College Press, 2010. — С. 44. — ISBN 1-84816-382-7. Extract of page 44
14. ↑ Good, Michael; Yen Chin Ong. Are Black Holes Springlike? (англ.) // Physical Review D : journal. — 2015. — February (vol. 91, no. 4). — P. 044031. — DOI:10.1103/PhysRevD.91.044031. — Bibcode: 2015PhRvD..91d4031G. — arXiv:1412.5432.
15. ↑ Wald, Robert. General Relativity (неопр.). — University Of Chicago Press (англ.)русск., 1984. — ISBN 978-0-226-87033-5.
16. ↑ Nielsen, Alex; Yoon. Dynamical Surface Gravity (англ.) // Classical Quantum Gravity : journal. — 2008. — Vol. 25.
17. ↑ Pielahn, Mathias; G. Kunstatter; A. B. Nielsen. Dynamical surface gravity in spherically symmetric black hole formation (англ.) // Physical Review D : journal. — 2011. — November (vol. 84, no. 10). — P. 104008(11). — DOI:10.1103/PhysRevD.84.104008. — Bibcode: 2011PhRvD..84j4008P. — arXiv:1103.0750.

Гравитационная энергия — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 ноября 2016; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 ноября 2016; проверки требуют 5 правок.

Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением.

Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя).

Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии, постоянна. Для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.

Гравитационная энергия играет очень важную роль на заключительных этапах эволюции звёзд, при их превращении в нейтронные звёзды и сверхновые^[1].

Для двух тяготеющих точечных тел с массами M и m гравитационная энергия Ug{\displaystyle U_{g}} равна:

 Ug=−GMmR,{\displaystyle \ U_{g}=-G{Mm \over R},}

где:

 G{\displaystyle \ G} — гравитационная постоянная;

 R{\displaystyle \ R} — расстояние между центрами масс тел.

Этот результат получается из закона тяготения Ньютона, при условии, что для бесконечно удалённых тел гравитационная энергия равна 0. Выражение для гравитационной силы имеет вид

Fg=GMmR2,{\displaystyle F_{g}=G{Mm \over R^{2}},}

где:

Fg{\displaystyle F_{g}} — сила гравитационного взаимодействия

С другой стороны согласно определению потенциальной энергии

Fg=dUgdR.{\displaystyle F_{g}={\frac {dU_{g}}{dR}}.}

Тогда:

Ug=const−GMmR.{\displaystyle U_{g}=const-G{Mm \over R}.}

Константа в этом выражении может быть выбрана произвольно. Её обычно выбирают равной нулю, чтобы при r, стремящемуся к бесконечности, Ug{\displaystyle U_{g}} стремилось к нулю.

Этот же результат верен для малого тела, находящегося вблизи поверхности большого. В этом случае R можно считать равным h+RM{\displaystyle h+R_{M}}, где RM{\displaystyle R_{M}} — радиус тела массой M, а h — расстояние от центра тяжести тела массой m до поверхности тела массой M.

На поверхности тела M имеем:

Ug=−GMmRM,{\displaystyle U_{g}=-G{Mm \over R_{M}},}

Если размеры тела M{\displaystyle M} много больше размеров тела m{\displaystyle m}, то формулу гравитационной энергии можно переписать в следующем виде:

Ug=−GMmRM+h=−mGMRM11+h/RM≈−mGMRM(1−hRM)=mgh−mGMRM,{\displaystyle U_{g}=-G{Mm \over R_{M}+h}=-mG{\frac {M}{R_{M}}}{\frac {1}{1+h/R_{M}}}\approx -mG{\frac {M}{R_{M}}}\left(1-{\frac {h}{R_{M}}}\right)=mgh-m{\frac {GM}{R_{M}}},}

где величину g=GMRM2{\displaystyle g={\frac {GM}{R_{M}^{2}}}} называют ускорением свободного падения. При этом член mGMRM{\displaystyle m{\frac {GM}{R_{M}}}} не зависит от высоты поднятия тела над поверхностью и может быть исключён из выражения путём выбора соответствующей константы. Таким образом для малого тела, находящегося на поверхности большого тела справедлива следующая формула

Ug=mgh.{\displaystyle U_{g}=mgh.}

В частности, эта формула применяется для вычисления потенциальной энергии тел, находящихся вблизи поверхности Земли.

В общей теории относительности наряду с классическим отрицательным компонентом гравитационной энергии связи появляется положительная компонента, обусловленная гравитационным излучением, то есть полная энергия гравитирующей системы убывает во времени за счёт такого излучения.

Теория гравитации Лесажа — Википедия

В 1690 году женевский математик^[1]Никола Фатио де Дюилье и в 1756 Жорж Луи ЛеСаж в Женеве предложили простую кинетическую теорию гравитации, которая дала механическое объяснение уравнению силы Ньютона.^[2] Из-за того, что работа Фатио не была широко известна и оставалась неопубликованной длительное время, именно описание теории Ле Сажем стало темой повышенного интереса в конце XIX века, когда данная теория была изучена в контексте только что открытой кинетической теории газов^[3]. Это механическое объяснение гравитации никогда не получало широкого признания и к началу XX века теория в целом считалась опровергнутой, в основном из-за проблем, поднятых Максвеллом^[4], Пуанкаре.^[5] Кроме того, во втором десятилетии XX века Альберт Эйнштейн создал общую теорию относительности, правда, признание к ней пришло несколько позже. Хотя теория Ле Сажа всё ещё изучается некоторыми исследователями, она обычно не рассматривается основным научным сообществом как жизнеспособная теория.

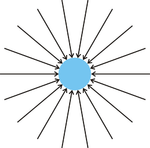
P1: Одно тело
Нет чистой направленной силы

Теория утверждает, что сила гравитации — это результат движения крошечных частиц, двигающихся на высокой скорости во всех направлениях во Вселенной. Интенсивность потока частиц предполагается одинаковой во всех направлениях, таким образом, изолированный объект A ударяется частицами со всех сторон, в результате чего он подвергается давлению вовнутрь объекта, но не подвергается направленной силе P1.

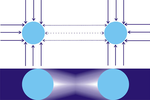
P2: Два тела «притягивают» друг друга

Однако, в случае присутствия второго объекта B, часть частиц, которые иначе бы ударили по объекту A со стороны B, перехватывается, таким образом B работает как экран, т.е. с направления В объект A ударит меньше частиц, чем с противоположного направления. Аналогично, объект B будет ударен меньшим количеством частиц со стороны A, по сравнению с противоположной стороной. То есть, можно сказать, что объекты A и B «экранируют» друг друга, и оба тела прижимаются друг к другу результирующим дисбалансом сил (P2). Таким образом, кажущееся притяжение между телами в данной теории на самом деле является уменьшенным давлением на тело со стороны других тел. По этой причине данную теорию иногда называют «push гравитация» или «теневая гравитация», хотя наиболее часто встречается название «гравитация Лесажа».

Природа столкновений[править | править код]

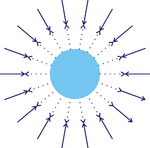
P3: Противоположные потоки

Если соударение тела A и гравитационной частицы полностью упруго, интенсивность отраженных частиц будет настолько же сильной, как и приходящих частиц, т.е. чистая направленная сила не возникнет. Данное утверждение верно и в том случае, если мы введём второе тело В, которое будет действовать как экран для гравитационных частиц в направлении тела A. Гравитационная частица C, которая в обычной ситуации ударила бы по объекту A, блокируется В, но другая частица D, которая в обычной ситуации не ударила бы по A, перенаправляется упругим отражением от объекта B на объект A, и следовательно заменяет C. Таким образом, если столкновение полностью упруго, отраженные частицы между объектами A и B полностью компенсируют любой «экранирующий» эффект. Чтобы объяснить суть гравитационной силы, мы должны предположить, что соударение частиц не является полностью упругим, или хотя бы то что отражённые частицы замедляются, т.е. их импульс уменьшается после столкновения. Это приведёт к тому что от объекта А отходит поток с уменьшенным импульсом, но приходит поток с неизменённым импульсом, таким образом появляется чистый направленный импульс к центру объекта A (P3). Если принять это предположение, то отраженные частицы в случае 2 взаимодействующих тел, полностью не компенсируют экранирующий эффект, из-за того, что отражённый поток слабее, чем падающий на тело поток.

Обратно-квадратичная зависимость[править | править код]

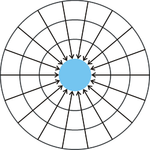
P4: Обратно-квадратичная зависимость

Из нашего предположения, что некоторые (или все) гравитационные частицы, сходящиеся на объекте, абсорбируются или замедляются данным объектом, следует, что интенсивность потока гравитационных частиц, испускаемого от массивного объекта, меньше чем интенсивность потока падающего на данный объект. Можно предположить, что этот дисбаланс импульса потока и соответственно силы приложенной на любое тело вблизи объекта, распределён по сферической поверхности с центром на данном объекте (P4). Дисбаланс импульса потока над всей сферической поверхностью, окружающей объект, не зависит от размера окружающей сферы, в то же время площадь поверхности сферы увеличивается пропорционально квадрату радиуса. Следовательно, дисбаланс импульса на единицу площади уменьшается в обратно-квадратичной зависимости от расстояния.

Пропорциональность массе[править | править код]

Из фактов, показанных выше, возникает сила, которая прямо пропорциональна только поверхности тела. Но сила гравитации пропорциональна также массам. Чтобы удовлетворить необходимость в пропорциональности от массы, теория утверждает, что: а) базовые элементы материи очень малы, таким образом, материя в основном состоит из пустого пространства; б) что гравитационные частицы настолько малы, что только очень малая часть из них перехватывается материей. В результате чего, «тень» каждого тела прямо пропорциональна поверхности каждого из базовых элементов материи. Если теперь предположить, что элементарные непрозрачные (для гравитационных частиц) элементы всей материи идентичны (т.е. имеют такое же отношение плотности к поверхности), то из этого следует, что экранирующий эффект (хотя бы приблизительно) пропорционален массе (P5).

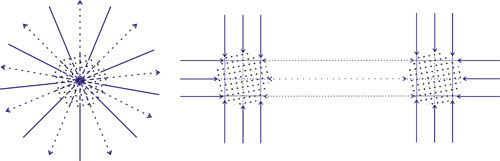
P5: Проницаемость, затухание и пропорциональность массе

Фатио[править | править код]

Фатио представил первую формулировку своих мыслей о гравитации в письме к Гюйгенсу весной 1690 года.^[1] Два дня спустя он зачитал содержание письма перед Лондонским Королевским обществом. В последующие годы Фатио написал несколько черновых рукописей своего главного труда «De la Cause de la Pesanteur». Некоторые фрагменты этих рукописей были в последующем приобретены Ле Сажем (см. ниже) и были найдены разбросанными среди бумаг Ле Сажа в 1944 году. На основании этих фрагментов и конспекта, сделанного самим Фатио, Бернар Ганьебен попытался восстановить труды Фатио.^[6] Ганьебен не знал, что полная копия одного из ранних черновиков, написанных в 1701 году, была найдена Карлом Боппом в 1915 году среди бумаг семьи Бернулли и легла в основу издания труда Фатио, опубликованного Боппом в 1929 году.^[7] Издание Боппа более подробное, чем издание Ганьебена, но издание Ганьебена включает в себя исправления сделанные Фатио до 1743 года включительно, на 40 лет позже создания черновика, на котором основывается издание Боппа. Для детального анализа труда Фатио и сравнением между изданиями Боппа и Ганьебена – смотрите публикации Цехе.^[8] Ниже приведённое описание в основном основано на издании Боппа. Они были названы Фатио «Проблемы I-IV», в то же время между Проблемой I и проблемой II формулируется 5 теорем. Проблемы II-IV составляют вторую половину издания Боппа и содержат математически наиболее передовые идеи теории Фатио, но они не были включены Ганьебеном в его издание трудов Фатио.

Некоторые свойства теории Фатио.[править | править код]

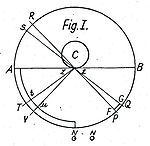
P6: Пирамида Фатио

Пирамида Фатио (Проблема I):^[9] Фатио предположил, что вселенная наполнена мельчайшими корпускулами, которые движутся с очень высокой скоростью беспорядочно и прямолинейно во всех направлениях. Чтобы проиллюстрировать свои мысли, он использовал следующий пример: Вообразим объект С, на котором расположена бесконечно маленькая плоскость zz и нарисована сфера с центром в zz. В эту сферу Фатио поместил пирамиду PzzQ, в которой некоторые корпускулы движутся в направлении zz, а также некоторые корпускулы, которые уже были отражены объектом C и, следовательно, покидают плоскость zz. Фатио предположил, что средняя скорость отражённых частиц меньше и следовательно импульс слабее чем у падающих на тело корпускул. В результате получается один поток, который толкает все тела по направлению к zz. Таким образом, с одной стороны скорость потока остаётся постоянной, но с другой стороны при большей близости к zz плотность потока увеличивается и следовательно его интенсивность пропорциональна 1/r². А так как можно нарисовать бесконечное количество таких пирамид вокруг C, пропорциональность 1/r² приложима ко всей области вокруг C.

Уменьшенная скорость: чтобы подтвердить предположение, что корпускулы после отражения движутся с уменьшенными скоростями, Фатио сделал следующие предположения:^[10] a) обыкновенное вещество или гравитационные корпускулы, или и то и другое – неупруги; b) столкновения полностью упруги, но корпускулы не абсолютно твёрдые, и следовательно переходят в состояние колебания после соударения и(или) c) из-за трения корпускулы начинают вращаться после столкновения. Эти отрывки теории Фатио – наиболее малопонятны, потому что он никогда точно не решил, какой из вариантов столкновений наиболее предпочтителен.^[11] Однако, в последней версии своей теории в 1742 году он сократил связанные отрывки и написал «полная упругость или пружинистая сила» для корпускул и «неполная упругость» для обыкновенного вещества, следовательно корпускулы должны быть отражены с уменьшенными скоростями.^[12]
Вдобавок, Фатио столкнулся с другой проблемой: что происходит, когда корпускулы сталкиваются друг с другом? Неупругое столкновение приводит к постоянному уменьшению скорости корпускул и следовательно к уменьшению гравитационной силы. Чтобы избежать данной проблемы, Фатио предположил, что диаметр корпускул очень мал по сравнению с расстоянием между ними, таким образом, взаимодействия между корпускулами происходят очень редко.

Конденсация:^[13] чтобы смягчить противоречия, которые возникли из-за того, что чем меньше скорость корпускул, тем больше корпускул будет аккумулироваться около тел, Фатио предположил, что корпускулы отражаются в пирамиду TzzV. В то же время, если корпускулы приходящие со стороны PQ достигают C, то отраженные частицы не достигают TV, а прибывают в tu. Однако, это не приводит к бесконечному накоплению частиц, а только к конденсации, т.к. увеличенная плотность остаётся постоянной. Фатио указал на то, что, продолжая увеличивать скорость, Tt может стать сколько угодно малым по отношению к TZ.

P7: Модель вещества с кристаллической решёткой (двадцатигранник)

Пористость обыкновенного вещества:^[14] чтобы обеспечить пропорциональность массе, Фатио предположил, что обыкновенное вещество чрезвычайно проницаемо для гравитационной жидкости (потока корпускул). Он сделал наброски 3 моделей, чтобы подтвердить своё предположение. a) Фатио предположил, что материя состоит из маленьких «шариков», диаметр которых по сравнению с расстоянием между ними «бесконечно» мал. Но он отбросил данное предположение, на основании того, что при таких условиях «шарики» будут стремиться друг к другу, и тело не будет оставаться «стабильным». b) После этого он сделал предположение, что «шарики» могут быть соединены линиями или прутьями, и формируют в некотором роде кристаллическую решетку. Однако он признал негодной и эту модель тоже. Если некоторые атомы находятся рядом друг с другом, то гравитационная жидкость не сможет проникнуть в эту структуру одинаково со всех сторон, и соответственно пропорциональность массе невозможна. c) В конце концов, Фатио убрал и «шарики», оставив только линии или сетку, сделав линии «бесконечно» меньшими по сравнению с расстоянием между ними, достигнув таким образом максимальной проницательной способности.

Сила давления корпускул (Проблема II):^[15] Уже в 1690 году Фатио предположил, что «толкающая сила», вызываемая корпускулами на ровной плоскости, в 6 раз меньше, чем сила, которая была бы создана этими же корпускулами, если бы они были расположены по нормали к поверхности. Фатио приводит доказательство своего предположения, путём определения силы, которая вызывается корпускулами на определённой точки плоскости zz. Он выводит формулу p=ρv²zz/6. Это решение очень похоже на формулу известную в кинетической теории газов p=ρv²/3, которая была найдена Даниилом Бернулли в 1738 году. Это первый раз, когда наблюдается близкая аналогия между таким видом гравитационных теорий и кинетической теорией газов – задолго до развития базовых концепций более поздней из теорий. Однако значение, полученное Бернулли, в 2 раза больше, чем значение Фатио, потому что (по Цехе) Фатио рассчитал только значение mv для изменения импульса после столкновения, а не 2mv и, следовательно, получил неправильный результат (его результат верен только для полностью неупругого столкновения). Фатио пытался использовать своё решение не только для объяснения гравитации, но также и для объяснения поведения газов. Он попытался сконструировать термометр, который должен был показывать «состояние движения» молекул воздуха и, следовательно, подсчитывать температуру. Но Фатио (в отличие от Бернулли) не идентифицировал теплоту с движением частиц воздуха, он использовал другую жидкость, которая должна быть ответственна за этот эффект.^[16] Также не известно, оказали ли труды Фатио влияние на Бернулли или нет.

Бесконечность (Проблема III):^[17] В этой главе Фатио исследует связь между понятием «бесконечность» и её отношением к своей теории. Фатио часто объяснял свои предположения тем фактом, что различные явления «бесконечно меньше или бесконечно больше» чем другие, и таким образом многие проблемы могут быть уменьшены до неопределяемого значения. Например, диаметр «переборок» «бесконечно меньше», чем расстояние между ними или что скорость корпускул «бесконечно больше», чем у обыкновенного вещества или разница в скорости между отраженными или неотраженными корпускулами «бесконечно маленькая».

Сопротивление среды (Проблема IV):^[18] Это математически самая сложная часть теории Фатио. Здесь он пытается оценить сопротивление потока корпускул движущемуся телу. Предположим, что u – скорость обыкновенного вещества, v – скорость гравитационных частиц и ρ – плотность среды. В случае если v << u и ρ = const, Фатио сделал вывод что сопротивление равно ρu². В случае если v >> u и ρ = const, сопротивление равно 4/3ρuv. В этом месте Ньютон констатировал, что отсутствие сопротивления орбитальному движению планет требует чрезвычайной разреженности любой среды в космосе. Поэтому Фатио уменьшил плотность среды и заявил, что чтобы сохранить достаточную гравитационную силу, это уменьшение должно быть компенсировано изменением v «обратно пропорционально квадратному корню плотности». Это следует из корпускулярного давления Фатио, которое пропорционально ρv². Согласно Цехе, идея Фатио увеличить v до очень больших значений действительно сделает сопротивление очень маленьким по сравнению с гравитацией (и вообще сколь угодно маленьким) из-за того, что сопротивление в модели Фатио пропорционально ρuv, а гравитация (т.е. давление корпускул) пропорциональна ρv².

Принятие теории Фатио научным сообществом[править | править код]

Фатио контактировал с некоторыми из самых известных учёных своего времени; отдельные из них подписали его рукопись.

P8: Подписи Галлея, Гюйгенса и Ньютона на бумаге Фатио

Мнения Ньютона о теории Фатио сильно различаются. Например, после описания необходимых условий механического объяснения гравитации, в 1692 году он написал в (неопубликованной) записке в своей собственной копии «Principia»:

Уникальная гипотеза, которая может объяснить гравитацию, была разработана самым гениальным геометром мистером Н. Фатио.^[19]

С другой стороны, сам Фатио заявлял, что хотя Ньютон лично прокомментировал, что теория Фатио является самым лучшим возможным механическим объяснением гравитации, он также признавал, что Ньютон склонялся к идее, что действительная причина тяготения не является механической. Также, Д. Грегори сделал заметку в своей «Memoranda» «Мистер Ньютон и мистер Галлей смеялись над манерой изложения гравитации Фатио». Это якобы было замечено им 28 декабря 1691 года. Однако, настоящая дата неизвестна, так как и чернила и перо, которые использовались, отличаются от остальной части страницы.^[20] После 1694 года отношения между двумя учёными охладели.

Гюйгенс был первым человеком, проинформированным Фатио о своей теории, но он никогда не признавал теорию верной. Фатио верил, что убедил Гюйгенса в состоятельности своей теории, но Гюйгенс опроверг это в своём письме к Лейбницу.^[21] Также существовала короткая переписка о теории между Фатио и Лейбницем. Лейбниц критиковал теорию Фатио за существование пустого пространства между частицами, существование которого отрицалось Лейбницом на философской почве.^[22]Якоб Бернулли проявил интерес к теории Фатио, и побудил Фатио записать свои мысли о гравитации в законченной рукописи, что и было сделано Фатио. Бернулли после этого скопировал рукопись, которая теперь находится в библиотеке университета Базеля, и на которой основано издание Боппа.^[23]

Тем не менее, теория Фатио оставалась в основном неизвестной (кроме некоторых исключений, например Крамера и Лесажа) из-за того, что a) он никогда не смог формально опубликовать свои работы и b) он попал под влияние группы религиозных фанатиков, называвшейся «Французские пророки» («French prophets»), принадлежавшей к французскому протестантскому течению камизаров (camisards), поднявшему восстание против религиозных преследований во Франции в этот исторический период, и его публичная репутация была подорвана.

Крамер, Редекер[править | править код]

В 1731 году швейцарский математик Габриель Крамер опубликовал диссертацию,^[24] в конце которой появился набросок теории абсолютно похожей на теорию Фатио (включая «сетевидную» структуру вещества, аналогию со светом, экранирование и т.д.), но без упоминания имени Фатио. Фатио было известно, что Крамер имел доступ к копии его главной работы, так что он обвинил Крамера в плагиате теории без понимания её. Крамер также проинформировал Лесажа о теории Фатио в 1749 году. В 1736 году германский врач Редекер тоже публикует похожую теорию.^[25] В соответствии с Превостом, Редекер предположил, что частицы в его модели абсолютно неупруги, но не дал точный анализ феномена. Существовала ли связь между Фатио и Редекером – неизвестно.^[26]

Ле Саж[править | править код]

Первое описание своей теории Essai sur l’origine des forces mortes, было отправлено Лесажем в Парижскую Академию наук в 1748 году, но оно никогда не было опубликовано (с. 154-158). Так, по словам Лесажа после создания и отправки своего эссе, он был проинформирован о теориях Фатио, Крамера и Редекера. Только в 1756 году в первый раз одно из описаний его теории было опубликовано,^[27] в 1758 году он отправил более детальное описание теории Essai de Chymie Méchanique, на конкурс в Академию наук Руана.^[28] В этом труде он пытался объяснить как природу гравитации так и силы химического притяжения. Описание теории, которое стало доступным широкой публике называлось Lucrèce Newtonien, в этом описании было раскрыто соответствие данной теории с представлениями Лукреция.^[29] Ещё одно описание теории из записок Лесажа было опубликовано после смерти автора в 1818 году Пьером Прево.^[30]

Критики теории Лесажа отмечали множество её слабых мест, особенно с точки зрения термодинамики. Джеймс Максвелл показал, что в модели Лесажа энергия непременно перейдёт в теплоту и быстро расплавит любое тело. Анри Пуанкаре подсчитал (1908), что скорость корпускул должна быть на много порядков выше скорости света, и их энергия испепелила бы все планеты^[31]. Были отмечены и непреодолимые логические трудности^[32]:

• Если тяготение вызвано экранированием, то Луна в те моменты, когда она находится между Землёй и Солнцем, должна существенно влиять на силу притяжения этих тел и, соответственно, на траекторию Земли, однако ничего подобного в реальности не наблюдается.
• Быстро движущееся тело должно испытывать спереди избыточное давление со стороны корпускул.

Попытка Джорджа Дарвина заменить корпускулы на волны в эфире оказалась также неудачной. В обзоре 1910 года модель Лесажа уверенно характеризуется как несостоятельная^[31].

• Богородский А. Ф. Всемирное тяготения. — Киев: Наукова думка, 1971. — 351 с.
• Роузвер Н. Т. Перигелий Меркурия. От Леверье до Эйнштейна = Mercury’s perihelion. From Le Verrier to Einstein. — М.: Мир, 1985. — 244 с.

1. ↑ ^{1 2} Fatio, 1690a
2. ↑ Le Sage, 1756
3. ↑ Thomson, W. 1873
4. ↑ Maxwell и 1875
5. ↑ Poincaré, 1908
6. ↑ Fatio, 1743
7. ↑ Fatio, 1701
8. ↑ Zehe, 1980
9. ↑ Fatio, 1690a; Fatio, 1701, pp. 32-35; Zehe, 1980, pp. 134-156
10. ↑ Fatio, 1690a; Fatio, 1701, p. 34;
11. ↑ Zehe, 1980, pp. 198-204.
12. ↑ Zehe, 1980, p. 385; Fatio, 1743, pp. 134-135.
13. ↑ Fatio, 1690a, p. 387; Fatio, 1690c, pp. 38-39;
14. ↑ Fatio, 1701, pp. 36-38 and 59-61; Zehe, 1980, pp. 206-214.
15. ↑ Fatio, 1701, pp. 47-49; Zehe, 1980, pp. 227-241 and 198-205
16. ↑ Zehe, 1980, p. 239
17. ↑ Fatio, 1701, pp. 49-50; Zehe, 1980, pp. 242-254.
18. ↑ Fatio, 1701, pp. 50-64. Zehe, 1980, pp. 255-276.
19. ↑ Newton, in Latin:«Hiijus autem generis Hypothesis est unica, per quam Gravitas explicari potest, eamque Geometra Ingeniossimus Pr. Fatius primus excogitavit.»; Fatio-c, p. 65;
20. ↑ Zehe, 1980, p. 374.
21. ↑ Zehe, 1980, p. 176
22. ↑ Zehe, 1980, pp. 173—175
23. ↑ Fatio, 1701, pp. 19-20
24. ↑ Cramer, 1731
25. ↑ Redeker, 1736
26. ↑ Le Sage, 1818, pp. XXXI-XXXII
27. ↑ Le Sage, G.-L. (1756), «Letter à une académicien de Dijon…», Mercure de France: 153-171 
28. ↑ Le Sage, G.-L. (1761), Essai de Chymie Méchanique, Not published — private print, <http://gallica.bnf.fr/ark:/12148/bpt6k110507m> 
29. ↑ Le Sage, G.-L. (1784), «Lucrèce Newtonien», Memoires de l’Academie Royale des Sciences et Belles Lettres de Berlin: 404-432, <http://bibliothek.bbaw.de/bibliothek-digital/digitalequellen/schriften/anzeige/index_html?band=03-nouv/1782&seite:int=0495>  An English translation appears in Le Sage, G.-L. (1898), The Newtonian Lucretius, in Langley, Samuel P., «The Le Sage theory of gravitation», Annual Report of the Board of Regents of the Smithsonian Institution: 139-160, June 30, 1898 
30. ↑ Le Sage, G.-L. (1818), «Physique Mécanique des Georges-Louis Le Sage», in Prévost, Pierre, Deux Traites de Physique Mécanique, Geneva & Paris: J.J. Paschoud, с. 1-186 
31. ↑ ^{1 2} Роузвер Н. Т., 1985, с. 133—138..
32. ↑ Богородский А. Ф., 1971, с. 31—34.