Формула силы трения — справочник для студентов и школьников
ОПРЕДЕЛЕНИЕ
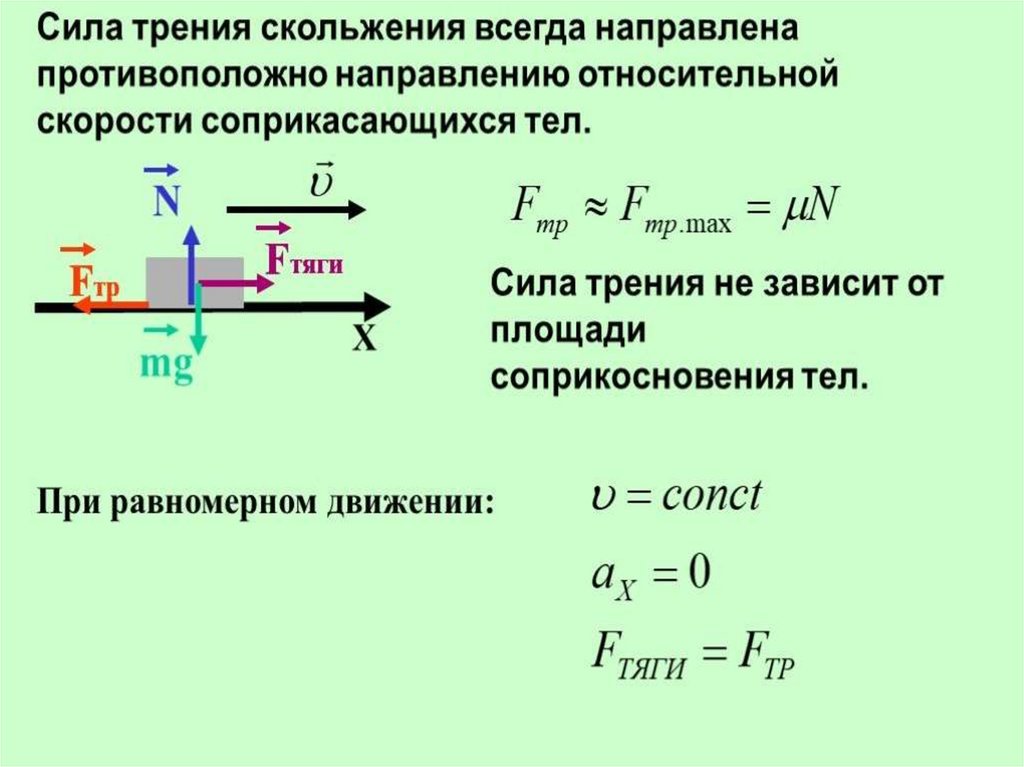
Сила трения равна коэффициенту трения, умноженному на силу реакции поддержки.
— сила трения, k — коэффициент трения, N — сила реакции опоры.
Единицей измерения силы является Н (Ньютон).
Существование силы трения объясняется взаимодействием неровностей на поверхностях тел. Он всегда существует, поскольку нет абсолютно гладких тел.
Сила трения всегда направлена в направлении, противоположном направлению движения, а сила реакции опоры перпендикулярна поверхности в направлении, противоположном силе тяжести. k зависит от взаимодействующих материалов и гладкости поверхностей трения, но не зависит от площади контакта трущихся тел. Это безразмерная величина.
Различают силу трения покоя и силу трения движения. Сила остаточного трения — минимальная сила, которую необходимо приложить, чтобы тело начало двигаться. Фрикционная сила движения — сила, которая препятствует движению, если движущая сила становится меньше, чем тело, тело остановится.
Примеры решения проблем на тему «Сила трения»
ПРИМЕР 1
Чтобы найти силу трения, действующую на движущееся тело, если ее масса равна 7H, а коэффициент трения равен 0,5.
Тело находится на опоре, поэтому его вес равен прочности реакции поддержки:
Так:
Сила трения равна
ПРИМЕР 2
Тело движется вверх вдоль плоскости, имеющей угол наклона . Известный коэффициент трения k, вес тела P.
Найдите формулу для силы трения для данного тела.
Сила реакции опоры направлена перпендикулярно линии движения, а масса тела направлена перпендикулярно горизонту. Таким образом, угол между этими векторами равен углу между линией движения и горизонтом, т.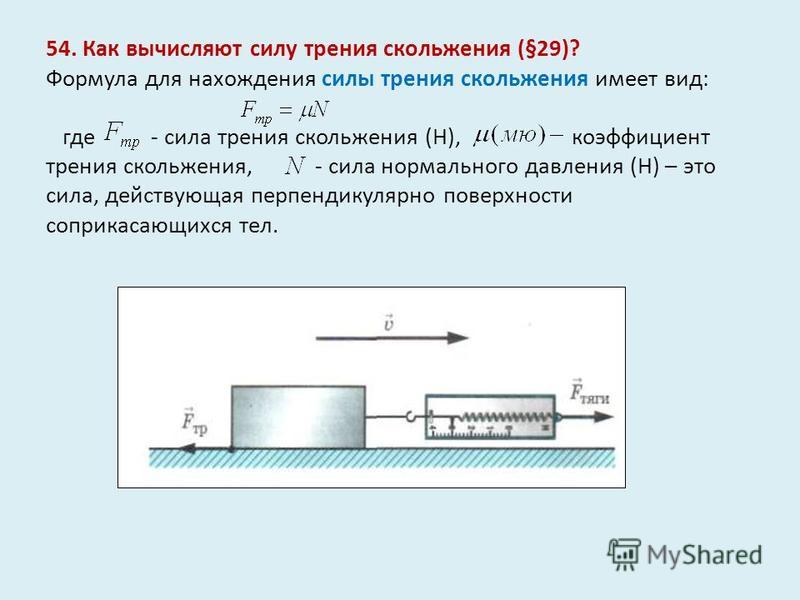
Е. . По определению косинус:
Согласно формуле, которую мы уже знаем:
Сила трения равна
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
9
Длина волны Гравитация и инерция.
Принципы эквивалентности Джеймс Чедвик, английский физик, лауреат Нобелевской премии по физике 1935 года Дисперсия и поляризация света Дэвид Джозеф Бом, ученый-физик
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Физика. 8 класс
Физика.
8 класс
ОглавлениеГлава 1. Общие сведения о движении§ 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ.  КООРДИНАТЫ ТЕЛА§ 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24.  ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ§ 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. 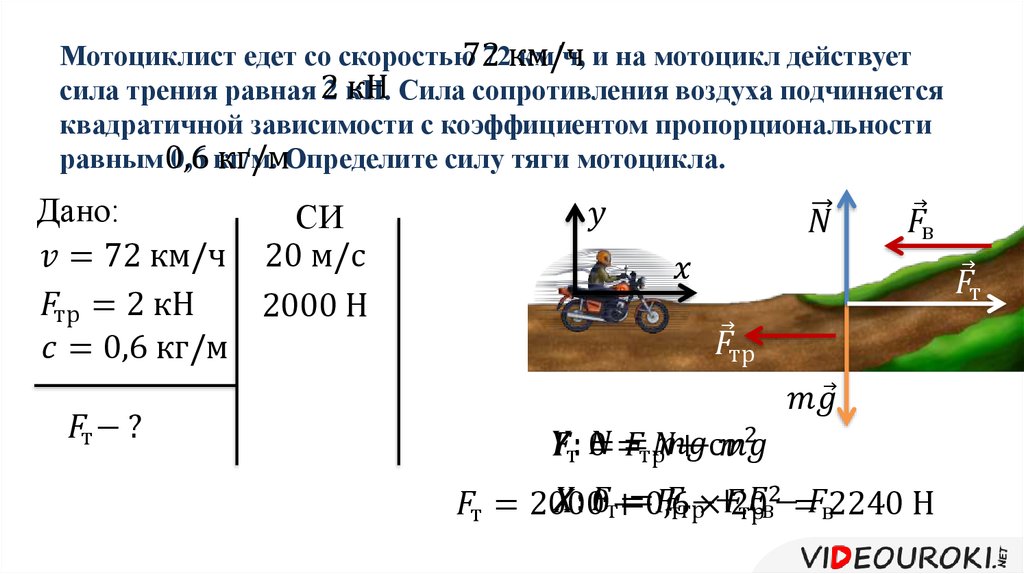 СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕГлава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. 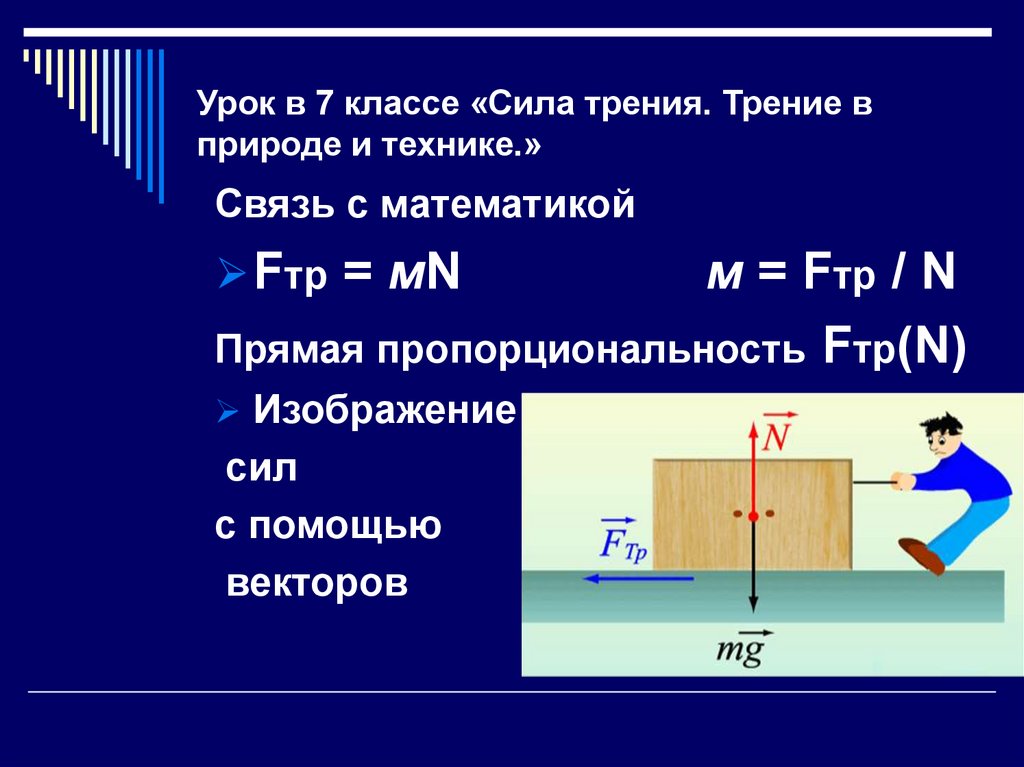 РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ§ 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87.  ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ§ 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям |
Трение качения: определение, коэффициент, формула (с примерами)
Трение является частью повседневной жизни. В то время как в идеализированных физических задачах вы часто игнорируете такие вещи, как сопротивление воздуха и сила трения, если вы хотите точно рассчитать движение объектов по поверхности, вы должны учитывать взаимодействия в точке контакта между объектом и поверхностью.
Обычно это означает работу с трением скольжения, трением покоя или трением качения, в зависимости от конкретной ситуации. Хотя катящийся объект, такой как мяч или колесо, явно испытывает меньшую силу трения, чем объект, который вы должны скользить, вам все равно нужно научиться рассчитывать сопротивление качению, чтобы описать движение таких объектов, как автомобильные шины по асфальту.
Определение трения качения
Трение качения — это тип кинетического трения, также известный как сопротивление качению , который относится к движению качения (в отличие от движения скольжения — другого типа кинетического трения) и противодействует движение качения по существу так же, как и другие формы силы трения.
Вообще говоря, качение не вызывает такого большого сопротивления, как скольжение, поэтому коэффициент трения качения на поверхности обычно меньше, чем коэффициент трения при скольжении или статике на той же поверхности.
Процесс качения (или чистого качения, т. е. без проскальзывания) сильно отличается от скольжения, поскольку качение включает в себя дополнительное трение по мере того, как каждая новая точка объекта соприкасается с поверхностью. В результате этого в каждый данный момент возникает новая точка соприкосновения, и ситуация мгновенно становится похожей на трение покоя.
Помимо шероховатости поверхности существует множество других факторов, которые также влияют на трение качения; например, величина деформации объекта и поверхности для качения при соприкосновении влияет на величину силы. Например, легковые или грузовые шины испытывают большее сопротивление качению, когда они накачаны до более низкого давления. Наряду с прямыми силами, воздействующими на шину, часть потерь энергии происходит из-за тепла, называемого 9.0011 гистерезисные потери .
Уравнение трения качения
Уравнение трения качения в основном такое же, как уравнения трения скольжения и статического трения, за исключением того, что вместо аналогичного коэффициента для других типов трения используется коэффициент трения качения.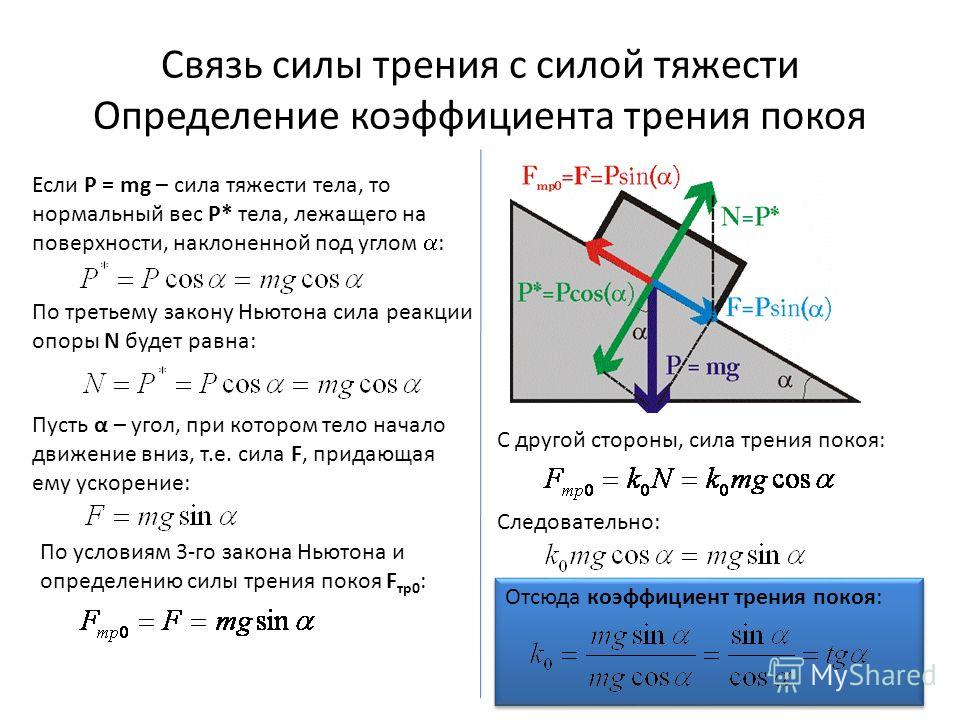
Использование F k,r для силы трения качения (т.е. кинетической, качения), F n для нормальной силы и μ k,r для коэффициента трения качения, уравнение:
F_{k,r} = µ_{k,r}F_n
F k,r — ньютоны. Когда вы решаете проблемы, связанные с телом качения, вам нужно будет найти конкретный коэффициент трения качения для ваших конкретных материалов. Engineering Toolbox, как правило, является фантастическим ресурсом для такого рода вещей (см. Ресурсы).
Как всегда нормальная сила ( F n ) имеет такую же величину веса (т.е. мг , где m – масса и г = 9,81 м/с 2 ) объект на горизонтальной поверхности (при условии, что никакие другие силы не действуют в этом направлении), и он перпендикулярен поверхности в точке контакта. Если поверхность наклонена под углом θ , величина нормальной силы определяется выражением мг cos ( θ ).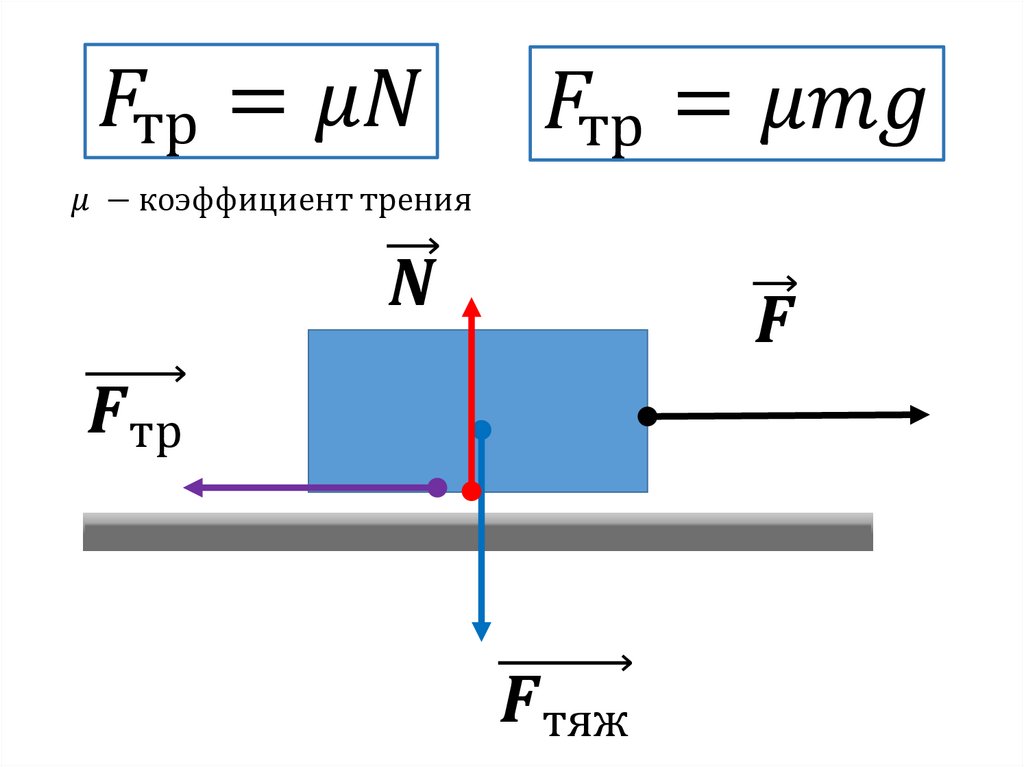
Расчеты с кинетическим трением
Расчет трения качения в большинстве случаев является довольно простым процессом. Представьте себе автомобиль массой m = 1500 кг, едущий по асфальту и имеющий μ k,r = 0,02. Каково сопротивление качению в этом случае?
Используя формулу, рядом F n = мг (на горизонтальной поверхности):
\begin{aligned} F_{k,r} &= μ_{k,r}F_n \\ &= μ_{k,r} мг \\ &= 0,02 × 1500 \;\text{кг} × 92 \\ &= 294 \;\text{N} \end{aligned}
Вы можете видеть, что сила трения качения в этом случае кажется существенной, однако, учитывая массу автомобиля и используя второй закон Ньютона, это составляет только замедление 0,196 м/с 2 . I
Если та же машина ехала по дороге с уклоном вверх в 10 градусов, вам нужно было бы использовать результат изменится:
\begin{aligned} F_{k,r} &= µ_{k,r}F_n \\ &= µ_{k,r} мг \cos(\theta)\\ &= 0,02 × 1500 \;\text{кг} × 92 × \cos (10°)\\ &= 289,5 \;\text{N} \end{aligned}
Поскольку нормальная сила уменьшается из-за наклона, сила трения уменьшается во столько же раз.
Вы также можете рассчитать коэффициент трения качения, если знаете силу трения качения и величину нормальной силы, используя следующую перестроенную формулу:
μ_{k,r} = \frac{F_{k ,r}}{F_n}
Представьте, что велосипедная шина катится по горизонтальной бетонной поверхности с F n = 762 Н и F k,r = 1,52 Н, коэффициент трения качения:
\begin{aligned} μ_{k,r} &= \frac{F_{ k,r}}{F_n} \\ &=\frac{1,52 \;\text{N}}{762 \;\text{N}} \\ &= 0,002 \end{aligned}
Коэффициент трения | Определение, единицы и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- В этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это лучший ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и многое другое. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
