Карта механики — скольжение и опрокидывание

Представьте себе ящик, стоящий на шероховатой поверхности, как показано на рисунке ниже. Теперь представьте, что мы начинаем толкать коробку сбоку. Первоначально сила трения будет сопротивляться силе толкания, и коробка будет стоять на месте. Однако по мере увеличения силы, толкающей коробку, произойдет одно из двух.

1. Сила толкания превысит максимальную силу трения покоя, и коробка начнет скользить по поверхности (скольжение).
2. Или сила толкания и сила трения создадут достаточно сильную пару, чтобы ящик повернулся и упал на бок (опрокидывание).

По мере увеличения силы толкания коробки она либо начнет скользить по поверхности (скольжение), либо начнет вращаться (опрокидывание). какой из двух вариантов произойдет первым. Чтобы определить это, мы обычно определяем как толкающую силу, необходимую для соскальзывания тела, так и толкающую силу, необходимую для опрокидывания тела. Вариант, требующий меньшего усилия, будет выполнен первым.

Определение силы, необходимой для «скольжения» объекта:

Тело будет скользить по поверхности, если толкающая сила превышает максимальную силу трения покоя, которая может существовать между двумя соприкасающимися поверхностями. Как и во всех задачах о сухом трении, этот предел силы трения равен статическому коэффициенту трения, умноженному на нормальную силу между телами. Если сила толкания превышает это значение, тело будет скользить.

Если сила толкания превышает максимальную силу трения покоя (u _s * F _N ), то тело начнет скользить.

Определение силы, необходимой для создания «наконечника» объекта

Нормальные силы, поддерживающие тела, являются распределенными силами. Эти силы не только предотвратят ускорение тела в земле из-за гравитационных сил, но они также могут перераспределиться, чтобы предотвратить вращение тела, когда на тело действуют силы, вызывающие момент. Это перераспределение приведет к смещению точечной нагрузки, эквивалентной нормальной силе, в ту или иную сторону. Тело опрокинется, когда нормальная сила больше не сможет перераспределяться, чтобы сопротивляться моменту, создаваемому другими силами (такими как сила толкания и сила трения).

В состоянии покоя (А) нормальная сила представляет собой равномерно распределенную силу, действующую на нижнюю часть тела. При приложении толкающей силы (В) распределенная нормальная сила перераспределяется, перемещая эквивалентную точечную нагрузку вправо. Это создает пару между силой тяжести и нормальной силой, которая будет противодействовать паре, создаваемой толкающей силой и силой трения. Если толкающая сила становится достаточно большой (С), пара, создаваемая гравитационной силой и нормальной силой, не сможет противостоять паре, создаваемой толкающей силой и силой трения.

Самый простой способ представить смещающую нормальную силу и опрокидывание — представить эквивалентную точечную нагрузку распределенной нормальной силы. Когда мы толкаем или тянем тело, нормальная сила будет смещаться влево или вправо.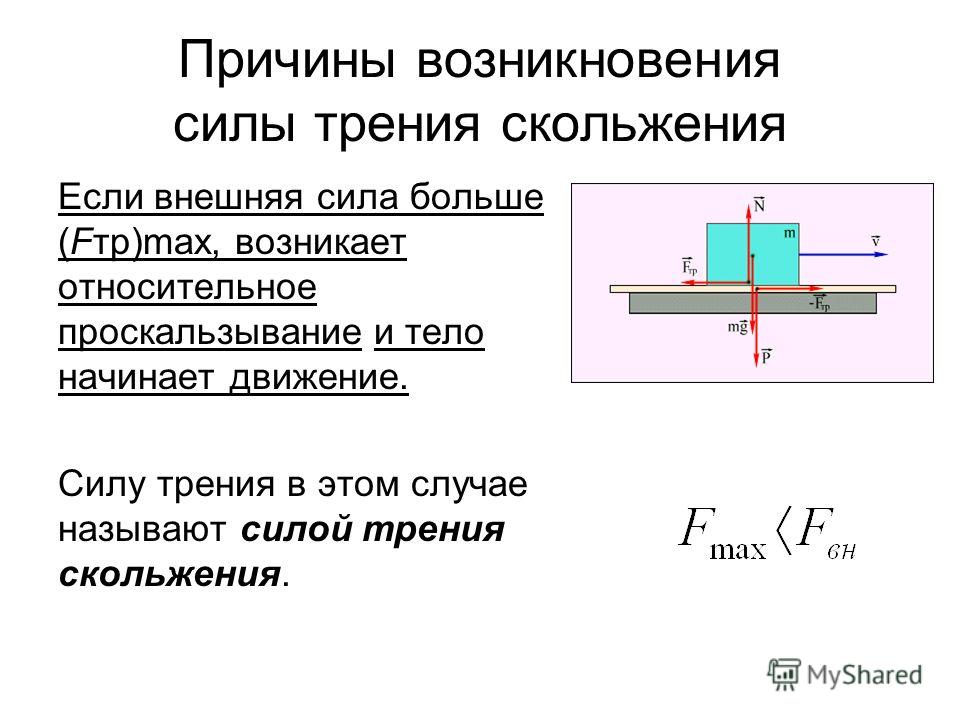 Эта нормальная сила и сила гравитации создают пару, создающую момент. Этот момент будет противодействовать моменту, создаваемому парой, образованной силой толкания и силой трения.

Поскольку нормальная сила является прямым результатом физического контакта, мы не можем сместить нормальную силу за пределы соприкасающихся поверхностей (т. е. края коробки). Если противодействие моменту толкающей силы и силы трения требует смещения нормальной силы за край ящика, то нормальная сила и сила тяжести не смогут противодействовать моменту и в результате ящик начнет вращать (иначе опрокидывать).

Тело опрокинется, когда момент сил толкания и трения превысит момент сил гравитации и нормальных сил. При надвигающемся движении нормальная сила будет действовать на самом краю тела.

Вопрос Видео: Кинематика объекта, скользящего по склону против трения

Стенограмма видео

Коробка массой 12,4 кг горки из положения покоя вниз по пандусу длиной 1,58 м с наклоном 23,3 градуса ниже горизонтали.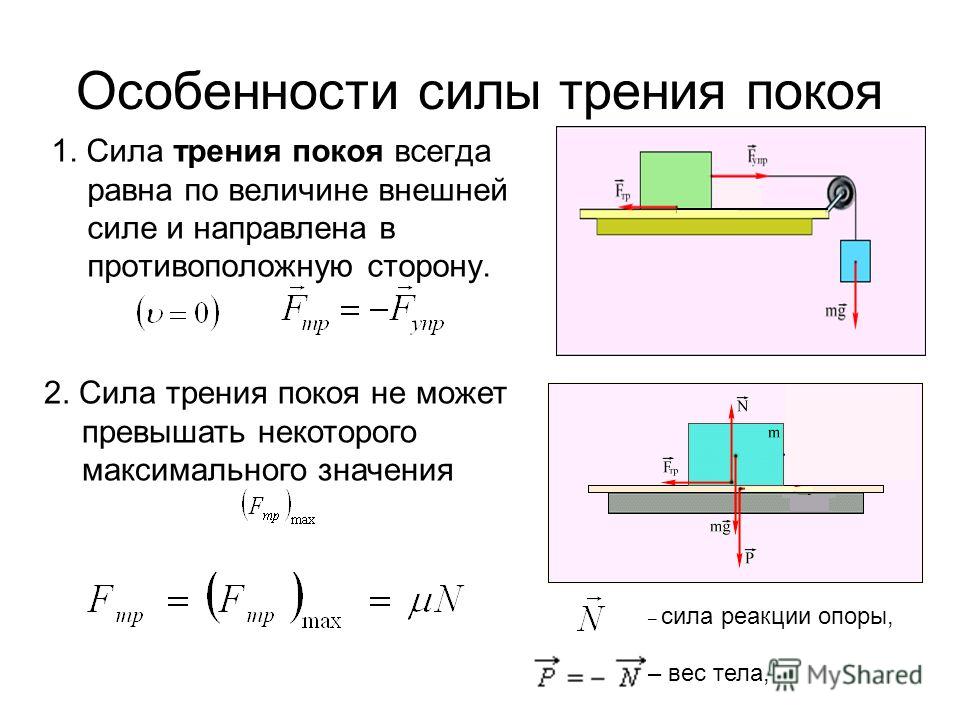 Коэффициент кинетического трения между коробкой и пандусом 0,0346. Какова величина коробки ускорение? Какова скорость ящика на внизу рампы?

Мы можем назвать ускорение коробки 𝑎 и скорость коробки в нижней части рампы 𝑣 sub 𝑓. Давайте начнем с нашего решения начертить схему подвижного ящика. В этом примере у нас есть коробка масса 𝑚 — 𝑚 равна 12,4 кг — на пандусе длиной 𝑙, где 𝑙 равно 1,58 метров. Пандус наклонен под углом мы назвали 𝜃, где 𝜃 на 23,3 градуса выше горизонтали. Под действием силы тяжести мы ожидайте, что коробка соскользнет с пандуса. и мы хотим решить для его ускорения, 𝑎, когда это произойдет. Мы также хотим узнать, насколько быстро коробка движется, когда она достигает нижней части пандуса.

В этом сценарии мы создали 𝑥- и 𝑦-координатная ось, так что положительное движение в 𝑥-направлении происходит вниз наклонное и положительное движение в 𝑦-направлении перпендикулярно плоскости.

Далее нарисуем свободное тело диаграмма массы 𝑚, то есть сил, действующих на нее. Мы знаем, что есть гравитация сила, действующая на 𝑚 прямо вниз, величина 𝑚 умноженная на 𝑔, где 𝑔, ускорение свободного падения равно 90,8 метра в секунду в квадрате. Также действует нормальная сила на массу, чтобы она не сместилась в плоскость. И, наконец, когда коробка скользит вниз В самолете есть кинетическая сила трения, которая сопротивляется его движению.

Глядя на эту диаграмму свободного тела, мы можем разделить силу веса на ее 𝑦- и 𝑥-составляющие, так что мы можем напишите уравнения баланса сил в 𝑦- и 𝑥-направлениях. И мы знаем, что с этой силой компоненты под прямым углом друг к другу, образуется треугольник, где верхняя угол это угол 𝜃.

Вспоминая второй закон Ньютона движения, что результирующая сила, действующая на объект, равна его ускорению, умноженному на его массу, мы можно рассмотреть силы в 𝑥-направлении в нашем сценарии. Это кинетическое трение сила и 𝑥-составляющая силы веса. Поскольку мы решили, что движение вниз по пандусу — это движение в положительном направлении, наше уравнение баланса сил для 𝑥-силы равны 𝑚𝑔 sin 𝜃 минус кинетическая сила трения равна массе объекта, умноженное на его ускорение.

Кинетическая сила трения, 𝑓 sub 𝑘, равно коэффициенту кинетического трения, 𝜇 sub 𝑘, умноженному на нормальная сила, действующая на объект. Это означает, что мы можем заменить 𝑓 sub 𝑘 с 𝜇 sub 𝑘 𝑓 sub 𝑛 в нашем уравнении баланса 𝑥-сил. А мы помним, что нам дано 𝜇 sub 𝑘 в условии задачи.

Глядя на этот баланс сил уравнения, мы видим, что если мы разделим обе части на массу 𝑚, мы увидим, что у нас есть выражение для ускорения 𝑎, которое мы хотим найти. Единственная проблема заключается в том, что мы еще не знать нормальную силу, 𝑓 sub 𝑛, которая действует на нашу массу.

Чтобы это выяснить, давайте посмотрим на силы в 𝑦-направлении на нашу массу.

Применение второго закона Ньютона к силы в этом направлении, мы пишем, что нормальная сила минус 𝑚𝑔 cos 𝜃, 𝑦-составляющая силы веса, равна произведению массы ящика на его ускорение в 𝑦-направлении. Но потому что коробка не уходит поверхности самолета это ускорение равно нулю. И наше уравнение упрощается до нормальная сила равна 𝑚𝑔, умноженной на косинус 𝜃. Это идеально, потому что теперь мы можем возьмите этот член для 𝑓 sub 𝑛 и подставьте его в наше уравнение в 𝑥-направление.

С этим расширенным выражением для ускорение 𝑎, мы видим, что масса ящика 𝑚 фигурирует во всех слагаемых в числитель и знаменатель. Так что отменяется. Вычтем ускорение из-за к гравитации, 𝑎 равно 𝑔 умноженному на величину sin 𝜃 минус 𝜇 sub 𝑘 cos 𝜃. Замена 𝑔, 𝜃 и 𝜇 sub 𝑘, когда мы вычисляем 𝑎 до трех значащих цифр, мы находим, что это 3,56 метра за секунду в квадрате. Это ускорение коробки когда он спускается по рампе.

Далее мы хотим решить скорость коробка имеет, когда она достигает нижней части пандуса длиной 1,58 метра. Чтобы понять это, мы знаем, что ускорение, которое испытывает ящик во время движения, постоянно. Это означает, что кинематическая уравнения движения применимы к движению этого ящика. Когда мы смотрим на эти четыре уравнения движения, мы ищем то, которое позволяет нам решить конечную скорость, 𝑣 sub 𝑓, с точки зрения информации, которую мы знаем.

Второе кинематическое уравнение написанное хорошо соответствует нашим условиям. Переписав его с точки зрения нашего переменных, конечная скорость ящика в квадрате равна начальной скорости ящика, что равно нулю, потому что коробка начинается с состояния покоя, плюс удвоенное значение коробки.