Элементарный учебник физики Т1

Ландсберг Г.С. Элементарный учебник физики. Т.1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1985. — 606 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ОТ ИЗДАТЕЛЬСТВА ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ ВВЕДЕНИЕ Глава I. Кинематика § 1. Движение тел § 2. Кинематика. Относительность движения и покоя. § 3. Траектория движения § 4. Поступательное и вращательное движения тела § 5. Движение точки § 6. Описание движения точки § 7. Измерение длины § 8. Измерение промежутков времени § 9. Равномерное прямолинейное движение и его скорость § 10. Знак скорости при прямолинейном движении § 11. Единицы скорости § 12. Графики зависимости пути от времени § 13. Графики зависимости скорости от времени § 14. Неравномерное прямолинейное движение § 15. Мгновенная скорость § 16. Ускорение при прямолинейном движении § 17. Скорость прямолинейного равноускоренного движения § 18. Знак ускорения при прямолинейном движении § 19. Графики скорости при прямолинейном равноускоренном движении § 20. Графики скорости при произвольном неравномерном движении § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости § 22. Путь, пройденный при равнопеременном движении § 23. Векторы § 24. Разложение вектора на составляющие § 25. Криволинейное движение § 26. Скорость криволинейного движения § 27. Ускорение при криволинейном движении § 28. Движение относительно разных систем отсчета § 29. Кинематика космических движений Глава II. Динамика § 30. Задачи динамики § 31. Закон инерции § 32. Инерциальные системы отсчета § 33. Принцип относительности Галилея § 34. Силы § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции § 36. Сила — вектор. Эталон силы § 37. Динамометры § 38. Точка приложения силы § 39. Равнодействующая сила § 40. Сложение сил, направленных по одной прямой § 41. Сложение сил, направленных под углом друг к другу § 42. Связь между силой и ускорением § 43. Масса тела § 44. Второй закон Ньютона § 45. Единицы силы и массы § 46. Системы единиц § 47. Третий закон Ньютона § 48. Примеры применения третьего закона Ньютона § 49. Импульс тела § 50. Система тел. Закон сохранения импульса § 51. Применения закона сохранения импульса § 52. Свободное падение тел § 53. Ускорение свободного падения § 54. Падение тела без начальной скорости и движение тела, брошенного вертикально вверх § 55. Вес тела § 56. Масса и вес § 57. Плотность вещества § 58. Возникновение деформаций § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении § 60. Деформации в покоящихся телах, вызванные силой тяжести § 61. Деформации тела, испытывающего ускорение § 62. Исчезновение деформаций при падении тел § 63. Разрушение движущихся тел § 64. Силы трения § 65. Трение качения § 66. Роль сил трения § 67. Сопротивление среды § 68. Падение тел в воздухе Глава III. Статика § 69. Задачи статики § 70. Абсолютно твердое тело § 71. Перенос точки приложения силы, действующей на твердое тело § 72. Равновесие тела под действием трех сил § 73. Разложение сил на составляющие § 74. Проекции сил. Общие условия равновесия § 75. Связи. Силы реакции связей. Тело, закрепленное на оси § 76. Равновесие тела, закрепленного на оси § 77. Момент силы § 78. Измерение момента силы § 79. Пара сил § 80. Сложение параллельных сил. Центр тяжести § 81. Определение центра тяжести тел § 82. Различные случаи равновесия тела под действием силы тяжести § 83. Условия устойчивого равновесия под действием силы тяжести § 84. Простые машины § 85. Клин и винт Глава IV. Работа и энергия § 86. «Золотое правило» механики § 87. Применения «золотого правила» § 88. Работа силы § 89. Работа при перемещении, перпендикулярном к направлению силы § 90. Работа силы, направленной под любым углом к перемещению § 91. Положительная и отрицательная работа § 92. Единица работы § 93. О движении по горизонтальной плоскости § 94. Работа силы тяжести при движении по наклонной плоскости § 95. Принцип сохранения работы § 96. Энергия § 97. Потенциальная энергия § 98. Потенциальная энергия упругой деформации § 99. Кинетическая энергия § 100. Выражение кинетической энергии через массу и скорость тела § 101. Полная энергия тела § 102. Закон сохранения энергии § 103. Силы трения и закон сохранения механической энергии § 104. Превращение механической энергии во внутреннюю энергию § 105. Всеобщий характер закона сохранения энергии § 106. Мощность § 107. Расчет мощности механизмов § 108. Мощность, быстроходность и размеры механизма § 109. Коэффициент полезного действия механизмов Глава V. Криволинейное движение § 110. Возникновение криволинейного движения § 111. Ускорение при криволинейном движении § 112. Движение тела, брошенного в горизонтальном направлении § 113. Движение тела, брошенного под углом к горизонту § 114. Полет пуль и снарядов § 115. Угловая скорость § 116. Силы при равномерном движении по окружности § 117. Возникновение силы, действующей на тело, движущееся по окружности § 118. Разрыв маховиков § 119. Деформация тела, движущегося по окружности § 120. «Американские горки» § 121. Движение на закруглениях пути § 122. Движение подвешенного тела по окружности § 123. Движение планет § 124. Закон всемирного тяготения § 125. Искусственные спутники Земли Глава VI. Движение в неинерциальных системах отсчета и силы инерции § 126. Роль системы отсчета § 127. Движение относительно разных инерциальных систем отсчета § 128. Движение относительно инерциальной и неинерциальной систем отсчета § 129. Поступательно движущиеся неинерциальиые системы § 130. Силы инерции § 131. Эквивалентность сил инерции и сил тяготения § 132. Невесомость и перегрузки § 133. Является ли Земля инерциальиой системой отсчета? § 134. Вращающиеся системы отсчета § 135. Силы инерции при движении тела относительно вращающейся системы отсчета § 136. Доказательство вращения Земли § 137. 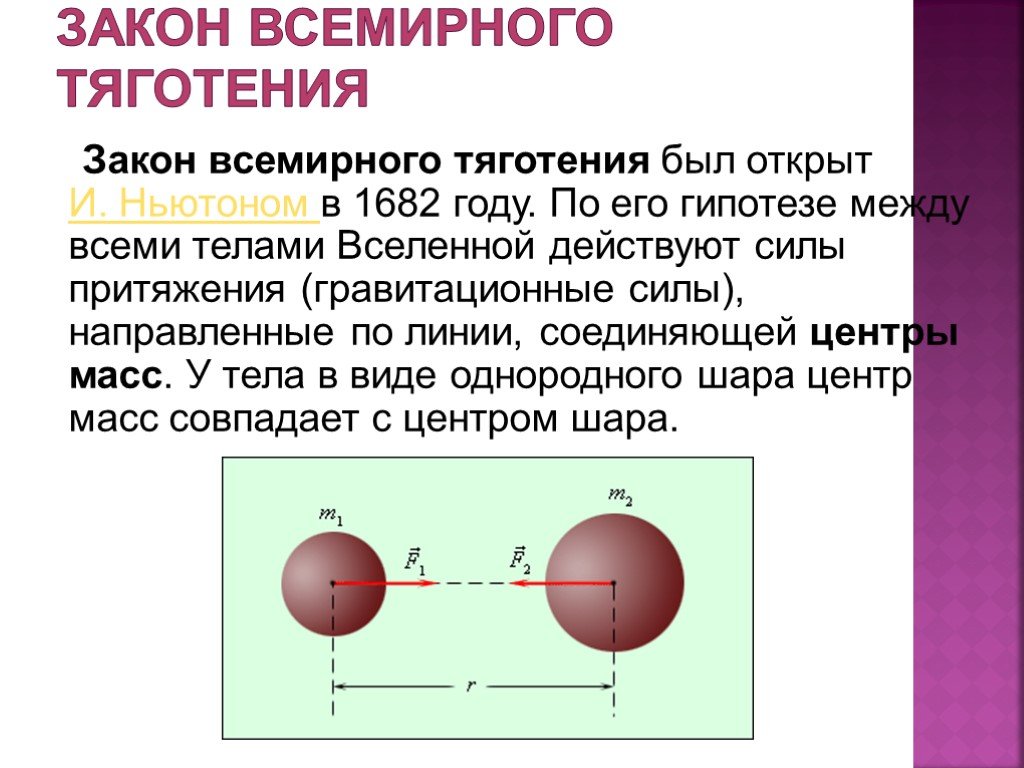Приливы Глава VII. Гидростатика § 138. Подвижность жидкости § 139. Силы давления § 140. Измерение сжимаемости жидкости § 141. «Несжимаемая» жидкость § 142. Силы давления в жидкости передаются во все стороны § 143. Направление сил давления § 144. Давление § 145. Мембранный манометр § 146. Независимость давления от ориентации площадки § 147. Единицы давления § 148. Определение сил давления по давлению § 149. Распределение давления внутри жидкости § 150. Закон Паскаля § 151. Гидравлический пресс § 152. Жидкость под действием силы тяжести § 153. Сообщающиеся сосуды § 154. Жидкостный манометр § 155. Устройство водопровода. Нагнетательный насос § 156. Сифон § 157. Сила давления на дно сосуда § 158. Давление воды в морских глубинах § 159. Прочность подводной лодки § 160. Закон Архимеда § 161. Измерение плотности тел на основании закона Архимеда § 162. Плавание тел § 163. Плавание несплошных тел § 164. Устойчивость плавания кораблей § 165. Всплывание пузырьков § 166. Тела, лежащие на дне сосуда Глава VIII. Аэростатика § 167. Механические свойства газов § 168. Атмосфера § 169. Давление атмосферы § 170. Другие опыты, показывающие существование атмосферного давления § 171. Разрежающие насосы § 172. Влияние атмосферного давления на уровень жидкости в трубке § 173. Максимальная высота столба жидкости § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид § 175. Распределение атмосферного давления по высоте § 176. Физиологическое действие пониженного давления воздуха § 177. Закон Архимеда для газов § 178. Воздушные шары и дирижабли § 179. Применение сжатого воздуха в технике Глава IX. Гидродинамика и аэродинамика § 180. Давление в движущейся жидкости § 181. Течение жидкости по трубам § 182. Закон Бернулли § 183. Жидкость в неинерциальных системах отсчета § 184. Реакция движущейся жидкости и ее использование § 185. Перемещение на воде § 186. Ракеты § 187. Реактивные двигатели § 188. Баллистические ракеты § 189. Взлет ракеты с Земли § 190. Сопротивление воздуха § 191. Эффект Магиуса и циркуляция § 192. Подъемная сила крыла и полет самолета § 193. Турбулентность в потоке жидкости или газа § 194. Ламинарное течение РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава X. Тепловое расширение твердых и жидких тел § 195. Тепловое расширение твердых и жидких тел § 196. Термометры § 197. Формула линейного расширения § 198. Формула объемного расширения § 199. Связь между коэффициентами линейного и объемного расширения § 200. Измерение коэффициента объемного расширения жидкостей § 201. Особенности расширения воды Глава XI. Работа. Теплота. Закон сохранения энергии § 202. Изменения состояния тел § 203. Нагревание тел при совершении работы § 204. Изменение внутренней энергии тел при теплопередаче § 205. Единицы количества теплоты § 206. Зависимость внутренней энергии тела от его массы и вещества § 207. Теплоемкость тела § 208. Удельная теплоемкость § 209. Калориметр. Измерение теплоемкостей § 210. Закон сохранения энергии § 211. Невозможность «вечного двигателя» § 212. Различные виды процессов, при которых происходит передача теплоты Глава XII. Молекулярная теория § 213. Молекулы и атомы § 214. Размеры атомов и молекул § 215. Микромир § 216. Внутренняя энергия с точки зрения молекулярной теории § 217. Молекулярное движение § 218. Молекулярное движение в газах, жидкостях и твердых телах § 219. Броуновское движение § 220. Молекулярные силы Глава XIII. Свойства газов § 221. Давление газа § 222. Зависимость давления газа от температуры § 223. Формула, выражающая закон Шарля § 224. Закон Шарля с точки зрения молекулярной теории § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы § 226. Закон Бойля — Мариотта § 227. Формула, выражающая закон Бойля — Мариотта § 228. График, выражающий закон Бойля — Мариотта § 229. Зависимость между плотностью газа и его давлением § 230. Молекулярное толкование закона Бойля — Мариотта § 231. Изменение объема газа при изменении температуры § 232. Закон Гей-Люссака § 233. Графики, выражающие законы Шарля и Гей-Люссака § 234. Термодинамическая температура § 235. Газовый термометр § 236. Объем газа и термодинамическая температура § 237. Зависимость плотности газа от температуры § 238. Уравнение состояния газа § 239. Закон Дальтона § 240. Плотность газов § 241. Закон Авогадро § 242. Моль. Постоянная Авогадро § 243. Скорости молекул газа § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна) § 245. Удельные теплоемкости газов § 246. Молярные теплоемкости § 247. Закон Дюлонга и Пти Глава XIV. Свойства жидкостей § 248. Строение жидкостей § 249. Поверхностная энергия § 250. Поверхностное натяжение § 251. Жидкостные пленки § 252. Зависимость поверхностного натяжения от температуры § 253. Смачивание и несмачивание § 254. Расположение молекул у поверхности тел § 255. Значение кривизны свободной поверхности жидкости § 256. Капиллярные явления § 257. Высота поднятия жидкости в капиллярных трубках § 258. Адсорбция § 259. Флотация § 260. Растворение газов § 261. Взаимное растворение жидкостей § 262. Растворение твердых тел в жидкостях Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое § 263. Введение § 264. Кристаллические тела § 265. Аморфные тела § 266. Кристаллическая решетка § 267. Кристаллизация § 268. Плавление и отвердевание § 269. Удельная теплота плавления § 270. Переохлаждение § 271. Изменение плотности веществ при плавлении § 272. Полимеры § 273. Сплавы § 274. Затвердевание растворов § 275. Охлаждающие смеси § 276. Изменения свойств твердого тела Глава XVI. Упругость и прочность § 277. Введение § 278. Упругие и пластические деформации § 279. Закон Гука § 280. Растяжение и сжатие § 281. Сдвиг § 282. Кручение § 283. Изгиб § 284. Прочность § 285. Твердость § 286. Что происходит при деформации тел § 287. Изменение энергии при деформации тел Глава XVII. Свойства паров § 288. Введение § 289. Пар насыщенный и ненасыщенный § 290. Что происходит при изменении объема жидкости и насыщенного пара § 291. Закон Дальтона для пара § 292. Молекулярная картина испарения § 293. Зависимость давления насыщенного пара от температуры § 294. Кипение § 295. Удельная теплота парообразования § 296. Охлаждение при испарении § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное § 298. Испарение при кривых поверхностях жидкости § 299. Перегревание жидкости § 300. Пересыщение паров § 301. Насыщение пара при возгонке § 302. Превращение газа в жидкость § 303. Критическая температура § 304. Сжижение газов в технике § 305. Вакуумная техника § 306. Водяной пар в атмосфере Глава XVIII. Физика атмосферы § 307. Атмосфера § 308. Тепловой баланс Земли § 309. Адиабатические процессы в атмосфере § 310. Облака § 311. Искусственные осадки § 312. Ветер § 313. Предсказание погоды Глава XIX. Тепловые машины § 314. Условия, необходимые для работы тепловых двигателей § 315. Паросиловая станция § 316. Паровой котел § 317. Паровая турбина § 318. Поршневая паровая машина § 319. Конденсатор § 320. Коэффициент полезного действия теплового двигателя § 321. Коэффициент полезного действия паросиловой станции § 322. Бензиновый двигатель внутреннего сгорания § 323. Коэффициент полезного действия двигателя внутреннего сгорания § 324. Двигатель Дизеля § 325. Реактивные двигатели § 326. Передача теплоты от холодного тела к горячему Ответы и решения к упражнениям Предметный указатель

Характеристика силы притяжения Земли и силы тяжести, действующих в ходе полета ракеты

Одной из основных сил, действующих на БЛА в полете, является сила земного притяжения:

,     (1)

где m – масса БЛА;  – вектор ускорения силы притяжения.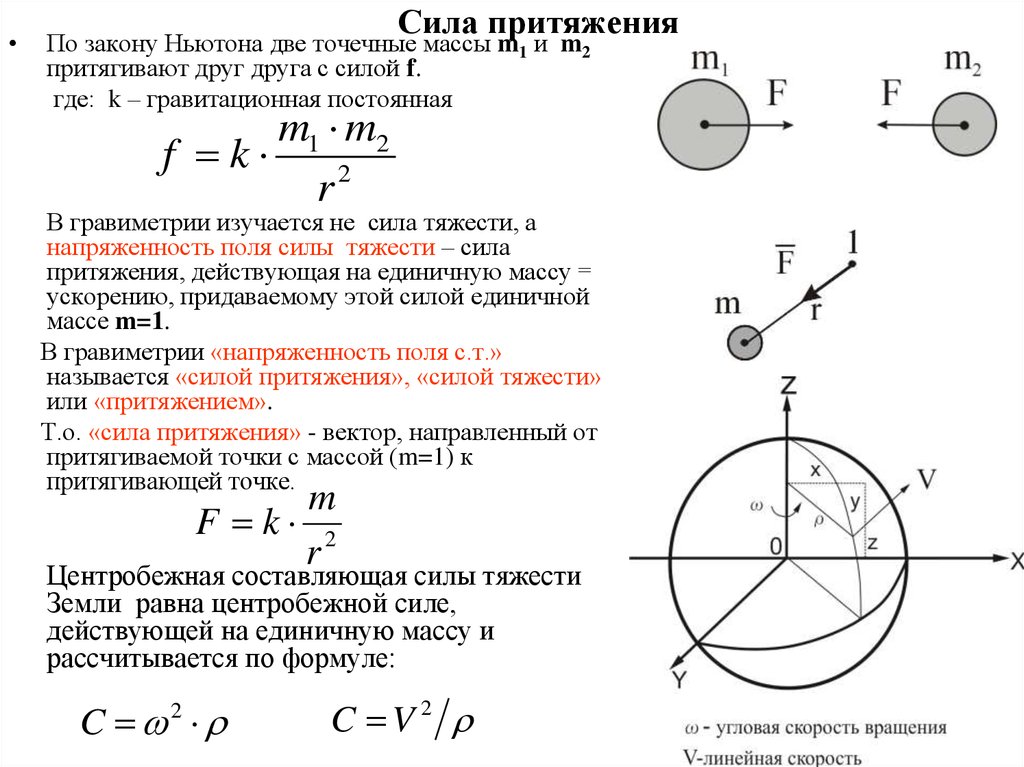

По своей физической природе сила притяжения Земли является гравитационной силой. Гравитационные силы возникают в результате взаимодействия гравитационных полей, которые создаются в окружающем пространстве материальными объектами, имеющими некоторую массу.

Общие закономерности гравитационного взаимодействия материальных объектов были установлены в 80-х годах ХVII века великим английским физиком и математиком Исааком Ньютоном. Согласно открытому им закону всемирного тяготения, всякая материальная точка притягивает другую материальную точку с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

.    (2)

Здесь f= 6,67∙10^-11 – универсальная постоянная тяготения, н∙м²/кг²; m₁ и m₂– массы материальных точек; R– расстояние между точками.

Силы F_1,2 и F_2,1 действуют по прямой, соединяющей точки m₁ и m₂, как показано на рисунке 1.

Рис. 1. Схема притяжения двух материальных тел

В соответствии с законом всемирного тяготения на движущийся в пространстве БЛА действуют силы притяжения Земли и других небесных тел. Однако, как показывают исследования и расчеты, сила притяжения Земли является определяющей даже при достаточно больших удалениях БЛА от ее поверхности. Поэтому с достаточно высокой степенью точности можно считать, что на БЛА, совершающий полет в околоземном пространстве, на удалениях, не превышающих нескольких тысяч километров, из гравитационных сил действует лишь сила притяжения Земли.

Сила притяжения Земли является потенциальной силой. Это значит, что работа силы притяжения Земли при перемещении БЛА зависит только от начального и конечного его положения в пространстве. Иными словами, работа этой силы вдоль произвольной замкнутой траектории движения БЛА тождественно равна нулю.

Потенциальный характер силы притяжения отражает потенциальный характер гравитационного поля Земли и имеет важное прикладное значение. Дело в том, что исчерпывающей силовой характеристикой потенциального поля является потенциальная функция или потенциал. Потенциалом силового поля называется скалярная функция координат, дифференциал которой равен элементарной работе создаваемой этим полем силы. Математически указанное свойство потенциала выражается формулой

dU(X,Y,Z) = dA,     (3)

где dU(X,Y,Z) – дифференциал потенциала силового поля U(X,Y,Z); dA – элементарная работа потенциальной силы.

Выражение потенциала притяжения тела произвольной формы с массой М и объемом V имеет вид:

,     (4)

где m – масса притягиваемого тела; M, V – области интегрирования, представляющие собой всю массу и весь объем притягивающего тела соответственно; R – расстояние от притягиваемой точки до элементарной массы  или элементарного объема притягивающего тела;  – объемная плотность притягивающего тела [1].

Однако, можно получить выражение, описывающее потенциал притяжения Земли точными аналитическими зависимостями, не удается из-за сложности ее фигуры (формы) и сложного характера распределения массы в теле планеты. Поэтому при решении практических задач Землю как притягивающее тело обычно представляют в идеализированном виде, позволяющем записать выражение для потенциала и вычислить силу притяжения Земли с требуемой точностью.

Сила тяжести. Земля совершает вращательное движение вокруг своей оси с угловой скоростью Ω_з=7,292116⋅10^-5с^-1 и годовое движение по слабоэллиптической орбите вокруг Солнца со средней скоростью 29,893 км/с. Вследствие того, что время полета БЛА во много раз меньше, чем период обращения Земли вокруг Солнца, влияние этого фактора на полет пренебрежимо мало. Можно считать, что в течение времени полета БЛА Земля движется по орбите прямолинейно и равномерно. Влияние же суточного вращения Земли во многих случаях необходимо учитывать.

Если БЛА находится на поверхности Земли, то справедливо следующее равенство:

,     (5)

где  – сила притяжения Земли;  – центробежная сила инерции;  – сила реакции опоры.

Таким образом, сила реакции опоры со стороны поверхности Земли уравновешивает силу притяжения и центробежную силу инерции, обусловленную ее вращением.

Равнодействующая  силы земного притяжения  и центробежной силы инерции от суточного вращения Земли , приложенная к материальному телу на поверхности Земли, называется силой тяжести. Формула для определения силы тяжести имеет вид:

,     (6)

что иллюстрируется рисунком 2.

Хотя при решении практических задач механики полета и теории наведения БЛА достаточно знать силу притяжения Земли (поскольку на БЛА в полете действует именно эта сила), рассмотрение силы тяжести целесообразно по двум причинам: во-первых, определение силы притяжения Земли пока в основном производится через определение силы тяжести; во-вторых, при решении задач наземной навигации приходится иметь дело только с силой тяжести и ее потенциалом.

Рис. 2. Схема действия силы тяжести

Величина центробежной силы инерции равна:

,    (7)

где  – расстояние от оси вращения Земли до материального тела, находящегося на ее поверхности; m – масса материального тела; R – расстояние от центра Земли до материального тела.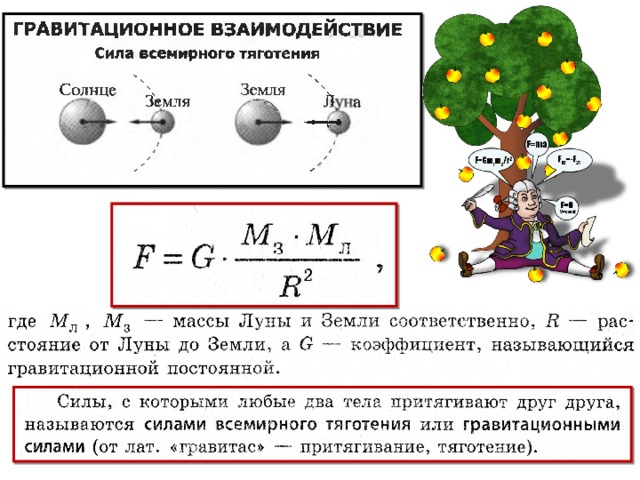

Центробежная сила инерции мала. Ее величина не превышает 0,35 % величины силы тяжести. Поэтому максимальное значение угла γ″, на который отклоняется линия действия силы тяжести от линии действия силы притяжения, также мало и составляет величину γ_max″=0,00173 рад=6′ на широте 45^о. Для сравнения укажем, что максимальное отклонение линии действия силы притяжения общего земного эллипсоида от направления к центру Земли γ_max‘=0,00335=11’5 также на широте 45^о.

Таким образом, на поверхности Земли эффект от центробежной силы инерции, обусловленной ее вращением, соизмерим с эффектом, вызываемой полярным сжатием (сплюснутостью) Земли.

Введение в международную формулу гравитации Hezar

Введение

Земля сфероидальна, и ее поверхность сфероидальна. В 1930 году была принята Международная формула силы тяжести (IGF) для расчета теоретического значения силы тяжести в любой точке сфероида. IGF 1930 года был основан на модели Клеро, впервые разработанной в 1777 году.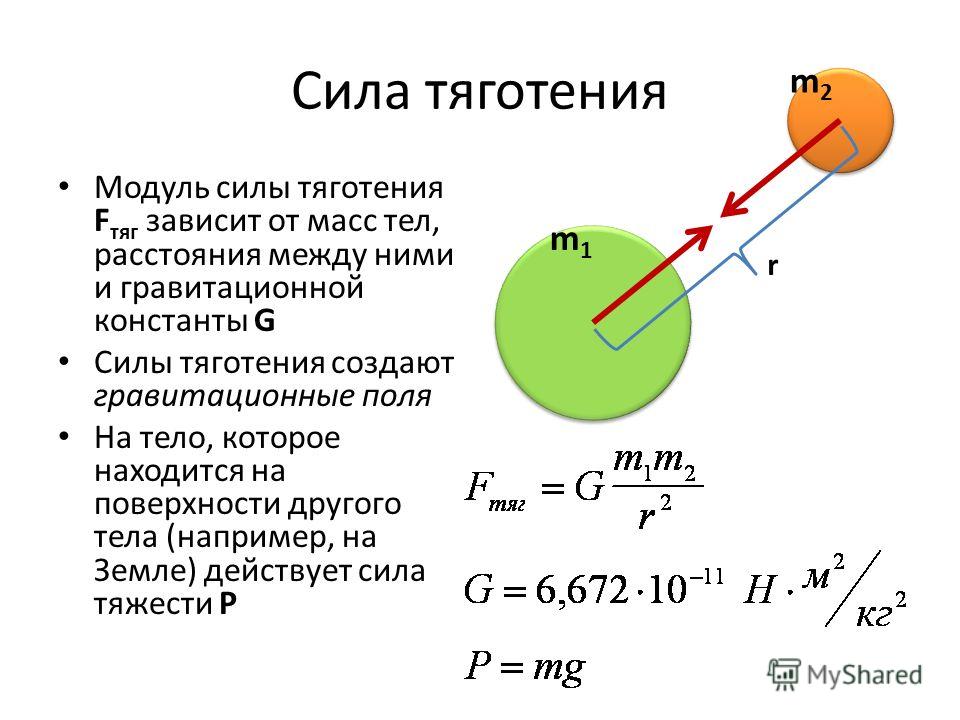 IGF 1930 года также включал данные Потсдама. Однако IGF 1930 года был дополнительно модифицирован в 1967 году Геодезической системой отсчета (GRS 67), которая затем была уточнена и описана Вуллардом в 1979 с использованием точных спутниковых данных Джейкобса в 1974 году. GRS 67 был совместим с данными Международной сети стандартизации гравитации 1971 года. Различия между IGF 1930 г. и GRS 67 обсуждались Lysonski [1]. IGF явно не зависит от уплощения Земли, потому что это теоретическая модель гравитации [2]. Более того, на топографической поверхности Земли наблюдались различные систематические ошибки вычисления нормальной гравитации [3]. Следовательно, новая формулировка силы тяжести требовала вычисления нормальной силы тяжести в разных точках. Две гравитационные модели Земли (EGM), которые являются лучшими моделями для расчета гравитации, включают EGM9.6 и EGM2008 [4], а наиболее известными IGF являются GRS30, GRS1967, GRS80 и WGS84 [5, 6]. Из них уравнение WGS84 было модифицировано несколькими учеными [1, 6–8].

Почти все вышеперечисленные модели являются теоретическими моделями для оценки гравитации Земли. Поэтому это исследование сосредоточено на разработке экспериментальной модели для оценки гравитации Земли. Исследование показало, что модель WGS84 не может объяснить экспериментальную гравитацию вершин и земной поверхности, в том числе разницу в гравитации −203 мГал между вершинами гор Хезар и Дамаванд (4,499,416 м и 5 605,730 м соответственно) [9]. По данным физико-геодезической съемки, выполненной Национальным картографическим центром Ирана (НКЦ), гравитация вершины Хезар на 203 мГал ниже, чем гравитация пика горы Дамаванд. Поэтому вершина Хезар неожиданно имеет низкое значение гравитации по всему Ирану. В настоящем исследовании мы ввели новую четырехкоэффициентную гравиметрическую формулу, в которой коэффициенты рассчитываются с использованием экспериментальных гравиметрических данных из четырехточечных наборов по всему миру. Это экспериментальное гравитационное уравнение было введено в виде Международной гравитационной формулы Хезара (HIGF). Гравитацию на разных высотах и ​​широтах можно измерить с помощью HIGF и сравнить с модифицированным IGF84 (WGS84) [8]. Главной новизной данного исследования является формулировка формулы силы тяжести с четырьмя коэффициентами, основанная на измерении силы тяжести над уровнем моря. В следующем разделе объясняются детали уравнения HIGF.

Формула четырех коэффициентов силы тяжести

Поскольку Земля имеет форму шара, сила тяжести рассчитывается по уравнению. 1:

g=GMr2(1)

Где G — гравитационная постоянная, M — масса Земли и r — расстояние от центра Земли.

Влияние несферической формы Земли, вращения Земли, расстояния до эллиптической Земли, поправки на свободный воздух [8] и феномена Бугера [10] на гравитацию также исследовались. IGF с четырьмя коэффициентами был введен как Eq. (2) [1, 5–7].

g=A+B⁡sin2⁡θ+C⁡sin22θ-Dh(2)

Где h и θ обозначают высоту и широту соответственно.

Изменения силы тяжести из-за высот эллипсоидальной Земли вводятся как 0,3086 ч [8]. Влияние аномалии Бугера, определяемое функцией плотности породы ( ρ = 2,65 г.м ³ ) и высоты ( h ), обозначается как 0,04193ρh [8]. Следовательно, точные гравитационные значения могут быть получены везде в зависимости от глобальной гравитационной аномалии Буге, показанной на рисунке 1 [11].

РИСУНОК 1 . Буге гравитационная аномалия мира [11].

Деталь для уравнения. (2) расчет приведен ниже:

Земля считается в трех формах. В первой форме Земля имеет однородную эллипсоидальную форму с радиусом r, где r = R _e ( –F Sin ² θ 0 9090 1 ), где 5 6 F 0 9016 обозначает в уравнении 3.

F=Re− RoRe(3)

F – параметр асимметрии шара, R _e — радиус Земли на экваторе, а θ — широта. Во второй форме считается, что геоид находится примерно от +150 до -150 м выше или ниже эллиптической Земли. Окончательная форма относится к неравномерному расстоянию на поверхности Земли ( ч ) от эллиптической Земли. В соответствии с несферичностью Земли и изменениями расстояния от центра Земли изменение интервала между каждой точкой Земли и центром Земли определяется в уравнении. (4):

r=Re(1 — F Sin2θ)+h(4)

r=Re(1-FSin2θ+hRe)(5)

g=ge(1-2hRe+2FSin2θ+3F2Sin4θ+3(hRe)2 -6Sin2θ)(6)

В соответствии с небольшим количеством последних двух членов (уравнение 6) может быть повторено как уравнение. 7.

g = ge(1+2FSin2θ+3F2Sin4θ)-2geReh(7)

Ускорение, вызванное вращением Земли, представлено уравнением 8.

aR=Rω2=(r + h)Cosθω2(8)

Составляющая aR в направлении r представлена ​​в виде уравнений 9, 10.

ar=aRCosθ(9)

ar=(r+h)Cos2θω2(10)

Используя уравнение (5) и (уравнение 10) также могут быть преобразованы в уравнение. 11.

ar=Reω2Cos2θ−F Re ω24Sin22θ+hω2Cos2θ(11)

Влияние вращения на гравитацию Земли получается путем подстановки уравнения 7 и (11) с уравнением. 12.

g=ge(1−Re ω2ge+(2F+Re ω2ge)Sin2θ+3F2Sin4θ+2F Re ω24 geSin22θ)−(2geRe+ω2Cos2θ)h(12)

Пренебрегая ω2Cos2θ, т. к. ω 2 2 90 1, ур. (12) выражается как уравнение. 13.

g=ge(1−Re ω2ge+(2F+Re ω2ge)Sin2θ+3F2Sin4θ+2F Re ω24 geSin22θ)−(2geRe)h(13)

Вторая часть уравнения. (13) с поправкой на свободный воздух представляет изменения силы тяжести из-за высоты эллипсоидальной Земли, 0,3086 ч [8]. Более того, влияние аномалии Бугера в уравнении (13) требует формулировки общего эффекта Бугера как функции плотности породы ( ρ = 2,65 г/см ³ ) и высоты ( h ), обозначаемой как 0,04193 ρh [ 8]. Следовательно, точная гравитация может быть измерена везде в зависимости от глобальной аномалии силы тяжести Бугера (рис. 1) [11].

Вводя A=ge(1-Re ω2ge), B=ge(2F+Re ω2ge) , C=F Re ω22 и D=(2geRe) , Ур. (13) можно переписать как уравнение. (2).

Коэффициенты A, B, C и D были рассчитаны посредством теоретического исследования IGF84. В этом исследовании были определены коэффициенты A, B, C и D, и формула HIGF была введена с использованием экспериментальных данных о земном тяготении. Формула HIGF показала высокое совпадение с экспериментальными данными по сравнению с формулой IGF84.

Существует множество гравитационных формул, основанных на формате уравнения. (2), включая FIG 1984 (WGS84) [5, 6], FIG 1987 (модифицированная версия WGS84) [1, 7] и предыдущую версию HIGF [9]. Эти формулы могут быть выражены в виде уравнений 14, 15 соответственно.

G84 = 978032.68 (1+0,0053024⁡Sin2⁡θ-0,0000058⁡Sin22θ) −0. 3086H (14)

G84M = 978032.68 (1+0,00193185138639⁡SIN22⁡L⁡ v 0,3086h(15)

Если поведение изменения силы тяжести в зависимости от высоты или воздействия свободного воздуха (−0,3073 h ) is close to Δg _h = — ( 0.3087691-0.0004398sin ² θ ) h+7.2125 × 10 ⁻⁸ h ² ≈ −0,3087   ч [12]. Влияние аномалии Бугера включается в уравнения (2), (14) и (15) добавлением члена0015 ч . Гравитация во многих точках Ирана и мира рассчитывалась по уравнениям (2), (14) без учета аномалии Бугера. Однако когда в уравнения была включена аномалия Бугера, гравитационные формулы давали те же значения смещения (0,1111 ч ). Между тем гравитация многих точек мира измерялась с помощью гравиметров CG-5 и других приборов [13, 15, 16] (табл. 1). Для сравнения, гравитация, рассчитанная с использованием уравнений (2), (14), показала небольшое отличие от экспериментальных данных. Следовательно, для оценки точной гравитации в этом исследовании была предложена новая формула гравитации с использованием алгоритма исключения матрицы Гаусса-Джордана и практических данных гравитации в качестве экспериментального HIGF.

ТАБЛИЦА 1 . Гравитация многих мест в мире рассчитана с использованием HIGF и IGF84 [13–15].

Представляем Hezar International Gravity Formula

Согласно формуле. (2) существует полиномиальное уравнение для гравитации Земли с использованием четырех постоянных коэффициентов. Эти четыре постоянных коэффициента можно определить с помощью точного измерения силы тяжести в четырех разных точках с разными координатами и высотами. Например, выбрав полюса, экватор, вершины Демавенда и Хезара в качестве четырех точек на Земле, четыре уравнения гравитации для четырех точек на Земле обозначены в уравнении. (16).

gd = a+bsin2θd+csin22θd -dhdgh = a+bsin2θh+csin22θh -dhhge = a+bsin2θe+csin22θe -dhegp = a+bsin2θp+csin22θp-dhp (16)

44, где g_{, g , g, где G 555555555 гг. , г Д , г Н ; θ P , θ E , θ D , θ H ; и h P , h E , h D , h H относятся к гравитации, широте и высоте полюсов, экватора, пиков горы Дамаванд и Хезар соответственно. Эти уравнения также можно представить в виде матрицы MX = Y , как в уравнении. (17).}

X=(ABCD),Y=(gDgHgEgP),M=(1Sin2θDSin22θD−hD1Sin2θHSin22θH−hh2Sin2θESin22θE−hE1Sin2θPSin22θP−hP)(17)

) Используя матричную геометрию и определения (Ур. до X = MM ⁻¹ Y , и, решив его, можно вычислить матрицу коэффициентов ( X ).

Средние экспериментальные коэффициенты A, B, C и D экспериментального HIGF были рассчитаны путем подстановки координат и гравитационных данных полюсов, экваториальных вершин, вершин Дамаванд и Хезар вместе с четырьмя другими наборами различных точек, представленных в таблице 1.

Результаты и обсуждение

Коэффициент связанной матрицы после разрешения был рассчитан и подставлен в уравнение. (1). Следовательно, экспериментальный HIGF представлен в виде уравнения. 18.

g=978031,85(1+0,0053024 sin2⁡θ-0,000032309786 sin22θ)-0,27h(18)

Гравитация многих точек мира рассчитана с использованием HIGF (уравнение (18)). Различия между HIGF и практическим гравитационным полем этих точек представлены в таблице 1.

На рис. 2 показано поведение g _84m and g ₈₄ by adding the free air effect or Δ _gh = − ( 0.3087691−0.0004398sin ² θ ) h + 7.2125 × 10 ^-8   h ² ≈ -0,3086 h к уравнениям (2), (14). На рис. 2 также показаны различия между g _84m и g ₈₄ на разных высотах и ​​широтах. Согласно рисунку 2, различий между g 9 и0055 84м и г ₈₄ составов. Таким образом, g ₈₄ или IGF84 с четырьмя коэффициентами использовали для сравнения/анализа различий между гравиметрическими составами HIGF и IGF84. На рисунке 3 показаны различия между гравитационными составами HIGF и IGF84 на разных высотах и ​​широтах. Согласно рисунку 3, HIGF и IGF84 продемонстрировали хорошее совпадение вблизи уровня моря и на разных высотах. Напротив, поведение HIGF не похоже на поведение IGF84 над уровнем моря, потому что состав HIGF основан на экспериментальных данных и является лучшим составом для извлечения силы тяжести над уровнем моря по сравнению с составом IGF84. В таблице 1 приведены значения гравитации во многих точках, рассчитанные с помощью HIGF и IGF84, их практические данные [13–15], а также различия между HIGF, IGF84 и практической гравитацией.

РИСУНОК 2 . Поведение g84 м и g84 в зависимости от широты на разных высотах.

РИСУНОК 3 . Поведение HIGF и IGF84 в зависимости от широты на разных высотах.

Таблицы 1 и 2 также изображают хи-квадрат {Sum [(Obs-Exp) ² /Exp]} для HIGF и IGF84 как (Obs) и практические данные как (Exp). Согласно таблице 2 значения хи-квадрата для данных Obs и Exp составили 0,291 008 и 0,787 851 соответственно. Следовательно, HIGF более соответствует экспериментальным результатам по сравнению с IGF84. На рис. 4 показаны практические данные на высотах 0–100 м и широтах 0–90° по сравнению с формулой HIGF и IGF84. Судя по рисунку, HIGF и IGF84 хорошо согласуются с экспериментальными результатами (треугольная метка) на более низких высотах. Однако над уровнем моря HIGF работал аналогично экспериментальным данным из-за низких значений хи-квадрата на больших высотах. Следовательно, HIGF более соответствует экспериментальным результатам по сравнению с IGF84.

ТАБЛИЦА 2 . Хи-квадрат HIGF, IGF84 и практические данные.

РИСУНОК 4 . Практические данные в диапазоне высот 0–100 м и широте 0–90° с профилями HIGF и IGF84.

Различия между гравитацией пиков Хезар и горы Дамаванд с использованием HIGF и IGF84 следующие: данные показали, что разница в силе тяжести пиков Хезар и горы Дамаванд составляла -203 мГал [9]. Согласно этим данным, разница между HIGF, IGF84 и экспериментальными данными составила 11 и 16 мГал. Таким образом, HIGF является лучшей формулой, чем IGF84. На основании результатов, представленных в таблице 1, HIGF может быть введен в качестве экспериментальной формулировки гравитации Земли для каждой точки в море и над уровнем моря.

Заключение

Вращающаяся эллипсоидальная Земля послужила основой для Международной Формулы Гравитации, принятой на Генеральной Ассамблее Международного Союза Геодезии и Геофизики (IUGG). Один конкретный эллипсоид вращения также называют нормальной Землей. Геодезическая система отсчета 1967 года, Геодезическая система отсчета 1980 года и Всемирная геодезическая система 1984 года — все это модели «нормальной Земли». Эта статья основана на формулировке теоретической модели нормальной Земли с 4 коэффициентами. Эти 4 коэффициента в Мировой геодезической системе 1984 были рассчитаны с использованием теоретических расчетов. Однако в данной работе они были извлечены экспериментальным расчетом. Таким образом, в этой статье было введено уравнение экспериментальной гравитации в виде международной формулы гравитации Хезара (HIGF) с использованием данных экспериментальной гравитации Земли. В заключение, HIGF дает точные результаты, поскольку он лучше согласуется с практическими данными по сравнению с IGF84.

Заявление о доступности данных

Первоначальные материалы, представленные в исследовании, включены в статью/дополнительный материал, дальнейшие запросы можно направлять соответствующим авторам.

Вклад авторов

MH, SK и MR внесли значительный вклад в проектирование, анализ, определение характеристик, эксперименты и применение. MR, внес свой вклад в концепцию и аналитический подход статьи к важному интеллектуальному содержанию. MRIF и MUK предоставили критическую доработку статьи.

Финансирование

Эта работа была поддержана грантом Исследовательского университета, Universiti Kebangsaan Malaysia, Dana Impak Perdana (DIP), код: 2020-018.

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Примечание издателя

Все утверждения, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций или издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.

Ссылки

1. Moritz H. Geodetic Reference System 1980. J Geodesy (2000) 74(1):128–33. doi:10.1007/s001

0278

CrossRef Full Text | Google Scholar

2. Абдель Захер М., Эльбарбари С., Эль-Шахат А., Месбах Х., Эмбаби А. Геотермальные ресурсы Египта, интегрированные с анализом на основе ГИС. J Volcanology Geothermal Res (2018) 365:1–12. doi:10.1016/j.jvolgeores.2018.09.013

CrossRef Полный текст | Google Scholar

3. Вайда П., Панисова Ю. Практическое сравнение формул для вычисления нормальной силы тяжести в точке наблюдения с акцентом на территории Словакии. Contrib Geophys Geodesy (2005) 35 (2): 173–88.

Google Scholar

4. Claessens SJ, Featherstone WE, Anjasmara IM. Гравитация, геоид и наблюдение Земли . Берлин, Гейдельберг: Springer (2010). п. 473–9. doi:10.1007/978-3-642-10634-7_63Действительно ли австралийские данные подтверждают EGM2008, или EGM2008 просто подтверждает/подтверждает австралийские данные?

Полнотекстовая перекрестная ссылка | Google Scholar

5. Хакни Р. Гравитация, данные по аномалиям. Энциклопедия геофизики твердой Земли . Дордрехт: Спрингер (2020). п. 1–10.

Полнотекстовая перекрестная ссылка | Google Scholar

6. Чу ПК. Уравнения динамики океана с реальной гравитацией. Научный представитель (2021) 11(1):1–10. doi:10.1038/s41598-021-82882-1

CrossRef Full Text | Google Scholar

7. Pail R, Goiginger H, Schuh WD, Höck E, Brockmann JM, Fecher T, et al. Комбинированная модель спутникового гравитационного поля GOCO01S Получена из GOCE и GRACE. Geophys Res Lett (2010) 37:1–5. Дои: 10.1029/2010gl044906

Полнотекстовая перекрестная ссылка | Google Scholar

8. Окоча ФК. Гравитационное исследование соляного купола Гастингса и связанных с ним разломов в округах Бразория и Галвестон, штат Техас. Техас: Государственный университет Стивена Ф. Остина (2017). Докторская диссертация. doi:10.1130/abs/2017sc-289183

Полный текст CrossRef | Google Scholar

9. Rezaie MR, Hosseinzadeh P. Hezar International Gravity Formula. В: Материалы ежегодной конференции по физике Ирана, 26-е, 11–14 сентября 2010 г. , Университет Бу-Али Сина, Хамадан, Иран (2010 г.). 1587-159 гг.0.

Google Scholar

10. Сабри Л.М., Сударсоно Б., Джамал Дж., Маварди С. Составление карты аномалий Бугера на основе аэрогравитационных данных (пример на юго-востоке Сулавеси). Elipsoida: Jurnal Geodesi dan Geomatika (2020) 3.

Google Scholar

11.ESA. Гравитационная аномалия Бугера (2015). Доступно по адресу: https://www.esa.int.

Google Scholar

12. Hinze WJ, Aiken C, Brozena J, Coakley B, Dater D, Flanagan G, et al. Новые стандарты обработки данных гравитации: Североамериканская база данных гравитации. Геофизика (2005) 70(4):J25–J32. doi:10.1190/1.1988183

CrossRef Полный текст | Google Scholar

13.TCL. НГКЛИ (2006). Доступно на: www.ncc.org.ir или http://gis.tavanir.org.ir/jeo86/sokan/y-hatam.pdf.

Google Scholar

14. Фукуда Ю., Такигучи Х., Казама Т., Нисидзима Дж., Гуляев С., Натуш Т. и др. Новые измерения абсолютной силы тяжести в Новой Зеландии. В: Международный симпозиум по гравитационным, геоидным и высотным системам , 2016. Cham: Springer (2017). п. 95–101. doi:10.1007/1345_2017_18

CrossRef Полный текст | Google Scholar

15. Фукуда Ю., Хигаси Т., Такемото С., Абэ М., Двипа С., Кусума Д.С. и другие. Первые измерения абсолютной гравитации в Индонезии. J Геодинамика (2004) 38 (3-5): 489–501. doi:10.1016/j.jog.2004.07.009

Полный текст CrossRef | Google Scholar

16. Робертсон Х.В., Гаррик Р.А. Измерения силы тяжести в Новой Зеландии с помощью Кембриджского маятникового аппарата. Новая Зеландия J Геология Геофиз (1960) 3(4):626–42. doi:10.1080/00288306.1960.10420150

CrossRef Full Text | Google Scholar

Местная сила тяжести: как рассчитать свою за 3 минуты

 

Введение

В метрологии знание местной силы тяжести важно, если вы выполняете сравнительные измерения, в которых участвуют силы, на которые влияет гравитация.

Основанная на третьей Генеральной конференции по мерам и весам в 1901 году, стандартная гравитация на Земле равна 9,80665 м/с ² или 32,174 фут/с ² .

Однако стандартная гравитация применима только к объекту или телу, находящемуся на уровне моря и геодезической широте 45 градусов. Скорее всего, это не относится к вашей лаборатории. Таким образом, вам может понадобиться рассчитать собственную местную гравитацию.

В этом руководстве вы узнаете, как рассчитать местную силу тяжести в вашей лаборатории, выполнив три простых шага:

1. Найдите широту и долготу,
2. Найти высоту над уровнем моря и
3. Рассчитайте местную гравитацию.

Кроме того, я отвечу на множество часто задаваемых вопросов о местной гравитации. Вот список разделов, включенных в это руководство:

1. Что такое стандартная гравитация
2. Что такое гравитация на уровне моря
3. Зачем вычислять местную гравитацию
4. Как рассчитать местную гравитацию
5. Формула местной гравитации
6. Популярные калькуляторы местной гравитации
7. Перевести гравитацию из миллигалов в м/с ²
8. Измерения, на которые влияет местная гравитация
9. Корректировка измерений с учетом местной гравитации

 
 

Что такое стандартная гравитация

Согласно Википедии, стандартная гравитация определяется как номинальное гравитационное ускорение объекта в вакууме вблизи поверхности Земли.

По данным Национального института стандартов и технологий (NIST), стандартное ускорение свободного падения равно 9,80665 м/с ² что приблизительно равно 32,17405 фут/с ² .

 

В брошюре BIPM SI и NIST SP330 стандартная гравитация указана как 980,665 см/с ² . Значение принимается Внутренней службой мер и весов и является законом в некоторых странах.

Посмотрите на изображение ниже, чтобы увидеть стандартную плотность, указанную в брошюре BIPM SI.

 

Вы можете узнать больше о стандартной гравитации, прочитав:

• Брошюра BIPM SI: Международная система единиц (СИ) – 9-е издание, или
• NIST SP 330: Международная система единиц (СИ), издание 2019 г.

 
 

Что такое сила тяжести на уровне моря? Это то же самое, что и стандартная гравитация, указанная выше.

В английских единицах ускорение силы тяжести вблизи поверхности Земли на уровне моря равно 32,17405 фут/с ² .

 
 

Зачем вычислять местную силу тяжести

В зависимости от выполняемых вами функций и процессов измерения вам может потребоваться знать местную силу тяжести, поскольку она может значительно повлиять на ваши результаты.

Например, возьмите два манометра и откалибруйте их в разных местах, где существует значительная разница в местной силе тяжести. Результаты будут другими, если они оба не будут скорректированы обратно к стандартной гравитации.

Таким образом, если вы не принимаете во внимание местную гравитацию, вы можете получить ошибочные результаты, которые могут привести к тому, что вы сообщите неверное заявление о соответствии.

Если вы выполняете следующие калибровки, вы должны знать свою местную гравитацию:

• Калибровка изделий под давлением с помощью грузопоршневого манометра,
• Калибровка устройств крутящего момента с колесами, рычагами, чашками и грузами,
• Калибровка предметов Силы собственным весом.

 
 

Как рассчитать местную силу тяжести

Чтобы найти местную силу тяжести, выполните следующие действия:

1. Найдите свою широту и долготу,
2. Найдите свою высоту над уровнем моря,
3. Рассчитайте местную гравитацию

В этом разделе мы углубимся в каждый из этих шагов, чтобы вы могли рассчитать местную гравитацию.

 
 

1. Найдите широту и долготу

Поскольку широта влияет на местную гравитацию, вам необходимо узнать географические координаты вашего местоположения. Благодаря современным технологиям GPS и Интернету эта задача стала очень простой.

Инструменты, которые я рекомендую использовать:

1. Карты Google,
2. Geo Planer или
3. Национальная карта Геологической службы США

 

Найти широту и долготу с помощью Google Maps

Найти широту и долготу с помощью Google Maps очень просто. Все, что вам нужно сделать, это зайти на веб-сайт Google Maps, ввести свой адрес и найти координаты широты и долготы в адресной строке браузера.

Чтобы найти свою широту и долготу в Картах Google, выполните следующие действия:

1. Перейти на Карты Google,
2. Введите свой адрес и
3. Найдите свои координаты в адресной строке браузера.

Посмотрите на изображение ниже, чтобы увидеть координаты широты и долготы в строке поиска.
 

 
Или вы можете просто зайти на Карты Google и включить геолокацию.

Взгляните на панель браузера на изображении ниже. Я зашел в карты Google, подождал около 3 секунд, и моя широта и долгота автоматически заполнились веб-адресом.

 

 
Если у вас возникли проблемы, прочитайте это руководство от Google.

 

Поиск широты и долготы с помощью Geo Planer

Раньше я использовал веб-сайт Geoplaner для определения широты, долготы и высоты. Поскольку сайт перестал давать данные о высоте, я им редко пользуюсь. Тем не менее, это все еще хороший сайт, чтобы легко найти широту и долготу. Поэтому я оставлю его в этом руководстве в качестве рекомендуемого инструмента.

Чтобы найти широту и долготу в Geo Planer, выполните следующие действия:

1. Перейти на веб-сайт Geo Planer,
2. Введите свой адрес и нажмите кнопку «ОК»,
3. Найдите и запишите свои координаты в формате «dd.ddddd» .

Нажмите на ссылку ниже и введите свой физический адрес, чтобы найти свои геодезические координаты.
https://www.geoplaner.com/

 

 
После того, как вы введете свой физический адрес, этот инструмент предоставит вам широту и долготу в нескольких форматах. Рекомендую записать координаты в ‘дд.ддддд’ формат .

 

 

Поиск широты и долготы с помощью национальной карты USGS

Чтобы быстро найти геодезические координаты (широту, долготу и высоту), воспользуйтесь веб-сайтом USGS National Map. Это отличный инструмент для получения всей информации, необходимой для расчета местной гравитации.

Чтобы найти широту и долготу с помощью национальной карты Геологической службы США, выполните следующие действия:

1. Увеличить ближе к вашему местоположению,
2. Нажмите кнопку возвышения точки,
3. Нажмите кнопку активации в окне высотной точки,
4. Введите свой адрес в верхнюю правую строку поиска (возможно, вам придется уменьшить масштаб до уровня 16),
5. Нажмите на точку вашего местоположения (это должна быть черная точка на карте), и
6. Запишите широту, долготу и высоту над уровнем моря.

Карта Геологической службы США покажет широту и долготу в двух разных форматах. Вы захотите записать значения в градусах. Они понадобятся вам позже для калькулятора предсказания гравитации.

 

Нажмите на ссылку ниже, чтобы попробовать национальную карту Геологической службы США.
https://apps.nationalmap. gov/viewer/

 
 

2. Найдите свою высоту над уровнем моря

После определения широты и долготы вам необходимо найти свою высоту над уровнем моря. Для некоторых людей эта задача может быть сложной. Тем не менее, я покажу вам, как легко найти высоту.

Раньше для просмотра топографических карт приходилось идти в местную библиотеку или правительственное учреждение. Сегодня вы можете найти топографические карты в Интернете.

Инструменты, которые я рекомендую использовать:

1. What is My Elevation или
2. Национальная карта Геологической службы США

 

Найдите высоту с помощью What is My Elevation

Если вам нужно быстро найти высоту, попробуйте whatismyelevation.com. Он чрезвычайно прост в использовании, и мгновенно дает вашу высоту .

Просто зайдите на сайт, и он автоматически покажет вашу высоту. Однако это может быть неточным (поначалу), потому что может не быть вашего точного местоположения. Итак, лучше всего нажать на ссылку «изменить местоположение» и ввести свой адрес, чтобы убедиться, что у вас есть наиболее точные результаты.

Чтобы узнать свою высоту, выполните следующие действия:

1. Перейдите на сайт whatismyelevation.com,
.
2. Нажмите на ссылку «Изменить местоположение»,
3. Введите свой адрес и
4. Найдите свою высоту.

На этом веб-сайте очень легко найти высоту. Это стоит проверить.

 

Найдите высоту с помощью национальной карты Геологической службы США

Раньше я рекомендовал веб-сайт Geoplaner, чтобы найти вашу высоту.

Однако на веб-сайте теперь трудно найти высоту, поэтому я начал рекомендовать программу просмотра карт USGS National Map Viewer как универсальный инструмент для определения широты, долготы и высоты.

По сравнению с другими топографическими картами онлайн, эта мне нравится больше всего. Однако будьте осторожны, чтобы не слишком сильно увеличить масштаб. Карта исчезнет, ​​если вы приблизитесь к уровню 16. Если это произойдет с вами, просто уменьшите масштаб, пока карта снова не появится.

Чтобы найти свою высоту, выполните следующие действия:

1. Приблизьтесь к вашему местоположению,
2. Нажмите кнопку точечной высоты (она выглядит как график с XY в верхнем левом углу),
3. Нажмите кнопку активации в окне высотной точки,
4. Введите свой адрес в верхнюю правую строку поиска (возможно, вам придется уменьшить масштаб до уровня 16),
5. Щелкните место вашего местоположения, и
6. Запишите широту, долготу и высоту над уровнем моря.

Карта Геологической службы США покажет вашу высоту как в метрах, так и в футах, что удобно. Используйте единицы измерения, которые вы предпочитаете. Если вы используете калькулятор предсказания силы тяжести NOAA, вы можете использовать любую единицу измерения для расчета местной силы тяжести.

 

 
 

3. Рассчитайте местную силу тяжести

Теперь, когда вы знаете широту, долготу и высоту над уровнем моря, пришло время рассчитать местную силу тяжести. Для выполнения этой задачи вы можете использовать уравнения или калькулятор локальной гравитации. Для оперативности воспользуемся онлайн-калькулятором.

Чтобы рассчитать местную гравитацию онлайн, я рекомендую использовать калькулятор NOAA Surface Gravity Prediction.

На изображениях ниже я собираюсь использовать веб-сайт NOAA Surface Gravity Prediction для расчета местной гравитации. Вам нужно будет ввести широту, долготу и высоту, которые вы записали на предыдущих шагах.

Чтобы рассчитать местную гравитацию, выполните следующие действия:

1. Посетите веб-сайт NOAA, посвященный прогнозу поверхностной гравитации,
.
2. Введите широту,
3. Введите долготу,
4. Введите вашу высоту,
5. Нажмите кнопку «Поехали», и
6. Запишите свою местную гравитацию.

 

 
После нажатия кнопки «Начать» вы будете перенаправлены на веб-страницу, похожую на изображение ниже. На странице будет указана ваша прогнозируемая местная сила тяжести с соответствующей оценкой неопределенности. Распечатайте страницу и сохраните ее для своих записей. Он может понадобиться вам во время оценки ISO/IEC 17025.

 

 
 

Формула местной гравитации

Если вы предпочитаете вычислять местную гравитацию с помощью уравнения, я рекомендую использовать формулу, которая раньше была опубликована на веб-сайте Национальной физической лаборатории.

http://www.npl.co.uk/reference/faqs/how-can-i-determine-my-local-values-of-gravitational-acceleration-and-altitude-(faq-pressure)

Эта веб-страница больше не существует (или была перемещена). Однако вы можете использовать изображение ниже, чтобы получить уравнение.

 

 
Используя Microsoft Excel, я создал калькулятор для расчета местной силы тяжести с использованием приведенного выше уравнения, включая оценку неопределенности, связанной со значением силы тяжести.

 

 
Если вам нужна копия этого калькулятора, нажмите на ссылку ниже и введите свой адрес электронной почты, чтобы загрузить его.

 
Нажмите здесь, чтобы бесплатно скачать калькулятор локальной гравитации!

 
 

Популярные калькуляторы местной гравитации

Чтобы рассчитать местную гравитацию (без использования длинных уравнений), вам понадобится калькулятор. Есть несколько бесплатных онлайн-калькуляторов. Вот список лучших онлайн-калькуляторов местной гравитации:

• Инструмент прогнозирования поверхностной гравитации NOAA (настоятельно рекомендуется)
• Калькулятор гравитационной информационной системы PTB — [удалено]
• Калькулятор прогноза силы тяжести BGI (настоятельно рекомендуется)
• SensorOne Калькулятор локальной силы тяжести
• Калькулятор локальной гравитации FlowSolv
• Калькулятор гравитации Земли Уолтера Бислина

 
 

Сравнение калькуляторов местной гравитации

Несмотря на то, что в Интернете доступно несколько калькуляторов местной гравитации, не все из них дают одинаковый результат.

Вот диаграмма, сравнивающая результаты каждого гравитационного калькулятора для одного и того же местоположения (т. е. широты, долготы и высоты).

 

 
Как видите, некоторые калькуляторы дают разные результаты. Вот обзор результатов:

• Результаты BGI и PTB почти идентичны.
• Результаты NOAA и PTB относительно схожи, но не согласуются с уравнением NPL.
Калькулятор Excel
• NPL, SensorOne, Walter Bislin и ISOBudgets дает одинаковые результаты и, скорее всего, использует одно и то же уравнение.
Результат калькулятора
• FlowSolv существенно отличается, поскольку он позволяет ввести только вашу широту и использует высоту по умолчанию 100 м.

 
 

Перевести гравитацию из миллигалов в м/с ²

Некоторые онлайн-калькуляторы гравитации дают результаты в миллигалах. Однако я предпочитаю получать результаты в метрах в секунду в квадрате. Поэтому я делю результат в миллигалах на 100 000, чтобы преобразовать гравитацию в метры на секунду в квадрате.

 

 
Чтобы преобразовать миллигалы в метры на секунду в квадрате, следуйте инструкциям ниже:

1. Найдите свою силу тяжести в миллигалах,
2. Разделите результат на 100 000 и
3. Запишите результат в м/с ^2.

 
 

Измерения, подверженные влиянию местной силы тяжести

Ниже приведен список функций измерения, на которые может влиять местная гравитация, где скорость ускорения является силой тяжести;

• Сила
• Вес
• Крутящий момент
• Давление

В этом разделе я покажу вам примеры измерений под влиянием местной гравитации.

 

Измерение силы с использованием собственного веса

Калибровка приборов силы с собственным весом требует поправки на местную гравитацию.

Посмотрите на приведенное ниже уравнение. Вы захотите использовать местную гравитацию вместо «g».

F = сила
м = масса
г = местное ускорение свободного падения
ρ _a = плотность воздуха
ρ _м = массовая плотность0009

Весы и балансы обычно калибруются в месте, где они используются для выполнения измерений, чтобы уменьшить влияние гравитации. Если весы или весы перемещаются в другое место после калибровки, это, вероятно, повлияет на их измерительные характеристики.

Приведенная ниже формула из руководства EURAMET CG-18 показывает взаимосвязь между массовым объектом, воздействующим на прибор, и его индикацией на дисплее.

I = Индикация на дисплее
K _S = коэффициент корректировки
M = масса
G = локальное ускорение гравитации
ρ _A = плотность воздуха
ρ _M = Массовая плотность

9000 4 00059 47 47474747474747474747474747474747 . .

Приведенная ниже формула используется для расчета давления на высоте или глубине в среде (например, газе или жидкости) с постоянной плотностью. Это обычно для манометров, но может использоваться в нескольких сценариях. Вы даже можете использовать его для расчета погрешности из-за разницы напора или высоты между эталоном и испытуемым устройством (UUT).

ρ = плотность жидкости (жидкости или газа)
g = местное ускорение свободного падения
h = высота или глубина в веществе с постоянной плотностью Тестер собственного груза требует необходимости внесения поправок на местную силу тяжести.

Посмотрите на приведенное ниже уравнение, чтобы увидеть формулу грузопоршневого манометра. Используйте местную гравитацию вместо «g».

 

Пневматическое давление

Это формула определения собственного веса, связанная с пневматической (т. е. газовой) средой под давлением, такой как воздух или азот.

P = давление
m = масса
g = местное ускорение свободного падения
ρ _a = плотность воздуха
ρ _m = массовая плотность
D = диаметр поршня
τ = поверхностное натяжение жидкости ^{A A = эффективная площадь поршня
α _c = коэффициент теплового расширения поршня цилиндра
α _p = коэффициент теплового расширения поршня
T _i = температура (во время испытания)
T _ref = эталонная температура
P _i = номинальное или заданное давление
ρ _f = плотность жидкости (т. е. N2)
h = высота от точки отсчета}

 

Гидравлическое давление

Это формула испытания собственным весом, связанная с гидравлической (т. е. жидкой) средой под давлением, такой как вода или масло.

P = давление
m = масса
g = местное ускорение свободного падения
ρ _a = плотность воздуха
ρ _m = массовая плотность
D = диаметр поршня
τ = поверхностное натяжение жидкости
A _{e = эффективная площадь поршня
α c = коэффициент теплового расширения поршневого цилиндра
α p = коэффициент теплового расширения поршня
T i = температура (во время испытания)
T ref = эталонная температура
P i = номинальное или заданное давление
ρ f = плотность жидкости
h = высота от эталона}

 

крутящий момент колеса или рычага, троса, поддона и грузов для создания желаемого крутящего момента.

Поскольку используется собственный вес, необходимо сделать поправку на местную силу тяжести.

Посмотрите на приведенное ниже уравнение, чтобы увидеть формулу, используемую для калибровки датчиков крутящего момента. Используйте местную гравитацию вместо «g». 9
m = масса
g = местное ускорение силы тяжести колеса или длины плеча/рычага

Как видите, существует множество примеров измерения, на которые влияет местная гравитация.

 
 

Корректировка измерений с учетом местной силы тяжести

Если вам необходимо скорректировать результаты измерений с учетом местной силы тяжести, используйте приведенное ниже уравнение. Как правило, это довольно распространено для давления, крутящего момента и силы (например, веса).

 

Стандартная сила тяжести в местную силу тяжести

Если вам нужно скорректировать результаты с учетом местной силы тяжести, все, что вам нужно сделать, это рассчитать поправочный коэффициент силы тяжести, используя приведенное ниже уравнение.

, где,
GCF = коэффициент коррекции гравитации
G _L = локальный гравитация
G _S = Стандартная гравитация (9,80665 м/с ² )

до контакта. , выполните следующие действия:

1. Рассчитайте местную гравитацию,
2. Разделите местную силу тяжести на стандартную силу тяжести,
3. Умножьте результат измерения на поправочный коэффициент гравитации.

 

Местная гравитация в стандартную гравитацию

Если вам нужно скорректировать результаты обратно в стандартную гравитацию, все, что вам нужно сделать, это инвертировать предыдущее уравнение.

 

Где
GCF = поправочный коэффициент силы тяжести
г _л = местная сила тяжести
g _S = стандартная сила тяжести (9,80665 м/с ² )

 

Разделите стандартную силу тяжести на вашу местную силу тяжести,

Умножьте результат измерения на поправочный коэффициент гравитации.