Резонанс | Формулы и расчеты онлайн

При заданных возмущающей силе F_max.возм и коэффициенте трения β амплитуда Y_m является функцией только угловой частоты возмущающей силы.

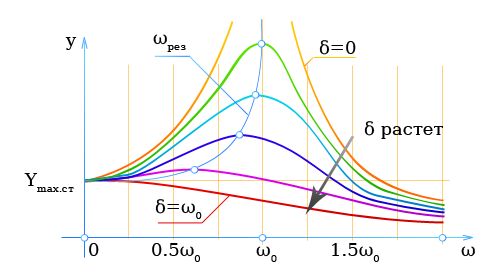
На рисунке показана зависимость Y_m от ω (резонансная кривая). Параметром служит коэффициент затухания δ.

При ω ≈ ω₀ она достигает особенно большого значения (резонанс).

При самых малых значениях δ величина Y_m резко возрастает.

Если δ > 0, то в случае резонанса ω < ω₀; величина Y_max.ст представляет собой статическое отклонение системы под действием постоянной силы Y_max.возм (ω = 0).

Для определения резонансной частоты необходимо найти максимум функции Ym = Ym(ω) и приравнять первую производную нулю; тогда, если

ωрез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω0	частота собственных незатухающих колебаний системы,	радиан/сек
m	масса колебательной системы,	кг
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

Частота резонанса

\[ ω_{рез} = \sqrt[-1.2]{ω_{0}^2 — \frac[-1.2]{β^2}{2m^2}} = \sqrt[-0.5]{ω_{0}^2 — 2δ^2} \]

Условие отсутствия резонанса

\[ δ ≥   \frac{ω_{0}}{\sqrt{2}} \]

Амплитуда резонанса

Чтобы найти величину амплитуды в резонансном случае, нужно подставить формулу (1) в формулу отклонения при вынужденных колебаниях.

Если

Ymax.рез	резонансная амплитуда колебаний системы,	метр
Fmax.возм	максимальное значение возмущающей силы,	Ньютон
m	масса колебательной системы,	кг
ωрез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω0	частота собственных незатухающих колебаний системы,	радиан/сек
ω	частота колебаний системы с затуханием,	радиан/сек
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

то имеем

\[ Y_m = \frac[-2.65] { F_{max.возм} } { β \sqrt[-1.25]{ ω_{0}^2 — \frac[-1.2]{β^2}{4m^2} } } \]

\[ Y_m = \frac{F_{max.возм}}{βω} \]

\[ Y_m = \frac{F_{max.возм}}{2δmω} \]

Согласно формуле, разность фаз α также зависит от частоты возмущающей силы. Параметром служит коэффициент δ.

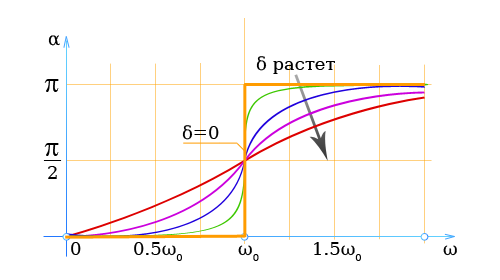
На рисунке представлена зависимость α от частоты.

Независимо от величины затухания при ω = ω₀ разность фаз составляет

\[ α = 90° \]

Резонанс играет большую роль в технике и в повседневной жизни. В большинстве механических устройств под действием внешних периодических сил могут возникать колебания. При резонансе происходит нарастание амплитуды колебаний, и это может привести к разрушениям («резонансная катастрофа»). В случае вращательного движения резонансную частоту называют критическим числом оборотов.

В помощь студенту

Резонанс	стр. 556

Резонанс — это… Что такое Резонанс?

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.

[1]^[2]

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (

высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит

все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

,

где  ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется

добротностью системы.

СВЧ

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Астрофизика

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.

Резонансный метод разрушения льда

Известно, что при движении нагрузки по ледяному покрову развивается система изгибных гравитационных волн (ИГВ). Это сочетание изгибных колебаний пластины льда и связанных с ними гравитационных волн в воде. Когда скорость нагрузки близка к минимальной фазовой скорости от ИГВ, вода прекращает поддержку ледяного покрова и поддержка осуществляется только упругими свойствами льда. Амплитуда ИГВ резко возрастает, и с достаточной нагрузкой, начинается разрушения. Потребляемая мощность в несколько раз ниже (в зависимости от толщины льда) по сравнению с ледоколами и ледокольными навесными оборудованиями. Этот метод разрушения льда известен как резонансный метод разрушения льда^[3][4]

Ученый Козин, Виктор Михайлович получил экспериментальные теоретические кривые, которые показывают возможности своего метода^[5].

Примечания

См. также

Литература

• Richardson LF (1922), Weather prediction by numerical process, Cambridge.
• Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457—472.
• Бломберген Н. Нелинейная оптика, М.: Мир, 1965. — 424 с.
• Захаров В. Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431—453.
• Арнольд В. И. Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны / Ред. А. В. Гапонов-Грехов. — М.: Наука, 1979. С. 116—131.
• Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275—309.
• Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
• Филлипс O.М. Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. — М.: Мир, 1984. — С. 297—314.
• Журавлёв В. Ф., Климов Д. М. Прикладные методы в теории колебаний. — М.: Наука, 1988.
• Сухоруков А.П Нелинейные волновые взаимодействия в оптике и радиофизике. — М.: Наука, 1988. — 232 с.
• Брюно А. Д. Ограниченная задача трёх тел. — М.: Наука, 1990.

Ссылки

Последовательный колебательный контур | Резонанс напряжений

Обозначение на схеме

Последовательный колебательный контур – это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно. На схемах идеальный последовательный колебательный контур обозначается вот так:

Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:

R  – это суммарное сопротивление потерь катушки и конденсатора

L – собственно сама индуктивность катушки

С – собственно сама емкость конденсатора

Колебательный контур и генератор частоты

Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:

Генератор у нас будет выдавать синус.

Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.

А вот и сама схема в реальности:

Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R – это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно “прячется” внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.

Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта U_ш , а также снимая осциллограмму с самого генератора U_ГЕН.

С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.

Влияние частоты на сопротивление колебательного контура

Итак,  погнали. В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.

Красная осциллограмма – это напряжение с генератора частоты, а желтая осциллограмма – отображение силы тока через напряжение на шунтовом резисторе.

Частота 200 Герц с копейками:

Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый

Добавляем частоту. 600  Герц с копейками

Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.

Добавляем частоту. 2 Килогерца

Сила тока стала еще больше.

3 Килогерца

Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.

4,25 Килогерц

Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.

И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.

Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.

Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.

Увеличиваем частоту еще больше

Сила тока начинает падать, а сдвиг фаз увеличивается.

22 Килогерца

74 Килогерца

Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.

Резонанс

Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:

Это явление носит название резонанса.

Не будем углубляться  в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.

Как вы помните, если у нас сопротивление  становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.

Формула Томсона

Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора X_L=X_C , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:

Реактивное сопротивление конденсатора вычисляется по формуле:

Приравниваем обе части и вычисляем отсюда F:

В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.

Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.

Замеряем индуктивность катушки:

И замеряем нашу емкость:

Высчитываем по формуле нашу резонансную частоту:

У меня получилось 5, 09 Килогерц.

С помощью  регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)

Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор – это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол 😉

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию  или с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как  среднеквадратичное напряжение  будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите – полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока – увы! Поэтому последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Давайте  обобщим, что у нас получилось в этих опытах.

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Добротность

Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:

Давайте посчитаем добротность в нашем случае.

Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала  генератора частоты 2 Вольта.

А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.

Считаем по формуле добротности:

Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.

Есть также вторая формула для вычисления добротности.

где

R – сопротивление потерь в контуре, Ом

L – индуктивность, Генри

С – емкость, Фарад

Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.

Также хочу добавить пару слов о добротности. Добротность контура – это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.

Резюме

Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.

Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.

На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.

При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.

При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.

При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.

Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.

На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса – индуктивную составляющую тока.

Резонанс — урок. Физика, 9 класс.

если вам случалось путешествовать на поезде, то наверняка вы обратили внимание на заметное, сильное  раскачивание железнодорожного вагона при случайном совпадении его собственной частоты колебаний на рессорах с частотой ударов колёс на стыках рельсов.

 

 

Ещё один очень яркий пример проявления явления резонанса — это несколько случаев обрушения мостов, когда по ним строевым шагом проходила рота солдат.

Чеканный шаг солдатских сапог совпал с собственной частотой колебаний моста. Мост стал колебаться с такой амплитудой, на которую его прочность не была рассчитана и… развалился. Тогда и родилась новая воинская команда «…не в ногу». Она звучит, когда пешая или конная рота солдат проходит по мосту.

Однако самый яркий пример разрушительного действия резонанса — это рухнувший \(7\) ноября \(1940\) года почти двухкилометровый Такомский подвесной мост в США (штат Вашингтон).

 

 

Данный случай и видео волнообразного раскачивания конструкции даже рекомендованы к просмотру на факультетах физики некоторых университетов — как самый хрестоматийный пример такого явления резонанса.

Разрушение подвесного моста под действием ветра — это иллюстрация того, как относительно постоянная сила вызывает резонанс. При этом происходит следующее:

 

1. порыв ветра отклоняет часть конструкции в сторону движения ветра — внешняя сила способствует возникновению колебаний;

2. при обратном движении конструкции сопротивления воздуха недостаточно, чтобы погасить колебание или значительно снизить его амплитуду;

3. вследствие упругости системы начинается новое движение по ветру, которое он (ветер) и усиливает, продолжая дуть в одном направлении.

Это пример поведения комплексного объекта, где резонанс развивается на фоне высокой добротности и значительной упругости под действием постоянного воздействия силы в одном направлении. К сожалению, Такомский мост — это не единственный пример обрушения конструкций. Случаи, аналогичные описанному, наблюдались и наблюдаются по всему миру, в том числе и в России.

Теория резонанса — Википедия

Теория резонанса — теория электронного строения химических соединений, в соответствии с которой распределение электронов в молекулах (в том числе сложных ионах или радикалах), является комбинацией (резонансом) канонических структур с различной конфигурацией двухэлектронных ковалентных связей. Резонансная волновая функция, описывающая электронную структуру молекулы, является линейной комбинацией волновых функций канонических структур^[1].

Иными словами, молекулярная структура описывается не одной возможной структурной формулой, а сочетанием (резонансом) всех альтернативных структур. Теория резонанса — это способ посредством химической терминологии и классических структурных формул визуализировать чисто математическую процедуру построения приближенной волновой функции сложной молекулы.

Следствием резонанса канонических структур является стабилизация основного состояния молекулы; мерой такой резонансной стабилизации является энергия резонанса — разность между наблюдаемой энергией основного состояния молекулы и расчетной энергией основного состояния канонической структуры с минимальной энергией^[2]. С позиций квантовой механики это означает, что более сложная волновая функция, представляющая собой линейную комбинацию волновых функций, каждая из которых соответствует одной из канонических структур, точнее описывает молекулу, чем волновая функция структуры с минимальной энергией.

Резонансные структуры циклопентадиенид-иона

Идея резонанса был введена в квантовую механику Вернером Гейзенбергом в 1926 году при обсуждении квантовых состояний атома гелия. Он сравнил структуру атома гелия с классической системой резонирующего гармонического осциллятора.

Модель Гейзенберга была применена Лайнусом Полингом (1928 год) к описанию электронной структуры молекулярных структур. В рамках метода валентных схем Полинг успешно объяснил геометрию и физико-химические свойства целого ряда молекул через механизм делокализации электронной плотности π-связей.

Сходные идеи для описания электронной структуры ароматических соединений были предложены Кристофером Ингольдом. В 1926—1934 годах Ингольд заложил основы физической органической химии, развив альтернативную теорию электронных смещений (теорию мезомерии), призванную объяснить структуру молекул сложных органических соединений, не укладывающуюся в обычные валентные представления. Предложенный Ингольдом для обозначения явления делокализации электронной плотности термин «мезомеризм» (1938), используется преимущественно в немецкой и французской литературе, а английской и русской преобладает «резонанс». Представления Ингольда о мезомерном эффекте стали важной составной частью теории резонанса. Благодаря немецкому химику Фрицу Арндту были введены, ставшие общепринятыми обозначения мезомерных структур при помощи двунаправленных стрелок.

СССР 1940-50 гг.[править | править код]

В послевоенном СССР теория резонанса стала объектом гонения в рамках идеологических кампаний и была объявлена «идеалистической», чуждой диалектическому материализму — и поэтому неприемлемой для использования в науке и образовании:

«Теория резонанса», будучи идеалистической и агностической, противостоит материалистической теории Бутлерова, как несовместимая и непримиримая с ней;… сторонники «теории резонанса» игнорировали её и извращали её существо. «Теория резонанса», будучи насквозь механистической, отрицает качественные, специфические особенности органического вещества и совершенно ложно пытается сводить закономерности органической химии к закономерностям квантовой механики…

…Мезомерийно-резонансная теория в органической химии представляет собою такое же проявление общей реакционной идеологии, как и вейсманизм-морганизм в биологии, как и современный «физический» идеализм, с которыми она тесно связана.

— Кедров Б.М. Против «физического» идеализма в химической науке. Цит. по ^[3]

В 1951 году на Всесоюзной конференции по состоянию теории химического состава органической химии под руководством академика А. Н. Несмеянова резонансная теория Полинга и теория мезомерии Ингольда были объявлены буржуазными и лженаучными^[4].

Гонения на теорию резонанса получили негативную оценку в мировой научной среде. В одном из журналов Американского химического общества в обзоре, посвящённом положению в советской химической науке, в частности, отмечалось^[5]:

В большинстве русских статей на эти темы (…), по-видимому, преобладает шовинистическая идея, что теория резонанса Лайнуса Полинга противоречит догмам диалектического материализма и поэтому должна быть отвергнута. Размах и резкость этого осуждения не имеет аналогов в истории химии

Оригинальный текст (англ.)

The large majority of Russian papers on these subjects (…) apparently arising from the chauvinistic idea that the resonance theory of Linus Pauling opposes the tenets of dialectical materialism and therefore must be rejected. The intensity and crudeness of this invective appear to be without parallel in the annals of chemistry.

Хотя гонения на теорию резонанса иногда называют «лысенковщиной в химии», история этих гонений имеет ряд отличий от гонений на генетику в биологии. Как отмечает Лорен Грэхэм: «Химики сумели отразить эту серьёзную атаку. Модификации теории носили скорее терминологический характер». В 50-х гг. химики, не опровергая критики теории резонанса, развивали аналогичные теоретические (в том числе — квантовохимические) построения, используя термин «гибридизация»^[4].

25. Вынужденные колебания. Явление резонанса. Резонансные кривые.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Второй закон Ньютона для такого осциллятора запишется в виде: 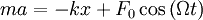. Если ввести обозначения:и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение: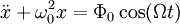

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид: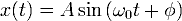

где A,φ произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение. Для этого подставим в уравнение решение вида: 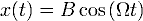и получим значение для константы: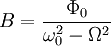

Тогда окончательное решение запишется в виде: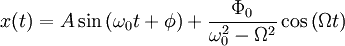

Резонаìнс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле: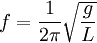

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс

Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.

Р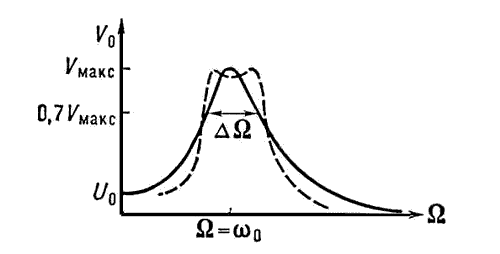езонансная кривая колебательного контура Резонансная кривая колебательного контура: w0 — частота собственных колебаний; W — частота вынужденных колебаний; DW — полоса частот вблизи w0, на границах которой амплитуда колебаний V = 0,7 Vmakc. Пунктир — резонансная кривая двух связанных контуров.

26. Основные понятия и исходные положения положения термодинамики. Обратимые и необратимые процессы. Круговые процессы (циклы).

Термодинамика — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии

Перечень начал термодинамики

Первое начало термодинамики представляет собой закон сохранения энергии в применении к термодинамическим системам.( Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил)

ΔU = Q − A

Второе начало термодинамики накладывает ограничения на направление термодинамических процессов, запрещая самопроизвольную передачу тепла от менее нагретых тел к более нагретым. Также формулируется как закон возрастания энтропии. dS≥0 (Неравенство Клаузиуса)

Третье начало термодинамики говорит о том, как энтропия ведет себя вблизи абсолютного нуля температур.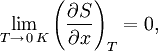

Обратимый процесс (то есть равновесный) — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.

Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.

Обратимые процессы дают наибольшую работу. Боìльшую работу от системы вообще получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.

Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, теплопроводность и др.

Термодинамиìческие циìклы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия) совпадают.

Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, циклы Стирлинга и Эрикссона), в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора

Явление резонанса и его возникновение. Примеры резонанса в механике, акустике, электрических цепях и атомах молекул

Под явлением резонанса стоит понимать мгновенный рост величины амплитуды колебаний объекта под воздействием внешнего источника энергии периодического характера воздействия с аналогичным значением частоты.

В статье мы рассмотрим природу возникновения резонанса на примере механического (математического) маятника, электрического колебательного контура и ядерного магнитного резонатора. Для того, чтобы проще представить физические процессы, статья сопровождается многочисленными вставками в виде практических примеров. Цель статьи — объяснить на примитивном уровне явление резонанса в разных областях его возникновения без математических формул.

Механические колебания маятника

Самая простая модель, которая может наглядно показать колебания, это простейший маятник, а точнее математический маятник. Колебания разделяют на свободные и вынужденные. Первоначально воздействующая энергия на маятник обеспечивает в теле свободные колебания без присутствия внешнего источника переменной энергии воздействия. Данная энергия может быть как кинетической, так и потенциальной.

Здесь не имеет значение насколько сильно или нет качается сам маятник, — время, потраченное на прохождения его пути в прямом и обратном направлении, сохраняется неизменным. Во избежание недоразумений с затуханием колебаний вследствие трения о воздух стоит выделить, что для свободных колебаний должны соблюдаться условия возврата маятника в точку равновесия и отсутствия трения.

А вот частота в свою очередь напрямую зависит от величины длины нити маятника. Чем короче нить, тем выше частота и наоборот.

Возникающая естественная частота тела под воздействием первоначально приложенной силы называется резонансной частотой.

Все тела, которым свойственны колебания, совершают их с заданной частотой. Для поддержания в теле незатухающих колебаний необходимо обеспечить постоянную периодическую энергетическую «подпитку». Это достигается воздействием в одновременный такт колебаний тела постоянной силы с определенным периодом. Таким образом возникающие колебания в теле под действием периодической силы снаружи называют вынужденными.

В какой-то момент внешних воздействий возникает резкий скачок амплитуды. Такой эффект возникает если периоды внутренних колебаний тела совпадают с периодами внешней силы и называется резонансом. Для возникновения резонанса достаточно совсем небольших величин внешних источников воздействия, но с обязательным условием повторения в такт. Естественно, при фактических расчетах в земных условиях не стоит забывать о действии сил трения и сопротивления воздуха на поверхность тело.

Простые примеры резонанса из жизни

Начнем с примера возникновения резонанса с которым сталкивался каждый из нас — это обычные качели на детской площадке.

Резонанс качелей

В ситуации с детскими качелями в момент приложения рукой силы при прохождения одной из двух симметричных высших точек возникает скачек амплитуды с соответствующим ростом энергии колебания. В быту явление резонанса могли наблюдать в ванной комнате любители вокала.

Звуковой акустический резонанс при пении в ванной

Каждый из поющих в ванной комнате из кафеля наверняка замечал как изменяется звук. Звуковые волны отражаясь о кафель в замкнутом пространстве ванной становятся громче и продолжительнее. Но этому воздействию подвержены не все ноты песни вокалиста, а лишь те, которые резонируют в один такт со звуковой резонансной частотой воздуха.

Для каждого из вышеперечисленного случая возникновения резонанса существует внешняя возбуждающая энергия: в случае с качелями элементарный толчок рукой, совпадающий с фазой колебания качели, и в случае с акустическим эффектом в ванной — голос человека, отдельные частоты которого совпадали с определенными частотами воздуха.

Звуковой резонанс бокала — опыт в домашних условиях

Данный опыт можно провести в домашних условиях. Для него необходим хрустальный бокал и закрытое помещение без посторонних шумов для чуткого восприятия аккустического эффекта. Смоченный водой палец передвигаем по краю бокала с «рваными» периодическими ускорениями. В процессе подобных движений вы можете наблюдать возникновение звенящего звука. Данный эффект возникает вследствие передачи энергии движения, частота колебание которой совпадает с собственными частотой колебания бокала.

На видео автор ролика передвигает смоченный палец с равномерной скоростью по окружноси бокала, наполовину наполненного водой. Возникает эффект «поющего бокала».

Разрушение мостов вследствие резонанса — случай с Такомским мостом

Все служившие в армии помнят, как при прохождении строем по мосту от командира звучала команда: «Отставить в ногу!». Почему же нельзя было проходить строем по мосту «в ногу»? Оказывается, при прохождении строем по мосту с одновременным поднятием выпрямленной ноги до уровня колена военнослужащие опускают плоскость подошвы в один такт с усилием, которое сопровождается характерным шлепком.

Шаг военнослужащих сливается в один единый такт, создавая скачкообразную внешнюю прикладываемую энергию для моста с определенной величиной колебаний. В случае если собственная частота колебаний моста совпадет с колебанием шага солдат «в ногу» — произойдет резонанс, энергия которого может привести к разрушительным воздействиям конструкции моста.

Хотя случаи полного разрушения моста и не зафиксированы при прохождении солдат «в ногу», но известнее случай разрушения Такомского моста через пролив Такома-Нэрроуз в штате Вашингтон США в 1940 году.

Одна из причин вероятных причин разрушения — механический резонанс, который возник вследствие совпадения частоты ветрового потока с внутренней собственной частотой моста.

Резонанс тока в электрических цепях

Если в механике явление резонанса можно объяснить сравнительно просто, то в электричестве все на пальцах не объяснить. Для понимания необходимы элементарные знания физики электричества. Резонанс, создаваемый в электрической цепи, может возникать при условии наличия колебательного контура. Какие элементы необходимы для создания колебательного контура в электрической сети? Прежде всего цепь должна быть подключена к источнику электрической энергии.

В электросети простейший колебательный контур состоит из конденсатора и катушки индуктивности.

Конденсатор, состоящий внутри из двух металлических пластин разделенных диэлектрическими изоляторами, способен хранить электрическую энергию. Аналогичным свойством обладает и катушка индуктивности, выполненная в виде спиралеобразных витков проводника электричества.

Взаимное соединение конденсатора и катушки индуктивности в электрической сети, образующей колебательный контур, может быть как параллельным так и последовательным. В следующем видеопособии для демонстрации резонанса приводят пример последовательного способа включения.

Колебания электрического тока внутри контура возникает под действием внешнего источника электроэнергии. Однако, не все поступающие сигналы, а точнее его частоты, служат источником возникновения резонанса, а лишь только те, частота которых совпадает с резонансной частотой контура. Остальные, не участвующие в процессе, подавляются в общем потоке сигнала. Регулировать резонансную частоту возможно при помощи изменения значений емкости конденсатора и индуктивности катушки.

Возвращаясь к физике резонанса в механических колебаниях, он особенно выражен при минимальных значениях сил трения. Показатель трения сопоставляется в электрической цепи сопротивлению, увеличение которого ведет к нагреву проводника встледствие превращения электрической энергии во втрутреннюю энергию проводника. Поэтому, как и в случае с механикой, в колебательном электрическом контуре резонанс четко выражен при низком активном сопротивлении.

Пример электрического резонанса в процессе настройки ТВ и радиоприемников

В отличие от резонанса в механике, который может негативно влиять на материалы конструкций вплоть до разрушения, в электрических целях его вовсю используют в полезном функциональном назначении. Один из примеров применения — настройка ТВ и радиопрограмм в приемниках.

Радиоволны соответствующей частоты достигают приемных антенн и вызывают небольшие электрические колебания. Далее сигнал, включающий весь пул транслируемых передач, поступает в усилитель. Настроенный на определенную частоту в соответствии со значением регулируемой емкости конденсатора, колебательный контур принимает только тот сигнал, частота которого совпадает с его собственной.

В радиоприемнике установлен колебательный контур. Для настройки на станцию вращают рукоятку конденсатора переменной емкости, меняя положение его пластин и соответственно меняя резонансную частоту контура.

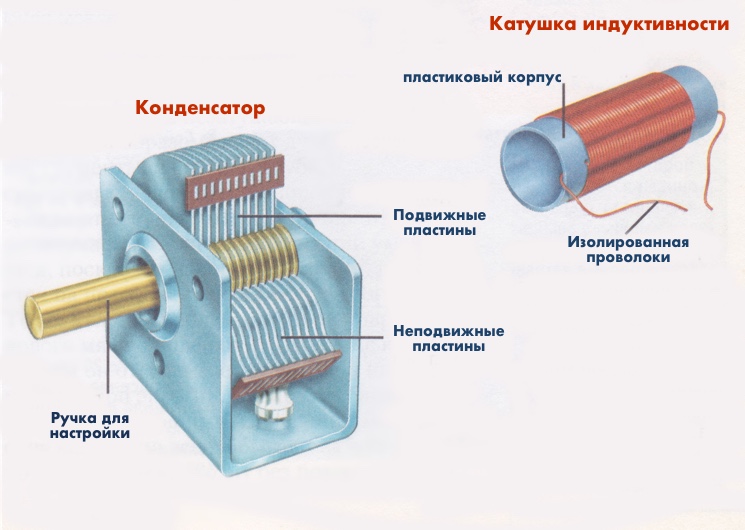
Вспомните аналоговый радиоприемник «Океан» времен СССР, ручка настройки каналов в котором есть ни что иное как регулятор изменения емкости конденсатора, положение которого меняет резонансную частоту контура.

Ядерный магнитный резонанс

Отдельные виды атомов содержат ядра, которые можно сравнить с миниатюрными магнитами. Под влиянием мощного внешнего магнитного поля ядра атомов меняют свою ориентацию в соответствии со взаимным расположением своего собственного магнитного поля по отношению к внешнему. Внешний сильный электромагнитный импульс поглощается атомом вследствие чего происходит его переориентация. Как только источник импульса прекращает свое действие ядра возвращаются на свои исходные позиции.

Ядра в зависимости от принадлежности к тому или иному атому способны принимать энергию в определенном диапазоне частот. Смена позиции ядра происходит в один такт с внешним колебаниям электромагнитного поля, что и служит причиной возникновения так называемого ядерного магнитного резонанса (сокращенно ЯМР). В научном мире этот вид резонанса используется в целях изучения атомных связей в рамках сложных молекул. Используемый в медицине метод отображения магнитного резонанса (ОМР) позволяет выводить результаты сканирования внутренних человеческих органов на дисплей для постановки диагноза и назначения лечения.

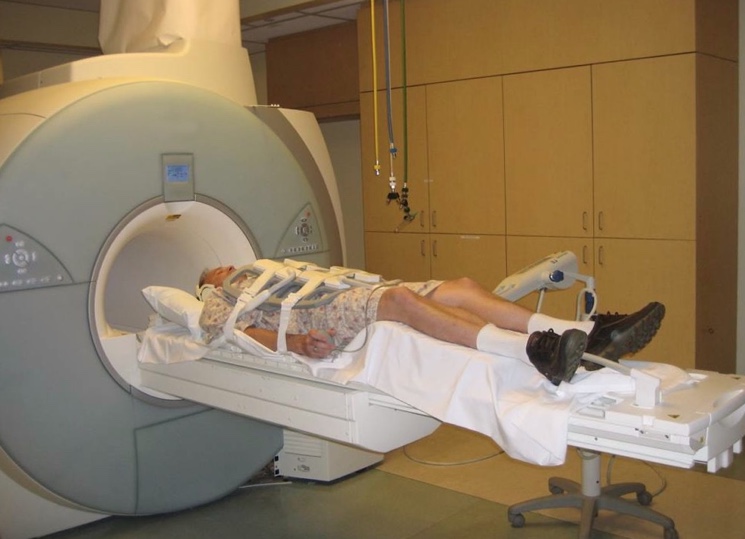
Магнитное поле ОМР сканера, формируемое при помощи катушек индуктивности, создает излучение высокой частоты под воздействием которого ядра атомов водорода изменяют свою ориентацию при условии совпадении своих собственных частот с внешним. В результате полученных данных с датчиков формируется графическая картинка на мониторе.

Если сравнивать метод ЯМР и ОМР относительно негативного влияния на организм человека излучения, то сканирование с помощью ядерного магнитного резонатора менее вредно, чем ОМР. Также при исследовании мягких тканей технология ЯМР показала большую эффективность в отражении детализации исследуемого участка ткани.

Что такое спектрография

Взаимная связь между атомами в молекуле не строго жесткая, при изменении которой молекула переходит в состояние колебания. Частота колебаний взаимных связей атомов меняет соответственно резонансную частоту молекул. С помощью излучения электромагнитных волн в ИК спектре можно вызвать вышеуказанные колебания атомных связей. Данный метод под названием инфракрасная спектрография используется в научных лабораториях для изучения состава исследуемого материала.