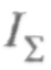Реактивная тяга — Википедия
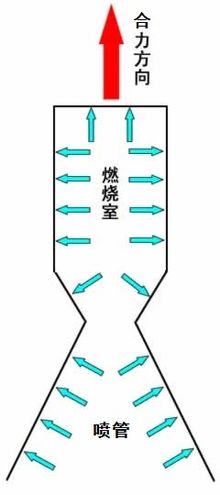 Направление реактивной тяги в реактивном двигателе показано красной стрелкой
Направление реактивной тяги в реактивном двигателе показано красной стрелкойРеактивная тяга — сила, возникающая в результате взаимодействия реактивной двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией[1].
В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:
- приложена непосредственно к корпусу реактивного двигателя;
- обеспечивает передвижение реактивного двигателя и связанного с ним объекта в сторону, противоположную направлению реактивной струи
Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена в противоположное направление движению плода[3].
Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.
Формула при отсутствии внешних сил[править | править код]
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}, где
- mp{\displaystyle m_{p}} — масса ракеты
- a→{\displaystyle {\vec {a}}} — её ускорение
- u→{\displaystyle {\vec {u}}} — скорость истечения газов
- ΔmtΔt{\displaystyle {\frac {\Delta m_{t}}{\Delta t}}} — расход массы топлива в единицу времени
Поскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном
Доказательство[править | править код]
До начала работы двигателей импульс ракеты и топлива был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю: mp⋅Δv→+Δmt⋅u→=0{\displaystyle m_{p}\cdot \Delta {\vec {v}}+\Delta m_{t}\cdot {\vec {u}}=0}, где
- Δv→{\displaystyle \Delta {\vec {v}}} — изменение скорости ракеты
mp⋅Δv→=−Δmt⋅u→{\displaystyle m_{p}\cdot \Delta {\vec {v}}=-\Delta m_{t}\cdot {\vec {u}}}
Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:
mp⋅Δv→Δt=−ΔmtΔt⋅u→{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}=-{\frac {\Delta m_{t}}{\Delta t}}\cdot {\vec {u}}}
Произведение массы ракеты m на ускорение её движения a по определению равно силе, вызывающей это ускорение:
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}
Уравнение Мещерского[править | править код]
Если же на ракету, кроме реактивной силы F→p{\displaystyle {\vec {F}}_{p}}, действует внешняя сила F→{\displaystyle {\vec {F}}}, то уравнение динамики движения примет вид:
mp⋅Δv→Δt=F→+F→p⇔{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+{\vec {F}}_{p}\Leftrightarrow } mp⋅Δv→Δt=F→+(−u→⋅ΔmtΔt){\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+(-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}})}
Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами F→{\displaystyle {\vec {F}}}, действующими на тело, но и реактивной силой F→p{\displaystyle {\vec {F}}_{p}}, обусловленной изменением массы движущегося тела:
a→=F→p+F→mp{\displaystyle {\vec {a}}={\frac {{\vec {F}}_{p}+{\vec {F}}}{m_{p}}}}
Формула Циолковского[править | править код]
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского[4]:
mtm=ev→u→{\displaystyle {\frac {m_{t}}{m}}=e^{\frac {\vec {v}}{\vec {u}}}}
Релятивистское обобщение этой формулы имеет вид:
mtm=(c→+v→c→−v→)c→2u→{\displaystyle {\frac {m_{t}}{m}}=\left({\frac {{\vec {c}}+{\vec {v}}}{{\vec {c}}-{\vec {v}}}}\right)^{\frac {\vec {c}}{2{\vec {u}}}}} , где c→{\displaystyle {\vec {c}}} — скорость света.
Реактивная сила Википедия
 Направление реактивной тяги в реактивном двигателе показано красной стрелкой
Направление реактивной тяги в реактивном двигателе показано красной стрелкойРеактивная тяга — сила, возникающая в результате взаимодействия реактивной двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией[1].
В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:
- приложена непосредственно к корпусу реактивного двигателя;
- обеспечивает передвижение реактивного двигателя и связанного с ним объекта в сторону, противоположную направлению реактивной струи[2].
Реактивное движение в природе[ | ]
Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена в противоположное направление движению плода[3].
Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.
Величина реактивной тяги[ | ]
Формула при отсутствии внешних сил[ | ]
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
F→p=mp⋅a→=−u→⋅ΔmtΔt
1.1.Принцип создания реактивной силы
ББК 39.65-02я73
К65 УДК 621.454.2.018(075.8)
Авторы: В. Г. Попов, Н. Л. Ярославцев
К65
Жидкостные ракетные двигатели /В.Г.Попов, Н.Л.Ярославцев.-М.: Издательско-типографский центр — «МАТИ» — КТУ им. К.Э. Циолковского , 2001, 171 с, ил. 103., табл. 3.ISBN5-230-21212-8
Даны классификация и характеристики жидкостных ракетных двигателей (ЖРД). Приведены основные схемы и параметры ракетных двигателей, особенности процессов горения, истечения и теплообмена в ракетных двигателях, сведения о конструкции основных узлов, агрегатов и систем автоматического регулирования ЖРД.
Для студентов высших учебных заведений, специализирующихся в области проектирования ракетных двигателей.
2705140400 — 255
К Без объявл.
038(01)-01
ББК 39.65-02я73
ISBN 5-230-21212-8
© «МАТИ» -Российский Государственный технологический Университет им.К.Э. Циолковского Издательско-типографский центр «МАТИ»- Российского государственного технологического университета им. К.Э.Циолковского
1. Принцип работы реактивного двигателя Основные понятия и определения
Возьмем замкнутый сосуд и создадим в нем избыточное давление Рк. Насосуд будет также действовать сила атмосферного давления Рн окружаю-шея среды, рис. 1.
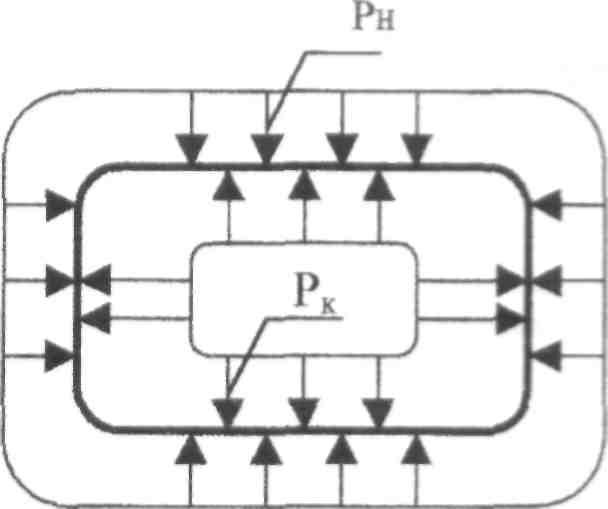
Рис.1
Если силы давления Рк и Рн уравновешены жесткостью стенок сосуда, то оностанется в покое.
Выполним в сосуде отверстие, рис.2, при этом равновесие сил Рк и Рн
нарушится и сосуд придет в движение (трение между наружной поверхностью
в и окружающей средой не учитывается). В результате этого возникнет
реактивная сила R, величина которой пропорциональна скорости и массе рабо-
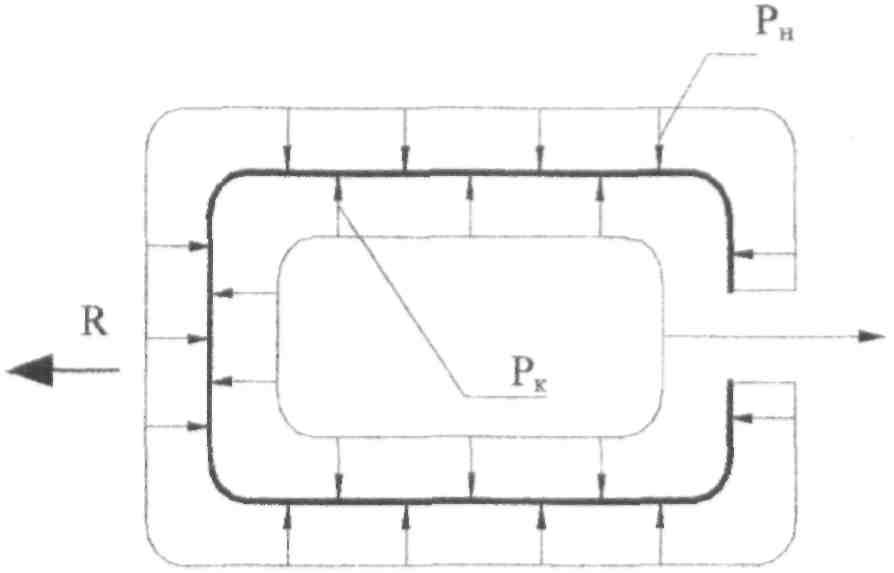
Рис.2
чего тела истекающего потока.
Потенциальная энергия избыточного давления будет преобразована в кинетическую энергию (Ек) истекающей струи. Реактивная сила R направлена в сторону, противоположную истечению реактивной струи.
На поверхность сосуда также действует сила, зависящая от величины давлений, воздействующих на его внутреннюю и наружную поверхности, т.е.
Р’ = Рк — Рн.
Тяга двигателя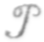 является
результирующей реактивной силыR
и сил давлений
Р’, воздействующих на поверхность сосуда
без учета сил внешнего аэродинамического
сопротивления
является
результирующей реактивной силыR
и сил давлений
Р’, воздействующих на поверхность сосуда
без учета сил внешнего аэродинамического
сопротивления
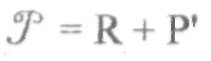
Для создания реактивной силы необходимо наличие 3х элементов:
первичного источника энергии;
рабочего тела;
собственно двигателя, в котором происходят преобразования.
Реактивный двигатель — устройство, обеспечивающее перемещение летательного аппарата ЛА в пространстве, путем преобразования первичного источника энергии в кинетическую энергию реактивной струи.
Различают реактивные двигатели прямой инепрямой реакции.
Для двигателя непрямой реакции характерно наличие движителя -устройства, обеспечивающего реактивную силу, например, винт в турбовинтовом двигателе.
Для создания реактивной силы движитель и двигатель используют разные рабочие тела. В качестве рабочего тела могут использоваться:
1.2. Классификация ракетных двигателей (РД) На рис. 3 представлена классификация ракетных двигателей.
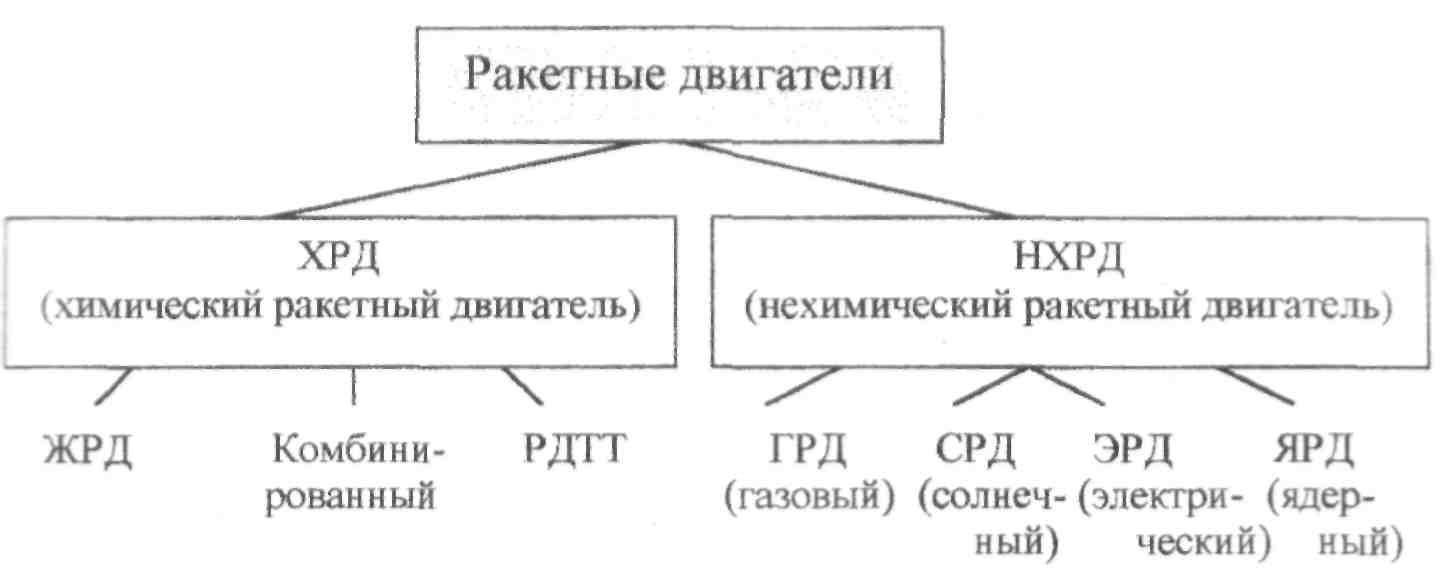
Рис.3
Если в качестве первичного источника энергии используется химическая реакция, то такой двигатель называется химическим.
Термическим РД называется двигатель, у которого энергия первичного источника преобразуется в тепло, а затем в кинетическую энергию истекающей струи. Химические РД являются термическими.
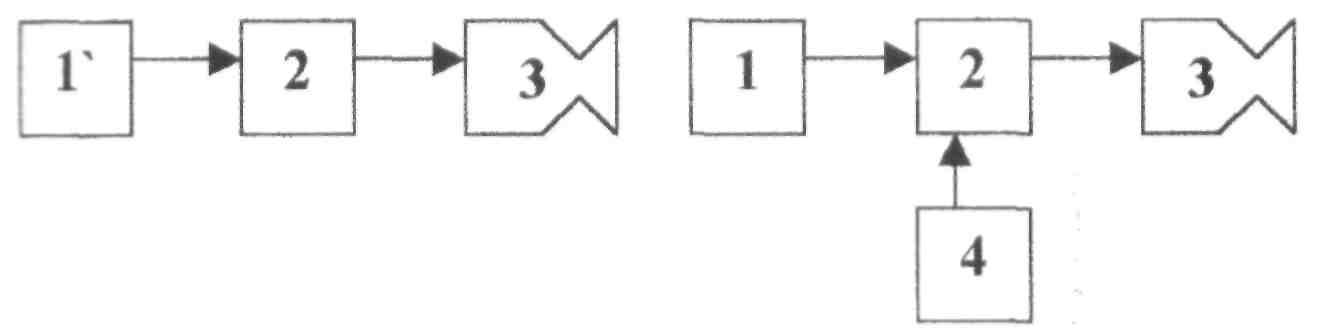
Структурные схемы ХРД и НХРД приведены на рис. 4
ХРД
(химический ракетный двигатель)
НХРД
(нехимический ракетный двигатель)
Г-
1-
2-3-4-
Рис.4
совмещённый источник первичной энергии и рабочего тела;
источник первичной энергии;
камера энергопреобразователь;
ускоритель;
источник рабочего тела.
1.3. Тяга ракетного двигателя
Вывод формулы тяги ракетного двигателя базируется на Ш-м законе Ньютона, при условии, что поток рабочего тела по тракту рассматривается стадион арным.
Стационарным называется движение, при котором расход газа во всех поперечных сечениях канала одинаков и не зависит от времени, а параметры газа в указанных сечениях, включая входное, постоянны и также не являются функцией времени.
Тяга реактивного двигателя является равнодействующей сил давления газов на внутренние и наружные поверхности камеры двигателя. Она возникает в результате преобразования химической энергии топлива в кинетическую энергию, истекающих из камеры, продуктов сгорания.
Тяга в пустоте —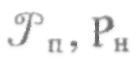 =0,
рис.5
=0,
рис.5
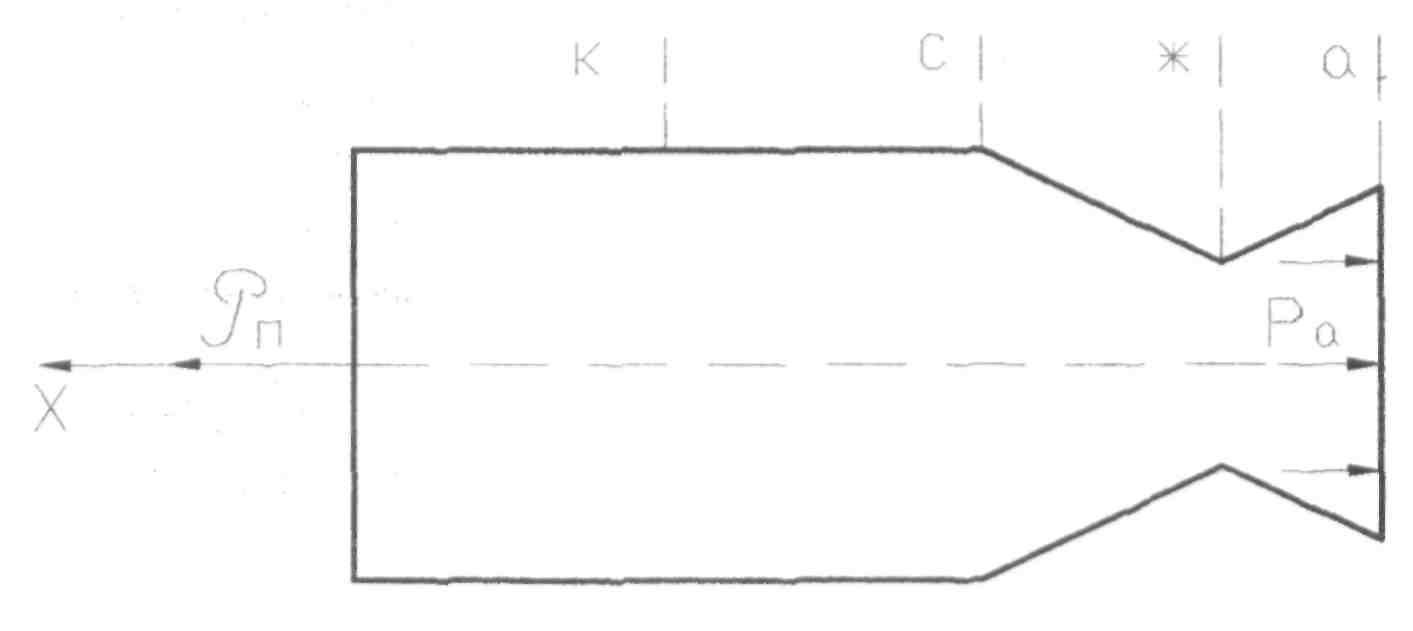
Рис.5
Определим
результирующую силу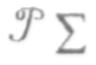
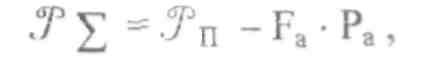
где Fa — площадь среза сопла, м2.
камеры двигателя:
Воспользуемся теоремой импульсов — импульс силы равен изменению количества движения:

где: 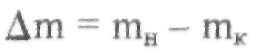 —
масса израсходованного топлива, тн— начальная масса
—
масса израсходованного топлива, тн— начальная масса
двигательной установки, тк—
конечная масса двигательной установки;
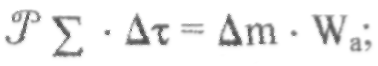
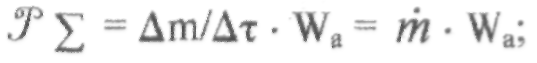
где т — массовый секундный расход, кг/с;
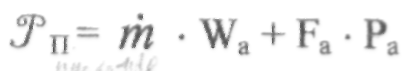
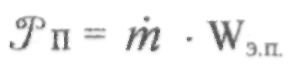
где: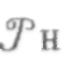 —
тяга ракетного двигателя в пустоте, Н;
—
тяга ракетного двигателя в пустоте, Н;
Wэ.п.— эффективная скорость истечения в пустоте, м/с;
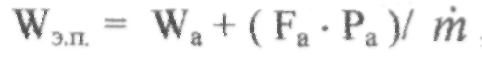
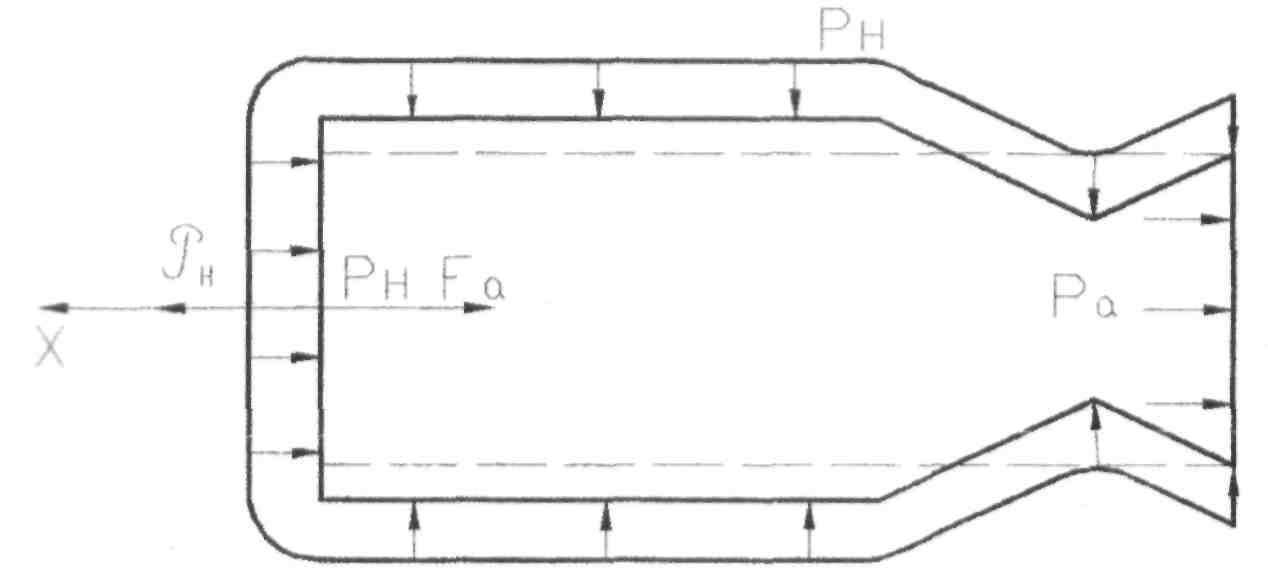
Рис.6
Тяга в условиях атмосферы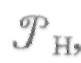 РнФ 0; рис.6
РнФ 0; рис.6 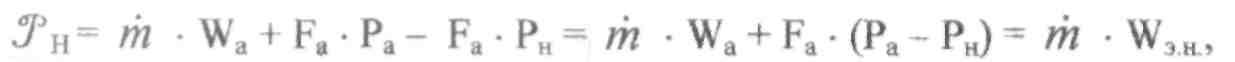
где:Wэн — эффективная скорость истечения при наличии давления окружающей среды, м/с.
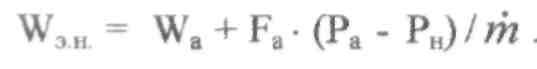
1.4. Мощностные параметры ракетных двигателей 1.Мощность реактивной струи, Вт.
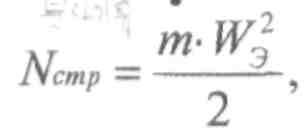
2.Мощность первичного источника энергии, Вт.
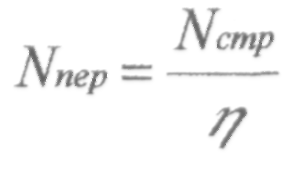
где: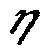 —
коэффициент полезного действия
двигательной установки.
—
коэффициент полезного действия
двигательной установки.
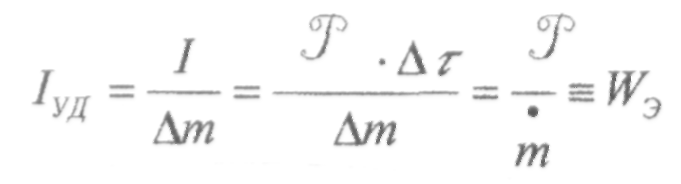
Удельный импульс
является основным параметром,
характеризующим совершенство
конструкции и эффективность преобразования
энергии в нём.
Величина удельного импульса не зависит
от тяги, создаваемой двигателем.
Для химических ракетных двигателей
величина удельного импульса лежит в
диапазоне 2000/4000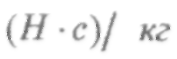
Вышеприведённый вывод формулы тяги осуществлялся при условии её постоянства во время работы двигательной установки. Однако на практике это не соответствует действительности. На рис.7 приведена зависимость тяги двигательной установки от времени её полёта. (Iвзл, Iпол, Iпд — значения импульса ДУ на режимах взлёта, полёта и выключения, Iпд- импульс последействия).
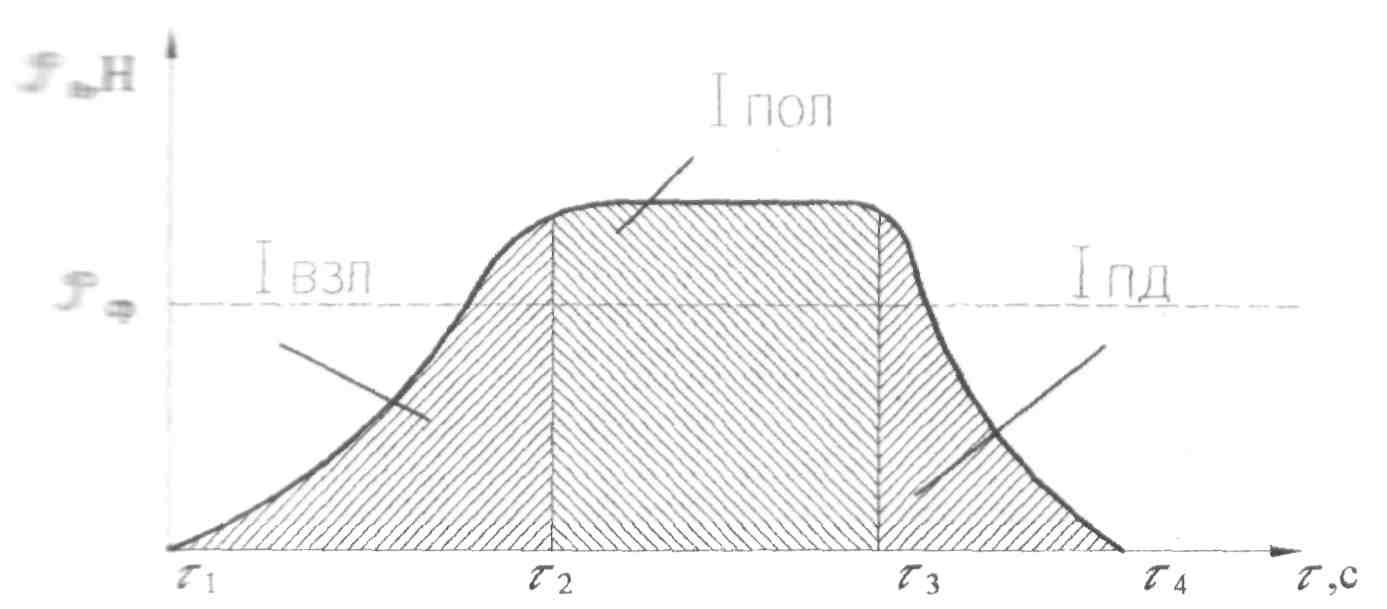
Рис7
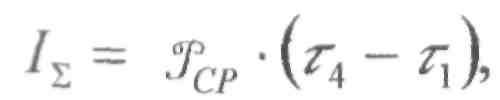
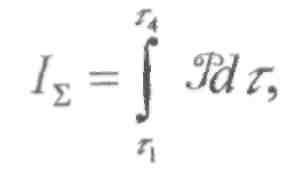
Суммарный импульс двигательной установки 1^, \н ■ с] можно оп-ршишь по следующим зависимостям:
Величину IПД стараются уменьшить, т.к. это обеспечивает точность доставки полезного груза к цели.
2) Удельный расход топлива, кг/Н • с .

Для химических ракетных двигателей величина удельного расхода топлива, существенно выше аналогичного параметра для воздушно-реактивных двигателей (ВРД). Поэтому время работы ВРД существенно больше, чем ХРД.
3) Удельная мощность реактивной струи, Вт/Н.
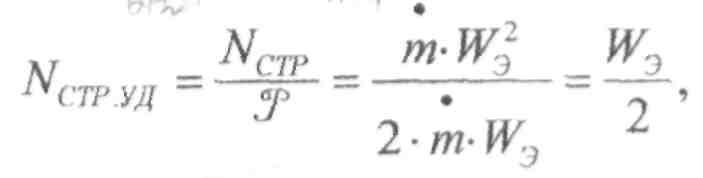
4) Удельная масса ДУ, кг/Н, кг/Т.
где: М — масса ДУ без учёта топлива.
Величины удельной массы двигателей различных типов приведены
ниже:
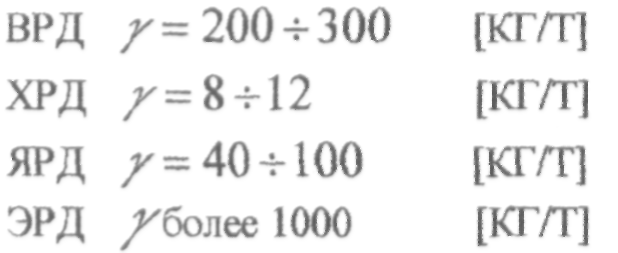 1т=104Н.
1т=104Н.
Дополнительные параметры, характеризующие работу ракетного двигателя
Тип рабочего тела — выбирается в зависимости от области применения.
Время работы двигателя.
ЖРД — 1000с РДТТ — 200 — 300с Если двигатель обладает системой многократного включения, то задаётся количество включений и интервал времени между ними.
Отклонение величины тяги от её номинального значения
 ном-
ном-Значения давлений в камере Рк и на срезе сопла Ра.
Величина суммарного импульса

Величина импульса последействия

Реактивная тяга или как устроен ионный реактивный двигатель / Habr
Не секрет, что все реактивные двигатели работают за счёт закона сохранения импульса. Именно из него вытекает, что реактивная тяга — это произведение массового расхода на скорость выхода рабочего тела из сопла.
Эту скорость принято называть удельным импульсом реактивного двигателя. Давайте для примера найдём реактивную тягу при стрельбе из автомата Калашникова, которая является основной составляющей отдачи. Пусть масса пули будет 0,016 кг, начальная скорость пули 700 м/с, а скорострельность 10 выстр./с. Тогда отдача F=700∙0,016∙10=112 Н (или 11 кгс). Большая отдача, но тут приведена техническая скорострельность 600 выстр./мин. В реальности стрельба ведётся очередями или одиночными и составляет ≈50 выстр./мин.
Выстрел из АКВернёмся к реальным реактивным двигателям, в которых вместо пуль обычно используются потоки выходящего с гиперзвуковой скоростью газа. Химические реактивные двигатели являются самыми распространёнными, но не единственными.
В этой статье, с большим предисловием, я хочу рассказать об ионных реактивных двигателях (далее ИРД). ИРД используют в качестве рабочего тела заряженные частицы — ионы. Ионы имеют массу, и если их разогнать электрическим полем, то можно создать реактивную тягу. Это всё в теории, а теперь подробнее. ИРД имеет некоторый запас газа, который ионизируют (т.е. нейтрально-заряженные атомы газа разбивают на отрицательные электроны и положительные ионы) с помощью газового разряда. Далее ионы разгоняются электрическим полем с помощью специальной системы сеток, и эта же система сеток блокирует движение электронов. После того, как положительные ионы вылетели из сопла, их нейтрализуют отрицательными электронами (в результате этого происходит рекомбинация и газ начинает светиться), чтобы ионы не притягивались обратно к двигателю, и тем самым не снижали его тяги.Почему ксенон?Обычно в ИРД в качестве рабочего тела используется газ ксенон, так как он имеет наименьшую энергию ионизации среди инертных газов.
Удельный импульс ионных реактивных двигателей достигает 50 км/с, что в 150 раз превышает скорость звука! Увы, но тяга таких двигателей составляет около 0,2 Н. Почему же так? Ведь удельный импульс очень большой. Дело в том, что масса ионов очень маленькая и массовый расход получается небольшим. Для чего тогда такие двигатели нужны, если они ничего не смогут сдвинуть с места? На Земле может быть не смогут, а вот в космосе, где нет сил сопротивления, они достаточно эффективные. Существует такое понятие как полный импульс — произведение тяги на время или произведение удельного импульса на массу топлива, который у ИРД является достаточно большим.
Решим следующую задачу. Пусть жидкостный ракетный двигатель имеет удельный импульс 5 км/с, а у нашего ИРД он будет 50 км/с. И давайте масса рабочего тела (в ЖРД она равна массе топлива) у обоих двигателей будет 50 кг. Примем массу космического аппарата равной 100 кг.
Найдём по формуле Циолковского конечную скорость аппарата (т.е. когда в нём закончится рабочая масса).
И что получается, если ионный и химический реактивные двигатели будут иметь одинаковую массу топлива, то ИРД сможет разогнать космический аппарат до больших скоростей, нежели химический РД. Правда на ИРД космический аппарат будет разгонятся дольше до конечной скорости, чем на ЖРД. Но в путешествиях к далёким планетам, высокая конечная (разгонная) скорость будет компенсировать этот недостаток.
Схема полёта к Марсу на ИРДИРД используются и в наше время. Например, аппарат Deep Space 1 сблизился с астероидом Брайль и кометой Борелли, передал на Землю значительный объём ценных научных данных и изображений.
Deep Space 1
Также космическая антенна LISA, которая сейчас находится на стадии проектирования, будет использовать ИРД для корректировки орбиты.
Laser Interferometer Space Antenna
И напоследок, давайте определим тягу ИРД, зная массу иона М=6,5∙10^-26 кг, ускоряющие напряжение U=50 кВ, ток нейтрализации I=0,5 А, элементарный заряд е=1,6∙10^-16 Кл.
Напряжение — это работа по переносу заряда, т.е. на выходе из сопла ион будет иметь кинетическую энергию равную произведению напряжения на заряд иона. Из кинетической энергии выражаем скорость (удельный импульс). Найдём массовый расход из определения тока, электрический ток — это проходящий заряд во времени. Получается, что массовый расход — это произведение массы иона и тока, делённое на заряд иона. Перемножая удельный импульс и массовый расход, получаем тягу равную 0,1 Н.
Подводя итог, хочу сказать, что существуют плазменные реактивные двигатели, у которых схожее устройство, но которые имеют намного больший массовый расход рабочего тела. Кто знает, может быть уже завтра на таких двигателях человечество будет летать на Марс и Луну.
Реактивная тяга — это… Что такое Реактивная тяга?
Реактивная тяга — сила, возникающая в результате взаимодействия двигательной установки с истекающей из сопла струей расширяющихся жидкости или газа, обладающих кинетической энергией[1].
В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя) . То есть, реактивная тяга:
Реактивное движение в природе
Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена в противоположное направление движению плода[3].
Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.
Величина реактивной тяги
Формула при отсутствии внешних сил
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
, где
- — масса ракеты
- — её ускорение
- — скорость истечения газов
- — расход массы топлива в единицу времени
Поскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном массовым секундным расходом топлива.[1]
Доказательство
До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю: , где
- — изменение скорости ракеты
Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:
Произведение массы ракеты m на ускорение ее движения a по определению равно силе, вызывающей это ускорение:
Уравнение Мещерского
Если же на ракету, кроме реактивной силы , действует внешняя сила , то уравнение динамики движения примет вид:
Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами , действующими на тело, но и реактивной силой , обусловленной изменением массы движущегося тела:
Формула Циолковского
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского[4]:
Релятивистское обобщение этой формулы имеет вид:
, где — скорость света.
См. также
Примечания
Ссылки
Реактивная сила Википедия
Направление реактивной тяги в реактивном двигателе показано красной стрелкойРеактивная тяга — сила, возникающая в результате взаимодействия реактивной двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией[1].
В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:
- приложена непосредственно к корпусу реактивного двигателя;
- обеспечивает передвижение реактивного двигателя и связанного с ним объекта в сторону, противоположную направлению реактивной струи[2].
Реактивное движение в природе
Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена в противоположное направление движению плода[3].
Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.
Величина реактивной тяги
Формула при отсутствии внешних сил
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}, где
- mp{\displaystyle m_{p}} — масса ракеты
- a→{\displaystyle {\vec {a}}} — её ускорение
- u→{\displaystyle {\vec {u}}} — скорость истечения газов
- ΔmtΔt{\displaystyle {\frac {\Delta m_{t}}{\Delta t}}} — расход массы топлива в единицу времени
Поскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном массовым секундным расходом топлива[1].
Доказательство
До начала работы двигателей импульс ракеты и топлива был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю: mp⋅Δv→+Δmt⋅u→=0{\displaystyle m_{p}\cdot \Delta {\vec {v}}+\Delta m_{t}\cdot {\vec {u}}=0}, где
- Δv→{\displaystyle \Delta {\vec {v}}} — изменение скорости ракеты
mp⋅Δv→=−Δmt⋅u→{\displaystyle m_{p}\cdot \Delta {\vec {v}}=-\Delta m_{t}\cdot {\vec {u}}}
Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:
mp⋅Δv→Δt=−ΔmtΔt⋅u→{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}=-{\frac {\Delta m_{t}}{\Delta t}}\cdot {\vec {u}}}
Произведение массы ракеты m на ускорение её движения a по определению равно силе, вызывающей это ускорение:
F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}
Уравнение Мещерского
Если же на ракету, кроме реактивной силы F→p{\displaystyle {\vec {F}}_{p}}, действует внешняя сила F→{\displaystyle {\vec {F}}}, то уравнение динамики движения примет вид:
mp⋅Δv→Δt=F→+F→p⇔{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+{\vec {F}}_{p}\Leftrightarrow } mp⋅Δv→Δt=F→+(−u→⋅ΔmtΔt){\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+(-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}})}
Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами F→{\displaystyle {\vec {F}}}, действующими на тело, но и реактивной силой F→p{\displaystyle {\vec {F}}_{p}}, обусловленной изменением массы движущегося тела:
a→=F→p+F→mp{\displaystyle {\vec {a}}={\frac {{\vec {F}}_{p}+{\vec {F}}}{m_{p}}}}
Формула Циолковского
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского[4]:
mtm=ev→u→{\displaystyle {\frac {m_{t}}{m}}=e^{\frac {\vec {v}}{\vec {u}}}}
Релятивистское обобщение этой формулы имеет вид:
mtm=(c→+v→c→−v→)c→2u→{\displaystyle {\frac {m_{t}}{m}}=\left({\frac {{\vec {c}}+{\vec {v}}}{{\vec {c}}-{\vec {v}}}}\right)^{\frac {\vec {c}}{2{\vec {u}}}}} , где c→{\displaystyle {\vec {c}}} — скорость света.
См. также
Примечания
Ссылки
Сила тяги реактивного (ракетного) двигателя
Тяга – равнодействующая всех реактивных сил, создаваемых агрегатами двигателя, определяется по формуле:
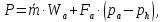
где 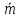 – массовый секундный расход топлива
реактивного двигателя;Wa – скорость газовой струи на срезе сопла; Fa – площадь среза сопла; ра – давление на срезе сопла; рh – давление
окружающей среды.
– массовый секундный расход топлива
реактивного двигателя;Wa – скорость газовой струи на срезе сопла; Fa – площадь среза сопла; ра – давление на срезе сопла; рh – давление
окружающей среды.
Первый член данного уравнения характеризует тягу, создаваемую за счет отбрасывания от сопла газов и эта часть – реактивная сила (статическая составляющая).
Второй член характеризует тягу, которая определяется разностью давлений на срезе сопла и давления окружающей среды и эта часть – переменная составляющая реактивной тяги (зависит от высоты полета).
Реактивный момент
Пусть
есть ракета с однокамерной двигательной
установкой (ДУ) рис.29: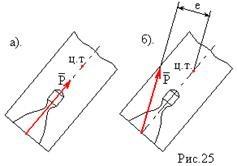
а) Если вектор тяги двигателя Р направлена вдоль оси, то реактивный момент отсутствует (рис. 29,а).
б) Если
вектор тяги (и результирующий вектор
тяги для многокамерной ДУ) действует с
некоторым эксцентриситетом относительно
центра тяжести (рис. 29,б),
то в этом случае действует реактивный
момент 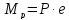 .
.
Рис.29
Аэродинамические схемы ла
Планером называется конструкция, объединяющая корпус, крылья, органы управления и стабилизации в единую аэродинамическую схему. Он предназначен для создания управляющих сил и размещения всей аппаратуры ракеты. Корпус планера обычно цилиндрической формы, за исключением ракеты типа «несущий конус», с конической (сферической) головной частью. Форма корпуса и головной части выбирается в целях получения наименьшей силы лобового сопротивления ракеты при полете. Материалом для корпуса служат легкие прочные металлы и сплавы
Аэродинамические поверхности планера служат для создания подъемной и управляющих сил. Подъемная сила, которая возникает при взаимодействии ракеты с воздухом во время ее полета, обеспечивает удержание ЛА в воздухе. Управляющие силы необходимы для изменения направления полета ракеты.
Различают подвижные и неподвижные аэродинамические поверхности (АП). Подвижные АП, предназначенные для управления полетом и стабилизацией ЛА, называются рулями, поворотными крыльями. Свои функции они выполняют путем поворота вокруг осей, перпендикулярных продольной оси корпуса ракеты, либо при выдвижении из корпуса на определенное время и в определенной последовательности.
Неподвижные АП служат для стабилизации полета ЛА (стабилизаторы) и для создания подъемной силы (несущие крылья, поверхности). По взаимному расположению рулей и неподвижных аэродинамических поверхностей можно выделить следующие аэродинамические схемы ракет (рис.30):
— нормальная или обычная;
— «утка»;
— «бесхвостка»;
— «поворотное крыло»;
В нормальной схеме рули и стабилизатор располагаются позади крыльев в хвостовой части ракеты.
Схема «бесхвостка». Данная схема является разновидностью нормальной схемы. Здесь крылья выполняют одновременно функции крыльев и стабилизаторов и отличаются большей стреловидностью и малым размахом. С целью увеличения подъемной силы в этой схеме увеличена площадь крыльев. При этом рули оказываются расположенными непосредственно за крыльями и связываются с ними конструктивно.
В
аэродинамической схеме «утка» рули
находятся в головной части ракеты
(впереди центра масс), а крылья, выполняющие
и функцию стабилизатора, расположены
в хвостовой части корпуса ракеты. Эта
схема удобна с точки зрения компоновки
ракеты, так как рулевые машинки могут
быть расположены близко к рулям. При
такой компоновке ракеты подъемная сила
рулей совпадает по направлению с
подъемной силой крыльев и корпуса.
Однако расположение рулей в носовой
части ракеты и возникновение скоса
воздушного потока при отклонении рулей
приводит к потере подъемной силы на
крыльях и возникновению значительных
моментов крена. Чтобы избежать «момента
косой обдувки» крыльевой блок делается
вращающимся вокруг оси ракеты, что
позволяет избежать воздействия скоса
воздушного потока на них.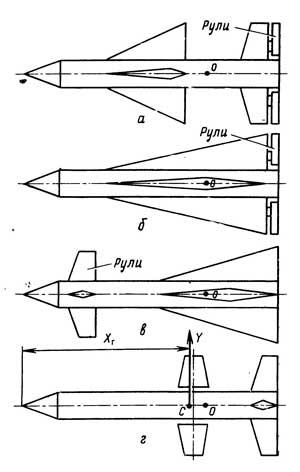
В схеме «поворотное крыло» подвижные поверхности (поворотные крылья) располагаются в районе центра тяжести и наряду с функцией крыла выполняют функцию рулей, а неподвижные стабилизаторы расположены в хвостовой части корпуса.
Рис. 30 Аэродинамические схемы: а)Нормальная; б)»Бесхвостка»; в)»Утка»; г)»Поворотное крыло».
Принципиально не существует наилучшей аэродинамической схемы. Выбор схемы аэродинамической компоновки определяется требуемыми высотами и дальностями полета ракеты, маневренностью и составом бортовой аппаратуры.
Таблица


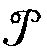 ном-
ном-