Формулы момента силы для статики и динамики. Работа момента силы

В общем курсе физики изучают два наиболее простых типа перемещения объектов в пространстве — это поступательное движение и вращение. Если динамика поступательного движения основана на использовании таких величин, как силы и массы, то для количественного описания вращения тел используют понятия моментов. В данной статье рассмотрим, по какой формуле момент силы вычисляют, и для решения каких задач пользуются этой величиной.

Момент силы

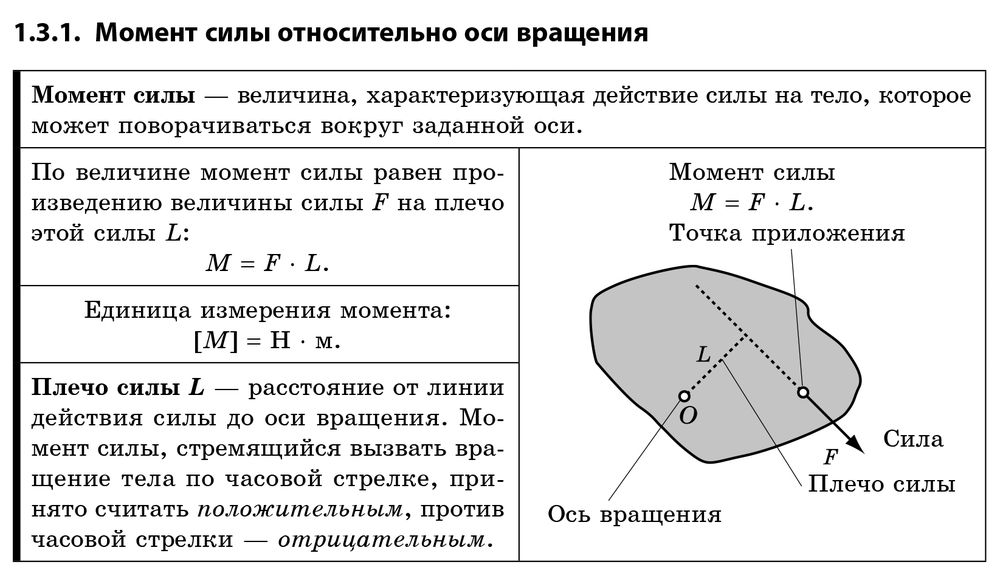
Представим себе простую систему, которая состоит из материальной точки, вращающейся вокруг оси на расстоянии r от нее. Если к этой точке приложить касательную силу F, которая будет перпендикулярна оси вращения, то она приведет к появлению углового ускорения точки. Способность силы приводить к вращательному движению систему называется крутящим моментом или моментом силы. Вычисляют по формуле следующей его:

M¯ = [r¯*F¯]

В квадратных скобках стоит векторное произведение радиус-вектора на силу. Радиус-вектор r¯ является направленным отрезком от оси вращения к точке приложения вектора F¯. Учитывая свойство векторного произведения, для значения модуля момента формула в физике запишется в таком виде:

M = r*F*sin(φ) = F*d, где d = r*sin(φ).

Здесь угол между векторами r¯ и F¯ обозначен греческой буквой φ. Величина d называется плечом силы. Чем оно больше, тем больший крутящий момент может создать сила. Например, если открывать дверь, надавливая на нее вблизи петель, то плечо d будет маленьким, поэтому необходимо приложить большую силу, чтобы повернуть дверь на петлях.

Как видно из формулы момента, величина M¯ — это вектор. Направлен он перпендикулярно плоскости, в которой лежат вектора r¯ и F¯. Направление M¯ определить легко с использованием правила руки правой. Чтобы им воспользоваться, необходимо четыре пальца руки правой направить вдоль вектора r¯ по направлению действия силы F¯. Тогда отогнутый большой палец покажет направление момента силы.

Рассмотренная величина является очень важной при вычислении условий равновесия системы тел, имеющих ось вращения. Таких условий в статике всего два:

• равенство нулю всех внешних сил, которые оказывают на систему то или иное воздействие;
• равенство нулю моментов сил, связанных с внешними силами.

Оба условия равновесия математически можно записать так:

∑_i(F_i¯) = 0;

∑_i(M_i¯) = 0.

Как видно, вычислять необходимо именно векторную сумму величин. Что касается момента силы, то принято считать за его положительное направление, если сила совершает поворот против хода стрелки часов. В противном случае перед формулой определения момента следует использовать знак минус.

Отметим, если в системе ось вращения расположена на некоторой опоре, то соответствующая сила реакции момента не создает, поскольку ее плечо равно нулю.

Момент силы в динамике

Динамика движения вращения вокруг оси имеет так же, как и динамика поступательного перемещения, основное уравнение, на основе которого решаются многие практические задачи. Оно называется уравнением моментов. Формула соответствующая записывается в виде:

M = I*α.

По сути, это выражение является вторым законом Ньютона, если момент силы заменить на силу, момент инерции I — на массу, а угловое ускорение α — на аналогичную линейную характеристику. Чтобы лучше понимать это уравнение, отметим, что момент инерции выполняет ту же самую роль, что обычная масса при поступательном движении. Момент инерции зависит от распределения массы в системе относительно оси вращения. Чем больше расстояние тела до оси, тем больше величина I.

Угловое ускорение α вычисляется в радианах в секунду в квадрате. Оно характеризует быстроту изменения вращения.

Если момент силы равен нулю, тогда система не получает никакого ускорения, что свидетельствует о сохранении ее момента импульса.

Работа момента силы

Поскольку изучаемая величина измеряется в ньютонах на метр (Н*м), то многие могут подумать, что ее можно заменить джоулем (Дж).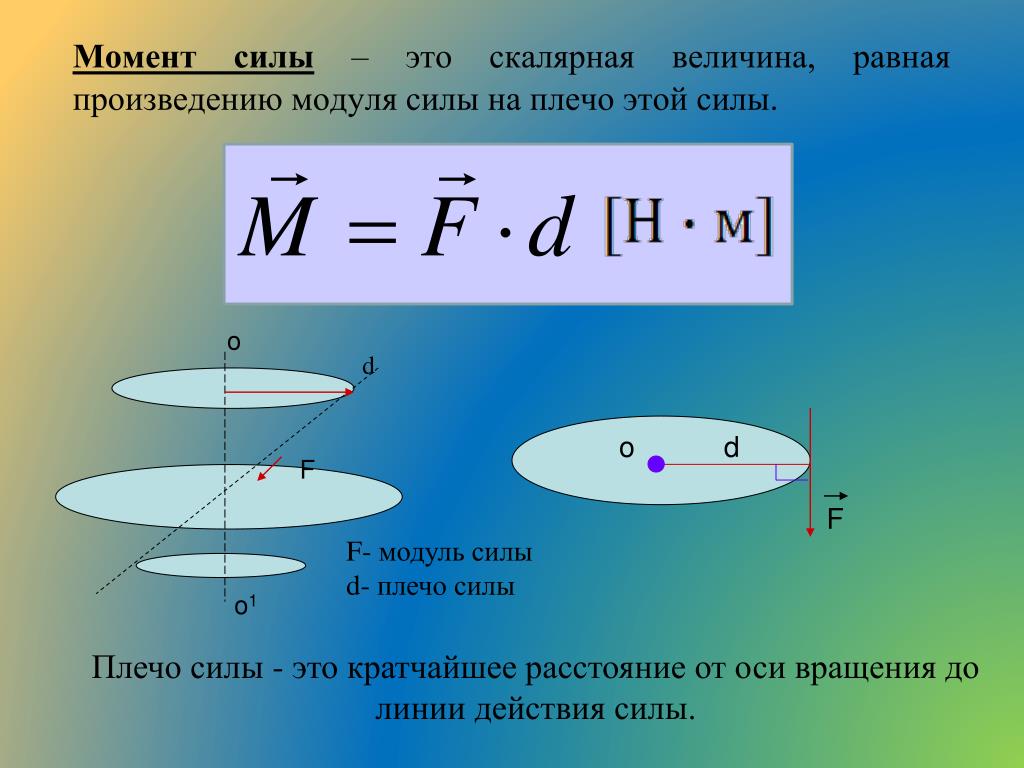 Однако этого не делают потому, что в джоулях измеряется некоторая энергетическая величина, момент силы же — это силовая характеристика.

Так же как сила, момент M тоже может совершать работу. Вычисляется она по такой формуле:

A = M*θ.

Где греческой буквой θ обозначен угол поворота в радианах, на который повернулась система в результате действия момента M. Заметим, что в результате умножения момента силы на угол θ, единицы измерения сохраняются, однако, уже используют именно единицы работы, то есть, Джоули.

Момент силы Калькулятор | Вычислить Момент силы

✖Сила — это любое взаимодействие, которое, если ему не противодействовать, изменит движение объекта. Другими словами, сила может заставить объект с массой изменить свою скорость.ⓘ Сила [F]		Атомная единица силыАттоньютонСантиньютонДеканьютонДециньютондинаэксаньютонFemtonewtonГиганьютонГрамм-силаГраве-силагектоньютонДжоуль / СантиметрДжоуль на метрКилограмм-силаКилоньютонКилопруд Килофунт-силаКип-силаМеганьютонМикроньютонMilligrave — силаМиллиньютонНаноньютонНьютонУнция-силаPetanewtonPiconewtonпрудФунт-фут в квадратную секундуПаундалФунт-силастенТераньютонТон-сила (Long)Тон-сила (метрическая система)Тон-сила (короткий)Йоттаньютон	+10% -10%
✖Перпендикулярное расстояние между силой и точкой является важным фактором при расчете момента силы. ⓘ Перпендикулярное расстояние между силой и точкой [rFP]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%

✖Момент силы – это произведение силы на расстояние, перпендикулярное линии действия силы. ⓘ Момент силы [M]

дина метрдина ммГрамм-сила-сантиметрграмм-сила-метрграмм-сила ммКилограмм-метрКилограмм-сила-сантиметрКилограмм-сила-метркгс ммКилоньютон-метрНьютон-сантиметрНьютон-метрНьютон Миллиметрунция силы-футУнция-сила-дюймфунт-сила футафунт силы дюйм

⎘ копия

👎

Формула

сбросить

👍

Момент силы Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1.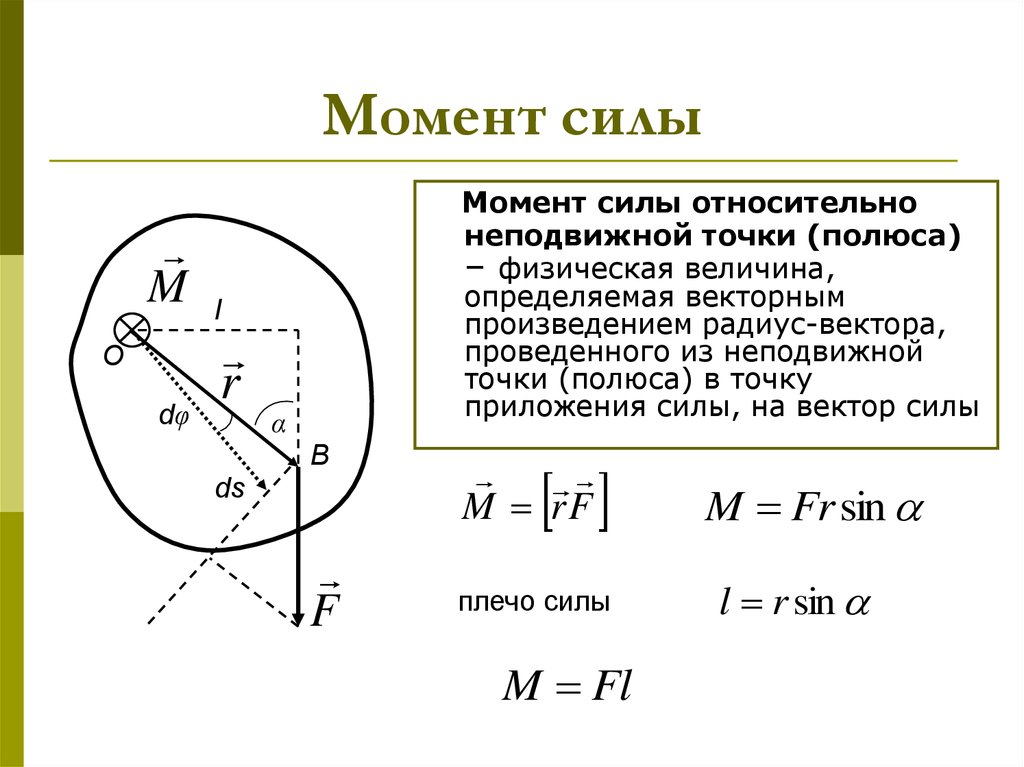 2) Идти

Момент силы

Момент силы = Сила*Перпендикулярное расстояние между силой и точкой Идти

Результат двух разнородных параллельных сил, не равных по величине

Равнодействующая сила = Первая сила-Вторая сила Идти

Результат двух сил, действующих на частицу под углом 180 градусов

Равнодействующая сила = Первая сила-Вторая сила Идти

Результат двух сил, действующих на частицу под углом 0 градусов

Равнодействующая сила = Первая сила+Вторая сила Идти

Результат двух одинаковых параллельных сил

Равнодействующая сила = Первая сила+Вторая сила Идти

Момент силы формула

Момент силы = Сила*Перпендикулярное расстояние между силой и точкой
M = F*r_FP

Что такое момент силы?

Момент силы — это мера ее тенденции заставить тело вращаться вокруг определенной точки или оси.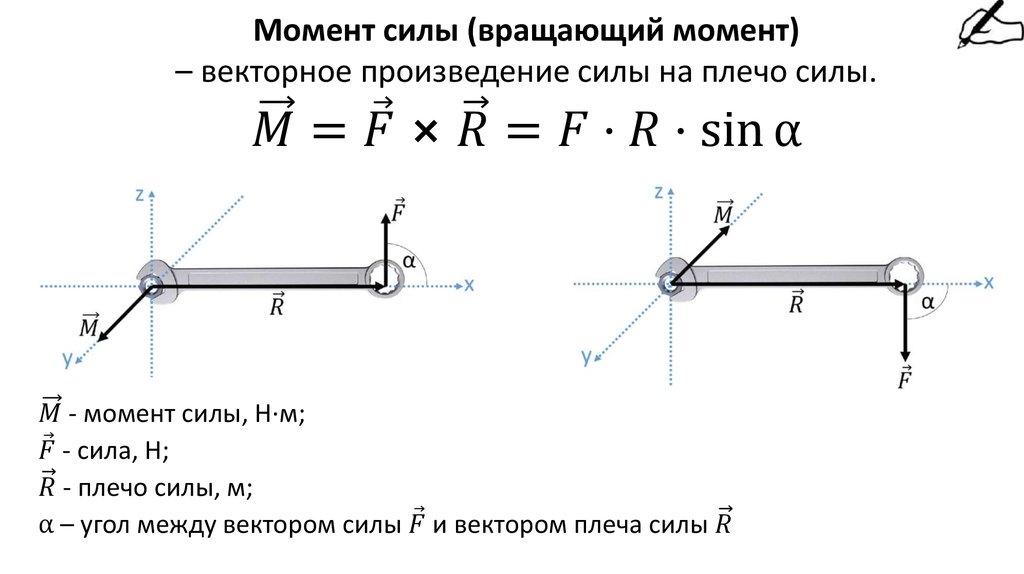

Чтобы на мгновение развиться, сила должна воздействовать на тело таким образом, чтобы оно начало скручиваться.

Share

Copied!

Расчет момента силы и крутящего момента – Excel Unusual

Это дополнение к предыдущему посту, знакомящее читателя с различными способами расчета момента силы и крутящего момента пары. Эта информация будет полезна в моделях динамики самолетов.

Расчет момента силы

Джордж Лунгу

– В этом руководстве представлены несколько способов расчета момента силы или крутящего момента. Это также
доказывает, что крутящий момент пары одинаков независимо от положения точки, относительно которой
вычисляется крутящий момент. Последствия в моделировании динамики самолета значительны.

Перекрестное произведение:

Перекрестное произведение или векторное произведение — это бинарная операция над двумя векторами
в трехмерном пространстве. В результате получается вектор, перпендикулярный плоскости
, содержащей первые два вектора.

Смысл вектора произведения — это направление продвижения правого винта, повернутого так, чтобы
первый вектор наложился на второй по кратчайшему пути.

Величина равна площади параллелограмма, заданного двумя векторами.
Определение момента силы:

Момент силы (иногда называемый крутящим моментом) относительно исходной точки представляет собой вектор, равный векторному произведению вектора положения источника силы (отсчитываемого от исходной точки) и силы вектор.

Три эквивалентных способа расчета момента силы:

 

– Три формулы для расчета момента силы F относительно точки O совершенно эквивалентны. О

– Эквивалентность получается из базовой тригонометрии в прямоугольных треугольниках

Полезная формула расчета момента силы в двухмерной декартовой системе координат:

– В большинстве случаев наша установка находится в декартовой системе координат

, где у нас уже есть координаты точек и x-y компоненты задействованных сил.

– Вот почему следующие формулы очень полезны (добавляем моментные вклады компонентов силы x и y).

Важное приложение:

— Если сила действует на тело в произвольной точке P, тело
будет испытывать линейное ускорение центра тяжести, а
— угловое ускорение вокруг центра тяжести, оба в соответствии с
Ньютоном второй закон.

– Если тело имеет момент инерции «I», мы можем записать F
угловую форму закона Ньютона (где a – угловое
ускорение – скорость изменения угловой скорости):

«Пара»:

-«Пара – это система параллельных, противоположных и равных сил
с равнодействующей моментом, но без равнодействующей силы.
Другой термин для пары — чистый момент. Его эффект состоит в том, чтобы создать
оборотов без какого-либо ускорения центра масс.
-Результирующий момент пары называется крутящим моментом. Это число
не следует путать с термином крутящий момент, поскольку он используется в физике
, где он является просто синонимом момента.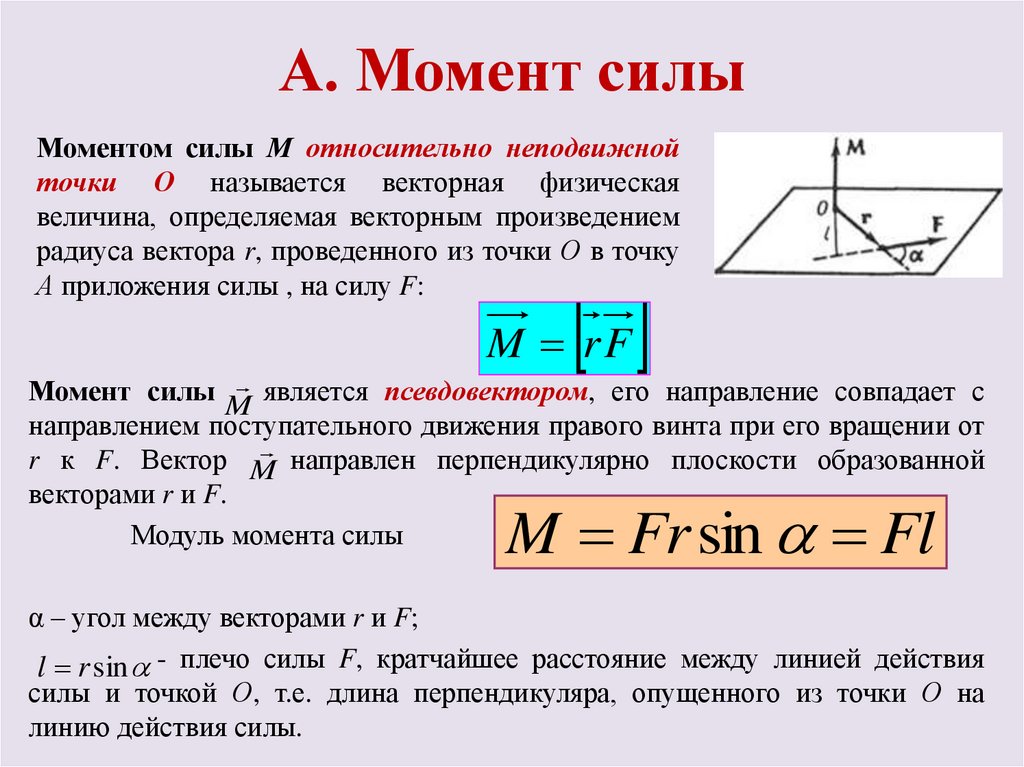 Вместо
— Момент пары, называемый крутящим моментом,
крутящий момент является частным случаем крутящего момента. Крутящий момент имеет специальное значение
, которое не зависит от свойств, которых момент не имеет, в частности свойство точки отсчета
быть независимым от точки отсчета относительно точки
, и его величина равна:
, которую он вычисляет». – Википедия

Демонстрация:

– Если мы вычислим результирующий импульс двух 1

противоположных сил относительно произвольной точки O, мы можем написать:

– Поскольку силы равны, параллельны, но противоположны, мы имеем:

— Но разность векторов зависит только от относительного положения источников силы, а не от
положения точки O. Это доказывает, что крутящий момент не зависит от положения точки относительно
, к которой он рассчитывается .
— Важным следствием является тот факт, что аэродинамический момент крыла или стабилизатора
напрямую добавляется к общему моменту самолета без какого-либо масштабирования.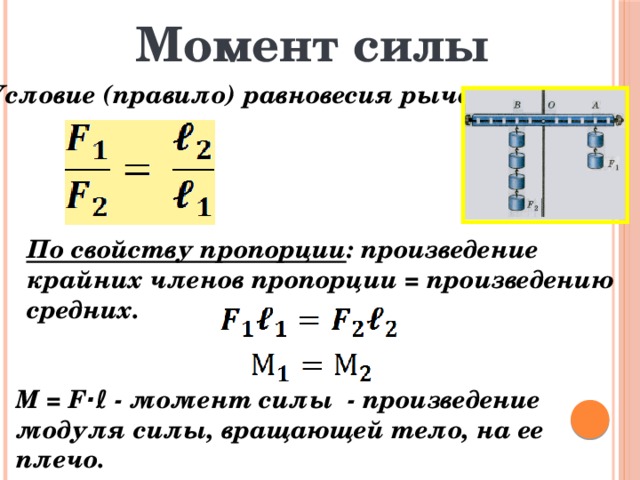
Конец.

Расчет моментов и сил. SINADRIVES Direct Drive Experts

Перейти к содержимому

Предыдущий

Расчет моментов и сил

Привет, мехатронисты,

Добро пожаловать в последний пост в блоге Sinadrives.

Сентябрь 2022

В сегодняшней статье мы обсудим, как рассчитать статические и динамические моменты силы. Эти простые расчеты позволяют нам определить, являются ли модули с выбранными линейными двигателями наиболее подходящими для разрабатываемого нами приложения.

Расчет статической силы

Начнем с физической части расчета, где мы будем использовать формулу 1:

F = m x g

Где:
F – сила в Н
м – масса в кг
г – ускорение свободного падения м/с2

Пример:
Если мы поместим на поверхность груз массой 10 кг, статическая сила, которую он оказывает, составит 98 Н (10 х 9,8 = 98 Н).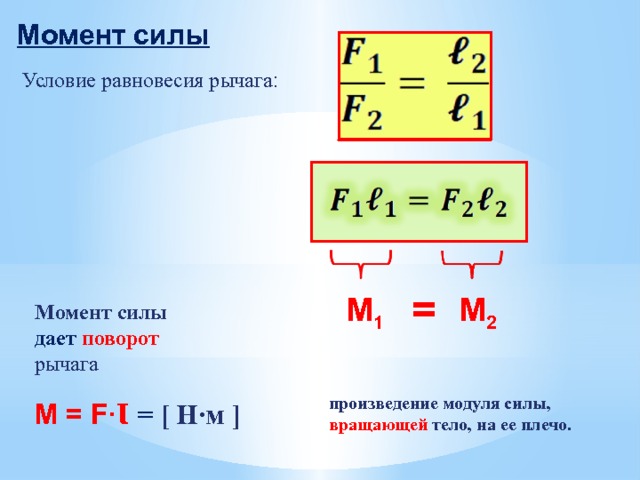

Расчет динамической силы

Для расчета динамической силы мы заменяем g (ускорение свободного падения) на A (ускорение). Важно знать, что это ускорение должно действовать в том же направлении, что и масса.

F = m x A

Где:
F – сила в Н
m – масса в кг
A – ускорение в м/с2

Пример:
и ускорить его в вертикальном направлении (A = 5 м/с2), динамическая сила, которую он оказывает, составляет 50 Н (10 х 5 = 50 Н).

Совместный расчет статических и динамических сил

Предположим, нам нужно рассчитать силу, с которой лифт действует на конструкцию здания при вертикальном движении.

Данные:

Масса лифта: 1000 кг
Ускорение: 4,5 м/S2

F = M x A + M x G = 1000 x 4,5 + 1000 x 9,8 = 4500 + 9800 = 14300N

. Расчет Static Moment

. Для расчета статического момента воспользуемся приведенной ниже формулой:

M = m x g x X

Где:
M – крутящий момент в Нм
X – расстояние между центром масс и зажимом в м
м – масса в кг
г – ускорение свободного падения м/с2

Пример:
Если мы поместим груз массой 10 кг на поверхность на расстоянии 300 мм, статический момент будет равен 29,4 Нм (10 х 9,8 х 0,3 = 29,4 Нм). Изображение 1 является примером приложения.

Расчет динамического момента

Для расчета динамического момента воспользуемся приведенной ниже формулой.

M = m x A x X

Где:
M – крутящий момент в Нм
X – расстояние между центром масс и зажимом в м
m – масса в кг
A – ускорение в м/с2

Пример:
Если поместить груз массой 10 кг на подвижную тележку на расстоянии 300 мм, а также переместить эту тележку с ускорением 15 м /с2 динамический момент составит 45 Нм (10 х 15 х 0,3 = 45 Нм).

На рис. 2 показан пример приложения.

Совместный расчет статических и динамических сил и моментов

Рассмотрим пример. Мы собираемся рассчитать статические и динамические силы и моменты. Мы будем использовать данные из двух приведенных выше примеров и применим порядок, как показано на рисунке 3.

В этом случае у нас есть:

Статические силы и моменты :
FZ = 98N
MX = 29,4 нм

Динамические силы и моменты :
MZ = 45 нм

Коэффициент.

выбрали линейный модуль MLE30420 для нашего приложения, и мы должны проверить моменты силы. На изображении ниже показаны значения по каталогу для модуля с линейным двигателем MLE30420HS:

. Если использовать формулу, приведенную в каталоге, получим:

Fy/Fycat + Fz/Fzcat + Mx/Mxcat + My/Mycat + Mz/Mzcat ≤ 1

Значения, рассчитанные в главах 1, 4 и 5, помещаем в верхнюю строку, а каталожные — в нижнюю. , что дает нам следующие результаты:

98/1500 + 29,4/180 + 45/320 = 0,07 + 0,16 + 0,14 = 0,23

Мы видим, что результат ≤ 1, что означает наличие хорошего запаса прочности. По каталогу результат меньше 1 гарантирует срок службы более 30 000 км.

Некоторые соображения

Отдельно рассчитанные значения никогда не могут превышать максимальное каталожное значение. Чем ниже это значение, тем дольше будет срок службы. Если скорость и ускорение превышают значения 3 м/с и 30 м/с2, соответственно, общая сумма не должна превышать 0,7, если не считается приемлемым более короткий срок службы.