Проводимость Калькулятор | Вычислить Проводимость
✖Сопротивление является мерой сопротивления току, протекающему в электрической цепи. Его единицей СИ является ом.ⓘ Сопротивление [R] | AbohmEMU сопротивленияESU сопротивленияExaohmГигаомкилооммегаоммикроомМиллиомНаномомПетаомПланка сопротивлениеКвантованная Hall СопротивлениеВзаимный СименсStatohmВольт на АмперYottaohmZettaohm | +10% -10% |
|
✖Проводимость (также известная как электрическая проводимость) определяется как способность вещества проводить электричество.ⓘ Проводимость [G] |
AbmhoАмпер / ВольтGemmhoГигасименскилосименсМегасименссименсМикромхомикросименсМиллисименсНаносименсПикозименсКвантованная зал КондактансСименсStatmho |
⎘ копия |
👎
Формула
сбросить
👍
Проводимость Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Сопротивление: 10.1 ом —> 10.1 ом Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.099009900990099 Сименс —>0.099009900990099 сименс (Проверьте преобразование здесь)
< 20 Электропроводность и проводимость Калькуляторы
Площадь поперечного сечения электрода с учетом проводимости и проводимости
Идти Площадь поперечного сечения электрода = (Проводимость*Расстояние между электродами)/(Удельная проводимость)
Расстояние между электродами с учетом проводимости и проводимости
Идти Расстояние между электродами = (Удельная проводимость*Площадь поперечного сечения электрода)/(Проводимость)
Электропроводность с учетом проводимости
Идти Удельная проводимость = (Проводимость)*(Расстояние между электродами/Площадь поперечного сечения электрода)
Проводимость с учетом проводимости
Идти Проводимость = (Удельная проводимость*Площадь поперечного сечения электрода)/(Расстояние между электродами)
Молярная проводимость при бесконечном разбавлении
Идти Молярная проводимость при бесконечном разбавлении = (Подвижность катиона+Подвижность аниона)*[Faraday]
Ограничение молярной проводимости катионов.
Идти Ограничение молярной проводимости = Ионная подвижность катиона при бесконечном разбавлении*[Faraday]
Ограничение молярной проводимости анионов.
Идти Ограничение молярной проводимости = Ионная подвижность аниона при бесконечном разбавлении*[Faraday]
Предельная молярная проводимость с учетом степени диссоциации
Идти Ограничение молярной проводимости = (Молярная проводимость раствора/Степень диссоциации)
Удельная проводимость с учетом молярности
Идти Удельная проводимость = (Молярная проводимость раствора*Молярность)/1000
Молярный объем раствора с учетом молярной проводимости
Идти Молярный объем = (Молярная проводимость раствора/Удельная проводимость)
Электропроводность с учетом молярного объема раствора
Идти Удельная проводимость = (Молярная проводимость раствора/Молярный объем)
Молярная проводимость с учетом проводимости и объема
Идти Молярная проводимость раствора = (Удельная проводимость*Молярный объем)
Эквивалентная проводимость
Идти Эквивалентная проводимость = Удельная проводимость*Объем раствора
Молярная проводимость с учетом молярности
Идти Молярная проводимость = Удельная проводимость*1000/Молярность
Постоянная ячейки с учетом проводимости и проводимости
Идти Постоянная ячейки = (Удельная проводимость/Проводимость)
Проводимость с учетом константы ячейки
Идти Удельная проводимость = (Проводимость*Постоянная ячейки)
Проводимость с учетом константы ячейки
Идти Проводимость = (Удельная проводимость/Постоянная ячейки)
Молярная проводимость
Идти Молярная проводимость = Удельная проводимость/Молярность
Удельная проводимость
Идти Удельная проводимость = 1/Удельное сопротивление
Проводимость
Идти Проводимость = 1/Сопротивление
Проводимость формула
Проводимость = 1/Сопротивление
G = 1/R
Что такое проводимость?
Проводимость (также известная как электрическая проводимость) определяется как способность вещества проводить электричество. Электропроводность — это мера того, насколько легко электрический ток (то есть поток заряда) может проходить через материал. Электропроводность — это обратное (или обратное) электрическое сопротивление, представленное как 1 / R.
Электропроводность — это мера того, насколько легко электрический ток (то есть поток заряда) может проходить через материал. Электропроводность — это обратное (или обратное) электрическое сопротивление, представленное как 1 / R.
Share
Copied!формула. Полупроводники. Структура полупроводников. Типы проводимости и возникновение тока в полупроводниках
Содержание:
- 1 Кристаллическая решетка кремния
- 2 Легирование полупроводников
- 3 Что такое удельная электропроводимость
- 4 Единицы проводимости
- 5 Области применения электропроводимости растворов
- 6 Температурный эффект, термокомпенсация
- 7 В чем разница между сопротивлением и проводимостью?
- 8 Единица измерения проводимости
- 9 Общее сопротивление параллельной цепи
- 10 Общая проводимость параллельной цепи
- 11 Строение атомов полупроводников.
- 12 Электропроводность полупроводника.
- 13 Электронно-дырочная проводимость.

- 13.1 Электронная проводимость.
- 13.2 Дырочная проводимость.
- 14 Свойства германия с примесями
- 14.1 Влияние примесей на проводимость полупроводника
Кристаллическая решетка кремния
В обычном состоянии, атомы кремния образуют кристаллическую решетку. На внешней электронной оболочке атома находятся четыре электрона. С их помощью, устанавливается ковалентная связь с четырьмя соседними атомами. Каждый электрон в такой связи принадлежит двум атомам одновременно.
Таким образом, у каждого атома на внешней электронной оболочке находиться восемь электронов. В результате, поскольку последний уровень электронной оболочки оказывается завершенным, у атома очень трудно забрать его электроны и материал ведет себя как диэлектрик (не проводит электрический ток).
Легирование полупроводников
Для того чтобы повысить проводимость полупроводников, их специально загрязняют примесями – атомами химических элементов с другим значением валентности. Примеси с меньшим количеством валентных электронов, чем у полупроводника, называются акцепторами. Примеси с большей валентностью – донорами.
Примеси с меньшим количеством валентных электронов, чем у полупроводника, называются акцепторами. Примеси с большей валентностью – донорами.
Сам этот процесс называется легированием полупроводников. Примерное соотношение — один атом примеси на миллион атомов полупроводника.
Что такое удельная электропроводимость
| Удельная проводимость (или удельная электролитическая проводимость) определяется, как способность вещества проводить электрический ток. Это величина, обратная удельному сопротивлению. При химическом очищении воды очень важно измерить удельную проводимость воды, зависящую от растворенных в воде ионных соединений. Удельная проводимость легко может быть измерена электронными приборами. Широкий спектр соответствующего оборудования позволяет сейчас измерять проводимость практически любой воды, от сверхчистой (очень низкая проводимость) до насыщенной химическими соединениями (высокая проводимость). |
Единицы проводимости
Основная единица измерения сопротивления — Ом. Удельная проводимость — величина обратная сопротивлению, она измеряется в Сименсах, ранее называвшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость — величина обратная сопротивлению, она измеряется в Сименсах, ранее называвшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость — это проводимость, измеренная между противоположными сторонами куба вещества со стороной 1 см. Единицей данного типа измерений является Сименс/см. При измерении проводимости воды чаще используются более точные мкС/см (микросименс) и мС/см (миллисименс).
Соответствующие единицы измерения сопротивления (или удельного сопротивления) — Ом/см, МегаОм/см и килоОм/см. При измерении сверхчистой воды чаще используют МегаОм/см, так как это дает более точные результаты. Сопротивление менее чистой воды, как например, водопроводной, измеряют в килоОм/см.
Большинство из нас, работая с практически чистой водой, используют единицы мкС/см и мС/см во время исследования воды с высокой концентрацией растворенных химических веществ. Использование удельной проводимости в данном приложении имеет преимущество почти прямой связи с примесями, особенно при низких концентрациях ионов, как, например, в системах охлаждения и бойлерах.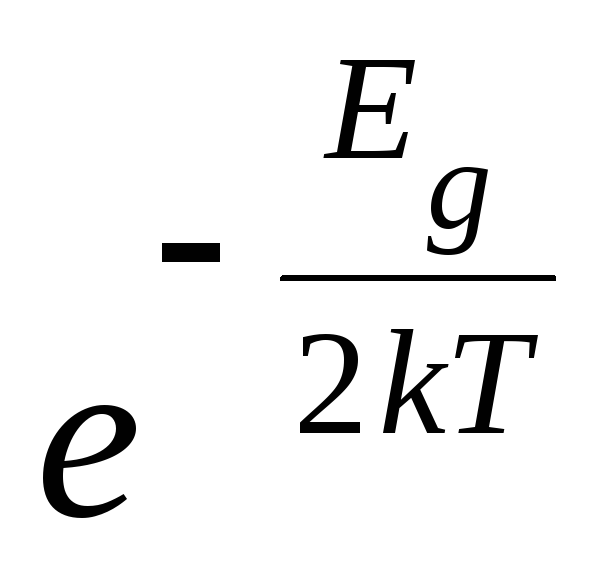 Таким образом, рост удельной проводимости указывает на рост примесей, и можно установить критический уровень для контроля максимального уровня примесей.
Таким образом, рост удельной проводимости указывает на рост примесей, и можно установить критический уровень для контроля максимального уровня примесей.
Удельная проводимость некоторых растворов 1000 мг. в л.:
| Состав | мкСм/см @ 25 C° | мСм/см |
| Бикарбонат натрия | 870 | 0,87 |
| Сульфат натрия | 1300 | 1,30 |
| Хлорид натрия | 1990 | 1,99 |
| Карбонат натрия | 1600 | 1,60 |
| Гидроксид натрия | 5820 | 5,82 |
| Гидроксид аммония | 189 | 0,19 |
| Соляная кислота | 11000 | 11,10 |
| Фтористоводородная кислота | 2420 | 2,42 |
| Азотная кислота | 6380 | 6,38 |
| Фосфорная кислота | 2250 | 2,25 |
| Серная кислота | 6350 | 6,35 |
Области применения электропроводимости растворов
Измерения удельной проводимости широко используются при исследовании воды, используемой в промышленности, муниципальных и коммерческих учреждениях, больницах c помощью кондуктометров (портативных, лабораторных, карманных или промышленных).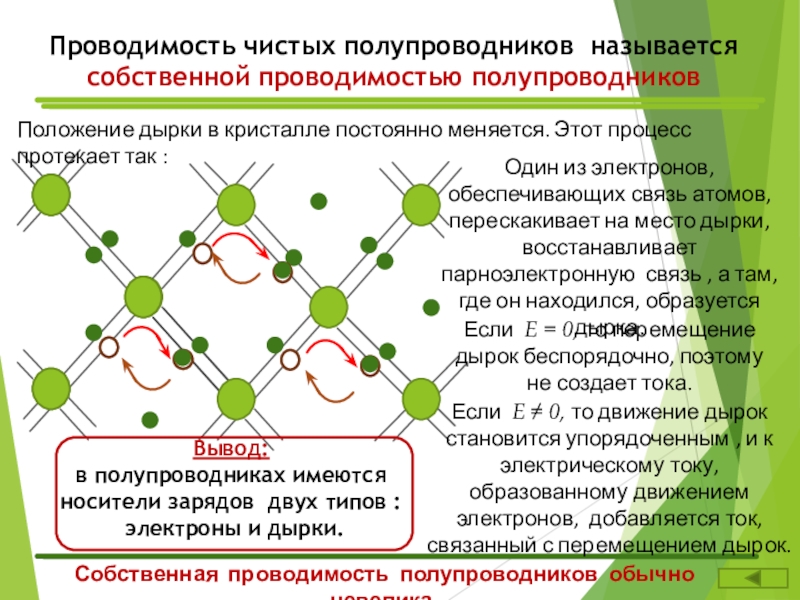 Пока индивидуальные ионы не могут быть определены это обычно не требуется, и удельная проводимость дает величину общих примесей.
Пока индивидуальные ионы не могут быть определены это обычно не требуется, и удельная проводимость дает величину общих примесей.
Ниже мы приводим самые распространенные правила измерения:
Проводимость в мкС/см х 0.5 = T.D.S. (общее солесодержание) мг. в л. как у NaCl или
Проводимость в мкС/см х 0.75 = T.D.S. (общее солесодержание) мг. в л. как таковая
Главный недостаток измерений удельной проводимости это то, что они не специфичны, не дают возможности распознавания различных типов ионов. Вместо этого определяется пропорция общего эффекта присутствия всех имеющихся ионов и некоторых ионов, как NaOH, HCI, представленных в значительно большей степени.
См. «Удельная проводимость 1000 мг. в л. растворов» см. выше.
Второй недостаток соотнесения удельной проводимости к концентрации заключается в том, что концентрированные растворы показывают слегка заниженное число мкС/см на каждый мг. в л. в отличие от разреженных, как показано на графике ниже. Этот эффект основан на снижении скорости движения ионов при увеличении концентрации, что лежит в основе теории межионного притяжения.
Некоторые соединения могут снижать точность измерений, осаждаясь на датчике или щупе, например, карбонат кальция. В большинстве случаев эти трудности не превращаются в серьезные помехи и могут быть достигнуты достаточно точные результаты. В целом, измерение удельной проводимости — это быстрый, надежный и недорогой способ измерения количества ионных соединений в протоке. Как правило, при повторных измерениях разброс значений не превышает 1%.
Скорость движения ионов прямо пропорциональна температуре. Поэтому оптимальная температура во время измерения — 25 °C. См. ниже о влиянии температуры и автоматической температурной компенсации. Тест-измерители удельной проводимости и контроллеры широко используются в самых различных областях.
Температурный эффект, термокомпенсация
Удельная проводимость в водных растворах из-за движения ионов и постоянно возрастающей температуры противоположна удельной проводимости металлов, но приближается к показателям графита. Это обусловлено природой самих ионов и вязкостью воды.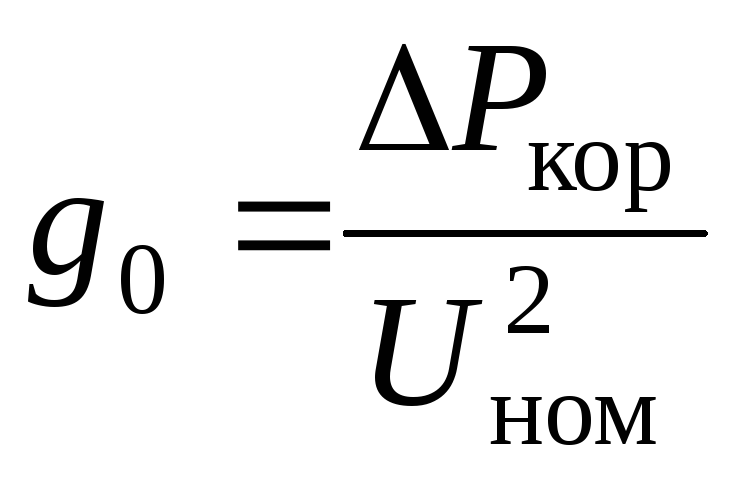 При низкой концентрации ионов (сверхчистая вода) ионизация воды позволяет определить часть проводящих ионов. Все эти процессы, а следовательно, и удельная проводимость существенно зависят от температуры.
При низкой концентрации ионов (сверхчистая вода) ионизация воды позволяет определить часть проводящих ионов. Все эти процессы, а следовательно, и удельная проводимость существенно зависят от температуры.
Эта зависимость обычно выражается, как относительное изменение удельной проводимости на градус C при конкретной температуре, а в особых случаях, как процент на градус C°., называемый наклонением конкретного раствора. Сверхчистая вода имеет наибольшее наклонение в 5.2% на градус C°., в то время, как наклонение большей части водопроводной воды и воды в охлаждающих системах находится в диапазоне 1.8 — 2.0% на градус C°.
Концентрированные соленые растворы, кислоты и щелочные растворы имеют наклонение около 1.5% на градус C. Теперь очевидно, что небольшая разница в температуре незначительно изменяет удельную проводимость. По этой причине, чаще всего удельную проводимость относят к 25 C°.
К счастью, доступны температурные датчики с характеристиками, близкими к раствору, в исследовании которого мы заинтересованы, и с использованием дополнительных резисторов и электронных схем можно получить температурные кривые почти для любого раствора.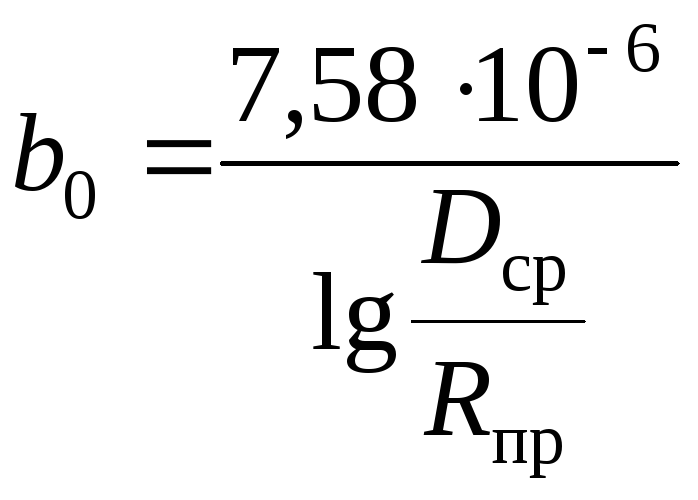
Температурный датчик используется как элемент регулировки электрической цепи, и значение проводимости автоматически приводится к эквивалентному значению при 25 C°.
Самые современные технологии используют микропроцессор и соответствующую таблицу, содержащую информацию о реакции раствора на температуру. Температура раствора измеряется, переводится в цифровой формат, затем сопоставляется с данными таблицы для получения точных значений.
В чем разница между сопротивлением и проводимостью?
Сопротивление, по определению, является мерой «трения», которое компонент представляет для прохождения через него тока. Сопротивление обозначается заглавной буквой «R» и измеряется в единицах «Ом». Однако мы также можем думать об этом электрическом свойстве с обратной ему точки зрения: насколько легко току течь через компонент, а не насколько трудно.
Если сопротивление – это термин, которое мы используем для обозначения меры того, насколько трудно току течь, то хорошим термином, чтобы выразить, насколько легко ток течет, будет проводимость. Математически проводимость – это величина, обратная сопротивлению:
Математически проводимость – это величина, обратная сопротивлению:
[проводимость = frac{1}{сопротивление}]
Чем больше сопротивление, тем меньше проводимость; и наоборот.
Это должно быть интуитивно понятно, потому что сопротивление и проводимость – противоположные способы обозначения одного и того же важного электрического свойства.
Если сравнивать сопротивления двух компонентов и обнаружится, что компонент «A» имеет сопротивление вдвое меньше сопротивления компонента «B», то в качестве альтернативы мы могли бы выразить это соотношение, сказав, что компонент «A» в два раза более проводящий, чем компонент «B». Если компонент «A» имеет сопротивление, равное только одной трети от сопротивления компонента «B», то мы можем сказать, что он в три раза более проводящий, чем компонент «B», и так далее.
Единица измерения проводимости
В продолжение этой идеи были придуманы символ и единица измерения проводимости. Символ представляет собой заглавную букву «G», а единицей измерения был mho, что означает «ohm» (ом), написанное в обратном порядке (вы думали, что у электронщиков нет чувства юмора?).
Несмотря на свою уместность, единицы измерения mho в последующие годы были заменены единицей Сименс (сокращенно «См», или, в англоязычной литературе, «S»). Это решение об изменении названий единиц измерения напоминает изменение единицы измерения температуры в градусах стоградусной шкалы (degrees centigrade – от латинских слов «centum», т.е. «сто», и «gradus») на градусы Цельсия (degrees Celsius) или изменение единицы измерения частоты c.p.s. (циклов в секунду) в герцы. Если вы ищете здесь какой-то шаблон переименования, то Сименс, Цельсий и Герц – это фамилии известных ученых, имена которых, к сожалению, о природе единиц говорят нам меньше, чем их первоначальные обозначения.
Возвращаясь к нашему примеру с параллельной схемой, мы должны быть в состоянии увидеть, что несколько путей (ветвей) для тока уменьшают общее сопротивление всей цепи, поскольку ток может легче проходить через всю цепь из нескольких ветвей, чем через любую из них отдельно. Что касается сопротивления, дополнительные ветви приводят к меньшему общему значению (ток встречает меньшее сопротивление). Однако с точки зрения проводимости дополнительные ветви приводят к большему общему значению (ток протекает с большей проводимостью).
Однако с точки зрения проводимости дополнительные ветви приводят к большему общему значению (ток протекает с большей проводимостью).
Общее сопротивление параллельной цепи
Общее сопротивление параллельной цепи меньше, чем любое из сопротивлений отдельных ветвей, потому что параллельные резисторы вместе «сопротивляются» меньше, чем по отдельности:
Рисунок 1 – Полное сопротивление параллельной цепи
Общая проводимость параллельной цепи
Общая проводимость параллельной цепи больше, чем проводимость любой из отдельных ветвей, потому что параллельные резисторы «проводят» вместе лучше, чем по отдельности:
Рисунок 2 – Полная проводимость параллельной цепи
Чтобы быть более точным, полная проводимость в параллельной цепи равна сумме отдельных проводимостей:
[G_{общ} = G_1 + G_2 + G_3 + G_4]
Если мы знаем, что проводимость – это не что иное, как математическая величина, обратная (1/x) сопротивлению, мы можем перевести каждый член приведенной выше формулы в сопротивление, подставив величину, обратную каждой соответствующей проводимости:
[frac{1}{R_{общ}} = frac{1}{R_{1}} + frac{1}{R_{2}} + frac{1}{R_{3}} + frac{1}{R_{4}}]
Решая приведенное выше уравнение для полного сопротивления (вместо значения, обратного общему сопротивлению), мы получим следующую формулу:
[R_{общ} = frac{1}{frac{1}{R_{1}} + frac{1}{R_{2}} + frac{1}{R_{3}} + frac{1}{R_{4}}}]
Итак, мы, наконец, пришли к нашей загадочной формуле сопротивления! Проводимость (G) редко используется в качестве практического параметра, поэтому при анализе параллельных цепей часто используется приведенная выше формула.
Строение атомов полупроводников.
Германий и кремний являются основными материалами многих полупроводниковых приборов и имеют во внешних слоях своих оболочек по четыре валентных электрона.
Атом германия состоит из 32 электронов, а атом кремния из 14. Но только 28 электронов атома германия и 10 электронов атома кремния, находящиеся во внутренних слоях своих оболочек, прочно удерживаются ядрами и никогда не отрываются от них. Лишь только четыре валентных электрона атомов этих проводников могут стать свободными, да и то не всегда. А если атом полупроводника потеряет хотя бы один электрон, то он становится положительным ионом.
В полупроводнике атомы расположены в строгом порядке: каждый атом окружен четырьмя такими же атомами. Причем они расположены так близко друг к другу, что их валентные электроны образуют единые орбиты, проходящие вокруг соседних атомов, тем самым связывая атомы в единое целое вещество.
Представим взаимосвязь атомов в кристалле полупроводника в виде плоской схемы.
На схеме красные шарики с плюсом, условно, обозначают ядра атомов (положительные ионы), а синие шарики – это валентные электроны.
Здесь видно, что вокруг каждого атома расположены четыре точно таких же атома, а каждый из этих четырех имеет связь еще с четырьмя другими атомами и т.д. Любой из атомов связан с каждым соседним двумя валентными электронами, причем один электрон свой, а другой заимствован у соседнего атома. Такая связь называется двухэлектронной или ковалентной.
В свою очередь, внешний слой электронной оболочки каждого атома содержит восемь электронов: четыре своих, и по одному, заимствованных от четырех соседних атомов. Здесь уже не различишь, какой из валентных электронов в атоме «свой», а какой «чужой», так как они сделались общими. При такой связи атомов во всей массе кристалла германия или кремния можно считать, что кристалл полупроводника представляет собой одну большую молекулу. На рисунке розовым и желтым кругами показана связь между внешними слоями оболочек двух соседних атомов.
Электропроводность полупроводника.
Рассмотрим упрощенный рисунок кристалла полупроводника, где атомы обозначаются красным шариком с плюсом, а межатомные связи показаны двумя линиями, символизирующими валентные электроны.
При температуре, близкой к абсолютному нулю полупроводник не проводит ток, так как в нем нет свободных электронов. Но с повышением температуры связь валентных электронов с ядрами атомов ослабевает и некоторые из электронов, вследствие теплового движения, могут покидать свои атомы. Вырвавшийся из межатомной связи электрон становится «свободным», а там где он находился до этого, образуется пустое место, которое условно называют дыркой.
Чем выше температура полупроводника, тем больше в нем становится свободных электронов и дырок. В итоге получается, что образование «дырки» связано с уходом из оболочки атома валентного электрона, а сама дырка становится положительным электрическим зарядом равным отрицательному заряду электрона.
А теперь давайте рассмотрим рисунок, где схематично показано явление возникновения тока в полупроводнике.
Если приложить некоторое напряжение к полупроводнику, контакты «+» и «-», то в нем возникнет ток.
Вследствие тепловых явлений, в кристалле полупроводника из межатомных связей начнет освобождаться некоторое количество электронов (синие шарики со стрелками). Электроны, притягиваясь положительным полюсом источника напряжения, будут перемещаться в его сторону, оставляя после себя дырки, которые будут заполняться другими освободившимися электронами. То есть, под действием внешнего электрического поля носители заряда приобретают некоторую скорость направленного движения и тем самым создают электрический ток.
Например: освободившийся электрон, находящийся ближе всего к положительному полюсу источника напряжения притягивается этим полюсом. Разрывая межатомную связь и уходя из нее, электрон оставляет после себя дырку. Другой освободившийся электрон, который находится на некотором удалении от положительного полюса, также притягивается полюсом и движется в его сторону, но встретив на своем пути дырку, притягивается в нее ядром атома, восстанавливая межатомную связь.
Образовавшуюся новую дырку после второго электрона, заполняет третий освободившийся электрон, находящийся рядом с этой дыркой. В свою очередь дырки, находящиеся ближе всего к отрицательному полюсу, заполняются другими освободившимися электронами. Таким образом, в полупроводнике возникает электрический ток.
Пока в полупроводнике действует электрическое поле, этот процесс непрерывен: нарушаются межатомные связи — возникают свободные электроны — образуются дырки. Дырки заполняются освободившимися электронами – восстанавливаются межатомные связи, при этом нарушаются другие межатомные связи, из которых уходят электроны и заполняют следующие дырки.
Из этого делаем вывод: электроны движутся от отрицательного полюса источника напряжения к положительному, а дырки перемещаются от положительного полюса к отрицательному.
Электронно-дырочная проводимость.
В «чистом» кристалле полупроводника число высвободившихся в данный момент электронов равно числу образующихся при этом дырок, поэтому электропроводность такого полупроводника мала, так как он оказывает электрическому току большое сопротивление, и такую электропроводность называют собственной.
Но если в полупроводник добавить в виде примеси некоторое количество атомов других элементов, то электропроводность его повысится в разы, и в зависимости от структуры атомов примесных элементов электропроводность полупроводника будет электронной или дырочной.
Электронная проводимость.
Допустим, в кристалле полупроводника, в котором атомы имеют по четыре валентных электрона, мы заменили один атом атомом, у которого пять валентных электронов. Этот атом своими четырьмя электронами свяжется с четырьмя соседними атомами полупроводника, а пятый валентный электрон останется «лишним» – то есть свободным. И чем больше будет таких атомов в кристалле, тем больше окажется свободных электронов, а значит, такой полупроводник по своим свойствам приблизится к металлу, и чтобы через него проходил электрический ток, в нем не обязательно должны разрушаться межатомные связи.
Полупроводники, обладающие такими свойствами, называют полупроводниками с проводимостью типа «n», или полупроводники n-типа. Здесь латинская буква n происходит от слова «negative» (негатив) — то есть «отрицательный». Отсюда следует, что в полупроводнике n-типа основными носителями заряда являются – электроны, а не основными – дырки.
Здесь латинская буква n происходит от слова «negative» (негатив) — то есть «отрицательный». Отсюда следует, что в полупроводнике n-типа основными носителями заряда являются – электроны, а не основными – дырки.
Дырочная проводимость.
Возьмем все тот же кристалл, но теперь заменим его атом атомом, в котором только три свободных электрона. Своими тремя электронами он свяжется только с тремя соседними атомами, а для связи с четвертым атомом у него не будет хватать одного электрона. В итоге образуется дырка. Естественно, она заполнится любым другим свободным электроном, находящимся поблизости, но, в любом случае, в кристалле такого полупроводника не будет хватать электронов для заполнения дырок. И чем больше будет таких атомов в кристалле, тем больше будет дырок.
Чтобы в таком полупроводнике могли высвобождаться и передвигаться свободные электроны, обязательно должны разрушаться валентные связи между атомами. Но электронов все равно не будет хватать, так как число дырок всегда будет больше числа электронов в любой момент времени.
Такие полупроводники называют полупроводниками с дырочной проводимостью или проводниками p-типа, что в переводе от латинского «positive» означает «положительный». Таким образом, явление электрического тока в кристалле полупроводника p-типа сопровождается непрерывным возникновением и исчезновением положительных зарядов – дырок. А это значит, что в полупроводнике p-типа основными носителями заряда являются дырки, а не основными — электроны.
Теперь, когда Вы имеете некоторое представление о явлениях, происходящих в полупроводниках, Вам не составит труда понять принцип действия полупроводниковых радиокомпонентов.
Свойства германия с примесями
В настоящее время из полупроводниковых элементов наибольшее применение нашли германий и кремний. Германий является очень редким элементом: содержание его в земной коре составляет менее 7·10-4%. Исходным продуктом для получения чистого германия является двуокись германия (GеO2), восстанавливаемая в водороде.
Кремний, наоборот, — один из самых распространенных элементов в природе и запасы его неисчерпаемы. Однако получение чистого кремния затруднено из-за высокой температуры плавления (более 1400° С) и большой химической активности в жидком состоянии.
Однако получение чистого кремния затруднено из-за высокой температуры плавления (более 1400° С) и большой химической активности в жидком состоянии.
| Если в четырехвалентный германий добавить пятивалентный мышьяк или фосфор (донорную примесь), то примесные атомы займут в кристаллической решетке места отдельных атомов германия. При этом около каждого атома примеси остается один валентный электрон, не связанный с окружающими атомами германия. |
При температуре, отличающейся от абсолютного нуля, этот электрон может покинуть атом примеси и стать свободным, причем возникновение свободных электронов не связано с появлением дырки. Для ионизации атома чистого германия необходима энергия 0,72 эв, тогда как для ионизации примесного атома требуется энергия 0,015 эв. Поэтому уже при комнатной температуре все свободные электроны донорной примеси находятся в зоне проводимости. Германий с донорной примесью называется германием n-типа. Если к нему приложить электрическое поле, то в полупроводнике появится ток.
При добавлении в четырехвалентный германий трехвалентного индия или галлия атом примеси, заняв место атома германия в кристаллической решетке, не будет иметь достаточного числа электронов для образования ковалентной связи. При температуре выше абсолютного нуля один из валентных электронов соседних атомов, получив достаточную энергию, заполнит недостающую связь. Примесный атом становится отрицательным ионом, а в том месте, откуда ушел электрон, образуется дырка. При этом свободный электрон не появляется, количество свободных электронов в зоне проводимости остается прежним. Для того чтобы электрон от атома германия перешел к атому примеси, ему надо сообщить энергию порядка 0,1 эв, в то время как для того, чтобы электрону от примесного атома перейти в зону проводимости, надо затратить энергию в 0,72 эв. При обычной комнатной температуре большинство электронов германия переходит к примесным атомам. Германий с акцепторной примесью называется германием р-типа.
В германии n-типа много свободных электронов, они рекомбинируют с дырками и уменьшают их количество; аналогично в германии р-типа много дырок, они рекомбинируют с электронами и уменьшают их количество.
Влияние примесей на проводимость полупроводника
Чистые полупроводники редко применяются в полупроводниковой технике. Обычно используются примесные полупроводники. Введение в полупроводник атомов соответствующей примеси способствует образованию дополнительных носителей тока, что приводит к повышению электропроводности иногда в десятки миллионов раз. В чистом полупроводнике «поставщиком» электронов в зону проводимости может быть валентная зона. Введение примесей в полупроводник должно способствовать переходу электронов в зону проводимости.
Существуют два вида примесей. В примесях первого вида энергетические уровни электронов примеси располагаются в запрещенной зоне полупроводника вблизи зоны проводимости. Поэтому атомы примеси, являясь поставщиками электронов в зону проводимости, легко отдают в нее электроны, поскольку электронам при этом следует сробщить меньшую энергию ∆Е1, а не ∆Е, как в полупроводнике без примеси. Примесные уровни при температуре выше абсолютного нуля отдают свои электроны в зону проводимости тем интенсивнее, чем выше температура полупроводника. Примесные уровни такого вида называются донорными уровнями, а сами примеси — донорами (donarе — дарить, лат.).
Примесные уровни такого вида называются донорными уровнями, а сами примеси — донорами (donarе — дарить, лат.).
Примесные уровни второго вида называются акцепторными, а сами примеси — акцепторами. Акцепторные уровни располагаются около валентной зоны. При абсолютном нуле температуры акцепторные уровни свободны, т. е. не заполнены. Поэтому при температуре, отличной от абсолютного нуля, на такие уровни могут перейти электроны из валентной зоны, и так как ∆Е2 < ∆Е, то число этих электронов будет больше, чем количество электронов, переходящих в зону проводимости. Уход электронов из валентной зоны дает возможность оставшимся здесь электронам, при наличии постороннего электрического поля, принять участие в проводимости в пределах этой зоны. При этом, как указывалось выше, дырки будут двигаться в направлении действия электрического поля.
Таким образом, электропроводность полупроводника можно увеличить путем введения донорной примеси (за счет возрастания электронов в зоне проводимости) либо путем введения акцепторной примеси (за счет возрастания числа дырок в валентной зоне). |
Источники
- http://hightolow.ru/semiconductors3.php
- https://www.ecoinstrument.ru/service/public/izmerenie_elektroliticheskoy_provodimosti/
- https://radioprog.ru/post/990
- https://sesaga.ru/poluprovodniki-struktura-poluprovodnikov-tipy-provodimosti-i-vozniknovenie-toka-v-poluprovodnikax.html
- https://www.elel.ru/provodimost.html
[свернуть]
Электрическая проводимость – формула, единица измерения, примеры и факты
Электрическая проводимость является обратной величиной удельного электрического сопротивления. Он также известен как удельная проводимость, которая отражает способность материала проводить электрический ток. Обычно мы обозначаем электропроводность греческой буквой σ (сигма). Однако в области электротехники мы представляем его как κ (каппа), а иногда используется γ (гамма). Единицей электропроводности в системе СИ является сименс на метр (См/м). Аналогично электрическому сопротивлению, у нас есть формула электропроводности и особый метод определения ее единицы, которую мы поймем на этой странице.
Здесь мы также рассмотрим различные примеры электропроводности в повседневной жизни.
Формула электропроводности
Предположим в идеальном случае, что кусок резистивного материала имеет однородное поперечное сечение и физический состав. Кроме того, электрическое поле и плотность тока параллельны и везде постоянны. Однако различные резисторы и проводники имеют однородное поперечное сечение с равномерным протеканием электрического тока и изготовлены из одного материала, так что это хорошая модель. Итак, в этом случае удельное электрическое сопротивление (ρ) можно рассчитать по следующей формуле:
$R=\rho {\frac{1}{2}}…….(1)$
Здесь
R — электрическое сопротивление однородного образца материала
— удельное сопротивление или удельное сопротивление
l — длина материала
A — площадь поперечного сечения материала
Мы знаем, что электропроводность данного материала прямо пропорциональна удельному сопротивлению, поэтому формула для этого утверждения:
$\sigma ={\frac{1}{2}}$
Теперь выведем единицу измерения электропроводности. 9{2}}{м}=Ом.м$
9{2}}{м}=Ом.м$
Обратное значение удельного сопротивления равно Ом-1м-1 или мОм/м.
Поскольку ом-1 записывается как S (Сименс), единицей электропроводности становится Сименс/метр или См/м….(2)
Кроме того, размерная формула электропроводности может быть получена как:
Мы знаем, что размерная формула сопротивления (Ом) равна [M1 L2 T-3 A-2], поэтому наоборот, т. е. mho становится [M-1 L-2 T-3 A2].
Этот mho эквивалентен S (Siemens) = [M-1 L-2 T3 A2] 91}$
При решении размерная формула электропроводности принимает вид:
[M-1 L-3 T3 A2]. Где-то вы можете найти эту формулу как [M-1 L-3 T3 I2].
Другая формула электропроводности
В идеальном случае удельное сопротивление в конкретной точке выражается как отношение напряженности электрического поля к плотности тока, создаваемого им в этой точке:
$\rho= \frac{ E}{J}$
Здесь,
⍴- Удельное сопротивление проводящего материала
E — величина электрического поля
Дж — величина плотности тока
Так как проводимость обратна удельному сопротивлению этого материала, то мы имеем следующее уравнение:
$\sigma= \frac {J}{E}$
Единицей плотности тока является ампер на квадратный метр, а размерная формула — [A1 L-2]. 1}$ = Kg-1m-3s3A2 или mho. м или С/м 9{1}}}$ = [M-1 L-3 T3 A2]
1}$ = Kg-1m-3s3A2 или mho. м или С/м 9{1}}}$ = [M-1 L-3 T3 A2]
Из приведенного выше уравнения (1) R и опишите, насколько трудно току течь через любой материал/вещество. Однако сопротивление — это внешнее свойство, а удельное сопротивление — внутреннее.
Под этим утверждением мы подразумеваем, что все провода из чистой меди (не подвергшиеся искажению их кристаллической структуры), независимо от их формы и размера, имеют одинаковое удельное сопротивление.
Однако длинный тонкий медный провод имеет гораздо большее сопротивление, чем толстый короткий медный провод.
Таким образом, каждый материал имеет свое характеристическое удельное сопротивление. Например, резина имеет гораздо большее удельное сопротивление, чем медь, поэтому проводимость меди выше, чем у резины.
Более того, говоря о металлах и жидкостях, у металлов больше свободных электронов, чем у жидкостей, а это означает, что металлы обладают электропроводностью, чем жидкости.
Теперь давайте разберемся в науке об электропроводности металлов и жидкостей.
Ниже приведены данные по электропроводности металлов при 20 ℃:
Электропроводность металлов с примерами
Материал | 90 111|
Серебро | 6,30 × 107 |
Медь | 5,8 × 107 |
Кальций | 2,82 × 107 |
Магний | 2,15 × 107 |
1,60 × 107 | |
Платина | 9,44 × 106 |
Факторы, влияющие на электропроводность грунтовых материалов, на которые влияют следующие причины:
Электропроводность жидкостей с примерами
Электропроводность жидкостей является мерой способности воды пропускать электрический ток. Эта способность напрямую связана с концентрацией ионов в воде.
Эта способность напрямую связана с концентрацией ионов в воде.
Кроме того, соединения, которые растворяются в ионы, известны как электролиты 40. Таким образом, чем больше присутствующих ионов, тем выше электропроводность воды.
Факторы, влияющие на электропроводность жидкостей:
Концентрация ионов,
Тип ионов, и
Температура раствора.
Примеры электропроводности
Металлы и плазма являются примерами материалов с высокой электропроводностью.
(изображение будет загружено в ближайшее время)
Одним из электрических проводников с наилучшей электропроводностью является серебро.
Факты об электропроводности
Хотя электричество проходит не через все жидкости, такие как лимонный сок, молоко, уксус, раствор поваренной соли, раствор серной кислоты, морская и дождевая вода, они могут проводить электричество.
 В то время как раствор сахара, дистиллированная вода и мед не могут проводить электричество.
В то время как раствор сахара, дистиллированная вода и мед не могут проводить электричество.
Питьевая вода имеет проводимость от 200 до 800 мкСм/см.
Электропроводность является важным параметром для измерения при мониторинге окружающей среды или процесса. Этот параметр полезен для определения различных изменений, таких как изменение проводимости, которое может указывать на загрязнение.
Итак, из нашего текста о том, что такое электропроводность, ее формула, единица измерения и примеры, мы резюмируем нашу тему утверждением, что материалы, через которые может легко проходить электрический ток, называются проводниками электричества. Электропроводность описывает способность вещества пропускать электрический ток, который можно рассчитать по формулам σ = $\frac{1}{\rho }$ и $\frac{J}{E}$.
Кроме того, твердые металлы и графит являются хорошими проводниками электричества и обладают высокой электропроводностью. Однако некоторые жидкости, такие как соленая вода и лимонный сок, также являются хорошими проводниками.
Однако некоторые жидкости, такие как соленая вода и лимонный сок, также являются хорошими проводниками.
Электропроводность | Определение, символ, формула, единица измерения
Что такое электропроводность?Электропроводность — это свойство материала, позволяющее проходить через него электрическому току. Другими словами, электропроводность — это мера электрического тока, проходящего через материал, когда градиент потенциала равен единице.
Таким образом, электропроводность измеряет способность проводника проводить электричество.
В электроэнергетике это один из важных факторов, который проектировщики учитывают при проектировании электрической системы. Медь и алюминий являются наиболее подходящими проводниками, так как их проводимость очень высока. Более высокая проводимость указывает на прохождение большего количества электронов через материалы без особых препятствий.
Материал с более высокой проводимостью имеет более низкое сопротивление и вызывает меньшие потери тепла (I2R) в проводнике. Например. печатная плата имеет сложную электрическую схему, и проводимость пути должна быть очень высокой, чтобы избежать помех протеканию электрического тока. Для этого применения лучше всего подходит оцинкованная медь.
Например. печатная плата имеет сложную электрическую схему, и проводимость пути должна быть очень высокой, чтобы избежать помех протеканию электрического тока. Для этого применения лучше всего подходит оцинкованная медь.
Электропроводность образца материала зависит от атомной конфигурации, длины и площади поперечного сечения материалов. Эти параметры остаются неизменными после расчета сопротивления, следовательно, они не изменяют проводимость. Однако проводимость снижается с повышением температуры. Почему это так?
Мы знаем, что ток в электрической цепи есть не что иное, как поток электронов. Большее количество электронов, проходящих через материал в секунду, означает, что материал имеет более высокую проводимость. Повышение температуры вызывает столкновения электрона с электроном и столкновение с атомом. В результате поток электронов через материал становится вялым, что вызывает снижение электропроводности материала.
Таким образом, можно сделать вывод, что проводник имеет более высокую проводимость при низких температурах. Вы бы слышали о сверхпроводимости. Что это такое? Сверхпроводимость — это свойство вещества, которое делает его способным проводить электричество без импеданса, что означает, что сопротивление равно нулю. Это возможно, если температура вещества ниже критической температуры.
Символ проводимостиСимвол электропроводности обозначается греческой буквой σ (Сигна). Электропроводность обратно пропорциональна удельному электрическому сопротивлению ( ρ ).
Соотношение между проводимостью и удельным сопротивлением приведено ниже.
σ = 1/ ρ
Формула электрической проводимости Сопротивление проводника в зависимости от проводимости материала, поперечной зоны и длины. На основании этих параметров можно вывести уравнение электропроводности.
Вывод уравнения электропроводности/ формула ∝ Л ——-(2) Р ∝ 1/ A ——-(3)
Таким образом,
R = 1/ σ ( 9027 0 L /A) ——-(4)
σ = 1/R x (L/A) ——-(5)
σ = S x (L/A) ——-(5) [Здесь S — проводимость и S = 1/R]
Взаимное сопротивление (R) является проводимостью (S) и взаимная OHM ( ω ) IS MHO (ω -1 или ℧)
здесь, R является сопротивлением в OHM ( ω )
.27. = Площадь поперечного сечения в см 2 или м 2
L = Длина проводника в сантиметрах (см) или метрах (м)
σ = Электропроводность материала ( Ом -см) или ( Ω -m)
S = электрическая проводимость
Удельное электрическое сопротивление материала непосредственно пропорционально площади поперечного сечения и обратно пропорционально длине.


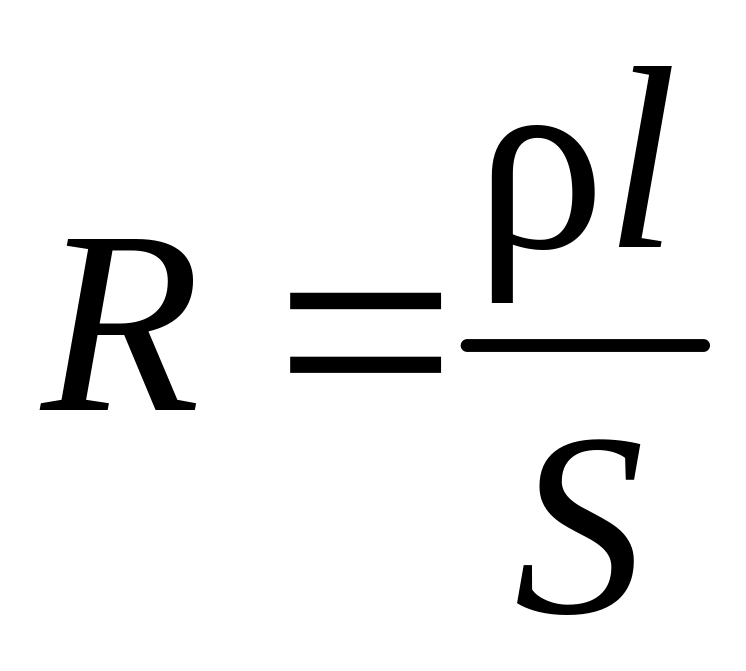
 В то время как раствор сахара, дистиллированная вода и мед не могут проводить электричество.
В то время как раствор сахара, дистиллированная вода и мед не могут проводить электричество.