Формула силы притяжения
Сила (F) — это результат взаимодействия тел друг с другом.
Зависимость силы тяготения от массы тел
Галилей доказал, что при свободном падении Земля сообщает всем телам в данном месте одно и то же ускорение независимо от их массы. Но ускорение по второму закону Ньютона обратно пропорционально массе: . Как же объяснить, что ускорение, сообщаемое телу силой притяжения Земли, одинаково для всех тел? Это возможно лишь в том случае, если сила притяжения к Земле прямо пропорциональна массе тела. В этом случае увеличение массы т, например, вдвое приведет к увеличению модуля силы F тоже вдвое, а ускорение, которое равно , останется неизменным. Обобщая этот вывод для сил тяготения между любыми телами, заключаем, что сила всемирного тяготения прямо пропорциональна массе тела, на которое эта сила действует.
Но
во взаимном притяжении участвуют, по
меньшей мере два тела.
Зависимость силы тяготения от расстояния между телами
Из опыта хорошо известно, что ускорение свободного падения равно 9,8 м/с2 и оно одинаково для тел, падающих с высоты 1, 10 и 100 м, т. е. не зависит от расстояния между телом и Землей. Это как будто бы означает, что и сила от расстояния не зависит. Но Ньютон считал, что отсчитывать расстояния надо не от поверхности, а от центра Земли. Но радиус Земли 6400 км. Понятно, что несколько десятков, сотен или даже тысяч метров над поверхностью Земли не могут заметно изменить значение ускорения свободного падения.
Чтобы
выяснить, как влияет расстояние между
телами на силу их взаимного притяжения,
нужно было бы узнать, каково ускорение
тел, удаленных от Земли на достаточно
большие расстояния.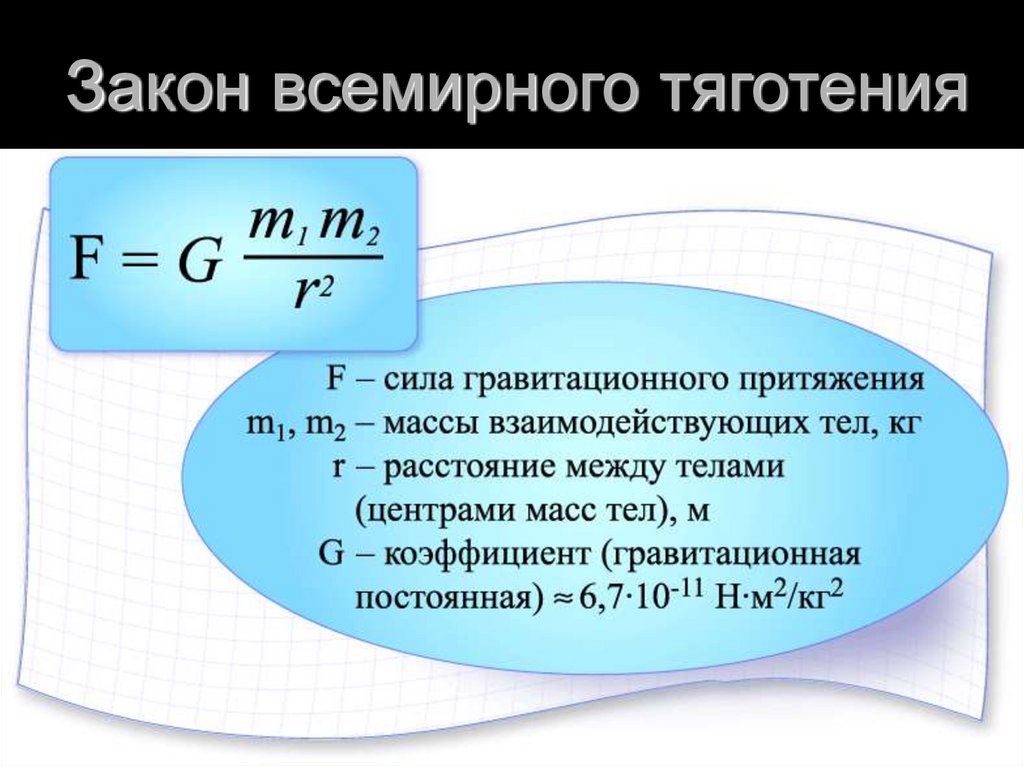
Однако наблюдать
и изучать свободное падение тела с
высоты в тысячи километров над Землей
трудно. Но сама природа пришла здесь на
помощь и дала возможность определить
ускорение тела, движущегося по окружности
вокруг Земли и обладающего, поэтому
центростремительным ускорением,
вызванным, разумеется, той же силой
притяжения к Земле. Таким телом является
естественный спутник Земли – Луна. Если
бы сила притяжения между Землей и Луной
не зависела от расстояния между ними,
то центростремительное ускорение Луны
было бы таким же, как ускорение тела,
свободно падающего близ поверхности
Земли. В действительности же
центростремительное ускорение Луны
равно 0,0027 м/с
Докажем это. Обращение Луны вокруг Земли происходит под действием силы тяготения между ними. Приближенно орбиту Луны можно считать окружностью. Следовательно, Земля сообщает Луне центростремительное ускорение. Оно вычисляется по формуле , где
Учитывая, что радиус Земли Rз ≈
6,4∙106 м,
получим, что центростремительное
ускорение Луны равно:м/с2.
Найденное значение ускорения меньше ускорения свободного падения тел у поверхности Земли (9,8 м/с2) приблизительно в 3600 = 602 раз.
Таким образом, увеличение расстояния между телом и Землей в 60 раз привело к уменьшению ускорения, сообщаемого земным притяжением, а следовательно, и самой силы притяжения в 602 раз.
Отсюда вытекает важный вывод: ускорение, которое сообщает телам сила притяжения к Земле, убывает обратно пропорционально квадрату расстояния до центра Земли
.
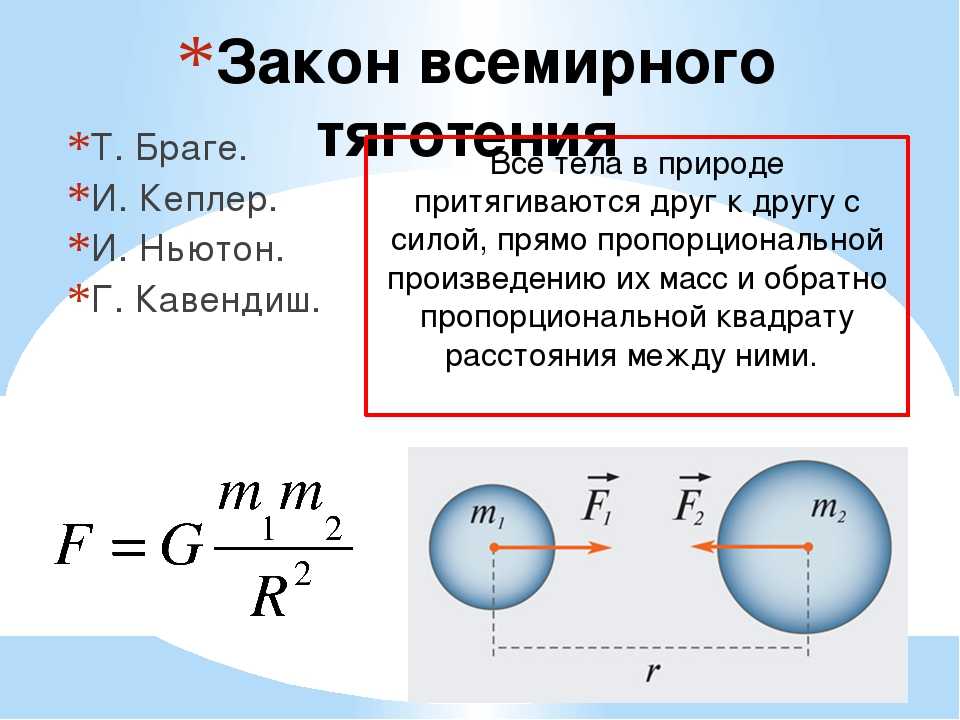
Закон всемирного тяготения
В 1667 г. Ньютон окончательно сформулировал закон всемирного тяготения:
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними
Коэффициент пропорциональности G называется гравитационной постоянной.
Закон всемирного тяготения справедлив только для таких тел, размеры которых пренебрежимо малы по сравнению с расстоянием между ними. Иначе говоря, он справедлив только для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис. 1). Подобного рода силы называются центральными.
Рис. 1
Для
нахождения силы тяготения, действующей
на данное тело со стороны другого, в
случае, когда размерами тел пренебречь
нельзя, поступают следующим образом.
Оба тела мысленно разделяют на столь
малые элементы, чтобы каждый из них
можно было считать точечным. Складывая
силы тяготения, действующие на каждый
элемент данного тела со стороны всех
элементов другого тела, получают силу,
действующую на этот элемент (рис. 2).
Проделав такую операцию для каждого
элемента данного тела и сложив полученные
силы, находят полную силу тяготения,
действующую на это тело.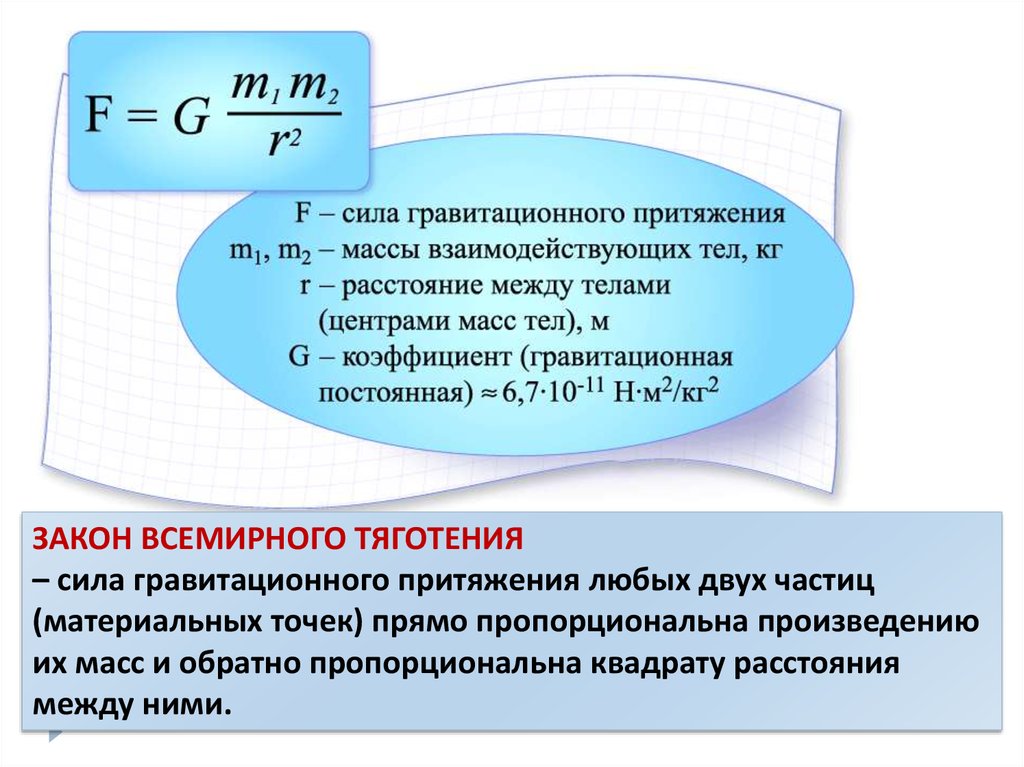
Рис. 2
Есть, однако, один практически важный случай, когда формула (1) применима к протяженным телам. Можно доказать, что сферические тела, плотность которых зависит только от расстояний до их центров, при расстояниях между ними, больших суммы их радиусов, притягиваются с силами, модули которых определяются формулой (1). В этом случае R – это расстояние между центрами шаров.
И наконец, так как размеры падающих на Землю тел много меньше размеров Земли, то эти тела можно рассматривать как точечные. Тогда под R в формуле (1) следует понимать расстояние от данного тела до центра Земли.
Между всеми телами действуют силы взаимного притяжения, зависящие от самих тел (их масс) и от расстояния между ними.
Закон всемирного тяготения. Калькулятор силы притяжения, массы и расстояния онлайн.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн калькулятор закона всемирного тяготения (гравитации) вычислит силу притяжения двух материальных точек, массу и расстояния между ними, а также даст подробное решение.
-24]Единица измерения расстояния r НанометрМиллиметрСантиметрМетрДециметрКилометрДюймФутЯрдМиляМорская миляАстрономическая единицаСветовой годПарсек
Калькулятор вычисления массы материальной точки через массу второй материальной точки, силу и расстояние.
Гравитационная постоянная G численно равна силе гравитационного притяжения между двумя телами, масса каждого тела равна 1 кг, находящимися на расстоянии 1 метра друг от друга.
G = 6.67 × 10-11 Н × м2 / кг2
Единица массы — килограмм, но также можно использовать и другие единицы, например грамм, тонна, миллиграмм и т.д.
Сила F = Ньютон (Н)Деканьютон даН (daN) × [10^1]Гектоньютон гН (hN) × [10^2]Килоньютон кН (kN) × [10^3]Меганьютон МН (MN) × [10^6]Гиганьютон ГН (GN) × [10^9]Тераньютон ТН (TN) × [10^12]Петаньютон ПН (PN) × [10^15]Эксаньютон ЭН (EN) × [10^18]Зеттаньютон ЗН (ZN) × [10^21]Иоттаньютон ИН (YN) × [10^24]Дециньютон дН (dN) × [10^-1]Сантиньютон сН (cN) × [10^-2]Миллиньютон мН (mN) × [10^-3]Микроньютон мкН (µN) × [10^-6]Наноньютон нН (nN) × [10^-9]Пиконьютон пН (pN) × [10^-12]Фемтоньютон фН (fN) × [10^-15]Аттоньютон аН (aN) × [10^-18]Зептоньютон зН (zN) × [10^-21]Иоктоньютон иН (yN) × [10^-24]
Расстояние r = НанометрМиллиметрСантиметрМетрДециметрКилометрДюймФутЯрдМиляМорская миляАстрономическая единицаСветовой годПарсек
Масса m2 = Миллиграмм мг (mg) = 10^-6 кгМикрограмм мкг (µg) = 10^-9 кгГрамм (г) = 10^-3 кгКилограмм кг (kg)Центнер ц = 10^2 кгТонна т (t) = 10^3 кг
Единица измерения массы m1 Миллиграмм мг (mg) = 10^-6 кгМикрограмм мкг (µg) = 10^-9 кгГрамм (г) = 10^-3 кгКилограмм кг (kg)Центнер ц = 10^2 кгТонна т (t) = 10^3 кг
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка.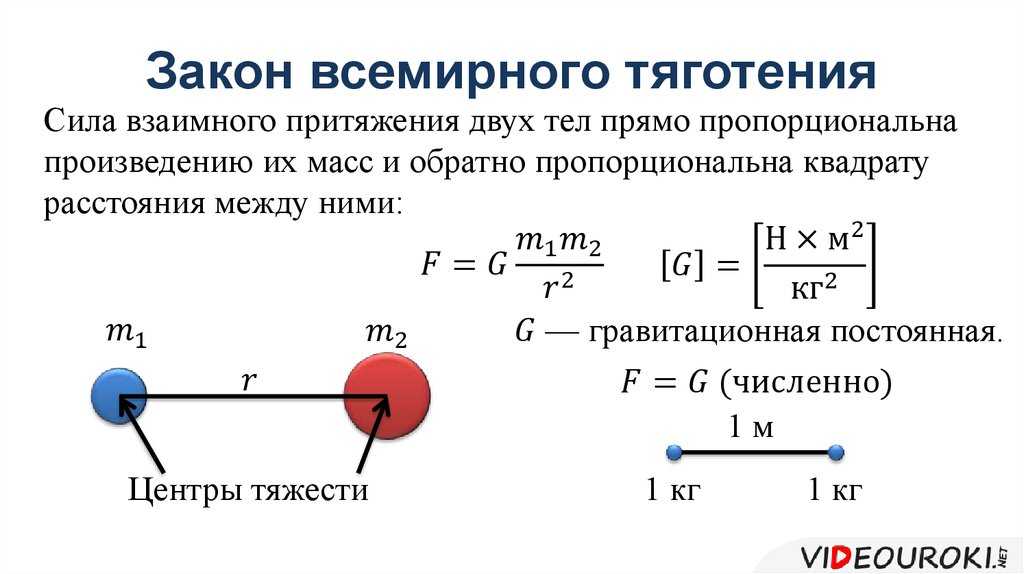 Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Формула силы притяжения — GeeksforGeeks
Сила притяжения определяется как сила, которая заставляет два или более объектов сближаться, даже если они не находятся рядом или не касаются друг друга. Это сила, которая притягивает тела ближе друг к другу. Согласно универсальному закону всемирного тяготения Ньютона, каждая масса, существующая в космосе, притягивает другую массу, и все, что брошено вверх, обязательно упадет обратно на землю.
Магнитная сила, электрическая сила, электростатическая сила и гравитационная сила являются некоторыми силами притяжения.
Формула силы притяжения
Сила притяжения между любыми двумя телами прямо пропорциональна их массам и обратно пропорциональна расстоянию между ними. Обозначается символом F g . Его единицей измерения является Ньютон (Н), а размерная формула задается как [M 1 L 1 T -2 ]. Его формула равна произведению гравитационной постоянной на отношение произведения масс тел на квадрат расстояния между ними.
F г = Gm 1 м 2 /r 2
где
9 F 90 сила притяжения,
- G — гравитационная постоянная со значением 6,67 × 10 −11 Н·м 2 /кг 2 ,
- м 1 — масса тела,
- м 2
0 — масса другого тела, между двумя телами.
Вывод
Рассмотрим систему из двух тел с массами m 1 и m 2 , разделенных расстоянием r.
Известно, что сила притяжения между этими двумя телами прямо пропорциональна произведению масс тел.
F ∝ м 1 м 2 ⇢ (1)
Кроме того, сила косвенно пропорциональна квадрату расстояния между двумя телами. Итак, мы получаем
F ∝ 1/r 2 ⇢ (2)
из (1) и (2),
F ∝ M 1 M 2 /R 2
Заменить знак пропорциональности на константу, мы получаем,
F г = Gm 1 m 2 /r 2
Здесь G известна как гравитационная постоянная.
Отсюда выводится формула силы притяжения между двумя телами.
Известно, что сила притяжения между этими двумя телами прямо пропорциональна произведению масс тел.Примеры задач
Задача 1. Вычислить силу притяжения между двумя телами массами 50 кг и 100 кг, находящимися на расстоянии 20 м друг от друга.
Решение:
m 1 = 50
m 2 = 100
r = 90 по формуле получаем 90
3 90 0002 F = Гм 1 м 2 / r 2
= (6,67 × 10 −11 × 50 × 100)/(20) 2
= 8,343 × 10 -10 9 002007 9 002003 Задача 2: Рассчитать гравитационную силу между два тела массами 100 кг и 150 кг, находящиеся на расстоянии 80 м.
Решение:
м 1 = 100
м 2 = 150
r = 80
3 Используя формулу
F = Гм 1 м 2 / r 2
= (6,67 × 10 −11 × 100 × 150)/(80) 2
= 1,5643 × 10 -10
2
20 Задача 3. Рассчитайте гравитационную силу между два тела массами 200 кг и 170 кг, находящиеся на расстоянии 1000 м.
0 г 2 = ( 6,67 × 10 −11 × 40 × 34)/(2,6 × 10 -11 )Решение:
м 1 = 200
м 2 = 170
r = 1000
2 3
F = Гм 1 м 2 / r 2
= (6,67 × 10 −11 × 200 × 170)/(1000) 2
= 2,26 × 10 -12
2 N
20 Задача 4. Вычислите массу тел, если сила тяжести между ними равна 2,8 × 10 -12 N так, что они имеют равные массы и находятся на расстоянии 120 м друг от друга.
8 10 -12Решение:
F = 2,8 × 10 -12
r = 120
Используя формулу получаем, 2
=> м 2 = Fr 2 /G
=> м 2 = (2,8 × 10 -12 × 120 × 120)/(6,67 × 10 −10 3 > 900 2 = 625
=> m = 25 кг
Задача 5.
Решение:
F = 1,89 × 10 -11
r = 60
Используя формулу получаем, /1r10 G0 2
=> м 2 = Пт 2 /З
=> м 2 = (1,89 × 10 -11 × 60 × 60)/(6,67 × 10 −11 )
=> м 2 = м 3 = 1023 900
Задача 6. Вычислить расстояние между телами массами 16 кг и 32 кг, если сила тяжести между ними равна 4,2 × 10 -12 Н.
Решение =
94002
м 1 = 16
м 2 = 32
Используя формулу получаем,
F = Gm 1 m 2 /r 2
=> r m 90 0 90 0 12 = Gm 90 90 9 2 /F
=> r 2 = (6,67 × 10 −11 × 16 × 32)/(4,2 × 10 -12 )
=> r 2 = 8100 м
r=> 57
Задача 7.
Решение:
Имеем,
F = 2,6 × 10 -11
м 0 9 1 0
м 2 = 34
Использование формулу получаем,
F = Gm 1 m 2 /r 2
=> r 2 = Gm 1 m 2 =>
/ F
0 3=> r 2 = 3600
=> r = 60 м
Формула силы притяжения. Определение, формула и примеры решения В природе преобладают многочисленные силы притяжения. Некоторыми из них являются магнитная сила, электрическая сила, электростатическая сила и гравитационная сила. Гравитационная сила — это очень хорошо идентифицируемый пример силы притяжения, поскольку она притягивает объекты к себе независимо от расстояния до них.
Где,
F сила притяжения
G гравитационная постоянная is m 2 ,
расстояние между двумя объектами равно d.Эта формула помогает вычислить силу, действующую между любыми двумя телами, имеющими большую массу, так как при меньших массах эта сила незначительна.
Решенные примеры
Пример 1: Рассчитайте силу тяжести, действующую между двумя телами массами 20 000 кг и 50 000 кг, разделенными расстоянием 50 м.
Ответ:
Известно:масса m 1 = 20000 кг,
масса m 2 = 50000 кг,
радиус r = 50 м,
Гравитационная постоянная G = 6,67 × 10 -11 Нм 2 /кг 2
Сила гравитации выражается как 9{-5}N\end{массив} \)
между двумя телами.
Вычислить массу тел, если сила притяжения между ними равна 1,89 × 10 -11 Н так, что они имеют равные массы и находятся на расстоянии 60 м друг от друга. .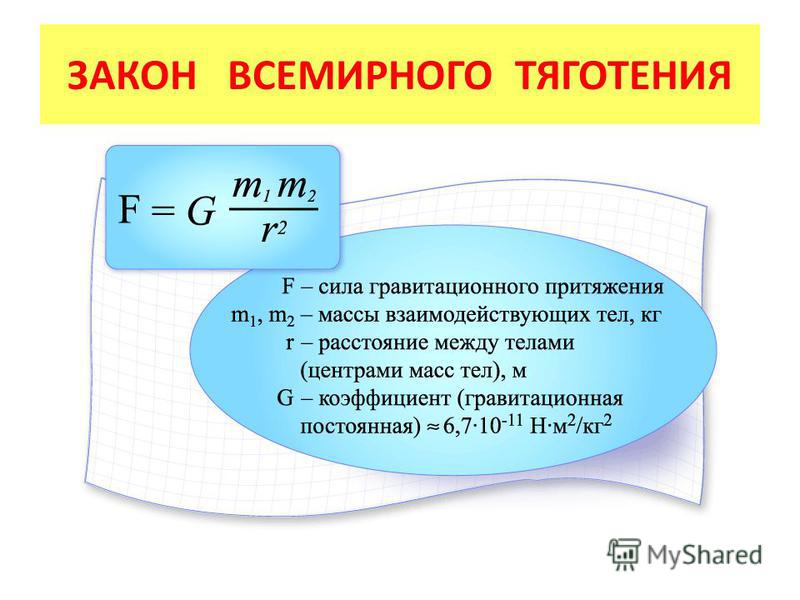 
Вычислить расстояние между телами массами 40 кг и 34 кг, если сила тяжести между ними равна 2,6 × 10 -11 N. 
Универсальный закон всемирного тяготения Ньютона многое объясняет о том, как действует эта сила. В нем говорится, что каждая масса, встречающаяся во Вселенной, притягивает ту или иную массу во Вселенной. Это подтверждает тот факт, что любой, кто брошен вверх, падает. 9{2}}\конец{массив} \)
