Правило моментов | Физика
С тех пор как Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский ученый П. Вариньон придал ему более общую форму, воспользовавшись понятием момента силы.
Моментом силы называется физическая величина, равная произведению силы на ее плечо:
M = Fl, (21.1)
где
М — момент силы, F — сила, l — плечо силы.
Докажем, что рычаг находится в равновесии, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки, т. е.
М1 = М2 (21.2)
Для доказательства этого равенства воспользуемся формулой (20.1). Используя свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), перепишем эту формулу в виде
F1l1 = F2l2
Но F2l2 = M2 — момент силы, стремящейся повернуть рычаг по часовой стрелке (см. рис. 50), а F
Формула (21.2) выражает правило моментов. Это правило справедливо для любого твердого тела, способного вращаться вокруг закрепленной оси. Таково, например, тело, изображенное на рисунке 53. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой O. Плечом силы F1 в данном случае является расстояние l1 от оси вращения до линии действия силы.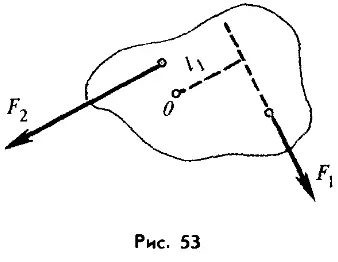
Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от ее плеча. Именно поэтому, например, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. С помощью небольшой силы при этом создают значительный момент, и дверь открывается. Открыть ее, оказывая давление около петель, значительно труднее. По той же причине гайку легче отворачивать более длинным гаечным ключом, шуруп легче вывернуть с помощью отвертки с более широкой ручкой и т. д.
Единицей момента силы в СИ является ньютон-метр (1 Н*м). Это момент силы 1 Н, имеющей плечо 1 м.
1. Что называют моментом силы? 2. Сформулируйте правило моментов. 3. Что характеризует момент силы? 4. Почему ручку у двери прикрепляют на противоположной от петель стороне? 5. Как находится момент силы в общем случае? 6. Что принимают за единицу момента силы?
Статика. Правило моментов
В задачах, связанных с равновесием тел, нужно, как правило, найти две силы (или больше) которые стремятся это тело повернуть по и против часовой стрелки. Если моменты этих сил равны, тело будет находиться в равновесии. А чтобы рассчитать момент, нужно также правильно определить плечо силы: это расстояние от оси вращения до линии действия силы.
Задача 1. К концу стержня длиной 2 м, укрепленного шарнирно одним концом к стене, а с другого конца поддерживаемого тросом длиной 2,5 м, подвешен груз массой 120 кг. Найдите силы, действующие на трос и стержень.
К задаче 1
Введем оси координат и напишем по каждой из осей уравнение по второму закону Ньютона. Удобно выбрать такое расположение координатных осей, как показано на рисунке. Тогда по оси :
Здесь угол .
По оси :
Из первого уравнения можем найти силу натяжения троса:
Тогда
Где
Подставим:
Теперь подставим численные данные:
Также нужно определить силу :
Ответ: Н, Н
Задача 2. Тяжелый однородный шар подвешен на нити, конец которой закреплен на вертикальной стене. Точка прикрепления шара к нити находится на одной вертикали с центром шара. Каков должен быть коэффициент трения между шаром и стенкой, чтобы шар находился в равновесии?
К задаче 2
Понятно, что из положения 1, как показано на рисунке, шар стремится повернуться в положение 2 – повернуться относительно своего центра масс. Не дает этого сделать сила трения, направленная вверх вдоль стенки. Введем систему координат и распишем уравнения по второму закону по координатным осям, а кроме того, добавим уравнение равновесия моментов. Ось направим вверх, а ось – вправо. Тогда по горизонтальной оси:
По вертикальной оси:
Правило моментов ( – плечо обеих сил относительно центра масс шара):
Чтобы шар не проворачивался, нужно, чтобы сила трения была больше чем , тогда
Или
Ответ: .
Задача 3. Какую силу надо приложить к рукоятке молотка, чтобы вырвать гвоздь, если сила сопротивления гвоздя 160 Н? Длина рукоятки 32 см. Расстояние от конца молотка до гвоздя 8 см.
К задаче 3. Вырываем гвоздь
Сила сопротивления гвоздя направлена внутрь дерева, в которое он вбит. То есть по отношению к точке упора молотка пытается этот молоток вращать против часовой стрелке. Сила, с которой мы давим на рукоять, наоборот, вращает рукоять по часовой стрелке. Тогда составим правило моментов относительно точки упора:
Ответ: 40 Н
Задача 4. Между двумя одинаковыми ящиками, стоящими на полу, вставлена палка, немного не доходящая до пола. К верхнему концу палки приложена горизонтальная сила. Какой из ящиков сдвинется быстрее? Рассмотреть два случая: трение между ящиком и полом отсутствует; трение между ящиками и полом есть.
К задаче 4. Исходное положение палки
Первый случай: трения нет. Тогда, как только мы начнем воздействовать на ящики с силой любой величины, они сразу сдвинутся с места, одновременно, потому что нет никакого противодействия этой силе.
Второй случай: трение есть. Тогда сила трения одинакова для обоих ящиков, ведь по условию они идентичны. Следовательно, сдвинется быстрее тот ящик, для которого мы эту силу трения преодолеем быстрее, то есть тот, на который палка давит с большей силой.
К задаче 4. Плечи сил, действующих на ящики
Палка упрется в правый ящик, точкой опоры для нее будет его верхний левый угол, значит, плечо силы будет равно , как показано на рисунке. В левый ящик палка упрется своим нижним концом, следовательно, плечом будет расстояние . Тогда
Так как , то – быстрее сдвинется правый ящик.
Статика. Правило моментов -2
В задачах, связанных с равновесием тел, нужно, как правило, найти две силы (или больше) которые стремятся это тело повернуть по и против часовой стрелки. Если моменты этих сил равны, тело будет находиться в равновесии. А чтобы рассчитать момент, нужно также правильно определить плечо силы: это расстояние от оси вращения до линии действия силы.
Задача
К задаче 1
Эта задача легко решается, если применить понятие центра масс. То есть будем считать всю массу доски сосредоточенной в одной точке – центре масс. Центр масс – такая точка, что если в ней установить опору, то предмет (в данном случае, доска) будет находиться в равновесии, потому что суммарный момент всех элементарных масс предмета относительно этой точки равен нулю. У однородных предметов (доска, балка, рельс, бревно, труба) центр масс находится посередине. Действительно, если подпереть ровную, одинаковую по толщине доску посередине – она будет находиться в равновесии. Это знают даже самые маленькие: ведь они любят кататься на качелях. Вернемся к задаче. Итак, раз доска однородна (ее толщина и ширина одинаковы по всей длине ), то ее центр масс находится в центре, а мы по условию подперли доску на расстоянии длины. Следовательно, если считать всю массу доски сосредоточенной в центре масс, то по правилу моментов
Ответ: доску придется удерживать с силой 100 Н, равной ее весу.
Задача 2. Бревно длиной м можно уравновесить в горизонтальном положении на подставке, отстоящей на м от его толстого конца. Если же подставка находится в м от толстого конца и на тонкий конец сядет рабочий массой 60 кг, бревно снова будет в равновесии. Определите массу бревна.
К задаче 2
Снова прибегнем к помощи центра масс. Если в первом случае бревно находилось в равновесии, то центр масс находится в трех метрах от толстого конца бревна. Будем считать весь вес бревна сосредоточенным в центре масс, тогда для второй ситуации запишем правило моментов:
Ответ: кг
Задача 3. Рельс длиной 10 м и массой 900 кг поднимают на двух параллельных тросах. Найдите силу натяжения тросов, если один из них укреплен на конце рельса, а другой – на расстоянии 1 м от другого конца.
К задаче 3
Составим два уравнения: сначала относительно точки крепления одного троса, затем – другого. Тогда для точки :
Относительно точки :
Из первого уравнения получим силу натяжения правого троса:
Из второго уравнения
Ответ: кН, кН.
Задача 4. К балке массой 200 кг и длиной 5 м подвешен груз массой 350 кг на расстоянии 3 м от одного из концов. Балка своими концами лежит на опорах. Каковы силы давления на каждую из опор?
Задача 4
Задача очень похожа на предыдущую. Снова запишем правило моментов относительно точек обеих опор.
Относительно точки :
Относительно точки :
Тогда:
Ответ: кН, кН.
Правило моментов 📕- Физика
С тех пор как Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский ученый П. Вариньон придал ему более общую форму, воспользовавшись понятием момента силы.
Моментом силы называется физическая величина, равная произведению силы на ее плечо:
M = Fl, (21.1)
Где
М — момент силы, F — сила, L — плечо силы.
Докажем, что рычаг находится в равновесии, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки, т. е.
М1 =
М2 (21.2)
Для доказательства этого равенства воспользуемся формулой (20.1). Используя свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), перепишем эту формулу в виде
F1l1 = F2l2
Но F2l2 = M2 — момент силы, стремящейся повернуть рычаг по часовой стрелке (см. рис. 50), а F1l1 = M1 — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, M1 = M2, что и требовалось доказать.
Формула (21.2) выражает Правило моментов. Это правило справедливо для любого твердого тела, способного вращаться вокруг закрепленной оси. Таково, например, тело, изображенное
на рисунке 53. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой O. Плечом силы F1 в данном случае является расстояние L1 от оси вращения до линии действия силы.
 В общем случае момент силы находят следующим образом. Сначала проводят линию действия силы. Затем из точки O, через которую проходит ось вращения, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы.
В общем случае момент силы находят следующим образом. Сначала проводят линию действия силы. Затем из точки O, через которую проходит ось вращения, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы.
Умножив силу на ее плечо, получают момент силы относительно оси вращения.
Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от ее плеча. Именно поэтому, например, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. С помощью небольшой силы при этом создают значительный момент, и дверь открывается.
Открыть ее, оказывая давление около петель, значительно труднее. По той же причине гайку легче отворачивать более длинным гаечным ключом, шуруп легче вывернуть с помощью отвертки с более широкой ручкой и т. д.
Единицей момента силы в СИ является ньютон-метр (1 Н*м). Это момент силы 1 Н, имеющей плечо 1 м.
1. Что называют моментом силы? 2. Сформулируйте правило моментов. 3. Что характеризует момент силы? 4. Почему ручку у двери прикрепляют на противоположной от петель стороне? 5. Как находится момент силы в общем случае?
6. Что принимают за единицу момента силы?
Статика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Основы статики
К оглавлению…
Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:
- Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
- Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться. В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
- Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Иными словами, векторная сумма всех сил, приложенных к телу должна быть равна нолю:

Момент силы. Правило моментов
К оглавлению…
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие — момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле:

Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками.
Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:


При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).
Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.
Алгоритм решения задач на правило моментов (задач по статике):
- Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
- Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
- Записать правило моментов относительно данной оси, на забывая про правило знаков.
- При необходимости записать также условие согласно которому равнодействующая сила равна нолю.
- Выразить искомую силу.
Рычаги и блоки
К оглавлению…
Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике:
- Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
- Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
- Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
- Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
- Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.
Центр тяжести тела
К оглавлению…
Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).
Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:
1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.
2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:

где: l1 – расстояние от центра масс до тела с массой m1, а l2 – до тела с массой m2.
3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:

Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).
4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.
5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:
Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:

Часто в физике приходится решать задачи на расчет равновесия в сложных системах, имеющих множество действующих сил, рычагов и осей вращения. В этом случае проще всего использовать понятие момента силы. В данной статье приводятся все необходимые формулы с подробными объяснениями, которые следует использовать для решения задач названного типа.
О чем пойдет речь?

Многие люди наверняка обращали внимание, что если воздействовать с какой-либо силой на предмет, закрепленный в некоторой точке, то он начинает вращаться. Ярким примером может служить дверь в дом или в комнату. Если ее взять за ручку и толкнуть (приложить силу), то она начнет открываться (поворачиваться на петлях). Этот процесс представляет собой проявление в быту действия физической величины, которая получила название момента силы.
Из описанного примера с дверью следует, что рассматриваемая величина указывает на способность силы совершать вращение, что является ее физическим смыслом. Также эту величину называют моментом кручения.
Определение момента силы
Перед тем как дать определение рассматриваемой величине, приведем простой рисунок.
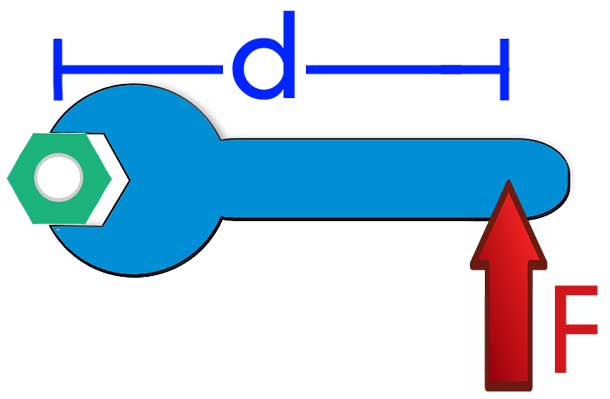
Итак, на рисунке изображен рычаг (синего цвета), который закреплен на оси (зеленый цвет). Этот рычаг имеет длину d, а к его концу приложена сила F. Что будет в этом случае происходить с системой? Верно, рычаг начнет вращаться против часовой стрелки, если смотреть на него сверху (отметим, что если напрячь немного свое воображение и представить, что взгляд направлен снизу на рычаг, то он будет вращаться по часовой стрелке).
Пусть точка закрепления оси называется O, а точка приложения силы — P. Тогда, можно записать следующее математическое выражение:
OP¯* F¯ = M¯FO.
Где OP¯ — это вектор, который направлен от оси к концу рычага, он также называется рычагом силы, F¯ — это вектор приложенной силы к точке P, а M¯FO — это момент силы относительно точки O (оси). Эта формула является математическим определением рассматриваемой физической величины.
Направление момента и правило правой руки
Выражение выше представляет собой векторное произведение. Как известно, его результатом также является вектор, который перпендикулярен плоскости, проходящей через соответствующие вектора-множители. Этому условию удовлетворяют два направления величины M¯FO (вниз и вверх).
Чтобы однозначно его определить, следует воспользоваться так называемым правилом правой руки. Его можно сформулировать таким образом: если согнуть в полудугу четыре пальца правой руки и направить эту полудугу так, чтобы она шла вдоль первого вектора (первый множитель в формуле) и направлялась к концу второго, тогда оттопыренный вверх большой палец укажет направление момента кручения. Отметим также, что перед тем как использовать это правило, необходимо установить умножаемые вектора так, чтобы они выходили из одной точки (их начала должны совпадать).
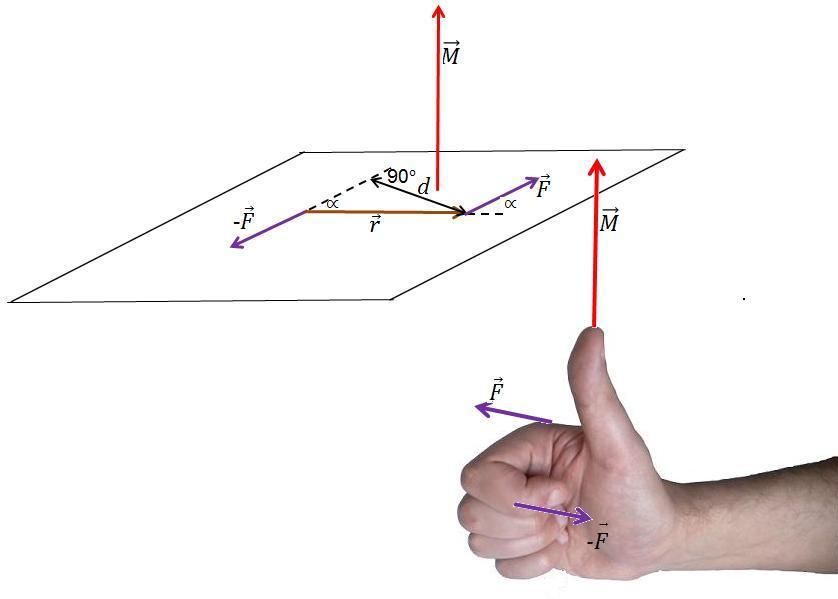
В случае рисунка в предыдущем пункте можно сказать, применив правило правой руки, что момент силы относительно оси будет направлен вверх, то есть на нас.
Помимо отмеченного способа определения направления вектора M¯FO, существует еще два. Приведем их:
- Момент кручения будет направлен таким образом, что если смотреть с конца его вектора на вращающийся рычаг, то последний будет двигаться против хода стрелки часов. Общепринято считать это направление момента положительным при решении разного рода задач.
- Если закручивать буравчик по часовой стрелке, то момент кручения будет направлен в сторону движения (углубления) буравчика.
Все приведенные определения являются эквивалентными, поэтому каждый может выбрать то, которое удобно для него.
Итак, было выяснено, что направление момента силы является параллельным оси, вокруг которой вращается соответствующий рычаг.
Приложенная под углом сила
Рассмотрим рисунок, который приведен ниже.
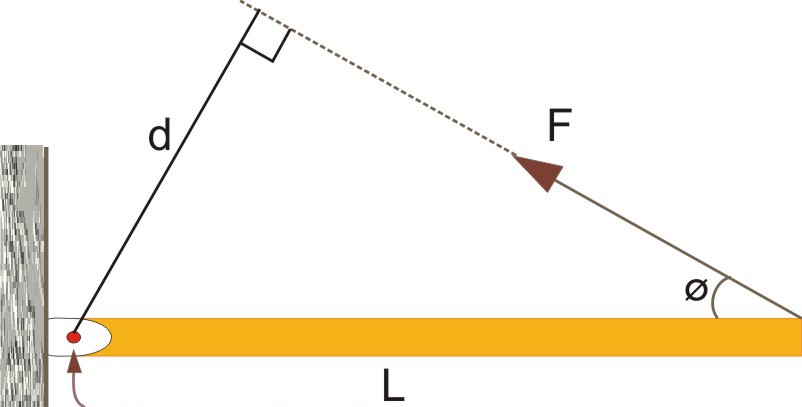
Здесь мы также видим рычаг длиной L, закрепленный в точке (указана стрелкой). На него действует сила F, однако, направлена она под некоторым углом Φ (фи) к горизонтальному рычагу. Направление момента M¯FO в этом случае будет таким же, как и на предыдущем рисунке (на нас). Чтобы вычислить абсолютное значение или модуль этой величины, необходимо воспользоваться свойством векторного произведения. Согласно ему для рассматриваемого примера, можно записать выражение: MFO = L*F*sin(180o-Φ) или, воспользовавшись свойством синуса, перепишем:
MFO = L*F*sin(Φ).
На рисунке приведен также достроенный прямоугольный треугольник, сторонами которого являются сам рычаг (гипотенуза), линия действия силы (катет) и сторона длиной d (второй катет). Учитывая, что sin(Φ) = d/L, указанная формула примет вид: MFO = d*F. Видно, что дистанция d — это расстояние от точки закрепления рычага до линии действия силы, то есть d — рычаг силы.
Обе рассмотренные в этом пункте формулы, которые следуют непосредственно из определения момента кручения, являются полезными при решении практических задач.
Единицы измерения момента кручения
Воспользовавшись определением, можно установить, что величина MFO должна измеряться в ньютонах на метр (Н*м). Действительно, в виде этих единиц она и используется в СИ.
Отметим, что Н*м — это единица измерения работы, которая выражается в джоулях, как и энергия. Тем не менее джоули для концепции момента силы не используют, поскольку эта величина отражает именно возможность осуществления последней. Однако связь с единицей работы имеется: если в результате действия силы F выполнен полный поворот рычага вокруг его точки вращения O, тогда совершенная работа будет равна A = MFO*2*pi (2*pi — угол в радианах, который соответствует 360o). В этом случае единицу измерения момента MFO можно выразить в джоулях на радиан (Дж/рад.). Последняя, наряду с Н*м, также используется в системе СИ.
Теорема Вариньона
В конце XVII века французский математик Пьер Вариньон, изучая равновесие систем с рычагами, впервые сформулировал теорему, которая теперь носит его фамилию. Она формулируется так: суммарный момент нескольких сил равен моменту результирующей одной силы, которая приложена к некоторой точке относительно той же оси вращения. Математически ее можно записать следующим образом:
M¯1+M¯2+…+M¯n = M¯ = d¯*∑ni=1(F¯i) = d¯*F¯.
Эту теорему удобно использовать для расчета моментов кручения в системах с несколькими действующими силами.
Далее приведем пример использования приведенный выше формул для решения задач по физике.
Задача с гаечным ключом
Один из ярких примеров демонстрации важности учета момента силы является процесс откручивания гаек ключом. Чтобы открутить гайку, нужно приложить некоторый момент кручения. Необходимо рассчитать, какую силу следует приложить в точке A, чтобы начать откручивать гайку, если эта сила в точке B равна 300 Н (см. рисунок ниже).
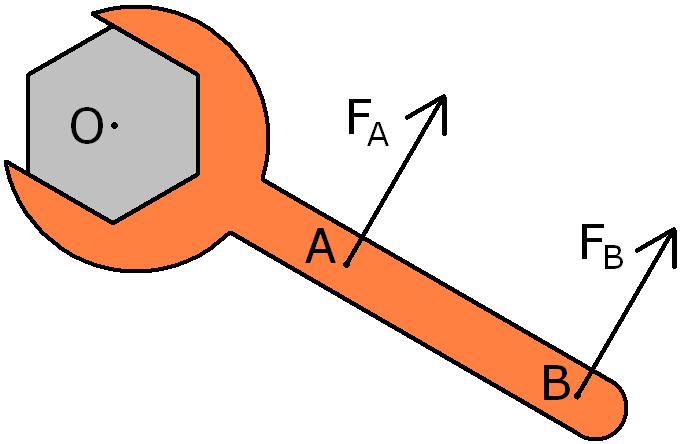
Из приведенного рисунка следуют две важные вещи: во-первых, расстояние OB в два раза больше, чем OA; во-вторых, силы FA и FB направлены перпендикулярно к соответствующему рычагу с осью вращения, совпадающей с центром гайки (точка O).
Момент кручения для этого случая можно записать в скалярной форме так: M = OB*FB = OA*FA. Поскольку OB/OA = 2, то это равенство будет выполняться только тогда, когда FA будет больше FB в 2 раза. Из условия задачи получаем, что FA = 2*300 = 600 Н. То есть, чем больше длина ключа, тем легче откручивать гайку.
Задача с двумя шарами разной массы
На рисунке ниже приведена система, которая находится в равновесии. Необходимо найти положение точки опоры, если длина доски равна 3 метра.

Так как система находится в равновесии, то сумма моментов всех сил равна нулю. На доску действуют три силы (веса двух шаров и сила реакции опоры). Поскольку сила опоры не создает момента кручения (длина рычага равна нулю), то остается только два момента, создаваемых весом шаров.
Пусть точка равновесия находится на расстоянии x от края, где лежит шар массой 100 кг. Тогда можно записать равенство: M1-M2 = 0. Поскольку вес тела определяется по формуле m*g, тогда имеем: m1*g*x — m2*g*(3-x) =0. Сокращаем g и подставляем данные, получаем: 100*x — 5*(3-x) = 0 => x = 15/105= 0,143 м или 14,3 см.
Таким образом, чтобы система находилась в равновесии, необходимо установить опорную точку на расстоянии 14,3 см от края, где будет лежать шар массой 100 кг.
Правило моментов для мощностей — Студопедия
В этом случае электрические нагрузки в узлах задаются расчетными мощностями. Переход от строгих выражений (12.13), (12.14) для токов к аналогичным выражениям для мощностей можно выполнить при введении допущения о равенстве напряжений во всех точках сети:

|
что равносильно неучету потерь мощности на участках сети. Действительно, при условии (12.17) выражение

|
обращается в нуль.
Теперь, если умножить левые и правые части выражений (12.13) и (12.14) на множитель  , то имеем
, то имеем

|
выражения для сопряженных мощностей

|
или, выполнив в формуле (12.18) операцию сопряжения, окончательно получим

|
В случае неравенства напряжений ( ) источников уравнительный поток мощности определяем по соотношению
) источников уравнительный поток мощности определяем по соотношению

|
где  – среднее напряжение источников. Тогда потоки мощностей головных участков вычисляем в виде
– среднее напряжение источников. Тогда потоки мощностей головных участков вычисляем в виде

|
Для проверки правильности расчетов потоков головных участков рекомендуется проверить выполнение баланса мощностей в электрической сети:

|
т. е. сумма мощностей, поступающих в сеть, должна быть равна сумме мощностей нагрузок в ее узлах. Аналогично должен выполняться баланс токов в сети:

|
Формулы моментов — определения, уравнения и примеры
СМОТРЕТЬ БОЛЬШЕ
Эффект поворота силы известен как момент.Это произведение силы, умноженное на перпендикулярное расстояние от линии воздействия силы до точки поворота или точки, в которой объект будет поворачиваться. СИ единица момента силы — Ньютон-метр (Нм). Это векторная величина.
Его направление задается правилом правого захвата, перпендикулярным плоскости силы и точки поворота, параллельной оси вращения.
𝝉 = F × d
где 𝝉 — момент силы / крутящего момента
F — сила
d — перпендикулярное расстояние от линии действия силы до оси
Пример:
Момент силы 10 Н около 3 Нм.Расстояние от точки приложения силы до точки равно
Момент силы = сила × расстояние
⇒ 3 Нм = 10 Н × r
⇒ r = 0,3 м
Вопрос:
Если получен однородный стержень массой 8 кг разворачивается на одном конце, каков чистый момент силы на планке.

Adam [1] — это адаптивный алгоритм оптимизации скорости обучения, разработанный специально для обучения глубоких нейронных сетей. Впервые опубликованный в 2014 году, Адам был представлен на очень престижной конференции для практиков глубокого обучения — ICLR 2015. В документе содержались некоторые очень многообещающие диаграммы, демонстрирующие огромный прирост производительности с точки зрения скорости обучения. Однако через некоторое время люди начали замечать, что в некоторых случаях Адам действительно находит худшее решение, чем стохастический градиентный спуск.Много исследований было сделано для решения проблем Адама.
Алгоритмы используют возможности методов адаптивных скоростей обучения, чтобы найти индивидуальные скорости обучения для каждого параметра. Он также имеет преимущества Adagrad [10], который действительно хорошо работает в условиях с редкими градиентами, но борется за невыпуклую оптимизацию нейронных сетей, и RMSprop [11], который решает некоторые проблемы Adagrad и работает действительно ну в настройках он-лайн. Популярность Адама растет в геометрической прогрессии, согласно статье Андрея Карпати «Взгляд на тенденции в машинном обучении».
В этой статье я сначала представлю алгоритм Адама, представленный в оригинальной статье, а затем пройдусь по последним исследованиям, которые демонстрируют некоторые потенциальные причины, по которым алгоритмы работают хуже, чем классический SGD в некоторых областях, и предоставляют несколько решений, которые сужают разрыв между SGD и Адамом.
Адама можно рассматривать как комбинацию RMSprop и Stochastic Gradient Descent с импульсом. Он использует квадратные градиенты для масштабирования скорости обучения, как RMSprop, и использует преимущество импульса, используя скользящее среднее значение градиента, а не сам градиент, как SGD с импульсом.Давайте подробнее рассмотрим, как это работает.
Адам — это метод адаптивной скорости обучения, то есть он рассчитывает индивидуальные скорости обучения для различных параметров. Его название происходит от адаптивной оценки моментов, и причина, по которой он назван, заключается в том, что Адам использует оценки первого и второго моментов градиента, чтобы адаптировать скорость обучения для каждого веса нейронной сети. Теперь, что такое момент? N-й момент случайной величины определяется как ожидаемое значение этой переменной в степени n.Более формально:
м — момент, X-случайная величина.Впервые может быть довольно сложно понять эту идею, поэтому, если вы не поймете ее полностью, вам все равно придется продолжать, вы все равно сможете понять, как работают алгоритмы. Обратите внимание, что градиент функции стоимости нейронной сети можно считать случайной величиной, поскольку он обычно оценивается на некотором небольшом случайном пакете данных. Первый момент — среднее значение, а второй момент — нецентрированная дисперсия (то есть мы не вычитаем среднее значение при расчете дисперсии).Позже мы увидим, как мы используем эти значения, сейчас мы должны решить, как их получить. Для оценки моментов Адам использует экспоненциально скользящие средние, вычисленные по градиенту, оцененному в текущей мини-партии:
Скользящие средние градиента и квадрат градиента.Где m и v — скользящие средние, g — градиент текущей мини-партии, а бетас — новые введенные гиперпараметры алгоритма. Они имеют действительно хорошие значения по умолчанию 0,9 и 0,999 соответственно. Почти никто никогда не меняет эти значения.Векторы скользящих средних инициализируются нулями на первой итерации.
Чтобы увидеть, как эти значения соотносятся с моментом, определенным как в первом уравнении, давайте посмотрим на ожидаемые значения наших скользящих средних. Так как m и v являются оценками первого и второго моментов, мы хотим иметь следующее свойство:
Ожидаемые значения оценщиков должны равняться параметру, который мы пытаемся оценить, как это бывает, параметр в нашем случае также является ожидаемое значение.Если бы эти свойства сохранялись, это означало бы, что у нас есть объективных оценок . (Чтобы узнать больше о статистических свойствах различных оценщиков, обратитесь к книге глубокого обучения Яна Гудфеллоу, глава 5 «Основы машинного обучения»). Теперь мы увидим, что это не относится к нашим скользящим средним. Поскольку мы инициализируем средние значения нулями, оценки смещены к нулю. Докажем, что для m (доказательство для v было бы аналогичным). Чтобы доказать, что нам нужно сформулировать m до самого первого градиента.Давайте попробуем развернуть пару значений m, чтобы увидеть шаблон, который мы будем использовать:
Как вы можете видеть, чем дальше мы расширяем значение m, тем меньше первых значений градиентов вносят вклад в общее значение , поскольку они умножаются на все меньше и меньше бета. Получив этот шаблон, мы можем переписать формулу для нашего скользящего среднего:
Теперь давайте посмотрим на ожидаемое значение m, чтобы увидеть, как оно соотносится с истинным первым моментом, поэтому мы можем исправить несоответствие двух :
Поправка смещения для первой оценки импульсаВ первом ряду мы используем нашу новую формулу для скользящего среднего, чтобы расширить m.Далее мы приближаем g [i] с помощью g [t]. Теперь мы можем вывести его из суммы, поскольку теперь оно не зависит от меня. Поскольку приближение имеет место, ошибка C появляется в формуле. В последней строке мы просто используем формулу для суммы конечного геометрического ряда. Из этого уравнения следует отметить две вещи.
- У нас есть предвзятая оценка. Это относится не только к Адаму, но и к алгоритмам, использующим скользящие средние (SGD с импульсом, RMSprop и т. Д.).
- Это не будет иметь большого эффекта, если это не начало обучения, потому что значение бета в силу t быстро стремится к нулю.
Теперь нам нужно исправить оценщик, чтобы ожидаемое значение было тем, которое нам нужно. Этот шаг обычно называют коррекцией смещения. Окончательные формулы для нашей оценки будут следующими:
Оценки с поправкой на смещение для первого и второго моментов.Осталось только использовать эти скользящие средние для индивидуального масштабирования скорости обучения для каждого параметра. То, как это делается в Adam, очень просто, чтобы выполнить обновление веса, мы делаем следующее:
Где w — вес модели, eta (похоже на букву n) — размер шага (он может зависеть от итерации).И это все, это правило обновления для Адама. Некоторым людям легче понять такие концепции в коде, поэтому вот возможная реализация Адама на python:
Есть два небольших варианта Адама, которых я не вижу на практике, но они реализованы в основном глубоко рамки обучения, поэтому стоит кратко их упомянуть.
Первый, называемый Adamax , был представлен авторами Адама в той же статье. Идея Adamax состоит в том, чтобы рассматривать значение v как норму L2 отдельных текущих и прошлых градиентов.Мы можем обобщить его до правила обновления Lp, но оно становится довольно нестабильным при больших значениях p. Но если мы используем специальный случай нормы L-бесконечности, это приводит к удивительно стабильному и хорошо работающему алгоритму. Вот как реализовать Adamax с помощью python:
Второй немного сложнее понять, он называется Надам [6]. Надам был опубликован Тимоти Дозатом в газете «Включение Нестерова Импульса в Адама». Как следует из названия, идея состоит в том, чтобы использовать термин импульса Нестерова для первых скользящих средних.Давайте рассмотрим правило обновления SGD с импульсом:
SGD с правилом обновления импульсаКак показано выше, правило обновления эквивалентно выполнению шага в направлении вектора импульса и затем шагу в направлении градиента. Однако шаг импульса не зависит от текущего градиента, поэтому мы можем получить более качественное направление шага градиента, обновив параметры с шагом импульса перед вычислением градиента. Для этого мы модифицируем обновление следующим образом:
f — функция потерь для оптимизации.Итак, с ускоренным импульсом Нестерова мы сначала делаем большой прыжок в направлении предыдущего накопленного градиента, а затем измеряем градиент, в котором мы оказались, чтобы сделать коррекцию. В лекционных заметках cs231n есть отличная визуализация:
sourec: лекционные заметки cs231n.Тот же метод можно включить в Адама, изменив первое скользящее среднее на ускоренный импульс Нестерова. Здесь можно применить одну вычислительную хитрость: вместо обновления параметров, чтобы сделать шаг импульса и изменить обратно, мы можем достичь того же эффекта, применяя шаг импульса временного шага t + 1 только один раз, во время обновления предыдущего временного шага. т вместо т + 1.Используя этот трюк, реализация Надама может выглядеть следующим образом:
Здесь я перечислю некоторые свойства Адама, для доказательства того, что они истинны, обратитесь к статье.
- Фактический размер шага, принятый Адамом в каждой итерации, приблизительно ограничен гиперпараметром размера шага. Это свойство добавляет интуитивное понимание к предыдущему гиперпараметру скорости неинтуитивного обучения.
- Размер шага правила обновления Адама не зависит от величины градиента, что очень помогает при прохождении областей с крошечными градиентами (такими как седловые точки или овраги).В этих областях SGD пытается быстро перемещаться по ним.
- Adam был разработан, чтобы объединить преимущества Adagrad, который хорошо работает с разреженными градиентами, и RMSprop, который хорошо работает в онлайн-настройках. Наличие обоих из них позволяет нам использовать Адама для более широкого круга задач. Адама также можно рассматривать как комбинацию RMSprop и SGD с импульсом.
Когда Адам был впервые представлен, люди были очень взволнованы его силой. Бумага содержала несколько очень оптимистичных диаграмм, показывающих огромный прирост производительности с точки зрения скорости обучения:
источник: оригинальная бумага АдамаЗатем бумага Надама представила диаграммы, которые показали еще лучшие результаты:
источник: бумага НадамаОднако через некоторое время люди начали отмечая, что, несмотря на превосходное время обучения, Адам в некоторых областях не сходится к оптимальному решению, поэтому для некоторых задач (таких как классификация изображений в популярных наборах данных CIFAR) современные результаты все еще достигаются только при применении SGD с импульсом ,Более того, Wilson et. [9] показали в своей статье «Предельное значение адаптивных градиентных методов в машинном обучении», что адаптивные методы (такие как Адам или Ададелта) не обобщают так же, как SGD с импульсом при тестировании на разнообразном наборе задач глубокого обучения, отговаривать людей использовать популярные алгоритмы оптимизации. С тех пор было проведено много исследований, чтобы проанализировать плохое обобщение Адама, пытающегося заставить его сократить разрыв с SGD.
Нитиш Шириш Кескар и Ричард Сошер в своей статье «Повышение производительности обобщения путем переключения с Адама на SGD» [5] также показали, что, переключаясь на SGD во время обучения, они смогли получить лучшую мощность обобщения, чем при использовании одного Адама. ,Они предложили простое исправление, которое использует очень простую идею. Они заметили, что на более ранних этапах обучения Адам все еще опережает SGD, но позже обучение насыщается. Они предложили простую стратегию, которую они назвали SWATS , в которой они начинают обучать глубокую нейронную сеть с Адамом, но затем переключаются на SGD, когда достигаются определенные критерии. Им удалось достичь результатов, сопоставимых с SGD с импульсом.
Одна важная вещь при выяснении того, что не так с Адамом, заключалась в анализе его конвергенции.Авторы доказали, что Адам сходится к глобальному минимуму в выпуклых настройках в их оригинальной статье, однако, несколько статей позже обнаружили, что их доказательство содержало несколько ошибок. Block et. Я [7] утверждал, что они обнаружили ошибки в исходном анализе сходимости, но все же доказал, что алгоритм сходится и предоставил доказательства в своей статье. Еще одна недавняя статья от сотрудников Google была представлена на ICLR 2018 и даже получила награду за лучшую статью. Чтобы углубиться в их работу, я должен сначала описать структуру, используемую авторами Адама для доказательства того, что она сходится для выпуклых функций.
В 2003 году Мартин Зинкевич представил задачу онлайн-выпуклого программирования [8]. В представленных настройках мы имеем последовательность выпуклых функций c1, c2 и т. Д. (Функция потери выполняется в i-й мини-партии в случае глубокой оптимизации обучения). Алгоритм, решающий проблему (Адам) в каждой временной метке t, выбирает точку x [t] (параметры модели) и затем получает функцию потерь c для текущей временной метки. Этот параметр приводит к множеству реальных проблем, например, читайте введение в статью.Чтобы понять, насколько хорошо работает алгоритм, значение сожаления алгоритма после T раундов определяется следующим образом:
Сожаление об алгоритме в онлайн-выпуклом программировании, где R — сожаление, c — функция потерь в t-й мини-партии, w — вектор параметров модели (весов), а w star — оптимальное значение вектора весов. Наша цель — доказать, что сожаление об алгоритме R (T) = O (T) или меньше, что означает, что в среднем модель сходится к оптимальному решению. Мартин Зинкевич в своей работе доказал, что градиентный спуск сходится к оптимальным решениям в этой постановке, используя свойство выпуклых функций:
. Известное свойство выпуклых функций.Тот же подход и структура использовали авторов Адама, чтобы доказать, что их алгоритм сходится к оптимальным решениям. Редди и соавт. [3] обнаружили несколько ошибок в своем доказательстве, главная из которых заключается в значении, которое отражено в работах Адама и Совершенствования Адама, подтверждающих сходимость:
Где V определяется как абстрактная функция, которая масштабирует скорость обучения для параметров, которые различаются для каждый отдельный алгоритм. Для Адама это скользящие средние градиентов прошлого квадрата, для Адаграда это сумма всех градиентов прошлого и текущего, для SGD — всего 1.Авторы обнаружили, что для того, чтобы доказательство сработало, это значение должно быть положительным. Легко видеть, что для SGD и Адаграда это всегда положительно, однако для Адама (или RMSprop) значение V может действовать неожиданно. Они также представили пример, в котором Адам не может сходиться:
Адам терпит неудачу в этой последовательностиДля этой последовательности легко увидеть, что оптимальное решение — x = -1, однако, как показывают авторы, Адам сходится к крайне неоптимальному значение x = 1. Алгоритм получает большой градиент C один раз каждые 3 шага, и в то время как другие 2 шага он наблюдает градиент -1, который перемещает алгоритм в неправильном направлении.Поскольку значения размера шага часто уменьшаются с течением времени, они предложили фиксировать максимальное значение V и использовать его вместо скользящего среднего для обновления параметров. Полученный алгоритм называется Amsgrad. Мы можем подтвердить их эксперимент с этой короткой записной книжкой, которую я создал, в которой показано, что различные алгоритмы сходятся в последовательности функций, определенной выше.
Amsgrad без коррекции смещенияНасколько это помогает на практике с реальными данными? К сожалению, я не видел ни одного случая, когда это помогло бы получить лучшие результаты, чем Адам.Филип Корзенёвский в своем посте описывает эксперименты с Амсградом, которые показывают результаты, аналогичные Адаму. Сильвен Гуггер и Джереми Ховард в своем посте показывают, что в своих экспериментах Амстердам на самом деле работает даже хуже, чем Адам. Некоторые рецензенты статьи также указали, что проблема может заключаться не в самом Адаме, а в структуре, которую я описал выше, для анализа сходимости, который не допускает значительной настройки гиперпараметров.
Илья Лощилов и Фрэнк Хаттер [4] предложили Адаму статью «Исправление регуляризации снижения веса в Адаме» [4].Эта статья содержит много вкладов и понимания Адама и снижения веса. Во-первых, они показывают, что, несмотря на распространенное мнение, регуляризация L2 не совпадает с затуханием веса, хотя она эквивалентна стохастическому градиентному спуску. Способ снижения веса был введен еще в 1988 году:
Где лямбда — гиперпараметр снижения веса для настройки. Я немного изменил обозначения, чтобы соответствовать остальной части поста. Как определено выше, снижение веса применяется на последнем этапе, при обновлении веса, штрафуя большие веса.Традиционно для SGD он реализуется через регуляризацию L2, в которой мы модифицируем функцию стоимости, чтобы она содержала норму L2 вектора весов:
Исторически методы стохастического градиентного спуска унаследовали этот способ реализации регуляризации спада веса, как и Адам , Однако регуляризация L2 не эквивалентна снижению веса для Адама. При использовании регуляризации L2 штраф, который мы используем для больших весов, масштабируется с помощью скользящего среднего от прошлого и текущего квадратов градиентов, и поэтому веса с большой типичной величиной градиента регулируются на меньшую относительную величину, чем другие веса.Напротив, снижение веса регулирует все веса одним и тем же фактором. Чтобы использовать снижение веса с Адамом, нам нужно изменить правило обновления следующим образом:
Правило обновления Адама с уменьшением весаПоказав, что эти типы регуляризации отличаются для Адама, авторы продолжают показывать, насколько хорошо оно работает с ними обоими. Разница в результатах очень хорошо показана на диаграмме из статьи:
Ошибка теста Top-1 ResNet на CIFAR-10, измеренная после 100 эпохНа этих диаграммах показана связь между скоростью обучения и методом регуляризации.Цвет представляет высокий уровень, ошибка теста для этой пары гиперпараметров. Как мы видим выше, не только Адам с уменьшением веса получает гораздо меньшую погрешность теста, но на самом деле помогает разделить скорость обучения и гиперпараметр регуляризации. На левой картинке мы можем видеть, что если мы изменим параметры, скажем, скорость обучения, то для того, чтобы снова достичь оптимальной точки, нам также потребуется изменить коэффициент L2, показывая, что эти два параметра взаимозависимы. Эта зависимость способствует тому, что настройка гиперпараметров иногда является очень сложной задачей.На правом рисунке мы видим, что, пока мы находимся в некотором диапазоне оптимальных значений для одного параметра, мы можем изменить другой независимо.
Другой вклад автора статьи показывает, что оптимальное значение, используемое для снижения веса, на самом деле зависит от количества итераций во время тренировки. Чтобы справиться с этим фактом, они предложили простую адаптивную формулу для настройки снижения веса:
, где b — размер партии, B — общее количество тренировочных точек за эпоху, а T — общее количество эпох.Это заменяет лямбда-гиперпараметр лямбда новым лямбда-нормализованным.
Авторы даже не остановились на этом, после исправления снижения веса, они попытались применить график скорости обучения с теплыми перезапусками с новой версией Адама. Тепловые перезапуски очень помогли при стохастическом градиентном спуске, я больше об этом говорю в своем посте «Улучшение нашей работы со скоростью обучения». Но ранее Адам сильно отставал от SGD. С новым снижением веса Адам получил намного лучшие результаты с перезапусками, но он все еще не так хорош, как SGDR.
Еще одна попытка исправить Адама, которую я практически не видел на практике, предложена Zhang et. в своей работе «Нормализованный Адам, сохраняющий направление» [2]. В статье отмечены две проблемы с Адамом, которые могут вызвать худшее обобщение:
- Обновления SGD лежат в диапазоне исторических градиентов, тогда как для Адама это не так. Это различие также наблюдалось в уже упомянутой работе [9].
- Во-вторых, хотя величины обновлений параметров Адама не зависят от удаления накипи градиента, влияние обновлений на одну и ту же общую сетевую функцию все еще зависит от величин параметров.
Для решения этих проблем авторы предлагают алгоритм, который они называют Нормализованным сохраняющим направление Адамом. Алгоритмы настраивают Адама следующими способами. Во-первых, вместо оценки средней величины градиента для каждого отдельного параметра он оценивает среднеквадратическую норму L2 вектора градиента. Поскольку теперь V является скалярным значением, а M является вектором в том же направлении, что и W, направление обновления является отрицательным направлением m и, следовательно, находится в диапазоне исторических градиентов w.Для второго алгоритмы перед использованием градиента проецируют его на единичную сферу, а затем после обновления веса нормализуются по их норме. Для более подробной информации следуйте их статье.
Адам, безусловно, является одним из лучших алгоритмов оптимизации для глубокого обучения, и его популярность очень быстро растет. В то время как люди заметили некоторые проблемы с использованием Адама в определенных областях, исследования продолжают работать над решениями, чтобы привести результаты Адама в соответствие с SGD с импульсом.
- Дидерик П.Кингма и Джимми Лей Ба. Адам: метод стохастической оптимизации. 2014. arXiv: 1412.6980v9
- Zijun Zhang et al. Нормализованный сохраняющий направление Адам. 2017. arXiv: 1709.04546v2
- Сашанк Дж. Редди, Сатьен Кале, Санджив Кумар. О сближении Адама и не только. 2018.
- Илья Лощилов, Фрэнк Хаттер. Фиксирование регуляции распада веса в Адаме. 2017. arXiv: 1711.05101v2
- Нитиш Шириш Кескар, Ричард Сошер. Повышение производительности генерализации путем переключения с Адама на SGD.2017 arXiv: 1712.07628v1
- Тимоти Дозат. Включение Нестерова импульса в Адама. 2016.
- Себастьян Бок, Йозеф Гоппольд, Мартин Вайс. Улучшение доказательства сходимости ADAM-оптимизатора. 2018. arXiv: 1804.10587в1
- Мартин Зинкевич. Выпуклое онлайн-программирование и обобщенный бесконечно малый градиентный подъем. 2003.
- Ашиа Уилсон, Ребекка Рулофс, Митчелл Стерн, Натан Сребро, Бенджамин Рехт. Предельная ценность адаптивных градиентных методов в машинном обучении.2017. arXiv: 1705.08292v2
- Джон Дючи, Эльад Хазан и Йорам Сингер. Адаптивные субградиентные методы для онлайн-обучения и стохастической оптимизации. Journal of Machine Learning Research, 12: 2121–2159, 2011.
- Тиджмен Тилеман и Джеффри Хинтон. Лекция 6.5-rmsprop: разделите градиент на скользящее среднее его недавней величины. COURSERA: нейронные сети для машинного обучения, 4 (2): 26–31, 2012.
Что такое правило 72?
Определение: Правило 72 — это математический способ подсчитать, сколько лет потребуется, чтобы ваши деньги удвоились с сложным процентом. Другими словами, это упрощенный метод, позволяющий определить, сколько времени нужно инвестировать, чтобы удвоить процентную ставку.
Для чего используется правило 72?
Инвесторы часто используют этот расчет при оценке разницы между аналогичными инвестициями.Они хотят, чтобы их инвестиции росли, поэтому они могут использовать полученные средства, чтобы инвестировать в новые возможности в будущем. Имейте в виду, что это не обязательно инвесторы или брокеры с Уолл-стрит.
Средние американцы могут использовать этот метод, чтобы оценить сумму денег, которую они будут иметь на пенсионном счете, или сколько будет стоить их доля во взаимном фонде через пять лет. Правило 72 будет рассчитывать, сколько времени потребуется, чтобы удвоить ваши деньги в инвестициях. Другими словами, это упрощенный, очень ограниченный калькулятор будущей стоимости, который рассчитает стоимость ваших инвестиций в будущем.
Эта формула является отличным сокращением, потому что уравнение полной длины для сложного процента длинно и сложно. Вы можете использовать это простое правило в качестве базовой оценки для инвестиций. Вот как это работает.
Формула
Формула правила 72 рассчитывается путем умножения инвестиционной процентной ставки на количество лет, вложенных в продукт, всегда равный 72.

Применив немного алгебры, мы можем перестроить уравнение правила 72, чтобы вычислить количество лет, необходимое для удвоения ваших денег с заданной процентной ставкой, составляемой ежегодно.

Или это может быть написано так, чтобы рассчитать годовой составной процентную ставку, необходимую для удвоения ваших инвестиций в данный период времени.

Имейте в виду, что определение правила 72 требует, чтобы проценты составлялись ежегодно. Этот метод не будет работать для инвестиций с полугодовым или ежеквартально сложным интересом, как есть. Если вы хотите использовать этот метод для возврата инвестиций, вам нужно будет изменить его.
Давайте рассмотрим пример.
Пример
Вот пример таблицы, в которой работает правило 72 калькулятора. Как видите, в первом столбце представлена годовая норма инвестиций, которая будет составляться в конце каждого года. Во втором столбце показано количество лет, в течение которых инвестиции удвоятся. Третий столбец всегда 72, потому что так работает формула. Коэффициент инвестиций, умноженный на число лет, всегда равен семидесяти двум.
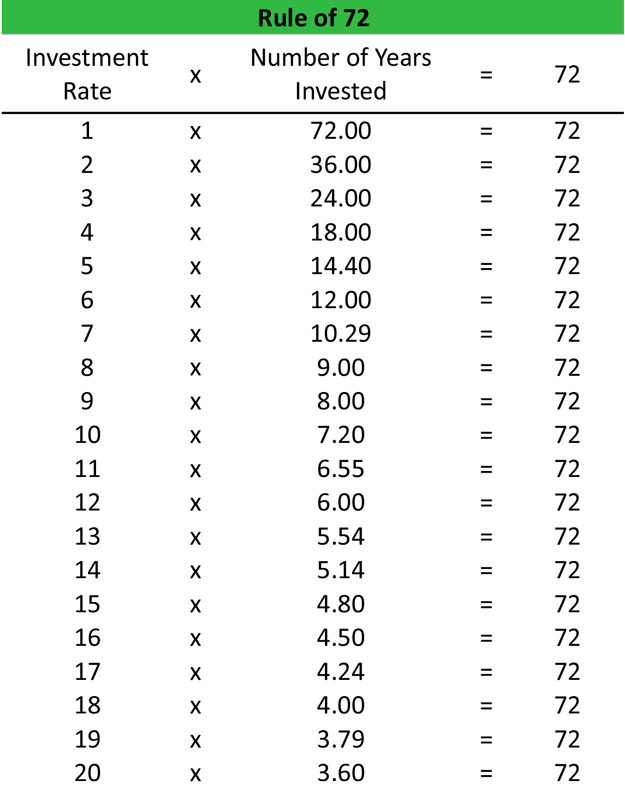
Предположим, у вас есть 10 000 долларов для инвестирования во взаимный фонд, и вы хотите знать, сколько потребуется времени, чтобы стать 20 000 долларов.Вы уверены, что вы можете получить среднюю прибыль 8 процентов в год. Из таблицы выше видно, что для достижения цели в 20 000 долларов потребуются около 9 лет ваших инвестиций.
Мы также можем сделать обратный расчет. Предположим, у вас есть 10000 долларов, и вы хотите знать, какую ежегодную ставку вам нужно будет удвоить за 5 лет. Возвращаясь к нашей таблице, вы можете увидеть, что для достижения цели в 20 000 долларов в течение 5 лет потребуется процентная ставка чуть более 14 процентов.
Как используется правило 72?
Очевидно, что мы могли бы использовать уравнение для расчета каждого из этих примеров, но я подумал, что таблица будет проще. Мы также можем использовать калькулятор будущей стоимости или формулу фактической будущей стоимости, чтобы убедиться, что эти цифры точны, но мы не обязаны это делать. Этот метод работает. Это отличный способ, потому что позволяет легко оценить стоимость ваших инвестиций в будущее без технических подробностей фактического уравнения будущей стоимости.В зависимости от процентной ставки, вы, вероятно, можете делать расчеты в своей голове.
Следует иметь в виду, что этот метод не учитывает другие будущие факторы, которые могут сорвать ваши инвестиционные планы. Например, уровень инфляции может измениться в течение жизни ваших инвестиций. Однако вы можете использовать правило 72 для расчета влияния инфляции на ваши деньги. Например, если уровень инфляции снизился с 3 до 4 процентов, ваши деньги потеряют половину своей стоимости через 18, а не через 24 года.
Вы можете даже сравнить рост текущих расходов, таких как обучение и медицинские расходы, с процентной ставкой. Это довольно возможно. Проверьте это сами. Вы можете использовать его для всех интересных вычислений будущей стоимости.
,
Турнирная таблица
2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 1997 1996 1995 1994 1993 1992 1991 1990 1989 1988 1987 1986 1985 1984 1983 1982 1981 1980 1979 1978 1977 1976 1975 1974 1973 1972 1971 1970 1969 1968 1967 1966 1965 1964 1963 1962 1961 1960 1959 1958 1957 1956 1955 1954 1953 1952 1951 1950
Гонки ВОДИТЕЛИ Команды DHL FASTEST LAP AWARD
Все Албон, Александр Боттас, Валттери Газли, Пьер Джовинацци, Антонио Грожан, Ромен Гамильтон, Льюис Хюлькенберг, Нико Кубица, Роберт Квят, Даниил Леклерк, Чарльз Магнуссен, Кевин Норрис, Ландо Перес, Серхио Риккардо, Даниэль Рассел, Джордж Райкконен, Кими Сайнс, Карлос Прогулка, Ланс Ферстаппен, Макс Феттель, Себастьян
,
