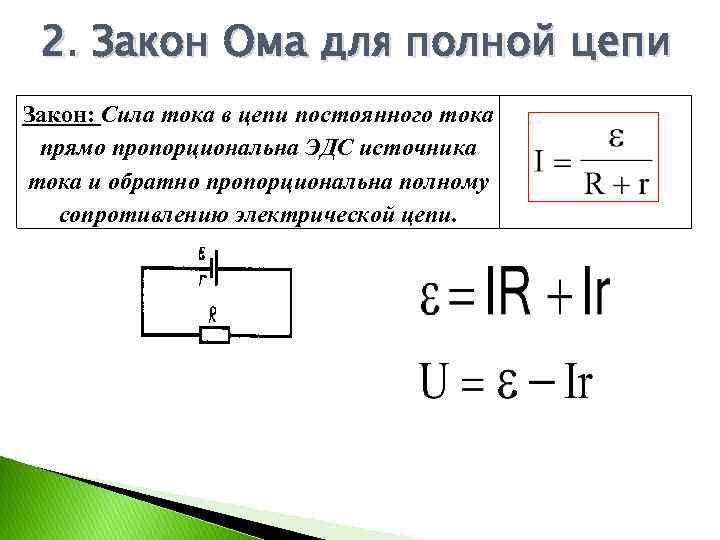
Закон полного тока для магнитного поля: физический смысл, формулы

В электрических цепях всегда присутствует магнитное поле, которое оказывает электромагнитное взаимодействие с токами этих цепей. Данный фактор учитывается при расчетах цепей, а закон полного тока для магнитного поля является инструментом для подобных вычислений.

Если поднести магнитную стрелку к проводнику, по которому течёт ток, её положение изменится. Это говорит о наличии вокруг проводника кроме электрического ещё и магнитного поля. В результате многочисленных исследований электромагнитных явлений установлено, что существует взаимное влияние полей, имеющих электрическую и магнитную природу.

Физический смысл закона

Рассмотрим упрощённый вариант влияния магнитной индукции на электрическое поле. Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I₁ и I₂. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.

В пределах плоскости, охватываемой контуром L, формируется магнитное поле, напряжённость которого распределена в соответствии с направлениями токов. При этом циркуляция вектора магнитного поля в плоскости замкнутого контура прямо пропорциональна сумме токов, пронзающих данный контур. Полный электрический ток равен векторной сумме его составляющих:

Направления векторов I₁ и I₂ определяется по правилу буравчика.

Приведённые выше рассуждения можно рассматривать в качестве примера изображающего упрощённую модель частного случая рассматриваемого закона. В действительности же, процессы взаимного влияния магнитных и электрических полей намного сложнее, и они описываются интегральными и дифференциальными уравнениями Максвелла.

Упрощенный подход

Выразить закон в дифференциальном представлении довольно сложно. Потребуется вводить дополнительные компоненты. Необходимо учитывать влияние молекулярных токов. Наличие вихревых токов является причиной образования магнитного вихревого поля в пределах контура.

Вектор электрического смещения сравним с вектором напряжённости присутствующего магнитного поля H. При этом Ориентация вектора смещения зависит от быстроты изменения магнитной индукции.

Для упрощения вычислений на практике часто пользуются формулами закона для магнитного поля полных токов, представленных в виде суммирования предельно малых участков контура, с учётом влияния вихревых полей. При реализации этого метода контур мысленно разбивают на бесконечно малые отрезки. На этих отрезках проводники считаются прямолинейными, а магнитное поле на таких участках контура считают однородным.

На одном дискретном участке вектор напряженности U_m определяется по формуле: U_m= H_L×ΔL, где H_L– циркуляция вектора напряжённости на участке ΔL контура L. Тогда суммарная напряжённость U_L вдоль всего контура вычисляется по формуле: U_L= Σ H_L× ΔL.

Закон в интегральном представлении

Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).

Воспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура).  Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ → 2π.

Из теоремы Остроградского-Гаусса вытекает формула:

Учитывая, что cos φ = 1,

следовательно:

Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ₀I, где μ₀ = 1/c² ε₀ – магнитная постоянная.

Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда

Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.

Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.

Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.

Если ток распределён в пространстве (произвольный ток), тогда

где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:

Отсюда вытекает:

1. Закон справедлив не только для бесконечно прямолинейного проводника, но и для контуров, произвольной конфигурации.
2. Циркуляция вектора магнитной индукции B сориентированного вдоль магнитных линий, всегда отлична от нуля.
3. Ненулевая циркуляция свидетельствует о том, что магнитное поле прямолинейного, бесконечно длинного проводника не потенциально. Такое поле называют вихревым, либо соленоидным.

Влияние среды

На результат взаимодействия магнитных потоков и постоянных токов влияет среда.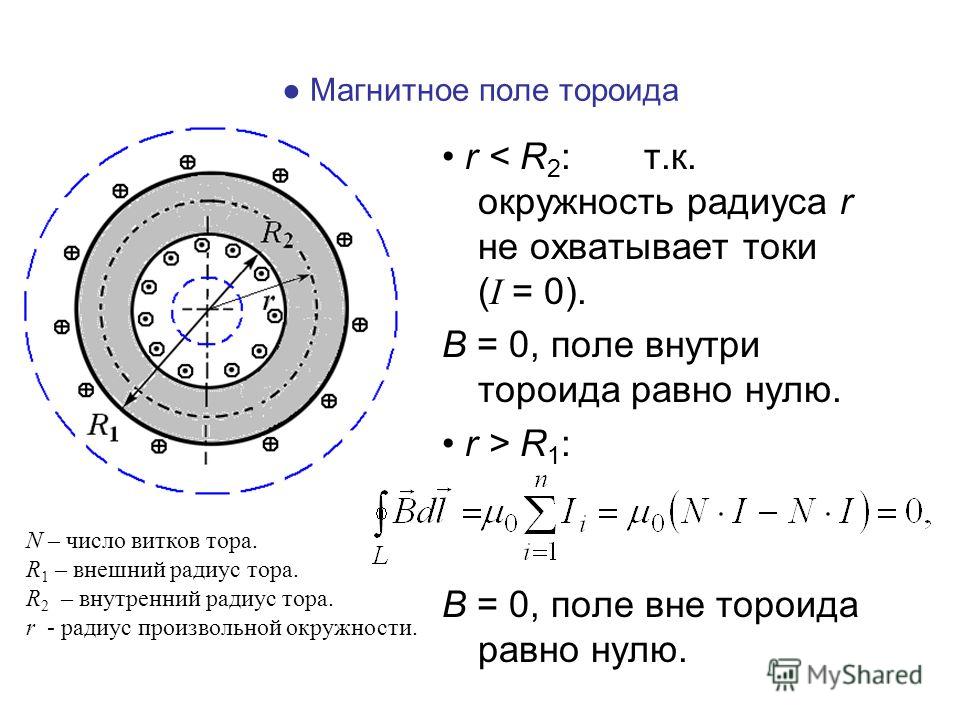 Вещества обладают магнитной проницаемостью в потоке вектора индукции, что вносит коррективы на взаимодействие магнитной среды с токами проводимости. В однородной изотопной среде, где значение вектора электромагнитной индукции одинаково во всех точках, векторы B и H связаны между собой следующим соотношением:

где H — напряжённость магнитного поля, символом μ обозначена магнитная проницаемость.

Носители электрических зарядов создают собственные микротоки. Циркуляция вектора, характеризующего электростатическое поле, всегда нулевая. Поэтому электростатические поля, в отличие от магнитных, являются потенциальными.

Вектор B отображает результирующее значение полей макро- и микротоков. Линии электростатической индукции всегда остаются замкнутыми, в том числе и на положительных зарядах.

Для полей, которые действуют в среде, состоящей из разных веществ, необходимо учитывать микротоки, характерные именно для конкретных структур, образующих данную среду.

Утверждение, изложенное выше, верно для полей соленоидов или любой другой структуры, обладающей свойствами конечной магнитной проницаемости.

Торойд

В электротехнике часто приходится иметь дело с катушками разных видов и размеров. Катушка, образованная витками намотанными на сердечник тороидальной формы (в виде бублика), называется тороидом. Важными характеристиками сердечника тора являются его радиусы — внутренний (R₁) и внешний (R₂).

Поле внутри соленоида на расстоянии r от центра равно:

Выводы

На основании изложенного, приходим к заключению:

1. Закон полного тока устанавливает зависимость между напряжённостью магнитного поля и перемещением в этом поле электрических зарядов.
2. Действие закона распространяется на все среды, при допустимых плотностях тока.
3. Закон также выполняется в полях постоянных магнитов.

При вычислениях не имеет значения, какую формулу мы используем – суть закона остаётся неизменной: он выражает взаимодействия, которые происходят между токами и создаваемыми ими магнитными полями, пронизывающими замкнутый контур.

Выводы закона учитываются при конструировании электромагнитных устройств. Наличие завихрений в электромагнитных полях приводит к снижению КПД. Кроме того, вихревые поля негативно влияют на работоспособность электронных элементов, расположенных в зоне их действий.

Конструкторы электротехнических приборов стремятся свести к минимуму таких влияний. Например, вместо обычных соленоидов применяют тороидальные катушки, за пределами которых отсутствуют электромагнитные поля.

Законы Ома для постоянного и переменного тока

Поиск по вики-сайту о сжатом воздухе

• Компрессоры
• Подготовка воздуха
• Промышленные газы
• Основная информация
• Рекомендации

Compressed Air Wiki Basic Theory Electricity

Чтобы получить из обычного воздуха сжатый воздух, требуется энергия. Эта энергия поступает в виде электричества: переменного или постоянного тока. В этой статье мы кратко рассмотрим законы Ома. Эти законы определяют сопротивление в виде отношения между током и напряжением.

Что такое закон Ома для постоянного тока?

Закон Ома утверждает, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению на этих двух точках. Вводя константу пропорциональности, сопротивление, получаем обычное математическое уравнение, которое описывает это соотношение:U = R x IГде I – ток в проводнике, выраженный в амперах, V – напряжение, измеренное на проводнике в вольтах, а R – сопротивление проводника в Омах. Если точнее, закон Ома утверждает, что R в этом соотношении является постоянной величиной и не зависит от тока.

Что такое закон Ома для переменного тока (и что такое самоиндукция)?

Переменный ток, проходящий через катушку, создает увеличение магнитного потока. Этот поток изменяет величину и направление аналогично электрическому току. При изменении потока в катушке генерируется ЭДС (электродвижущая сила) в соответствии с законами индукции.ЭДС направлена против напряжения подключенного полюса. Это явление называется самоиндукцией. Самоиндукция в блоке переменного тока приводит к частичному смещению фазы между током и напряжением, а также частично к индуктивному падению напряжения. Полное сопротивление устройства переменному току становится больше, чем рассчитанное или измеренное при постоянном токе.Смещение фазы между током и напряжением представлено углом φ. Индуктивное сопротивление (так называемое реактивное сопротивление) обозначено X. Сопротивление обозначено R. Полное сопротивление блока или проводника обозначено Z.

Другие статьи по этой теме

Electrical Installation in Compressor Systems

In this article we will take a look at the electrical system that makes sure the compressor works like it should.

Read more

Введение в электричество

Узнайте об основах электричества и о той роли, которую оно играет в сжатии воздуха. Некоторые основные термины и определения.

Read more

Электродвигатель

Узнайте об основах электродвигателей и о том, как они используются в современных воздушных компрессорах.

Read more

Законы Кирхгофа — Закон Кирхгофа для тока и закон напряжения

Закон Кирхгофа является одним из основных законов, который используется в электростатике для решения сложных вопросов схем. Закон Кирхгофа дан Густавом Робертом Кирхгофом, известным немецким физиком, он дал нам два закона: закон тока Кирхгофа и закон напряжения Кирхгофа, которые обсуждаются в этой статье.

История Густава Роберта Кирхгофа

Густав Роберт Кирхгоф был немецким физиком русского происхождения, его работа заключалась в исследовании электропроводности. Закон Кирхгофа о цепи представляет собой комбинацию закона Кирхгофа о напряжении (KVL) и закона Кирхгофа о токе (KCL), которые были опубликованы в 1845 году. Анализ цепи проводится с использованием этих законов. Они полезны при расчете тока и напряжения в различных потоках по сети.

Что такое законы Кирхгофа?

Законы Кирхгофа — это основной закон, используемый в анализе цепей для решения сложных проблем схем. Густав Роберт Кирхгоф дал нам два закона: закон Кирхгофа о напряжении (KVL) и закон Кирхгофа о токе (KCL), которые широко используются при анализе цепей. Закон напряжения Кирхгофа (KVL) аналогичен закону сохранения энергии, тогда как закон тока Кирхгофа (KCL) подобен закону сохранения заряда.

Этот закон гласит, что «общий ток или заряд, входящий в соединение или узел, в точности идентичен общему току или заряду, выходящему из узла, поскольку в узле не теряется заряд». Другими словами, алгебраическая сумма всех токов, входящих в узел и выходящих из него, должна быть равна нулю. Текущий закон Кирхгофа (KCL) также известен как I закон Кирхгофа.

Примечание: 

Закон Кирхгофа (I) аналогичен Закону сохранения заряда . Таким образом, Nord или узел — это точка в цепи, которая не служит источником или приемником заряда.

Следовательно,

ⁿ ∑ _k=1 I _K = 0

Где n обозначает общее количество ветвей в узле с токами, текущими к нему или от него.

т. е. 

I _(выход) +I _(вход) = 0

Например, ,

Из сети резисторов сконцентрируйтесь на узле А. Этот узел связан с пятью ветвями. Три входящих тока i ₃ , i ₄ и i ₅ и два входящих тока i ₁ и i ₂ . Сумма полных входящих и исходящих токов в узле А теперь будет равна нулю в соответствии с текущим законом Кирхгофа.

Рассмотрим два тока, которые входят в узел, i _1, и i ₂ , как положительные, а два тока, выходящие из узла, i ₃ и i ₄ , как отрицательные.

I ₁ +I ₂ –i ₃ –i ₄ = 0

( Iвх1  +  Iвх2  +  Iвх3 ) + ( -Iвых1  +  -Iвых2  +  -Iвых3 ) =  0  .
 

  vAB + vBC + vCD + (-vDA) = 0 
  

  VR1 + VR2 + (-V1) = 0  

  VR1 = (i1) x 4
ВР1 = 4 (i1) 
 

  VR2 = (i1 + i2) x 2
VR1 = 2 {(i1) + (i2)}  

. .

Так по КВЛ

  VR1 + VR2 + (-V1) = 0 
  VR1 + VR2 + (-V1) = 0 
  4 (i1) + 2 {(i1) + (i2)} - 28 =  

  4 (i1) + 2 (i1) + 2 (i2) – 28 = 0
6 (il) + 2 (i2) = 28 …………………….. Уравнение 1  

Давайте рассчитаем второй цикл .

В этом случае ток течет в направлении против часовой стрелки .

То же, что и предыдущий, разность потенциалов между R3, R2 и V2 при протекании тока по часовой стрелке равна нулю.

  VR3 + VR2 + V1 = 0  

Найдем разность потенциалов на этих резисторах.

В случае VR3

Будет отрицательным из-за направления против часовой стрелки.

По закону Ома V = IR (I = ток и R = сопротивление в омах)

 
VR3 = -(i2) х 1
VR3 = -1 (i2)  

В случае VR2,

Также будет отрицательным из-за направления против часовой стрелки ,

R2 общий для обоих шлейфов . Таким образом, общий ток, протекающий через этот резистор, представляет собой сумму обоих токов, таким образом, I через R2 составляет (i1 + i2) .

Итак,

  В соответствии с законом Ома V = IR (I = ток и R = сопротивление в омах)
VR2 = -(i1 + i2) x 2
VR2 = -2 {(i1) + (i2)}  

В случае V2

Поскольку ток течет против часовой стрелки , разность потенциалов будет положительной, точно противоположной V1, то есть 7В.

Так, по КВЛ

  VR3 + VR2 + V2 = 0 
  VR3 + VR2 + V2 = 0 
  -1 (i2) - 2 {(i1) + (i2)} + 7 = 0  

  -1 (i2) - 2 (i1) - 2 (i2) + 7 = 0
-2 (il) - 3 (i2) = -7 …………………….. Уравнение 2  

Теперь решим эти два Одновременное уравнений, получаем i1 это 5А и i2 это -1 А .