Формула Гаусса — Остроградского — Википедия

Материал из Википедии — свободной энциклопедии

Фо́рмула Гаусса — Остроградского связывает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность и интеграл от дивергенции этого поля по объёму, ограниченному этой поверхностью.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности и наоборот.

Пусть тело V{\displaystyle V} ограничено замкнутой поверхностью S{\displaystyle S}. Тогда для любого векторного поля F{\displaystyle \mathbf {F} } выполняется равенство

∭VdivF=∬S⟨F,n⟩,{\displaystyle \iiint \limits _{V}\mathrm {div} \,\mathbf {F} =\iint \limits _{S}\langle \mathbf {F} ,\mathbf {n} \rangle ,}

то есть интеграл от дивергенции векторного поля F{\displaystyle \mathbf {F} }, распространённый по объёму V{\displaystyle V}, равен потоку вектора через поверхность S{\displaystyle S}.

Замечания[править | править код]

В работе Остроградского формула записана в следующем виде:

∫(dPdx+dQdy+dRdz)ω=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)s,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)\omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )s,}

где ω{\displaystyle \omega } и s{\displaystyle s} — дифференциалы объёма и поверхности соответственно. P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z){\displaystyle P=P(x,\;y,\;z),\;Q=Q(x,\;y,\;z),\;R=R(x,\;y,\;z)} — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью^[1].

Современная запись формулы:

∫(dPdx+dQdy+dRdz)dΩ=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)dS,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)d\Omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )dS,}

где cos⁡αdS=dydz{\displaystyle \cos \alpha \,{dS}={dy}{dz}}, cos⁡βdS=dxdz{\displaystyle \cos \beta \,{dS}={dx}{dz}} и cos⁡γdS=dxdy{\displaystyle \cos \gamma \,{dS}={dx}{dy}}. В современной записи ω=dΩ{\displaystyle \omega =d\Omega } — элемент объёма, s=dS{\displaystyle s=dS} — элемент поверхности^[1].

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

Впервые теорема была установлена Лагранжем в 1762^[2].

Общий метод преобразования тройного интеграла к поверхностному впервые показал Карл Фридрих Гаусс (1813, 1830) на примере задач электродинамики

[3].

В 1826 году М. В. Остроградский вывел формулу в общем виде, представив её в виде теоремы (опубликовано в 1831 году). Многомерное обобщение формулы М. В. Остроградский опубликовал в 1834 году^[3]. С помощью данной формулы Остроградский нашёл выражение производной по параметру от n{\displaystyle n}-кратного интеграла с переменными пределами и получил формулу для вариации n{\displaystyle n}-кратного интеграла.

За рубежом формула как правило называется «теоремой о дивергенции» (англ. divergence theorem), иногда — формулой Гаусса или «формулой (теоремой) Гаусса—Остроградского».

• Остроградский М. В. Note sur les integrales definies. // Mem. l’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
• Остроградский М. В. Memoire sur le calcul des variations des integrales multiples. // Mem. l’Acad., 1, стр. 35—58, 24/1 1834 (1838).

1. ↑ ^{1 2} Ильин В. А. и др. Математический анализ. Продолжение курса / В. А. Ильин, В. А. Садовничий, Бл. X. Сендов. Под ред. А. Н. Тихонова. — М.: Изд-во МГУ, 1987.— 358 с.
2. ↑ В работе по теории звука в 1762 г. Лагранж рассматривает частный случай теоремы: Lagrange (1762) «Nouvelles recherches sur la nature et la propagation du son» (Новые исследования о природе и распространении звука), Miscellanea Taurinensia (Mélanges de Turin), 2: 11 — 172. Репринтное издание: «Nouvelles recherches sur la nature et la propagation du son» в кн.: J.A. Serret, ed., Oeuvres de Lagrange, (Paris, France: Gauthier-Villars, 1867), vol. 1, pages 151—316; на страницах 263—265 Лагранж преобразовывает тройные интегралы в двойные с помощью интегрирования по частям.
3. ↑ ^{1 2} Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 150—151.

Формула Остроградского-Гаусса

Доказательство.

\(\circ\) Докажем сначала формулу Остроградского Гаусса в одном важном частном случае, когда область \(G\) еще и элементарна относительно всех трех координатных осей. Напомним, что область \(G\) называется элементарной относительно оси \(z\), если найдутся две такие непрерывные в замыкании области \(\Omega \subset \boldsymbol{R}^{2}\) функции \(\varphi(x, y)\) и \(\psi(x, y)\), что

$$
G = \{(x, y, z): \varphi(x, y) < z < \psi(x, y),\ (x, y) \ \in \Omega\}.\nonumber
$$

Применяя формулу сведения тройного интеграла к повторному, получаем
$$
\iiint\limits_{G} \frac{\partial R}{\partial z} (x, y, z)\ dx\ dy\ dz = \iint\limits_{\Omega} dx\ dy \int\limits_{\varphi(x, y)}^{\psi(x, y)}\frac{\partial R}{\partial z} (x, y, z)\ dz =\\=\iint\limits_{\Omega} R(x, y, \psi(x, y))\ dx\ dy-\iint\limits_{\Omega} R(x, y, \varphi(x, y))\ dx\ dy =\\= \iint\limits_{\Sigma_{1}} R(x, y, z)\ dx\ dy+\iint\limits_{\Sigma_{2}} R(x, y, z)\ dx\ dy.\label{ref3}
$$

Здесь \(\Sigma_{1}\) — поверхность, являющаяся графиком функции \(\psi(x, y)\), a \(\Sigma_{2}\) — поверхность, являющаяся графиком функции \(\varphi(x, y)\).

Мы воспользовались выражением поверхностного интеграла второго рода через двойной интеграл и тем, что поверхность \(\Sigma_{1}\) ориентирована внешними к \(\partial G\) нормалями, которые составляют с осью \(z\) острый угол, а на поверхности \(\Sigma_{2}\) внешние к \(\partial G\) нормали составляют с осью \(z\) тупой угол (рис. 56.1). Добавляя к двум поверхностным интегралам в формуле \eqref{ref3} еще равный нулю интеграл \(\displaystyle\iint\limits_{\Sigma_{3}}R\ dx\ dy\) по куску цилиндрической поверхности, построенной на \(\partial G\), и замечая, что \(\partial G = \displaystyle\bigcup_{i=1}^{3}\Sigma_{i}\), получаем
$$
\iiint\limits_{G} \frac{\partial R}{\partial z} (x, y, z)\ dx\ dy\ dz = \iint\limits_{\partial G} R\ dx\ dy.\label{ref4}
$$

Рис. 56.1

Аналогично, воспользовавшись элементарностью области относительно осей \(x\) и \(y\), докажем, что
$$
\iiint\limits_{G} \frac{\partial P}{\partial x} dx\ dy\ dz = \iint\limits_{\partial G} P\ dy\ dz,\quad \iiint\limits_{G} \frac{\partial Q}{\partial y} dx\ dy\ dz = \iint\limits_{\partial G} Q\ dz\ dx.\label{ref5}
$$
Складывая равенства \eqref{ref4} и \eqref{ref5}, получим формулу \eqref{ref2}.

Примерами областей, элементарных относительно всех трех координатных осей, являются шар, куб, симплекс (фигура, получающаяся при пересечении четырех полупространств (рис. 56.2)).

Рис. 56.2

Точки \(A\), \(B\), \(C\), \(D\) — вершины симплекса, треугольники \(ABC\), \(ABD\), \(ACD\) и \(BCD\) — грани симплекса.

Дальнейшая схема последовательного расширения класса областей, для которых справедлива формула \eqref{ref2}, такая же, как и при доказательстве формулы Грина на плоскости.

Будем называть область \(G\) объемно односвязной, если для любой ограниченной области \(\Omega\) из условия \(\partial \Omega \subset G\) следует, что и \(\Omega \subset G\). Для простоты будем говорить просто “односвязная область”. Формулу \eqref{ref2} теперь можно обобщить на ограниченную односвязную область \(G\) с кусочно гладкой границей, которая кусочно гладкой перегородкой делится на две области, \(G_{1}\) и \(G_{2}\), элементарные относительно всех трех координатных осей. При этом \(\partial G_{1} = \Sigma_{1} \cup \Sigma_{3}\), \(\partial G_{2} = \Sigma_{2} \cup \Sigma_{3}^{-}\), \(\partial G = \Sigma_{1} \cup \Sigma_{2}\). Если \(\partial G_{1}\) и \(\partial G_{2}\) ориентированы внешними нормалями, то \(\Sigma_{3}\) и \(\Sigma_{3}^{-}\) ориентированы противоположно (рис. 56.3).

Рис. 56.3

Применяя формулу \eqref{ref2} к каждой из областей \(G_{1}\) и \(G_{2}\), получаем
$$
\iiint\limits_{G_{1}} \operatorname{div}\ \boldsymbol{a}\ dx\ dy\ dz = \iint\limits_{\partial G_{1}} (\boldsymbol{a}, \boldsymbol{n})\ dS = \iint\limits_{\Sigma_{1}} (\boldsymbol{a}, \boldsymbol{n})\ dS+\iint\limits_{\Sigma_{3}} (\boldsymbol{a}, \boldsymbol{n})\ dS,\nonumber
$$
$$
\iiint\limits_{G_{2}} \operatorname{div}\ \boldsymbol{a}\ dx\ dy\ dz = \iint\limits_{\partial G_{2}} (\boldsymbol{a}, \boldsymbol{n})\ dS = \iint\limits_{\Sigma_{2}} (\boldsymbol{a}, \boldsymbol{n})\ dS+\iint\limits_{\Sigma_{3}^{-}} (\boldsymbol{a}, \boldsymbol{n})\ dS.\nonumber
$$

Складывая эти формулы и учитывая, что потоки через перегородку взаимно уничтожаются, получаем формулу \eqref{ref2} для области \(G\).

Далее индукцией формула \eqref{ref2} распространяется на односвязные области с кусочно гладкой границей, которые при помощи \(n\) непересекающихся гладких перегородок разбиваются на области, элементарные относительно всех трех координатных осей. Примером таких областей являются выпуклые многогранники, возникающие как пересечение конечного числа полупространств. Их всегда можно представить как объединение симплексов. Можно распространить формулу \eqref{ref2} и на произвольные многогранники — связные множества в \(\boldsymbol{R}^{3}\), являющиеся объединением конечного числа симплексов, причем два симплекса могут пересекаться только по одной из граней и каждая грань может быть общей не более чем для двух симплексов.

Предельный переход от многогранников к произвольной односвязной области с кусочно гладкой границей требует преодоления некоторых нетривиальных технических трудностей. \(\bullet\)

Формула Гаусса — Остроградского / Поверхностный интеграл / 3dstroyproekt.ru

Формула Гаусса — Остроградского является аналогом формулы Грина — Остроградского. Эта формула связывает поверхностный интеграл второго рода по замкнутой поверхности с тройным интегралом по пространственной области, ограниченной этой поверхностью.

Для вывода формулы Гаусса — Остроградского надо воспользоваться рассуждениями, подобными тем, которые использовались при нахождении формулы Грина — Остроградского.

Рассматривается сначала поверхность, ограниченная сверху и снизу некоторыми поверхностями, заданными известными уравнениями, а сбоку ограниченную цилиндрической поверхностью. Затем рассматривается вариант когда поверхность ограничена цилиндрической поверхностью с образующими, параллельными двум другим координатным осям.

После этого полученные результаты обобщаются, приводя к формуле Гаусса — Остроградского:

$ \iint\limits_S { Pdydz+Qdzdx+Rdxdy } =\iiint\limits_V { \left( { \frac { \partial P(x,y,z) } { \partial x } +\frac { \partial Q(x,y,z) } { \partial y } +\frac { \partial R(x,y,z) } { \partial z } }\right)dxdydz } $

Отметим, что эта формула применима для вычисления поверхностных интегралов по замкнутой поверхности.

На практике формулу Гаусса — Остроградского можно применять для вычисления объема тел, если известна поверхность, ограничивающая это тело.

Имеют место формулы:

$ V=\iint\limits_S { xdydz } =\iint\limits_S { ydxdz } =\iint\limits_S { zdxdy } =\iiint\limits_V { dxdydz } $

Пример 1

Найти формулу вычисления объема шара.

В поперечных сечениях шара { сечения параллельны плоскости $XOY$ } получаются окружности.

Уравнение шара имеет вид: $x^2+y^2+z^2=R^2$

Найти объем шара можно по формуле: $ V=\int\limits_ { -R } ^R { \int\limits_ { -\sqrt { R^2-x^2 } } ^ { \sqrt { R^2-x^2 } } { \int\limits_ { -\sqrt { R^2-x^2-y^2 } } ^ { \sqrt { R^2-x^2-y^2 } } { dzdydx } } } =8\int\limits_0^R { dx\int\limits_ { -\sqrt { R^2-x^2 } } ^ { \sqrt { R^2-x^2 } } { \sqrt { R^2-x^2-y^2 } dy } } = \\ $ $ \begin{array} { l } = 8\int\limits_0^R { \left[ { \frac { y\sqrt { R^2-x^2-y^2 } } { 2 } +\frac { R^2-x^2 } { 2 } \arcsin \frac { y } { \sqrt { R^2-x^2 } } }\right]\mathop { \left| { dx }\right. } \limits_0^ { \sqrt { R^2-x^2 } } } =8\int\limits_0^R { \frac { R^2-x^2 } { 2 } \cdot \frac { \pi } { 2 } dx } =2\pi \left[ { R^2x-\frac { x^3 } { 3 } }\right]\mathop { \left| \right. } \limits_0^R = \frac { 4\pi R^3 } { 3 } \end{array} $

Для решения этой же задачи можно воспользоваться преобразованием интеграла к сферическим координатам. Это значительно упростит интегрирование.

$ V=\int\limits_0^\pi { d\theta } 2\int\limits_0^\pi { d\varphi } \int\limits_0^R { \rho ^2\sin \varphi d\rho } =2\int\limits_0^\pi { d\theta } \int\limits_0^\pi { \frac { R^3 } { 3 } \sin \varphi d\varphi } =\frac { 2 } { 3 } \int\limits_0^\pi { 2R^3d\theta } =\frac { 4\pi R^3 } { 3 } . $

Формула Гаусса — Остроградского — Википедия

Материал из Википедии — свободной энциклопедии

Фо́рмула Гаусса — Остроградского связывает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность и интеграл от дивергенции этого поля по объёму, ограниченному этой поверхностью.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности и наоборот.

Формулировка

Пусть тело V{\displaystyle V} ограничено замкнутой поверхностью S{\displaystyle S}. Тогда для любого векторного поля F{\displaystyle \mathbf {F} } выполняется равенство

∭VdivF=∬S⟨F,n⟩,{\displaystyle \iiint \limits _{V}\mathrm {div} \,\mathbf {F} =\iint \limits _{S}\langle \mathbf {F} ,\mathbf {n} \rangle ,}

то есть интеграл от дивергенции векторного поля F{\displaystyle \mathbf {F} }, распространённый по объёму V{\displaystyle V}, равен потоку вектора через поверхность S{\displaystyle S}.

Замечания

В работе Остроградского формула записана в следующем виде:

∫(dPdx+dQdy+dRdz)ω=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)s,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)\omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )s,}

где ω{\displaystyle \omega } и s{\displaystyle s} — дифференциалы объёма и поверхности соответственно. P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z){\displaystyle P=P(x,\;y,\;z),\;Q=Q(x,\;y,\;z),\;R=R(x,\;y,\;z)} — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью^[1].

Современная запись формулы:

∫(dPdx+dQdy+dRdz)dΩ=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)dS,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)d\Omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )dS,}

где cos⁡αdS=dydz{\displaystyle \cos \alpha \,{dS}={dy}{dz}}, cos⁡βdS=dxdz{\displaystyle \cos \beta \,{dS}={dx}{dz}} и cos⁡γdS=dxdy{\displaystyle \cos \gamma \,{dS}={dx}{dy}}. В современной записи ω=dΩ{\displaystyle \omega =d\Omega } — элемент объёма, s=dS{\displaystyle s=dS} — элемент поверхности^[1].

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

История

Впервые теорема была установлена Лагранжем в 1762^[2].

Общий метод преобразования тройного интеграла к поверхностному впервые показал Карл Фридрих Гаусс (1813, 1830) на примере задач электродинамики^[3].

В 1826 году М. В. Остроградский вывел формулу в общем виде, представив её в виде теоремы (опубликовано в 1831 году). Многомерное обобщение формулы М. В. Остроградский опубликовал в 1834 году^[3]. С помощью данной формулы Остроградский нашёл выражение производной по параметру от n{\displaystyle n}-кратного интеграла с переменными пределами и получил формулу для вариации n{\displaystyle n}-кратного интеграла.

За рубежом формула как правило называется «теоремой о дивергенции» (англ. divergence theorem), иногда — формулой Гаусса или «формулой (теоремой) Гаусса—Остроградского».

См. также

Литература

• Остроградский М. В. Note sur les integrales definies. // Mem. l’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
• Остроградский М. В. Memoire sur le calcul des variations des integrales multiples. // Mem. l’Acad., 1, стр. 35—58, 24/1 1834 (1838).

Примечания

1. ↑ ^{1 2} Ильин В. А. и др. Математический анализ. Продолжение курса / В. А. Ильин, В. А. Садовничий, Бл. X. Сендов. Под ред. А. Н. Тихонова. — М.: Изд-во МГУ, 1987.— 358 с.
2. ↑ В работе по теории звука в 1762 г. Лагранж рассматривает частный случай теоремы: Lagrange (1762) «Nouvelles recherches sur la nature et la propagation du son» (Новые исследования о природе и распространении звука), Miscellanea Taurinensia (Mélanges de Turin), 2: 11 — 172. Репринтное издание: «Nouvelles recherches sur la nature et la propagation du son» в кн.: J.A. Serret, ed., Oeuvres de Lagrange, (Paris, France: Gauthier-Villars, 1867), vol. 1, pages 151—316; на страницах 263—265 Лагранж преобразовывает тройные интегралы в двойные с помощью интегрирования по частям.
3. ↑ ^{1 2} Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 150—151.

Формула Гаусса — Остроградского — Википедия

Материал из Википедии — свободной энциклопедии

Фо́рмула Гаусса — Остроградского — математическая формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

∭VdivFdV=∬S⊂⊃F⋅ndS,{\displaystyle \iiint \limits _{V}\mathrm {div} \,\mathbf {F} \,dV=\iint \limits _{S}\!\!\!\!\!\!\!\!\!\!\!\;\!\!\;\subset \!\!\supset \mathbf {F} \cdot \mathbf {n} \,dS,}

то есть интеграл от дивергенции векторного поля F{\displaystyle \mathbf {F} }, распространённый по некоторому объёму V{\displaystyle V}, равен потоку вектора через поверхность S{\displaystyle S}, ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде:

∫(dPdx+dQdy+dRdz)ω=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)s,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)\omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )s,}

где ω{\displaystyle \omega } и s{\displaystyle s} — дифференциалы объёма и поверхности соответственно. P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z){\displaystyle P=P(x,\;y,\;z),\;Q=Q(x,\;y,\;z),\;R=R(x,\;y,\;z)} — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью^[1].

Современная запись формулы:

∫(dPdx+dQdy+dRdz)dΩ=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)dS,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)d\Omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )dS,}

где cos⁡αdS=dydz{\displaystyle \cos \alpha \,{dS}={dy}{dz}}, cos⁡βdS=dxdz{\displaystyle \cos \beta \,{dS}={dx}{dz}} и cos⁡γdS=dxdy{\displaystyle \cos \gamma \,{dS}={dx}{dy}}. В современной записи ω=dΩ{\displaystyle \omega =d\Omega } — элемент объёма, s=dS{\displaystyle s=dS} — элемент поверхности^[1].

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

История

Впервые теорема была установлена Лагранжем в 1762^[2].

Общий метод преобразования тройного интеграла к поверхностному впервые показал Карл Фридрих Гаусс (1813, 1830 гг.) на примере задач электродинамики^[3].

В 1826 году М. В. Остроградский вывел формулу в общем виде, представив её в виде теоремы (опубликовано в 1831 году). Многомерное обобщение формулы М. В. Остроградский опубликовал в 1834 году

[3]. С помощью данной формулы Остроградский нашёл выражение производной по параметру от n{\displaystyle n}-кратного интеграла с переменными пределами и получил формулу для вариации n{\displaystyle n}-кратного интеграла.

За рубежом формула как правило называется «теоремой о дивергенции» (англ. divergence theorem), иногда — формулой Гаусса или «формулой (теоремой) Гаусса—Остроградского».

См. также

Литература

• Остроградский М. В. Note sur les integrales definies. // Mem. l’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
• Остроградский М. В. Memoire sur le calcul des variations des integrales multiples. // Mem. l’Acad., 1, стр. 35—58, 24/1 1834 (1838).

Примечания

1. ↑ ^{1 2} Ильин В. А. и др. Математический анализ. Продолжение курса / В. А. Ильин, В. А. Садовничий, Бл. X. Сендов. Под ред. А. Н. Тихонова. — М.: Изд-во МГУ, 1987.— 358 с.
2. ↑ В работе по теории звука в 1762 г. Лагранж рассматривает частный случай теоремы: Lagrange (1762) «Nouvelles recherches sur la nature et la propagation du son» (Новые исследования о природе и распространении звука), Miscellanea Taurinensia (Mélanges de Turin), 2: 11 — 172. Репринтное издание: «Nouvelles recherches sur la nature et la propagation du son» в кн.: J.A. Serret, ed., Oeuvres de Lagrange, (Paris, France: Gauthier-Villars, 1867), vol. 1, pages 151—316; на страницах 263—265 Лагранж преобразовывает тройные интегралы в двойные с помощью интегрирования по частям.
3. ↑ ^{1 2} Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 150—151.

Формула Остроградского – Гаусса.

Пусть компоненты векторного поля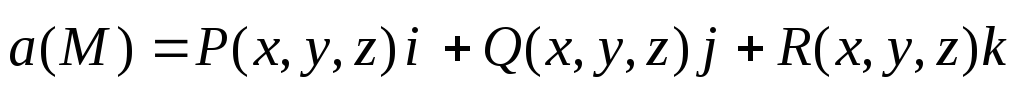

непрерывны и имеют непрерывные частные производные в пространственно односвязной замкнутой областиV и на ее кусочно гладкой границе .

Тогда справедлива формула Остроградского – Гаусса

.

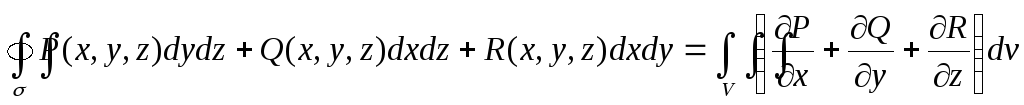Заметим, что левая часть формулы представляет собой поток векторного поля 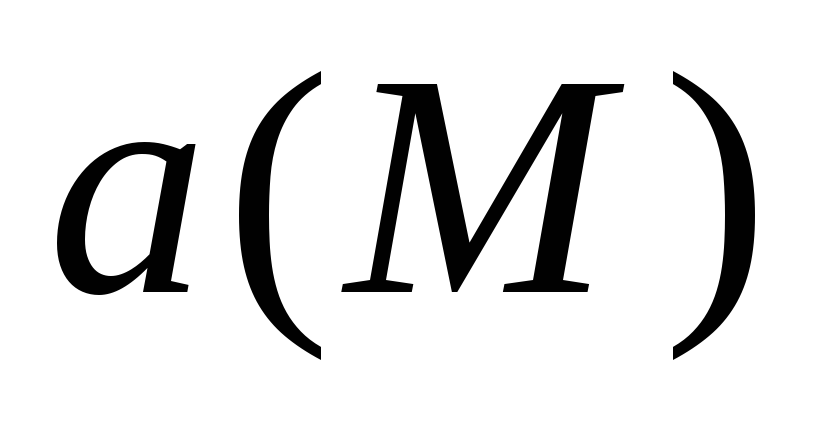через поверхность .

Доказательство. 1) Формула Остроградского – Гаусса, в силу произвольностиP, Q, Rсостоит из трех частей, в каждую из которых входит одна из компонент векторного поляP, Q, R. В самом деле, можно взятьP = 0, Q = 0 и доказывать отдельно часть формулы в которую входит толькоR. Остальные части формулы (приP= 0, R= 0, Q= 0, R = 0) доказываются аналогично. Будем доказывать часть формулы

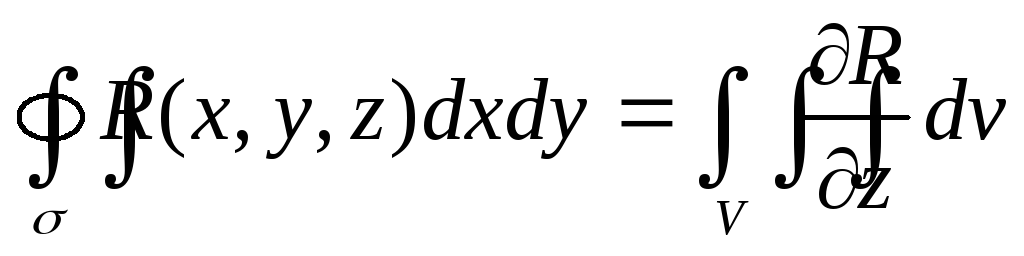
2) Для доказательства выбранной части формулы представим пространственную область Vв виде объединения конечного числа цилиндрических тел, не имеющих общих внутренних точек, с образующими, параллельными осиOZ. Доказательство можно проводить для цилиндрического тела. В самом деле, тройной интеграл в правой части равен сумме тройных интегралов по цилиндрическим телам (свойство аддитивности). Поверхностный интеграл в левой части также равен сумме поверхностных интегралов по полным поверхностям цилиндрических тел, причем при суммировании интегралы по общим границам соседних цилиндрических тел будут сокращаться из-за противоположного направления внешних нормалей на общих границах.

Итак, будем доказывать соотношение 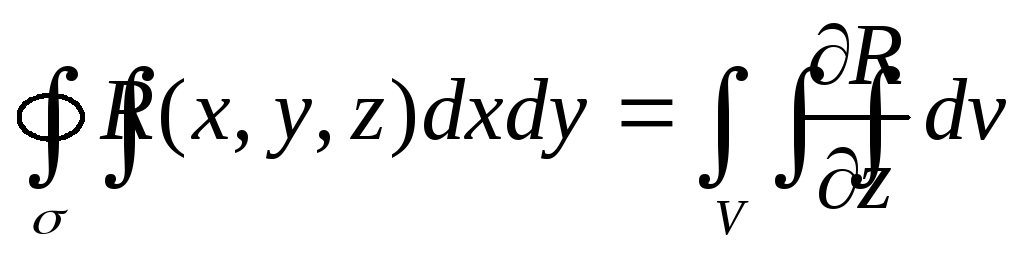для цилиндрического телаV, проектирующегося в областьDна плоскостиOXY. Пусть «верхняя» граница цилиндрического тела – поверхность

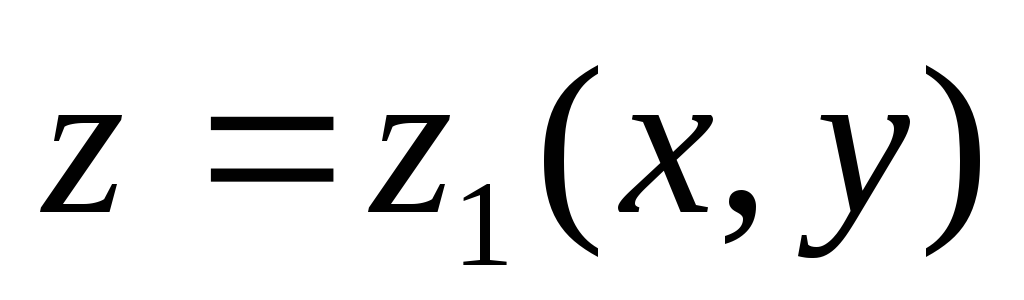описывается уравнением , «нижняя» граница – поверхность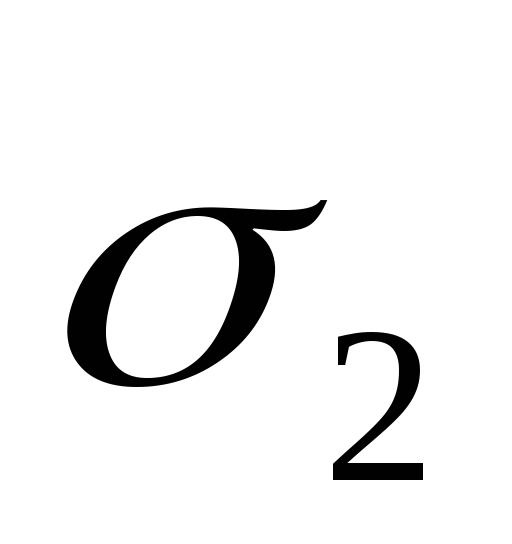 описывается уравнением 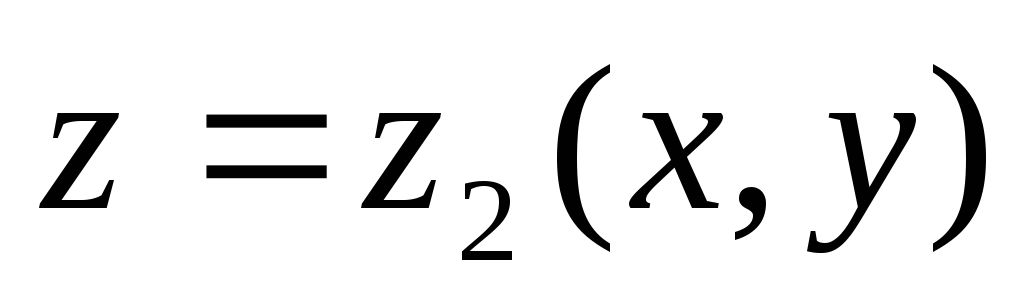. Боковую поверхность цилиндрического тела, параллельную осиOZ, обозначим.

Сразу заметим, что поток векторного поля через боковую поверхность равен нулю. Действительно, 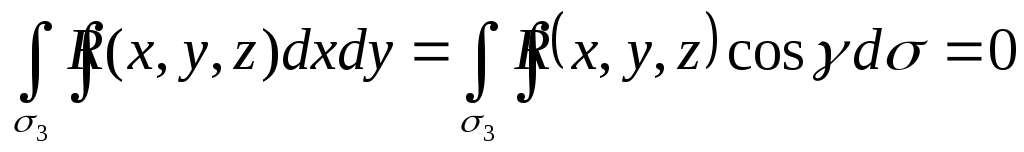, так как нормаль на боковой поверхности ортогональна осиOZи.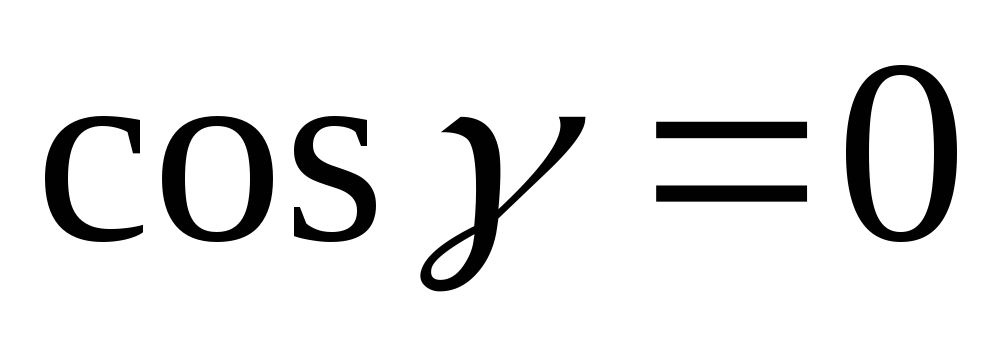

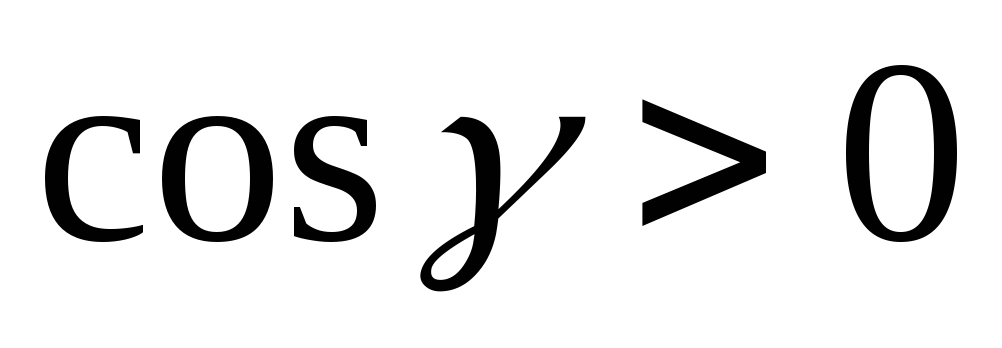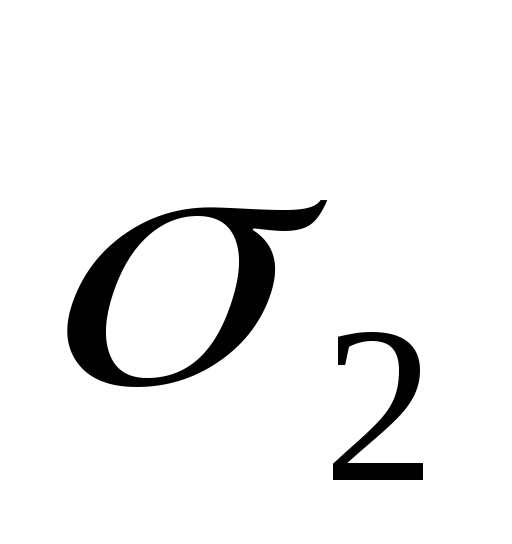
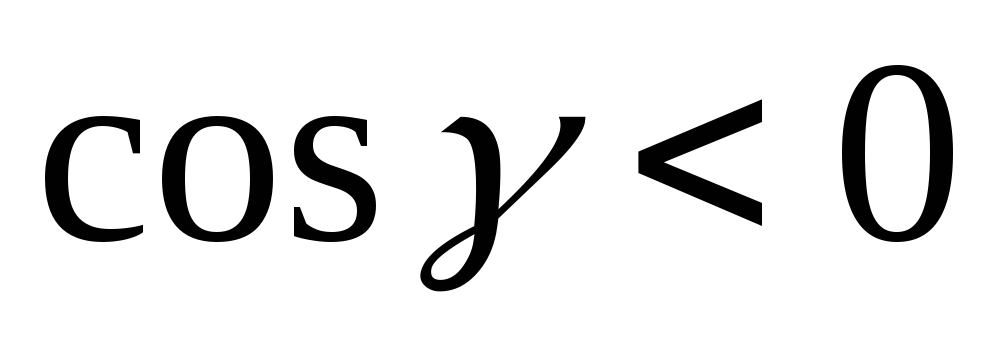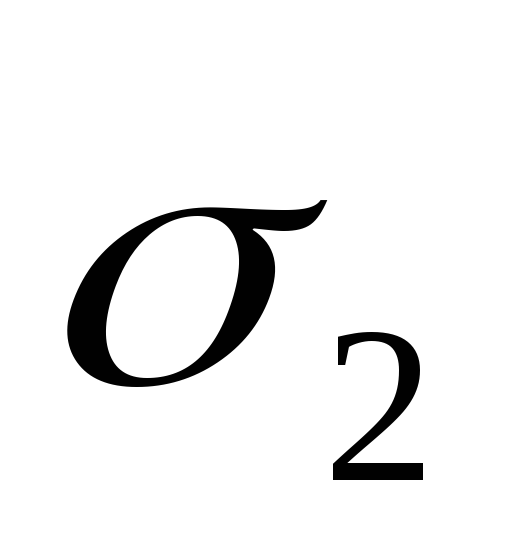Заметим также, что на «верхней» поверхности , а на «нижней поверхности. Поэтому при переходе от поверхностного интеграла пок двойному интегралу по областиDи обратно надо менять знак, а при переходе от поверхностного интеграла пок двойному интегралу по областиDи обратно менять знак не надо .

Замечание.Формулу Остроградского – Гаусса можно записать в «полевом» виде

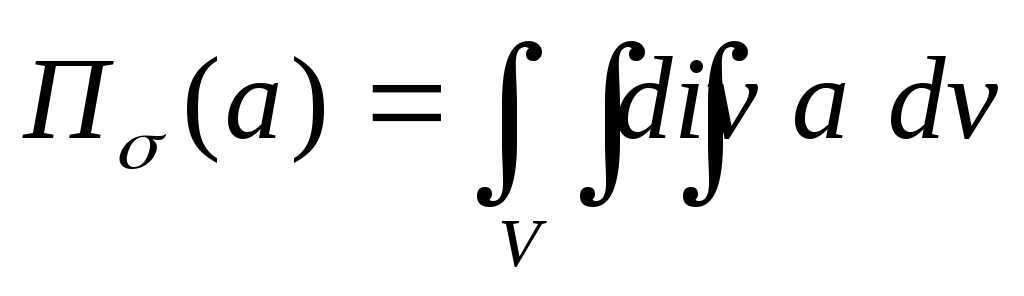— поток векторного поля через замкнутую поверхность равен объемному интегралу от дивергенции поля по области, ограниченной поверхностью .

Дивергенция векторного поля (расходимость) есть .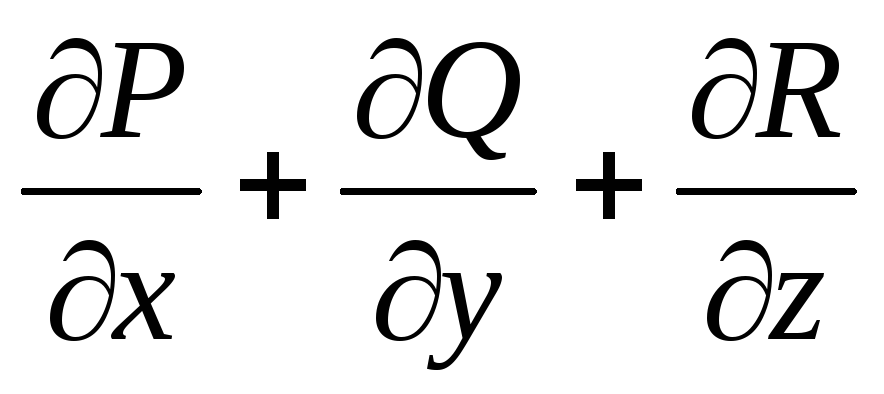

Дивергенция – это характеристика векторного поля, инвариантная относительно системы координат. Покажем это.

Инвариантное определение дивергенции.

Рассмотрим произвольную точку M в пространственной области V. Выберем ее окрестностьV_M – шар радиусаrс центром в точкеM. Обозначим— ее границу – сферу радиусаr. По теореме о среднем для тройного интеграла

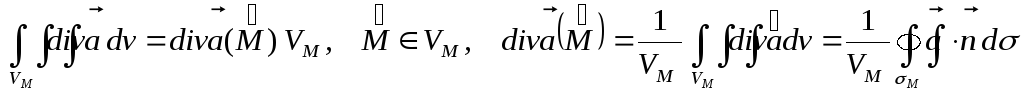(по формуле Остроградского – Гаусса).

Стягиваем окрестность к точке M, получаем дивергенцию векторного поля в точкеM.

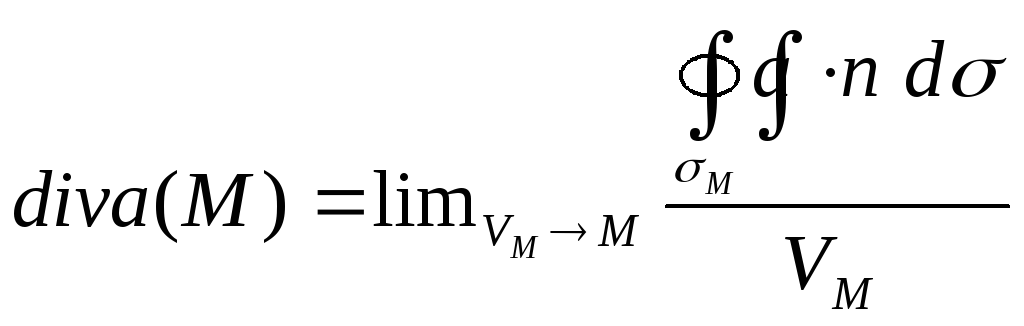. Это и естьинвариантное определение дивергенции.

Поэтому дивергенция векторного поля в точке M имеет смысл объемной плотности потока векторного поля через окрестность этой точки и характеризует мощность источника (если 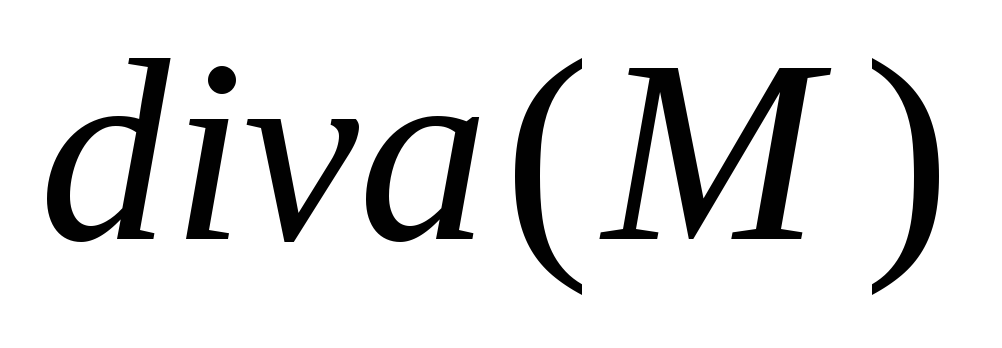>0) или стока (если <0) векторного поля в точке M.

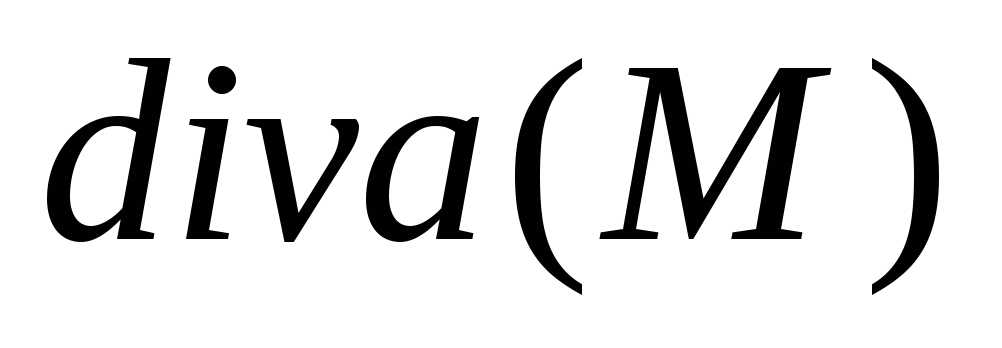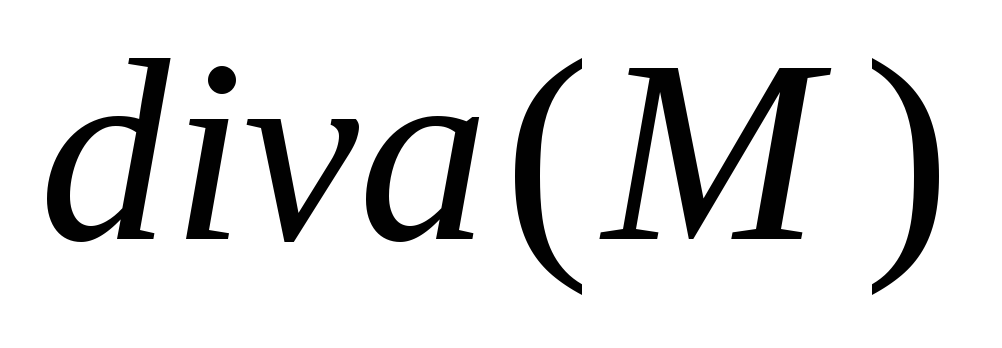Если >0, то точкаM– источник векторного поля, если<0, то точка M– сток векторного поля. Если в некоторой области дивергенция равна нулю, то в этой области нет ни источников, ни стоков, поток векторного поля через границу такой области равен нулю – «сколько поля втекает в область, столько и вытекает из нее».

Пример.Определить расположение источников и стоков векторного поля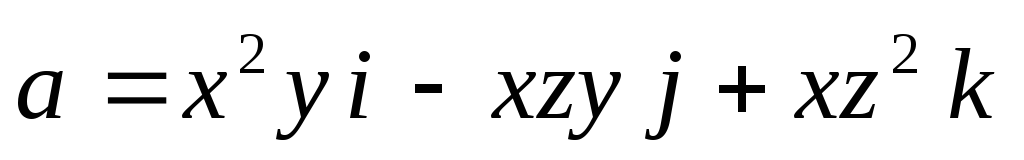. Выяснить, является ли точкаM(1,2,3)источником или стоком.

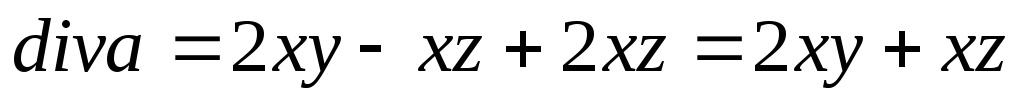. Все точки, для которых 2xy+xz >0 – источники, все точки, для которых 2xy+xz <0– стоки. На поверхности 2xy+xz = 0 нет ни источников, ни стоков. Точка M– источник, так как.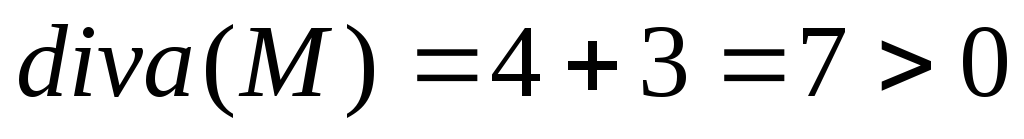

Формула Гаусса — Остроградского — Википедия

Материал из Википедии — свободной энциклопедии

Фо́рмула Гаусса — Остроградского — математическая формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

∭VdivFdV=∬S⊂⊃F⋅ndS,{\displaystyle \iiint \limits _{V}\mathrm {div} \,\mathbf {F} \,dV=\iint \limits _{S}\!\!\!\!\!\!\!\!\!\!\!\;\!\!\;\subset \!\!\supset \mathbf {F} \cdot \mathbf {n} \,dS,}

то есть интеграл от дивергенции векторного поля F{\displaystyle \mathbf {F} }, распространённый по некоторому объёму V{\displaystyle V}, равен потоку вектора через поверхность S{\displaystyle S}, ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде:

∫(dPdx+dQdy+dRdz)ω=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)s,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)\omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )s,}

где ω{\displaystyle \omega } и s{\displaystyle s} — дифференциалы объёма и поверхности соответственно. P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z){\displaystyle P=P(x,\;y,\;z),\;Q=Q(x,\;y,\;z),\;R=R(x,\;y,\;z)} — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью^[1].

Современная запись формулы:

∫(dPdx+dQdy+dRdz)dΩ=∫(Pcos⁡α+Qcos⁡β+Rcos⁡γ)dS,{\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)d\Omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )dS,}

где cos⁡αdS=dydz{\displaystyle \cos \alpha \,{dS}={dy}{dz}}, cos⁡βdS=dxdz{\displaystyle \cos \beta \,{dS}={dx}{dz}} и cos⁡γdS=dxdy{\displaystyle \cos \gamma \,{dS}={dx}{dy}}. В современной записи ω=dΩ{\displaystyle \omega =d\Omega } — элемент объёма, s=dS{\displaystyle s=dS} — элемент поверхности^[1].

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

История

Впервые теорема была установлена Лагранжем в 1762^[2].

Общий метод преобразования тройного интеграла к поверхностному впервые показал Карл Фридрих Гаусс (1813, 1830 гг.) на примере задач электродинамики^[3].

В 1826 году М. В. Остроградский вывел формулу в общем виде, представив её в виде теоремы (опубликовано в 1831 году). Многомерное обобщение формулы М. В. Остроградский опубликовал в 1834 году^[3]. С помощью данной формулы Остроградский нашёл выражение производной по параметру от n{\displaystyle n}-кратного интеграла с переменными пределами и получил формулу для вариации n{\displaystyle n}-кратного интеграла.

За рубежом формула как правило называется «теоремой о дивергенции» (англ. divergence theorem), иногда — формулой Гаусса или «формулой (теоремой) Гаусса—Остроградского».

Видео по теме

См. также

Литература

• Остроградский М. В. Note sur les integrales definies. // Mem. l’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
• Остроградский М. В. Memoire sur le calcul des variations des integrales multiples. // Mem. l’Acad., 1, стр. 35—58, 24/1 1834 (1838).

Примечания

1. ↑ ^{1 2} Ильин В. А. и др. Математический анализ. Продолжение курса / В. А. Ильин, В. А. Садовничий, Бл. X. Сендов. Под ред. А. Н. Тихонова. — М.: Изд-во МГУ, 1987.— 358 с.
2. ↑ В работе по теории звука в 1762 г. Лагранж рассматривает частный случай теоремы: Lagrange (1762) «Nouvelles recherches sur la nature et la propagation du son» (Новые исследования о природе и распространении звука), Miscellanea Taurinensia (Mélanges de Turin), 2: 11 — 172. Репринтное издание: «Nouvelles recherches sur la nature et la propagation du son» в кн.: J.A. Serret, ed., Oeuvres de Lagrange, (Paris, France: Gauthier-Villars, 1867), vol. 1, pages 151—316; на страницах 263—265 Лагранж преобразовывает тройные интегралы в двойные с помощью интегрирования по частям.
3. ↑ ^{1 2} Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 150—151.