формулы и расчеты, закон Био-Савара-Лапласа

Одним из фундаментальных понятий всех происходящих в природе электромагнитных явлений выступает магнитное поле, важнейшей характеристикой которого служит напряжённость.

• Определение и формула напряжённости магнитного поля
• Физический смысл
• Закон Био-Савара-Лапласа
• Циркуляция вектора напряжённости магнитного поля
• Формулы

Определение и формула напряжённости магнитного поля

Вокруг постоянного магнита или проводника с протекающим по нему электрическим током всегда присутствует магнитное поле. Эта одна из форм существования электромагнитного поля, естественного или искусственного происхождения. Как и всякая физическая величина, она имеет свои характеристики, одной из которых выступает напряжённость магнитного поля.

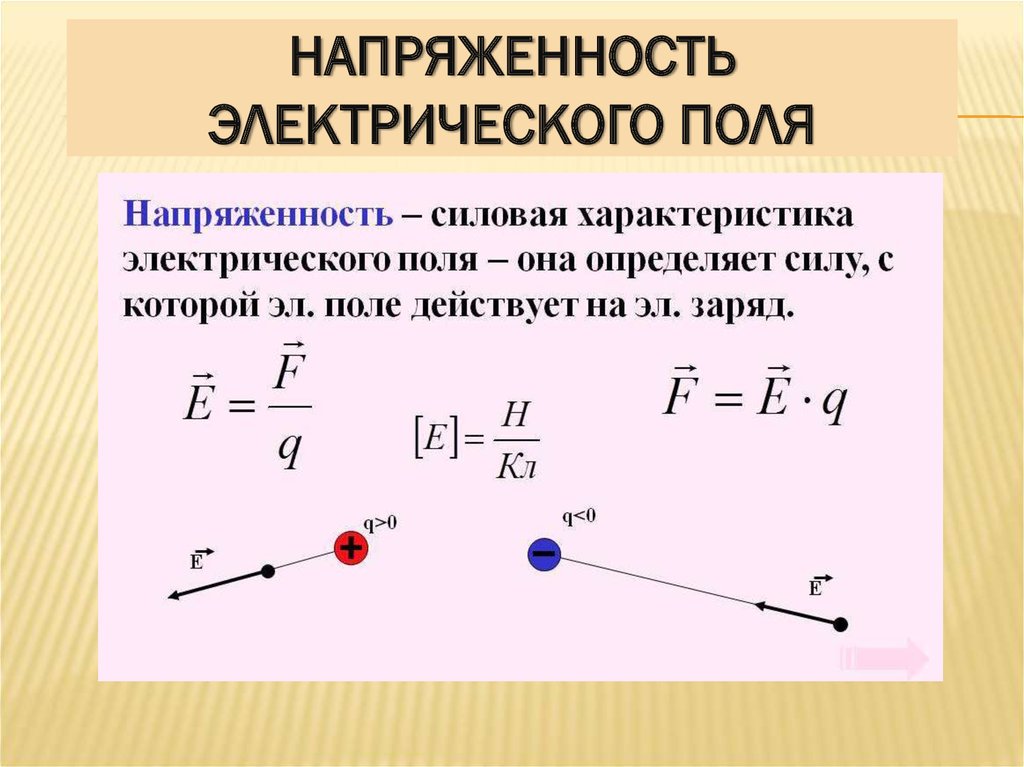
Из курса физики известно, что напряжённость магнитного поля H – это векторная (не скалярная, то есть определённым образом направленная в пространстве) величина, являющейся геометрической разницей между векторами магнитной индукции B и вектором намагниченности M.

Небольшое пояснение. Магнитная индукция B – это силовая векторная характеристика магнитного поля в конкретной точке пространства, которая характеризует силу воздействия на электрический заряд определённой величины, движущийся в этом поле.

Намагниченность M – это векторный показатель, демонстрирующий магнитное состояние тела, являющегося источником возникшего магнитного поля. Формулы, описывающие величину напряжённости магнитного поля в разных системах единиц измерения, выглядят следующим образом:

В системе СИ (Международной системе единиц):

H = 1/μ₀·B – M,

где μ

0 – магнитная постоянная, равная 4π10⁻⁷ Гн/м, или менее точно 1,2566370614 10^-6 Н/А². Единицей измерения напряжённости здесь выступает ампер на метр. 1А/м = 4π/1000Э = 0,01256637Э.

В системе СГС (сантиметр-грамм-секунда):

H = B – 4 πM.

Здесь единицей измерения служит эрстед (Э).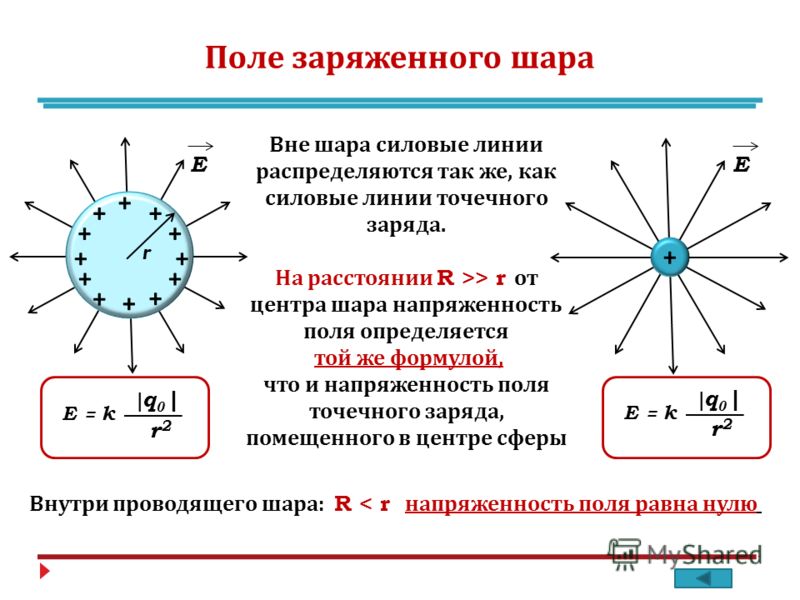 1Э = 1000/4πА/м = 79,5775 А/м. При этом надо в обязательном порядке учитывать, что намагниченность зависит от магнитной проницаемости среды следующим образом:

M = ((μ-1)/4πμ)B, где μ – магнитная проницаемость, составляющая:

• для диамагнетиков (стекло, медь, вода) – 0,99999;
• для парамагнетиков (алюминий, воздух, кислород) – 1,0000;
• для ферромагнетиков: никель – 1100; железо – 8000.

Физический смысл

Физический смысл напряжённости находится в прямой зависимости от среды формирования магнитного поля:

• при её отсутствии или в вакууме, напряжённость и вектор магнитного поля – H и B, совпадают между собой с точностью до величины магнитной постоянной μ₀;
• в магнитной среде напряжённость – H представляет собой величину воздействия «внешнего» поля. Поля, имеющего место быть при отсутствии самого магнитного материала. То есть она соответствует вектору магнитной индукции – B внешних полей воздействия.

Закон Био-Савара-Лапласа

Главный закон магнитостатики, действие которого экспериментально было обнаружено в начале XIX века французскими учёными Био и Саваром, принял свою формулировку благодаря другому французскому исследователю маркизу де Лапласу. Именно он показал, что «магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока». Аналогичный вывод несколько позже был сделан исходя из двух уравнений Максвелла, составляющих совместно с выражениями для силы Лоренца теоретическую основу классической электродинамики.

В обобщённом виде закон выглядит следующим образом:

Пользуясь системой единиц СИ, для вакуума получаем:

где I – ток; dl – вектор, совпадающий и сонаправленный с протекающим током, r – модуль радиус-вектора, направленный в точку определения dB, α – угол между dl и r.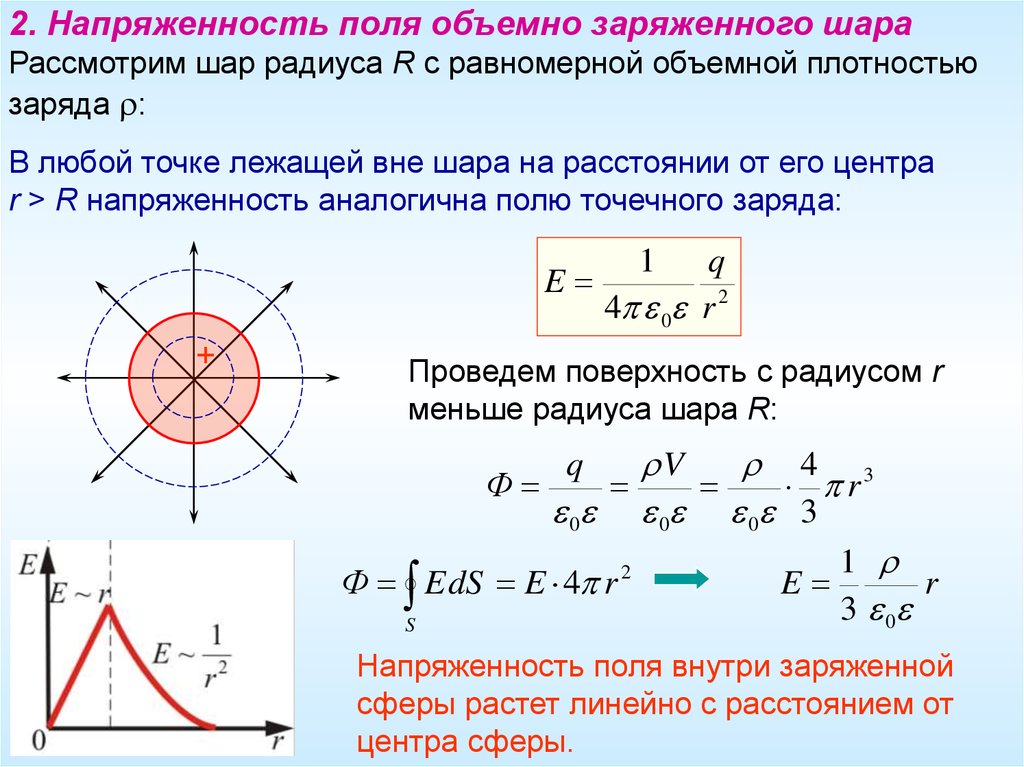

Циркуляция вектора напряжённости магнитного поля

В 1826 году ещё один французский учёный – Андре Мари Ампер сформулировал теорему о циркуляции магнитного поля (позже она также была подтверждена шотландцем Максвеллом), гласящую, что «Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающий контур циркуляции».

Из которой следует, что циркуляция вектора напряжённости магнитного поля соответствует сумме свободных токов, сцепленных с контуром. Связанные токи, образованные в магнетике под воздействием внешних полей, явно здесь не присутствуют.

Формулы

что в дифференциальной форме выглядит следующим образом:

где j – плотность тока, а c – скорость света в вакууме.

Напряжённость магнитного поля в цилиндрической катушке

Напряжённость магнитного поля в цилиндрической катушке прямо пропорциональна силе тока, зависящей, в свою очередь, от прикладываемого напряжения, а также сопротивления, определяемого числом витков катушки и обратно пропорциональна длине катушки.

H = (I·n)/L

В приведённой формуле:

• I – сила протекающего тока;
• n – число витков катушки;
• L – длина цилиндрической катушки.

Вокруг прямолинейного проводника

Магнитное поле, окружающее прямолинейный проводник, напрямую зависит от величины и направления протекающего тока:

H = I/2πr

Где I – величина тока, а r – расстояние точки замера от проводника.

В центре витка с током

Здесь формула расчёта напряжённости практически аналогична случаю прямолинейного проводника:

H = I/2R

Лишь R – обозначает радиус токопроводящего витка.

Определение напряжённости магнитного поля, измерение его величины в разных местах и условиях имеет большое практическое значение. Прежде всего, потому что все мы живём в магнитном поле земли и нередко подвергаемся воздействию внеземных магнитных полей.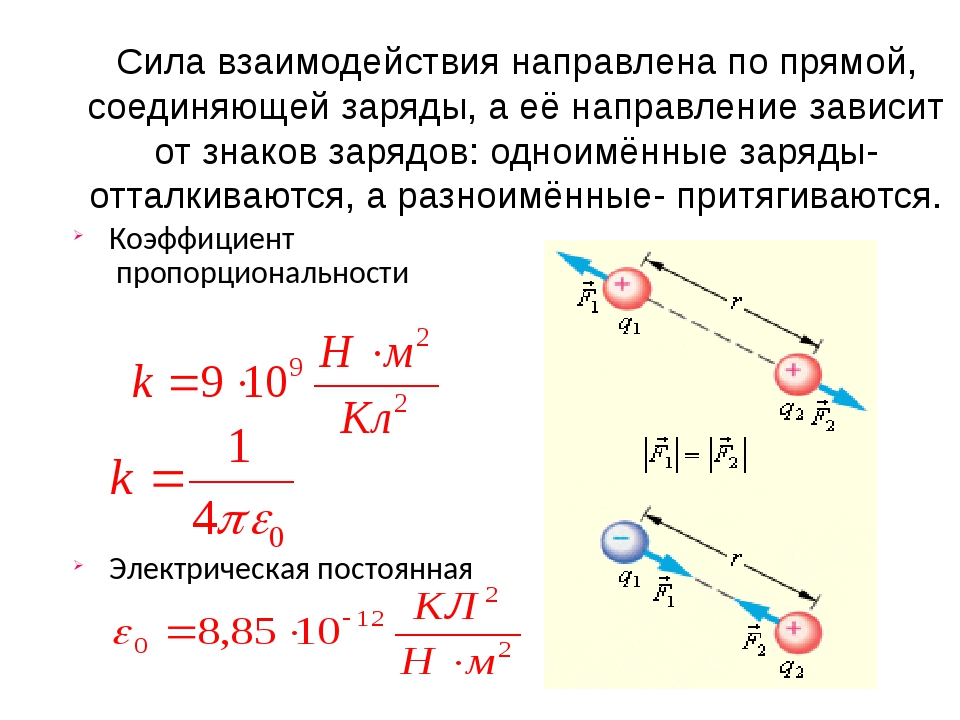

Кроме того, данная величина важна с электротехнических позиций, вследствие электромагнитного воздействия на физические тела, попадающие в зону влияния магнитного поля. Так большое практическое значение находит использование тороидального магнитного поля, образованного катушкой с сердечником, внутри которой оно максимально; а вне её – равняется нулю.

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 2 чел.
Средний рейтинг: 5 из 5.

Формула напряженности магнитного поля в физике

Определение и формула напряженности магнитного поля

Определение

Напряженностью магнитного поля

$\bar{H}$ называют векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:
$$\bar{H}=\frac{\bar{B}}{\mu_{0}}-\bar{J}(1)$$
где $\bar{B}$ – вектор магнитной индукции, $\mu_{0}=4 \pi \cdot 10^{-7}$ Гн/м(Н/А2)- магнитная постоянная, $\bar{j}$ – вектор намагниченности среды в исследуемой точке поля.

Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:

$$\bar{H}=\frac{\bar{B}}{\mu_{0}}$$

В изотропной среде формула (1) преобразуется к виду:

$$\bar{H}=\frac{\bar{B}}{\mu_{0} \mu}$$

где $\mu$ – скалярная величина, называемая относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности магнитного поля и магнитной индукции совпадают по направлению.

Иногда напряженность магнитного поля $d \bar{H}$ определяют как векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:

$$d H=\frac{d F}{\mu_{0} I d l}$$

Намагничивание ферромагнетиков

В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μr и магнитной восприимчивости χ. Большинство веществ являются диамагнетиками (χ = -10-8 … -10-7 и μr < 1) и парамагнетиками (χ = 10-7 … 10-6 и μr > 1), несколько реже встречаются ферромагнетики (χ = 103 … 105 и μr >> 1). Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.

Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.

Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.

На данном графике показана основная кривая намагничивания ферромагнетика. Изначально намагниченность J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика. Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения JНАС. Данное явление называется магнитным насыщением. В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.

Закон Био-Савара-Лапласа

Это важнейший в электромагнетизме закон. Он определяет вектор напряженности $d \bar{H}$ в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:

$$d \bar{H}=\frac{1}{4 \pi} \frac{I}{r^{3}} d \bar{l} \times \bar{r}(5)$$

где $d \bar{l}$ – вектор элемента проводника, который по модулю равен длине проводника, направление совпадает с направлением тока; $\bar{r}$ – радиус–вектор, который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля; $r=|\bar{r}|$ .

Вектор $d \bar{H}$ – перпендикулярен плоскости, в которой находятся векторы $d \bar{l}$ и $\bar{r}$, и направлен так, что из его конца вращение вектора $d \bar{l}$ по кратчайшему пути до совмещения с вектором $\bar{r}$ происходило по часовой стрелке. Для нахождения направления вектора $d \bar{H}$ можно использовать правило буравчика (Буравчик (винт) вращаем так, чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением вектора напряженности поля, которое создает рассматриваемый ток).

Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.

Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует векторно суммировать все элементарные напряженности $d \bar{H}$, порождаемые элементами проводника и найденные по формуле (4).

Закон Ампера. Магнитная индукция поля

Из глубокой древности известны магнитные свойства некоторых железных руд, которые получили свое применение более чем за тысячу лет до нашей эры в устройстве магнитного компаса (устройства, в котором магнитная стрелка свободно вращается вокруг своей оси и показывает направление север — юг).

Практические опыты убеждают, что магниты (куски железных руд) способны создавать вокруг себя особое магнитное поле, которое способно влиять на другой находящийся в данном поле магнит.

Магнитные силы прямого магнита (прямолинейный стержень) сосредоточены в основном на его концах, которые называют полюсами магнита. Например, магнитная стрелка будет поворачиваться около концов магнита (направление вращения стрелки зависит от полюса), но будет оставаться неподвижной, если помещена у средней части магнита.

В магнитном поле магнит будет вести себя точно также как и электрический диполь в электростатическом поле – будет стремиться повернуться по полю.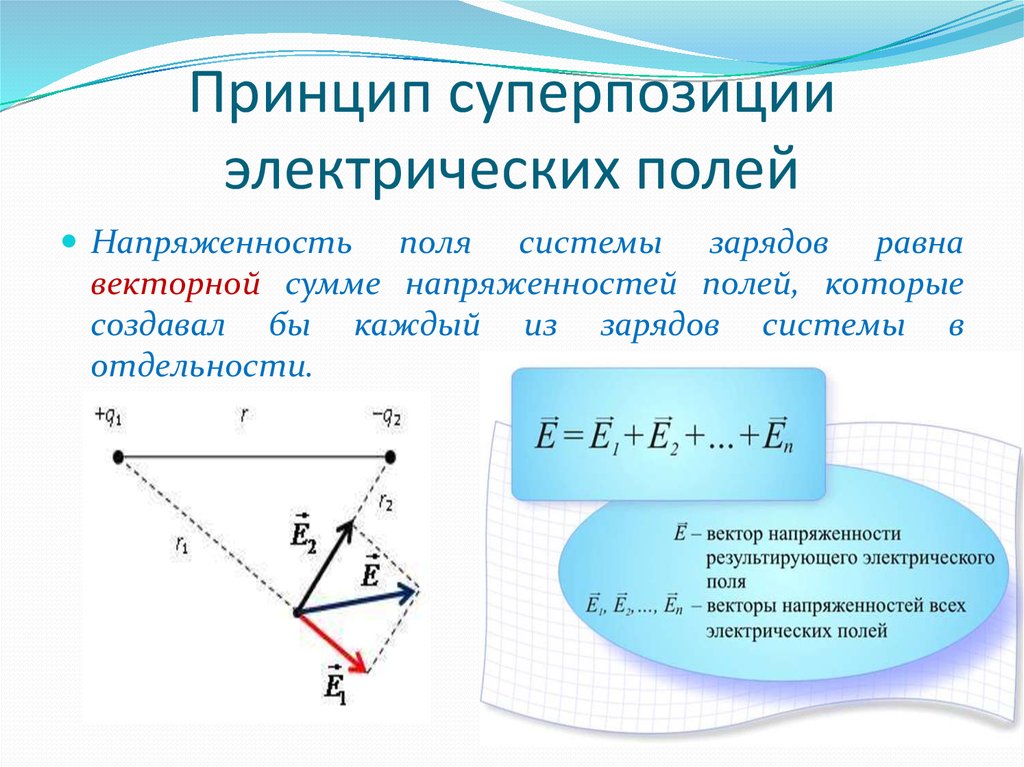 Но есть важный нюанс – если диполь можно разделить на положительный и отрицательный заряды, то при разломе магнита пополам получится два новых магнита, каждый из которых будет иметь свои полюса (северный и южный).

В 1820 году Эрстедом было установлено, что проводники, по которым проходят токи, также взаимодействуют с магнитной стрелкой. Положение магнитной стрелки, которую поместили рядом с проводником с током, также изменяется вместе с изменением величины и направления тока, но при этом стрелка совершенно не реагирует на неподвижные электрические заряды. Из этого явления был сделан вывод, что создавать магнитное поле могут лишь движущиеся электрические заряды (электрический ток), а вокруг неподвижных зарядов существует лишь электростатическое поле.

Магнитное поле, возникающее рядом с проводником с током, как и электрическое поле, обусловленное неподвижными электрическими зарядами, является одним из видов материи. У него имеются определенные физические свойства, такие как инерция, и характеризуется энергией.

Магнитное поле взаимодействует не только с магнитами, но и с электрическими зарядами, находящимися в движении, поскольку они способны сами создавать магнитное поле. Именно поэтому проводники, по которым протекает электрический ток, отталкиваются или притягиваются в зависимости от направления протекающего тока.

Вектор магнитной индукции В является основной характеристикой магнитного поля. Данная величина пропорциональна силе, которая действует на северный конец бесконечно маленькой магнитной стрелки, которая помещена в данную точку магнитного поля. В разных точках поля по направлению и величине индукция имеет различные значения.

Действия магнитного поля на проводник с током было исследовано Ампером. Отсюда и название – закон Ампера.

Если проводник с током помещен во внешнее магнитное поле, например между полюсами магнита, на этот проводник начнет действовать сила F (рисунок ниже), которую можно измерить:

Направление силы F, указанное на рисунке выше, соответствует тому случаю, когда вектор B направлен так, как указывают стрелки, а ток течет перпендикулярно «на нас». При этом было обнаружено, что действующая на прямолинейный проводник с током сила F, прямо пропорциональна силе тока I в проводнике, его длине l, sin α (в данном случае α это угол между вектором В и направлением тока) и магнитной индукции В:

В данном случае k – коэффициент пропорциональности, который зависит от выбранной системы единиц.

Данная формула справедлива для случая однородного поля (в котором вектор В постоянен) и прямолинейного проводника.

В случае, когда поле неоднородно и проводник имеет произвольную форму, формула (1) примет вид:

Данное выражение носит название закон Ампера.

В системе СИ закон Ампера для прямолинейного проводника конечной длины l и однородного поля записывается в виде:

А для системы СГС выражение будет иметь вид:

Здесь с – электродинамическая постоянная, имеющая значение 3·1010 см/с, α – угол между вектором В и направлениями тока в проводнике.

Направление вектора В или силы F определяют с использованием правила левой руки (рисунок ниже):

Правило левой руки звучит так: если указательный палец левой руки направить по полю, а средний по направлению тока, то отогнутый большой палец покажет направление силы, которая действует на проводник с током.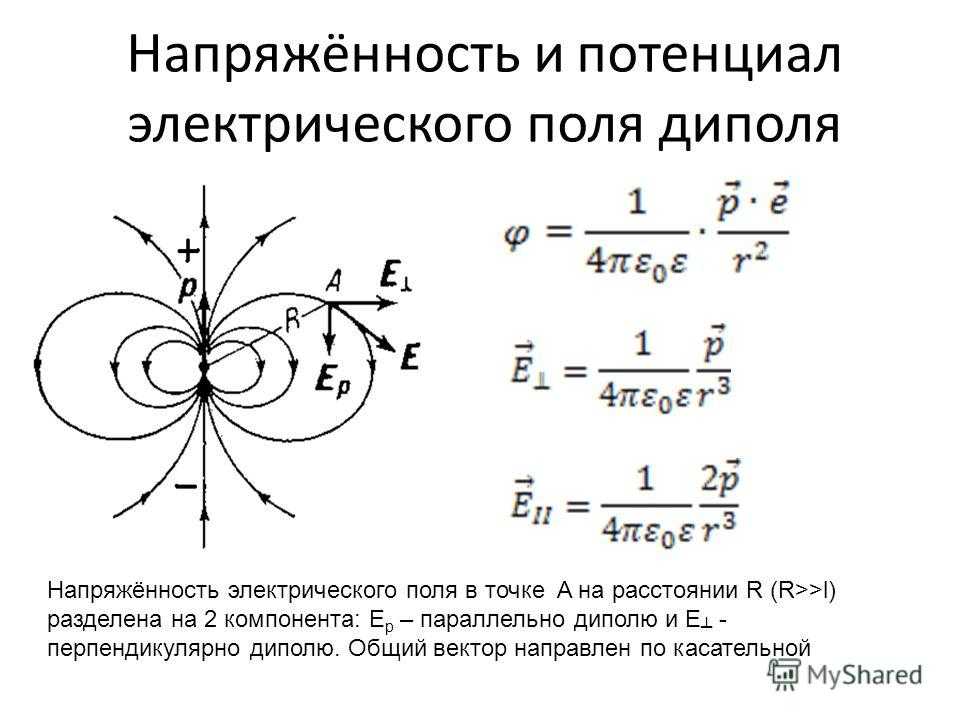

Подтверждением закона Ампера может служить следующий опыт. По свободно провисающему между двумя изоляторами проводнику протекает электрический ток (рисунок ниже):

Когда к проводнику подносят постоянный магнит, то он по мере приближения магнита отклоняется в сторону. Магнит действует на проводник с током с силой F. Проводник также действует на постоянный магнит с силой F, но направленной противоположно и приложенной в данном случае к северному полюсу магнита.

Так же как и электрическое поле, магнитное поле можно отображать графически с магнитных силовых линий или линий магнитной индукции.

Кривые, касательные к которым в каждой точке совпадают с направлением вектора В в этих точках называют линиями магнитной индукции (линии поля В). В отличии от силовых линий электростатического поля линии магнитной индукции всегда замкнуты. Они выходят из северного полюса магнита, входят в южный, и замыкаются внутри магнита.

Линии поля магнита Вмагн. показаны на рисунке выше, а также на рисунке изображены линии поля, созданного проходящим по проводнику электрическим током (Втока). В случае прямолинейного проводника линии магнитной индукции представляют собой концентрические окружности (рисунок ниже):

Направление данных линий определяют с помощью правила буравчика – если по направлению тока ввинчивать буравчик (винт справа), то вращение рукоятки буравчика покажет направление линий B.

Похожие материалы:

• Эквипотенциальные поверхности. Потенциал…
• Связь между напряженностью и потенциалом…
• Условия потенциальности поля. Вихри (ротор)
• Закон Джоуля – Ленца

Магнитный поток

Для характеристики воздействия индукционного фона на контур из металла используют такую величину, как поток. Она является скалярной. В контексте этого необходимо узнать, индукция в чем измеряется. Она зависит от количества идущих через единицу сечения проводящего элемента силовых линий. В международной системе СИ за измерительную единицу принимается Тесла (Тл). Отсюда и название устройства, предназначенного для замеров – теслометра. 1 Тл – индукция, возникающая в полевом пространстве, в котором момент силы в 1 Н*м оказывает воздействие на контур площадью 1 квадратный метр, по которому течет ток в 1 ампер.

Магнитный поток

Магнитное взаимодействие

Французский физик Андре-Мари Ампер в 1820 г. обнаружил, что два проводника, по которым пропущен электрический ток, расположенные параллельно друг другу, притягиваются, если направления токов совпадают, и отталкиваются, если токи направлены в разные стороны. Ампер назвал этот эффект электродинамическим взаимодействием.

Рис. 1. Опыт Ампера по взаимодействию токов в параллельных проводниках.

Для объяснения этого явления Ампер ввел понятие магнитного поля, которое возникает вокруг любого движущегося электрического заряда. Магнитное поле непрерывно в пространстве и проявляет себя, оказывая силовое воздействие на другие движущиеся электрические заряды.

Предшественники Ампера пытались построить теорию магнитного поля по аналогии с электрическим полем с помощью магнитных зарядов с разными знаками (северным N и южным S).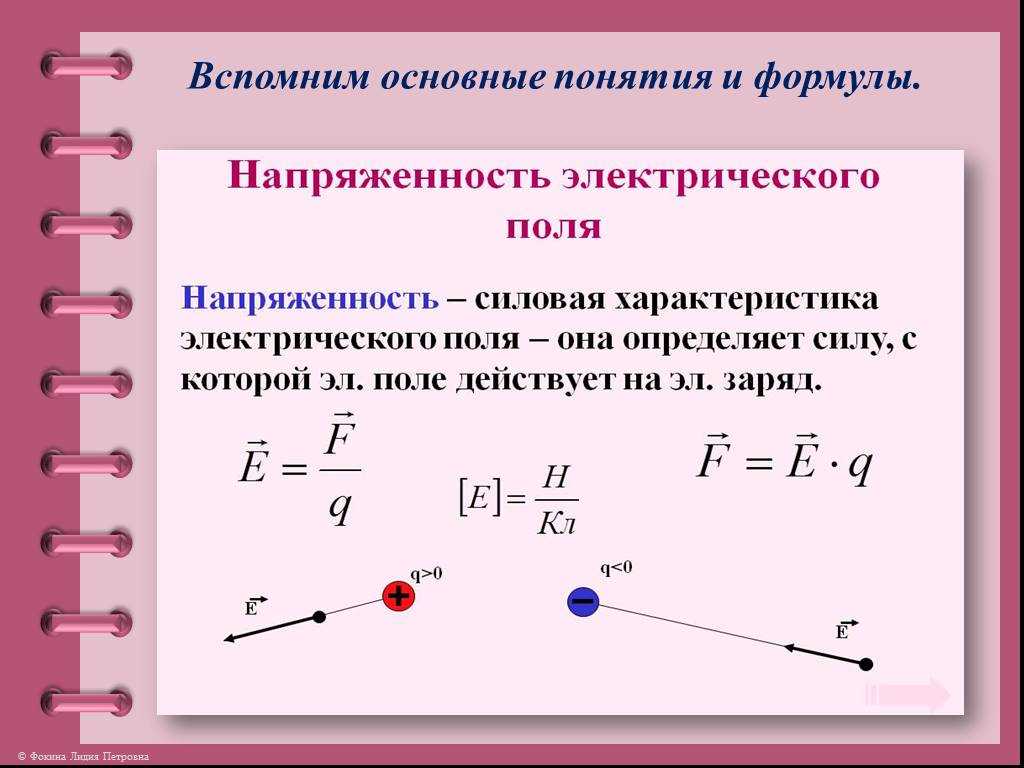

Однако, эксперименты показали, что отдельных магнитных зарядов в природе не существует. Магнитное поле возникает только в результате движения электрических зарядов.

Единица измерения индукции

Единица индукции в системе СИ определяется как индукция такого магнитного поля, в котором на 1 м проводника при силе тока действует сила Ампера величиной 1 Н. Единица называется тесла (Тл).

$1 Тл = {1 Н\over {1 A*1 м}}$ (3).

Единица индукции названа в честь выдающегося сербского инженера, физика Николы Тесла (1856-1943 г.г.). Тесла изобрел электромеханические генераторы, высокочастотный трансформатор. Исследовал свойства токов высокой частоты, изобрел многофазный электродвигатель и системы передачи электроэнергии с помощью переменного тока. Тесла сформулировал основные принципы радиосвязи, изобрел мачтовую антенну для приемки и передачи радиосигналов.

Рис. 3. Портрет Никола Тесла.

Применение силы Лоренца

Данное явление используется в датчиках, применяемых для непрямого замера электротока в локаторах, кабелях, выявления скорости транспорта или турбины.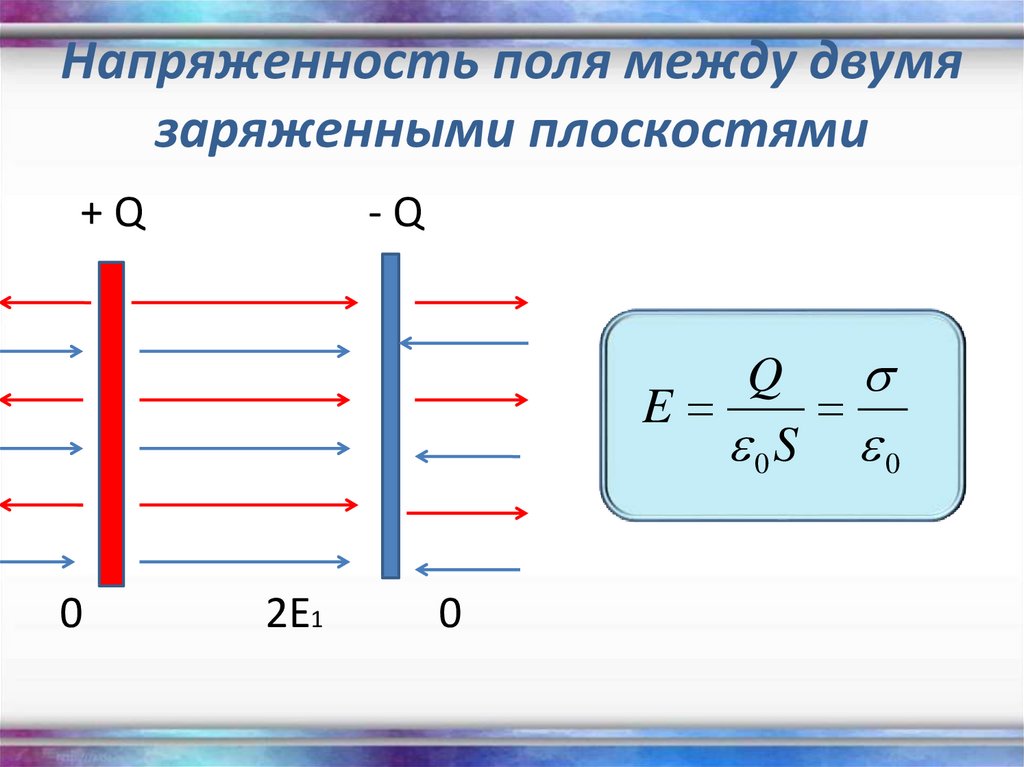 Масс-спектрометры, работая с данной силой, вычисляют удельные заряды элементарных частиц. Лоренцово воздействие заставляет заряды двигаться по кругу. Замерив радиус траектории движения, можно вычислить удельную величину, представляющую собой отношение заряда к массе.

Выглядит выражение так:

Q/m=v/(B*r).

Масс-спектрометр

Формула натяжения — DewWool

Натяжение — это сила, действующая по всей длине веревки, струны, проволоки или тросов. Специальной формулы напряжения не существует. Напряжение является разновидностью контактной силы. Основные законы физики можно применить для расчета силы натяжения струны или веревки. Натяжение всегда представляет собой тянущую силу и проявляется в веревке только тогда, когда ее тянет сила. Здесь, в этой статье, мы обсуждаем формулу напряжения в разных сценариях.

При решении числовых величин, связанных с натяжением, мы принимаем во внимание некоторые допущения, без которых трудно рассчитать натяжение, используя основные законы физики. Это можно рассматривать как идеальный случай, который не всегда соответствует действительности в сценариях реальной жизни.

• Натяжение одинаково во всех точках веревки.
• Рассматриваемый канат не имеет массы.
• Игнорируйте незначительные эффекты трения, сопротивления воздуха и других нежелательных факторов, если не указано иное.
• Все расчеты сделаны для планеты Земля и значения g (ускорение свободного падения составляет 9,8 м/с ² .

В этой статье мы вычисляем формулу напряжения для следующих 10 сценариев:

1. Натяжение каната, тянущего блоки горизонтально
2. Натяжение каната, тянущего блоки горизонтально с участием кинетического трения
3. Натяжение веревки во время перетягивания каната
4. Натяжение вертикально подвешенного провода с грузом
5. Натяжение каната, прикрепленного к грузу под углом
6. Напряжение в лифте
7. Человек, идущий по натянутой веревке
8. Натяжение проволоки при круговом движении
9. Натяжение троса шкива
10. Натяжение троса с наклоном и шкивом

Формула для натяжения веревки, тянущей блоки по горизонтали Натяжение веревки, тянущей блоки по горизонтали

Это наиболее распространенная форма натяжения в задаче о струне.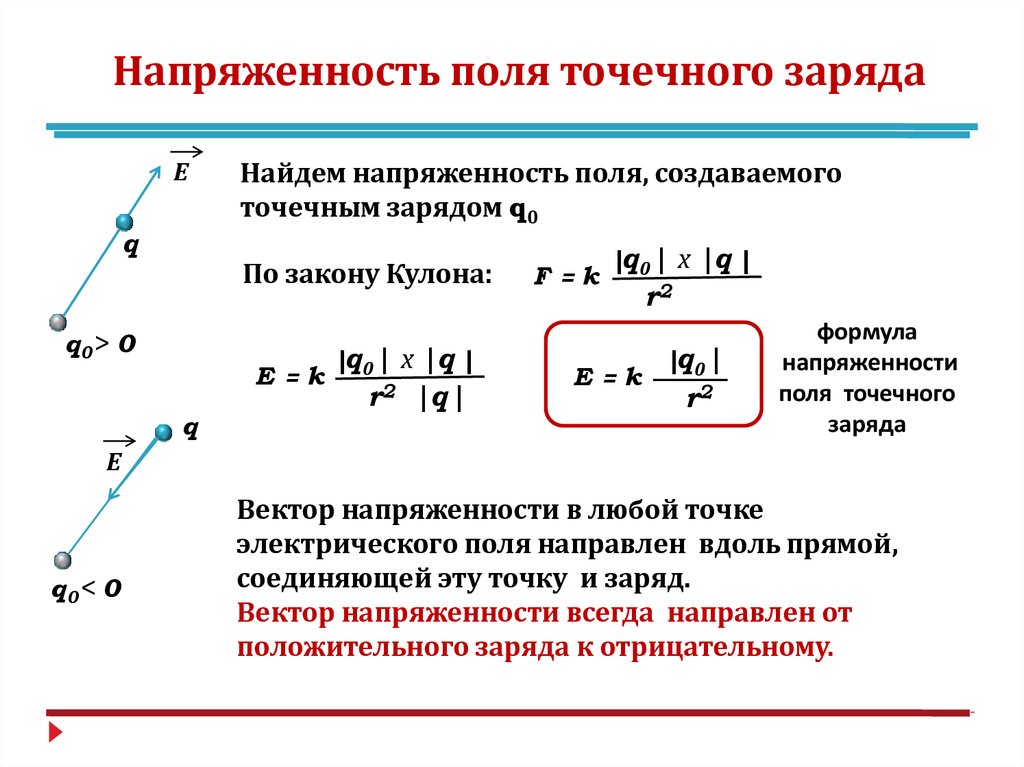 Веревкой тянут два блока, находящихся на расстоянии друг от друга. Блоков может быть n, но натяжение каждой веревки будет разным. Здесь сила F тянет блоки массами M1 и M2 по поверхности без трения (uk=0).

Для всей системы: Fnet(для всей системы) = Общая масса*ускорение => Ускорение(a) = F/(M ₁ +M ₂ )

Используя диаграмму свободного тела как показано выше, мы сосредоточились на двух блоках по отдельности и рассчитали формулу для натяжения.

T = M ₁ *a T = F + M ₂ *a

Оба уравнения можно использовать для определения значения натяжения веревки. Значения напряжения будут одинаковыми. Единицей силы натяжения в системе СИ является Ньютон. Вы можете прочитать наш блог о единицах силы для более подробной информации.

Формула натяжения веревки, тянущей блоки по горизонтали с учетом кинетического трения

Кинетическое трение – это противодействующая сила между двумя телами, движущимися относительно друг друга. В идеальном случае проблем с напряжением всегда будет Фактор трения. Обычно мы опускаем его для упрощения вычислений. Статическое трение будет иметь место в случаях, когда сила, приложенная к системе, меньше предельного трения.

Формула для натяжения веревки, тянущей блоки по горизонтали с учетом трения.

Здесь результирующая сила системы будет включать приложенную силу тяги, силу натяжения плюс силу трения в направлении, противоположном приложенной силе. Следует отметить, что сила трения будет применяться к каждому объекту с массой.

Формула трения = μ _k *N => μ _k * (m*g) [где μ _k — коэффициент кинетического трения] Трение всей системы = μ _k ( m1+m2)*g Трение блока1 = m1*g Трение блока2 = m2*g

Используя диаграмму свободного тела, как показано выше,

Блок 1: Сила натяжения и сила трения действуют в противоположных направлениях.

Fnet = T – трение => T = μ _k *m ₁ *g + m ₁ *a

Блок 2: Сила приложена вправо. Натяжение и сила трения действуют в одном направлении.

Fnet = F – T – трение => T = F – μ _k *m ₂ *g – m ₂ *a   

Формула натяжения веревки во время перетягивания каната

В игре «Перетягивание каната» две команды тянут одну веревку навстречу друг другу в противоположных направлениях. Побеждает та команда, которая перетянет противника на свою сторону. Сила команды передается через натяжение веревки, чтобы тянуть противника. Найдем формулу напряженности в таком сценарии.

Формула натяжения каната для перетягивания каната

F = масса x ускорение => F _net = общая масса x a _net => a _net = F _net /общая масса

Ускорение во всей системе будет одинаковым. Используем это значение ускорения в уравнении сил для обоих тел и вычисляем формулу натяжения. Вы можете прочитать здесь для подробного вывода.

T = F1 – [(M ₁ +M ₂ )*ускорение] T = F2 – [(M ₃ +M ₄ )*ускорение]

Формула натяжения вертикально подвешенного троса с грузом Натяжение вертикально подвешенного троса с грузом груз под углом

Струны не всегда будут крепиться в вертикальном или горизонтальном положении. Как правило, они крепятся под углом в соответствии с удобством. Например, серийные провода освещения сделаны так, чтобы свободно висеть в елке. Возможно, вы видели линию свешивания ткани, которая никогда не бывает прямой, она изгибается из-за веса. Попробуем рассчитать натяжение струн такого подобного случая.

Натяжение нити, закрепленной под углом

Здесь груз (масса m) подвешен на двух тросах с натяжением T1 и T2. Поскольку задействовано два провода, натяжение может быть разным. Угол, который провода образуют с потолком, обозначен как a и b.

Сначала мы нарисуем диаграмму свободного тела для блока. Силы натяжения разрешаются в горизонтальном и вертикальном направлениях. Сила mg будет действовать вниз за счет гравитационного притяжения, а натяжение будет действовать в противоположном направлении, т.е. вверх.

T1 sin(a) + T2 sin(b) = m*g ———-(1)

T1cos(a) = T2cos(b)———————(2)

Решая уравнения (1) и (2), мы можем получить решение для T1 и T2. Заметим, что если угол a=b, то натяжение T1 будет равно T2.

Формула для натяжения в лифте Натяжение тросов в лифте

Это классическая численная задача физики для определения силы натяжения. Когда кто-нибудь подвешен на веревке в состоянии покоя, тогда натяжение равно весу тела. Но когда веревку тянут вверх или вниз с ускорением, значение натяжения изменяется. Напряжение всегда будет выше при подтягивании тела вверх по сравнению с опусканием.

T = m*g [Когда лифт стоит]

T = m*(g-a) [Когда лифт идет вниз]

T = m*(g+a) [Когда лифт движение вверх]

Человек, идущий по канату Натяжение каната: Человек массой m, идущий по канату

Возможно, вы видели или слышали о каскадерах, идущих по канату. Эта задача аналогична гире, подвешенной на двух тросах. Вес человека можно принять как блок, свободно подвешенный на двух тросах, образующих угол с потолком. Натяжение будет разным на двух участках веревки, за исключением случаев, когда человек находится точно в середине.

T1 sin(a) + T2 sin(b) = m*g ———-(1)

T1cos(a) = T2cos(b)———————(2)

Формула натяжения проволоки при круговом движении Натяжение струны при круговом движении

Вы когда-нибудь раскачивали груз, прикрепленный к струне? Вы бы почувствовали натяжение струны в своих руках.

Здесь сила mg груза под действием силы тяжести будет действовать вниз, а натяжение будет действовать к нам, от груза. На груз действует еще одна дополнительная сила. Это называется центростремительной силой. Это сила, которая пытается притянуть объект к центру, т.е. к вам. Итак, на тело действуют три силы: гравитационная, натяжная и центростремительная.

У нас есть три вектора, поэтому мы решаем векторы и находим формулу для натяжения струны.

Натяжение = sqrt[(mg) ² +(mv ² /r) ² ]

Формула натяжения каната шкива Формула натяжения каната Шкив

Шкив используется для уменьшения усилий при подъеме тяжелых предметов. Он состоит из неподвижного колеса, по которому свободно проходит веревка или веревка. При определении силы натяжения мы предполагаем, что трение между канатом и шкивом равно нулю.

В системе шкивов есть два случая. Веревка может двигаться вверх или вниз с ускорением а. Напряжение в обоих сегментах будет одинаковым. Запишем уравнение для чистой силы в каждом из блоков и рассчитаем натяжение веревки из двух уравнений.

Для блока 1: движение вверх против силы тяжести с ускорением a

м ₁ *a = T – m*g [чистая сила = натяжение – сила тяжести]
T = m ₁ *а + м ₁ *g

Для блока 2: движение вниз под действием силы тяжести с ускорением а T = m ₁ *g – m ₁ *a

Формула натяжения каната с наклоном и шкивом Натяжение каната с наклоном и шкивом

В реальной жизни, сила, действующая на объект, будет строго горизонтальной или вертикальной. Он всегда будет под углом. Итак, давайте посмотрим на этот пример, где два блока прикреплены к канату шкива. Один блок помещается под наклоном, что также связано с кинетическим трением о поверхность.

На блок m1 будут действовать четыре силы. Вес, нормальная сила, натяжение и кинетическая сила трения. Мы должны решить силы, чтобы составить уравнение в горизонтальном и вертикальном направлениях.

Чистая сила (M₁) = T – m₁gsinθ – трение T = M₁a – M₁gsinθ – μ _k M₁g

На блок m2 будут действовать две силы. Вес и натяжение веревки.

Чистая сила (M₂) = M₂g – натяжение T = M₂g – M₂a

Используя приведенные выше два уравнения, мы можем найти значение силы натяжения.

Исследование силы натяжения:

Натяжение струн в гитаре может влиять на издаваемый ею звук. Натяжение струны регулируется при настройке гитары, чтобы получить определенную ноту. Прочтите эту статью «Влияние изменения натяжения струн на воспринимаемую высоту звука классической гитары», чтобы узнать больше об этом.

Может ли напряжение иметь отрицательное значение?

Если значение натяжения отрицательное, то это означает, что сила направлена ​​в противоположном направлении. Во-вторых, поскольку сила направлена ​​в противоположную сторону, в большинстве случаев на веревку может действовать сила сжатия, а не сила натяжения.

Одинаково ли значение натяжения во всех точках каната?

Для простоты считаем, что веревка при расчете не имеет массы. На самом деле веревка будет иметь некоторую массу. И значение натяжения веревки будет разным в разных местах веревки.

Предположим, например, что вы тянете веревку с потолка с силой F1, тогда натяжение ближнего к вам конца веревки будет примерно F1. Но, по мере продвижения дальше, значение напряжения будет уменьшаться.

См. также:

• Формула натяжения — Перетягивание каната
• Формула натяжения — натяжение каната, тянущего блоки горизонтально
• Формула натяжения — Веревка, тянущая блоки горизонтально с участием кинетического трения
• Формула натяжения — канат
• Формула натяжения: Натяжение вертикально подвешенной проволоки с грузом
• Элеватор натяжения
• Формула натяжения при круговом движении
• Система шкивов

Натяжение струн: уравнение, размеры и расчет

Сила натяжения — это сила, возникающая в веревке, струне или кабеле при растяжении под действием приложенной силы.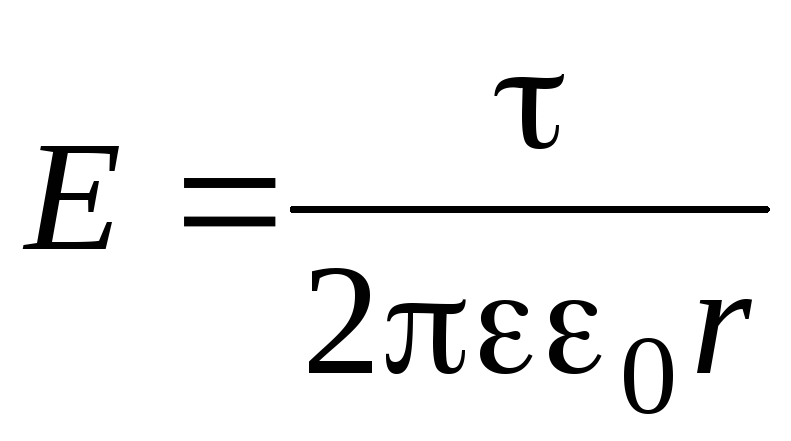

Это сила, возникающая при приложении нагрузки к концам объекта, обычно к его поперечному сечению. Его также можно назвать тянущей силой, напряжением или напряжением.

Этот тип силы проявляется только при контакте между кабелем и объектом. Натяжение также позволяет передавать силу на относительно большие расстояния.

Натяжение при отсутствии ускорения

Предположим, у нас есть тело массой (m) на отрезке нити, как показано ниже. Гравитация тянет его вниз, что составляет его вес:

Натяжение струны

Чтобы струна не разгонялась вниз из-за своей массы, ее нужно тянуть обратно вверх с равной силой. Это то, что мы называем напряжением. Если он не ускоряется, мы можем сказать, что T = mg.

Напряжение при ускорении

в лифте, поднимающем людей на верхние этажи здания, напряжение не может быть таким же, как вес груза — оно обязательно будет больше. Итак, откуда берется дополнение? Напряжение = усилие для балансировки + дополнительная сила для ускорения. Это моделируется математически как:

Т = мг + мА

Т = м (г + а).

Другой сценарий, когда лифт спускается вниз. Натяжение не будет равно 0, что приведет к свободному падению. Он будет немного меньше веса предмета. Итак, если выразить это уравнение словами, напряжение = сила, необходимая для баланса, — сила сбрасывается. Математически это будет

T = mg — ma

T = m (g — a).

Примеры работы

Давайте посмотрим на пару примеров работы.

Когда частицы высвобождаются из состояния покоя на приведенной ниже диаграмме, каково натяжение удерживающей их струны?

Пример натяжения струны

Ответ:

В такой ситуации упадет частица с наибольшей массой, а поднимется частица с наименьшей массой. Возьмем частицу массой 2 кг за частицу a, а частицу массой 5 ​​кг за частицу b.

Чтобы уточнить вес каждой частицы, мы должны умножить ее массу на силу тяжести.

Вес a = 2 г

Вес b = 5 г

Теперь вы можете смоделировать уравнение для ускорения и напряжения каждой частицы.

T -2g = 2a [Частица a] [Уравнение 1]

5g -T = 5a [Частица b] [Уравнение 2]

Теперь вы решаете это одновременно. Добавьте оба уравнения, чтобы исключить переменную T.

3g = 7a

Если брать газ

Вы можете подставить ускорение в любое из уравнений, чтобы получить напряжение.

Подставьте ускорение в уравнение 1.

T — 19,6 = 8,4

T=28N

Имеются две частицы, одна массой 2 кг сидит на гладком столе, а другая массой 20 кг висит сбоку стола над шкивом, соединяющим обе частицы – показано ниже. Эти частицы удерживались на месте все это время, и теперь они высвобождаются. Что будет дальше? Чему равны ускорение и натяжение струны?

Натяжение струны с одной частицей на гладком столе

Ответ: Дополним диаграмму, чтобы увидеть, с чем мы работаем.

Натяжение нити с одной частицей на гладком столе

Примем частицу массой 2 кг за частицу А.

А частицу массой 20 кг за частицу В.

Теперь разложим частицу А по горизонтали.

T = ma [уравнение 1]

Разделение частицы B по вертикали

mg -T = ma [уравнение 2]

Подставляем в них числа:

T = 2a [Уравнение 1]

20g — T = 20a [Уравнение 2]

Теперь мы можем сложить оба уравнения, чтобы исключить напряжения.

20g = 22a

Теперь разложите ускорение в любом из уравнений. Мы бы сделали первое.

T=17.8N

Натяжение под углом

Мы можем рассчитать натяжение веревки, прикрепленной к грузу под углом. Давайте возьмем пример, чтобы увидеть, как это делается.

Найдите натяжение каждой части струны на диаграмме ниже.

Растяжение под углом

Ответ: нам нужно будет составить из всей диаграммы два уравнения – одно для вертикальных сил, а другое для горизонтальных. Итак, что мы собираемся сделать, так это разделить натяжение обеих струн на их соответствующие вертикальную и горизонтальную составляющие.

Натяжение под углом

[Уравнение 1] [Вертикальное]

[Уравнение 2] [Горизонтальное]

Поскольку у нас есть два уравнения и два неизвестных, мы собираемся использовать процедуру одновременного уравнения, чтобы сделать это путем замены.

Теперь перестроим второе уравнение и подставим его в первое уравнение.

Теперь, когда у нас есть значение для , мы можем подставить его в любое из уравнений. Воспользуемся вторым.

Натяжение струн.