Механическая работа. Мощность 7 класс онлайн-подготовка на Ростелеком Лицей

Работа – физическая величина

 

В нашем повседневном опыте слово «работа» встречается очень часто. Но следует различать работу физиологическую и работу с точки зрения науки физики. Когда вы приходите с уроков, вы говорите: «Ой, как я устал!». Это работа физиологическая. Или, к примеру, работа коллектива в народной сказке «Репка».

 

Рис. 1. Работа в повседневном смысле слова

Мы же будем говорить здесь о работе с точки зрения физики.

Механическая работа совершается, если под действием силы происходит перемещение тела. Работа обозначается латинской буквой А. Более строго определение работы звучит так.

Работой силы называется физическая величина, равная произведению величины силы на расстояние, пройденное телом в направлении действия силы.

 

Рис. 2. Работа – это физическая величина

Формула  справедлива, когда на тело действует постоянная сила.

В международной системе единиц СИ работа измеряется в джоулях.

Это означает, что если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа 1 джоуль.

Единица работы названа в честь английского ученого Джеймса Прескотта Джоуля.

 

Рис. 3. Джеймс Прескотт Джоуль (1818 – 1889)

 

Работа может равняться нулю и быть отрицательной

 

 

Из формулы для вычисления работы  следует, что возможны три случая, когда работа равна нулю.

 

Первый случай – когда на тело действует сила, но тело не перемещается. Например, на дом действует огромная сила тяжести. Но она не совершает работы, поскольку дом неподвижен.

Второй случай – когда тело перемещается по инерции, то есть на него не действуют никакие силы. Например, космический корабль движется в межгалактическом пространстве.

Третий случай – когда на тело действует сила, перпендикулярная направлению движения тела. В этом случае, хотя и тело перемещается, и сила на него действует, но нет перемещения тела в направлении действия силы.

Рис. 4. Три случая, когда работа равна нулю

Следует также сказать, что работа силы может быть отрицательной. Так будет, если перемещение тела происходит против направления действия силы. Например, когда подъемный кран с помощью троса поднимает груз над землей, работа силы тяжести отрицательна (а работа силы упругости троса, направленная вверх, наоборот, положительна).

 

Мощность – быстрота выполнения работы

 

 

Предположим, при выполнении строительных работ котлован необходимо засыпать песком. Экскаватору для этого понадобится несколько минут, а рабочему с помощью лопаты пришлось бы трудиться несколько часов. Но и экскаватор, и рабочий при этом выполнили бы одну и ту же работу.

 

Рис. 5. Одну и ту же работу можно выполнить за разное время

Чтобы охарактеризовать быстроту выполнения работы в физике используется величина, называемая мощностью.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.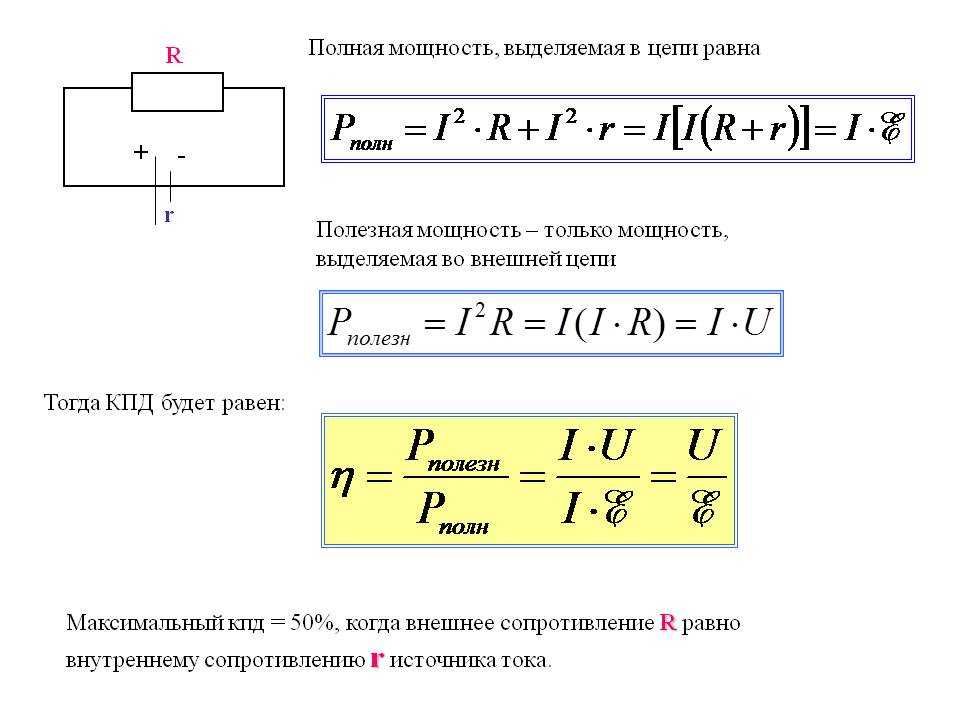

Мощность обозначается латинской буквой N.

Единицей измерения мощности я системе СИ является ватт.

Один ватт – это мощность, при которой работа в один джоуль совершается за одну секунду.

Единица мощности названа в честь английского ученого, изобретателя паровой машины Джеймса Уатта.

 

Рис. 6. Джеймс Уатт (1736 – 1819)

 

Еще одна формула для вычисления мощности

 

 

Объединим формулу для вычисления работы  с формулой для вычисления мощности.

 

Вспомним теперь, что отношение пути, пройденного телом, S, ко времени движения t представляет собой скорость движения тела v.

Таким образом, мощность равна произведению численного значения силы на скорость движения тела в направлении действия силы.

Этой формулой удобно пользоваться при решении задач, в которых сила действует на тело, движущееся с известной скоростью.

 

Список литературы

1. Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
2. Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
3. Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «physics.ru» (Источник)
2. Интернет-портал «festival.1september.ru» (Источник)
3. Интернет-портал «fizportal.ru» (Источник)
4. Интернет-портал «elkin52.narod.ru» (Источник)

 

Домашнее задание

1. В каких случаях работа равна нулю?
2. Как находится работа на пути, пройденном в направлении действия силы? В противоположном направлении?
3. Какую работу совершает сила трения, действующая на кирпич, при его перемещении на 0,4 м? Сила трения равна 5 Н.

 

Помогите посчитать мощность насоса. № 714 ГДЗ Сборник задач по физике 7-9 класс Лукашик. – Рамблер/класс

Помогите посчитать мощность насоса. № 714 ГДЗ Сборник задач по физике 7-9 класс Лукашик. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Определите среднюю мощность насоса, который,
преодолевая силу тяжести, подает воду объемом 4,5 м³ на
высоту 5 м за 5 мин.
 

ответы

Привет. Лови!

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

№ 179 Сборник задач по физике 7-9 класс Лукашик. Почему патрон продолжает вращаться?

У кого есть ответ?
Почему после выключения двигателя сверлильного станка патрон продолжает вращаться?
 

ГДЗФизика7 класс8 класс9 классЛукашик В.И.

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!

ГИА9 класс

7.4 Мощность – общая физика с использованием вычислений I

7 Работа и кинетическая энергия

Цели обучения

К концу этого раздела вы сможете:

• Соотносить работу, выполненную в течение интервала времени, с передаваемой мощностью
• Найти мощность, затрачиваемую силой, действующей на движущееся тело

Понятие работы включает в себя силу и перемещение; теорема о работе-энергии связывает чистую работу, совершаемую над телом, с разницей его кинетической энергии, вычисленной между двумя точками на его траектории. Ни одна из этих величин или отношений не включает время в явном виде, однако мы знаем, что время, доступное для выполнения определенного объема работы, часто так же важно для нас, как и сам объем. На открывающем главу рисунке несколько спринтеров могли достичь одинаковой скорости на финише и, следовательно, выполнить одинаковый объем работы, но победитель гонки выполнил ее за наименьшее количество времени.

Мы выражаем отношение между выполненной работой и интервалом времени, затрачиваемым на ее выполнение, вводя понятие мощности. Поскольку работа может меняться в зависимости от времени, мы сначала определим среднюю мощность как работу, выполненную за интервал времени, деленную на интервал

.

[латекс] {P} _ {\ text {ave}} = \ frac {\ Delta W} {\ Delta t}. [/latex]

Затем мы можем определить мгновенную мощность (часто называемую просто мощностью ).

Мощность

Мощность определяется как скорость выполнения работы или предел средней мощности для интервалов времени, приближающихся к нулю,

[latex]P=\frac{dW}{dt}. [/latex]

 

Если мощность постоянна в течение временного интервала, средняя мощность для этого интервала равна мгновенной мощности, а работа, выполненная агентом, поставляющим мощность, равна [latex]W=P\Delta t[/latex]. Если мощность в течение интервала меняется со временем, то выполненная работа есть интеграл мощности по времени,

[латекс]W=\int Pdt.[/латекс]

Теорема о работе-энергии описывает, как работа может быть преобразована в кинетическую энергию. Поскольку существуют и другие формы энергии, как мы обсудим в следующей главе, мы также можем определить мощность как скорость передачи энергии. Работа и энергия измеряются в джоулях, поэтому мощность измеряется в джоулях в секунду, которой в системе СИ присвоено название ватт, аббревиатура Вт: [латекс]1\,\текст{Дж/с}=1\, \text{W}[/латекс]. Другой распространенной единицей измерения мощности повседневных устройств является мощность в лошадиных силах: [latex]1\,\text{hp}=746\,\text{W}[/latex].

Пример

Сила подтягивания

Военнослужащий массой 80 кг делает 10 подтягиваний за 10 с (рисунок). Какую среднюю мощность развивают мышцы тренирующегося при перемещении его тела? ( Подсказка: Сделайте разумные оценки для любых необходимых количеств.)

Рисунок 7.14 Какая мощность затрачивается на выполнение десяти подтягиваний за десять секунд?

Стратегия

Работа, совершаемая против силы тяжести при движении вверх или вниз на расстояние [латекс]\Delta y[/latex], равна [latex]mg\Delta y.[/latex] (Если вы поднимаете и опускаете себя с постоянной скоростью , сила, которую вы прикладываете, компенсирует гравитацию на протяжении всего цикла подтягивания.) Таким образом, работа, выполняемая мышцами тренирующегося (движущими, но не ускоряющими свое тело) за полное повторение (вверх и вниз), составляет [латекс]2 мг\ Delta y.[/latex] Предположим, что [латекс]\Delta y=2\text{ft}\примерно 60\,\text{см}\text{.}[/latex] Также предположим, что длина ветвей составляет 10 % от массы тела и не входят в подвижную массу. При этих предположениях мы можем рассчитать работу, проделанную за 10 подтягиваний, и разделить на 10 с, чтобы получить среднюю мощность. 9{2})(0,6\,\text{m})}{10\,\text{s}}=850\,\text{W}\text{.}[/latex]

 

Значимость

Это типично для расхода энергии при напряженных упражнениях; в бытовых единицах это несколько больше одной лошадиной силы [латекс](1\,\text{hp}=746\,\text{W}).[/latex]

Проверьте свои знания

Оцените мощность, затрачиваемую тяжелоатлетом, поднимающим штангу массой 150 кг на 2 м за 3 с.

Show Solution

980 Вт

Сила, необходимая для перемещения тела, также может быть выражена через действующие на него силы. Если сила [латекс]\mathbf{\overset{\to }{F}}[/latex] действует на тело, которое смещается [латекс]d\mathbf{\overset{\to }{r}}[/latex ] за время dt , сила затрачиваемая силой

[латекс] P = \ frac {dW} {dt} = \ frac {\ mathbf {\ overset {\ to {F}} \ cdot d \ mathbf {\ overset {\ to} {r}}} {dt } = \ mathbf {\ overset {\ to} {F}} \ cdot (\ frac {d \ mathbf {\ overset {\ to {r}}} {dt}) = \ mathbf {\ overset {\ to} {F}}\cdot\mathbf{\overset{\to}}{v}},[/latex]

, где [латекс]\mathbf{\overset{\to }{v}}[/латекс] — скорость тела. Тот факт, что пределы, подразумеваемые производными, существуют для движения реального тела, оправдывает перестановку бесконечно малых величин.

Пример

Мощность автомобиля при движении вверх по склону

Сколько мощности должен затратить автомобильный двигатель, чтобы поднять автомобиль массой 1200 кг на подъем с уклоном 15% со скоростью 90 км/ч (рисунок)? Предположим, что 25% этой мощности рассеивается на преодоление сопротивления воздуха и трения.

Рисунок 7.15 Мы хотим рассчитать мощность, необходимую для движения автомобиля в гору с постоянной скоростью.

Стратегия

При постоянной скорости кинетическая энергия не изменяется, поэтому чистая работа, затраченная на перемещение автомобиля, равна нулю. Следовательно, мощность двигателя, необходимая для движения автомобиля, равна мощности, затрачиваемой на преодоление силы тяжести и сопротивления воздуха. По предположению, 75% мощности передается против силы тяжести, что равно ,\text{sin}\,\theta ,[/latex], где [latex]\theta[/latex] — угол наклона.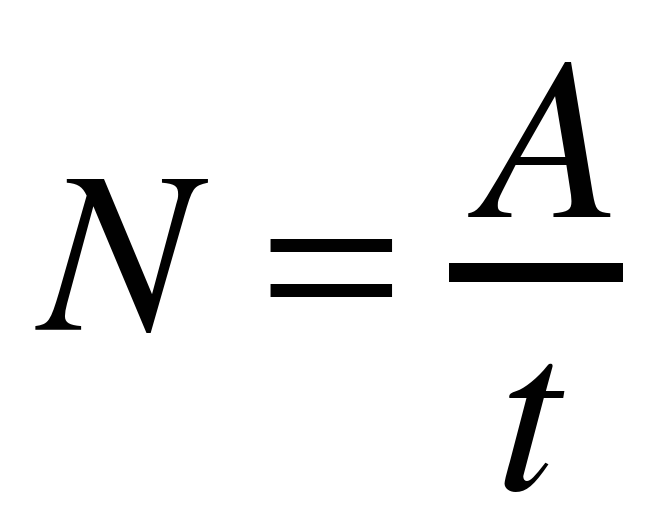 Оценка 15% означает [латекс]\текст{тангенс}\,\тета = 0,15.[/латекс] Это рассуждение позволяет нам определить требуемую мощность. 9\circ)}{0,75}=58\,\text{кВт,}[/latex]

или около 78 л.с. (Вы должны указать шаги, используемые для преобразования единиц.)

Значимость

Это разумное количество мощности для двигателя автомобиля малого и среднего размера, чтобы обеспечить [латекс](1\,\text{hp}= 0,746\,\text{кВт}\text{).}[/latex] Обратите внимание, что это только мощность, затраченная на движение автомобиля. Большая часть мощности двигателя уходит куда-то еще, например, на отработанное тепло. Вот почему автомобилям нужны радиаторы. Любая оставшаяся мощность может быть использована для ускорения или для управления аксессуарами автомобиля.

Резюме

• Мощность – это скорость выполнения работы; то есть производная работы по времени.
• В качестве альтернативы, работа, выполненная за интервал времени, является интегралом мощности, подаваемой за интервал времени.
• Мощность, передаваемая силой, действующей на движущуюся частицу, представляет собой скалярное произведение силы и скорости частицы.

Ключевые уравнения

«>

Работа силы над бесконечно малым перемещением	[латекс] dW = \ mathbf {\ overset {\ to {F}} \ cdot d \ mathbf {\ overset {\ to {r}} = | \ mathbf {\ overset {\ to {F}} ||d\mathbf{\overset{\to}}{r}}|\text{cos}\,\theta[/latex]
Работа силы, действующей на пути от А до В	[латекс] {W} _ {AB} = \ underset {\ text {path} AB} {\ int} \ mathbf {\ overset {\ to {F}} \ cdot d \ mathbf {\ overset {\ to {r}}[/латекс]
Работа, совершаемая постоянной силой кинетического трения	[латекс]{W}_{\text{fr}}=\text{−}{f}_{k}|{l}_{AB}|[/latex] 9{2}}{2 м}[/латекс]
Теорема о работе-энергии	[латекс] {W} _ {\ text {net}} = {K} _ {B} — {K} _ {A} [/ латекс]
Мощность как скорость выполнения работы	[латекс]P=\frac{dW}{dt}[/латекс]
Мощность как скалярное произведение силы и скорости	[латекс] P = \ mathbf {\ overset {\ to {F}} \ cdot \ mathbf {\ overset {\ to {v}} [/latex]

Концептуальные вопросы

Мощность большинства электроприборов измеряется в ваттах. Зависит ли этот рейтинг от того, как долго прибор включен? (В выключенном состоянии это устройство с нулевой мощностью.) Объясните с точки зрения определения мощности.

Показать решение

Приборы оцениваются по потребляемой энергии за относительно небольшой интервал времени. Не имеет значения, как долго прибор включен, важна лишь скорость изменения энергии в единицу времени.

Объясните с точки зрения определения мощности, почему потребление энергии иногда указывается в киловатт-часах, а не в джоулях. Какова связь между этими двумя энергетическими единицами?

Искра статического электричества, которую можно получить от дверной ручки в холодный сухой день, может иметь мощность в несколько сотен ватт. Объясните, почему вы не ранены такой искрой.

Показать решение

Искра возникает в течение относительно короткого промежутка времени, поэтому вашему телу передается очень небольшое количество энергии.

Зависит ли работа, совершаемая при подъеме предмета, от скорости его подъема? Зависит ли затрачиваемая мощность от того, как быстро он поднимается?

Может ли мощность, затрачиваемая силой, быть отрицательной?

Показать решение

Если сила антипараллельна или направлена ​​в направлении, противоположном скорости, затрачиваемая мощность может быть отрицательной.

Как 50-ваттная лампочка может потреблять больше энергии, чем 1000-ваттная духовка?

Проблемы

Человек в хорошей физической форме может выдавать 100 Вт полезной мощности в течение нескольких часов подряд, возможно, крутя педали механизма, который приводит в действие электрогенератор. Пренебрегая любыми проблемами эффективности генератора и практическими соображениями, такими как время отдыха: (a) Сколько людей потребуется, чтобы запустить электрическую сушилку для белья мощностью 4,00 кВт? б) Сколько человек потребуется, чтобы заменить крупную электростанцию ​​мощностью 800 МВт?

Показать раствор

а. 40; б. 8 миллионов

Какова стоимость эксплуатации электрических часов мощностью 3,00 Вт в течение года, если стоимость электроэнергии составляет 💲0,0900 за [латекс]\текст{кВт}\cdot \text{ч}[/латекс]?

Большой бытовой кондиционер может потреблять 15,0 кВт электроэнергии. Какова стоимость эксплуатации этого кондиционера 3,00 часа в день за 30,0 дня, если стоимость электроэнергии составляет 💲0,110 за [латекс]\текст{кВт}\cdot \text{ч}[/латекс]?

Показать решение

💲149

(a) Какова средняя потребляемая мощность в ваттах устройства, потребляющего 5,00 [латекс]\текст{кВт}\cdot \текст{ч}[/латекс] энергии в день? б) Сколько джоулей энергии потребляет этот прибор в год? 9{6}\,\text{J}[/latex] полезной работы за 8 часов? б) За какое время при такой скорости этот человек поднимет 2000 кг кирпичей на высоту 1,50 м? (Работа, проделанная для подъема его тела, может быть опущена, поскольку здесь она не считается полезной. )

Показать решение

a. 208 Вт; б. 141 с

Драгстер массой 500 кг разгоняется из состояния покоя до конечной скорости 110 м/с на расстоянии 400 м (около четверти мили) и сталкивается со средней силой трения 1200 Н. Какова его средняя выходная мощность в ваттах и ​​лошадиных силах, если это занимает 7,30 с?

(a) За какое время автомобиль массой 850 кг с полезной выходной мощностью 40,0 л.с. (1 л.с. равен 746 Вт) достигнет скорости 15,0 м/с без учета трения? б) Сколько времени займет это ускорение, если при этом автомобиль поднимется на холм высотой 3,00 м?

Показать раствор

а. 3,20 с; б. 4,04 с

а) Найдите полезную мощность двигателя лифта, который поднимает груз массой 2500 кг на высоту 35,0 м за 12,0 с, если он также увеличивает скорость из состояния покоя до 4,00 м/с. Обратите внимание, что общая масса уравновешенной системы составляет 10 000 кг, так что в высоту поднимается только 2 500 кг, но ускоряются полные 10 000 кг. (b) Сколько это стоит, если электричество стоит 💲0,09{5}\text{-kg}[/latex] самолет с двигателями мощностью 100 МВт, способный развивать скорость 250 м/с и высоту 12,0 км, если бы сопротивление воздуха было пренебрежимо малым? (b) Если это действительно занимает 900 с, какова мощность? в) Какова средняя сила сопротивления воздуха при этой мощности, если самолету потребуется 1200 с? ( Подсказка: Вы должны найти расстояние, которое самолет проходит за 1200 с при постоянном ускорении.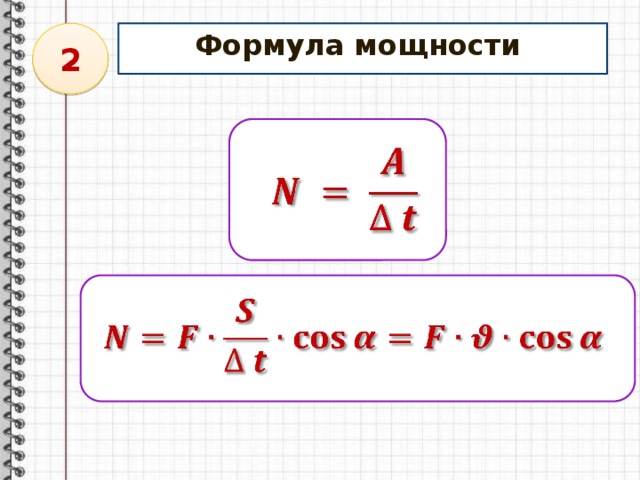 \circ[/латекс] с той же скоростью. Предположим, что тормозящая сила трения в обоих случаях одинакова.

Показать решение

1,7 кВт

Дополнительные задачи

Тележку тянут на расстояние D по плоской горизонтальной поверхности под действием постоянной силы F , действующей под углом [латекс]\тета[/латекс] к горизонтальному направлению. Другими силами, воздействующими на объект в это время, являются сила тяжести ([латекс]{F}_{w}[/латекс]), нормальные силы ([латекс]{F}_{N1}[/латекс]) и ([латекс ]{F}_{N2}[/latex]), и трения качения [латекс]{F}_{r1}[/латекс] и [латекс]{F}_{r2}[/латекс], как показано ниже. . Какую работу совершает каждая сила?

Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to}{F}}}_{1}=(3\ ,\text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется по x -ось от [латекс]х=0[/латекс] до [латекс]х=5\,\текст{м}[/латекс] за некоторый интервал времени. Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?

Показать решение

[латекс]15\,\текст{N}\cdot \текст{м}[/латекс]

Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to }{F}}}_{1}=(3\,\ text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется сначала по x -ось от [latex]x=0[/latex] до [latex]x=5\,\text{m}[/latex] и затем параллельно y -ось от [latex]y=0 [/latex] to [latex]y=6\,\text{m}\text{.}[/latex] Какую работу выполняет [latex]{\mathbf{\overset{\to} }{F}} }_{1}[/латекс]?

Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to }{F}}}_{1}=(3\,\ text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется по прямому пути от декартовой координаты (0 м, 0 м) до (5 м, 6 м). Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?

Показать решение

[latex]39\,\text{N}\cdot \text{m}[/latex]

Рассмотрим частицу, на которую действует сила, зависящая от положения частицы. Эта сила определяется как [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {1} = (2y) \ mathbf {\ hat {i}} + (3x) \ mathbf {\ hat { j}}.[/latex] Найдите работу, совершаемую этой силой при перемещении частицы из начала координат в точку, расположенную на 5 метров вправо на 9\circ[/latex] над горизонталью на том же расстоянии?

Показать раствор

а. [латекс]208\,\текст{N}\cdot \текст{м}[/латекс]; б. [латекс] 240\,\текст{N}\cdot \текст{м}[/латекс]

Вынести ящик массой 200 кг с площадки 1 этажа в квартиру 3 этажа. Рабочие знают, что они могут либо сначала воспользоваться лифтом, а затем переместить его по третьему этажу в квартиру, либо сначала передвинуть ящик в другое место, отмеченное буквой C ниже, а затем подняться на лифте на третий этаж и сдвинуть его на третий. пол меньшее расстояние. Беда в том, что третий этаж очень неровный по сравнению с первым этажом. Учитывая, что коэффициент кинетического трения между ящиком и поверхностью пола равен 0,100, а между ящиком и поверхностью третьего этажа равен 0,300, найдите работу, которую затрачивают рабочие на каждом пути, показанном на рисунке 9.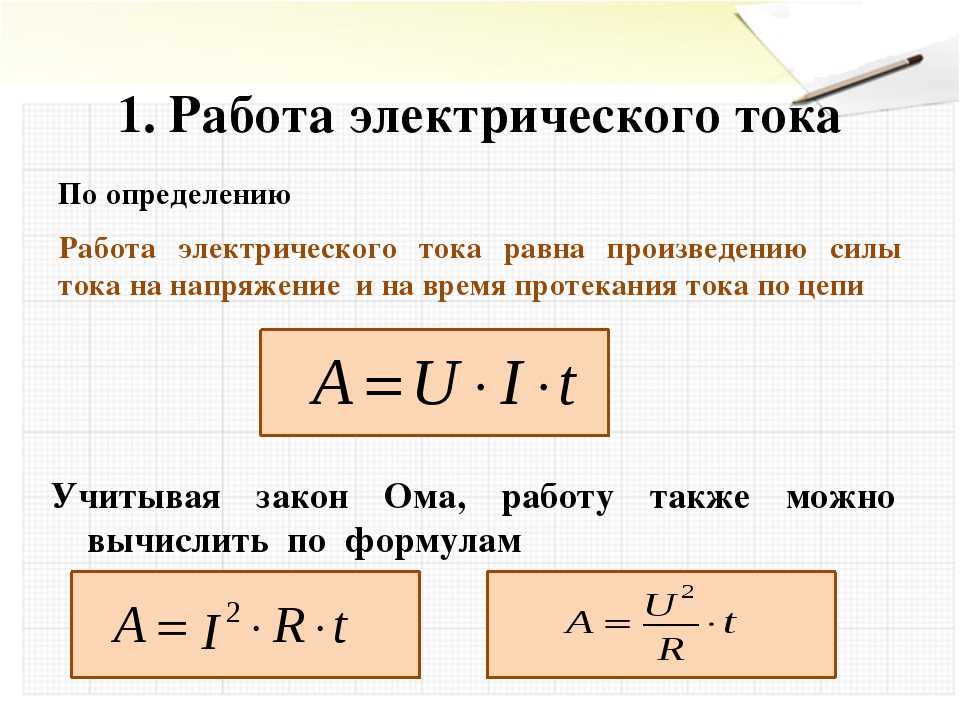 0049 А до Е . Предположим, что силы, которую должны приложить рабочие, достаточно, чтобы сдвинуть ящик с постоянной скоростью (нулевое ускорение). Примечание: Работа лифта против силы тяжести не выполняется рабочими.

Хоккейная шайба массой 0,17 кг брошена по шероховатому полу с разной шероховатостью в разных местах, что можно описать зависящим от положения коэффициентом кинетического трения. Для шайбы, движущейся по x -ось, коэффициент кинетического трения является следующей функцией x , где x в м: [латекс]\мю (х)=0,1+0,05х.[/латекс] Найдите выполненную работу кинетической силой трения хоккейной шайбы, когда она перемещается (a) из [латекс]x=0[/латекс] в [латекс]x=2\,\text{m}[/латекс] и (б) из [латекс]x=2\,\text{m}[/латекс] в [латекс]x=4\,\текст{м}[/латекс].

Показать раствор

а. [латекс]\текст{−}0,9\,\текст{N}\cdot \text{м}[/латекс]; б. [латекс]-0,83\,\текст{N}\cdot \текст{м}[/латекс]

Требуется горизонтальная сила 20 Н, чтобы удержать ящик массой 5,0 кг, движущийся с постоянной скоростью по наклонной поверхности без трения при изменении высоты по вертикали на 3,0 м. а) Какова работа силы тяжести при этом изменении высоты? б) Какую работу совершает нормальная сила? в) Какую работу совершает горизонтальная сила?

Коробка массой 7,0 кг скользит по горизонтальному полу без трения со скоростью 1,7 м/с и сталкивается с относительно невесомой пружиной, которая сжимается на 23 см, прежде чем коробка останавливается. а) Какой кинетической энергией обладает ящик до столкновения с пружиной? б) Вычислите работу, совершенную пружиной. в) Определите жесткость пружины.

Показать раствор

а. 10. Дж; б. 10. Дж; в. 380 Н/м

Вы едете на автомобиле по прямой дороге с коэффициентом трения между шинами и дорогой 0,55. Большой кусок обломков падает прямо перед вашим взором, и вы тут же нажимаете на тормоза, оставляя след длиной 30,5 м (100 футов) перед остановкой. Полицейский видит, что ваша машина остановилась на дороге, смотрит на след заноса и выписывает вам штраф за превышение скорости 13,4 м/с (30 миль/ч). Стоит ли оспаривать штраф за превышение скорости в суде?

По неровной поверхности пола толкают ящик. Если к ящику не приложено никакой силы, ящик замедлится и остановится. Если ящик массой 50 кг, движущийся со скоростью 8 м/с, останавливается через 10 с, с какой скоростью сила трения, действующая на ящик, отбирает энергию у ящика?

Show Solution

160 Дж/с

Предположим, что для поддержания скорости 8 м/с ящика массой 50 кг требуется горизонтальная сила 20 Н. а) Какова мощность этой силы? (b) Обратите внимание, что ускорение ящика равно нулю, несмотря на то, что сила 20 Н действует на ящик горизонтально. Что происходит с энергией, переданной ящику в результате работы этой силы в 20 Н? 9\circ[/latex] наклон горизонтальной силой [латекс]\mathbf{\overset{\to }{F}}.[/latex] Коэффициент кинетического трения между ящиком и наклоном равен [латекс]{\mu }_{k}=0,40.[/latex] Рассчитайте работу, совершаемую (а) приложенной силой, (б) силой трения, (в) силой тяжести и (г) результирующей силой.

Показать решение

Если ящик поднимается: a. 3,46 кДж; б. −1,89 кДж; в. −1,57 кДж; д. 0; Если ящик опускается: a. −0,39 кДж; б. −1,18 кДж; в. 1,57 кДж; д. 0

Поверхность предыдущей задачи изменена так, что коэффициент кинетического трения уменьшен. К ящику приложена такая же горизонтальная сила, и после того, как его толкнули на 8,0 м, его скорость составила 5,0 м/с. Какую работу теперь совершает сила трения? Предположим, что ящик находится в состоянии покоя.

Сила F ( x ) зависит от положения, как показано ниже. Найдите работу, совершаемую этой силой над частицей при ее перемещении из [латекс]x=1,0\,\text{m}[/latex] в [латекс]x=5,0\,\text{m}\text{.} [/latex]

Показать решение

8,0 Дж

Найдите работу, совершаемую той же силой на рисунке, между теми же точками [латекс]A=(0,0)\,\text{и}\,B =(2\,\text{m},2\,\text{m})[/latex], по дуге окружности радиусом 2 м с центром в точке (0, 2 м). Оцените интеграл пути с помощью декартовых координат. ( Подсказка: Возможно, вам понадобится обратиться к таблице интегралов. )

Ответьте на предыдущую задачу, используя полярные координаты.

Показать раствор

35,7 Дж

Найдите работу, совершаемую той же силой на рисунке, между теми же точками [латекс]A=(0,0)\,\text{и}\,B=(2\,\text{m},2\ ,\text{m})[/latex], по дуге окружности радиусом 2 м с центром в точке (2 м, 0). Оцените интеграл пути с помощью декартовых координат. ( Подсказка: Вам, вероятно, потребуется свериться с таблицей интегралов.) 9{3\text{/}2}.[/latex]

Предположим, что сопротивление воздуха, с которым сталкивается автомобиль, не зависит от его скорости. Когда автомобиль движется со скоростью 15 м/с, его двигатель передает на колеса мощность 20 л.с. а) Какая мощность передается на колеса, если автомобиль движется со скоростью 30 м/с? б) Сколько энергии затрачивает автомобиль, чтобы проехать 10 км со скоростью 15 м/с? При 30 м/с? Предположим, что двигатель имеет КПД 25%. в) Ответьте на те же вопросы, если сила сопротивления воздуха пропорциональна скорости автомобиля. (d) Что эти результаты, а также ваш опыт потребления бензина говорят вам о сопротивлении воздуха?

Показать раствор

а. 40 л.с.; б. 39,8 МДж, независимо от скорости; в. 80 л.с., 79,6 МДж при 30 м/с; д. Если сопротивление воздуха пропорционально скорости, автомобиль получает около 22 миль на галлон при 34 милях в час и половину этого при удвоенной скорости, что ближе к реальному опыту вождения.

Рассмотрим линейную пружину, как на рисунке (а), с массой M , равномерно распределенной по ее длине. Левый конец пружины неподвижен, а правый конец в положении равновесия [латекс]х=0,[/латекс] движется со скоростью v в направлении x . Чему равна полная кинетическая энергия пружины? ( Подсказка: Сначала выразите кинетическую энергию бесконечно малого элемента пружины дм через полную массу, равновесную длину, скорость правого конца и положение вдоль пружины; затем проинтегрируйте.)

Глоссарий

средняя мощность

работа, выполненная за интервал времени, деленный на интервал времени

мощность

(или мгновенная мощность) скорость выполнения работы

Формула энергии в физике и уравнениях для классов 10, 11 и 12

Содержание

Формула энергии Физика

Идея энергии имеет важное значение для физики. Энергия есть не что иное, как способность выполнять труд. Простейший Под действием энергии предмет может совершать работу. Другими словами, объект может работать только тогда, когда в нем присутствует энергия. Мы можем получать энергию из различных источников, включая свет, атомы, тепло и другие вещи, которые порождают различные типы энергии. Здесь мы изучим основы энергии и формулы энергии с помощью решенных математических задач.

Формула энергии. Физика. Определение энергии.

Энергия – это способность выполнять любой тип физического действия. Способность объекта действовать называется его энергией. Суммарная работа, которую может совершить объект, называется его энергией. Следовательно, энергия и работа равны. Итак, единица энергии и единица действия одна и та же.
Мы знаем Закон сохранения энергии, что Энергия никогда не создается и не уничтожается, только мы можем преобразовать ее из одной формы в другую. В. во всей Вселенной общее количество энергии постоянно. Когда мы включаем вентилятор, электронная энергия преобразуется в механическую энергию. Энергия существует во многих формах. Механическая энергия, Тепловая энергия, Световая энергия, Звуковая энергия, Магнитная энергия, Электрическая энергия, Химическая энергия Атомная энергия. В этом разделе мы подробно узнаем о формулах механической энергии.

Формула энергии Физика — Единицы измерения энергии (Джоули)

Как мы уже знаем, способность вещества совершать работу называется его энергией. Единицей измерения энергии является джоулей (Дж) , широко известная как ньютон-метров, , которая является единицей энергии в системе СИ. Используемая энергия измеряется в джоулях или ньютон-метрах, когда объект подвергается воздействию определенной силы в ньютонах и перемещается на определенное расстояние в метрах.

Формула энергии по физике для 10, 11 и 12 классов

Энергия в основном подразделяется на два типа. Кинетическая энергия и потенциальная энергия.
Формула для определения кинетической энергии объекта: – K.E = ½ mv²

[где m= масса объекта, V = скорость объекта]

Формула для определения потенциальной энергии объект равен – PE = mgh

Где m обозначает массу объекта, g обозначает ускорение свободного падения, а h обозначает высоту.

Давайте разберемся с этими терминами и формами один за другим.

Что такое формула механической энергии в физике?

Способность объекта выполнять работу благодаря его движению, положению или форме, или всем этим трем, называется его механической энергией. Механическая энергия делится на две части: (i) кинетическую энергию и (ii) потенциальную энергию.

Кинетическая энергия

Без помощи уравнений движения Ньютона можно анализировать динамику механической системы, используя идеи работы и кинетической энергии. Многие сложные события могут быть просто проанализированы, особенно когда применяется это понятие. Но закон движения Ньютона служит краеугольным камнем идеи работы-кинетической энергии. Поэтому результат один и тот же независимо от того, как ведется диалог.

Определение кинетической энергии

Способность движущегося объекта выполнять работу за счет его движения называется его кинетической энергией. Чтобы остановить движущийся объект, необходимо приложить внешнюю силу. Количество работы, которую объект совершает против приложенной силы, прежде чем он остановится, является мерой кинетической энергии объекта.

Примеры кинетической энергии

В нашей повседневной жизни мы видим много примеров, когда сила передается объекту, когда он находится в движении, и объект способен совершать работу. Например,
(i) Пули, выпущенные из оружия, могут пробить оконное стекло. Но если пуля остановится на стекле, пуля не сможет пробить стекло. Так что понятно, что пули способны что-то сделать для скорости.

(II) При забивании гвоздя в стену молоток не только прижимается к шляпке гвоздя. Поднеся молоток с некоторого расстояния и с большой скоростью ударив по шляпке гвоздя, он пробивает стену. Динамический молот способен действовать за счет своего движения.

Кинетическая энергия воды и ветра используется для различных целей человеческого благосостояния. Электричество вырабатывается с помощью динамо-машин, использующих кинетическую энергию быстрых потоков воды в водопадах и бурных горных реках. Используя поток воздуха, машина гонит зерно и забирает воду из колодца.

Вывод формулы кинетической энергии в физике

Предположим, что имеется объект массой m. движется по прямой со скоростью. Чему равна кинетическая энергия тела? Предположим, что к объекту приложена некоторая сила F, чтобы остановить его движение. В результате объект замедляется, проходит расстояние и останавливается. Как мы знаем, S — это мера кинетической энергии объекта по отношению к F до его остановки. следовательно,

Кинетическая энергия объекта = работа, совершаемая против силы
F = F. s = mas [F = ma] …….(1)
Инерционная скорость объекта может быть записана как v = 0,

V² = u² – 2ас. [Используя формулу v² = u²+ 2as]

или, 2as = u²
или, as = u²/2 ……. (2)

Подставляя значение как в (1) из (2), получаем
Кинетическая энергия объекта = ½ мк²
Линейная кинетическая энергия объекта = 2 x масса x (линейная скорость) ²

Мы можем заключить, что когда объект ускоряется силой, его скорость увеличивается, но когда он замедляется, его импульс уменьшается.

Потенциальная энергия. Определение потенциальной энергии

Способность объекта действовать из-за его определенного положения или формы называется его потенциальной энергией.

Здесь состояние (т. е. положение или форма) объекта считается доказательством или стандартным состоянием, за исключением того, что все другие условия называются особыми условиями. Количество работы, проделанной объектом при возвращении его из определенного положения или формы в исходное положение или форму, является мерой статической энергии объекта. Обратите внимание, что доказательство или нормальное состояние объекта также называется нулевым состоянием.

Пример потенциальной энергии

Гидроэлектроэнергия вырабатывается в основном за счет использования статической энергии воды. Вода в реке удерживается плотиной на высоком месте. Эта вода оснащена стабильностью. Эта статическая энергия преобразуется в кинетическую энергию при падении. Затем турбина вращается за счет кинетической энергии воды. В результате вырабатывается электричество.

Вывод формулы потенциальной энергии в физике

Допустим, предмет массой (m) поднят на высоту h над поверхностью.

Сила, действующая на объект = Сила тяжести = мг

Работа против силы тяжести = сила × перемещение = мг ч
Эта работа сохраняется в объекте в виде статической энергии.

Статическая энергия вещества = mgh = Масса объекта x Ускорение свободного падения × Высота объекта от поверхности отсчета радиус Земли ]

Формула энергии Физика в терминах силы: задачи

Q . Найти кинетическую энергию тела массой 10 кг непосредственно перед тем, как оно упадет с высоты 10 м на землю. g = 980 см/с².

→ Скажем, скорость вещества непосредственно перед тем, как оно коснется земли

V² = 2gh = 2 x 9,8 x 10 (здесь h = 10 м )

= 196 м²/с² (ответ)

Q. Тело массой 1 кг брошено вертикально вверх со скоростью 250 см/с с высоты 8 м над землей. Какова будет кинетическая энергия тела в момент касания земли?

→  Предположим, что скорость объекта равна v непосредственно перед тем, как он коснется земли
Верхняя сторона находится на положительной стороне, v²=u²+2gh
= (2,5)²+2 x 9,8 x 8
[” u” = 250 см/с = 2,5 м/с, g = 9,8 м/с] 90 241 и h = -8 м] 90 241 = 163,05 м²/с² 90 241 Следовательно, кинетическая энергия объекта непосредственно перед тем, как он коснется земли, равна ½ mv²

= ½x 1×163,05 = 81,525 Дж. ( Ответ )

Связанный пост:

• Законы движения Ньютона — примеры для детей 9 класса& 11
• Простая схема микроскопа, формула, определение, открытие и увеличение силы
• Законы движения — первый, второй, третий закон с приложениями
• Правило большого пальца левой руки Флеминга используется для
• Uidai. Gov.In Aadhar — новая регистрация, обновление, загрузка для школы
• Столицы штатов и союзных территорий Индии 2022
• Чрезвычайная ситуация в Индии и ее последствия
• Формула куба — объем, площадь поверхности в математике для класса 10
• Схема круговорота воды для детей 3 класса с объяснением
• Квадрат и куб от 1 до 30 [ Скачать PDF ]

Формула энергии в физике: часто задаваемые вопросы

В. Что вы подразумеваете под энергией?

Энергия определяется как способность выполнять работу. Энергия – это способность выполнять любой вид физического действия. Способность объекта действовать называется его энергией. Суммарная работа, которую может совершить объект, называется его энергией.

В. По каким формулам определяется энергия вещества?

Энергия в основном подразделяется на два типа. Кинетическая энергия и потенциальная энергия.
Формула для определения кинетической энергии объекта: – K.