Мощность через эдс формула

На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб!

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• III. Основы электродинамики
• Найти мощность источника ЭДС
• Переменный ток
• Электрическая мощность
• III. Основы электродинамики
• Полная мощность
• Полезная мощность
• Формулы мощности для источников э.д.с. и источников тока

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: физика МОЩНОСТЬ единицы мощности 7 класс Перышкин

III. Основы электродинамики

Определить мощность тока в электрической лампе, если при напряжении В сила тока в ней мА. Определить мощность тока в электрической лампе, если сопротивление нити акала лампы Ом, а напряжение на нити В. Определить силу тока в лампе электрического фонарика, если напряжение на ней 4,5 В, а мощность 1,5 Вт. В каком из двух резисторов мощность тока больше при последовательном см.

Ученики правильно рассчитали, что для освещения елки нужно взять 12 имеющихся у них электрических лампочек.

Соединив их последовательно, можно будет включить их в городскую сеть. Почему меньшее число лампочек включать нельзя? Как изменится расход электроэнергии, если число лампочек увеличить до 14? В горном ауле установлен ветряной двигатель, приводящий в действие электрогенератор мощностью 8 кВт. Сила тока в паяльнике 4,6 А при напряжении В.

Определите мощность тока в паяльнике. Одинакова ли мощность тока в проводниках? На баллоне первой лампы написано В; Вт, а на баллоне второй — В; Вт. Лампы включены в сеть с напряжением, на которое они рассчитаны. У какой лампы сила тока больше; во сколько раз? Определите показания амперметров А1 и А и сопротивление резистора, если амперметр А2 показывает силу тока 2 А. Найти ЭДС и внутреннее сопротивление источника тока.

Какую мощность будет потреблять каждая из лампочек, если их подключить к сети последовательно? Выберите дальнейшие действия:.

Ваш e-mail не будет опубликован. Ноябрь 17, Категории Физика Физика 8. Теги 8 класс. Проверить свои знания по Физике.

Июнь 10, в дп. Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован. Send this to a friend Your email Recipient email Send Cancel. Мощность тока. Мощность источника тока в замкнутой цепи.

Найти мощность источника ЭДС

Сторонние силы. Источники тока. Но при движении зарядов от одного конца к другому концу проводника, разность потенциалов будет уменьшаться до нуля и ток, в конце концов, прекратится рис. Положительные заряды всегда двигаются в сторону уменьшения потенциала, а отрицательные, наоборот — в сторону увеличения потенциала. Для того чтобы поддерживать ток в проводнике, необходимо поддерживать разность потенциалов, а для этого необходимо положительные заряды, пришедшие на конец с меньшим потенциалом , отводить на их первоначальное положение — на конец проводника с потенциалом. Силы электрического поля с такой задачей не могут справиться, так как они не могут заставить двигаться положительные заряды в сторону увеличения потенциала.

Это могут сделать только силы не электрического происхождения.

I- сила тока в цепи; Е- электродвижущая сила источника тока, Следовательно, полная мощность, выделяемая во всей цепи, определится формулой.

Переменный ток

I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока. Следовательно, функция Р 1 имеет максимум. Значение R 0 , соответствующее максимальной мощности, можно получить, дифференцируя Р 1 по R и приравнивая первую производную к нулю:. Из формулы 3 , с учётом того, что R и r всегда положительны, а Е? Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока. При этом сила тока в цепи 5. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного. Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла.

Электрическая мощность

Задача взята из задачника по физике класса, автор А. Правильные ответы: 20 А, в, В, 2 кВт. Напишите ход решения, плиззз. Грабцевич Разделите напряжение на зажимах на сумму сопротивлений ламп 50 ламп включены параллельно и проводов, получите ток в цепи. ЭДС генератора найдете как произведение тока в цепи на полное сопротивление.

Закон Ома для замкнутой цепи. Основные понятия.

III. Основы электродинамики

При этом. График зависимости Р а I — парабола, ветви которой направлены вниз рис Задача 1. При каком токе полезная мощность батареи равна 8 Вт? Какова наибольшая полезная мощность батареи? Дано: Решение.

Полная мощность

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:. Если ток внутри ЭДС противонаправлен градиенту потенциала течёт внутри ЭДС от плюса к минусу , то мощность поглощается источником ЭДС из сети например, при работе электродвигателя или заряде аккумулятора , если сонаправлен течёт внутри ЭДС от минуса к плюсу , то отдаётся источником в сеть скажем, при работегальванической батареи или генератора.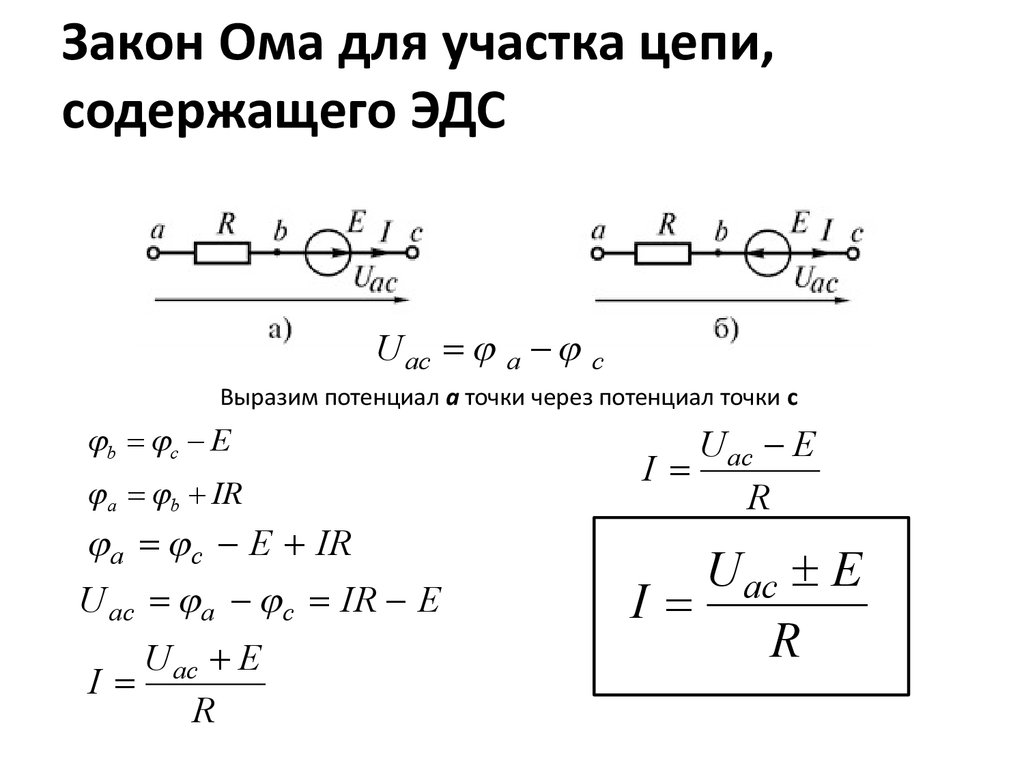

При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой. Мощность, развиваемая источником тока во всей цепи, называется полной мощностью. В общем виде электрическая цепь состоит из внешнего участка нагрузки с сопротивлением R и внутреннего участка с сопротивлением R 0 сопротивлением источника тока. Заменяя в выражении полной мощности величину э. При линейной нагрузке сила тока в цепи пропорциональна мгновенному напряжению, вся потребляемая мощность является активной.

Мощность. Сопротивление. Ток. Напряжение. Закон Ома. all-audio.pro — Инженерный справочник. r = внутреннее сопротивление источнка ЭДС. ε = ЭДС.

Полезная мощность

Электрический ток, на каком угодно участке цепи совершает некоторую работу А. Допустим, что у нас есть произвольный участок цепи рис. Работа, которая выполняется при перемещении заряда равного 1 Кл между точками A и B рис. В том случае, если через проводник протекает ток силой I за время равное по указанному выше участку пройдет заряд q равный:.

Формулы мощности для источников э.д.с. и источников тока

При подключении электроприборов к электросети обычно имеет значение только мощность и КПД самого электроприбора. Но при использовании источника тока в замкнутой цепи важна полезная мощность, которую он выдаёт. В качестве источника могут применяться генератор, аккумулятор, батарея или элементы солнечной электростанции. Для расчётов это принципиального значения не имеет. При подключении электроприборов к электропитанию и создании замкнутой цепи, кроме энергии Р, потребляемой нагрузкой, учитываются следующие параметры:. Не следует путать КПД источника и нагрузки.

При протекании тока по однородному участку цепи электрическое поле совершает работу. Эту работу называют работой электрического тока.

Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток. Единицей измерения в Международной системе единиц СИ является ватт русское обозначение: Вт , международное: W. Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Введём обозначения:. Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало.

Работа и мощность в цепи постоянного тока. Электродвижущая сила. Закон Ома для полной цепи Закон Ома для полной цепи 1.

5. Дайте понятие эдс, мощность источника и приёмника электрической энергии. Сформулируйте баланс мощностей. Приведите пример в общем виде.

Источник электрической энергии осуществляет направленное перемещение электрических зарядов по всей замкнутой цепи (рис. 2.3).

Энергия W, которую затрачивает или может затратить источник на пере­мещение единицы положительного заряда по всей замкнутой цепи, характеризует электродвижущую силу источника Е (ЭДС):

(1)

Исходя из формулы (1) следует, что энергия, затраченная источником, равна

W_ист= Eq = EIt, (2)

так как q = It, что вытекает из определения величины тока

Во всех элементах электрической цепи происходит преобразо­вание энергии

Скорость такого преобразования энергии определяет электриче­скую мощность элементов электрической цепи

Р= (3)

Таким образом, мощность источника электрической энергии определяется выражением

(4)

Энергия, затраченная на перемещение единицы положительного заряда на каком-либо участке замкнутой цепи, характеризует на­пряжение или падение напряжения на этом участке (внутреннем или внешнем):

(5)

Если воспользоваться законом Ома для участка электрической цепи, то полезную мощность можно определить следующим вы­ражением:

(6)

Уравнение баланса мощностей:

Сумма мощностей источников электрической энергии равна сумме мощностей приёмников

∑ Е ∙I  = ∑  I^2∙ R  , (7)

где

I – ток в ветви,А;

Е-ЭДС,В;

R-сопротивление, Ом.

E₁I₁+E₂I₂=I₁²R₁+I₂²R₂+I₃²R₃+I₄²R₄+I₅²R₅

6.Объясните принцип построения потенциальной диаграммы электрической цепи. Приведите пример в общем виде.

Потенциал точки – это напряжение между этой точкой и землёй, при этом надо помнить, что потенциал точки из которой ток вытекает больше, чем потенциал точки, в которую он втекает.

Положительный полюс источника имеет потенциал больший, чем отрицательный на величину ЭДС.

Потенциальная диаграмма представляет собой график изменения потенциалов точек цепи от величины сопротивлений участков между этими точками.

Для построения диаграммы необходимо:

1. Определить все токи в ветвях данного контура.

2. Одну из точек электрической цепи условно заземлить (потенциал этой точки равен нулю).

3. Потенциал остальных точек определить по правилу:

Если обходить цепь по направлению тока, то потенциал в каждой точке определяется потенциалом предыдущей точки плюс ЭДС источника, работающего в режиме генератора, минус ЭДС источника, работающего в режиме потребителя, и минус падения напряжения на участке между этими точками цепи. Если контур обходить против тока, то знаки перед ЭДС и падением напряжения изменяются на противоположные.

4. Изобразить координатные оси, по оси ОХ откладываем величину сопротивлений, по оси ОУ потенциалы соответствующих точек. Выбрать масштаб.

График представляет собой ломаную линию .

7. Раскройте понятия: электрическое сопротивление, удельная электрическая проводимость. (Сформулируйте определения, запишите формулы для расчета и единицы измерения, укажите какими параметрами определяется сопротивление проводника). Сформулируйте закон Ома. Подтвердите примером

Электрическое сопротивление проводника — это способность проводника препятствовать прохождению электрического тока через него.

Обозначается электрическое сопротивле­ние буквой R. Единицей измерения сопротивления является Ом:

[R] = Ом.

Сопротивление R зависит от длины проводникаl, площади по­перечного сеченияS и материала проводника :

где удельное сопротивление проводника, зависящее от свойства материала проводника.

Единицей измерения удельного сопротивления является

[] = Ом• м,

поскольку []

Однако на практике сечение проводников выражают в мм².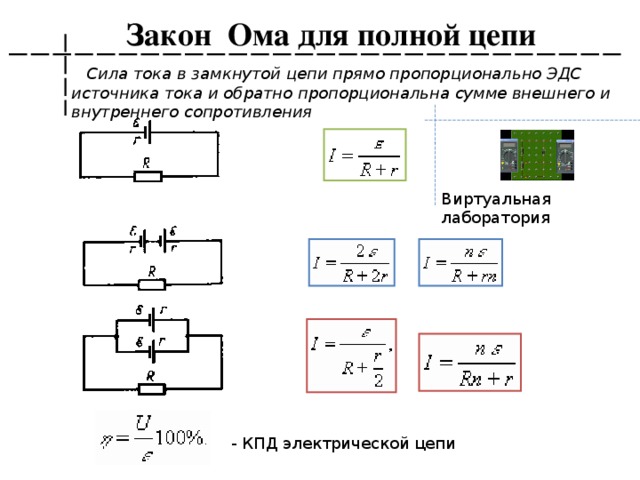 Поэтому []₌

Удельное сопротивление проводника определяет область его применения. Так, например, для соединения источника с потре­бителем применяются металлические провода с малым удельным сопротивлением — алюминий, медь. Для обмоток реостатов на­гревательных приборов применяются сплавы с большим удель­ным сопротивлением — нихром, фехраль (при этом уменьшается длина проводника ).

Величину, обратную сопротивлению, называют проводимостью

Единицей проводимости является сименс

[g] = См (сименс).

Элементы электрической цепи, характеризующиеся сопротив­лением R, называют резистивными, а промышленные изделия, предназначенные для выполнения роли сопротивления электри­ческому току, называются резисторами. Резисторы бывают регу­лируемые и нерегулируемые, проволочные и непроволочные, пленочные, композиционные и др.

Сопротивление проводников зависит от их температуры.

Сопротивление проводника при любой температуре (с доста­точной степенью точности при изменении температуры в преде­лах 0-100 °С) можно определить выражением

_(2.1)

где R₂ — сопротивление проводника при конечной температуре t°₂; R₁— сопротивление проводника при начальной температуреt₁°; — температурный коэффициент сопротивления.

Для различных проводников температурный коэффициент со­противления имеет различные значения.

Закон Ома для замкнутой цепи

Сила тока в электрической цепи с одним источником э.д.с. прямо пропорциональна электродвижущей силе и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участка цепи

где

R₀ — сопротивление источника, Ом;

R — сопротивление потреби­теля,Ом;

Е-ЭДС,В;

I-ток в цепи,А.

Электрогенераторы | Физика

Цели обучения

К концу этого раздела вы сможете:

• Рассчитать ЭДС, индуцируемую в генераторе.
• Рассчитайте пиковую ЭДС, которая может быть наведена в конкретной генераторной системе.

Электрические генераторы индуцируют ЭДС, вращая катушку в магнитном поле, как кратко описано в ЭДС индукции и магнитном потоке. Теперь мы рассмотрим генераторы более подробно. Рассмотрим следующий пример.

Пример 1. Расчет ЭДС, индуцированной в катушке генератора

Катушка генератора, показанная на рисунке 1, поворачивается на четверть оборота (от θ = 0º до θ = 90º) за 15,0 мс. Круглая катушка из 200 витков имеет радиус 5,00 см и находится в однородном магнитном поле 1,25 Тл. Чему равна средняя ЭДС индукции?

Рис. 1. Когда катушка этого генератора поворачивается на четверть оборота, магнитный поток Φ изменяется от своего максимума до нуля, индуцируя ЭДС.

Стратегия

Мы используем закон индукции Фарадея, чтобы найти среднюю ЭДС, индуцированную за время Δ t :

[латекс]\text{ЭДС}=-N\frac{\Delta\Phi}{\ Дельта т}\\[/латекс].

Мы знаем, что N  = 200 и Δ t = 15,0 мс, поэтому мы должны определить изменение потока Δ Φ , чтобы найти ЭДС.

Решение

Поскольку площадь петли и напряженность магнитного поля постоянны, мы видим, что

[латекс]\Delta\Phi =\Delta\left(BA\cos\theta\right)=AB\Delta\left(\cos\theta \right)\\[/latex].

Теперь Δ (cos θ ) = −1,0, поскольку было дано, что θ изменяется от 0° до 90°. Таким образом, Δ Φ  = − AB и

[латекс]\text{emf}=N\frac{AB}{\Delta t}\\[/latex].

Площадь петли A = πr ² = (3,14…)(0,0500м) ² = 7,85 × 10 ⁻³ м ² . Ввод этого значения дает 9{-3}\text{ s}}=131\text{ V}\\[/latex].

Обсуждение

Это практическое среднее значение, аналогичное 120 В, используемому в домашнем хозяйстве.

ЭДС, рассчитанная в приведенном выше примере 1 , представляет собой среднее значение за одну четвертую оборота. Чему равна ЭДС в каждый момент времени? Оно изменяется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высотой ℓ в однородном магнитном поле, как показано на рисунке 2.

Рисунок 2. Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, которая изменяется синусоидально во времени . Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот.

Заряды в проводах петли испытывают магнитную силу, так как движутся в магнитном поле. На заряды в вертикальных проводах действуют силы, параллельные проводу, вызывающие токи. Но находящиеся в верхнем и нижнем сегментах ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения принимается равной ЭДС = 9.0013 Bℓv , где скорость v перпендикулярна магнитному полю B . Здесь скорость составляет угол θ с B , так что ее составляющая, перпендикулярная B , равна v sin θ (см. рис. 2). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС = Bℓv sin θ , и они имеют одинаковое направление. Суммарная ЭДС вокруг петли тогда равна

[латекс]\текст{ЭДС}=2{B\ell v}\sin\theta\\[/латекс].

Это выражение верно, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью ω . Угол θ связан с угловой скоростью соотношением θ  =  ωt , так что

[латекс]\текст{ЭДС}=2{B\ell v}\sin\omega t\\[/ латекс].

Теперь линейная скорость v связана с угловой скоростью ω соотношением v  =  rω . Здесь r = w /2, так что v = ( w /2) ω , и

[латекс]\text{emf}=2 B\ell \frac }{2}\omega\sin\omega t=\left(\ell w\right)B\omega\sin\omega t\\[/latex].

Заметив, что площадь петли равна A  =  ℓ w , и учитывая N петель, мы находим, что

[латекс]\text{emf}=NAB\omega\sin\omega t\\[/latex]

— ЭДС , индуцированная в катушке генератора N витков и площадь A вращающаяся с постоянной угловой скоростью ω в однородном магнитном поле B . Это также может быть выражено как

[латекс]\text{emf}={\text{emf}}_{0}\sin\omega t\\[/latex],

, где

[латекс]{\ text{emf}}_{0}=NAB\omega\\[/latex]

— максимальная (пиковая) emf . Обратите внимание, что частота колебаний равна f = ω /2π , а период равен T = 1/ f = 2π/ ω . На рис. 3 показан график зависимости ЭДС от времени, и теперь кажется разумным, что переменное напряжение является синусоидальным.

Рис. 3. ЭДС генератора подается на лампочку с показанной системой колец и щеток. На графике показана зависимость ЭДС генератора от времени. emf0 — пиковая эдс. Период T = 1/ f = 2π/ω, где f — частота. Обратите внимание, что буква E означает emf.

Тот факт, что пиковая ЭДС, ЭДС ₀  = NABω , имеет смысл. Чем больше количество катушек, тем больше их площадь, и чем сильнее поле, тем больше выходное напряжение. Интересно, что чем быстрее раскручивается генератор (больше ω ), тем больше ЭДС. Это заметно на велосипедных генераторах, по крайней мере, на более дешевых. Один из авторов, будучи подростком, находил забавным ехать на велосипеде достаточно быстро, чтобы сжечь его фары, пока однажды темной ночью ему не пришлось ехать домой без света. На рисунке 4 показана схема, с помощью которой можно сделать генератор для получения импульсного постоянного тока. Более сложное расположение нескольких катушек и разъемных колец может обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.

Рис. 4. Разъемные кольца, называемые коммутаторами, в этой конфигурации создают на выходе импульсную ЭДС постоянного тока.

Пример 2. Расчет максимальной ЭДС генератора

Рассчитать максимальную ЭДС, ЭДС ₀ , генератора, рассмотренного в Примере 1. , определено, ЭДС ₀  = NABω  можно использовать для нахождения ЭДС ₀ . Все остальные величины известны.

Решение

Угловая скорость определяется как изменение угла в единицу времени:

[латекс]\омега =\фракция{\Дельта\тета}{\Дельта t}\\[/латекс].

Одна четвертая оборота составляет π/2 радиана, а время составляет 0,0150 с; таким образом,

[латекс]\begin{array}{lll}\omega & =& \frac{\pi /2\text{rad}}{0,0150 \text{s}}\\ & =& 104,7\text{ рад/с}\end{массив}\\[/latex].

104,7 рад/с — это ровно 1000 об/мин. Подставляем это значение на 9{2}\right)\left(1.25\text{ T}\right)\left(104.7 \text{ рад/с}\right)\\ & =& 206\text{ V}\end{массив}\\ [/латекс].

Обсуждение

Максимальная ЭДС больше, чем средняя ЭДС 131 В, найденная в предыдущем примере, как и должно быть.

В реальной жизни электрические генераторы выглядят совсем иначе, чем на рисунках в этом разделе, но принцип тот же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра. На рис. 5 показан вид в разрезе паровой турбины; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора.

Рисунок 5. Паровая турбина/генератор. Пар, образующийся при сжигании угля, воздействует на лопатки турбины, вращая вал, соединенный с генератором. (кредит: Nabonaco, Wikimedia Commons)

Генераторы, показанные в этом разделе, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически двигатель становится генератором, когда его вал вращается. Некоторые ранние автомобили использовали свой стартер в качестве генератора. В разделе «Обратная ЭДС» мы дополнительно исследуем работу двигателя как генератора.

Резюме раздела

• Электрический генератор вращает катушку в магнитном поле, индуцируя ЭДС, определяемую как функция времени

  [латекс]\text{emf}=2{B\ell v}\sin\omega t\\[/latex],

  где A  является площадью N -витковой катушки, вращающейся с постоянной угловой скоростью ω в однородном магнитном поле B .

• Пиковая ЭДС ЭДС ₀ генератора равна

  эдс ₀  = NABω

Концептуальные вопросы

1. Используя RHR-1, покажите, что ЭДС на сторонах контура генератора на рисунке 4 одинаковы, и, таким образом, добавьте.
2. Источником электрической энергии генератора является работа, совершаемая для вращения его катушек. Как работа, необходимая для поворота генератора, связана с законом Ленца?

Задачи и упражнения

1. Рассчитайте пиковое напряжение генератора, который вращает катушку из 200 витков диаметром 0,100 м со скоростью 3600 об/мин в поле 0,800 Тл.

2. При какой угловой скорости в об/мин пиковое напряжение генератора составит 480 В, если его 500-витковая катушка диаметром 8,00 см вращается в поле 0,250 Тл?

3. Какова пиковая ЭДС, создаваемая вращением катушки диаметром 20,0 см из 1000 витков в магнитном поле Земли 5,00 × 10 ⁻⁵  Тл, если плоскость катушки изначально перпендикулярна полю Земли и поворачивается параллельно полю за 10,0 мс?

4. Какова пиковая ЭДС, создаваемая катушкой радиусом 0,250 м, состоящей из 500 витков, которая поворачивается на четверть оборота за 4,17 мс, первоначально имея плоскость, перпендикулярную однородному магнитному полю. (Это 60 об/с.)

5. (a) Велосипедный генератор вращается со скоростью 1875 рад/с, производя пиковую ЭДС 18,0 В. Он имеет прямоугольную катушку размером 1,00 на 3,00 см в поле 0,640 Тл. Сколько витков в катушке? (b) Практично ли такое количество витков провода для катушки размером 1,00 на 3,00 см?

6. Интегрированные понятия Эта задача относится к велосипедному генератору, рассмотренному в предыдущей задаче. Он приводится в движение колесом диаметром 1,60 см, которое катится по внешнему ободу велосипедной шины. а) Какова скорость велосипеда, если угловая скорость генератора равна 1875 рад/с? б) Какова максимальная ЭДС генератора, когда велосипед движется со скоростью 10,0 м/с, учитывая, что в первоначальных условиях она составляла 18,0 В? (c) Если сложный генератор может изменять свое собственное магнитное поле, какая напряженность поля ему потребуется при скорости 5,00 м/с, чтобы произвести 90,00 В максимальная ЭДС?

7. (a) Автомобильный генератор вращается со скоростью 400 об/мин, когда двигатель работает на холостом ходу. Его 300-витковая прямоугольная катушка размером 5,00 на 8,00 см вращается в регулируемом магнитном поле, так что она может создавать достаточное напряжение даже при низких оборотах. Какая напряженность поля необходима для создания пиковой ЭДС 24,0 В? (b) Обсудите, как эта требуемая напряженность поля соотносится с напряженностью поля, доступной для постоянных и электромагнитов.

8. Покажите, что если катушка вращается с угловой скоростью ω , период ее выхода переменного тока равен 2π/ ω .

9. Катушка диаметром 10,0 см из 75 витков вращается с угловой скоростью 8,00 рад/с в поле 1,25 Тл, начиная с плоскости катушки, параллельной полю. а) Чему равна пиковая ЭДС? б) В какой момент времени достигается максимальная ЭДС? в) В какой момент ЭДС достигает своего максимального отрицательного значения? (d) Каков период выходного напряжения переменного тока?

10. а) Если ЭДС катушки, вращающейся в магнитном поле, равна нулю при t = 0 и возрастает до своего первого пика при t = 0,100 мс, какова угловая скорость катушки? б) В какое время произойдет ее следующий максимум? в) Каков период выпуска продукции? (d) Когда объем выпуска составляет первую четверть своего максимума? (e) Когда она составляет следующую четверть своего максимума?

11. Необоснованные результаты Катушка из 500 витков площадью 0,250 м ² вращается в поле Земли 5,00 × 10 ⁻⁵ Тл, производя максимальную ЭДС 12,0 кВ. а) С какой угловой скоростью должна вращаться катушка? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

Глоссарий

электрогенератор:

Устройство для преобразования механической работы в электрическую энергию; он индуцирует ЭДС, вращая катушку в магнитном поле

ЭДС, индуцированная в катушке генератора:

э.д.с. = NAB ω sin ωt , где A – площадь N -витковой катушки, вращающейся с постоянной угловой скоростью ω B, за период 001

в однородном магнитном поле. времени т

пиковая ЭДС:

эдс ₀  = NABω

Избранные решения задач и упражнений

1. 474 В

3. 0,247 В

5. (а) 50 (б) да

7. (а) 0,477 Тл (б) Эта напряженность поля достаточно мала, чтобы ее можно было получить с помощью либо постоянного магнит или электромагнит.

9. (а) 5,89 В (б) При t = 0 (в) 0,393 с (г) 0,785 с

11. (а) 1,92 × 10 ⁶ рад/с (б) Эта угловая скорость неоправданно высока, выше, чем может быть получена для любой механической системы. (c) Предположение, что можно получить напряжение до 12,0 кВ, неразумно.

 

электричество — Назад $ЭДС$ и мощность?

спросил 8 лет, 7 месяцев назад

Изменено 8 лет, 7 месяцев назад

Просмотрено 606 раз

$\begingroup$

Формула, связывающая ток с противо-ЭДС: $V-E=IR$, где $V$ — источник pd, а $E$ — противо-ЭДС.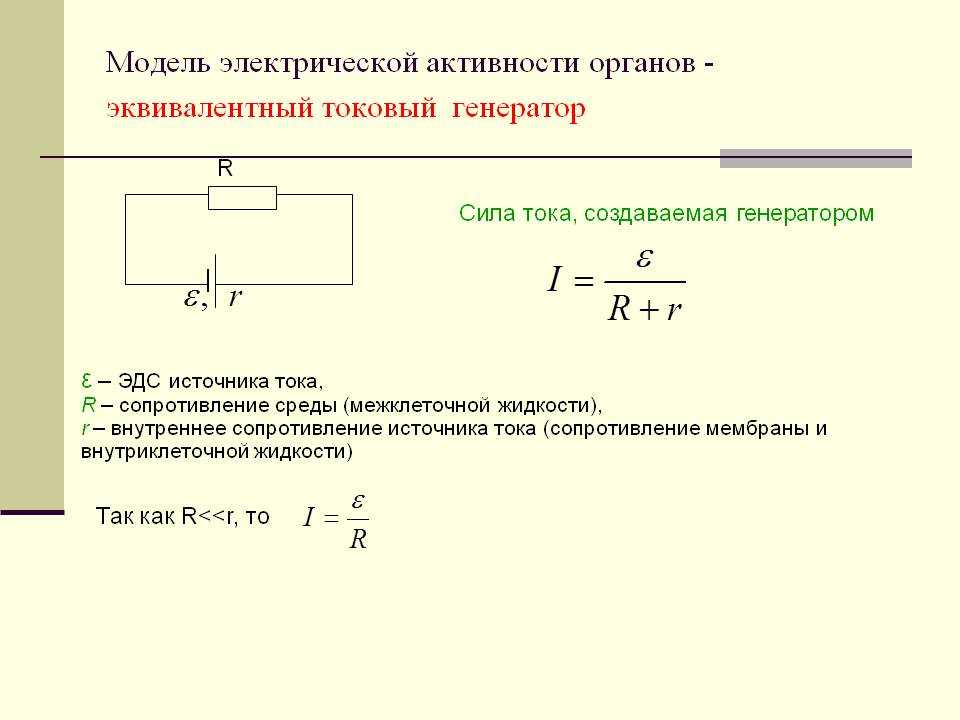 Таким образом, можно видеть, что по мере увеличения противоЭДС ток уменьшается. Но каково значение мощности ($PV$), передаваемой через источник и через компонент. Я предполагаю, что и то, и другое просто уменьшается, иначе энергия будет потеряна, правильно ли это, и если да, то не могли бы вы объяснить?

• электричество
• электрические цепи
• электрический ток

$\endgroup$

1

$\begingroup$

Предположим, мы имеем дело с идеальным двигателем, в котором нет ни трения, ни резистивных потерь. Если мы приложим напряжение, двигатель будет ускоряться до тех пор, пока противо-ЭДС не станет равной напряжению, и в этом состоянии мы имеем:

$$ P = (V — E)I = 0 $$

Мощность равна произведению тока на падение напряжения, но и ток, и падение напряжения равны нулю, поэтому ток не течет и мощность не рассеивается. Теперь предположим, что мы нагружаем двигатель, то есть заставляем двигатель выполнять некоторую работу. Нагрузка замедляет двигатель, поэтому обратная ЭДС $E$ уменьшается, но приложенное напряжение остается постоянным, поэтому теперь:

$$ P = (V — E)I > 0 $$

и мощность потребляется. Куда уходит сила? Ну, это входит в работу, проделанную двигателем над нагрузкой, которую мы к нему приложили. Если угловая скорость двигателя равна $\omega$, а развиваемый им крутящий момент равен $T$, то мощность равна $\omega T$, поэтому имеем:

$$ (V — E)I = \omega T $$

Энергия не теряется, мотор преобразует ее в работу.

$\endgroup$

$\begingroup$

Подводимая мощность представляет собой произведение напряжения на силу тока. Для описанной вами системы напряжение равно $(V-E)$, а ток равен $I$. Таким образом, отдаваемая мощность уменьшается с увеличением E. $$P = (V — E) \times I$$ При работе с несколькими напряжениями постоянного тока на одном узле следует применять принцип суперпозиции.