Энергетические характеристики сигналов. Спектральная плотность энергии
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
Страница проекта на GitHub.
Содержание
Энергия и средняя мощность сигналов Скалярное произведение сигналов. Обобщенная формула Рэлея Равенство Парсеваля Спектральная плотность энергии сигнала Список литературыЭнергия и средняя мощность сигналов
Пусть дан некоторый сигнал , который характеризует изменение напряжения или силы тока во времени. Тогда будет определять мгновенную мощность, выделяемую на сопротивлении 1 Ом.
Проинтегрируем мгновенную мощность на некотором интервале времени и получим энергию сигнала на данном интервале:(1)
Тогда средняя мощность сигнала на данном интервале времени равна:(2)
Если сигнал является периодическим, то среднюю мощность можно получить путем усреднения на одном периоде повторения сигнала. В случае абсолютно-интегрируемого непериодического сигнала , интервал интегрирования может быть расширен на всю ось времени:Таким образом, периодические сигналы, повторяющиеся на все оси времени мы можем характеризовать конечной средней мощностью , поскольку их энергия бесконечна. Непериодические сигналы характеризуются конечной энергией , потому что их средняя мощность на все оси времени равна нулю.
Выражения (1)–(3) справедливы и для комплексного сигнала . В этом случае, мгновенную мощность можно определить как .
Скалярное произведение сигналов. Обобщенная формула Рэлея
Пусть даны два сигнала и , в общем случае комплексные. Скалярным произведением сигналов называется величина равная:
(4)
Интеграл (4) возвращает одно число (скаляр), в общем случае комплексное.Заметим, что скалярное произведение сигнала с самим собой возвращает энергию данного сигнала:
(5)
Тогда скалярное произведение (4) можно трактовать как величину взаимной энергии сигналов и , т.е. степень взаимного влияния одного сигнала на другой. Если два сигнала и имеют нулевое скалярное произведение, то говорят, что они ортогональны.Подставим в (4) вместо обратное преобразование Фурье его спектральной плотности . Тогда:
(6)
Поменяем в (6) порядок интегрирования:(7)
Можно сделать вывод: скалярное произведение сигналов во временно́й области, с точностью до множителя , равно скалярному произведению спектральных плотностей данных сигналов. Выражение (7) носит название обобщенной формулы Рэлея [1, стр. 67].
Равенство Парсеваля
Ранее мы уже рассматривали равенство Парсеваля, связывающее среднюю мощность периодического сигнала. Для непериодических сигналов мы можем получить аналогичное равенство энергии сигнала во времени и в частотной области. Для этого в обобщенную формулу Рэлея подставим и получим:
(8)
или с учетом (4) равенство Парсеваля [2, стр. 49]:(9)
Таким образом, энергия сигнала во временно́й и частотной областях равна с точностью до множителя .
Если в выражениях (7)–(9) использовать частоту , выраженную в герц, вместо циклической частоты , измеряемой в единицах рад/c, то и множитель сокращается:
(10)
(11)
Спектральная плотность энергии сигнала
При рассмотрении предельного перехода к преобразованию Фурье было введено понятие спектральной плотности сигнала и была приведена аналогия поясняющая понятие спектральной плотности, и ее отличие от спектра периодического сигнала.
Из равенства (9) следует, что энергия сигнала может быть представлена как интеграл по всей оси частот:
(12)
Тогда использую ту же аналогию, что и в разделе , в частности сравнивая (12) с , можно заключить, что представляет собой спектральную плотность энергии сигнала. Проинтегрировав по всей оси , мы получим полную энергию сигнала, равно как проинтегрировав плотность стержня по длине мы получим полную массу. Спектральная плотность энергии представляет собой квадрат АЧХ сигнала. Кроме того является вещественной неотрицательной функцией частоты . Спектральная плотность энергии сигнала измеряется в единицах джоуль на герц (Дж/Гц) или ватт, умноженный на секунду в квадрате (Втс).Спектральные плотности сигналов имеют убывающий по частоте характер , и на практике анализ поведения убывающей спектральной плотности с ростом частоты имеет важное значение. Однако графический анализ бывает затруднителен ввиду высокой скорости убывания спектральной плотности по частоте, а в случае спектральной плотности энергии затруднителен вдвойне, поскольку возведение АЧХ в квадрат только ускоряет убывание. Поэтому широкое распространение получило представление спектральной плотности энергии в логарифмическом масштабе, выраженной в единицах децибел (дБ):
(13)
В качестве примера на рисунке 1 приведены спектральные плотности энергии прямоугольного, треугольного, двустороннего экспоненциального и гауссова импульсов в линейном и логарифмическом масштабе.
Рисунок 1. Спектральная плотность энергии некоторых сигналов
а — в линейном масштабе; б — в логарифмическом масштабе
Как видно из рисунка 1а, спектральные плотности энергии импульсов в линейном масштабе практически сливаются и очень сложно различимы.
В логарифмическом масштабе (рисунок 1б), спектральные плотности энергии обнаруживают значительные отличия. Треугольный и экспоненциальный импульсы имеют одинаковую скорость убывания спектральной плотности энергии, а прямоугольный импульс имеет очень медленное затухание спектральной плотности энергии с ростом частоты. Гауссов импульс, напротив, отличается очень быстрым затуханием .Выводы
В данном разделе мы рассмотрели энергетические характеристики периодических и непериодических сигналов. Мы показали, что периодические сигналы имеют бесконечную энергию, но конечную среднюю мощность. Средняя мощность непериодических сигналов стремится к нулю, а их энергия конечна.
Было введено понятие скалярного произведения сигналов и получена обобщенная формула Релея,связывающая скалярное произведение во временной и частотной областях.
Установлено равенство Парсеваля для непериодических сигналов, как частный случай формулы Релея.
Введено понятие спектральной плотности энергии как квадрата модуля спектральной плотности сигнала. Также рассмотрено представление спектральной плотности энергии в линейном и логарифмическом масштабе для различных сигналов.
Смотри также
Преобразования Фурье непериодических сигналовСвойства преобразования Фурье
Спектральные плотности некоторых сигналов
Информация была полезна? Поделитесь с друзьями!
Список литературы
[1] Баскаков, С.И. Радиотехнические цепи и сигналы Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4
[2] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.
[3] Bracewell, R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6
© Бахурин Сергей 2015 — 2020. Все права защищены. Любое копирование материалов сайта без разрешения автора запрещено.
4 Энергия и мощность сигнала
Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся в резисторе мощность будет равна:
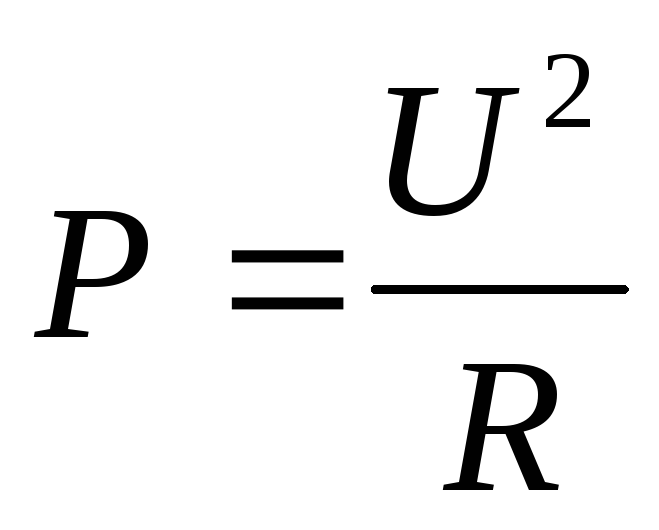
За время Т в этом резисторе выделяется тепловая энергия:
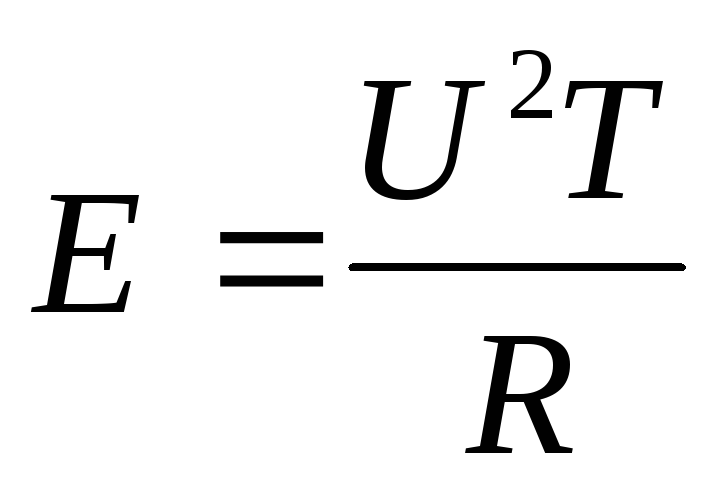
Пусть теперь к тому же резистору приложено не постоянное напряжение, а сигнал S(t). Рассеивающаяся в резисторе мощность при этом тоже будет зависеть от времени (речь идет о мгновенной мощности).
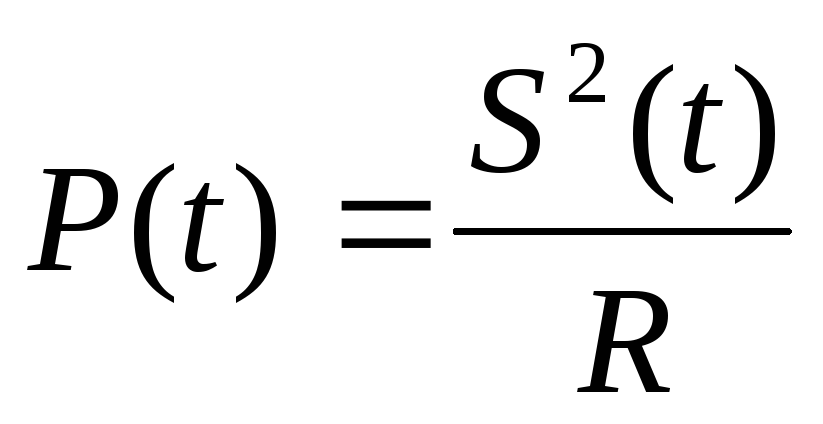
Чтобы вычислить теряющуюся за время T энергию, мгновенную мощность необходимо проинтегрировать:
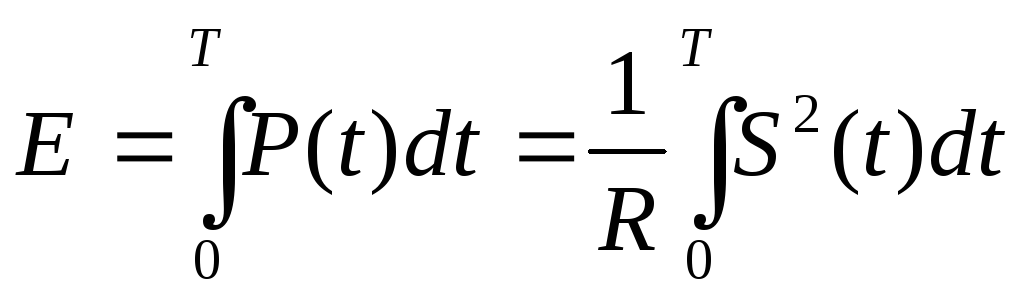
Можно ввести и понятие средней мощности за заданный промежуток времени, разделив энергию на длительность временного интервала:
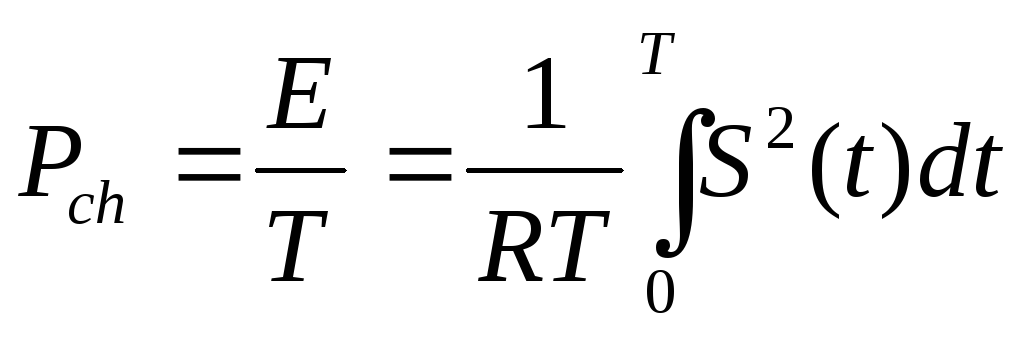
Во все приведенные формулы входит сопротивление нагрузки R. Если энергия и мощность интересуют нас не как физические величины, а как средние сравнения различных сигналов, этот параметр можно из формул исключить (принять R=1). Тогда мы получим определение энергии мгновенной мощности и средней мощности, принятой в теории сигналов
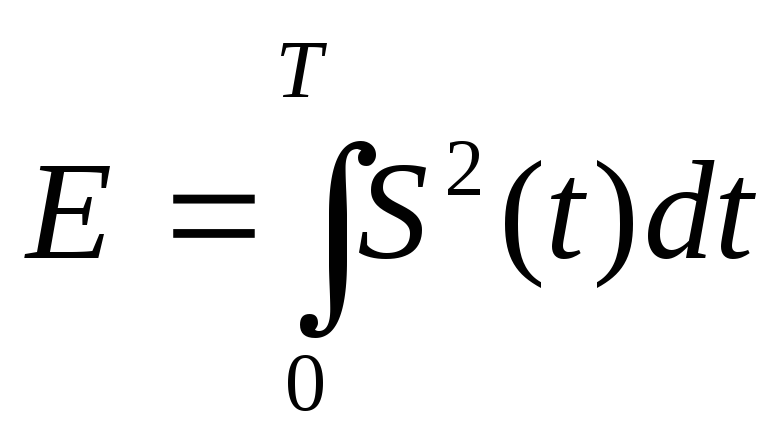 — энергия сигнала
— энергия сигнала
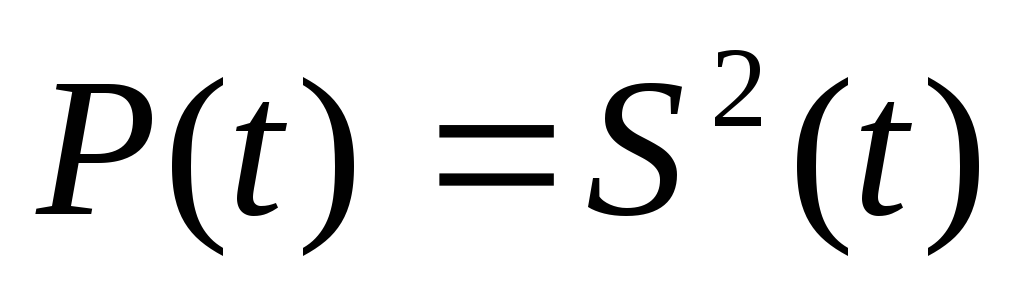 — мгновенная
мощность
— мгновенная
мощность
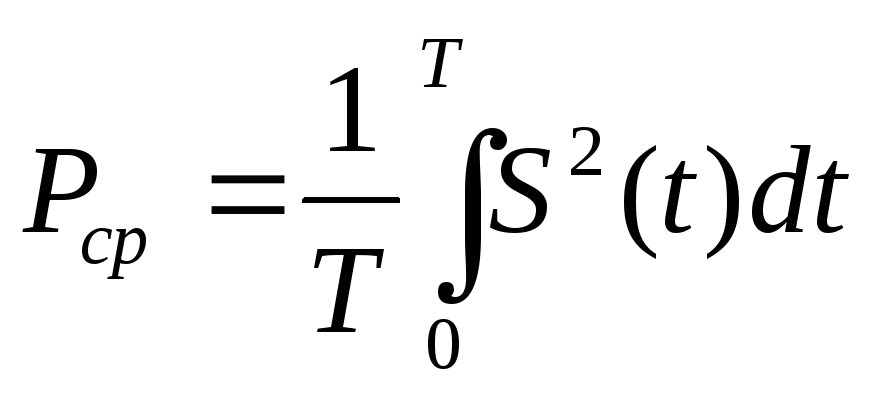 (1)
(1)
Данные параметры иногда называются удельной мощностью и энергией, чтобы подчеркнуть, подразумевая при этом единичное значение сопротивления нагрузки.
Энергия сигнала может быть конечной или бесконечной. Любой сигнал конечной длительности будет иметь конечную энергию, а любой периодический – бесконечную. Если энергия сигнала бесконечна, можно определить его среднюю мощность на всей временной оси. Для этого из формулы (1) путем предельного перехода, устремив интервал усреднения в бесконечность
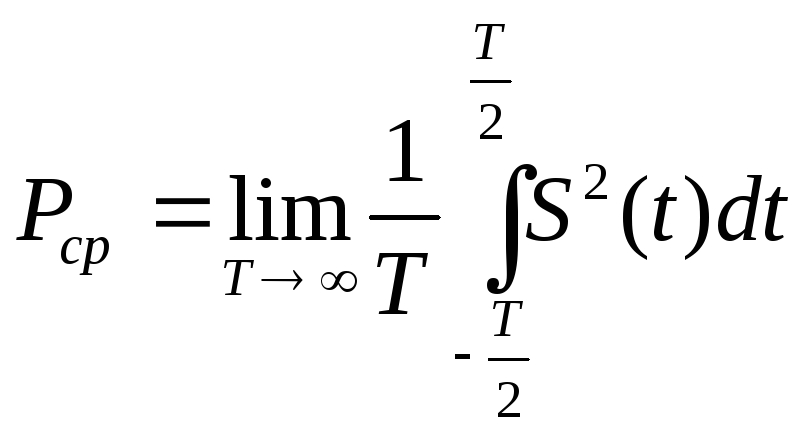 (2)
(2)
Квадратный корень из Рср даст среднеквадратичное значение мощности сигнала
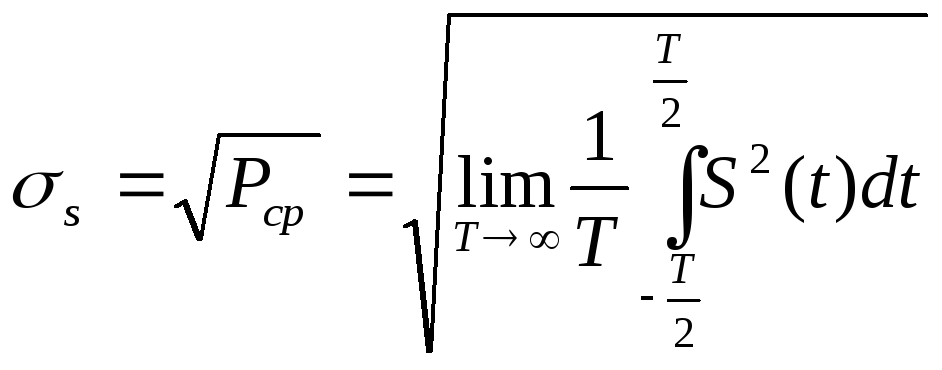 (3)
(3)
5 Спектральный анализ периодических сигналов. Условия Дирихле. Ряд Фурье.
Для периодического сигнала с периодом Т выполняется соотношение:S(t+nT) = S(t) при любом t.
где n — произвольное целое число; Т – период сигнала.Величина обратная периоду называется частотой повторения сигнала (f = 1/T). Используют понятие круговой частоты. (ω = 2πf)
Разложению в ряд Фурье могут подвергаться периодические сигналы.
Чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:
не должно быть разрывов 2-го рода (с уходящими в бесконечность ветвями функции)
число разрывов 1-го рода (скачков) должно быть конечным
число экстремумов должно быть конечным
Различают несколько форм записи ряда Фурье:
синусно – косинусная
вещественная
комплексная
Синусно-косинусная форма записи ряда Фурье
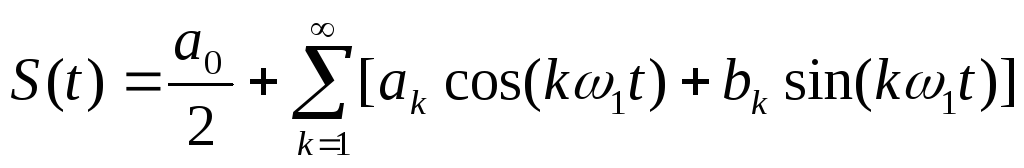
Входящие в формулу кратные основной частоте (ω1) частоты называются гармониками. Гармоники нумеруются в соответствии с индексом k, частота ω k = k ω 1 называется к-ой гармоникой сигнала.
Коэф-ты, входящие в данный ряд определяются след образом:
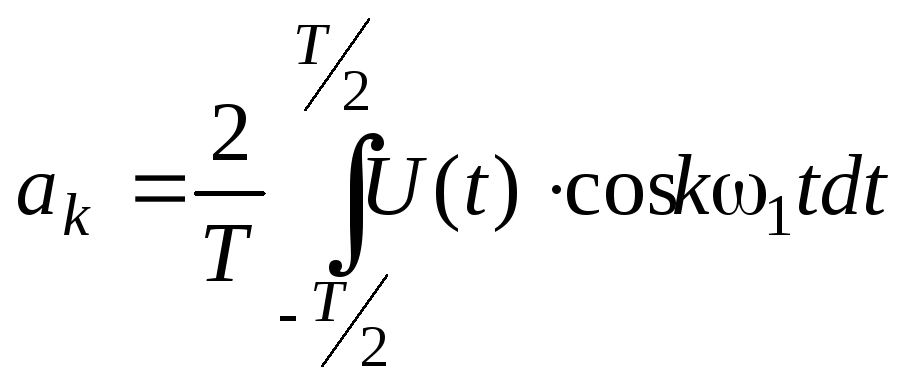 ;
; 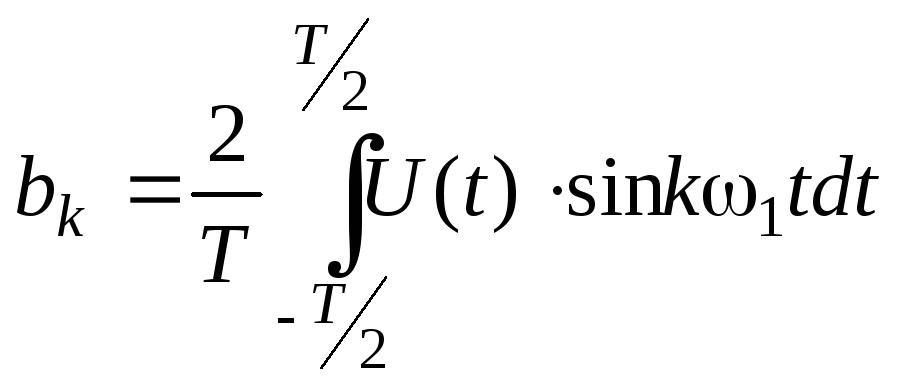 ;
;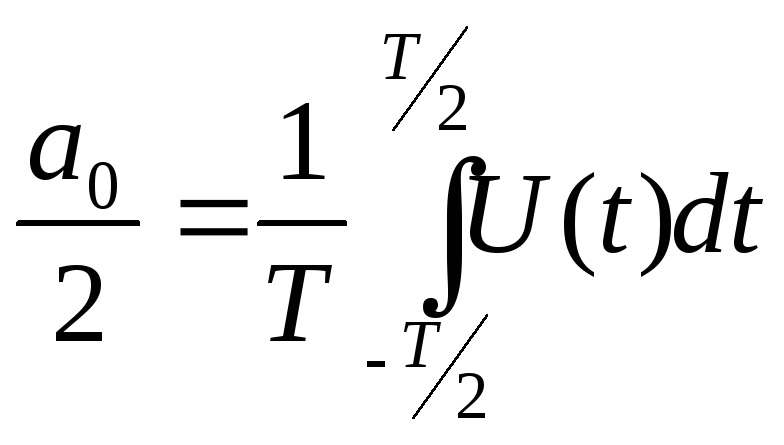
a0/2 – среднее значение с-ла на периоде.
Если S(t) — чётная ф-ция, то все bк = 0 и в ф-ле ряда Фурье будут только косинусные слагаемые. Если S(t) — нечётная ф-ция, то все ак = 0 и в ф-ле ряда Фурье будут только синусные слагаемые.
Вещественная форма записи
Некоторое неудобство синусно-косинусной формы ряда Фурье состоит в том, что для каждого значения индекса суммирования к в формуле фигурируют два слагаемых синус и косинус.
,
где 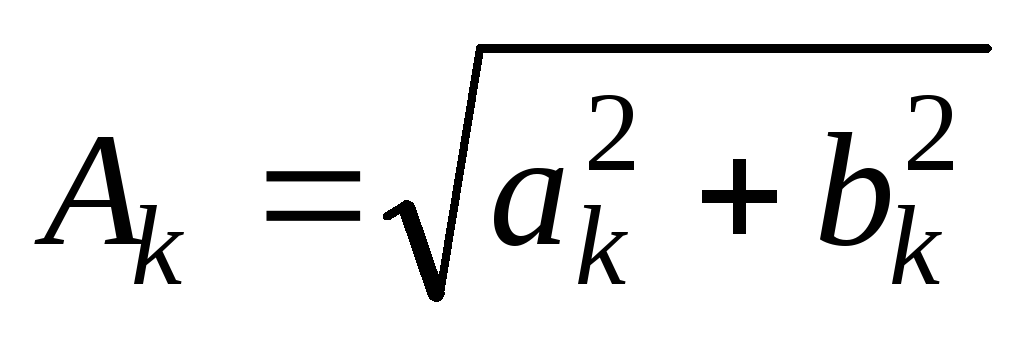 ;
;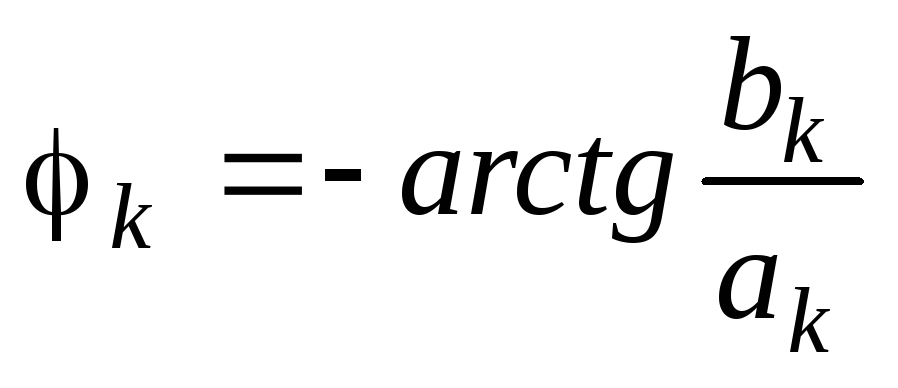 — фазаk—ой
гармоники.
— фазаk—ой
гармоники.
Если S(t) является чётной функцией фазы φк могут принимать значения 0 и π, а если S(t) функция нечётная, то возможны значения фазы ±π/2.
Комплексная форма записи
Данная форма представления является наиболее употребимой в радиотехнике. Она получается из вещественной формы представления косинуса в виде полусуммы комплексных экспонент. Вытекает из формулы Эйлера: еjx = cos(x) + jsin(x), cos(x) = ½ ( ejx + e—jx ).
Применив данное преобразование к вещественной форме ряда Фурье получим:
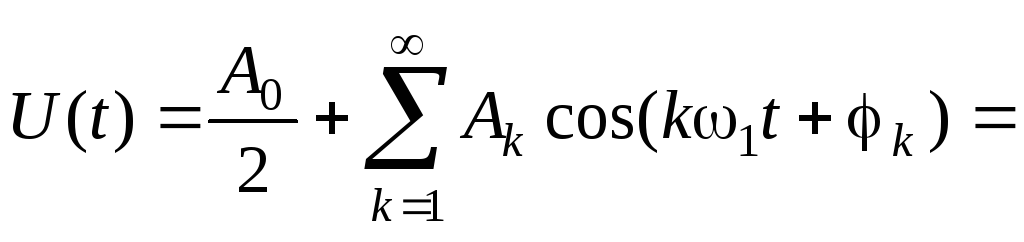
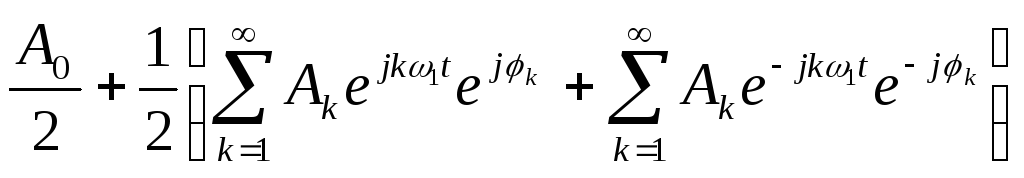 .
.
Учитывая, что 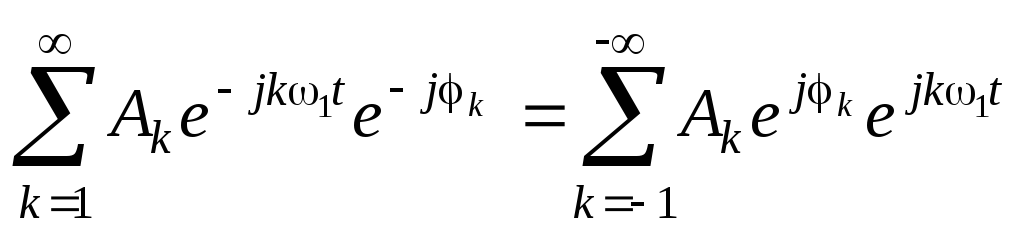 ,получим
,получим 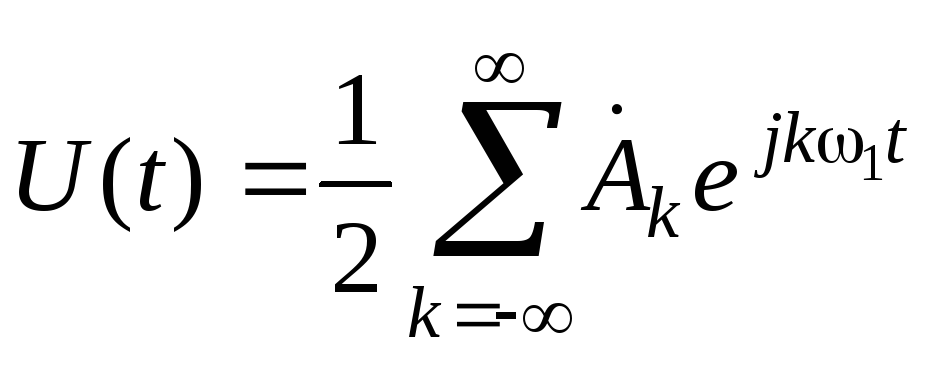 .
Формулы называются парой преобразований
Фурье. Вторая формула из них позволяет
найти спектр, т.е. совокупность
гармонических составляющих, образующих
в сумме колебание
.
Формулы называются парой преобразований
Фурье. Вторая формула из них позволяет
найти спектр, т.е. совокупность
гармонических составляющих, образующих
в сумме колебание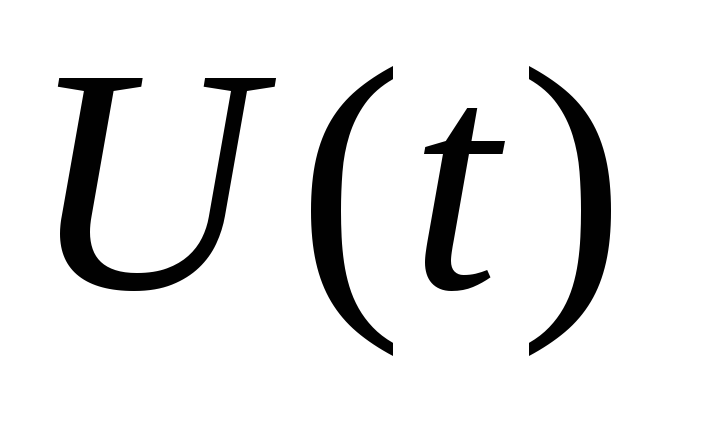 .
.
Спектр периодической
последовательности импульсов состоит
из постоянной составляющей и множества
гармонических составляющих, частоты
которых образуют дискретный ряд значений 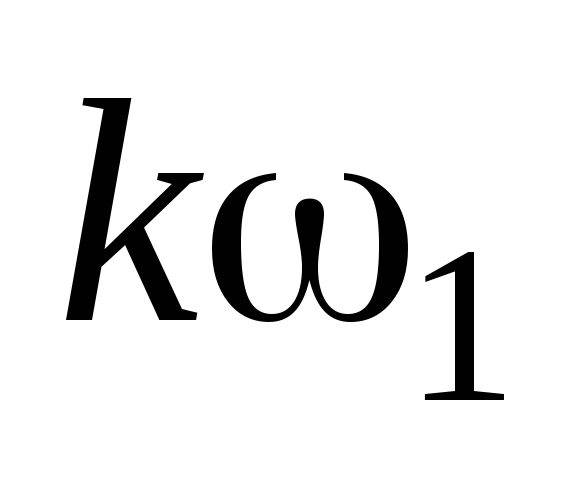 (
(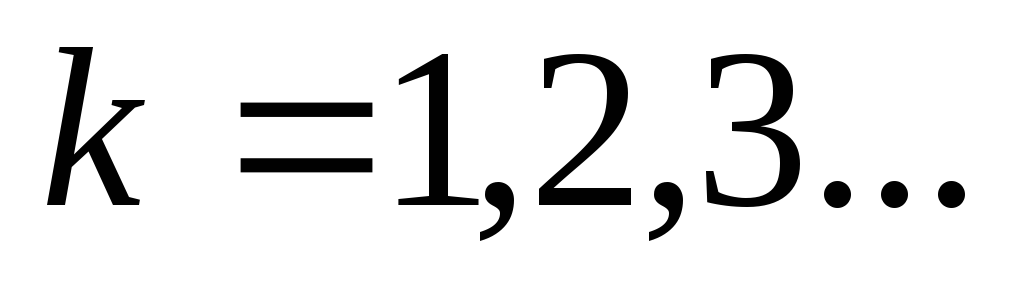 )
кратных основной частоте колебаний
)
кратных основной частоте колебаний .
Амплитуды гармонических составляющих
или сокращенно гармоник равны
.
Амплитуды гармонических составляющих
или сокращенно гармоник равны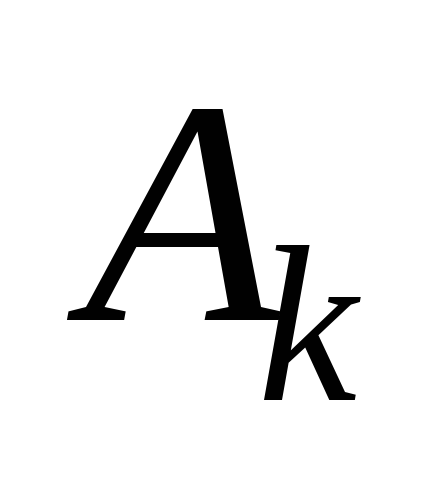 ,
а начальные фазы
,
а начальные фазы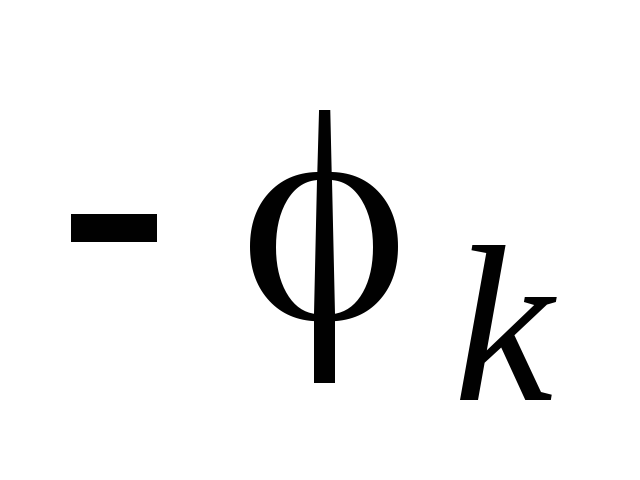 .
Такой спектр называется дискретным или
линейчатым. Постоянную составляющую
можно рассматривать как гармонику с
нулевой частотой колебания и амплитудой
.
Такой спектр называется дискретным или
линейчатым. Постоянную составляющую
можно рассматривать как гармонику с
нулевой частотой колебания и амплитудой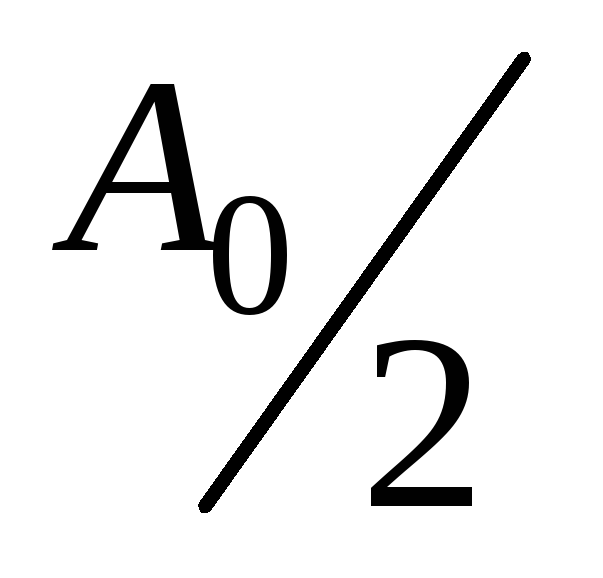 .
.
1.3. Спектральная плотность. 1. Сигналы и спектры. Теоретические основы цифровой связи
1.3.1. Спектральная плотность энергии
1.3.2. Спектральная плотность мощности
Спектральная плотность (spectral density) характеристик сигнала — это распределение энергии или мощности сигнала по диапазону частот. Особую важность это понятие приобретает при рассмотрении фильтрации в системах связи. Мы должны иметь возможность оценить сигнал и шум на выходе фильтра. При проведении подобной оценки используется спектральная плотность энергии (energy spectral density — ESD) или спектральная плотность мощности (power spectral density — PSD).
1.3.1. Спектральная плотность энергии
Общая энергия действительного энергетического сигнала 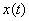 , определенного в интервале
, определенного в интервале 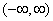 описывается уравнением (1.7). Используя теорему Парсеваля [1], мы можем связать энергию такого сигнала, выраженную во временной области, с энергией, выраженной в частотной области:
описывается уравнением (1.7). Используя теорему Парсеваля [1], мы можем связать энергию такого сигнала, выраженную во временной области, с энергией, выраженной в частотной области:
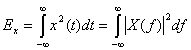 , (1.13)
, (1.13)
где 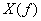 — Фурье-образ непериодического сигнала
— Фурье-образ непериодического сигнала 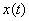 . (Краткие сведения об анализе Фурье можно найти в приложении А.) Обозначим через
. (Краткие сведения об анализе Фурье можно найти в приложении А.) Обозначим через 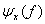 прямоугольный амплитудный спектр, определенный как
прямоугольный амплитудный спектр, определенный как
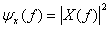 (1.14)
(1.14)
Величина 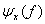 является спектральной плотностью энергии (ESD) сигнала
является спектральной плотностью энергии (ESD) сигнала 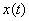 . Следовательно, из уравнения (1.13) можно выразить общую энергию
. Следовательно, из уравнения (1.13) можно выразить общую энергию 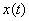 путем интегрирования спектральной плотности по частоте.
путем интегрирования спектральной плотности по частоте.
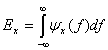 (1.15)
(1.15)
Данное уравнение показывает, что энергия сигнала равна площади под 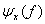 на графике в частотной области. Спектральная плотность энергии описывает энергию сигнала на единицу ширины полосы и измеряется в Дж/Гц. Положительные и отрицательные частотные компоненты дают равные энергетические вклады, поэтому, для реального сигнала
на графике в частотной области. Спектральная плотность энергии описывает энергию сигнала на единицу ширины полосы и измеряется в Дж/Гц. Положительные и отрицательные частотные компоненты дают равные энергетические вклады, поэтому, для реального сигнала 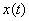 , величина
, величина 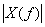 представляет собой четную функцию частоты. Следовательно, спектральная плотность энергии симметрична по частоте относительно начала координат, а общую энергию сигнала
представляет собой четную функцию частоты. Следовательно, спектральная плотность энергии симметрична по частоте относительно начала координат, а общую энергию сигнала 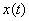 можно выразить следующим образом.
можно выразить следующим образом.
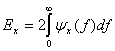 (1.16)
(1.16)
1.3.2. Спектральная плотность мощности
Средняя мощность 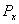 действительного сигнала в периодическом представлении
действительного сигнала в периодическом представлении 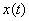 определяется уравнением (1.8). Если
определяется уравнением (1.8). Если 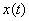 — это периодический сигнал с периодом
— это периодический сигнал с периодом 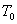 , он классифицируется как сигнал в периодическом представлении. Выражение для средней мощности периодического сигнала дается формулой (1.6), где среднее по времени берется за один период
, он классифицируется как сигнал в периодическом представлении. Выражение для средней мощности периодического сигнала дается формулой (1.6), где среднее по времени берется за один период 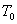 .
.
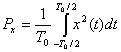 (1.17,а)
(1.17,а)
Теорема Парсеваля для действительного периодического сигнала [1] имеет вид
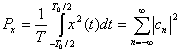 , (1.17,б)
, (1.17,б)
где члены 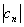 являются комплексными коэффициентами ряда Фурье для периодического сигнала (см. приложение А).
являются комплексными коэффициентами ряда Фурье для периодического сигнала (см. приложение А).
Чтобы использовать уравнение (1.17,6), необходимо знать только значение коэффициентов 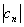 . Спектральная плотность мощности (PSD)
. Спектральная плотность мощности (PSD) 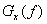 периодического сигнала
периодического сигнала 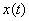 , которая является действительной, четной и неотрицательной функцией частоты и дает распределение мощности сигнала
, которая является действительной, четной и неотрицательной функцией частоты и дает распределение мощности сигнала 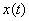 по диапазону частот, определяется следующим образом.
по диапазону частот, определяется следующим образом.
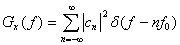 (1.18)
(1.18)
Уравнение (1.18) определяет спектральную плотность мощности периодического сигнала 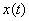 как последовательность взвешенных дельта-функций. Следовательно, PSD периодического сигнала является дискретной функцией частоты. Используя PSD, определенную в уравнении (1.18), можно записать среднюю нормированную мощность действительного сигнала.
как последовательность взвешенных дельта-функций. Следовательно, PSD периодического сигнала является дискретной функцией частоты. Используя PSD, определенную в уравнении (1.18), можно записать среднюю нормированную мощность действительного сигнала.
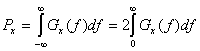 (1.19)
(1.19)
Уравнение (1.18) описывает PSD только периодических сигналов. Если 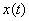 — непериодический сигнал, он не может быть выражен через ряд Фурье; если он является непериодическим сигналом в периодическом представлении (имеющим бесконечную энергию), он может не иметь Фурье-образа. Впрочем, мы по-прежнему можем выразить спектральную плотность мощности таких сигналов в пределе. Если сформировать усеченную версию
— непериодический сигнал, он не может быть выражен через ряд Фурье; если он является непериодическим сигналом в периодическом представлении (имеющим бесконечную энергию), он может не иметь Фурье-образа. Впрочем, мы по-прежнему можем выразить спектральную плотность мощности таких сигналов в пределе. Если сформировать усеченную версию 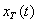 непериодического сигнала в периодическом представлении
непериодического сигнала в периодическом представлении 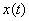 , взяв для этого только его значения из интервала (
, взяв для этого только его значения из интервала (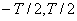 ), то
), то 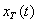 будет иметь конечную энергию и соответствующий Фурье-образ
будет иметь конечную энергию и соответствующий Фурье-образ 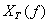 . Можно показать [2], что спектральная плотность мощности непериодического сигнала
. Можно показать [2], что спектральная плотность мощности непериодического сигнала 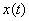 определяется как предел.
определяется как предел.
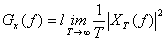 (1.20)
(1.20)
Пример 1.1. Средняя нормированная мощность
а) Найдите среднюю нормированную мощность сигнала 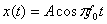 , используя усреднение по времени.
, используя усреднение по времени.
б) Выполните п. а путем суммирования спектральных коэффициентов.
Решение
а) Используя уравнение (1.17,а), имеем следующее.
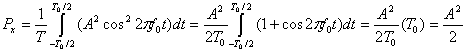
б) Используя уравнения (1.18) и (1.19), получаем следующее.
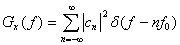
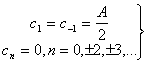 (см. приложение А)
(см. приложение А)
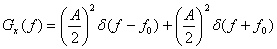
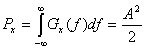
Основы радиолокации — Импульсная и средняя мощность
коэффициент заполнения
средняя мощность
импульсная мощность
длительность импульса
период повторения импульсов
Рисунок 1. К пояснению понятий «коэффициент заполнения», «импульсная мощность», «средняя мощность»
коэффициент заполнения
средняя мощность
импульсная мощность
длительность импульса
период повторения импульсов
Рисунок 1. К пояснению понятий «коэффициент заполнения», «импульсная мощность», «средняя мощность»
Импульсная и средняя мощность
Энергия, излучаемая радиолокатором непрерывного излучения может быть легко определена, поскольку передатчик такого радиолокатора работает непрерывно. Однако у импульсного радиолокатора передатчик включается и выключается, чтобы обеспечить получение информации о дальности цели с каждым импульсом. Знать количество энергии, излучаемой в таком случае, важно, поскольку оно связано с мощностью на выходе передатчика, от которой прямо зависит максимальная дальность действия радиолокатора. Чем большую энергию излучает радиолокатор, тем большей будет дальность обнаружения им цели.
Энергия импульса равна произведению импульсной (пиковой, максимальной) мощности на длительность импульса. Однако измерительные средства (датчики), используемые в радиолокаторах для измерения мощности, выполняют измерение в течение интервала времени, превышающего длительность импульса. По этой причине период повторения импульсов включен в формулы для расчета мощности передатчика. Мощность, измеренная в течение такого периода, называют средней мощностью. Соотношение между средней и импульсной мощностью поясняется на Рисунке 1 и описывается следующей формулой:
Импульсная мощность должна вычисляться чаще, чем средняя мощность. Это вызвано тем, что большинство измерительных средств измеряют среднюю мощность напрямую, как правило, путем оценки нагрева чувствительного элемента датчика. Формула (1) определяет общий подход к расчету импульсной мощности по средней мощности и наоборот.
Поскольку некоторое количество энергии накапливается в модуляторе, система электропитания должна обеспечивать потребляемую мощность передатчика, лишь немного большую, чем средняя излучаемая мощность.
Коэффициент заполнения
Произведение длительности импульса (τ) на частоту повторения импульсов (prf), являющуюся величиной, обратной периоду повторения импульсов (Τ) в формуле (1), называют коэффициентом заполнения радиолокатора. Коэффициент заполнения показывает какую часть рабочего периода (периода повторения импульсов) система находится в «активном» состоянии.
Иногда при расчетах импульсной и средней мощности используется величина, обратная коэффициенту заполнения. Такая величина называется скважностью. Она показывает сколько импульсов укладывается в интервал времени, равный периоду повторения.
Сущность коэффициента заполнения можно пояснить на таком примере (Рисунок 1). Предположим, передатчик работает в течение 1 микросекунды и выключается на 99 микросекунд, затем снова запускается на 1 микросекунду и так далее. В таком случае передатчик работает в течении одной из ста микросекунд или 1/100 всего рабочего времени, то есть его коэффициент заполнения составляет 1/100 или 1 процент. Значение коэффициента заполнения используется при расчетах как импульсной мощности, так и средней мощности радиолокационной системы.
Что такое Сигнал (Информация) — Типы и Парметры Сигналов
В этой статье Вы узнаете что такое информация и сигнал, какие бывают сигналы, их виды, параметры. Увидите реальную спектральную плотность мощности. Что происходит с сигналом в канале связи. Познакомимся с эффектом Доплера. Узнаем больше о шумах и помехах.


Что такое информация
Под информацией понимают совокупность сведений о каких-либо событиях, явлениях или предметах, предназначенных для передачи, приёма, обработки, преобразования, хранения.
К.Э. Шеннон, как один из основателей теории информации образно её определил так: «Информация – послание, которое уменьшает неопределённость».
Если я Вам скажу что-то, что для Вас известно, то это не будет для Вас информацией. Я если скажу, то что Вы не знали, уменьшу вашу неопределенность, то это уже будет для Вас информацией.
Что такое сигнал
Сигнал – это некоторый физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением. Пример – электрический сигнал, радиосигнал, как частный случай электромагнитного сигнала, акустический сигнал, оптический и т.д. В зависимости от того, в какой среде идет распространение сигнала. Сигнал – это материальный носитель информации.
Обычно сигнал, независимо от его физической природы, представляют, как некоторую функцию времени x(t). Такое представление есть общепринятая математическая абстракция физического сигнала.
Типы сигналов
- Детерминированный, или регулярный – это сигнал, закон изменения которого известен и известны все его параметры.
Такой сигнал передает информацию? Информация уменьшает неопределенность. В детерминированном сигнале мы знаем все, мы знаем какой он будет через минуту, через год. Детерминированный сигнал информацию в себе никакую не несет. Например, сигнал с гетеродина, мы сами его сформировали, задали частоту, амплитуду, фазу.
- Квазидетерминированный — это сигнал, закон изменения которого известен, но один или несколько параметров является случайной величиной.
Пример: x(t)=Asin(wt+j), где амплитуда А и j — случайная величина.
Например, мы знаем его частоту, но не знаем амплитуду и фазу — это квазидетерминированный сигнал, “квази”-почти, почти определенный сигнал. Информация вносит некоторую случайность. Если мы знаем амплитуду, частоту и фазу, значит информации там нет. Квазидетерминированный сигнал передает информацию, передача информации идет в тех параметрах, которые случайны, в нашем примере амплитуда и фаза случайные величины. Именно в этих величинах передается информация. Информация всегда несет в себе хаос, случайность. Все модулированные сигналы, ЧМ, ФМ это квазидетерминированные сигналы.
- Случайным называют сигнал, мгновенные значения которого не известны, а могут быть лишь предсказаны с некоторой вероятностью.
Кроме этого все сигналы могут быть непрерывными (аналоговыми) и дискретными (цифровыми или импульсными).
О случайном сигнале мы можем судить о его вероятностных характеристиках. Мы можем знать его плотность вероятности, но какое значение примет сигнал через секунду, минуту мы не знаем. Когда мы работаем со случайным сигналом, мы всегда работаем с вероятностью.
Параметры сигналов
Какие параметры мы будем использовать? Это энергия за некоторый интервал времени T. X(t) это сам сигнал, чтобы определить энергию мы должны взять по модулю, возвести в квадрат, проинтегрировать на некотором промежутке времени и получим энергию.


Средняя мощность за некоторое время t. Это энергия деленная на время.


Мгновенная мощность, если средняя мощность измеряется на некотором участке времени, то мгновенная измеряется в один, конкретный момент времени.


Средняя мощность измеряется на промежутке времени, а мгновенная в точке.


Спектральная плотность энергии и мощности
Спектральная плотность сигнала характеризует распределение энергии или мощности сигнала по диапазону частот. Спектральная плотность энергии, это как у нас энергия распределяется по частотному диапазону. Вычисляется через преобразование Фурье.


И соответственно, СПМ это, как у нас распределяется мощность по частотному диапазону.
В формуле, модуль в квадрате это спектральная плотность энергии, поделили ее на время T и по определению, время T должно стремиться к бесконечности. Но на практике, никто не ждет бесконечности, все оценивают СПМ на некотором интервале времени.
СПМ это некоторая функция зависящая от частоты. По шкале СПМ возьмем 10 Вт/Гц, и окрестности в 1 Гц по частоте. То в полосе 1 Гц будет заключено 10 Вт мощности.


Есть два сигнала и представлены их спектральные плотности мощности. ВОПРОС. Мощность какого сигнала больше?


Мы должны определить площадь под кривой, проинтегрировать. S1=2*10=20 Вт, S2=1*30=30 Вт. В первом случае S1 имеет мощность 20 Вт, а во втором 30 Вт.
СПМ реального сигнала, отображаемая на спектральном анализаторе.


Современные анализаторы спектра могут считать автоматически площадь, вы включаете определение мощности, задаете частотный интервал в котором он должен измерить эту мощность и он сам вычисляет канальную мощность сигнала.
Что происходит с сигналом в канале связи
С ним происходят ослабления, задержка, доплеровский сдвиг, шумы и тому подобное.
Ослабление
Сигнал ослабевает за счет рассеивания в пространстве. Например, у нас есть источник радиосигнала, всенаправленный и изотропный, т.е. он во все стороны излучает одинаково. Получается сферический фронт волны. На одном расстоянии r1 и на другом r2.


Пусть излучаемая мощность 100 Вт, все эти 100 ватт распределяются по всей сфере. Приемные антенны не большие, они охватывают только небольшой участок пространства. И количество мощности, проходящее через небольшой участок пространства, будет разный на расстоянии r1 и r2. Потому что плотность мощности на расстоянии r1 будет выше, чем на расстоянии r2.
Площадь сферы равна S=4pi*R^2. И эта формула фигурирует во всех формулах оценки дальности радиосвязи. Потому что радиоволна равномерно рассеивается в пространстве. И помимо того, что сигнал сам ослабевает по мере распространения в пространстве, электромагнитная волна проходит через некую среду, которую пытается нагреть и за счет этого теряет свою энергию.
Задержка распространения сигнала
Не смотря на то, что электромагнитная волна, это самое быстрое, что есть у нас во вселенной, тем не менее скорость распространения этой волны конечна. И поддается измерениям. Например, на 1 км задержка распространения ~3.3 мкс.
На что влияет задержка распространения? Обычно, мы точно не знаем расстояние между передатчиком и приемником с точность до микрон. И задержка распространения, которая нам неизвестна, мы не знаем расстояние и не знаем за какое время примем этот сигнал. И соответственно мы не знаем начальную фазу сигнала.
Доплеровский сдвиг частоты
Приняли сигнал с частотой, который отличается от той, которую мы передали. Это дало информацию о скорости объекта. Доплеровский сдвиг частоты появляется, когда у нас либо приемник, или передатчик, двигаются относительно друг друга. Либо двигается отражающая среда, передатчик излучил, радиосигнал отразился от какого-то объекта, если этот объект тоже двигается, то возникает доплеровский сдвиг частоты. Более подробно читайте полную статью “Доплеровский сдвиг частоты”.
Воздействие помех и шумов
И в эфире есть шумы и собственные шумы приемника. Про шумы подробнее в отдельной статье.
Замирания сигнала
Замирания сигнала это процесс, когда у сигнала, случайным образом скачет амплитуда и фаза. То больше амплитуда, то меньше. Выделяют:
- Быстрые замирания (интерференционное замирание) — накладывание собственных копий сигнала от переотражений с разными фазами. Вызываются многолучевым распространением сигнала.
Когда есть источник, есть приемник, есть множество путей распространения радиоволны, одна волна может прийти прямой, другая переотраженной.
Например, одна волна прошла 100 км, другая 101 км, к чему это приводит? Если две электромагнитные волны проделали разный путь, то фазы у этих сигналов тоже будут разные. Соответственно, если сигналы сложились в противофазе, то сигналы друг друга подавили, если сложились в фазе, то друг друга усилили.


Из-за многолучевого распространения, каждый луч проделывает разное расстояние, это приводит к тому, что начальная фаза каждого луча отличается. И когда в приемнике эти сигналы складываются, они могут друг друга усиливать либо ослаблять. Это приводит к тому, что амплитуда результирующего сигнала постоянно изменяется, это и есть быстрые замирания.
- Медленные замирания (затенение) – возникновение препятствий на пути следования радиоволны. Если радиоволна распространяется в пространстве и встречает препятствия, причем эти препятствия то появляются, то исчезают.


На рисунке ниже представлен характер изменения амплитуды сигнала от времени. Сплошной линией показаны быстрые замирания, пунктирной медленные. Медленные замирания происходят из за затенения, быстрые из-за многолучевого распространения. Получается, что амплитуда постоянно скачет на десятки дБ.


Межсимвольная интерференция
Возникает из-за многолучевого распространения.
Линейные искажения
Канал связи всегда имеет АЧХ и ФЧХ. Какие-то частоты он усиливает, какие-то ослабляет, фаза где-то поворачивается в одну сторону, где-то в другую это и есть линейные искажения.
Если мы хотим сделать модель канала связи, то чем больше этих параметров мы учтем, тем точнее будет эта модель.
Audio Digital Signal Processing: Мощность цифрового сигнала
В аналоговом мире значение сигнала определяется в Вольтах (Volt), а мощность сигнала в Ваттах (Watt). Мгновенная мощность электрического сигнала определяется, как квадрат напряжения, разделенный на сопротивление в цепи, через которую проходит сигнал.
Сигнал после оцифровки x(t) является аналогом напряжения, а мощность цифрового сигнала определяется, как квадрат значения сигнала — x(t)2. Среднеквадратичное или действующее значение сигнала (RMS) определяется, как квадратный корень из усредненного значения мощности сигнала.Рассмотрим эти величины на примере. Выберем частоту дискретизации сигнала 44100 Гц (Fs), период дискретизации (Ts) рассчитывается, как обратная величина к частоте. Будем генерировать сигнал с частотой 441Гц (очень близко к ноте ля первой октавы 440Гц).
Сгенерируем 4 полных периода синусоидального сигнала на заданной частоте. Мы специально подобрали соотношение частоты дискретизации и сигнала (добавив 1Гц), чтобы количество отсчетов (N) было целым числом. Определим дискретное время (t) в пределах от 0 до N−1. Рассчитаем значения функции синус для всех значений заданного времени.
Полученный сигнал x(t) на графике отображается красной линией. Мы видим все 4 периода. Амплитуда сигнала в диапазоне от −1 до 1.
Рассчитаем значение мощности сигнала (P), как среднее всех мгновенных мощностей сигнала и среднеквадратичное значение (RMS), как корень из мощности (P).
Видим что значение мощности равно 0.5, а среднеквадратичное значение 0.707.. или точнее корень из двух на два.
Рассмотрим, как изменится мощность и среднеквадратичное значение, если мы умножим сигнал на это значение — на графике сигнал y(t) отображен синим цветом. Видим, что размах амплитуды ограничен этим значением, а мощность сигнала (Py) уменьшилась в два раза.
Часто понятия мощность и среднеквадратичное значения сигнала путают, причем эта путаница происходит в гигантских масштабах.Производители звукового оборудования (например Harman/Kardon, Marantz и прочие аудиофильские бренды) пишут RMS и измеряют это значение в Ваттах.
Мощность и энергия сигналов
Понятия мощности и энергии в теории сигналов не относятся к характеристикам каких-либо физических величин сигналов, а являются их количественными характеристиками, отражающими определенные свойства сигналов и динамику изменения их значений (отсчетов) во времени, в пространстве или по любым другим аргументам.
Для произвольного, в общем случае комплексного, сигнала s(t) = a(t)+jb(t), где а(t) и b(t) — вещественные функции, мгновенная мощность (instantaneous power) сигнала по определению задается выражением:
w(t) = s(t) s*(t) = [a(t)+jb(t)] [a(t)-jb(t)] = a2(t)+b2(t) = |s(t)|2, (21)
т.е. функция распределения мгновенной мощности по аргументу сигнала равна квадрату функции его модуля, для вещественных сигналов — квадрату функции амплитуд.
Аналогично для дискретных сигналов:
wn = sn s*n = [an+jbn] [an-jbn] = an2 + bn2 = |sn|2, (21′)
Энергия сигнала (также по определению) равна интегралу от мощности по всему интервалу существования или задания сигнала. В пределе:
Еs =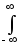 w(t)dt
=
w(t)dt
=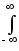 |s(t)|2dt.
(22)
|s(t)|2dt.
(22)
Es =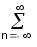 wn =
wn =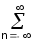 |sn|2.
(22′)
|sn|2.
(22′)
Мгновенная мощность w(t) является плотностью мощности сигнала, так как измерения мощности возможны только через энергию на интервалах ненулевой длины:
w(τ) = (1/t)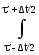 |s(t)|2dt
|s(t)|2dt
Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.
Как правило, сигналы изучаются на определенном интервале Т, для периодических сигналов — в пределах одного периода Т, при этом средняя мощность сигнала:
WT(τ)
= (1/T)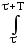 w(t)
dt = (1/T)
w(t)
dt = (1/T)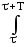 |s(t)|2 dt. (23)
|s(t)|2 dt. (23)
Понятие средней мощности может быть распространено и на незатухающие сигналы, энергия которых бесконечно велика. В случае неограниченного интервала Т строго корректное определение средней мощности сигнала должно производиться по формуле:
Ws = 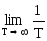
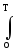 w(t)
dt. (23′)
w(t)
dt. (23′)
Квадратный корень из значения средней мощности характеризует действующее (среднеквадратическое) значение сигнала.
Применительно к электрофизическим системам, данным понятиям мощности и энергии соответствуют вполне конкретные физические величины. Допустим, что функцией s(t) отображается электрическое напряжение на резисторе, сопротивление которого равно R Ом. Тогда рассеиваемая в резисторе мощность, как известно, равна (в вольт-амперах):
w(t) = |s(t)|2/R,
а полная выделенная на резисторе тепловая энергия определяется соответствующим интегрированием мгновенной мощности w(t) по интервалу задания напряжения s(t) на резисторе R. Физическая размерность мощности и энергии в этом случае определяется соответствующей физической размерностью функции напряжения s(t) и сопротивления резистора R. Для безразмерной величины s(t) при R=1 это полностью соответствует выражению (2.2.1). В теории сигналов в общем случае сигнальные функции s(t) не имеют физической размерности, и могут быть формализованным отображением любого процесса или распределения какой-либо физической величины, при этом понятия энергии и мощности сигналов используются в более широком смысле, чем в физике. Они представляют собой метрологические характеристики сигналов.
Из сравнения выражений (19) и (22) следует, что энергия и норма сигнала связаны соотношениями:
Es = ||s(t)||2, ||s(t)|| = 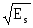 (24)
(24)
Вычислим энергию суммы двух произвольных сигналов u(t) и v(t)
E
=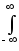 [u(t)+v(t)]2 dt = Eu + Ev + 2
[u(t)+v(t)]2 dt = Eu + Ev + 2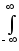 u(t)v(t)
dt.(25)
u(t)v(t)
dt.(25)
Как следует из этого выражения,энергия сигналов (а равно и их мощность), в отличие от самих сигналов, в общем случае не обладают свойством аддитивности. Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию
Euv = 2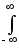 u(t)v(t)
dt.(26)
u(t)v(t)
dt.(26)
Нетрудно заметить, что энергия взаимодействия сигналов равна их удвоенному скалярному произведению
Euv= 2u(t), v(t). (26′)
При обработке данных используются также понятия мощности взаимодействия двух сигналов x(t) и y(t):
wxy(t) = x(t) y*(t), (27)
wyx(t) = y(t) x*(t),
wxy(t) = w*yx(t).
Для вещественных сигналов:
wxy(t) = wyx(t) = x(t) y(t). (28)
С использованием выражений (27-28) интегрированием по соответствующим интервалам вычисляются значения средней мощности взаимодействия сигналов на определенных интервалах Т и энергия взаимодействия сигналов.
Скалярное произведение произвольных сигналовu(t) и v(t) отражает степень их связи (сходства) по форме и положению в пространстве сигналов, и обозначается как u(t), v(t).
u(t), v(t) = ||u(t)||||v(t)|| cos , (29)
Физическую сущность скалярного произведения векторов в двумерном пространстве можно определить как произведение «длины» (нормы) одного вектора на проекцию второго вектора по «направлению» первого вектора.
Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение
u(t),
v(t) =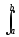 u(t)v(t)
dt = 0.
u(t)v(t)
dt = 0.
Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными (угол между сигналами равен φ = 90о), полностью независимыми друг от друга (некоррелированными, r = cos φ=0, и имеют нулевую энергию взаимодействия (Euv= 0).
Энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности, т.к. имеют нулевое значение скалярного произведения и, соответственно, нулевую энергию взаимодействия.
Вычисление скалярного произведения обычно производится непосредственно по сигнальным функциям. Для аналоговых сигналов:
s(t),
v(t)
=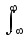 s(t)v(t) dt. (30)
s(t)v(t) dt. (30)
Для дискретных сигналов в N-мерном пространстве:
sn, vn=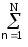 sn vn. (30′)
sn vn. (30′)
Линейное пространство аналоговых сигналов с таким скалярным произведением называется гильбертовым пространством Н (второе распространенное обозначение — L2). Линейное пространство дискретных и цифровых сигналов — пространством Евклида (обозначение пространства — R2). В этих пространствах справедливо фундаментальное неравенство Коши-Буняковского
|s,v|||s||||v||, (31)
т.к. модуль косинуса в (2.1.4) может быть только равным или меньше 1
Для комплексного гильбертова пространства скалярное произведение вычисляется по формуле
s(t),
v(t)
=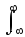 s(t)v*(t)
dt. (32)
s(t)v*(t)
dt. (32)
При определении функций в пространстве L2[a,b] вычисление скалярного произведения производится соответственно с пределами интегрирования от а до b.
Косинус угла между сигналами:
cos =s(t),v(t)/(||s||||v||). (33)
Однако при рассмотрении выражения (33) совместно с выражением для квадрата метрики сигналов
2(s,v)
=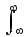 [s(t)-v(t)]2dt = ||s||2+ ||v||2— 2||s||||v||
cos.
[s(t)-v(t)]2dt = ||s||2+ ||v||2— 2||s||||v||
cos.
можно отметить следующие закономерности. При φ=0 (cos φ = 1) сигналы «совпадают по направлению» и расстояние между ними минимально. При φ = π/2 (cos φ = 0) сигналы «перпендикулярны друг другу» (иначе говоря – ортогональны), и проекции сигналов друг на друга равны 0. При φ = π (cos φ = -1) сигналы «противоположны по направлению» и расстояние между сигналами максимально. Фактор расстояния между сигналами играет существенную роль при их селекции в многоканальных системах.
Корреляция сигналов.
Значение косинуса в (33) изменяется от 1 до -1, и не зависит от нормы сигналов («длины» векторов). Максимальное значение cos φ = 1 соответствует полной тождественности относительной динамики сигналов, минимальное значение cos φ = -1 наблюдается при полной противоположности значений относительной динамики сигналов. По существу, коэффициент r = cos φ является интегральным коэффициентом степени сходства формы сигналов по пространству их задания. С учетом этого он и получил название коэффициента корреляции сигналов.
Однако количественные значения коэффициентов корреляции существенно зависят от выбора нулевой точки сигнального пространства.
Для получения значений коэффициентов корреляции, независимых от нуля сигнального пространства и от масштаба единиц измерений, необходимо вычислять коэффициент по центрированным сигналам, при этом в оценках коэффициента появляется знаковый параметр совпадения или несовпадения по «направлению» корреляции и исчезает зависимость от масштаба представления сигналов. Это позволяет вычислять коэффициенты корреляции различных сигналов вне зависимости от физической природы сигналов и их величины.
Разложение сигнала в ряд. Произвольный сигнал s(t) H (пространство Гильберта), заданный на интервале [a, b], может быть разложен в ряд по упорядоченной системе ортонормированных базисных функций uk(t)
s(t)
=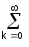 ckuk(t).
(34)
ckuk(t).
(34)
Для нахождения значений коэффициентов сk умножим обе части данного выражения на базисную функцию um(t) с произвольным номером m и проинтегрируем результаты по переменной t, при этом получим
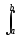 s(t)um(t)
dt =
s(t)um(t)
dt =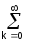 ck
ck 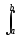 umuk dt.
umuk dt.
С
учетом ортонормированности функций
ui(t),
в правой части этого равенства остается
только один член суммы с номером m = k при 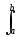 ukuk dt =1, который, по левой части уравнения,
представляет собой скалярное произведение
сигнала и соответствующего m = k базисного
вектора, т.е. проекцию сигнала на
соответствующее базисное направление
ukuk dt =1, который, по левой части уравнения,
представляет собой скалярное произведение
сигнала и соответствующего m = k базисного
вектора, т.е. проекцию сигнала на
соответствующее базисное направление
ck =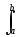 s(t)uk(t)
dt. (35)
s(t)uk(t)
dt. (35)
Таким образом, в геометрической интерпретации коэффициенты сk представляют собой проекции вектор — сигнала s(t) на соответствующие базисные направления uk(t), т.е. координаты вектора s(t) по координатному базису, образованному системой ортогональных функций u(t), в пределе — бесконечномерной. При практическом использовании количество членов ряда (34) ограничивается определенным значением N, при этом для любого значения N совокупность коэффициентов ck обеспечивают наименьшее по средней квадратической погрешности приближение к заданному сигналу.
Соответственно, энергия взаимодействия двух сигналов x(t) и y(t) может вычисляться по скалярному произведению их координатных проекций, которое, с учетом взаимной ортогональности всех проекций, будет равно:
x(t),
y(t)=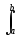 x(t)y(t)
dt =
x(t)y(t)
dt =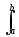 [
[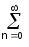 anun(t)]
[
anun(t)]
[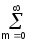 bmum(t)]
dt =
bmum(t)]
dt =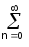 anbn.
(36)
anbn.
(36)
Косинус угла между векторами x(t) и y(t) с использованием выражения (36):
cos
=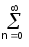 anbn /(||x(t)||||y(t)||).
anbn /(||x(t)||||y(t)||).
Возможность разложения непрерывных сигналов и функций в обобщенные ряды по системам ортогональных функций имеет огромное принципиальное значение, так как позволяет вместо изучения несчетного множества точек сигнала ограничиться счетной системой коэффициентов ряда.
К системам базисных функций, которые используются при разложении сигналов, предъявляют следующие основные требования:
— для любого сигнала ряд разложения должен сходиться;
— при ограничении ряда по уровню остаточной погрешности расхождения с заданным сигналом количество членов ряда должно быть минимальным;
— базисные функции должны иметь достаточно простую аналитическую форму;
— коэффициенты разложения в ряд должны вычисляться относительно просто.
Согласно теореме Дирехле, любой сигнал s(t), имеющий конечное число точек нарушения непрерывности первого рода, и конечный по энергии на интервале [a, b], может быть разложен по системе ортонормальных функций, если существуют интегралы модуля сигнала и модуля его первой производной, т.е.:
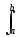 |s(t)|
dt < ,
|s(t)|
dt < , 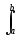 |s'(t)|
dt <
.
|s'(t)|
dt <
.
Наибольшее распространение в качестве базисных функций частотного разложения нашли комплексные экспоненциальные функции exp(pt) при p = jf (преобразование Фурье) и p = s+jf (преобразование Лапласа), от которых с использованием формул Эйлера
exp(jωt) = cos(ωt) + j sin(ωt), exp(-jωt) = cos(ωt) — j sin(ωt),
cos(ωt) = [ехр(jωt)+exp(-jωt)]/2, sin(ωt) = [ехр(jωt)-exp(-jωt)]/2j
всегда можно перейти к вещественным синус-косинусным функциям. Термин «частотное разложение» обязан своим происхождением независимой переменной частотного представления сигналов, которая измеряется в единицах, обратных единицам времени, т.е. в единицах частоты f = 1/|t|. Однако понятие частотного преобразования не следует связывать только с временным представлением сигналов, т.к. математический аппарат преобразования не зависит от физического смысла переменных. Так, например, при переменной «х», как единице длины, значение f будет представлять собой пространственную частоту — число периодических изменений сигнала на единице длины с размерностью 1/|х|.
Разложение энергии сигнала. Допустим, что сигнал s(t) разложен в обобщенный ряд Фурье по гармоническим функциям. Вычислим энергию сигнала непосредственной подстановкой выражения (2.3.2) в выражение (2.2.2)
Es =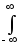 s2(t)
dt =
s2(t)
dt =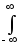
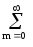
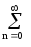 cmcnumun dt
=
cmcnumun dt
=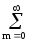
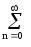 cmcn
cmcn 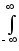 umun dt.
(37)
umun dt.
(37)
В этом выражении, в силу ортонормированности базисной системы, отличны от нуля только члены с номерами m = n. Отсюда
Es =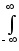 s2(t)
dt =
s2(t)
dt =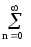 cn2,
(38)
cn2,
(38)
т.е. при разложении сигнала в обобщенный ряд Фурье, энергия сигнала не изменяется и равна сумме энергии всех составляющих ряда. Это соотношение называют равенством Парсеваля.

