Формула расчета момента инерции — Центрсельстрой
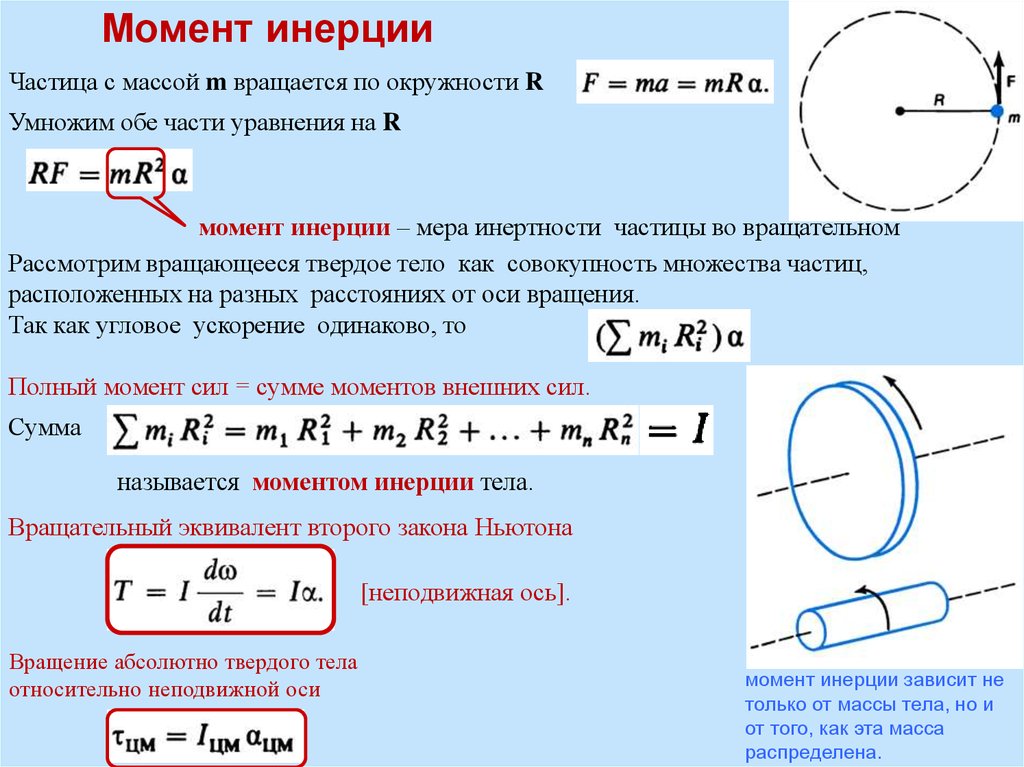
Что такое момент инерции?
Момент инерцииназываемый также моментом инерции массы или угловой массой, (единицы СИ кг м2) — это мера сопротивления объекта изменению скорости вращения. Это вращательный аналог массы. То есть, это инерция жесткого вращающегося тела по отношению к его вращению.
Момент инерции играет во вращательной динамике практически ту же роль, что и масса в основной динамике, определяя связь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также некоторыми другими величинами. Хотя для многих ситуаций достаточно простой скалярной обработки, более продвинутая тензорная обработка позволяет анализировать такие сложные системы, как вращающиеся вершины и движение гироскопа.
Для обозначения момента инерции обычно используется символ I и иногда J.
Момент инерции объекта относительно данной оси описывает, насколько трудно изменить его угловое движение относительно этой оси.
Например, рассмотрим два диска (A и B) одинаковой массы. Диск А имеет больший радиус, чем диск В. Если предположить, что толщина и распределение массы равномерны, то для ускорения диска А (изменения его угловой скорости) требуется больше усилий, поскольку его масса распределена дальше от оси вращения: масса, находящаяся дальше от оси, должна для данной угловой скорости двигаться быстрее, чем масса, находящаяся ближе. В этом случае диск A имеет больший момент инерции, чем диск B.
Момент инерции имеет две формы: скалярную форму I (используется, когда известна ось вращения) и более общую тензорную форму, которая не требует знания оси вращения. Скалярная форма I (часто называемая просто «моментом инерции») позволяет кратко проанализировать многие простые проблемы в динамике вращения, такие как скатывание объектов по наклонной плоскости и поведение шкивов.
Например, хотя блок любой формы будет скользить вниз по наклонной плоскости с одинаковой скоростью, катящиеся объекты могут спускаться с разной скоростью, в зависимости от их моментов инерции.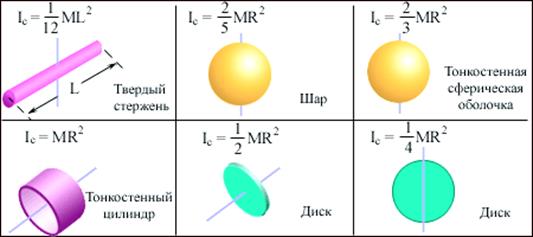
Обруч будет спускаться медленнее, чем сплошной диск равной массы и радиуса, потому что большая часть его массы расположена далеко от оси вращения и, следовательно, должна двигаться быстрее, если обруч катится с той же угловой скоростью.
Однако для (более сложных) задач, в которых ось вращения может меняться, скалярный метод неадекватен, и необходимо использовать тензорный метод (хотя в особых ситуациях возможны сокращения). Примеры, требующие такого обращения, включают гироскопы, вершины и даже спутники — все объекты, чья центровка может меняться.
Момент инерции не следует путать с полярным моментом инерции, который является мерой способности объекта сопротивляться кручению (скручиванию).
Формула момента инерции:
Простая формула момента инерции любого объекта, будь то точечная масса или 3D-структура, дается следующим образом:
где
dm — масса бесконечно малой части тела
и r — (перпендикулярное) расстояние точечной массы до оси вращения.
Подробный анализ
(Скалярный) момент инерции точечной массы, вращающейся вокруг известной оси, определяется следующим образом
I является аддитивным.
Таким образом, для твердого тела, состоящего из N точечных масс mi с расстояниями ri до оси вращения, общий I равен сумме моментов инерции точечных масс:
Для твердого тела, описываемого непрерывной функцией плотности массы ?(r), I вокруг известной оси может быть вычислена путем интегрирования квадрата расстояния (взвешенного по плотности массы) от точки тела до оси вращения:
V — объем, занимаемый объектом.
? — функция пространственной плотности объекта, и
координаты точки внутри тела.
Диаграмма для расчета I диска. Здесь k — 1/2, а r — радиус, используемый при определении момента.
Исходя только из анализа размеров, I неточечного объекта должна иметь вид:
M — масса
R — радиус объекта от центра масс (в некоторых случаях вместо него используется длина объекта).
k — безразмерная постоянная, называемая константой инерции, которая изменяется в зависимости от рассматриваемого объекта.
Инерционные константы используются для учета различий в размещении массы от центра вращения.
Примеры включают:
k = 1, тонкое кольцо или тонкостенный цилиндр вокруг своего центра,
k = 2/5, твердая сфера вокруг своего центра
k = 1/2, твердый цилиндр или диск вокруг своего центра.
Теорема о параллельных осях
После того как момент инерции вычислен для вращения вокруг центра масс твердого тела, его можно удобно пересчитать и для всех параллельных осей вращения, не прибегая к формальному определению. Если ось вращения смещена на расстояние R от оси центра масс (например, вращение диска вокруг точки на его периферии, а не через центр), то смещенный и центральный моменты инерции связаны следующим образом:
Эта теорема также известна как правило параллельных осей и является частным случаем теоремы Штейнера о параллельных осях.
Теорема о перпендикулярных осях
Теорему о перпендикулярных осях для плоских объектов можно продемонстрировать, рассмотрев вклад в трехосные моменты инерции от произвольного элемента массы. Из момента массы точки, вклады в каждый из осевых моментов инерции составляют
Составные тела
Если тело может быть разложено (физически или концептуально) на несколько составных частей, то момент инерции тела вокруг данной оси получается суммированием моментов инерции каждой составной части вокруг той же заданной оси.
Моменты инерции распространенных форм
Читайте далее:
- Испытание маятника на кручение металлической проволоки.
- Испытание маятника на кручение металлической проволоки.
- Что такое потенциальная функция скорости и функция потока?.
- Что такое формула Чези для открытых каналов? Как определить постоянную Чези?.
- Метод распределения моментов в структурном анализе.
- ПРОЕКТИРОВАНИЕ СТАЛЬНЫХ КОМПРЕССИОННЫХ ЭЛЕМЕНТОВ.
- Теория линии текучести для проектирования перекрытий — допущения, методы анализа.
Вывод рабочей формулы для экспериментального определения момента инерции.
Рис. 4.1
При экспериментальном
определении момента инерции используется
маятник Обербека, который представляет
собой крестовину с четырьмя закрепленными
на ней на одинаковых расстояниях от оси
одинаковыми грузами. На ось крестовины
насажен двухступенчатый шкив, на который
намотана нить с подвешенным к ней грузом.
При движении груза вниз шкив начинает
вращаться. Для вывода рабочей формулы
рассмотрим упрощенную схему установки,
выделив систему связанных движущихся
тел: поступательно движущийся груз и
вращающийся шкив (рис. 4.1). Поступательное
движение груза описывается уравнением:
mg – T = ma (4.1)
Вращательный момент шкива создает сила натяжения нити Т1, которая по третьему закону Ньютона равна силе
ТR=Iε (4.2)
Если отсутствует проскальзывание нити, то тангенциальное ускорение элементов нити, вращающихся вместе со шкивом, равно линейному ускорению груза:
аτ = а = εR (4.3)
Решая систему
уравнений (4.1), (4.2) и (4.
3), получим для
момента инерции выражение: .
Линейное ускорение груза можно вычислить по измеренным высоте падения груза и времени его падения:
Таким образом, получена рабочая формула для экспериментального определения момента инерции:
(4.4)
Вывод формулы для теоретического вычисления момента инерции.
Момент инерции является аддитивной величиной, то есть момент инерции системы тел равен сумме моментов инерции всех тел, входящих в систему. Маятник Обербека состоит из шкива (включая ось и втулку крестовины), четырех стержней крестовины и грузов, укрепленных на крестовине. Момент инерции шкива указан на установке. Момент инерции стержня относительно оси, проходящей через его конец, равен m2lc2/3, где
Грузы, укрепленные на
крестовине, приближенно можно считать
за точечные массы. Тогда момент инерции
каждого груза равен m1l2,
где m1 − масса одного груза (указана на
установке), l − расстояние от оси вращения до центра
масс груза (измеряется при выполнении
работы).Теоретический момент инерции после суммирования вычисляется по формуле:
Описание экспериментальной установки
Рис. 4.2
Внешний вид
установки представлен на рис.4.2.
Регулировочные винты 1 обеспечивают
горизонтальную установку основания 2,
к которому крепится вертикальная колонка
3, на которой нанесена миллиметровая
шкала. К этой колонке прикреплены
неподвижный кронштейн 4 и верхний
подвижный 5, с помощью которого можно
регулировать длину пути груза h.
Через диск 6 перекинута нить 7, один конец
которой прикреплен к шкиву 8, а на втором
конце закреплены грузы 9. Кронштейн 11
снабжен резиновым амортизатором для
ограничения движения грузов. Включение
прибора производится нажатием клавиши
«сеть» 12, обнуление миллисекундомера
производится клавишей «сброс» 13, клавиша
«пуск» 14 включает миллисекундомер.
Время падения груза высвечивается на
индикаторе 15.
Понимание момента инерции площади
Момент инерции площади , также называемый вторым моментом площади , является параметром, который определяет, какое сопротивление форма (например, поперечное сечение балки) должна выдерживать. изгибается из-за своей геометрии.
https://www.youtube.com/watch?v=Bls5KnQOWkYВидео не может быть загружено, так как отключен JavaScript: понимание момента инерции площади (https://www.youtube.com/watch?v=Bls5KnQOWkY)
Рассмотрим тонкую доску, которая выдерживает нагрузку в 100 кг. Планка будет намного менее жесткой, когда нагрузка будет приложена к более длинному краю поперечного сечения.
Это связано с тем, что сопротивление изгибу зависит от того, как материал поперечного сечения распределен относительно оси изгиба. Доска слева имеет больше материала, расположенного дальше от оси изгиба, что делает ее намного более жесткой. 94$. Он отражает, как площадь поперечного сечения распределяется относительно той или иной оси. Это не уникальное свойство поперечного сечения — оно меняется в зависимости от рассматриваемой оси изгиба.
Давайте сравним значения $I$, рассчитанные для нескольких различных сечений, для оси изгиба, показанной ниже:
Значения момента инерции площади (в мм 4 ) для трех форм материалы вдали от оси изгиба имеют большие моменты инерции – их труднее согнуть. Это одна из причин Двутавровая балка — такое широко используемое поперечное сечение для конструкционных применений — большая часть материала расположена далеко от оси изгиба, что делает ее очень эффективной при сопротивлении изгибу при использовании минимального количества материала.
Момент инерции площади против второго момента площади
Используются оба термина: «секундный момент площади» и «площадной момент инерции». Второй момент площади часто предпочтительнее, чтобы избежать путаницы с моментом инерции, который является совершенно другим параметром, описывающим сопротивление тела угловому ускорению, хотя и рассчитывается аналогичным образом. 92 dA}$$
Нижние индексы $x$ и $y$ указывают, что момент инерции площади соответствует изгибу вокруг осей $x$ и $y$ соответственно.
Давайте рассмотрим пример того, как это уравнение можно применить для расчета $I$ для прямоугольного поперечного сечения.
Пример – прямоугольное сечение
Мы будем использовать приведенное выше уравнение для расчета $I$ для изгиба вокруг оси $x$ для следующего поперечного сечения: 93ч{12}$$
К счастью, вам не нужно выполнять этот процесс интегрирования всякий раз, когда вам нужно вычислить $I$ для поперечного сечения и оси изгиба.
Если это довольно стандартная форма, вы можете просто найти уравнение, которое уже было получено для вашего конкретного поперечного сечения. Большинство учебников по сопротивлению материалов содержат таблицы, подобные приведенной ниже, в которых перечислены уравнения $I$ для обычных поперечных сечений.
| Сечение | Площадь Момент инерции 92$$ Утверждается, что момент инерции площади вокруг любой оси $I_x$ может быть рассчитан из момента инерции площади относительно параллельной оси $I_{xc}$, проходящей через центр тяжести поперечного сечения, площадь поперечного сечения $A$ и расстояние между двумя осями $d$. Иллюстрация теоремы о параллельных осях, которую можно использовать для вычисления $I_x$ на основе $I_{xc}$, $d$ и площади поперечного сечения $A$. C — центр тяжести поперечного сечения. В справочных текстах обычно приводятся уравнения для $I$ для центроидальных осей, поэтому теорема о параллельных осях является мощным инструментом для распространения этих уравнений на любые другие параллельные оси. Сложение и вычитание моментов инерции площадиМоменты инерции площади можно суммировать и вычитать для расчета значений составных сечений. На изображении ниже показано, как этот метод можно использовать для расчета $I_x$ для полого сечения. Пример расчета $I$ для составного поперечного сечения путем прибавления или вычитанияПри использовании этого метода необходимо убедиться, что значения $I$ для сечений компонентов ($I_{xA}$ и $I_{xB}$ в приведенном выше примере) соответствуют правильной оси изгиба, иначе сначала вам нужно будет применить теорему о параллельной оси, чтобы получить значения $I$ для правильной оси. Применение момента инерции площадиМомент инерции площади является важным параметром для любого применения, связанного с изгибом элемента конструкции, что означает, что он постоянно присутствует в 92}$$ Если вы хотите узнать больше об этих областях применения, ознакомьтесь со страницами , отклонение балки и , изгиб . Как показывают два приведенных выше примера, момент инерции площади часто появляется в уравнениях вместе с модулем Юнга $E$. Термин $EI$ получил название изгибной жесткости . $I$ представляет собой жесткость поперечного сечения балки из-за ее геометрии , а $E$ представляет собой жесткость поперечного сечения Полярный момент инерцииВ дополнение к расчету момента инерции площади для осей $x$ и $y$, находящихся в той же плоскости, что и поперечное сечение, мы также можем рассчитать момент инерции площади для оси это перпендикулярно поперечному сечению. Это называется полярным моментом инерции и обычно обозначается буквой $J$ или $I_z$. Он часто используется в задачах, связанных с деформацией кручения, которая является 9-й.2 dA}$$ $J$ учитывает, как площадь поперечного сечения распределяется радиально относительно оси вращения или кручения $z$. Как и в случае с $I_x$ и $I_y$, $\rho$ член в уравнении возведен в квадрат, а это означает, что наибольший вклад в значение $J$ вносят участки поперечного сечения, расположенные далеко от оси вращения. Вот почему трансмиссионные валы полые — центральная часть поперечного сечения не сильно влияет на сопротивление скручиванию, поэтому более эффективно использовать полые валы. Мы можем сделать интересное наблюдение: полярный момент инерции относительно оси, проходящей через определенную точку поперечного сечения, равен сумме площадных моментов инерции двух перпендикулярных осей, проходящих через одну и ту же точку. Это называется теоремой перпендикулярных осей. Теорема о перпендикулярной оси $$J = I_x + I_y$$ Вывод этой теоремы довольно прост — посмотрите видео «Понимание площади момента инерции», если хотите его увидеть. Сопутствующие темыФермы — это конструкции (например, мосты или крыши), состоящие из элементов, способных воспринимать только растягивающие или сжимающие осевые нагрузки. Узнать больше Напряжение и деформация — это фундаментальные понятия, относящиеся к внутренним силам и деформациям тела в ответ на приложенные нагрузки. Узнать больше Как рассчитать момент инерции?Момент инерции, называемый угловой массой или инерцией вращения относительно оси вращения, представляет собой величину, определяющую величину крутящего момента, необходимого для достижения желаемого углового ускорения, или характеристику тела, препятствующую угловому ускорению. Момент инерции рассчитывается как произведение массы каждой частицы на квадрат ее расстояния от оси вращения. Момент инерции Термин «момент инерции» относится к величине, которая описывает, как тело сопротивляется угловому ускорению, и рассчитывается как произведение массы каждой частицы на квадрат расстояния частицы от оси вращения. Момент инерции системы из n частиц
Как рассчитать момент инерции?Для расчета момента инерции любого вращающегося объекта используется несколько способов.
Формулы для Sympulation Moment of Sonertia.
Solved Examples of Moment of InertiaПример 1: Определить момент инерции твердого шара массой 22 кг и радиусом 5 м. Ответ :
2 и радиусом 10 м. Ответ :
Пример 3. Если однородная плита имеет массу 23 кг, длину 10 м и ширину 7 м, определить его момент инерции. Ответ :
Пример 4: Когда однородный полый прямоугольный круговой конус имеет момент инерции 98 кг m 2 и масса 20 кг определяют радиус конуса. Ответ :
Пример 5: I. масса 10 кг и радиус 7 м, определить момент инерции полого цилиндра. Ответ :
| |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Член $\rho$ — это расстояние от оси $z$ (которая на изображении ниже направлена за пределы экрана) до элемента dA.
Или, другими словами, можно сказать, что это величина, определяющая, какой крутящий момент требуется для определенного углового ускорения вращающейся оси. Момент инерции часто называют вращательной инерцией или угловой массой. кг·м 2 — единица момента инерции в системе СИ.
в этой таблице.
0076
