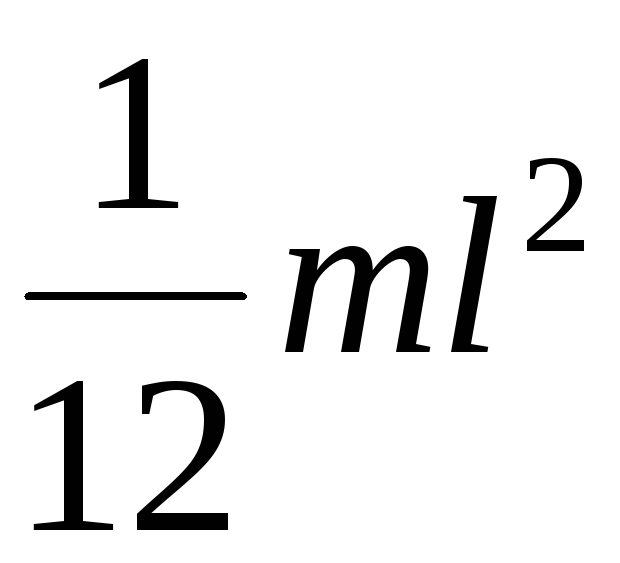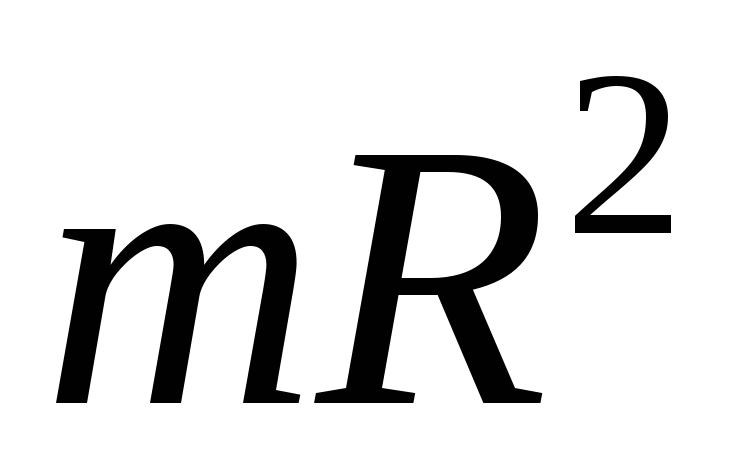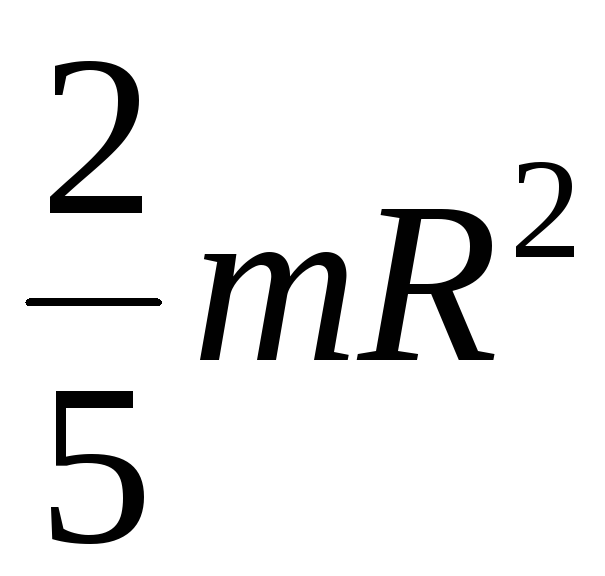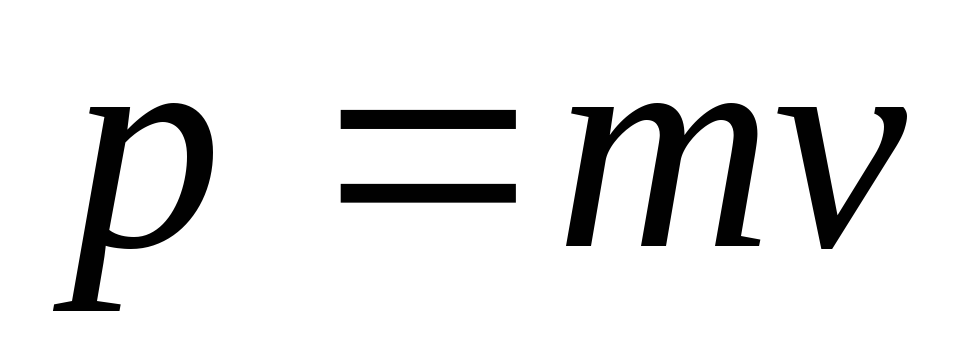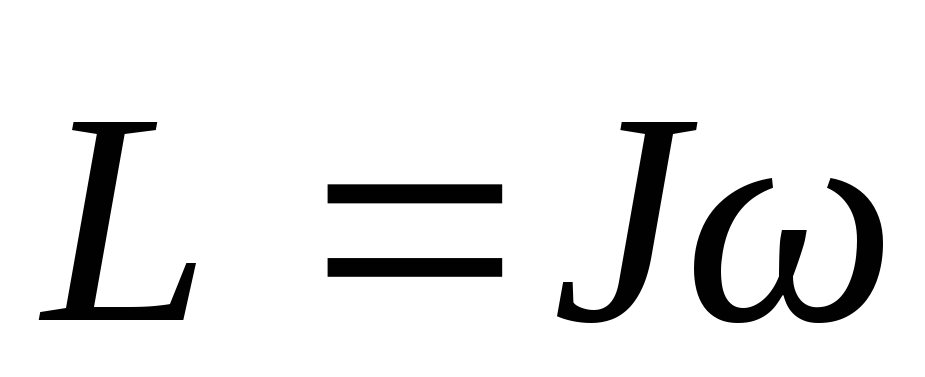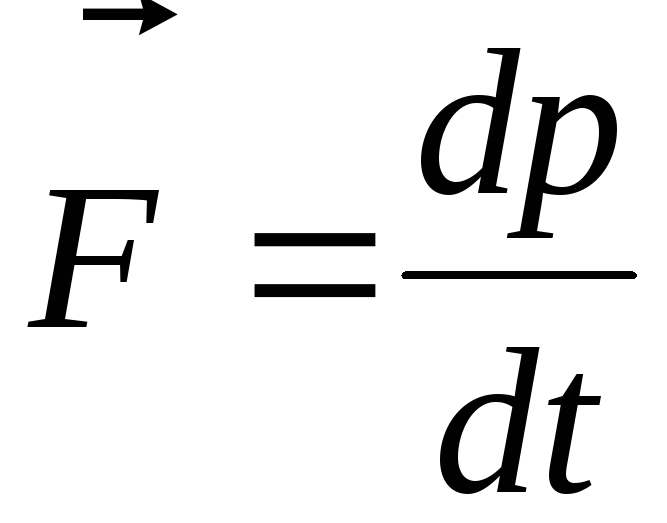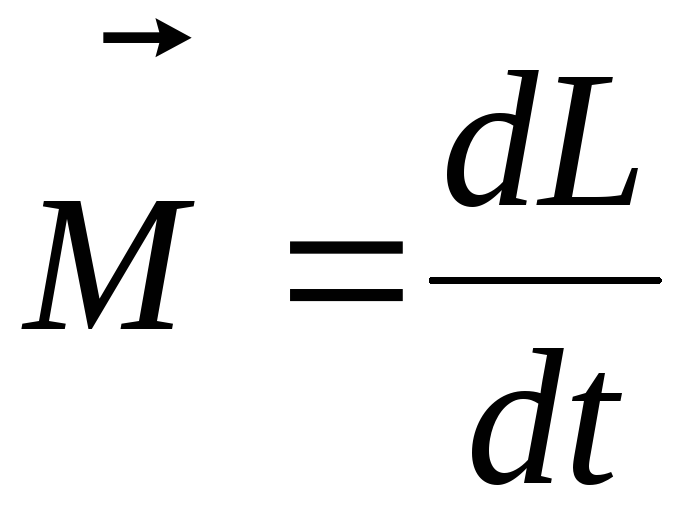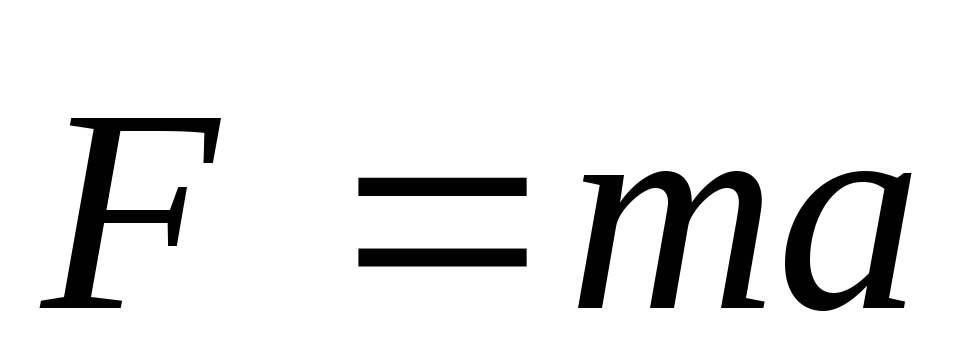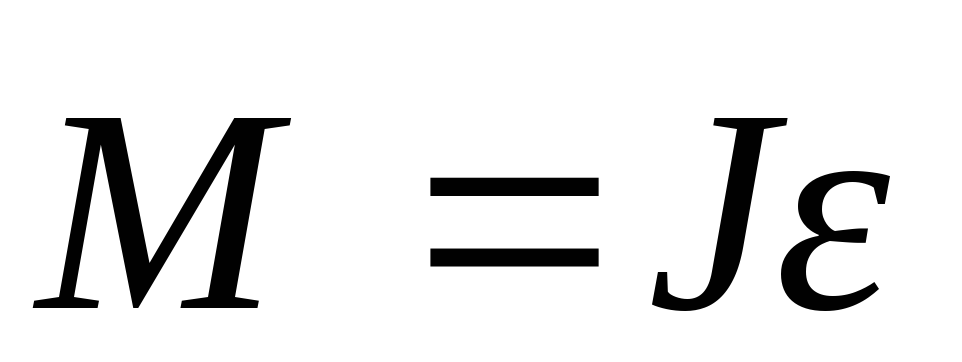Формула момента инерции, J

Момент инерции тела

Момент инерции является скалярной (в общем случае тензорной) физической величиной, которую находят как сумму произведений масс материальных точек () (на которые следует провести разбиение рассматриваемого тела) на квадраты расстояний () от них до оси вращения:

   

Если тело считают непрерывным, то суммирование в выражении (1) заменяется интегрированием, массы элементов тела обозначают как :

   

где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела. Если тело является однородным:

   

Момент инерции материальной точки

Роль массы при движении по окружности материальной точки выполняет момент инерции (J), который равен:

   

где r- расстояние от материальной точки до оси вращения. Для материальной точки, которая движется по окружности, момент инерции является постоянной величиной.

Момент инерции является аддитивной величиной. Это означает то, что если в системе не одна, а несколько материальных точек, то момент инерции системы (J) равен сумме моментов инерции () отдельных точек:

   

Примеры моментов инерции некоторых тел

Момент инерции тонкого стержня вращающегося около оси, проходящей через его один конец и перпендикулярно стержню, равен:

   

Момент инерции прямого круглого конуса, массы высоты h и радиуса r вращающегося около своей оси:

   

Момент инерции однородного твердого параллелепипеда, c геометрическими параметрами и массой m вращающегося относительно своей самой длинной диагонали, вычисляют по формуле:

   

Момент инерции тонкой прямоугольной пластины массы m, ширины w и длины d, вращающейся относительно оси, которая проходит через точку пересечения диагоналей этого прямоугольника перпендикулярно плоскости пластины:

   

где m – масса шара; R – радиус шара. Шар вращается около оси, которая проходит через его центр.

Примеры формул для вычисления моментов инерции других тел можно посмотреть в разделе «Момент инерции». В этом же разделе можно ознакомиться с теоремой Штейнера.

Примеры решения задач по теме «Момент инерции»

Момент инерции материальной точки

Для динамического описания движения материальной точки по окружности используют следующие величины: момент силы (), момент импульса () и момент инерции (J). При этом основной закон динамики вращательного движения записывают в виде:

   

Кроме этого, описывая движение по окружности вместо радиус-вектора () пользуются углом поворота (), вместо вектора скорости () используют вектор угловой скорости ().

Момент инерции

Роль массы при движении по окружности материальной точки выполняет момент инерции (J), который равен:

   

где r- расстояние от материальной точки до оси вращения. Для материальной точки, которая движется по окружности, момент инерции является постоянной величиной. При этом изменение момента импульса происходит только за счет изменения угловой скорости:

   

Используя момент инерции основное уравнение динамики (1) для движения материальной точки по окружности можно записать как:

   

где – угловое ускорение материальной точки. Уравнение (4) отражает тот факт, что при движении материальной точки по окружности, момент силы исполняет роль силы (в поступательном движении), момент инерции – роль массы, угловое ускорение – роль линейного ускорения. Это легко увидеть, если записать второй закон Ньютона и сравнить его с уравнением (4):

   

Мерой инертности материальной точки при движении по окружности служит момент инерции.

Момент инерции является аддитивной величиной. Это означает то, что если в системе не одна, а несколько материальных точек, то момент инерции системы (J) равен сумме моментов инерции () отдельных точек:

   

где – масса ой материальной точки; расстояние от данной материальной точки до оси вращения. Момент инерции системы материальных точек зависит от распределения этих точек в пространстве. Чем ближе материальные точки находятся от оси вращения, тем меньше момент инерции данной системы. У твёрдых тел, которые можно представить как непрерывную совокупность материальных точек, момент инерции относительно оси является постоянной величиной.

Примеры решения задач

простое пояснение, значении в физике, формулы, примеры

Что такое инерция?

Определение момента инерции

Формула момента инерции

Теорема Гюйгенса – Штейнера

Моменты инерции простейших объектов

Рекомендованная литература по теме и полезные ссылки

Момент инерции, видео

Что такое инерция?

Инерция в физике – способность тел определенное время сохранять состояние движения при отсутствии действия внешних сил. Впрочем, понятие инерции имеет частое применение не только в физике, но и в нашей повседневной жизни. Так обычно «инертным» называют человека, который совершенно не проявляет никакой инициативы, делают только то, что ему скажут другие, и делает это крайне медленно, без какого-либо энтузиазма. «Движется по инерции», – говорим мы, когда хотим подчеркнуть, что что-то делается без какого-либо смысла, а просто потому, что так было заведено когда-то или в силу наработанной годами привычки. И если с понятием инерции все более-менее понятно, благодаря таким вот житейским примерам, то термин «момент инерции» требует более детального пояснения, чем мы и займемся в нашей статье.

Определение момента инерции

Со школьной программы по физике мы прекрасно знаем, что масса тела является мерой его инертности. Например, если в супермаркете сильно толкнуть две тележки, одна из которых будет пустой, а вторая нагруженной разными товарами, то впоследствии остановить будет труднее тележку, нагруженную товарами в силу ее большей массы. Другими словами, чем больше у тела масса, тем большее на него воздействие инерции и тем больше нужно сил, чтобы изменить движение такого тяжелого тела.

В приведенном примере тележка движется по прямой линии, то есть иными словами совершает поступательное движение. И если при поступательном движении какого-либо теле его масса является мерой его инерции, то при вращательном движении тела вокруг своей оси мерой его инерции будет величина, которая собственно и называется – момент инерции.

Момент инерции – скалярная физическая величина, мера инертности тела при его вращении вокруг оси. Обычно обозначается буквой J и измеряется в килограммах, умноженных на квадратный метр. Такое академическое определение того, что такое момент инерции.

Формула момента инерции

Как рассчитать точное значение момента инерции? Для этого есть общая формула, помогающая физикам определять момент инерции любого тела. Если тело разбить на бесконечно маленькие кусочки с массой dm, то момент инерции будет равным сумме произведения этих элементарных масс на квадрат расстояния до оси вращения. Формула будет иметь такой вид:

J – момент инерции, r – расстояние до оси вращения.

Для материальной точки массы m, которая вращается вокруг оси на расстоянии r, данная формула будет иметь такой вид:

Теорема Гюйгенса – Штейнера

Говоря о моменте инерции невозможно не упомянуть о теореме двух математиков Гюйгенсе и Штейнере, которые дали формулировку определению характеристики параллельных осей.

Теорема Гюйгенса – Штейнера гласит: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Если записать вышесказанное математической формулой, то получится следующее:

Где d – расстояние между осями

Эта теорема значительно облегчает решения многих физических задач, связанных с инерцией. К примеру, у Вас имеется объект произвольной формы, центробежная сила которого известна. При помощи формулы Штейнера можно вычислить момент инерции тела относительно любой оси параллельной линии, которая проходит через середину фигуры.

Моменты инерции простейших объектов

Несмотря на внешнюю простоту, вычисление моментов инерции для разных предметов предполагает знание интегралов, этих важных инструментов высшей математики. Для упрощения задачи создана таблица с вычислениями инерции для простых геометрических фигур: круга, квадрата, цилиндра и т. д.

Так выглядят математические расчеты вычисления моментов инерции для круга и кольца.

Аналогичным образом будет рассчитываться момент инерции цилиндра.

Предлагаем вашему вниманию более детальную таблицу с формулами для расчета момента инерции для основных геометрических фигур: шара, сферы, диска, цилиндров, и т. д.

Рекомендованная литература и полезные ссылки

• Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
• Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — DOI:10.1126/science.286.5437.77. — PMID 10506564.
• Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.)русск. : journal. — 2012. — Vol. 117. — DOI:10.1029/2012JE004161.
• Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3

Момент инерции, видео

И в завершение образовательное видео по теме нашей статьи.

Эта статья доступна на английском языке – Moment of Inertia.

формула. Момент инерции тела :: SYL.ru

Чтобы изменить скорость перемещения тела в пространстве, необходимо приложить некоторое усилие. Этот факт относится ко всем видам механического движения и связан с наличием инерционных свойств у объектов, имеющих массу. В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.

Что такое вращение с точки зрения физики?

Ответ на этот вопрос может дать каждый человек, поскольку этот физический процесс ничем не отличается от его понятия в обиходе. Процесс вращения представляет собой перемещение объекта, обладающего конечной массой, по круговой траектории вокруг некоторой воображаемой оси. Можно привести следующие примеры вращения:

• Движение колеса автомобиля или велосипеда.
• Вращение лопастей вертолета или вентилятора.
• Движение нашей планеты вокруг оси и вокруг Солнца.

Какие физические величины характеризуют процесс вращения?

Перемещение по окружности описывается набором величин в физике, основные из которых перечислены ниже:

• r — расстояние до оси материальной точки массой m.
• ω и α — угловая скорость и ускорение, соответственно. Первая величина показывает, на сколько радиан (градусов) поворачивается тело вокруг оси за одну секунду, вторая величина описывает скорость изменения во времени первой.
• L — момент импульса, который подобен аналогичной характеристике при линейном движении.
• I — момент инерции тела. Эта величина рассматривается ниже в статье подробно.
• M — момент силы. Он характеризует степень изменения величины L, если приложена внешняя сила.

Перечисленные величины связаны друг с другом следующими формулами вращательного движения:

1. L = I*ω

2. M = I*α

Первая формула описывает круговое движение тела в отсутствие действия внешних моментов сил. В приведенном виде она отражает закон сохранения момента импульса L. Второе выражение описывает случай ускорения или замедления вращения тела в результате действия момента силы M. Оба выражения часто используются при решении задач динамики по круговой траектории.

Как видно из этих формул, момент инерции относительно оси (I) в них используется в качестве некоторого коэффициента. Рассмотрим подробнее эту величину.

Откуда появляется величина I?

В этом пункте рассмотрим самый простой пример вращения: круговое перемещение материальной точки массой m, дистанция которой от оси вращения составляет r. Эта ситуация приведена на рисунке.

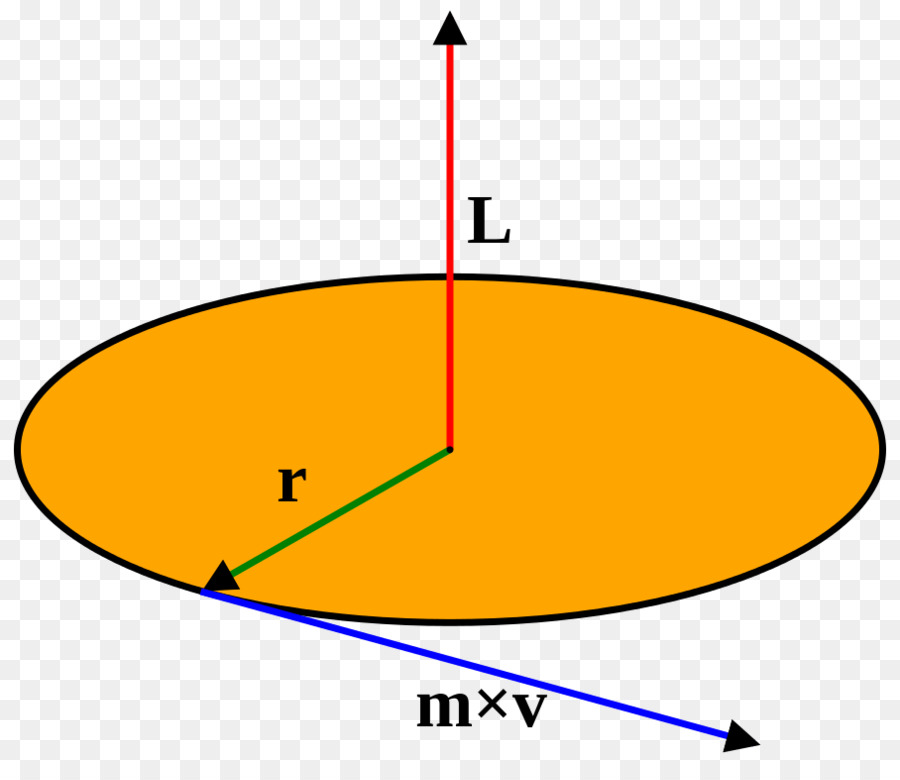
Согласно определению, момент импульса L записывается, как произведение плеча r на линейный импульс p точки:

L = r*p = r*m*v, поскольку p = m*v

Учитывая, что линейная и угловая скорость связаны друг с другом через расстояние r, это равенство можно переписать так:

v = ω*r => L = m*r²*ω

Произведение массы материальной точки на квадрат расстояния до оси вращения принято называть моментом инерции. Формула выше перепишется в таком случае следующим образом:

I = m*r² => L = I*ω

То есть мы получили выражение, которое было приведено в предыдущем пункте, и ввели в использование величину I.

Общая формула для величины I тела

Выражение для момента инерции массой m материальной точки является базовым, то есть оно позволяет рассчитать эту величину для любого тела, имеющего произвольную форму и неоднородное распределение массы в нем. Для этого необходимо разбить рассматриваемый объект на маленькие элементы массой m_i (целое число i — номер элемента), затем, умножить каждый из них на квадрат расстояния r_i² до оси, вокруг которой рассматривают вращение, и сложить полученные результаты. Описанную методику нахождения величины I можно записать математически так:

I = ∑_i(m_i*r_i²)

Если тело разбито таким образом, что i->∞, тогда приведенная сумма заменяется интегралом по массе тела m:

I = ∫_m(r_i²*dm)

Этот интеграл эквивалентен другому интегралу по объему тела V, поскольку dV=ρ*dm:

I = ρ*∫_V(r_i²*dV)

Все три формулы используются для вычисления момента инерции тела. При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.

Свойства величины I и ее физический смысл

Описанная процедура получения общего выражения для I позволяет сделать некоторые выводы о свойствах этой физической величины:

• она является аддитивной, то есть полный момент инерции системы можно представить, как сумму моментов отдельных ее частей;
• она зависит от распределения массы внутри системы, а также от расстояния до оси вращения, чем больше последнее, тем больше I;
• она не зависит от действующих на систему моментов сил M и от скорости вращения ω.

Физический смысл I заключается в том, насколько сильно система препятствует любому изменению скорости ее вращения, то есть момент инерции характеризует степень «плавности» возникающих ускорений. Например, колесо велосипеда можно легко раскрутить до больших угловых скоростей и также легко его остановить, но чтобы изменить вращение маховика на коленвале автомобиля, понадобится приложить значительное усилие и некоторое время. В первом случае имеет место система с маленьким моментом инерции, во втором — с большим.

Значение I некоторых тел для оси вращения, проходящей через центр масс

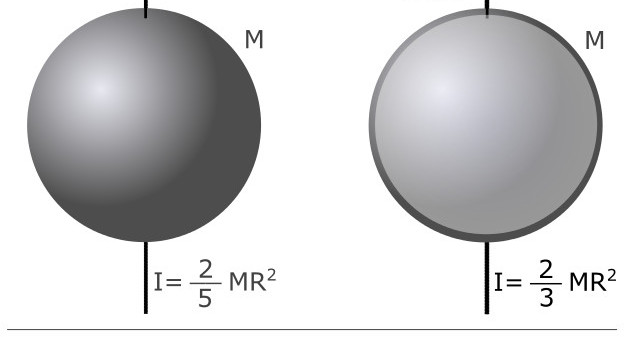
Если применить интегрирование по объему для любых тел с произвольным распределением массы, то можно получить для них величину I. В случае однородных объектов, которые имеют идеальную геометрическую форму, эта задача уже решена. Ниже приводятся формулы момента инерции для стержня, диска и шара массой m, в которых составляющее их вещество распределено равномерно:

• Стержень. Ось вращения проходит перпендикулярно ему. I = m*L²/12, где L — длина стержня.
• Диск произвольной толщины. Момент инерции с осью вращения, проходящей перпендикулярно его плоскости через центр масс, вычисляется так: I = m*R²/2, где R — радиус диска.
• Шар. В виду высокой симметрии этой фигуры, для любого положения оси, проходящей через ее центр, I = 2/5*m*R², здесь R — шара радиус.

Далее приведем два примера решения задач на применение общей формулы для расчета I и на использование свойства аддитивности этой величины.

Задача на расчет значения I для системы с дискретным распределением массы

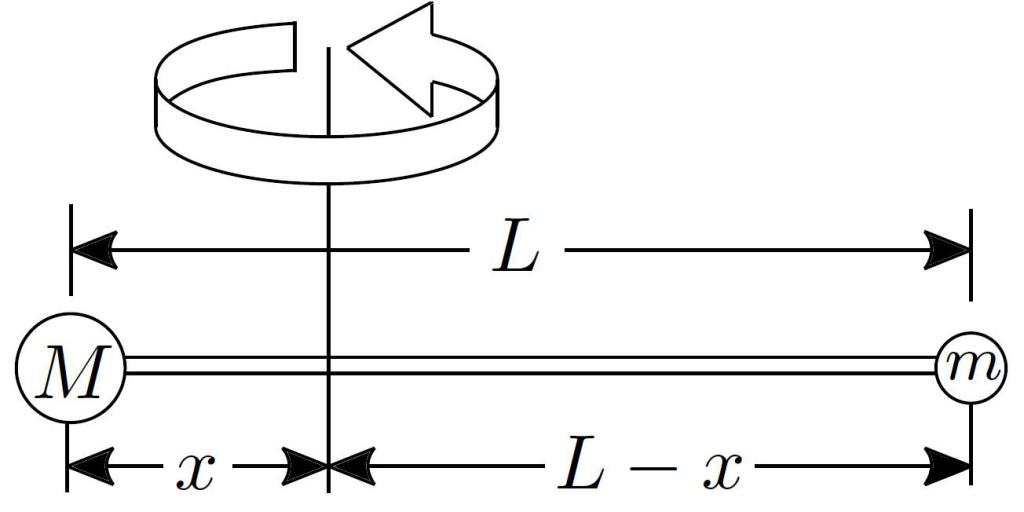
Представим себе стержень длиною 0,5 метра, который сделан из твердого и легкого материала. Этот стержень закреплен на оси таким образом, что она проходит перпендикулярно ему точно посередине. На этот стержень подвешены 3-и груза следующим образом: с одной стороны оси имеются два груза массами 2 кг и 3 кг, находящиеся на расстояниях 10 см и 20 см от его конца, соответственно; с другой стороны подвешен один груз массой 1,5 кг к концу стержня. Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.

Поскольку массой стержня можно пренебречь, тогда необходимо рассчитать момент I для каждого груза и сложить полученные результаты, чтобы получить полный момент системы. Согласно условию задачи от оси груз массой 2 кг находится на расстоянии 0,15 м (0,25-0,1), груз 3 кг — 0,05 м (0,25-0,20), груз 1,5 кг — 0,25 м. Воспользовавшись формулой для момента I материальной точки, получаем:

I = I₁+I₂+I₃ = m₁*r₁² + m₂*r₂² + m₃*r₃² = 2*(0,15)²+3*(0,05)²+1,5*(0,25)² = 0,14 625 кг*м².

Обратим внимание, что при выполнении вычислений все единицы измерения были переведены в систему СИ.

Чтобы определить угловую скорость вращения стержня после действия силы, следует применить формулу с моментом силы, которая была приведена во втором пункте статьи:

M = I*α

Поскольку α = Δω/Δt и M = r*F, где r — длина плеча, получаем:

r*F = I*Δω/Δt => Δω = r*F*Δt/I

Учитывая, что r = 0,25 м, подставляем числа в формулу, получаем:

Δω = r*F*Δt/I = 0,25*50*10/0,14625 = 854,7 рад/с

Полученная величина является достаточно большой. Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:

f = Δω/(2*pi) = 854,7/(2*3,1416) = 136 с^-1

Таким образом, приложенная сила F к концу стержня с грузами за 10 секунд раскрутит его до частоты 136 оборотов в секунду.

Расчет значения I для стержня, когда ось проходит через его конец

Пусть имеется однородный стержень массой m и длиной L. Необходимо определить момент инерции, если ось вращения расположена на конце стержня перпендикулярно ему.

Воспользуемся общим выражением для I:

I = ρ*∫_V(r_i²*dV)

Разбивая рассматриваемый объект на элементарные объемы, заметим, что dV может быть записано, как dr*S, где S — площадь сечения стержня, а dr — толщина элемента разбиения. Подставляя это выражение в формулу, имеем:

I = ρ*S*∫_L(r²*dr)

Этот интеграл вычислить достаточно просто, получаем:

I = ρ*S* (r³/3)∣₀^L => I = ρ*S*L³/3

Поскольку объем стержня равен S*L, а масса — ρ*S*L, то получаем конечную формулу:

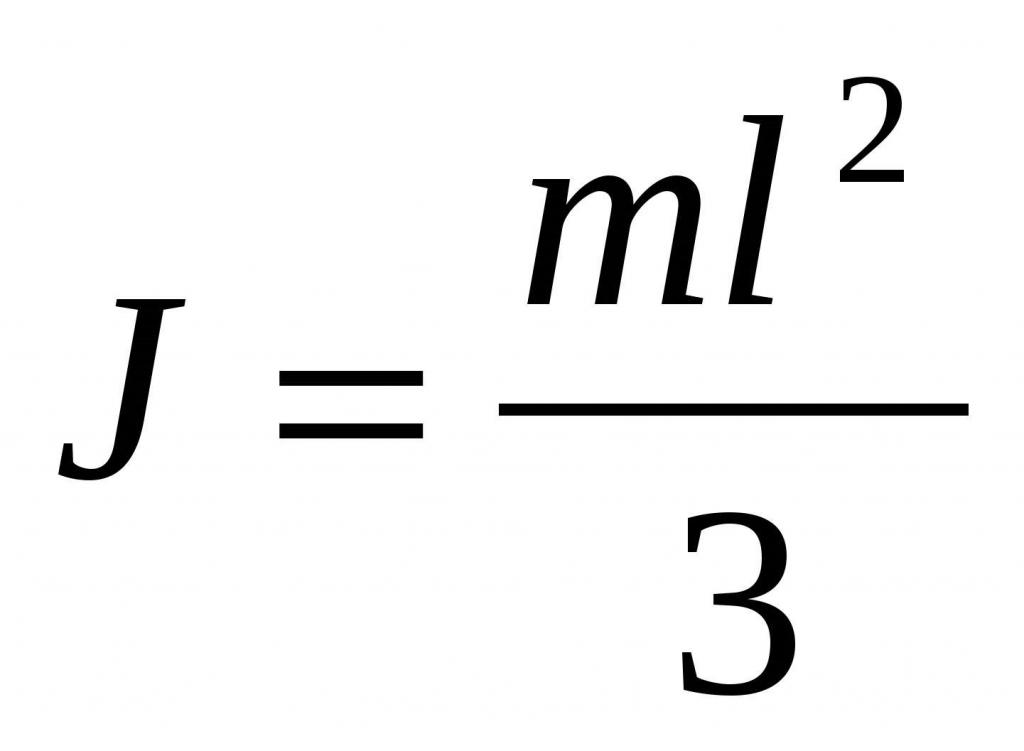
Любопытно отметить, что момент инерции для того же стержня, когда ось проходит через его центр масс, в 4 раза меньше полученной величины (m*L²/3/(m*L²/12)=4).

2. Динамика вращательного движения материальной точки и твердого тела Краткая теория

Эффективность воздействия силы на тело, которое может вращаться вокруг неподвижной оси, определяется векторным произведением:

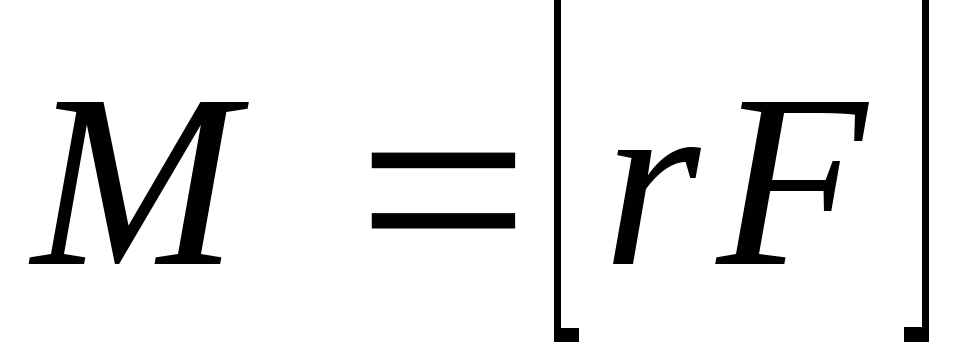, (2.1)

где 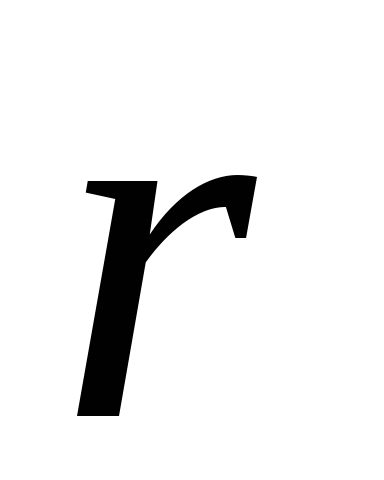— радиус-вектор точки приложения силы, — момент силы относительно оси вращения (рис. 2.1). На рис. 2.1. ось вращения проходит через точку О перпендикулярно плоскости рисунка. Модуль момента силы можно представить в виде:

,

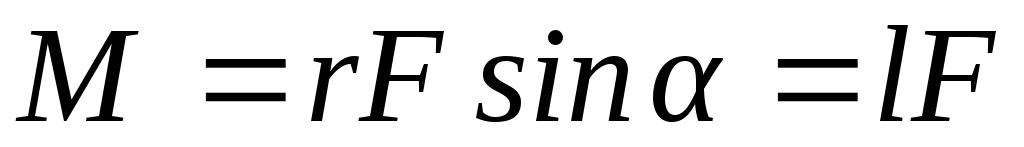где —плечо силы относительно точки О (т. е. длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила). Рисунок 2.1 выполнен в предположении, что точка О, относительно которой берется момент силы 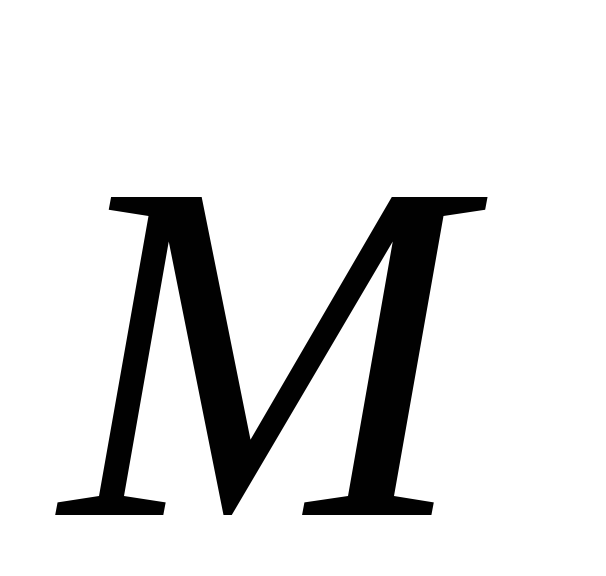, и векторлежат в плоскости рисунка. Вектор

перпендикулярен к плоскости рисунка и направлен от нас.

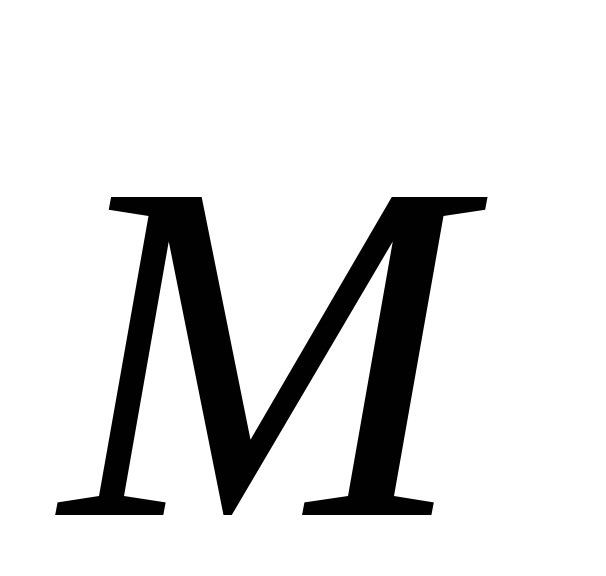
Для отдельно взятой частицы момент импульса относительно точки О (рис. 2.2) определяется векторным произведением:

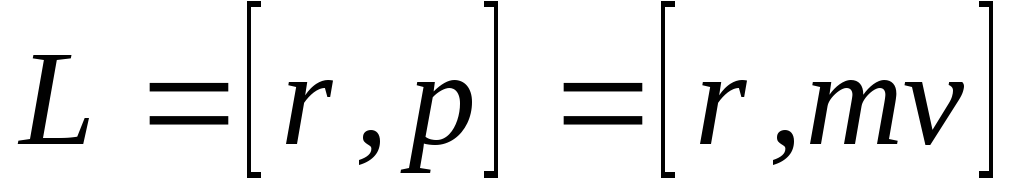, (2.2)

где

— импульс частицы. Модуль вектора момента импульса можно представить в виде:

г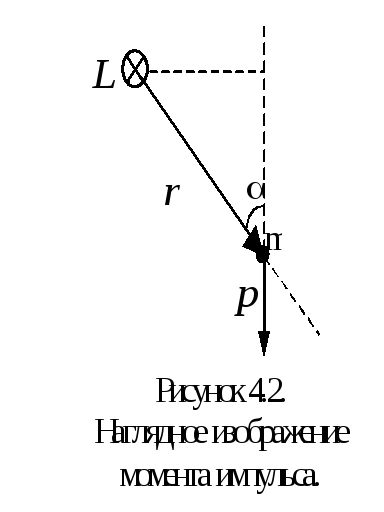

O

де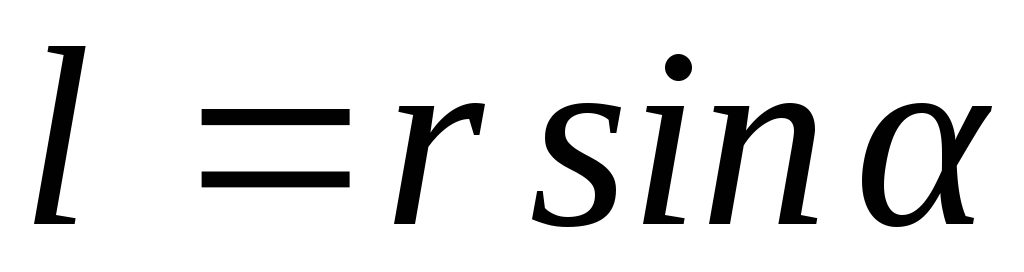— длина перпендикуляра, опущенного из точкиО на прямую, вдоль которой направлен импульс частицы. Эта длина называется плечом импульса относительно точки О.

l

Р

2.1

Рис.2.2. Наглядное изображение момента импульса 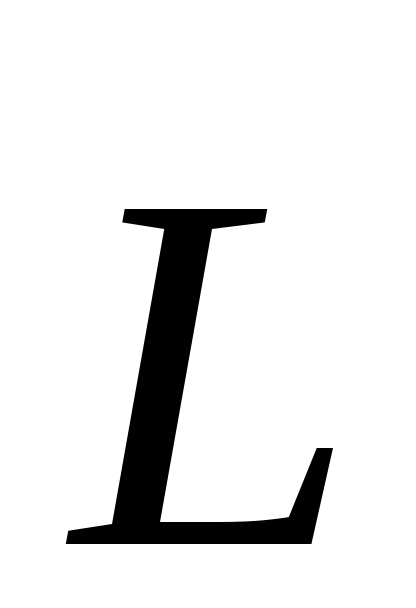частицы массойm относительно точки О

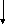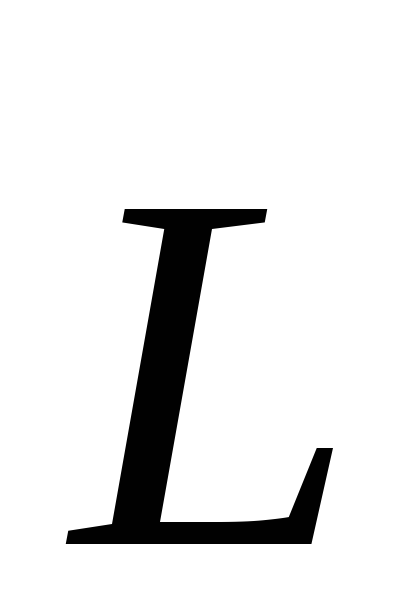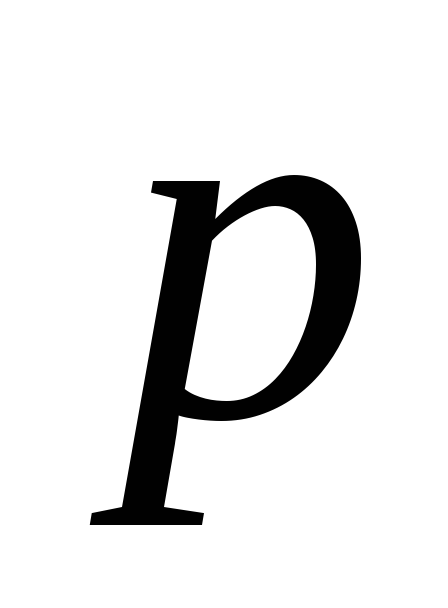исунок 2.2. выполнен в предположении, что точкаО, относительно которой берется момент импульса , и векторлежат в плоскости рисунка. Вектор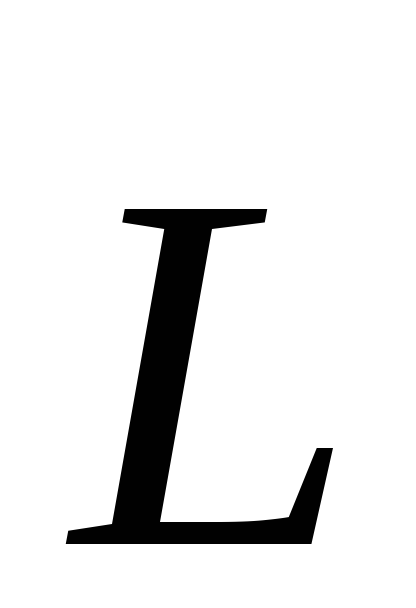перпендикулярен к плоскости рисунка и направлен от нас.

Момент инерции J материальной точки относительно оси вращения равен произведению m массы точки на квадрат расстояния r от этой точки до оси вращения:

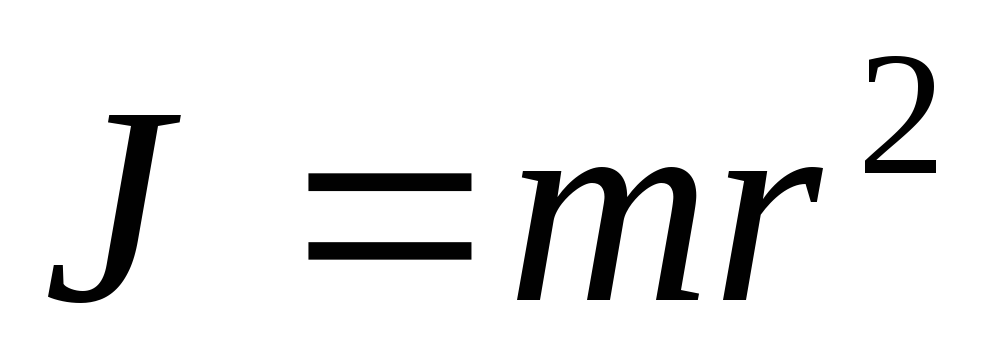. (2.3)

Момент инерции твердого тела относительно неподвижной оси называется физическая величина, характеризующая способность данного тела запасать количество вращательного движения (т. е. момента импульса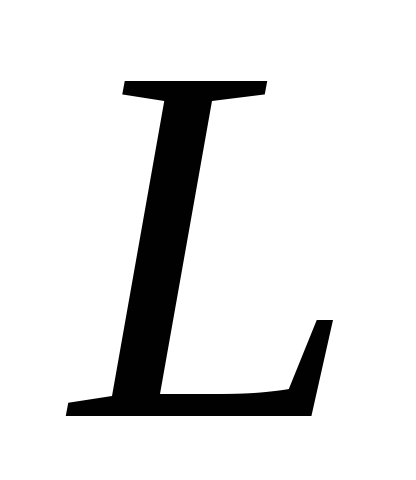

):

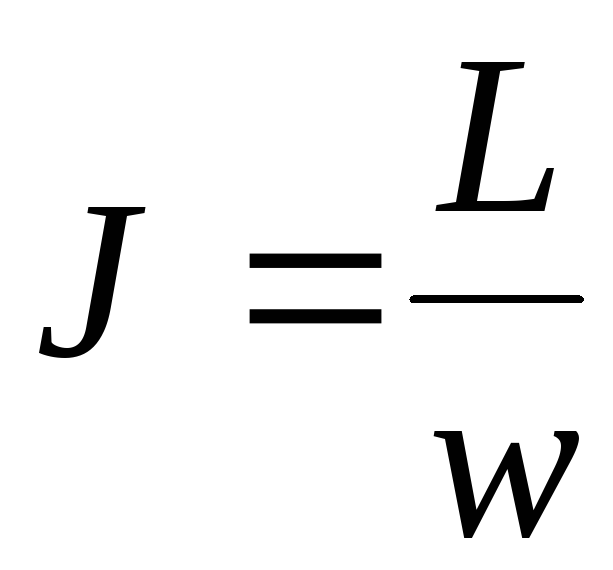, (2.4)

где w— угловая скорость. Момент инерции твердого тела относительно оси вращения зависит от распределения массы данного тела вокруг выбранной оси и может быть рассчитан по формуле:

,

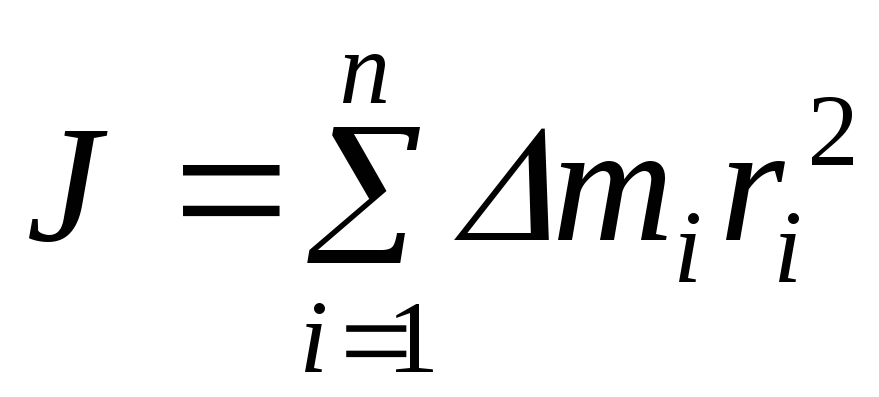где r_i – расстояние элемента массы

от оси вращения. То же в интегральной форме:

.

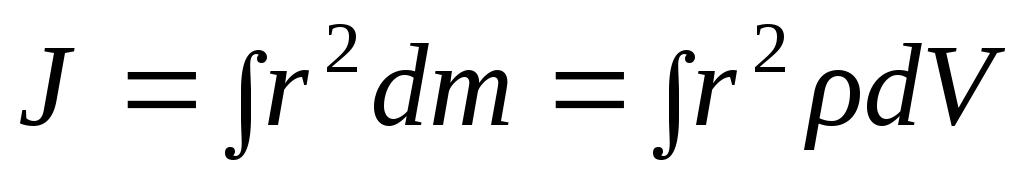Если тело однородно, т. е. его плотность 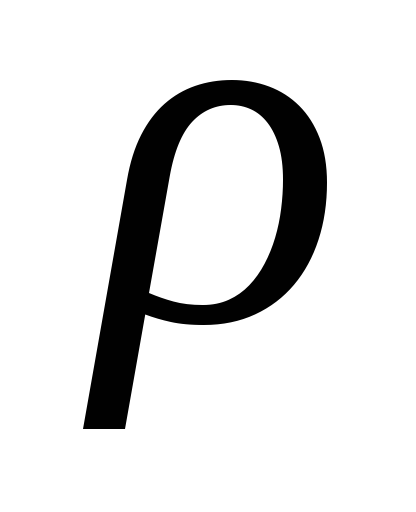одинакова по всему объемуV, то:

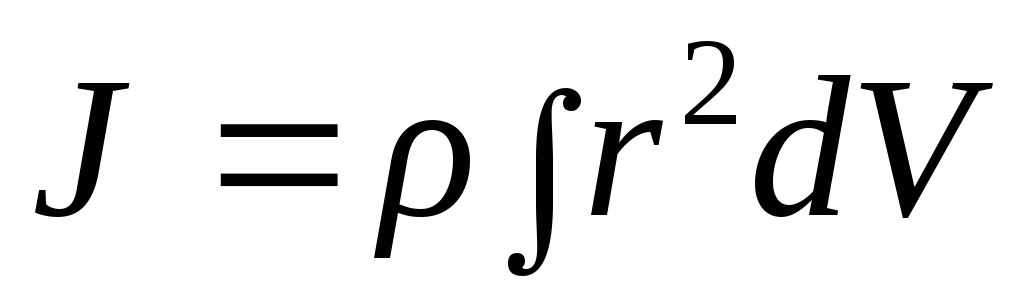. (2.5)

Моменты инерции некоторых тел правильной геометрической формы:

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции
Однородный тонкий стержень массой m и длиной l	Проходит через центр тяжести стержня перпендикулярно стержню
	Проходит через конец стержня перпендикулярно стержню
Тонкие кольцо, обруч, труба радиусом R и массой m	Проходит через центр перпендикулярно плоскости основания
Круглый однородный диск (цилиндр) радиусом R и массой m	Проходит через центр диска перпендикулярно плоскости основания
Однородный шар массой m и радиуса R	Проходит через центр шара

Теорема Штейнера. Момент инерции J тела относительно произвольной оси:

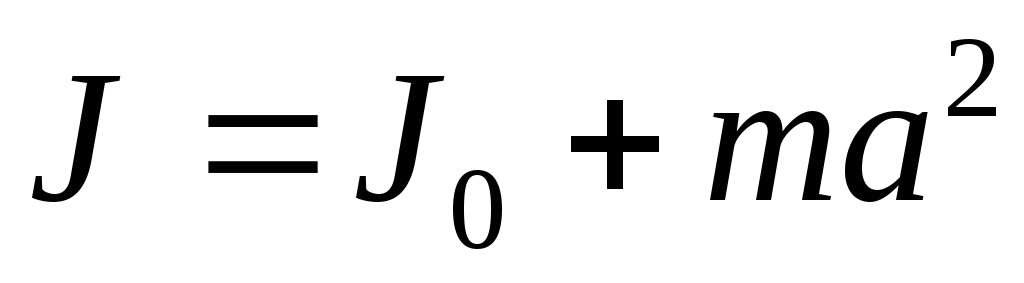, (2.6)

где J₀ – момент инерции этого тела относительно оси, проходящей через центр масс тела параллельно заданной оси; — расстояние между осями;m – масса тела.

При вращении вокруг закрепленной оси выполняются законы, аналогичные первому и второму законам Ньютона для прямолинейного движения.

Первый закон Ньютона для вращательного движения: всякое тело находится в состоянии покоя или равномерного вращения c постоянной угловой скоростью если равнодействующая всех моментов сил, действующих на тело, равна нулю:

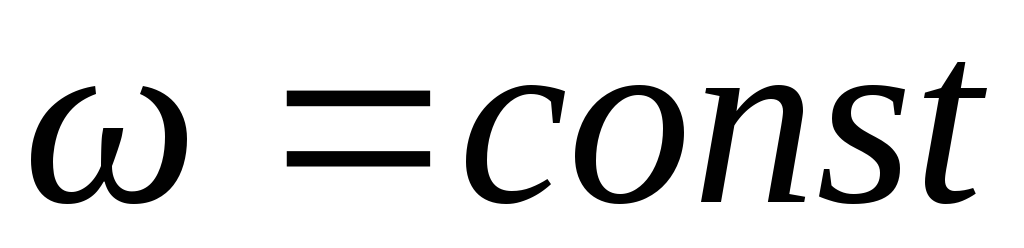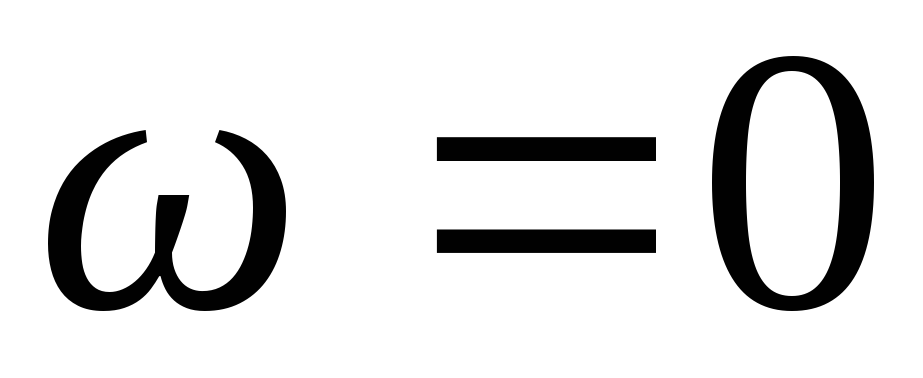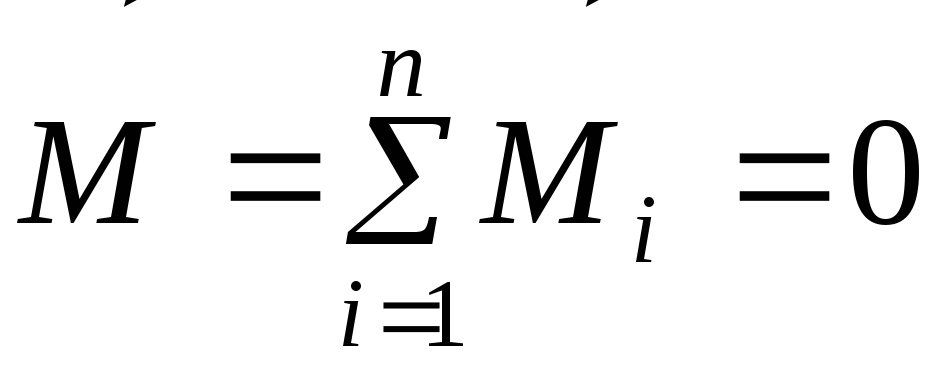():. (2.7)

Второй закон Ньютона для вращательного движения: под действием момента внешних сил тело приобретает угловое ускорение

, (2.8)

Основное уравнение динамики вращательного движения для изолированной материальной точки:

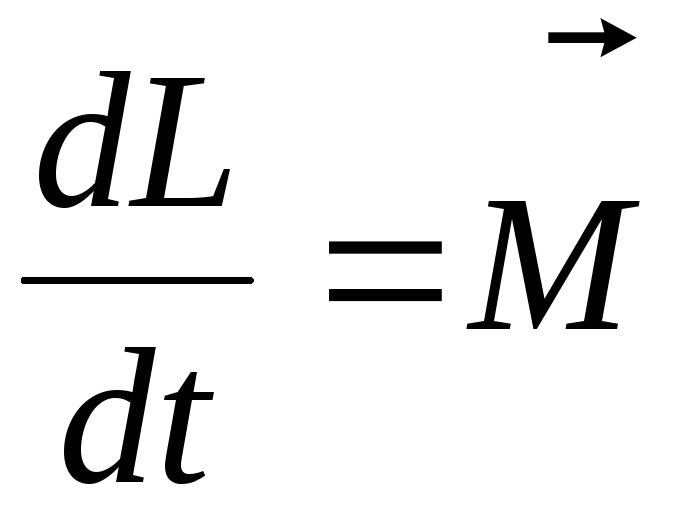, (2.9)

где 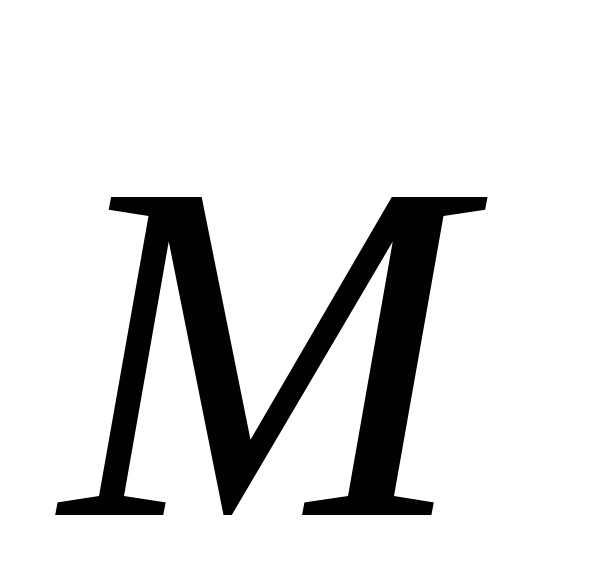— результирующий момент внешних сил, действующих на материальную точку, 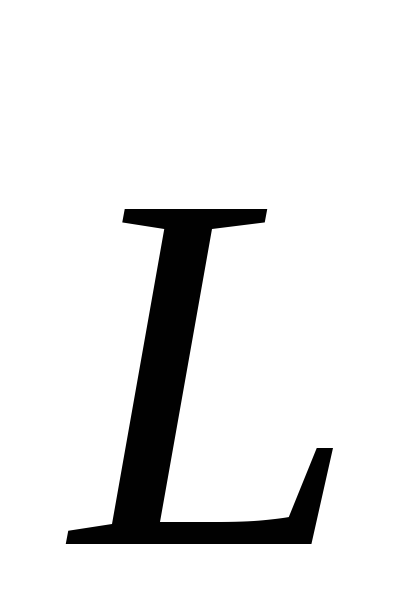— момент импульса материальной точки.

Разбив тело на элементарные массы m_i, можно представить его как систему материальных точек, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием как внутренних сил, обусловленных ее взаимодействием с другими элементарными массами рассматриваемого тела, так и внешних сил. Тогда основное уравнение динамики вращательного движения для материальной точки, входящей в систему точек имеет вид:

, (2.10)

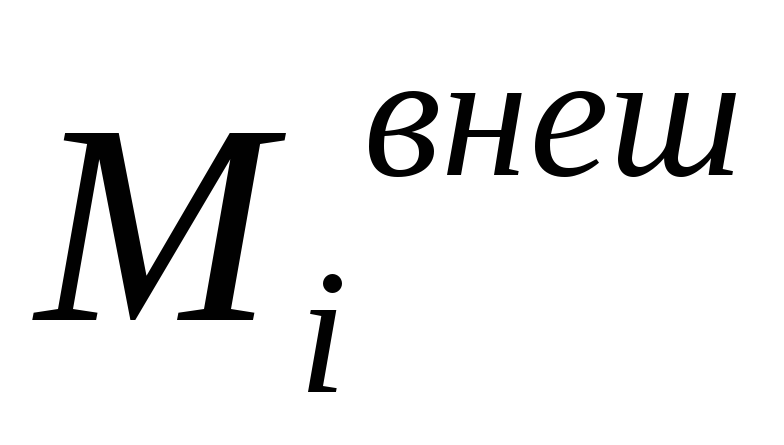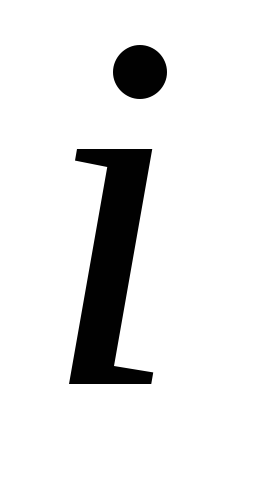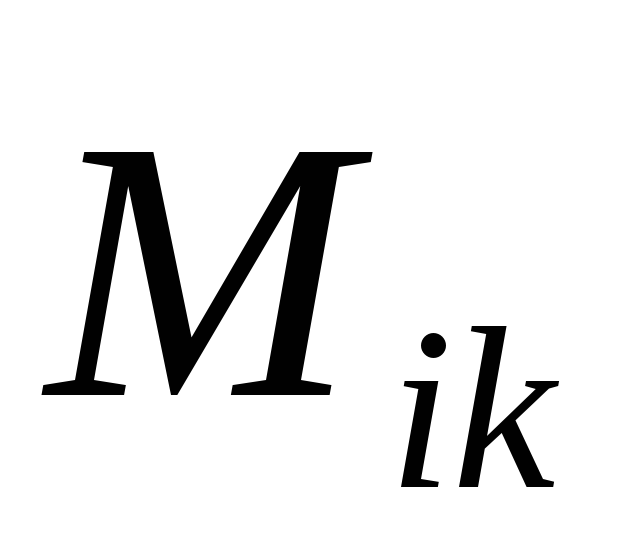где — результирующий момент внешних сил, действующих на-ю точку системы;— момент внутренних сил, действующих со стороны-ой точки на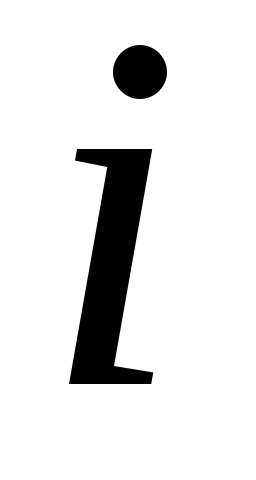-ю;n — число точек в системе; -момент импульсаi—ой точки, входящей в состав системы.

Основное уравнение динамики вращательного движения системы материальных точек:

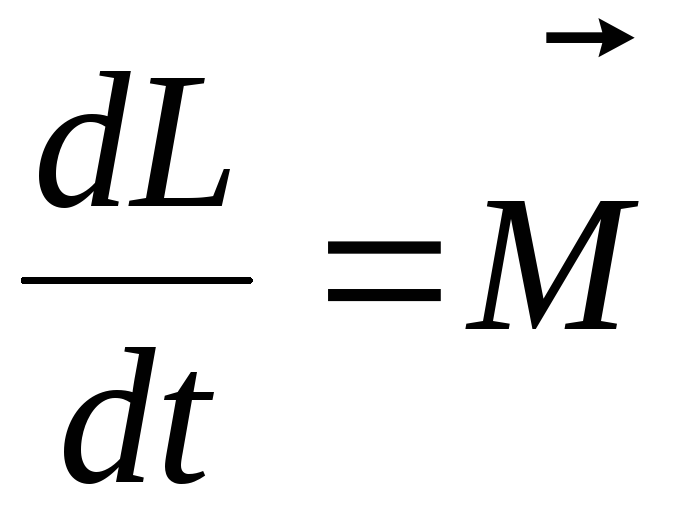, (2.11)

где =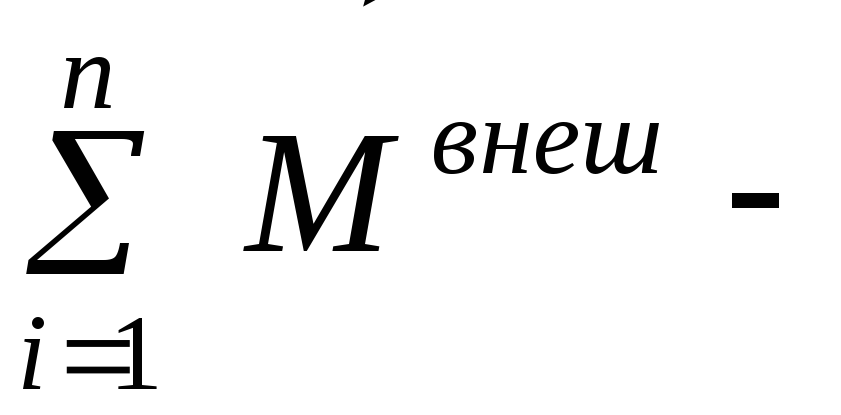главный момент внешних сил, действующих на систему материальных точек, 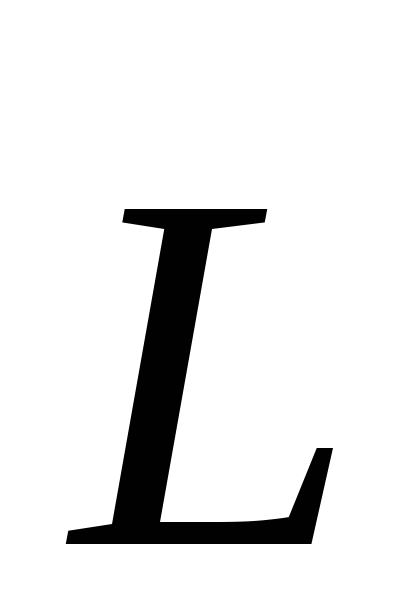= 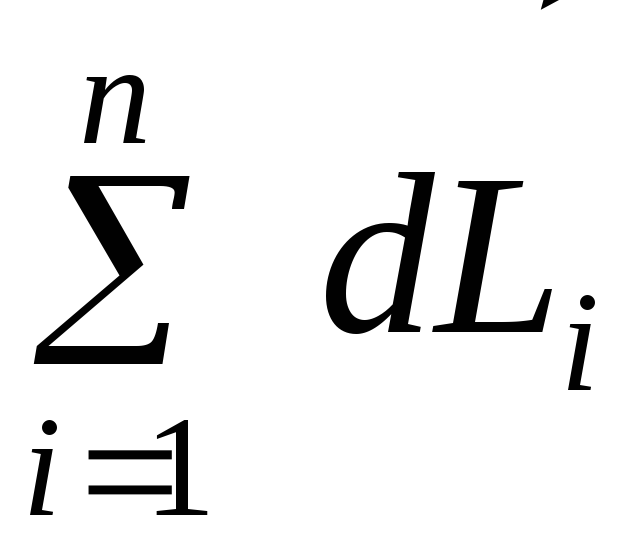-момент импульса системы точек.

Частный случай системы материальных точек – твердое тело. Для твердого тела расстояние между точками не изменяется. Поэтому уравнение (2.11) справедливо и для твердого тела. В последнем случае 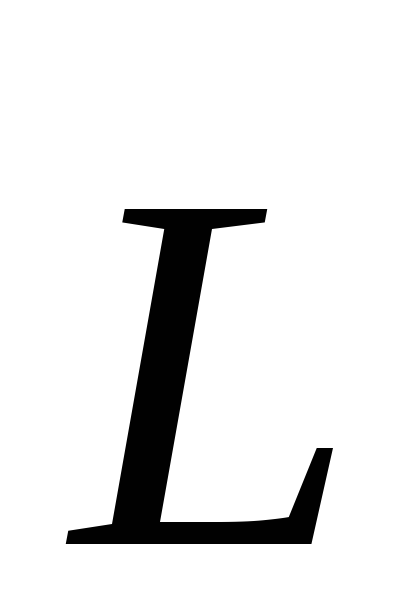есть момент импульса тела, 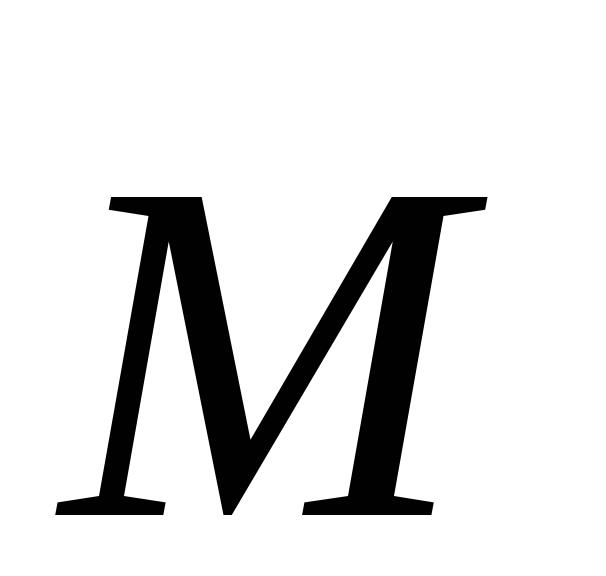— сумма моментов внешних сил, действующих на тело.

ТАБЛИЦА АНАЛОГИЙ

ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ	ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Глава 3. Динамика вращательного движения

§ 3.1 Момент силы. Момент импульса.

Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси ОО’ (рис. 1.14).

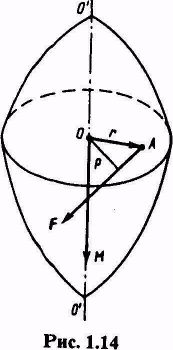
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль мо­мента силы относительно точки О:

М = Fp=Frsinα.

Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:

(3.1) Единица момента силы — ньютон-метр (Н • м).

Направление М можно найти с помощью правила правого винта.

Моментом импульса частицы называется векторное произведение радиус-вектора частицы на её импульс:

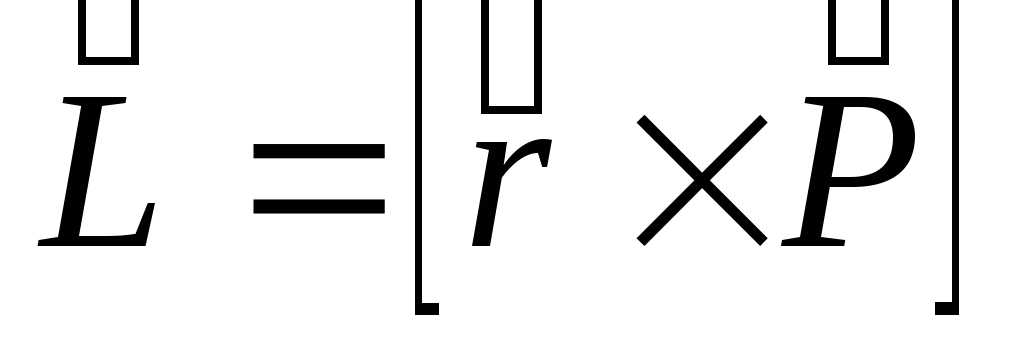или в скалярном виде L = гPsinα

Эта величины векторная и совпадает по направлению с векторами ω.

§ 3.2 Момент инерции. Теорема Штейнера

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, назы­ваемая моментом инерции тела относительно оси вращения.

Моментом инерции материальной точки относительно оси враще­ния называют произведение массы этой точки на квадрат расстояния её от оси:

I_i=m_ir_i² (3.2)

Момент инерции тела относительно оси вращения называют сумму мо­ментов инерции материальных точек, из которых состоит это тело:

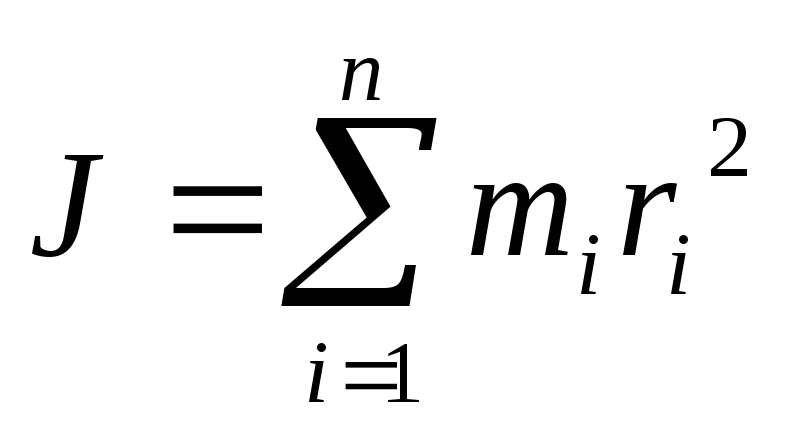(3.3)

В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm, момент инерции определяется интегрированием:

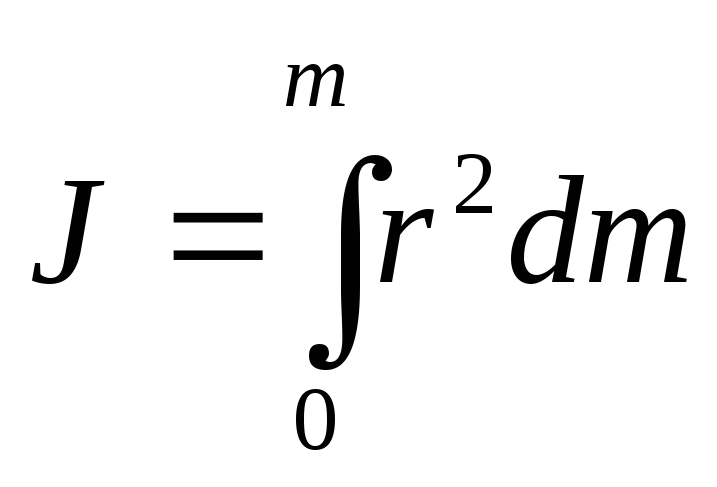(3.4)

[r — расстояние от оси вращения до элемента массой dm].

Если тело однородно и его плотность 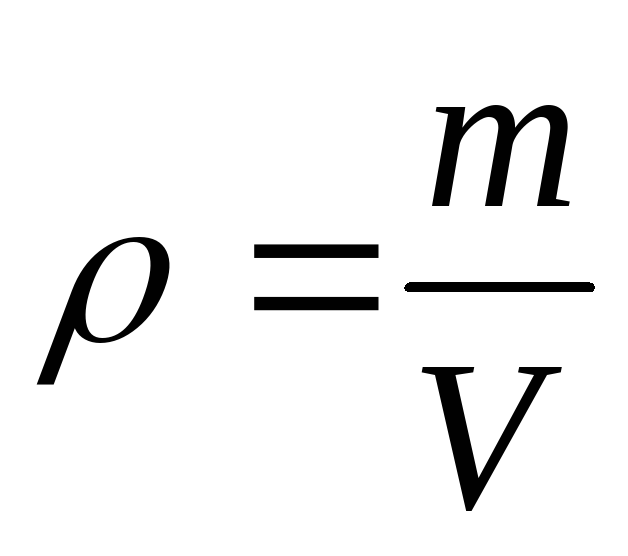, то момент инерции тела

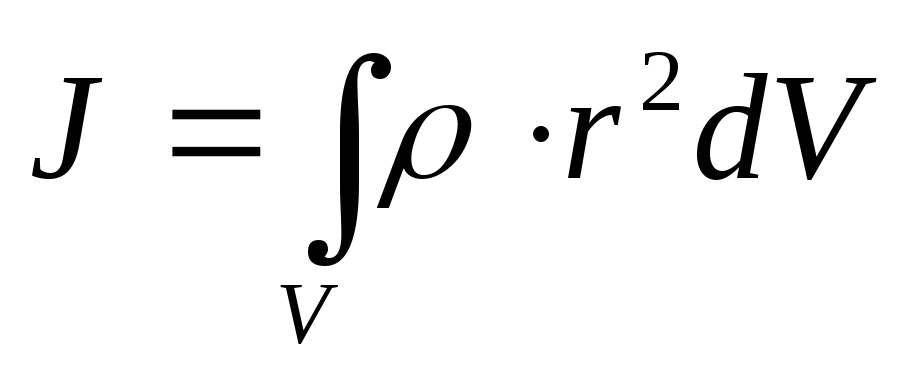(3.5)

Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.

• Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню

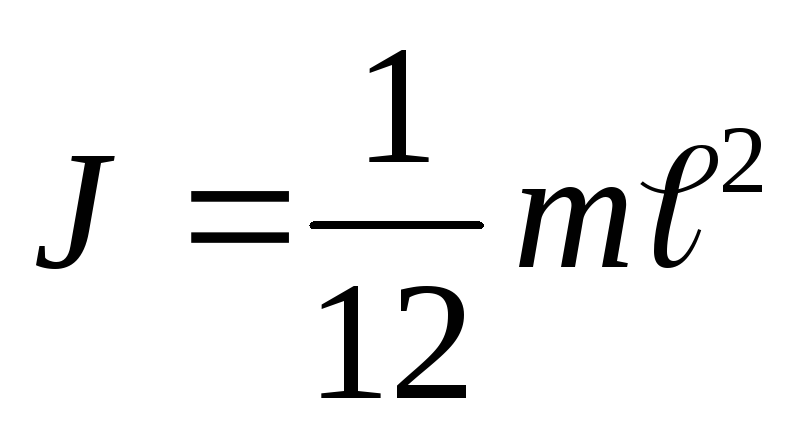(3.6)

• Момент инерции однородного цилиндра относительно оси, перпен­дикулярной его основанию и проходящей через центр инерции,

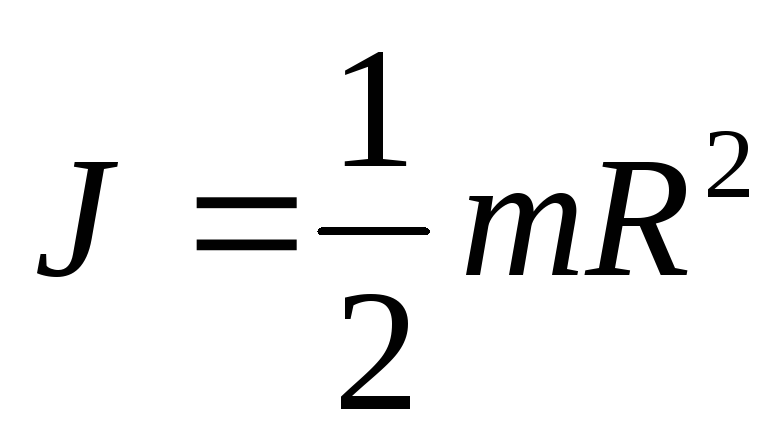(3.7)

• Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр,

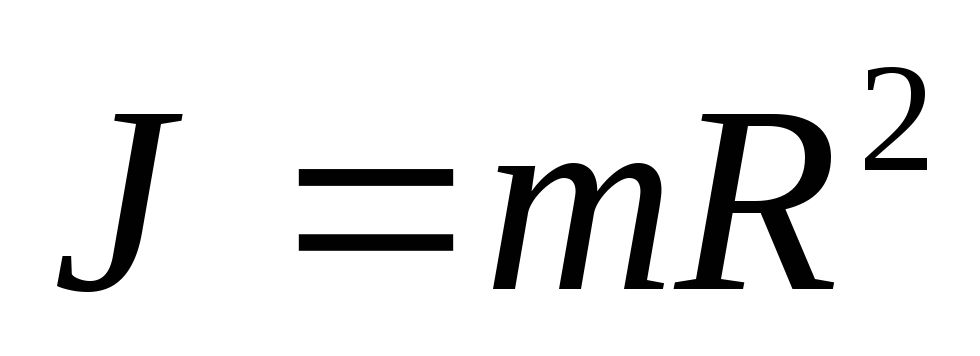(3.8)

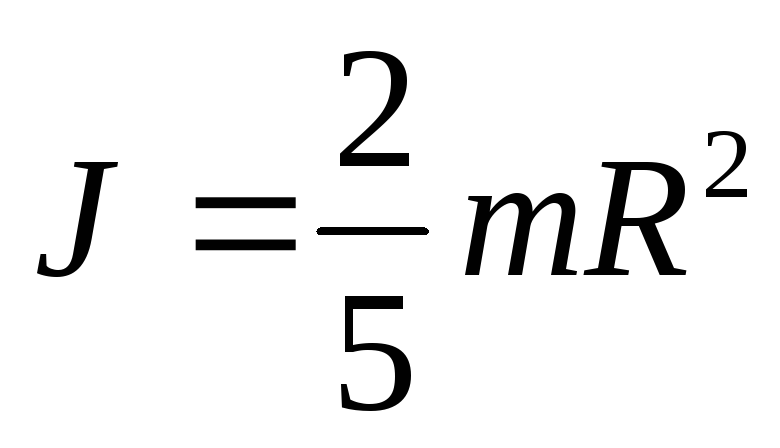(3.9)

Рассмотрим пример. Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоско­сти вращения. Масса диска — m, радиус — R.

Площадь кольца (рис. 3.2), заключенного между

r и r + dr, равна dS = 2πr·dr . Площадь диска S = πR².

Следовательно, 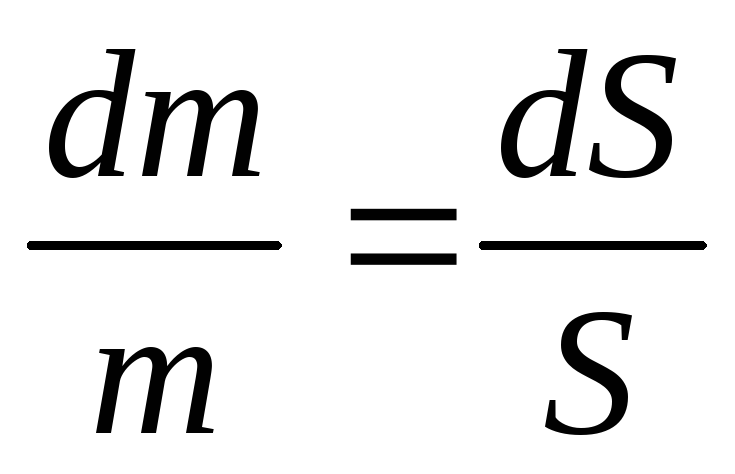. Тогда

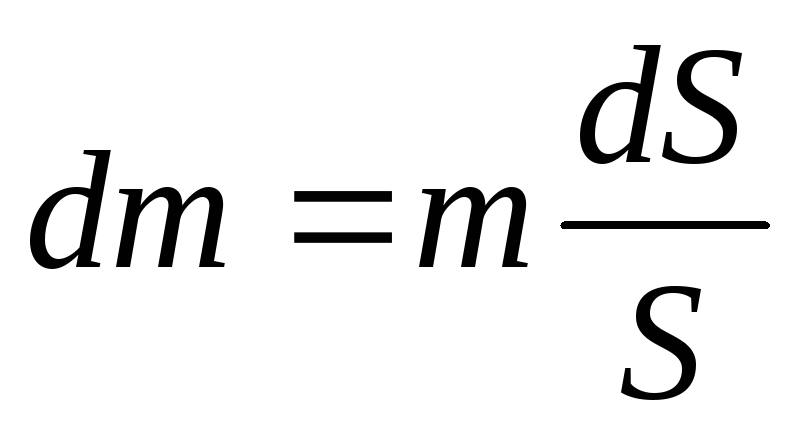или

Согласно

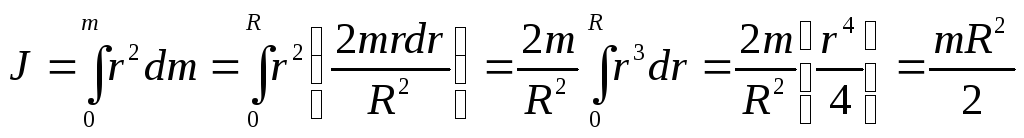(3.10)

Приведенные формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

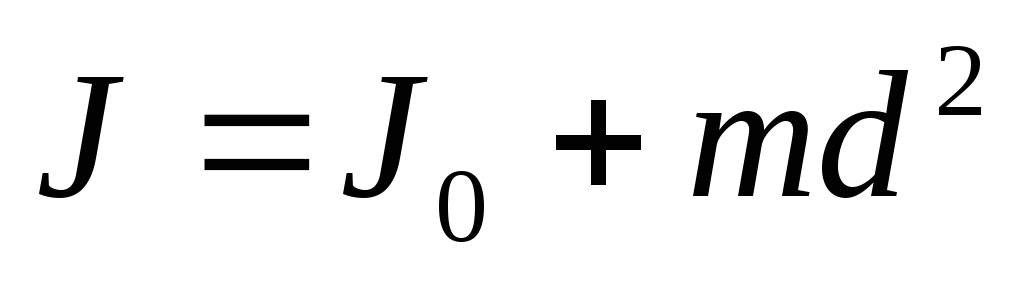(3.11)

[m — масса тела, d — расстояние от центра масс до выбранной оси вра­щения (расстояние между осями)].

Единица момента инерции — килограмм-метр в квадрате (кг· м²).

Так, момент инерции однородного стержня относительно оси, проходящей через его конец, по теореме Штейнера равен

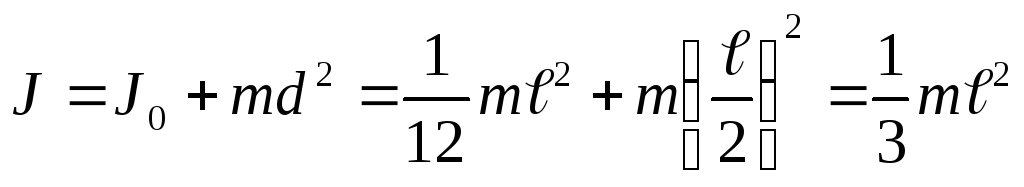(3.12)

1.Напишите основное уравнение динамики вращательного движения (2ой закон Ньютона для вращательного движения).

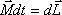
Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 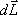, равно импульсу момента  всех внешних сил, действующих на это тело.

2.Чему равен момент силы? (формула в векторном и скалярном виде, рисунки).

Момент   силы  (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы – векторная величина ( М̅)

(векторный вид) М̅= |r̅*F̅|,r– расстояние от оси вращения, до точки приложения силы.

(вроде как скалярный вид) |М|=|F|*d

Вектор момента силы – совпадает с осью О₁О₂, его направление определяется првилом правого винта.Момент   силы  измеряется в ньютон-метрах. 1 Н•м —  момент   силы , который производит сила 1 Н на рычаг длиной 1 м.

3.Что называется вектором: поворота, угловой скорости, углового ускорения. Куда они направлены, как определить это направление на практике?

Векторы – это псевдовекторы или аксиальные векторы, не имеющие определённую точку приложения: они откладываются на оси вращения из любой её точки.

1. Угловое перемещение — это псевдовектор, модуль которого равен углу поворота , а направление совпадает с осью, вокруг которой тело поворачивается, и определяется правилом правого винта: вектор направлен в ту сторону, откуда поворот тела виден против хода часовой стрелки(измеряется в радианах)

2. Угловая скорость — величина, характеризующая быстроту вращения твёрдого тела, равная отношению элементарного угла поворота и прошедшего времени dt, за который прошёл этот поворот.

Вектор угловой скоростинаправлен вдоль оси вращения по правилу правого винта, так же, как и вектор .

3. Угловое ускорение— величина, характеризующая быстроту перемещения угловой скорости.

Вектор направлен вдоль оси вращения в сторону вектора при ускоренном вращении и противоположно вектору при замедленном вращении.

4.Чем полярный вектор отличается от аксиального?

Полярный вектор обладает полюсом, а аксиальный — нет.

5.Что называется моментом инерции материальной точки, твердого тела?

Момент   инерции  — величина, характеризующая меру  инерции   материальной   точки при её вращательном движении вокруг оси. Численно она равна произведению массы на квадрат радиуса (расстояния до оси вращения). Для  твердого   тела  момент  инерции равен сумме  моментов  инерции  её частей, и поэтому может быть выражена в интегральной форме:

I=∫ r² dү.

6.От каких параметров зависит момент инерции твердого тела?

1. От массы тела

2. От геометрических размеров

3. От выбора оси вращения

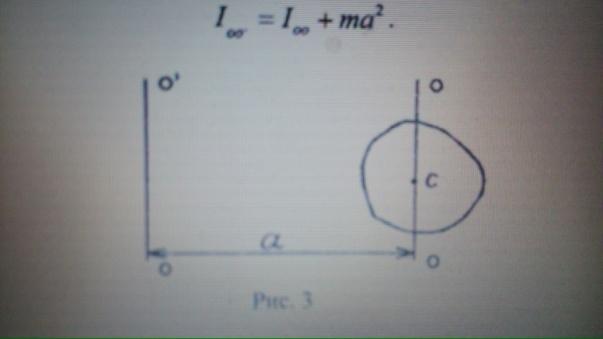
7.Теорема Штейнера (поясняющий рисунок).

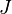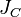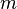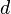Теорема: момент инерции тела относительно произвольной оси равен сумме момента инерции этого телаотносительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния между осями: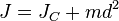

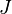— искомый момент инерции относительно параллельной оси

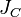— известный момент инерции относительно оси, проходящей через центр масс тела

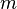— масса тела

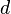— расстояние между указанными осями

8.Момент инерции шара, цилиндра, стержня, диска.

Моментом инерции м.т. относительно полюса называют скалярную величину, равную  произведению массы этой. точки  на квадрат расстояния  до полюса..

Момент инерции м.т. можно найти по формуле

где m — масса м.т., R — расстояние до полюса 0.

Единицей измерения момента инерции в СИ является килограмм умноженный на метр в квадрате (кг×м²).

1.Прямой тонкий стержень длины lи массыm 1)Ось перпендикулярна к стержню и проходит через его центр масс

2)Ось перпендикулярна к стержню и проходит через его конец

2.Шар радиуса rи массыm

Ось проходит через центр шара

3.Полый тонкостенный цилиндр или кольцо радиуса rи массыm

Ось цилиндра

4.Сплошной цилиндр или диск радиуса rи массыm Ось цилиндра

5.Сплошной цилиндр длины l, радиусаrи массыm

Ось перпендикулярна к цилиндру и проходит через его центр масс

9.Как определить направление момента силы?

Момент силы относительно некоторой точки — это векторное произведение силынакратчайшее расстояниеот этой точки до линии действия силы.

[M]₌ Ньютон · метр

M— момент силы (Ньютон · метр),F— Приложенная сила (Ньютон),r— расстояние от центра вращения до места приложения силы (метр),l— длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр),α— угол, между вектором силыFи вектором положенияr

M₌ F·l₌ F·r·sin(α)

M=F*r

(м,F,r-векторные величины)

Момент силы — аксиальный вектор. Он направлен вдоль оси вращения.

Направление вектора момента силы определяется правилом буравчика, а величина его равнаM.

10.Как складываются момент сил, угловые скорости, моменты импульса?

Момент сил

Если на тело, которое может вращаться вокруг какой-либо точки, действует одновременно несколько сил, то для сложения моментов этих сил следует использовать правило сложения моментов сил.

Правило сложения моментов сил гласит — Результирующий вектор момента силы равен геометрической сумме составляющих векторов моментов с

Для правила сложения моментов сил различают два случая

1. Моменты сил лежат в одной плоскости, оси вращения параллельны. Их сумма определяется путем алгебраического сложения. Правовинтовые моменты входят в сумму со знаком минус. Левовинтовые — со знаком плюс

2. Моменты сил лежат в разных плоскостях, оси вращения не параллельны. Сумма моментов определяется путем геометрического сложения векторов.

Угловые скорости

Углова́я ско́рость(рад/с) — физическая величина, являющаяся аксиальным вектором и характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени

направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Угловые скорости откладываются на оси вращения и могут складываться в том сллучае если они направлены в одну сторону, в противоположную — вычитаются

Момент импульса

В Международной системе единиц (СИ) импульс измеряется в килограмм-метр в секунду (кг·м/с).

Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Если имеется материальная точка массой , двигающаяся со скоростью и находящаяся в точке, описываемой радиус-вектором , то момент импульса вычисляется по формуле:

где  — знак векторного произведения

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторнопросуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

11.Сформулируйте закон сохранения полной механической энергии применительно к телу, вращающемуся вокруг неподвижной оси.

MgH=(IоW^2)/2

потенциальная энергия максимальна в начальной точке движения маятника. Потенциальная энергия MgH переходит в кинетическую, которая максимальна в момент приземления маятника на землю.

Iо-момент инерции относительно оси для одного грузика ( их у нас 4 )

I= 4Iо=4ml^2 ( Io=ml^2)

следовательно

MgH=2ml^2W^2

12.Сформулируйте закон сохранения полной механической энергии применительно к телу, вращающемуся вокруг неподвижной оси.

Момент импульса вращающегося тела прямо пропорционален скорости вращения тела, его массе и линейной протяженности. Чем выше любая из этих величин, тем выше момент импульса.

В математическом представлении момент импульса Lтела, вращающегося с угловой скоростьюω, равенL = Iω, где величинаI, называемаямоментом инерции

скорость вращения маятника многократно возрастает вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции I, тем выше угловая скоростьωи, как следствие, короче период вращения, обратно пропорциональный ей.

Момент импульса вращающегося тела   

 

где  – масса тела;  – скорость;  – радиус орбиты, по которой перемещается тело;  – момент инерции;  – угловая скорость вращающегося тела.

Закон сохранения момента импульса:

– для вращательного движения

 при ;

13.Каким выражением определяется работа момента сил

= МОМЕНТ_СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон* метр, а УГОЛ в радианах

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ_СИЛЫ * *

14.Получите формулу, определяющую мощность, развиваемую моментом сил.

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работ. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ

В системе CИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.