Что такое Сила Лоренца?

Определение + формула

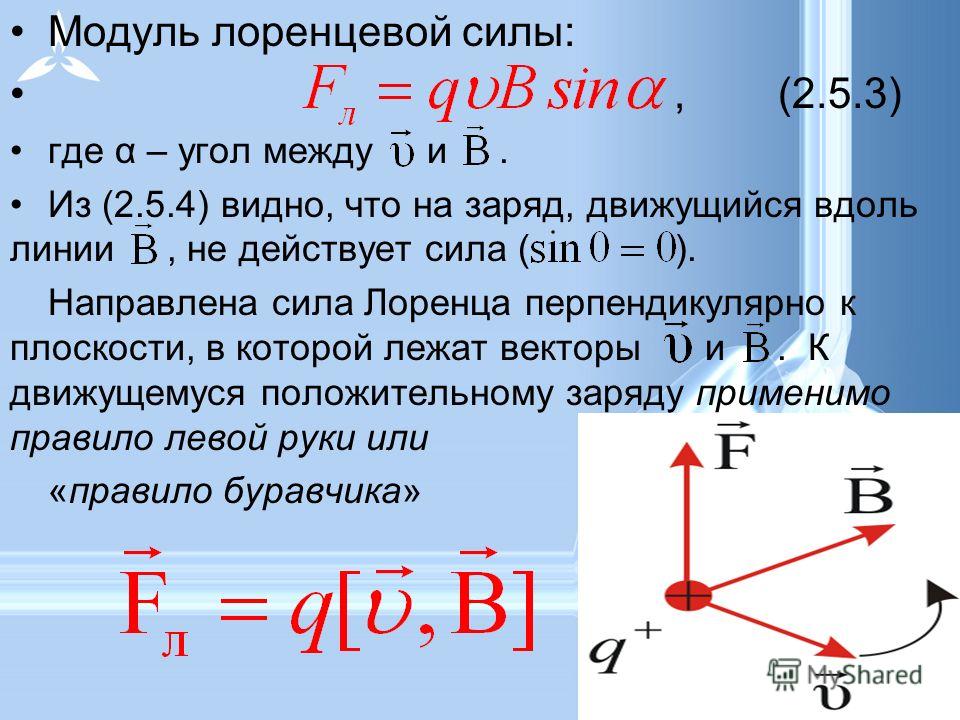
Сила Лоренца – сила, оказывающая воздействие на движущийся электрический заряд со стороны электромагнитного поля. Названа она по фамилии ученого-физика, который впервые описал это явление. Зачастую, обозначение сила Лоренца применяют в формуле имея в виду лишь магнитную силу:

\[\mathrm{F}=\mathrm{q}(E+v B)\]

Где магнитная сила обозначена B, заряд частицы – q, напряжение электрополя – E, скорость движущейся частицы – v.

Сила Ампера, оказывающая воздействие на фрагмент проводника, имеющего длину Δl с определенной силой тока l, во время его нахождения в магнитном поле B, F = I ⋅ B ⋅ Δ l ⋅ sin α может быть выражена через силы, воздействующие на определенные носители заряда.

Обозначим заряд конкретного носителя как q. При этом n представляет собой значение концентрации в проводнике носителей свободного заряда.

Таким образом выражение n ⋅ q ⋅ υ ⋅ S, где S применяется для обозначения площади поперечного сечения предлагаемого проводника, а u – является модулем скорости упорядоченного перемещения носителей в представленном проводнике, будет соответствовать току, текущему в проводнике: I = q ⋅ n ⋅ υ ⋅ S

Формула 2

Формула силы Ампера выглядит следующим образом:

\[\mathrm{F}=\mathrm{q} \cdot \mathrm{n} \cdot \mathrm{S} \cdot \Delta \mathrm{l} \cdot \mathrm{u} \cdot \mathrm{B} \cdot \sin \alpha\]

Исходя из того, что переменная N, с помощью которой обозначено число носителей свободного заряда, движущихся в проводнике с площадью сечения S и длиной Δl равна произведению n ⋅ S ⋅ Δ l, мы можем говорить, что сила, действующая на каждую из заряженных частиц, равна выражению:

\[F_{Л}\] = q ⋅ υ ⋅ B ⋅ sin α.

Сила, которую мы нашли называют — силой Лоренца. Формула показывает, что значение угла α соответствует углу, образованному вектором магнитной индукции \[\vec{B}\] и скоростью \[\vec{v}\].

По принципу действия сила Лоренца имеет большое сходство с силой Ампера. Отличие состоит в том, что действие последней распространяется на весь проводник, нейтральный в электрическом смысле, а первая описывает как влияет электромагнитное поле на отдельную движущуюся заряженную частицу.

Направление силы Лоренца

Определяя направление силы Лоренца, исходим из того, что она всегда будет перпендикулярна вектору магнитной индукции. Это значит, что \[\vec{B}\] соответствует тому выделенному направлению в пространстве, вдоль которого действие магнитных сил не распространяется. Вектор силы Лоренца имеет направление перпендикулярное вектору \[\vec{v}\]. Для определения окончательного направления силы можно воспользоваться правилом левой руки.

Ладонь необходимо расположить таким образом, чтобы четыре пальца были вытянуты вдоль направления движения заряда, а положение отставленного большого пальца соответствовало вектору магнитной индукции поля. Именно большой палец будет указывать направление силы Лоренца, которая действует на положительный заряд.

Если заряд отрицательный, направление силы станет противоположным.

Рисунок 1. Правило левой руки

На рис. 2 можно увидеть демонстрацию взаимного расположения векторов \[\vec{v}\] и \[\vec{B}\] для положительно заряженной частицы.

Рисунок 2. Взаимное расположение векторов \[\vec{v} \vec{B}\] и \[\vec{F}_{Л}\].

Модуль силы Лоренца − \[\vec{F}_{Л}\] равен площади параллелограмма, построенного на векторах  \[\vec{v}\] и  \[\vec{B}\], умноженной на заряд q.

Сила Лоренца имеет нормальное, то есть перпендикулярное направление относительно векторов \[vec{v}\] и \[\vec{B}\].

Работа силы Лоренца всегда имеет нулевое значение, поскольку эта сила всегда перпендикулярна скорости и движению заряда. Величина скорости не изменяется под влиянием магнитного поля, его воздействие приводит к изменению лишь направления скорости. Поэтому заряженная частица, движущаяся под воздействием силы Лоренца перпендикулярно магнитному полю, при условии его однородности, и скорости лежащей в плоскости, направленной нормально относительно вектора \[\vec{B}\] , будет иметь траекторию в виде окружности. Радиус можно рассчитать, используя формулу:

R = m ν q B

В таких случаях магнитная сила Лоренца выступает в роли центростремительной силы. Это проиллюстрировано на рис. 3.

Рисунок 3. Круговая траектория движения заряженной частицы в условиях однородного магнитного поля.

Формула 3

Период кругового движения частицы внутри однородного магнитного поля можно определить по формуле:

\[T=2 \pi R u=2 \pi m q B\]

Данное выражение подтверждает, что заряженные частицы с заданной массой m не зависят от скорости u и радиуса круговой траектории R.

Применение силы Лоренца

Формула 4 + определение

Для определения угловой скорости кругового движения заряженной частицы применяется следующая формула:

\[\omega=u R=u q B m u=q B m\]

Частота, с которой заряженная частица обращается в однородном магнитном поле именуется циклотронной. Она не зависит от скорости, с которой движется частица, а также от ее кинетической энергии.

Благодаря данному обстоятельству становится возможным применение силы Лоренца для циклотронов, если конкретнее – ускорителей тяжелых частиц, известных как ионы, протоны. Рисунок 4 демонстрирует принципиальную схему циклотрона.

Рисунок 4. Траектория движения заряженных частиц внутри вакуумной камеры циклотрона.

Определение 3

Дуант — один из двух полых металлических полуцилиндров, размещенных в вакуумной камере циклотрона между двух полюсов электромагнита в качестве ускоряющего D-образного электрода.

Дуанты подвергаются воздействию переменного электрического напряжения, частота которого равна частоте циклотрона. В центре камеры происходит инжектирование заряженных частиц. Электрическое поле, создаваемое в зазоре между двух дуантов ускоряет движение частиц. Двигаясь по полуокружностям они подвергаются воздействию силы Лоренца. Рост энергии частиц приводит к увеличению радиуса полуокружностей. Электрическое поле вызывает ускорение заряженных частиц, а на заданной траектории ее удерживает магнитное поле. Энергия за счет ускорения протонов в циклотронах может увеличиваться до 20 МэВ.

Однородные магнитные поля нашли свое применение в самых разных устройствах – в частности, в масс-спектрометрах.

Приборы делают возможным разделение изотопов – ядер, имеющих одинаковый заряд, но различную массу. Например, ²⁰Ne, ²²Ne.

Элементарный масс-спектрометр можно увидеть на рисунке 5.

Рисунок 5. Селектор скоростей и масс-спектрометр.

Ионы, вылетая из источника S преодолевают несколько мелких отверстий и образуют узкий пучок. После попадания в селектор скоростей они продолжают движение в альянсе однородного электрического, образованного в промежутке между пластин плоского конденсатора и магнитного поля, формирующегося в зазоре, возникающего между разнозаряженными полюсами электромагнита. Направление начальной скорости \[\vec{v}\] заряженных частиц перпендикулярно относительно векторов \[\vec{E}\] и \[\vec{B}\].

Во время движения в зоне скрещенных электрического и магнитного полей на частица воздействует электрическая сила — \[\vec{q E}\] и магнитная сила Лоренца. {6}\] K с практически одинаковой плотностью положительных и отрицательных зарядов. Для доведения вещества до подобного состояния используют установки типа «Токамак». Такие процедуры проводят в процессе изучения управляемых реакций термоядерного типа. Необходимо исключить попадание плазмы на стенки. Достигнуть необходимого уровня термоизоляции получается за счет формирования магнитного поля определенной конфигурации.

Траекторию движения заряженной частицы внутри магнитной «бутылки» или ловушки можно увидеть на рисунке 7.

Рисунок 7. Магнитная «бутылка». Заряженные частицы не покидают пределов магнитного поля. Для его создания применяют две круглые катушки с током.

Аналогичное явление наблюдается в магнитном поле нашей планеты, которое обеспечивает надежную защиту всего живого, выступая в качестве преграды на пути потока заряженных частиц из космоса.

Магнитное поле Земли осуществляет «перехват» быстрых заряженных частиц из космического пространства. В результате происходит формирование радиационных поясов. Внутри этих магнитных ловушек частицы стремительно перемещаются по спиралевидным траекториям в одну сторону и в другую между северным и южным магнитным полюсом. Движение совершается за доли секунды.

В полярных областях частицы могут прорываться и оказываться в верхних слоях атмосферы. Это явление известно, как «северное сияние». Размеры радиационных поясов Земли (рис.8) могут занимать как 500 км, так и десятки радиусов Земли. Считаем нелишним напомнить, что южный магнитный полюс располагается неподалеку от северного географического полюса Земли на северо-западе острова Гренландия. На сегодняшний день секреты природы земного магнетизма пока еще не раскрыты.

Рисунок 8. Радиационные пояса Земли.

Практическое применение силы Лоренца. Примеры

Силу Лоренца широко используют в электродвигателя, генераторах. На ней основано функционирование электронных приборов, оказывающих воздействие на заряженные частицы – ионы, электроны. Среди таких устройств можно выделить телевизионные электронно-лучевые трубки, масс- спектрометры, МГД-генераторы.

Практическое применение сила Лоренца находит в рельсотронах, циклотронах, фильтрах скорости, магнетронах. Она задает орбиту движения заряженных частиц в специальных ускорителях.

Рисунок 9. Модель движения заряженных частиц в магнитном поле.Рисунок 10. Модель масс-спектрометра.Рисунок 11. Модель селектора скоростей.

Сила лоренца правило формула. 5 Сила Лоренца. Формула Лоренца. Движение заряженных частиц в электрическом и магнитных полях.

ГлавнаяРазноеСила лоренца правило формула

5 Сила Лоренца. Формула Лоренца. Движение заряженных частиц в электрическом и магнитных полях.

Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой

(114.1)

где В — индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q > 0 направления I и v совпадают, для Q < 0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца (см. (114.1)) равен

где  — угол между v и В.

Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F = Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия QvB = mv2/r, откуда

(115. 1)

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

Подставив сюда выражение (115.1), получим

(115.2)

т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v ≪ c). На этом основано действие циклических ускорителей заряженных частиц (см. § 116).

Если скорость v заряженной частицы направлена под углом  к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v1 = vcos; 2) равномерного движения со скоростью v = vsin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v = vsin). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. {-19} Кл. \]

При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.

Сила Лоренца действующая на электрон и протон

Величина и направление силы Лоренца определяются соотношением

\[ \vect{F_{L}}= e \vect{v} × \vect{B} \]

где $\vect{v}$, $\vect{B}$ и $\vect{F}$ образуют правую систему.

Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:

\[ F_{L} = evB \]

Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.

Вычислить, найти силу Лоренца действующую на электрон или протон

Радиус траектории электрона в магнитном поле

Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу. {-19} Кл. \]

При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.

Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.

Сила Лоренца действующая на протон

Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.

Радиус траектории протона в магнитном поле

Если

rmppvB

радиус круговой траектории протона,	метр
1,67 · 10-27 кг — масса протона,	кг
1,602 · 10-19 Кл — элементарный электрический заряд,	Кулон
скорость протона,	м/с
магнитная индукция,	Тесла

Радиус траектории для протона будет вычисляться по аналогичной формуле

\[ r = \frac{m_{p} · v}{pB} \]

Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц

В помощь студенту

Сила Лоренца

стр. 665

www.fxyz.ru

Сила Лоренца

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:

I = qnvS ( 2 )

Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:

F = | I |B Δl sin α

Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:

F = | q | nvS Δl B sin α = v | q | NB sin α, где N = nSΔl — число заряженных частиц в рассматриваемом объеме.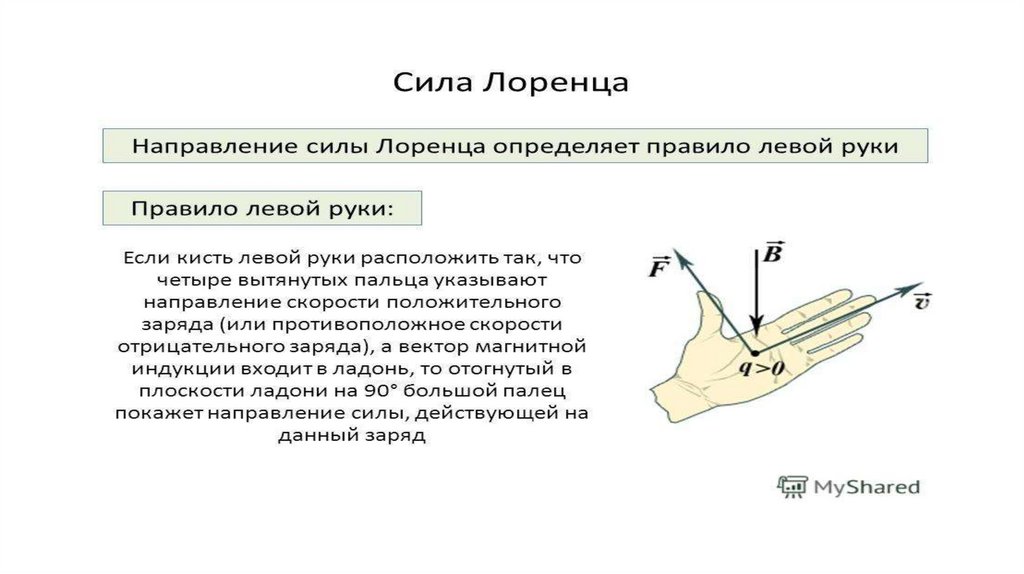 Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная: где α — угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

Другие заметки по физике

edu.glavsprav.ru

Сила Лоренца — fizikatyt

Сила Лоренца — сочетание электрического и магнитного взаимодействия, которое возникает, когда положительно или отрицательно заряженная частица движется в электромагнитном поле. Она перпендикулярна направлениям векторов магнитной индукции и скорости заряда. Под её действием частица изменяет траекторию своего движения и скорость.

Этот вид сил впервые описал Джеймс Максвелл в 1865 году, а в 1892 году голландский физик Хендрик Лоренц записал для неё математическое выражение. Хотя первый вывод формулы исследователи приписывают Оливеру Хевисайду.

Вариация этой базовой силы действует на проводник с током, когда его помещают между полюсами магнита. Если в проводнике существует ток, то он будет отклоняться во внешнем магнитном поле, так как сила Лоренца будет действовать на все движущиеся в нём электроны. В какую сторону отклонится провод с током наглядно продемонстрирует правило левой руки.

Это явление и возникающую силу используют в экспериментальной физике для:

• увеличения скорости элементарных частиц и ионов в различных циклотронах и других ускорителях;
• определения удельного заряда и массы положительных ионов, относительной атомной массы изотопов химических элементов в масс-спектрографии;
• в магнетронах и скоростных фильтрах.

В быту такое воздействие на заряженную частицу нашло применение в телевизорах с электронно-лучевой трубкой, электродвигателях, колонках, генераторах.

Какова природа силы?

Эта сила принадлежит спектру сил электромагнитного взаимодействия. Магнитное поле создают заряженные частицы, такие как протон или электрон, во время своего движения. Движущийся заряд поместим во внешнее поле, например, между полюсами магнита. Поле точечного заряда и внешнее поле будут взаимодействовать определённым образом: притягиваться или отталкиваться. Это зависит от знака заряда и от взаимного расположения линий магнитной индукции полей.

Формула для вычисления модуля силы Лоренца демонстрирует её зависимость от скорости частицы v, абсолютного значения её заряда q, от модуля индукции внешнего магнитного поля B и угла α, показывающего взаимное расположение векторов скорости и магнитной индукции.

На рисунке представлены все величины, фигурирующие в формуле:

Из уравнения видно, что если v (скорость) стремится к нулю, то на точечный заряд не будет действовать и сила Лоренца. Кроме того, если заряд перемещается в направлении, параллельном направлению вектора магнитной индукции, то есть sin (0) = 0, снова будем наблюдать отсутствие внешней силы (Fл=0). А при движении, перпендикулярном линиям внешнего магнитного поля, сила Лоренца становится центростремительной и искривляет траекторию объекта (наблюдается движение по окружности). Протон представлен на рисунке а), рисунок б) описывает электрон.

Правило левой руки

Для положительно заряженной частицы необходимо расположить ладонь левой руки, чтобы четыре вытянутых пальца направить параллельно её движению, а линии магнитной индукции входили в ладонь перпендикулярно, то отогнутый на 90° большой палец покажет направление силы Лоренца. А для отрицательного заряда силу Лоренца направляем в противоположную сторону.

fizikatyt.ru

46.7 Сила Лоренца. | FizPortal

46.7 Сила Лоренца.

 Магнитное поле действует с некоторой силой на каждую движущуюся заряженную частицу, эта сила называется силой Лоренца (названной в честь голландского физика Генриха Антона Лоренца). Можно считать, что рассмотренная выше сила Ампера является суммой сил Лоренца, действующих на каждую заряженную частицу, направленное движение которых и образует электрический ток. Для того чтобы получить формулу для этой силы представим выражение для элемента тока в виде (рис. 423)

рис. 423 здесь S − площадь поперечного проводника, j = nqv − вектор плотности тока1, q − электрический заряд движущихся частиц, v − их скорость, n − число частиц в единице объема (концентрация заряженных частиц). Подставим это выражение в формулу для силы Ампера и заметим, что величина nSΔl = N равна общему числу заряженных частиц в выделенном участке проводника. Поэтому сила, действующая на одну частицу (сила Лоренца) равна  Модуль силы Лоренца рассчитывается по формуле где α − угол между векторами скорости частицы и индукции магнитного поля (рис. 424).рис. 424  Сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости частицы v и индукции магнитного поля B. Направление этой силы можно определить по правилу левой руки, аналогичному правилу для определения направления силы Ампера. Также можно говорить, что на заряженную частицу, действует сила со стороны компоненты поля B⊥, перпендикулярной вектору скорости. Частица, движущаяся параллельно вектору индукции (то есть вдоль силовой линии магнитного поля), действия силы Лоренца не испытывает.  В некоторых учебниках, особенно по теоретической физике, сначала дается формула для силы Лоренца как следствие определения вектора магнитной индукции и обобщения экспериментальных данных, а затем на ее основе выводится выражение для силы Ампера. То, что мы поступили наоборот, несущественно, так обе эти силы имеют одинаковую природу − действие магнитного поля на движущийся заряд. 1Напомним, что за направление силы тока принято направление движения положительно заряженных частиц, поэтому излагаемые здесь правила для определения направления силы Лоренца справедливы для положительных зарядов. Для отрицательно заряженных частиц направление силы Лоренца противоположное.

fizportal.ru

Сила Лоренца | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Тема:

Электромагнетизм

Силой Лоренца F̅Л называют силу, дейст­вующую на электрически заряженную час­тицу, которая движется, испытывая действия электрического и магнитного полей одно­временно.

Это выражается формулой

F̅Л = F̅Э + F̅М.

где F̅Э, — электрическая составная силы Ло­ренца, описывающая взаимодействие частицы с электрическим полем; F̅М — магнитная составная силы Лоренца, которая описывает взаимодействие частицы с магнитным по­лем.

Рис. 6.21. Графическое изображение на­правления силы Лоренца

Сила Лоренца направлена всегда под уг­лом к скорости частицы, поэтому она при­дает ей центростремительное ускорение (рис. 6.21).

Для случая, когда α = 90°,

qvB = mv2 / R.

Отсюда

R = mv / qB.

Рис. 6.22. Магнитное поле смещает элект­ронный луч

Таким об­разом, заря­жен­ная час­тица, по­падая в магнитное поле, начинает двигаться по дуге окружности. Материал с сайта http://worldofschool.ru

При иных значениях 0 < α < 90° траекто­рия движения заряженной частицы в маг­нитном поле приобретает форму спирали.

Наблюдать действие силы Лоренца мож­но с помощью электронно-лучевой трубки (рис. 6.22). Если включить питание осцилло­графа, то на экране его электронно-лучевой трубки будем наблюдать светлое пят­но — место падения на экран движущихся электронов. Если поднести к трубке осцил­лографа магнит, то пятно сместится, что свидетельствует о действии магнитного поля на движущиеся электроны.

На этой странице материал по темам:

• Доклад по физике применение силы лоренца

• Лекция по физике сила лоренца

• Доклад на тему сила лоренца

• Физический смысл величин входящих в формулу полной силы лоренца?

• Реферат на тему сила ампера

Вопросы по этому материалу:

worldofschool. ru

---

• Туристические фонарики
• Освещение подъезда в многоквартирном доме
• Как соединить несколько розеток подряд
• Декоративные освещения
• Схема 380 в 220
• Что такое электрочайник
• Кухни с подсветкой
• Резонанса напряжений условие
• Какой фирмы пылесос выбрать для дома
• Как сделать терморегулятор
• Какое реле напряжения лучше по качеству

Калькулятор силы Лоренца | Как рассчитать силу Лоренца?

Используя данные о заряде частиц, магнитном поле и скорости частиц, Калькулятор силы Лоренца может помочь вам найти силу Лоренца. Этот превосходный инструмент значительно упростит вычисления уравнения силы Лоренца.

Дано

Найти силу|Дано B,q,VНайти магнитное поле|Дано F,q,VНайти заряд|Дано F,B,VНайти скорость|Дано F,q,V

Магнитное поле B

TeslamTeslaμTesla

Заряд q

ПикоКулонынаноКулоныМикроКулоныМиллиКулоныКулоныАмперчасымиллиамперчасыЭлементарный заряд

Скорость V

метр/секунда-километр/час-фут/с-миль/час-узел-фут/мин

Калькулятор силы Лоренца: Вы пытаетесь узнать, как магнитное поле влияет на заряженные частицы? Используйте наш простой Калькулятор силы Лоренца, чтобы получить силу Лоренца.

Продолжайте читать, чтобы узнать больше о силе Лоренца, ее формуле и ее применении в нашей повседневной жизни. Изучая силу Лоренца и науку, стоящую за ней, вы лучше поймете ее значение.

Сила Лоренца определяется как результат воздействия электромагнитных полей на точечный заряд электрическими и магнитными силами. Он утверждает, что на движущуюся заряженную частицу действует магнитное поле.

Сила Лоренца, с другой стороны, зависит от силы магнитного поля, заряда и скорости. Направление силы в этом случае не совпадает ни с направлением движения частицы, ни с направлением магнитного поля. И направление частицы, и магнитное поле перпендикулярны силе Лоренца.

Сила Лоренца Формула выражается как F = q v B sin(α)

• Где, F = результирующая сила
• v = скорость частицы
• B = напряженность магнитного поля
• α = угол между направлением траектории частицы и направлением магнитного поля
• q = заряд частицы

Чтобы рассчитать силу Лоренца, следуйте простым инструкциям здесь.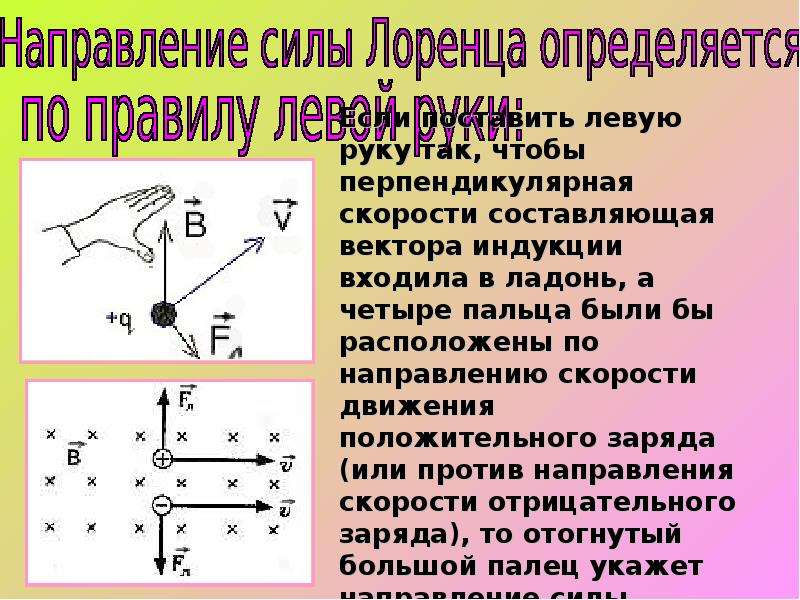

Они на одном пути.

• Сначала определите заряд частицы, скорость частицы, напряженность магнитного поля и угол.
• Замените все эти входные данные в формуле силы Лоренца, F = q v B sin(α )
• Если упростить уравнение, то легко найти силу Лоренца.

Ниже приведена процедура использования калькулятора силы Лоренца.

Чтобы получить результат, нажмите кнопку Рассчитать ‘x’.

Наконец, в поле вывода будет показано значение x.

Для получения дополнительных концепций посетите веб-сайт physicscalculatorpro.com, чтобы получить быстрые ответы с помощью этого бесплатного инструмента.

Сила Лоренца имеет широкий спектр применения. Он используется в науке для ускорения частиц в циклотронах при поиске фундаментальных законов физики элементарных частиц. Его также можно найти в масс-спектрометрах, которые могут идентифицировать атомы и молекулы. Электродвигатели, громкоговорители и, возможно, реже рельсотроны — все это практические повседневные приложения.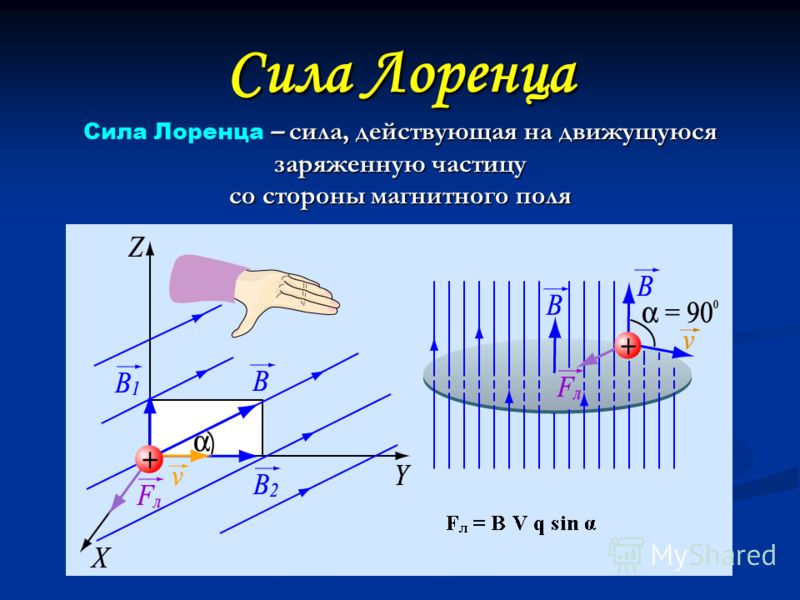

• Мгновенные вычисления
• Копируемые результаты в другие приложения
• Формула включена в качестве руководства.
• Поддерживается до 16 знаков после запятой.
• Обеспечьте поддержку различных единиц измерения для каждого входа.

1. Как вычисляется сила Лоренца?

Сила Лоренца — это сила, действующая на заряженную частицу q, движущуюся между электрическим полем E и магнитным полем B со скоростью v. Сила Лоренца (названная в честь голландского ученого Хендрика А. Лоренца) определяется как F = qE + qv B для всей электромагнитной силы F, действующей на заряженную частицу.

---

2. Является ли сила Лоренца инвариантной?

Поскольку сила является вектором, а не скаляром, она не может быть лоренц-инвариантной.

---

3. Где действует сила Лоренца?

Во многих технологиях, таких как циклотроны и другие ускорители частиц с круговым маршрутом, используется сила Лоренца.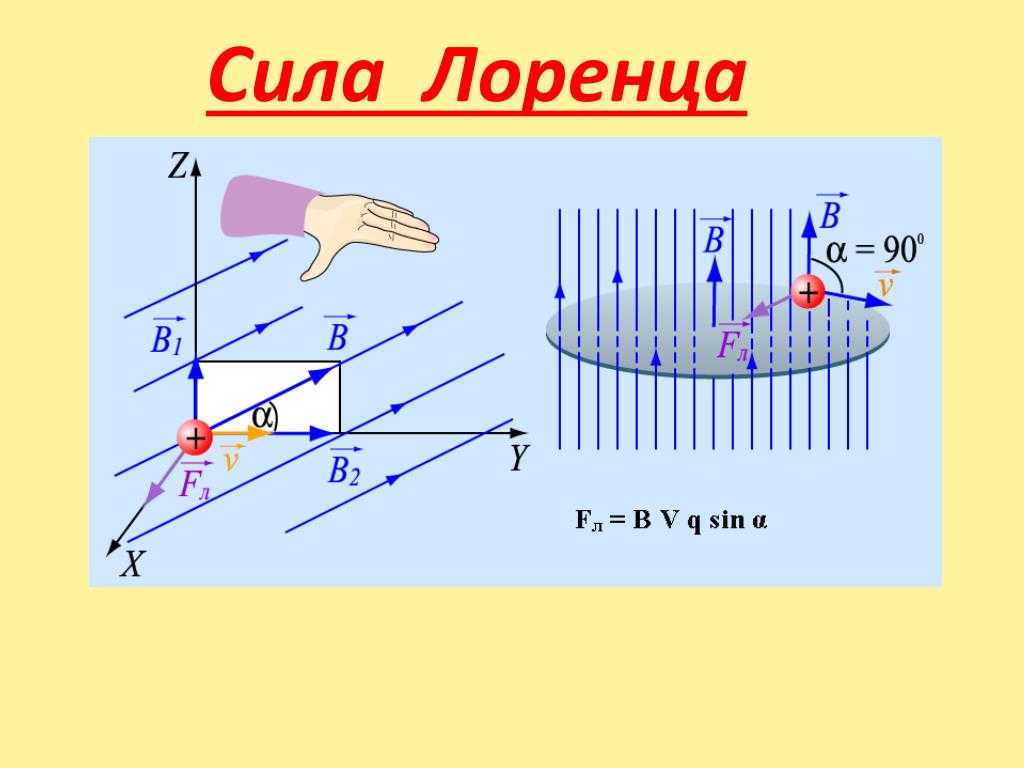 Масс-спектрометры представляют собой разновидность масс-спектрометров. Velocity Filters — это разновидность скоростных фильтров.

---

4. Что такое Лоренц-инвариантные величины?

Разные инерциальные наблюдатели получают разные значения E и p для энергии и импульса, но формула дает одно и то же значение для энергии покоя частицы. В результате энергия покоя частицы m0c2 является лоренц-инвариантной величиной.

---

5. Инвариантны ли уравнения Максвелла Лоренца?

Другими словами, ее основные правила, суммированные четырьмя уравнениями Максвелла и законом силы Лоренца, являются формоинвариантными относительно преобразований Лоренца, т. е. при переходе от одной инерциальной системы отсчета к другой.

---

404 — СТРАНИЦА НЕ НАЙДЕНА

Почему я вижу эту страницу?

404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.

Другие возможные причины

Вы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.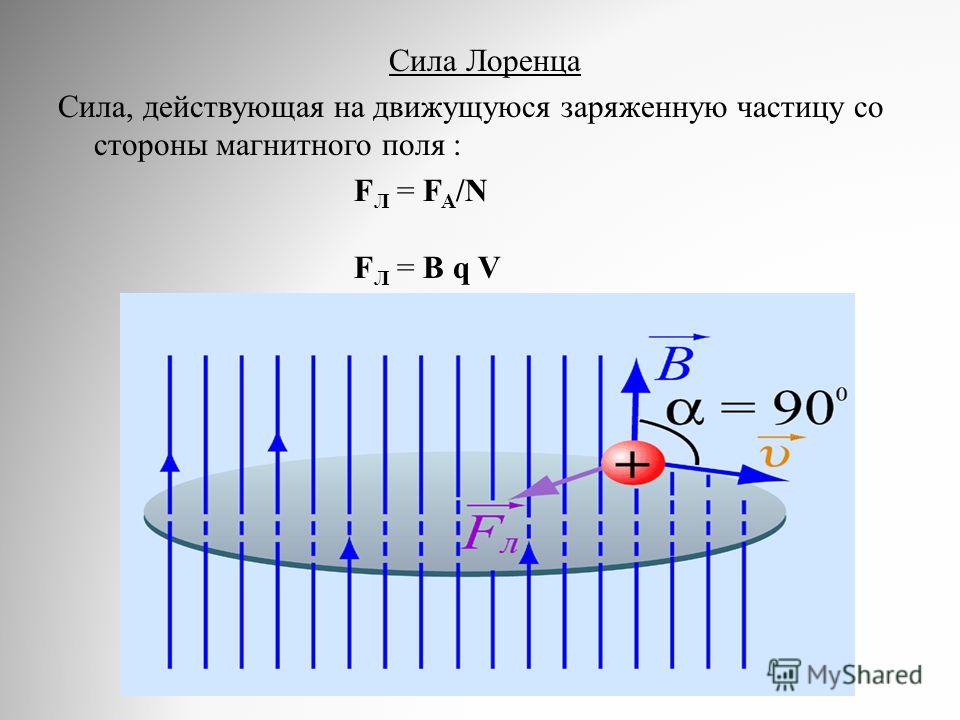

Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.

Также возможно, что вы непреднамеренно удалили корневую папку документа или ваша учетная запись должна быть создана заново. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.

Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.

Как найти правильное написание и папку

Отсутствующие или поврежденные файлы

Когда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.

http://example.com/example/Example/help.html

В этом примере файл должен находиться в папке public_html/example/Example/

Обратите внимание, что CaSe важен в этом примере.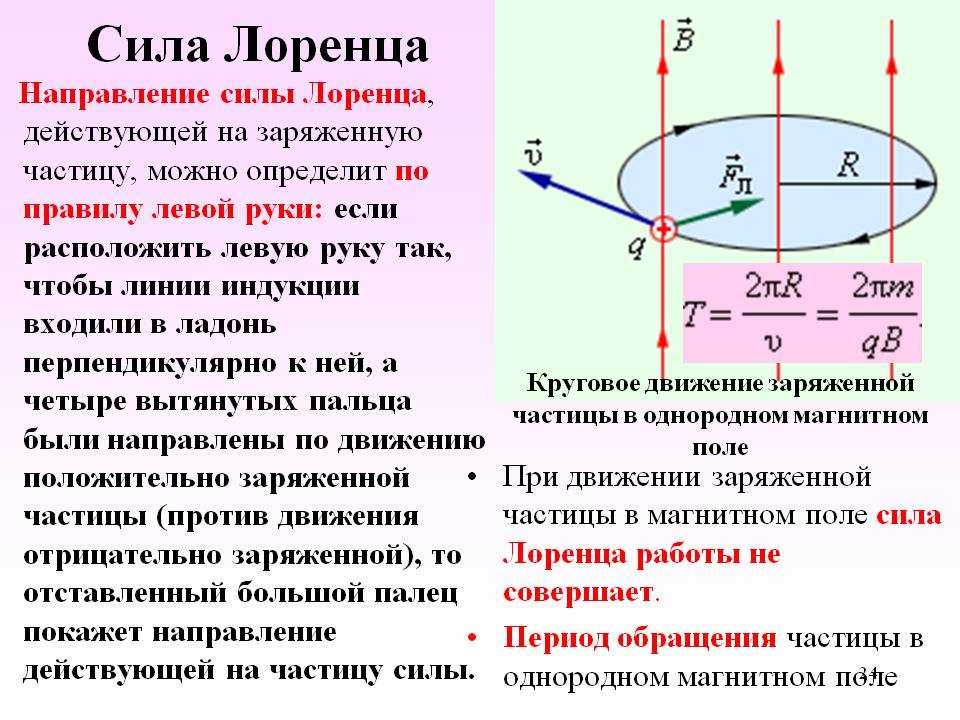 На платформах с учетом регистра e xample и E xample не совпадают.

Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.

Разбитое изображение

Если на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным цветом X , где отсутствует изображение. Щелкните правой кнопкой мыши на X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.

Это зависит от браузера, если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотр информации о странице» и перейдите на вкладку «Мультимедиа».

http://example.com/cgi-sys/images/banner.PNG

В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/

Обратите внимание, что в этом примере важен CaSe .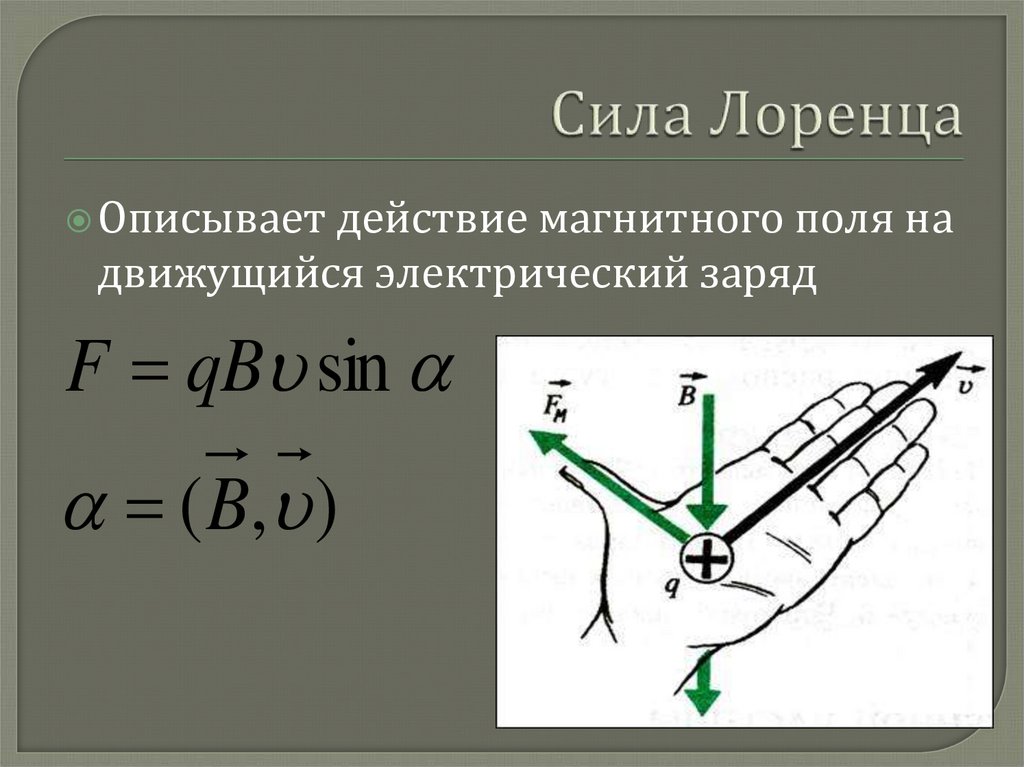 На платформах с учетом регистра PNG и png не совпадают.

Ошибки 404 после перехода по ссылкам WordPress

При работе с WordPress ошибки 404 Page Not Found часто могут возникать при активации новой темы или изменении правил перезаписи в файле .htaccess.

Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.

Вариант 1. Исправьте постоянные ссылки

1. Войдите в WordPress.
2. В меню навигации слева в WordPress нажмите  Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
3. Выберите  По умолчанию .
4. Нажмите  Сохранить настройки .
5. Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
6. Нажмите  Сохранить настройки .

Во многих случаях это сбросит постоянные ссылки и устранит проблему. Если это не сработает, вам может потребоваться отредактировать файл .htaccess напрямую.

Вариант 2. Измените файл .htaccess

Добавьте следующий фрагмент кода 9index.php$ — [L]
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]

# Конец WordPress

Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.

Как изменить файл .htaccess

Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.

Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .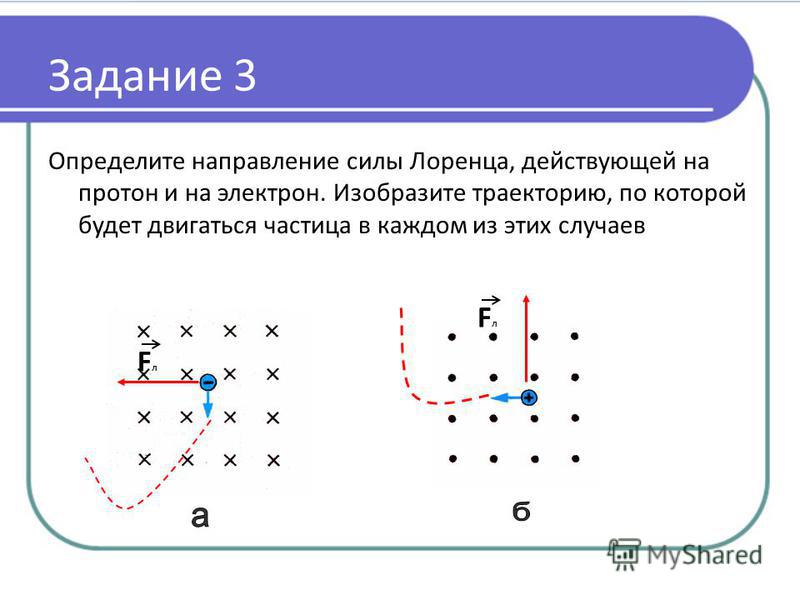 htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.

Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассказывается, как редактировать файл в cPanel, но не о том, что нужно изменить. статьи и ресурсы для этой информации.)

Существует множество способов редактирования файла .htaccess

• Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
• Использовать режим редактирования программы FTP
• Использовать SSH и текстовый редактор
• Используйте файловый менеджер в cPanel

Самый простой способ отредактировать файл .htaccess для большинства людей — через диспетчер файлов в cPanel.

Как редактировать файлы .htaccess в файловом менеджере cPanel

Прежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.

Откройте файловый менеджер

1. Войдите в cPanel.
2. В разделе «Файлы» щелкните значок «Диспетчер файлов ».
3. Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
4. Убедитесь, что установлен флажок Показать скрытые файлы (точечные файлы) «.
5. Нажмите  Перейти . Файловый менеджер откроется в новой вкладке или окне.
6. Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.

Чтобы отредактировать файл .htaccess

1. Щелкните правой кнопкой мыши файл .htaccess и выберите  Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
2. Может появиться диалоговое окно с вопросом о кодировании.