Моделирование в электроэнергетике — Описание электроэнергетического режима через изменение мгновенных значений электрических параметров.

Режим работы электроэнергетической системы в любой момент времени характеризуется изменяющимися мгновенными значениями тока и напряжения. Изменение данных параметров происходит с течением времени по закону, который можно записать следующим математическим выражением:

 – амплитудные значения тока и напряжения;

 – начальная фаза тока;

 – начальная фаза напряжения;

– круговая частота (угловая частоты).

Как видно из представленных соотношений изменение тока и напряжения осуществляется с течением времени по синусоидальному закону (см. рис. 1). Основными величинами, которые определяют синусоидальный сигнал, являются: амплитуда, угловая частота и начальная фаза.

Рис.1. Изменение тока и напряжения с течением времени при произвольном выборе начало отсчета

Для описания характеристики интенсивности (силы действия) электрических параметров используется такое понятие, как действующее значение. Под действующим значением переменного тока понимают такое значение, при котором за время одного периода в проводнике выделяется столько же теплоты, сколько при постоянном токе. Математически данное утверждение записывается в следующем виде:

где I – постоянный ток;

i(t) – мгновенное значение переменного тока;

T – период изменения переменного тока.

В результате получаем, что действующее значение переменного тока определяется как среднеквадратичное значение переменного тока за период.

Аналогичным образом определяется действующее значение переменного напряжения:

В зарубежной литературе для обозначения действующего значения сигнала, используется аббревиатура RMS (root mean square). Однако измерительные приборы, которые промаркированы аббревиатурой RMS, не всегда измеряют действующие значения сигнала по вышеописанному методу. В большинстве измерительных приборов старого образца применяется способ измерения действующих значений тока (или напряжения) основанный на измерении среднего выпрямленного значения за полупериод. Затем полученное среднее значение ставилось в соответствие действующему значению (градуировка прибора), так как действующее значение синусоидального сигнала может быть определено через среднее значение умноженное на коэффициент «1,1». Данный способ определения действующего значения был связан с тем, что принцип работы большинства аналоговых приборов (стрелочных приборов) основан на измерении какого-то действия за определенный промежуток времени, т.е. определение среднего значения сигнала. В результате, измерительные приборы с меткой RMS могут отображать правильный результат только при синусоидальном сигнале.

Рис.2. Результат измерений действующих сигналов в зависимости от разной формы кривой

В современных устройствах (в микропроцессорной технике) применяются алгоритмы, которые определяют действующее значение тока за период в соответствии с вышеописанным методом. В результате полученные устройства показывают правильные результаты при любом негармоническом сигнале с некоторыми ограничениями по форме и частоте входного сигнала. Данные устройства в зарубежной литературе получили аббревиатуру TRMS (True Root Mean Squared – истинное среднеквадратичное значение).

Средним значением синусоидального тока (или напряжения) называется среднее арифметическое всех его значений за полупериод. Математически данное утверждение записывается в следующем виде:

Следует отметить, что среднее значение синусоидального тока (или напряжения) за период равно нулю, так как на протяжении первого полупериода ток имеет одно направление, а на протяжении второго полупериода – обратное.

Однако в случае выпрямления переменного тока, постоянный ток имеет одинаковое направление, и величина выпрямленного тока определяется среднеарифметическим всех мгновенных значений. Математически данное утверждение записывается в следующем виде:

 

Полная мощность в сети переменного тока

Величиной, которая определяет фактические электрические нагрузки на провода линий электропередачи или кабельные линии, обмотки силовых трансформаторов, аппаратуру распределительных устройств, является полная мощность электрической сети. Полная мощность – величина,  равная произведению действующих значений периодического электрического тока в цепи и напряжения на ее зажимах. Полная мощность трехфазной сети переменного тока определяется следующим образом:

где – действующее значение фазного напряжения;

– действующее значение линейного напряжения;

– действующее значение фазного тока.

Полная мощность состоит из двух составляющих – активной и реактивной мощности. Данные переменные связаны между собой  следующим образом:

– активная мощность;

– реактивная мощность.

Активная мощность в сети переменного тока

Протекание синусоидальных токов по участкам электрической цепи сопровождается потреблением энергии. Так как ток и напряжение постоянно меняют своё значение, то потребляемая мощность будет меняться в каждый момент времени. Данная мощность называется мгновенной мощностью , которая определяется произведением мгновенного значения напряжения на мгновенное значение тока в этой цепи.

Рис.3. Изменение мгновенной мощности с течением времени.

Мгновенная мощность на графике обозначена заштрихованной областью. Из представленного графика видно, что мгновенная мощность имеет постоянную составляющую и гармоничную составляющую, частота которой в два раза больше частоты напряжения и тока.

Следует отметить, что мгновенная мощность в случае активно-индуктивной или активно-емкостной нагрузки может менять свой знак, который зависит от сдвига фаз между током и напряжением. Когда мгновенная мощность отрицательна, то энергия возвращается из двухполюсника к источнику питания. Такой возврат энергии к источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника.

Чтобы понять какое количество энергии потребляется в сети переменного тока, необходимо взять среднюю мощность за период. Таким образом, среднее арифметическое значение мгновенной мощности за период называется активной мощностью. Формула для определения активной мощности записывается следующим образом:

 Введем понятия об угле сдвига между током и напряжением , который определяется разностью начальной фазы напряжения и начальной фазой тока. Формула для определения угла сдвига между током и напряжением записывается следующим образом:

Из представленной формулы видно, что сдвиг фаз между током и напряжением может быть как положительным, так и отрицательным:

— Положительный сдвиг фаз между током и напряжением  указывает на то, что напряжение по фазе опережает ток (нагрузка активно-индуктивная).

— Отрицательный сдвиг фаз между током и напряжением  указывает на то, что напряжение по фазе отстает от тока (нагрузка активно-емкостная).

Таким образом, формула для  активной мощности в одной фазе может быть записана в следующем виде:

Для трехфазной сети переменного тока значение активной мощности будет определяться по следующему выражению:

Реактивная мощность в сети переменного тока

Реактивная мощность периодически циркулирует между источником и приемником, так как в процессе каждого периода реактивные элементы (емкость и индуктивность) накапливают энергию, а затем возвращают ее источнику.  Реактивная мощность не может преобразоваться в тепловую или механическую энергию, таким образом, данная энергия не выполняет никакой работы. Реактивная мощность определяет небаланс между полной и активной мощностями. Таким образом, формула для определения реактивной мощности в одной фазе может быть записана в следующем виде:

Для трехфазной сети переменного тока значение реактивной мощности будет определяться по следующему выражению:

Следует отметить, что угол сдвига фаз между током и напряжением может быть как положительным, так и отрицательным:

— Положительный сдвиг фаз между током и напряжением  указывает на то, что напряжение по фазе опережает ток — нагрузка активно-индуктивная. В таком режиме работы сети реактивная мощность будет положительна 

— Отрицательный сдвиг фаз между током и напряжением  указывает на то, что напряжение по фазе отстает от тока (нагрузка активно-емкостная). В таком режиме работы сети реактивная мощность будет отрицательна

         В качестве примера, рассмотрим один из способов измерения реактивной мощности в сети переменного тока с помощью одного ваттметра, который подключается специальным образом. Следует обратить внимание на то, что данный метод измерения является фиктивным, так как ваттметр осуществляет измерение только активной мощности в сети. В связи со специфичным подключением ваттметра измеренное значение активной мощности будет пропорциональна величине реактивной мощности в сети переменного тока.

         В соответствии с данным методом ваттметр подключается по цепям тока — в рассечку любой фазы (например, фаза А), а по цепям напряжения — к линейному напряжению оставшихся фаз (например, к линейному напряжению В-С). Схема соединения ваттметра в сети переменного тока показана на схеме (см. рис.4).

Рис.4. Схема включения ваттметра для измерения мощности в симметричной трехфазной сети, которая по величине пропорциональна значению реактивной мощности, и векторная диаграмма

         Вектор линейного напряжения будет определяться разностью фазных напряжений:

         В результате к ваттметру подводится ток в фазе «А» и линейное напряжение, которое отстает от тока на угол:

Подключенный таким образом ваттметр будет измерять следующее значение активной мощности:

         Полная реактивная мощность в сети переменного тока будет определяться следующим соотношением:

         Таким образом, данный метод позволяет определить величину реактивной мощности в сети переменного тока, которая пропорциональна величине активной мощности, измеряемой ваттметром. Данным методом можно пользоваться только в симметричной трехфазной сети. Следует отметить, что данная схема используется редко, так как в случае незначительной асимметрии фаз применение данного метода дает значительную погрешность.

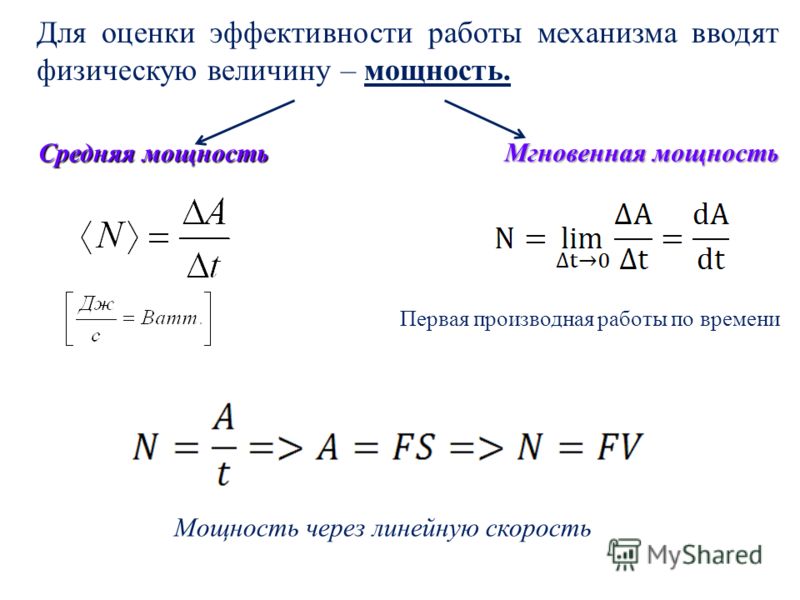
Мощность | Работа и энергия

Итак, есть два пауэрлифтера: Б-кий и М-кий. Под присмотром своего тренера они работают с одинаковыми штангами, вес которых составляет 90 кг.

Из рисунка видно, что они поднимают свои снаряды на одну и ту же высоту (2 метра). Но есть небольшое различие между спортсменами: Б-кий поднимает штангу очень быстро, в течение одной секунды, в то время как М-кий перемещает свой гриф на то же самое расстояние за три секунды.

В прошлых статьях мы весьма подробно говорили о работе. Конечно, ее можно определить как скалярное произведение вектора силы и вектора перемещения, но сейчас лучше рассматривать работу как количество энергии, которое один объект передает или, наоборот, отнимает у другого.

Какую работу в нашем случае совершает каждый атлет, перемещая свой груз? Поднимая штангу и сообщая ей тем самым потенциальную энергию, каждый спортсмен совершает работу против силы тяжести:

A=mgh=90\thickspaceкг×9. 2×2\thickspaceм=1764\thickspaceДж

Работа у пауэрлифтеров будет одинаковой. Они поднимают один и тот же груз на одну и ту же высоту. Но, как я уже сказал, они делают свою работу по-разному: один быстрее, другой медленнее.

Чтобы охарактеризовать подобные различия, вводят специальную физическую величину, которая называется мощностью. Мощность – это скалярная величина, показывающая, как быстро совершается та или иная работа. Обычно ее обозначают буквой P. Измеряется она в ваттах (Вт). Мы найдем мощность, если разделим сделанную работу на время, в течение которого она была сделана:

P=\dfrac{A}{t}

Б-кий совершает работу в 1764 джоулей за одну секунду. Значит, его мощность равна:

P=\dfrac{A}{t}=\dfrac{1764\thickspaceДж}{1\thickspaceс}=1764\thickspaceВт

М-кий совершает ту же самую работу за три секунды:

P=\dfrac{A}{t}=\dfrac{1764\thickspaceДж}{3\thickspaceс}=588\thickspaceВт

Теперь рассмотрим другой пример.

Автомобиль массой 1500 килограмм разогнался за 4 секунды из состояния покоя до 30 м/с. 2}{2×4\thickspaceс}=168750\thickspaceВт\approx169\thickspaceкВт

Та мощность, которую мы сейчас нашли, – это средняя мощность. Можно обозначить ее так: P_{ср}. Средняя мощность равна отношению работы тела к промежутку времени, за который эта работа была совершена:

P_{ср}=\dfrac{A}{t}

При этом мощность двигателя могла меняться. Поэтому существует еще и мгновенная мощность – это уже мощность в определенный момент времени. Обозначим ее вот так: P(t).

Теперь поговорим о том, как мы можем найти величину мгновенной мощности.

Во-первых, если мощность двигателя постоянна, мгновенная мощность совпадает по величине со средней мощностью:

P(t)=P_{ср}

Есть еще один способ. Обратимся к уравнению для расчета мощности и заменим механическую работу ее определением:

P(t)=\dfrac{A}{t}=\dfrac{Fs\cos\alpha}{t}

Формула для расчета скорости содержится в этом выражении:

P(t)=F×\dfrac{s}{t}×\cos\alpha=Fv\cos\alpha

Если нам известна величина скорости тела в определенный момент времени, мы можем узнать его мгновенную мощность, используя эту формулу. Стоит отметить, что в этом уравнении под углом \alpha подразумевается угол между вектором скорости и вектором силы, приложенной к телу.

ньютоновская механика — Как найти мгновенную мощность?

спросил 5 лет, 5 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 7к раз

$\begingroup$

Мне интересно, есть ли способ найти мгновенную мощность, когда вам не дано уравнение, связывающее работу со временем, а только численные значения таких величин, как сила, масса тела, ускорение и время, при которых вы хотите найти мощность. 92}{2млн.$$ Если конкретное взаимодействие не задано, потенциальной энергии нет, следовательно, полная энергия — это просто кинетическая энергия. Если внешний агент изменяет эту энергию, то мощность этого внешнего агента равна $$P=\frac{dE}{dt}=\frac{p}{m}\frac{dp}{dt}$$ Если мы теперь используйте второй закон Ньютона $F=\frac{dp}{dt}$ мы получаем $$P=\frac{p}{m}F$$

В вопросе OP говорится, что числовое значение силы дано, следовательно Я предполагаю, что сила постоянна.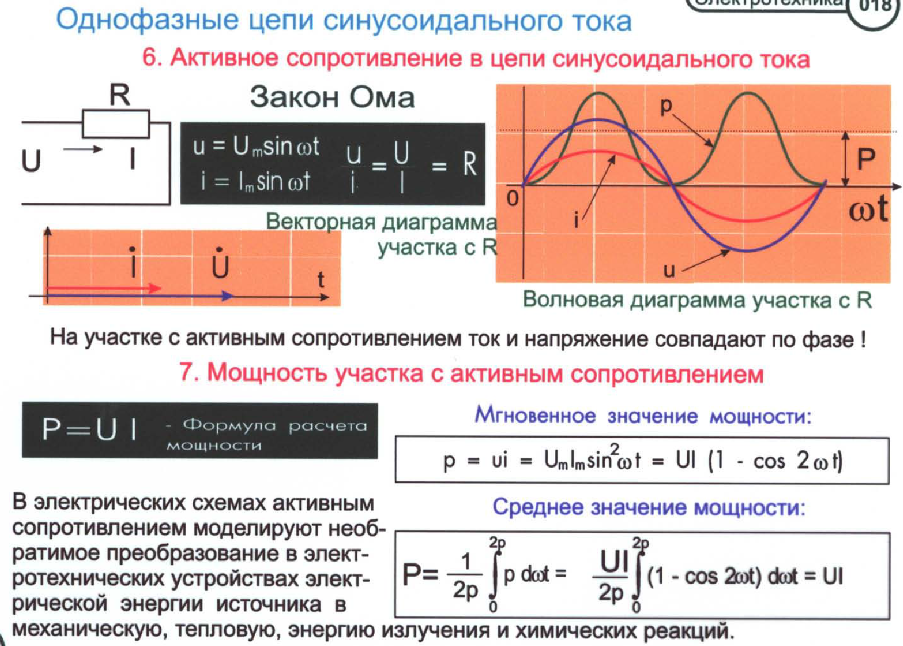 2}{m}t$$

$\endgroup$

0

$\begingroup$

Сила определяется как $P=\vec{F}\cdot\vec{v}$, так что это может быть вам полезно, если у вас есть скорость вашего тела в какой-то момент времени.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Средняя мощность и мгновенная мощность

спросил 7 лет, 5 месяцев назад

Изменено 2 года, 1 месяц назад

Просмотрено 21к раз

$\begingroup$

Меня смущает использование терминов «средняя мощность» и «мгновенная мощность». В чем основное различие между ними?

$\endgroup$

4

$\begingroup$

Объем работы, выполненной за «период времени»

$\Rightarrow $ Средняя мощность $= \frac{\Delta W}{\Delta t}$

например, работа $W_1=3 \, \mathrm{ J} $ в момент времени $t_1= 2\ , \mathrm{ сек.

}$ и $W_2=7 \, \mathrm{ J} $ в момент времени $t_2= 13\, \mathrm{ сек.}$

$\Rightarrow $ продолжительность $\Delta t = t_2-t_1=13-2\, (\mathrm{ сек.}) $

$\Rightarrow $ объем работы $\Delta W = W_2-W_1=7-3\, (\mathrm{ J}) $

$\Rightarrow $ Средняя мощность $\frac{\Delta W}{\Delta t}=\frac{7-3}{13-2}=\frac{4}{11}\, (\mathrm {Дж/с}) $

Если интервал времени $\Delta t \to 0 \Rightarrow \Delta t=dt, \Delta W=dW$

(Означает, что Мощность в какой-то момент. )

$\Rightarrow $ Мгновенная Мощность $ = \frac{d W}{d t}$

$\endgroup$

$\begingroup$

«Мгновенная мощность». или «IPP». Это будет количество энергии, подаваемой или требуемой в течение ОЧЕНЬ короткого промежутка времени… но НЕ в течение какого-либо «длительного периода», например, необходимого пусковому двигателю… для проворачивания автомобильного двигателя. Это «IPP» уровень может быть ОЧЕНЬ высоким. . целых 250-400 AMPS.. или около 4 киловатт.. но ТОЛЬКО на 2-3 секунды и меньше на прогретом двигателе. ЗАТЕМ… двигатель запускается… и мощность, требуемая пусковым двигателем, падает до НУЛЯ… Итак… в «ваттах», измеренных в «ватт-часах», ИСТИННАЯ потребляемая мощность может составлять 2 Вт или МЕНЬШЕ… так как для производства 1 часа требуется 3600 секунд.Так что..если вам нужно 300 ампер, но только в течение 3 СЕКУНД..тогда ничего..ОБЩЕЕ использование «ватт-часов» будет всего несколько ватт/часов.

«Средняя мощность», с другой стороны… это мощность, используемая в течение определенного периода ВРЕМЕНИ, например, час или более. Возьмем кондиционер, скажем, 10 тыс. БТЕ или около того. Если он постоянно работает на высокой скорости в течение часа и потребляет «1100 Вт», то ОБЩАЯ потребляемая мощность составит 1,1 кВт/час. Мощность в значительной степени постоянна … в течение всего периода времени в один час … по сравнению с запуском двигателя … где мощность, необходимая в течение нескольких секунд, огромна, но затем падает до нуля за несколько секунд.