Контрольные вопросы

1. Объяснить характер движения грузов. В каких пределах измеряется натяжение нити?

2. Каков смысл коэффициента трения скольжения?

3. Выведите формулы для определения коэффициента трения скольжения динамическим и энергетическим методами.

4. Какова причина сил сухого трения?

5. К какому виду взаимодействия относится сила трения? В чем особенность неконсервативных сил?

Принадлежности: установка для определения коэффициента силы трения скольжения, прямоугольный треугольник с масштабом в миллиметрах, двойной лист бумаги из школьной тетради, установка ФПМ-07 для определения силы трения качения.

Цель работы: 1. изучить закон сухого трения (трения скольжения, трения качения).

2. экспериментально определить коэффициенты трения скольжения и трения качения.

Теория

Силы трения появляются при перемещении соприкасающихся тел (или их частей) друг относительно друга. Трение, возникающее при относительном перемещении двух соприкасающихся тел, называется внешним; трение между частями одного и того же сплошного тела (например, жидкости или газа) носит название внутреннего трения.

Трение между поверхностями двух соприкасающихся твердых тел при отсутствии между ними жидкой (или газообразной) прослойки (смазки) называется сухим.

Трение между телом и жидкой (или газообразной) средой, а так же между слоями такой среды называется вязким (или жидким).

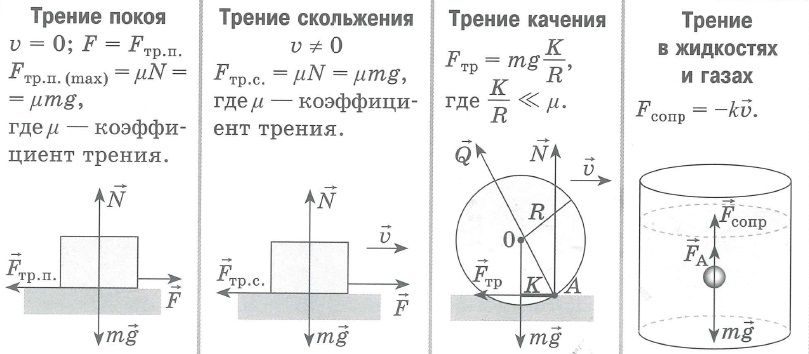
В данной работе изучаются законы сухого трения. Различают три вида сухого трения: трение покоя, трение скольжения и трение качения.

Сухое трение возникает не только при скольжении одного тела по поверхности другого, но и при всякой попытке вызвать такое скольжение. Трение, возникающее при попытке вызвать движение одного тела по поверхности другого, называется трением покоя или трением сцепления.

Пусть на горизонтальной поверхности находится тело. Приложим к нему переменную горизонтальную силу. Можно убедиться, что не любая приложенная к телу сила может вызвать её скольжение по поверхности. Это отсутствие движения можно объяснить тем, что приложенная сила уравновешивается какой-то другой силой. Этой силой является сила трения покоя. Таким образом, сила трения покоя автоматически принимает значение приложенной силы. Приложенную силу данного направления можно менять от нуля до сколь угодно большого значения, а сила трения покоя имеет предельное значение, которое называется максимальной силой трения покоя. Максимальная сила трения покоя выражается формулой, установленной опытным путём французским учёным Амонтоном ещё в 1699 году:

Рис. 15.2



F₀

-F₀

(15.1)

где k – коэффициент трения покоя, зависит от свойств (физической природы и качества обработки) поверхностей соприкасающихся тел,

Q – сила нормального давления.

Рис. 15.1

F₀

-F₀



F_ТР

До тех пор, пока внешняя сила не превосходит максимальную силу трения покоя F_0, скольжение не возникает (явление застоя). Если сила F, действующая на тело, больше максимальной силы трения покоя (F > F₀), начинается скольжение и сила трения покоя переходит в силу трения скольжения. Тело получает ускорение , и его скорость начинает расти.

В общем случае сила трения при скольжении зависит от относительной скорости трущихся тел. Характер этой зависимости различен для различных пар трущихся тел. В некоторых случаях зависимость силы трения от скорости может иметь вид, приведенный на рис.15.1. Как видно из графика, для некоторого интервала при малых скоростях силу трения скольжения можно считать постоянной, не зависящей от скорости и равной максимальной силе трения покоя (закон Кулона, установленный в 1781 году).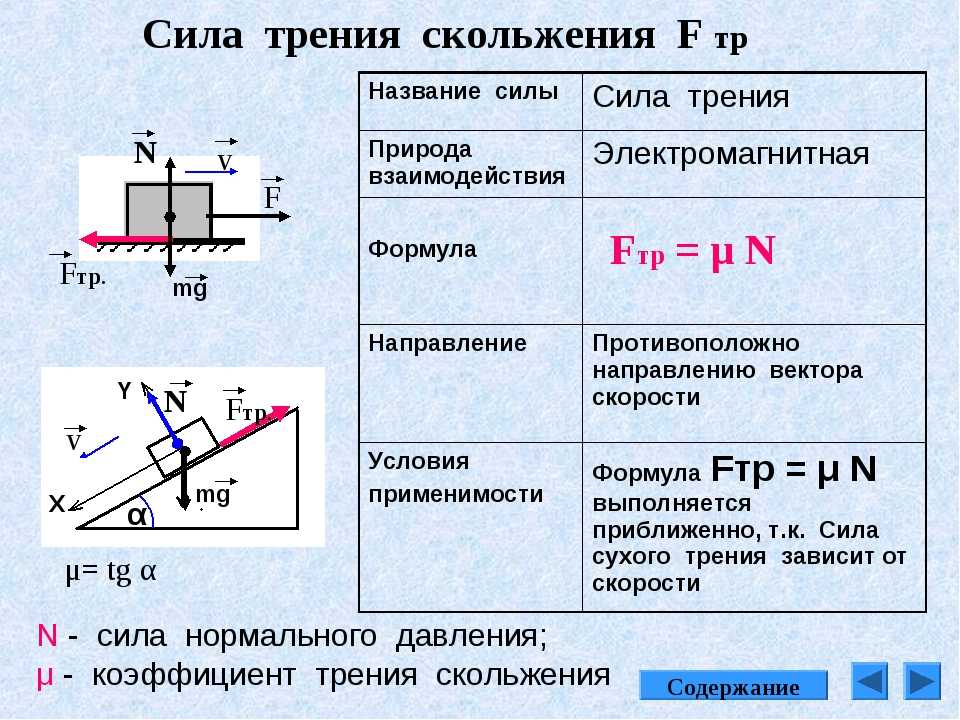 Опыты подтверждают это с достаточной точностью. В этом случае характер зависимости силы трения от скорости имеет вид, приведенный на рис.15.2.

Закон Кулона для силы трения скольжения имеет вид:

, (15.2)

где k – коэффициент силы трения скольжения, равный коэффициенту силы трения покоя. Как видно из (15.2), коэффициент k не имеет размерности. Законы Амонтона и Кулона являются приближёнными, т.к. коэффициент трения k зависит не только от физической природы и качества обработки поверхностей трущихся тел, но также от загрязнений, давления между телами, от температуры и т.п. Кроме того, k зависит от большого числа причин, многие из которых не поддаются учёту (наличие на соприкасающихся поверхностях окислов, влаги, адсорбированных газов и др.). Поэтому результаты измерений коэффициентов трения скольжения, полученные для одних и тех же материалов в разных опытах, могут противоречить друг другу. Причиной, вызывающей силу трения (покоя и скольжения) между грубо обработанными поверхностями, является возникновение сил при зацеплении неровностей (выступов и впадин).

Эти силы направлены в сторону, противоположную действующей силе. При улучшении качества обработки поверхностей сила трения уменьшается, однако в случае идеально гладких поверхностей мила трения может стать бесконечно большой (поверхности прилипнут друг к другу), вследствие молекулярного или атомного сцепления.

Рис. 15.3

Psin



Распространенным методом определения коэффициента трения скольжения (а также коэффициента трения покоя) является метод предельного угла. Пусть тело находится на наклонной плоскости (угол наклона ) (рис.15.3). На тело вдоль наклонной плоскости действует составляющая силы тяжести Psin, однако скольжение наблюдается, начиная с определенного (предельного) угла ₀. Следовательно, при отсутствии движения сила Psin уравновешивается с силой трения покоя F.

(15. 3)

При предельном угле ₀, начинается скольжение, т.е. трение покоя переходит в трение скольжения F_тр.

Согласно (15.2),

(15.4)

Тогда при  = ₀ из формул (15.3) и (15.4) можно получить:

(15.5)

Рассмотрим теперь механизм возникновения трения качения (без скольжения). Тело (цилиндр или шар), катящееся по ровной горизонтальной поверхности без скольжения, постепенно останавливается под действием силы трения качения, зависящей от физических свойств материалов плоскости и катящегося тела (а так же силы сопротивления воздуха).

При качении тело и плоскость деформируются под действием силы, прижимающей тело к плоскости. Так как для окончательного суждения неважно, что деформируется: тело или плоскость или то и другое, то для простоты рассуждений предположим, что тело (цилиндр или шар) не деформируется, а деформируется только поверхность, по которой катится тело. Какой характер имеет эта деформация?

Д опустим, что деформация носит упругий характер (рис. 15.4), тогда силы взаимодействия между телом и плоскостью будут совершенно симметричны относительно вертикальной плоскости ab, проходящей через ось тела. Каждой силе

f с фронтальной стороны катящегося тела будет соответствовать равная ей сила на симметрично расположенном участке площади соприкосновения с тыльной стороны катящегося тела.

Результирующая всех сил упругой деформации поверхности качения будет вертикальна, и сумма моментов этих сил относительно оси тела так же будет равна нулю. Поэтому силы упругих деформаций тела и плоскости при качении не скажутся на скорости качения, и движение будет происходить так, как будто никаких деформаций нет. Никаких сил трения качения в этом случае не возникает, и тело будет катиться бесконечно долго.

Следовательно, для объяснения сил трения качения следует считать деформации тела и плоскости качения неупругими, что фактически всегда имеет место. Очевидно, что силы, действующие на тело со стороны плоскости качения, не должны быть симметричными относительно плоскости ab: сила f больше силы на симметричном участке, расположенном сзади плоскости ab. Поэтому результирующая этих сил обязательно имеет горизонтальную составляющую, направленную назад, и момент этих сил относительно оси цилиндра также не равен нулю, причем, он тормозит вращение тела.

Найдём силу трения качения. Точка приложения результирующей не может быть расположена ни в вертикальной плоскости ab, проходящей через центр, ни сзади неё, ибо тогда эта сила сообщила положительное угловое ускорение телу, т.е. ускоряла бы его. Следовательно, остаётся последний вариант: точка приложения силы Q (реакция опоры) должна находится впереди, причём, линия силы Q должна проходить выше центра тела, в противном случае она сообщила бы положительное угловое ускорение. Таким образом, на катящееся тело действует сила трения качения, которая направлена и приложена так, как показано на рис.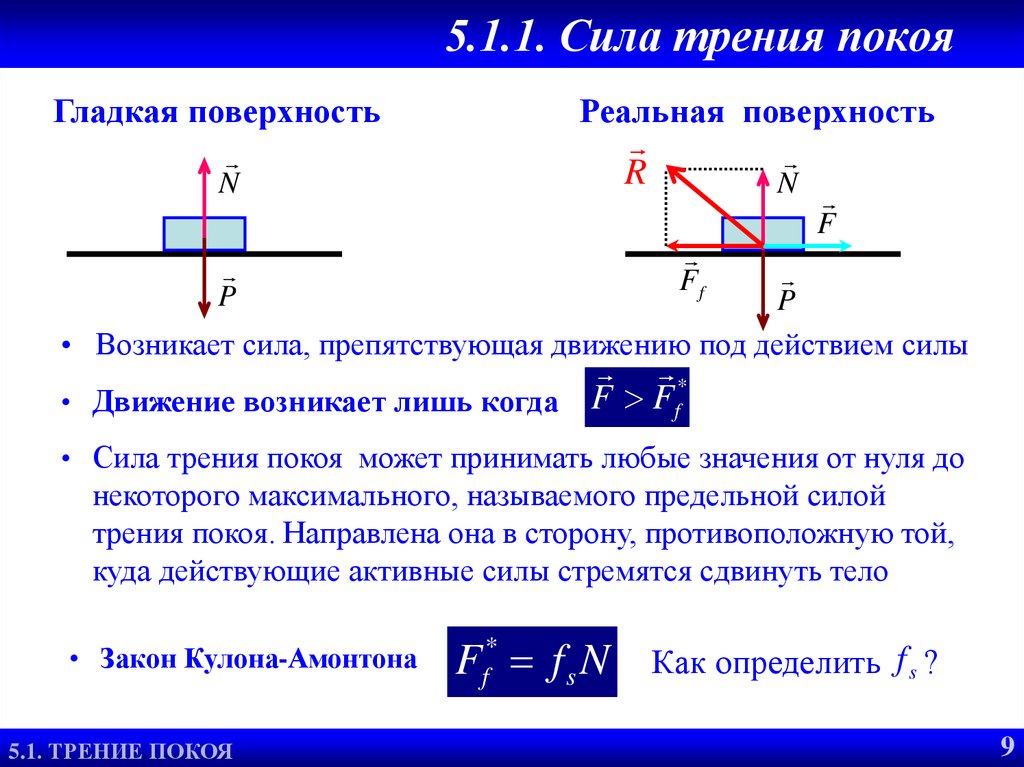 15.5.

Горизонтальная компонента силы Q представляет собой силу трения качения f_K. Так как расстояние S (расстояние от точки приложения силы Q до плоскости ab) практически очень мало по сравнению с радиусом тела R, и угол наклона  очень мал, то абсолютная величина Q почти равна силе давления, прижимающей тело к плоскости, в данном случае силе тяжести тела P. Связь между силой трения качения и другими величинами определяют опытным путём.

Пусть к оси вращения равномерно катящегося по горизонтальной плоскости тела приложена постоянная горизонтальная сила F в направлении движения, равная силе трения качения f_K. Так как вращение тела равномерное и угловое ускорение его равно нулю, то сила Q должна проходить через ось тела. Две другие силы: сила тяжести P и внешняя сила F по условию проходят через ось тела.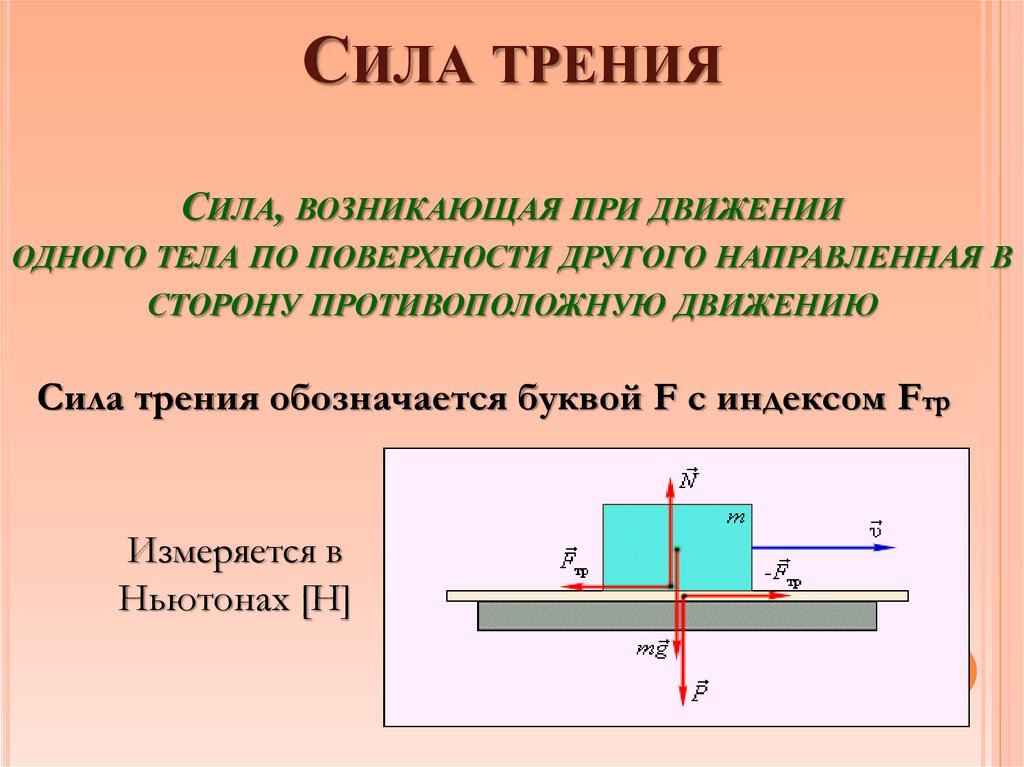 Следовательно,

. (15.6)

Так как угол  мал, то (15.6) можно записать в виде:

(15.7)

Обычно говорят не о силе трения качения, а о моменте силы трения качения:

(15.8)

Таким образом, момент силы трения качения равен силе нормального давления P, умноженной на S. Величину S называют коэффициентом трения качения и обычно обозначают через k (имеет размерность длины).

Курс физики (Грабовский Р.И.)

Курс физики (Грабовский Р.И.)

Грабовский Р.И. Курс физики. Учеб. пособие для с/х ин-тов. Изд. 4-е, перераб. и доп. М., «Высш. школа», 1974. — 552 с. Учебник составлен в соответствии с программой по физике для сельскохозяйственных институтов. В нем приводится достаточное количество примеров, связанных с агробиологическими науками и сельскохозяйственным производством. Настоящее издание (3-е вышло в 1970 г.) отличается от предыдущих некоторыми (небольшими по объему) дополнениями и изменениями, способствующими улучшению содержания. Предназначается для студентов неинженерных факультетов сельскохозяйственных вузов. Многие разделы учебника могут быть использованы и студентами инженерных факультетов. Оглавление Предисловие Введение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 10. Силы упругости § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III. Работа и энергия § 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. 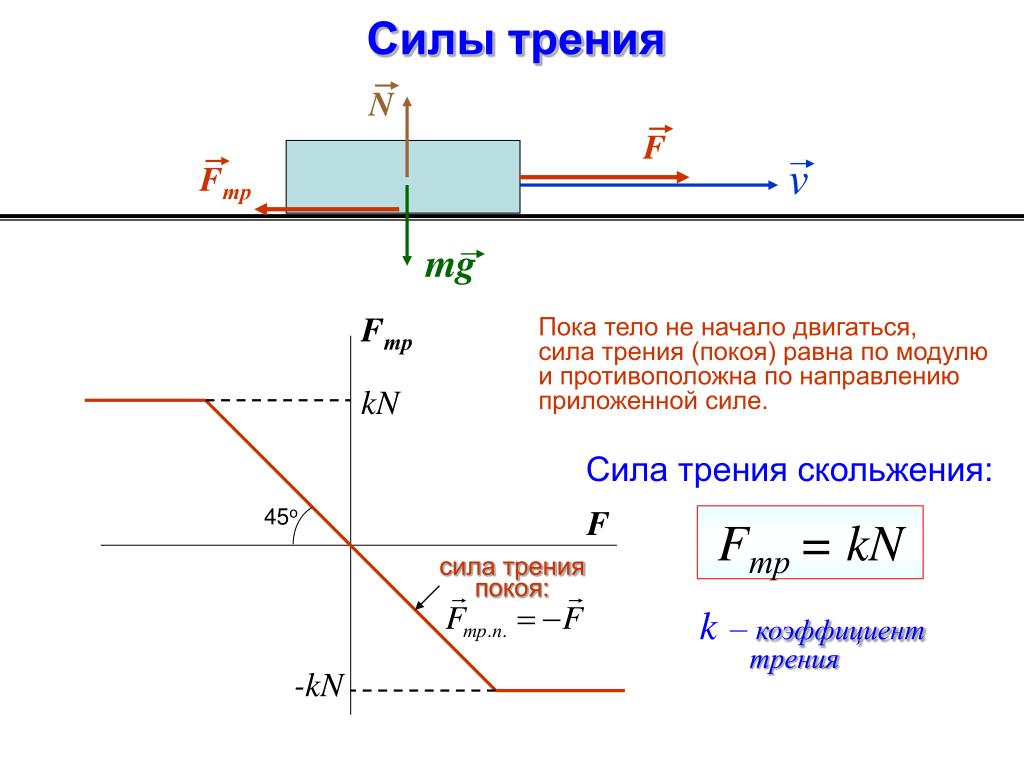О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35. Основные положения молекулярно-кинетической теории § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. 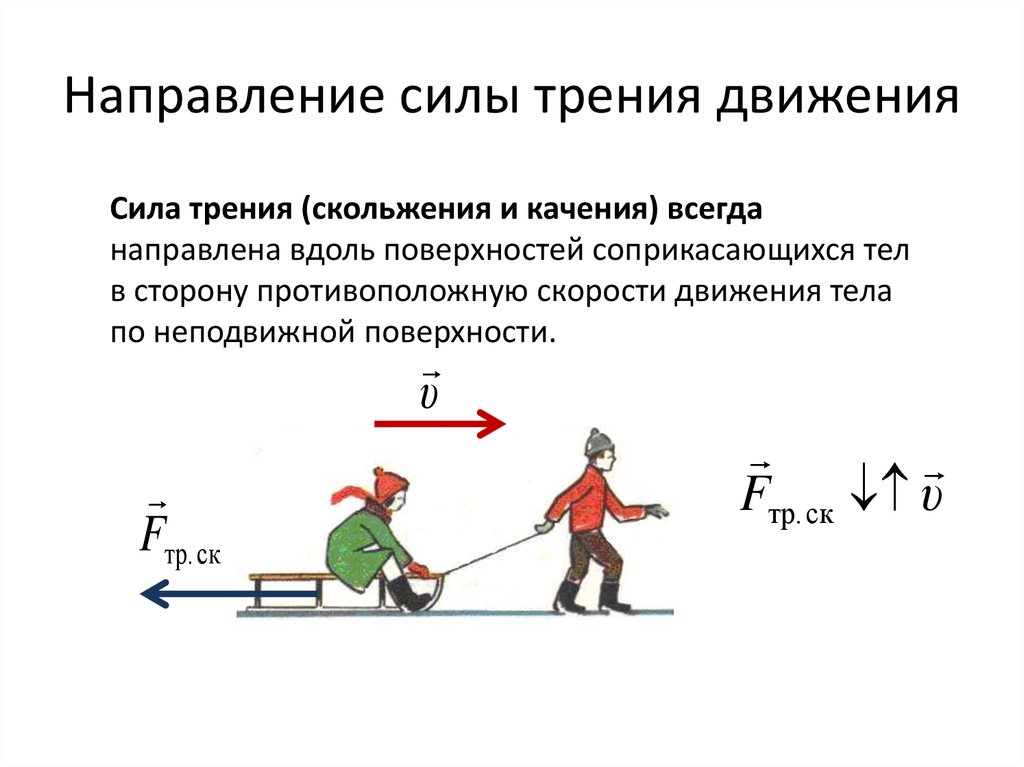Средняя кинетическя энергия поступательного движения молекулы идеального газа § 43. О числе степеней свободы. Внутренняя энергия газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50. Внутреннее трение (вязкость) Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. Тепловое расширение твердых и жидких тел § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором § 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции § 83. Конденсатор. Энергия электрического поля Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов § 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. 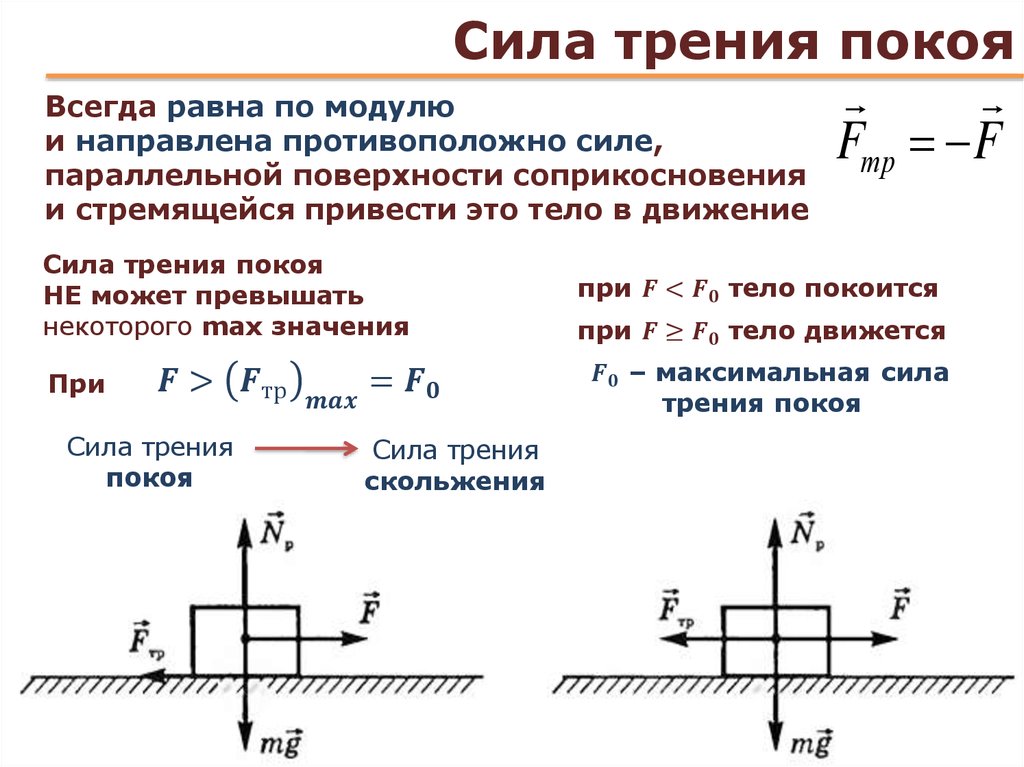Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока § 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. 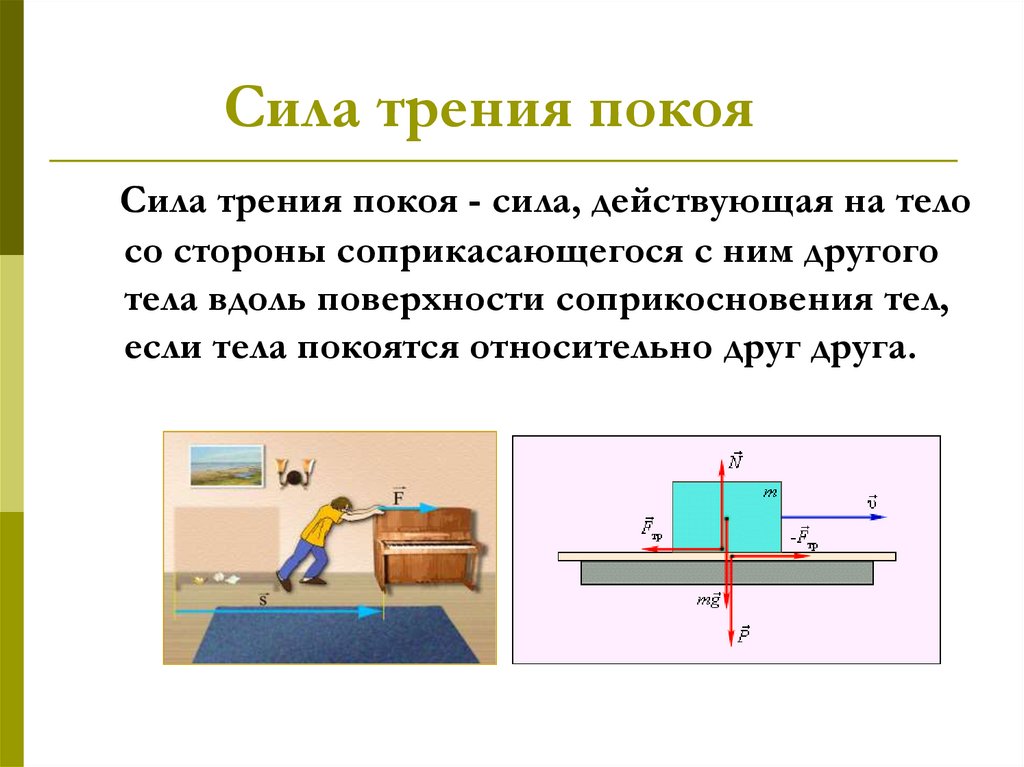Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122. Об интерференции света, отраженного от прозрачных пленок § 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. 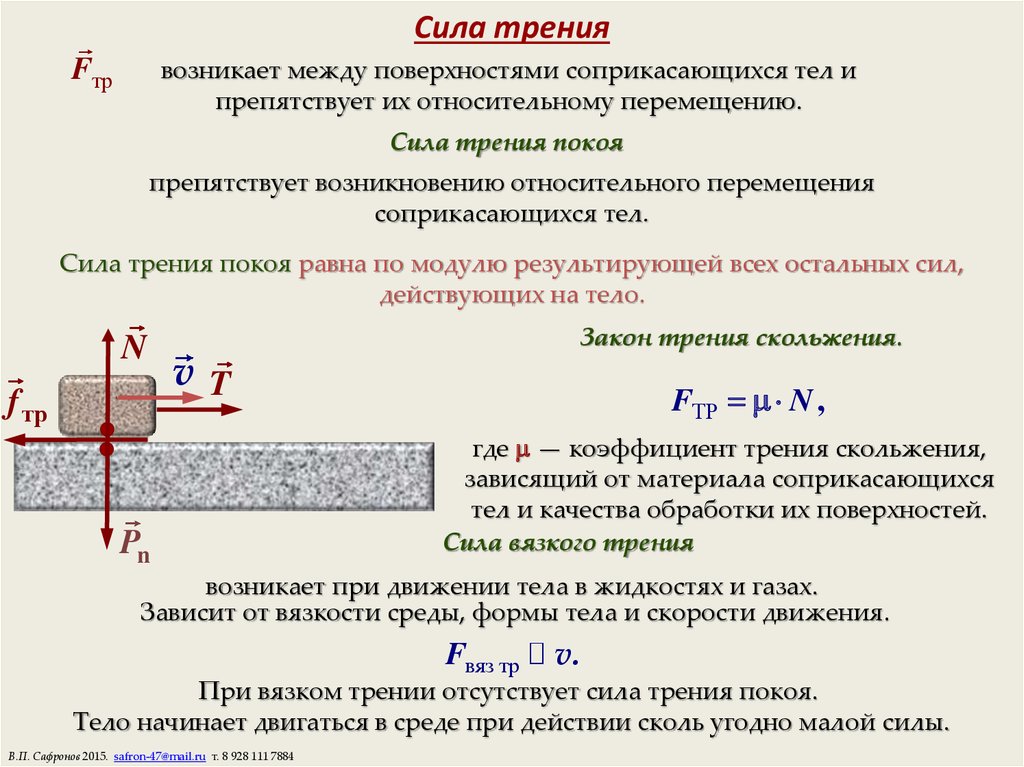Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии

Статическое трение: определение, взаимосвязь и формулы

Трение очень важно в нашей повседневной жизни, так как оно помогает предотвратить скольжение автомобильных шин на льду зимой и позволяет автомобилю останавливаться при торможении. Человек, прыгающий с парашютом при спуске, ощущает сопротивление воздуха, представляющее собой силу жидкостного трения, оказываемую воздухом на движущееся тело. Кроме того, мяч, катящийся по земле, будет замедляться до тех пор, пока в конечном итоге не остановится из-за трения качения, оба из которых являются примерами контактных сил.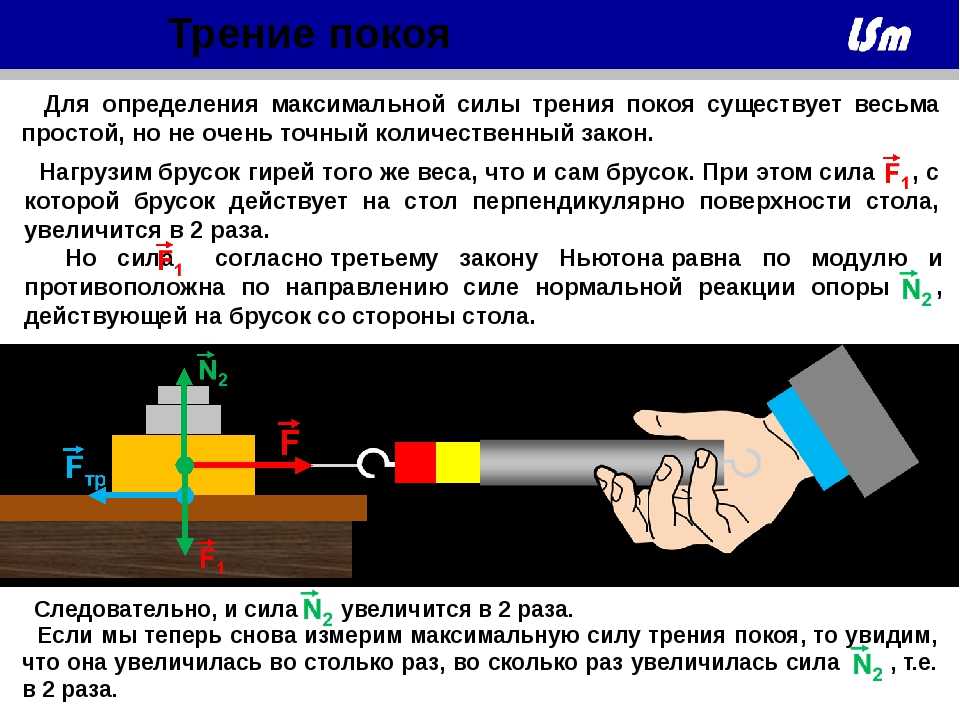

Рис. 1. Люди пытаются преодолеть силу трения покоя, чтобы столкнуть заглохший автомобиль с дороги.

Если два тела касаются друг друга напрямую, они соприкасаются. Контактные силы используются для объяснения взаимодействия между двумя телами. Некоторые примеры контактных сил включают нормальную силу и силу трения. Есть два основных типа сил трения, в которые попадают все остальные; статическое и кинетическое трение. В этой статье мы сосредоточимся на силе трения покоя и объясним ее математическое представление. Мы также обсудим различия между статическим и кинетическим трением.

Статическое трение: определение

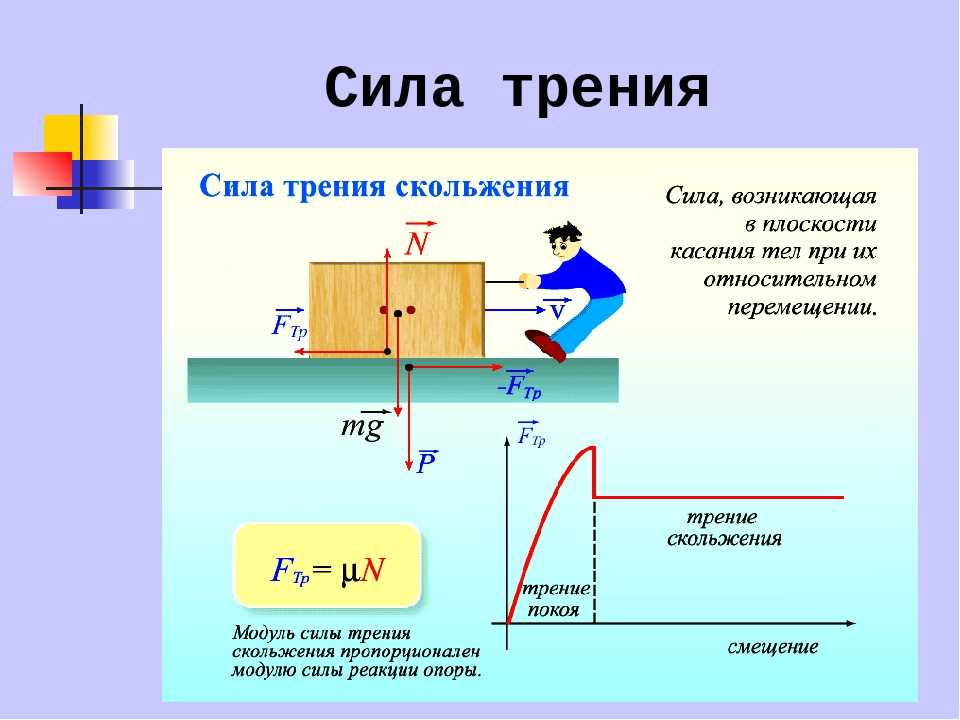
Если у нас есть коробка на полу, и мы пытаемся толкнуть ее с некоторой силой, коробка может просто стоять на месте и не двигаться. Это происходит из-за силы статического трения . Статическая сила трения возникает, когда объект и поверхность покоятся друг относительно друга. Нет движения одного относительно другого. Из-за статического трения объект будет оставаться неподвижным на поверхности, не скользя. Пол создает силу статического трения, которая равна по величине и противоположна по направлению приложенной силе, пока приложенная сила не превысит максимальную силу статического трения. Сила трения покоя может быть представлена ​​как \(\overset\rightharpoonup{f_{\mathrm s}}\).

Важно отметить, что это не имеет никакого отношения к третьему закону Ньютона, так как пара сил действия-противодействия всегда действует на разные объекты.

Рис. 2. Коробка, изначально находящаяся в состоянии покоя, испытывает приложенную силу \(\overset\rightharpoonup F\) для преодоления силы трения покоя.

На рисунке выше мы видим коробку, которая изначально находится в состоянии покоя. Нормальная сила \(\overset\rightharpoonup N\) направлена ​​вверх и действует на коробку со стороны пола, а вес \(\overset\rightharpoonup W\) действует вниз. Поскольку ящик находится в равновесии, величины нормальной силы и веса равны.

Затем к ящику прикладывается сила \(\overset\rightharpoonup F\), которая тянет его вправо, со временем величина этой приложенной силы постепенно увеличивается. Коробка некоторое время будет находиться в состоянии покоя. Это связано с тем, что даже если сила увеличивается, сила трения покоя также увеличивается, чтобы уравновесить величину с силой \(\overset\rightharpoonup F\).

Сила, необходимая для перемещения ящика, равна и противоположна максимальной силе статического трения. Максимальное значение силы статического трения показано как \({(f _ {\mathrm s})}_\max\), и оно пропорционально величине нормальной силы. Коэффициент пропорциональности отображается как \(\mu_{\mathrm s}\) и называется коэффициент трения покоя . Как только максимальная сила статического трения будет преодолена, коробка начнет скользить вправо.

Статическое трение: Формула

Реальное значение статического трения может варьироваться от нуля (когда на объект не действует сила) до максимального значения, которое математически представляется как

$$f_s\leq{(f_s) }_{max}=\mu_sN.$$

Согласно математическому представлению, отношение статического трения находится между величинами, так как величина статического трения пропорциональна как величине нормальной силы, так и шероховатости между двумя поверхностями в контакт. Следовательно, направления не имеют значения, как в векторных отношениях.

Итак, что означает эта формула?

• Когда приложенная сила \(\overset\rightharpoonup F\) равна значению, при котором начинается движение, можно использовать формулу для расчета величины силы трения покоя.
• Если сила \(\overset\rightharpoonup F\) не заставляет объект двигаться, то величина силы трения покоя должна быть меньше \(\mu_sN\). В этом случае величина силы трения покоя будет просто равна величине приложенной силы \(\overset\rightharpoonup F\).

Предельное трение

Мы упоминали, что существует предел, при котором сила \(\overrightarrow F\) превышает максимальное значение силы статического трения. Если предел превышен, коробка начинает двигаться. Когда сила статического трения максимальна и движение вот-вот начнется, сила трения называется ограничивающим трением . Когда движение начинается, объект больше не будет испытывать статическое трение.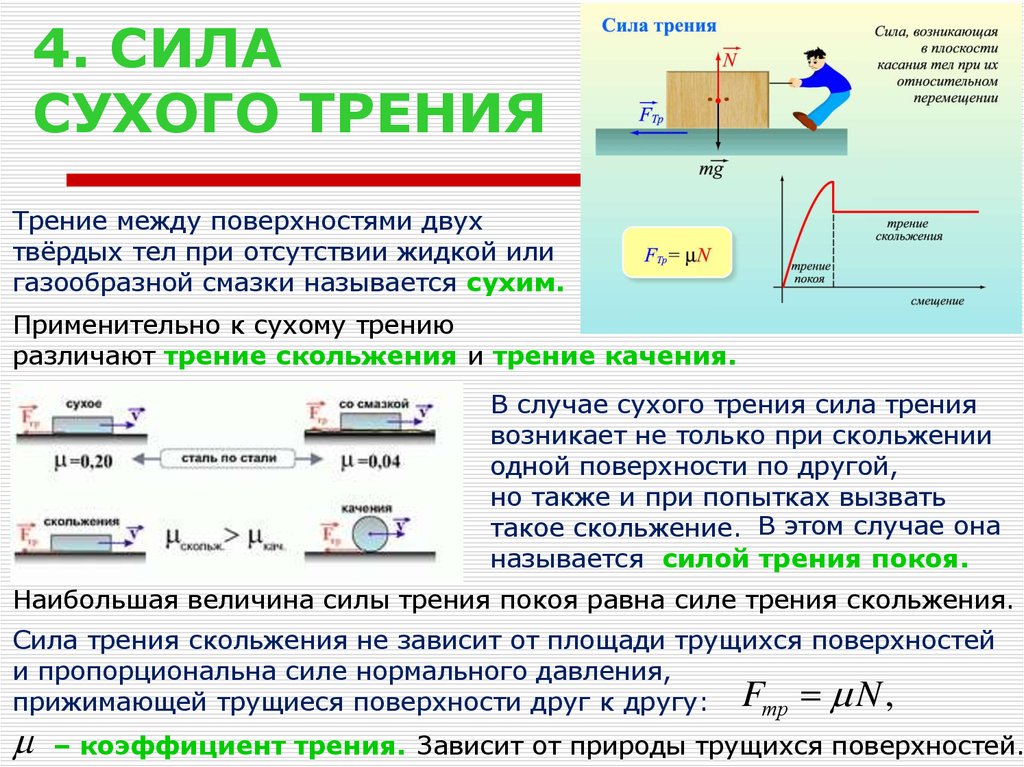 Вместо этого объект испытывает силу кинетического трения.

Рис. 3. Диаграмма, показывающая, как силы статического и кинетического трения изменяются с увеличением приложенной силы.

Если мы посмотрим на приведенный выше график, мы увидим, что с увеличением приложенной силы \(\overset\rightharpoonup F\) величина силы статического трения также начинает увеличиваться, пока не достигнет пика, где величина равна величине предельное трение. После этого объект начинает двигаться, и действует уже не статическая сила трения, а кинетическая сила трения.

Примеры статического трения

Теперь давайте рассмотрим несколько примеров, связанных с силой статического трения.

Рис. 4 – Ящик в покое. Приложенная сила недостаточно велика, чтобы преодолеть силу трения покоя.

Вопросы

а) Ящик массой \(4\,\mathrm{kg}\) покоится на поверхности. Когда к ящику приложена сила \(10\,\mathrm N\), он все еще находится в состоянии покоя, какова величина силы трения покоя?

b) Если значение максимальной силы трения покоя равно \(20\,\mathrm N\), то каков коэффициент трения покоя \(\mu_{\mathrm s}\) для \(10\,\ матрм кг\) коробка? (\(g=10\,\frac{\mathrm m}{\mathrm s^2}\))

Решения

а) Когда объект находится в состоянии покоя и к нему приложена сила, величина силы равна величине силы трения покоя.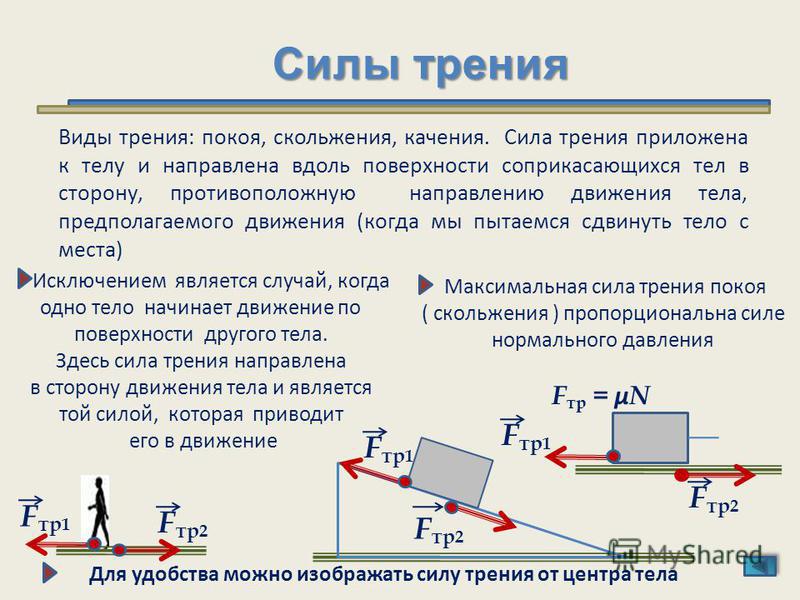 Поскольку приложена сила \(10\,\mathrm N\), величина силы трения покоя также равна \(10\,\mathrm N\).

б) Величина максимальной силы трения покоя равна \(\mu_{\mathrm s}N\).

Поскольку значение максимальной силы трения покоя равно \(20\,\mathrm N\), его можно вставить вместо \({\left(f_s\right)}_\max\). Также указана масса объекта. Итак, мы можем рассчитать вес. 92\right),\\\mathrm W&=40\,\mathrm N.\end{align*}$$

Поскольку вес и нормальная сила имеют одинаковую величину, мы можем определить коэффициент трения покоя \(\ му _ {\ mathrm s} \).

$$\begin{align*}f _{\mathrm s}&=\mu _{\mathrm s}N,\\\mu _{\mathrm s}&=\frac{{\mathrm f}_{\mathrm s}}{\mathrm N},\\\mu _{\mathrm s}&=\frac{20\,\mathrm N}{40\,\mathrm N},\\\mu _{\mathrm s}&= 0.5.\end{align*}$$

Статическое трение против кинетического трения

Итак, что такое разница между статическим трением и кинетическим трением?

Различия между силами статического трения и кинетического трения можно обобщить следующим образом:

1. Статическое трение применяется только тогда, когда объект неподвижен, а кинетическая сила трения применяется, когда объект движется. (Способ запомнить ключевое различие между ними состоит в том, чтобы критически подумать об их определениях. В то время как статика означает отсутствие движения, кинетика означает отношение к движению или результат его действия.)
2. Максимальное значение силы статического трения всегда больше величины кинетической силы трения, потому что объекту всегда легче поддерживать движение, чем начать движение из состояния покоя.
3. Величина силы кинетического трения о сухую поверхность практически постоянна, независимо от скорости объекта. В то время как величина статического трения увеличивается с приложенной силой, пока не достигнет предельного трения.

Статическое трение — основные выводы

• Сила трения покоя прилагается, когда объект находится в состоянии покоя.

• Когда приложенная сила \(\overset\rightharpoonup F\) достигает значения, при котором начинается движение, можно использовать формулу для расчета величины силы трения покоя.

• Если сила \(\overset\rightharpoonup F\) меньше этого значения, то величина силы трения покоя должна быть меньше \(\mu_{\mathrm s}N\). В этом случае величина силы трения покоя будет просто равна величине приложенной силы \(\overset\rightharpoonup F\).

• Тип трения, при котором сила трения покоя максимальна и движение вот-вот начнется, называется предельным трением.

• Разница между статической и кинетической силой трения заключается в том, что статическая сила трения действует, когда объект неподвижен, а кинетическая — когда объект движется. Статика означает стояние, кинетическое движение.

---

Каталожные номера

1. Рис. 1 – Люди выталкивают заглохший автомобиль с улицы (https://www.flickr.com/photos/nathaninsandiego/5421942474) Натана Руперта под лицензией CC BY-NC-ND 2.0 (https://creativecommons.org/licenses/by-nc-nd/2.0/).
2. Рис. 2. Преодоление статического трения, StudySmarter Originals.
3. Рис. 3 — Статическое трение, Предельное трение, Кинетическое трение (https://commons.wikimedia.org/wiki/File:Static_friction.png), адаптировано из Ilevanat, лицензировано GNU (https://www.gnu.org). /licenses/fdl-1.3.html).
4. Рис. 4. Ящик в покое, StudySmarter Originals.

Максимальное трение покоя при прижатии предмета к стене

спросил 3 года, 1 месяц назад

Изменено 3 года, 1 месяц назад

Просмотрено 355 раз

$\begingroup$

На картинке выше $m$ объект не движется. Если мы увеличим силу $F$, будет ли максимум увеличение статического трения также?

Если я использую формулу $$(f_s)_{max} = \mu_s N$$, то ответ положительный ($N=F$), но кто-то говорит:

Вы не должны использовать эту формулу для этой ситуации (нажатие объекта на вертикальной стене). Это исключение, и максимальное статическое трение равно статическому трению и здесь постоянно.

Я согласен с тем, что статическое трение постоянно, потому что единственная вертикальная сила (кроме трения) — это вес (мг), и он не меняется, а составляет около максимум статическое трение Не могу с ним согласиться.

Кто не прав?

Я знаю, что это простой вопрос, но я не мог его понять. Извини! 🙂

• трение

$\endgroup$

$\begingroup$

Да, максимальное статическое трение увеличится, но трение не может вызвать ускорение объекта, поэтому сила трения всегда будет равна весу, $mg$. Это связано с тем, что $F_r \le \mu N$ может принимать любое значение меньше $\mu N$, чтобы сбалансировать вес.

$\endgroup$

$\begingroup$

Вы и «кто-то» спорите о противоположных целях, поскольку вы говорите о разных значениях фразы «максимальное статическое трение».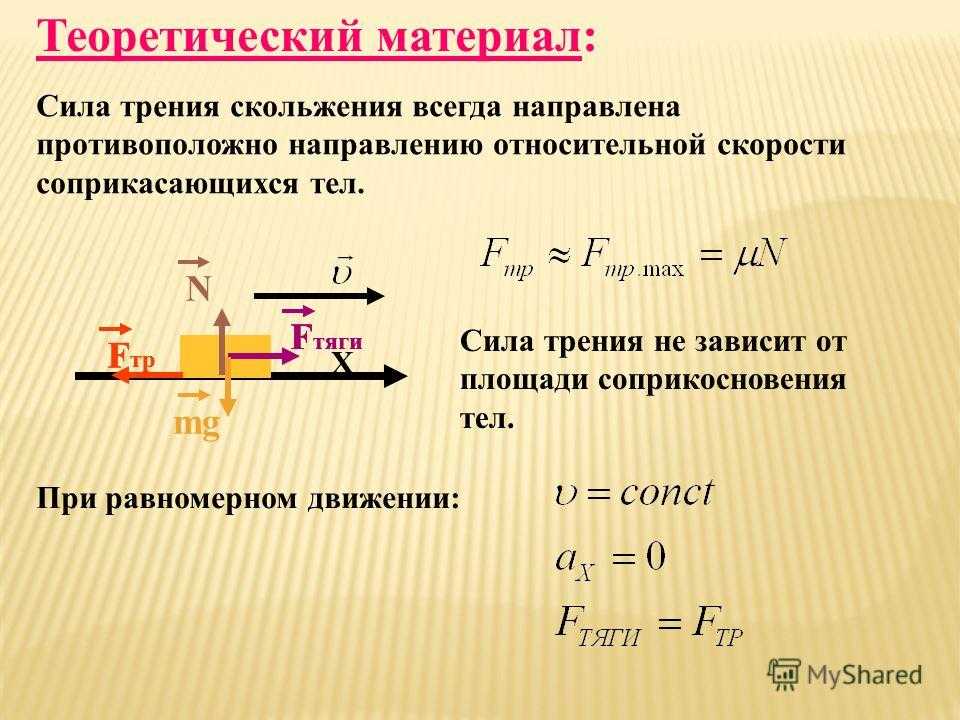

Вы используете эту фразу для обозначения максимальной силы, которую трение может противодействовать движению объекта. В этом смысле максимум пропорционален приложенной силе F и поэтому будет линейно возрастать (в первом приближении) с F.

‘Кто-то’ принимает «максимальное статическое трение» как фактическую максимальную силу, вызванную трением в показанном сценарии, которая остается mg, даже если вы увеличиваете величину F.

Различие между двумя интерпретациями станет очевидным в любом из двух сценариев. Во-первых, если вы уменьшите величину F до точки, в которой «максимальное статическое трение» в вашем смысле станет меньше, чем mg, и в этом случае объект будет скользить по стене. Другой был бы, если бы вы приложили дополнительную силу, тянущую объект вниз, и в этом случае сила трения будет увеличиваться, чтобы противостоять движению, пока не будет достигнут предел «максимального статического трения».

В общем, я думаю, что ваше использование термина «максимальное статическое трение» больше соответствует его общему смыслу.

$\endgroup$

$\begingroup$

Да, если вы увеличиваете $F$, вы увеличиваете максимальную силу статического трения. Однако это не увеличивает реальную силу статического трения.

Я думаю, что человек использует термин «максимальная статическая сила трения», когда на самом деле имеет в виду реальную силу статического трения $f_s$. Фактическая сила трения покоя постоянна просто потому, что сила, которой она противодействует, $mg$, оказывается постоянной. В примерах с горизонтальными поверхностями сила, противодействующая трению покоя, обычно является переменной в зависимости от приложенной горизонтальной силы, что делает силу трения покоя также переменной вплоть до максимально возможной силы трения покоя.

В этом примере максимально возможная сила трения покоя равна $uF$. Этого можно было бы достичь, если бы, например, вы постепенно подвешивали дополнительный вес к имеющемуся весу.