Масса и плотность вещества, теория и онлайн калькуляторы

Масса и плотность вещества, теория и онлайн калькуляторы

Коэффициенты пропорциональности между ускорением и силой, постоянные для конкретного тела, отличаются для разных тел. Этот коэффициент связан с таким свойством тела как инертность. Чем больше инертность, тем меньше ускорение тела, которое сообщает телу действующая на него сила.

Физическая величина, которая численно характеризует свойство инертности тела — это масса (инертная масса). Обозначается масс буквой $m$. Применяя понятие массы связь между ускорением и силой можно выразить как:

\[\overline{a}=\frac{\overline{F}}{m}\left(1\right).\]

Масса — мера инертности

Масса, которая входит в формулу (1) является мерой инертности. Данный параметр не зависит от силы, оказывающей воздействие на тело и других условий, в которых находится тело, например, температуры, гравитации и т.д.

Свойства массы

Эмпирически получены такие свойства массы, как:

1. Масса — аддитивная скалярная величина, которая не зависит от места положения тела в пространстве. Аддитивность означает, что масса тела равна сумме масс частей тела. Это свойство в точности выполняется для макроскопических тел и нарушается, если энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в ядро атома. То, что масса является скалярной величиной, значит, что инертные свойства тел одинаковы во всех направлениях.
2. Масса тела не зависит от скорости, если она много меньше скорости света.

Массу можно определять при помощи взвешивания или используя динамический способ. Динамический способ нахождения массы заключается в следующем. Если один раз для рассматриваемого тела измерить ускорение и действующую на тело силу одновременно, то можно применяя формулу (1) вычислить массу. Зная массу тела можно рассчитывать ускорение тела по известной силе и по известному ускорению находить силу.

Гравитационная масса

В определении массы на основе тяготения используют закон гравитации:

\[F=\gamma \frac{m_1m_2}{r^2}\left(2\right). \]

Измерение гравитационной массы проводят при помощи взвешивания. Тела располагают неподвижно относительно Земли и сравнивают действующие на них силы тяготения. Определенная таким способом масса называется гравитационной.

Эмпирически показывают, что гравитационные массы инертные массы совпадают. В механике Ньютона совпадение инертной и гравитационной масс не имеет физической основы. Это просто экспериментальный факт, который установлен с высокой точностью, если это было бы не так, то классическая динамика не пострадала бы. В релятивистской теории тяготения равенство инертной и гравитационной массы имеет принципиальное значение и положено в основу теории.

И так, масса тела — это количественная мера инертных и гравитационных свойств тела.

Единицей измерения массы в Международной системе единиц является килограмм:

\[\left[m\right]=кг.\]

Плотность вещества

Если из одного и того же вещества изготовить тела разных объемов ($V$), то их массы будут разными. Но экспериментально установлено, что отношение масс этих тел к их объемам буде постоянной величиной:

\[\frac{m_1}{V_1}=\frac{m_2}{V_2}=const\ \left(3\right).\]

Отношение массы тела к его объему служит характеристикой вещества и называется плотностью. Обозначают плотность буквой $\rho $.

\[\rho =\frac{m}{V}\left(4\right).\]

Плотность вещества зависит от температуры, внешнего давления, агрегатного состояния. Плотность можно еще определить как массу единицы объема вещества. Плотность является скалярной физической величиной. Для однородного тела плотность является постоянной величиной для всей массы тела.

Для неоднородных тел, используется понятие средней плотности ($\left\langle \rho \right\rangle $):

\[\left\langle \rho \right\rangle =\frac{m}{V}\left(5\right).\]

Иногда применяют понятие плотность тела в точке, которая равна:

\[\rho ={\mathop{\lim }_{\Delta V\to 0} \frac{\Delta m}{\Delta V}\left(6\right),\ }\]

где $\Delta m$ — элементарная масса тела (малая часть массы тела), содержащая исследуемую точку тела; $\Delta V$ — объем данного элемента тела. 3}$.

Плотность смеси веществ нельзя вычислить как сумму плотностей отдельных составляющих смеси.

Примеры задач с решением

Пример 1

Задание. Какова плотности смеси газов, если температура равна T, давление $p$, масса первой компоненты $m_1$ (ее молярная масса ${\mu }_1$), масса второй компоненты $m_2$ (ее молярная масса ${\mu }_2$)? Считайте газы в смеси идеальными.

Решение. Плотность смеси ($\rho $) равна:

\[\rho =\frac{m}{V}\left(1.1\right),\]

где массу смеси ($m$) найдем как:

\[m=m_1+m_2\left(1.2\right).\]

Так как газы можно считать идеальными, то объем смеси будем искать, используя уравнение Менделеева — Клапейрона:

\[pV=\nu RT\ \left(1.3\right),\]

где $\nu ={\nu }_1+{\nu }_2=\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2}-\ $число молей вещества; $R$ — универсальная газовая постоянная. Из (3) выразим объем смеси идеальных газов:

\[V=\frac{\nu RT}{p}=\frac{(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2})RT}{p}\left(1.4\right).\]

Подставим правую часть (1.4) вместо объема и правую часть (1.2) вместо массы в формулу (1.1):

\[\rho =\frac{\left(m_1+m_2\right)p}{(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2})RT}.\]

Ответ. $\rho =\frac{\left(m_1+m_2\right)p}{(\frac{m_1}{{\mu }_1}+\frac{m_2}{{\mu }_2})RT}$

Пример 2

Задание. Под действием силы $F$ тело движется прямолинейно так, что его скорость изменяется в соответствии с графиком рис.1. Какова масса тела?

Решение. Основой для решения задачи служит второй закон Ньютона, который запишем, учитывая, что движение тела в нашей задаче прямолинейное:

\[F=ma=m\frac{dv}{dt}\left(2.1\right).\]

Уравнение изменения скорости ($v(t)$), исходя из графика имеет вид:

\[v\left(t\right)=Ct-B\ \left(2. 2\right).\]

Вычислим:

\[\frac{dv}{dt}=C\ \left(2.3\right).\]

Используя формулы (2.1) и (2.3) выразим массу тела:

\[F=m\cdot C\to m=\frac{F}{C}.\]

Ответ. $m=\frac{F}{C}$

Читать дальше: начальная фаза колебаний.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Физик: Массу определяем через инертность, а инертность — через массу. И смотри, дурак, не перепутай!

Во-первых, заметьте, и намека нет на то, что где-то, скажем, в классической механике, или в каких-то иных случаях, масса может быть количеством вещества. Нет! Только мера инертности! Везде и всегда! Во-вторых, что значит «Прежде М. определяли как «количество вещества»? Я что – жил, учился и работал в XIX веке и только вчера очутился сразу в XXI?

Наконец, кто и когда противопоставлял количество вещества энергии?? В формуле потенциальной энергии сила умножается на расстояние. Но сила это действие, придающее ускорение не мере инертности, а КОЛИЧЕСТВУ ВЕЩЕСТВА! В формуле кинетической энергии половина КОЛИЧЕСТВО ВЕЩЕСТВА, а не мера инертности, умножается на квадрат скорости. Как это «прежде» массу противопоставляли энергии, если без нее – без количества вещества — не рассчитаешь ни силу, ни энергию?? О чем пишет энциклопедия?

По-прежнему, не понимая, как такая чушь могла появиться в энциклопедии, беру более позднее издание – «Краткий политехнический словарь», подписанный в печать в 1955 году. В нем «МАССА – величина, пропорциональная количеству вещества в теле». И все! И никаких «мер инертности»!

И получается, что начиная с 30-х, а может и 20-х годов прошлого века, существуют две различные физики. Причем, не «классическая» и «современная», поскольку «современная» претендует на включение в себя «классической», а вообще две разные – «нормальная» и «современная». Нормальная физика для тех физиков и инженеров, кто занимается реальным делом (для них политехнические словари), а «современная» для тех «ученых», кто выколачивает себе в доход деньги налогоплательщиков из бюджета (в их распоряжении энциклопедии). Эти физики до того разные, что, как видите, даже понятие масса в них означает совершенно разные и не сочетаемые вещи.

Да и не только. В одной физике волны (акустические, в различных средах) не имеют частиц и для этой физики понятие «частица волны» является глупостью. А другая физика увлеченно изучает кванты – частицы электромагнитных волн.

Самое знаменитое уравнение

Ну, да ладно. В те далекие годы студенчества у меня не вызывала сомнений эта пресловутая формула Е=mс2 («самое знаменитое уравнение в мире») потому, что это модификация банальной формулы кинетической энергии, а я был уверен, что масса m в ней — это количество вещества, но только полностью, а не половина, как в уравнении кинетической энергии. Ведь только в этом случае уравнение Е=mс2 имеет физический смысл и смысл вообще.

Смотрите: если в каком-то объекте выделится вся внутренняя энергия, то осколки этого объекта разлетятся с некой скоростью. Количество вещества всех этих осколков, умноженное на квадрат той скорости каждого осколка, с которой он летит, даст в сумме кинетическую энергию всех осколков. И эта сумма действительно будет пропорциональна внутренней энергии этого объекта.

Если осколки будут разлетаться со скоростью света, то их кинетическую энергию, естественно, можно записать как половинное количество вещества в них, умноженное на квадрат скорости света, естественно, это может быть пропорционально энергии самого объекта. Правильно это уравнение или нет, но физический смысл Е=mс2 был налицо.

Но если в этом пресловутом уравнении масса m это не количество вещества, то тогда что получается?

Начнем с вопроса: а что такое «мера инертности»? Чтобы не домысливать, начал переходить по ссылкам в Википедии, ведь «мера инертности» это физическая величина, определение обязано быть! И выяснил, что определения меры инертности нет, что статьи «Масса» и «Инертность» кивают друг на друга: в статье «Инертность» мера инертности это масса, а в статье «Масса» масса это мера инертности. (По методе Васусуалия Лоханкина – «веревка это вервие простое»). Определения всех физических величин – «количества вещества», «скорости», даже «воздействия» есть, а определения меры инертности нет! Современная физика до сих пор не в курсе дела, что это такое, так что ли?

Первый вопрос, а почему эти умные физики не называют вещи своими именами и не дают свое определения мере инертности, как остальным величинам, мало того, подменяют названия? Почему они свою меру инертности называют не «мерой инертности», а «массой»? Предположения выскажу позже, а сейчас еще вопрос, а почему эйнштейнисты меру инертности, которая «неизвестно что», продолжают измерять килограммами?

Ведь масса это физическая величина, до сих пор характеризующая только количество вещества, и эталон килограмма, хранящийся в Международном бюро мер и весов (расположенном в городе Севр у Парижа, копия эталона есть в Москве), до сих пор является эталоном КОЛИЧЕСТВА ВЕЩЕСТВА. Теряющем, кстати, за сто лет 3×10−8 своего вещества, а не «меры инертности».

Взглянем на дело с другой стороны: какой физической величиной – в каких единицах — должна измеряться «мера инертности»?

Инертность это явление сохранения скорости тела в случае, если внешние воздействия на него отсутствуют или взаимно скомпенсированы, то есть, способность тела без воздействия силы сохранять скорость. (Состояние покоя это нулевая скорость). Но разве эту способность килограммами надо измерять?

Примеры. Стоит автомобиль, в котором количество вещества, положим, тысячу килограмм. В него сели четыре блондинки. Количество вещества в автомобиле изменилось процентов на 20, а автомобиль, как стоял, так и стоит, – его скорость не изменилась. Летит вокруг Земли космическая станция, из нее в открытый космос вышел космонавт, изменив количество вещества станции. А скорость станции не изменилась. Так при чем тут килограммы к способности тела не менять скорость?

Ясно, что для изменения способности тела изменять скорость, нужна работа, энергия, и мерой инертности может быть только работа или энергия.

Но опять не буду сам домысливать, а возьму из Википедии определение массы, даваемое этими самыми умными физиками (выделено мною, — Ю.М.):«Ма́сса — одна из важнейших физических величин. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя).

Сначала просто отметим, что и по «современным» представлениям, масса, если считать ее мерой инертности, это то же самое, что и энергия! Но продолжим чтение.

«В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта:

Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии, и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.

Инертная масса, которая характеризует меру инертности тел и  фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу».

Начнем с первого предложения.

Читаю определение количества вещества в «современной физике»: «Количество вещества — физическая величина, характеризующая количество однотипных структурных единиц, содержащихся в веществе». Однотипных! Атом состоит из разнотипных структурных единиц – протонов, нейтронов и электронов. Это как? В атоме нет никакого количества вещества? Сталь – это смесь атомов и молекул. Это как? В ней тоже нет никакого количества вещества? Или кто-то считает количество стали не тоннами, а молями? Ладно, это химия, не буду дальше.

Но «Физи́ческая величина́ — физическое свойство материального объекта, физического явления, процесса, которое может быть охарактеризовано количественно». Подчеркну: физическая величина предназначена для количественного описания ОДНОГО свойства. А современная физика, как видите, давая определение тому, что она называет «массой», цинично утверждает, что эта физическая величина описывает «два различных свойства физического объекта»! А почему эти свойства не описывают свои физические величины для этих свойств?? Почему прицепились к массе?

Теперь о том, какие именно свойства современная физика называет массой.

Начнем с «инертной» массы. Смотрите, как изящно современные физики излагают. Это, оказывается, не мера инертности тела (что естественно), это только то, что ее характеризует. И это то, что при одинаковой силе дает одинаковой ускорение. А что это такое? А это и есть количество вещества, хоть ты прямо так напиши, хоть заумно, как это сделано современными физиками. Ведь смысл зауми определения «инертной» массы в том, чтобы и сообщить читателям, что это количество вещества, но ни в коем случае не показать прямо, что это количество вещества. Как иначе объяснить натужное определение того, что такое масса: не прямо, как это делают нормальные физики, а как силы, деленной на ускорение? Ну, ладно, это все же количество вещества и размерность этой массы в килограммах не вызывает возражений.

Но то, что современные физики называют «гравитационной» массой, это ведь вес или, иными словами, сила притяжения. Это то, что в мое время в школе требовали никак не путать с массой, для чего в учебнике были даже картинки, поясняющие образно, что вес (сила притяжения масс друг к другу) определяется пружинными весами, а масса – чашечными, сравнивающими отношение весов замеряемой массы с весом гирь. Но, как видим, современные физики умышленно подменяют физическую величину «сила» притяжения, физической величиной «масса». Зачем?

Затем, что это еще не все свойства объекта, на которые современные физики налепили название масса. Вернитесь к концу первого абзаца: современные физики сообщают, что масса это то же самое, что и энергия (по современным представлениям —масса  эквивалентна энергии покоя).

То есть, три различных и НЕ ОБЪЕДИНЯЕМЫХ свойства объекта – количество вещества в теле, силу, с которой тело притягивается к другому телу и работу, которую необходимо выполнить, чтобы изменить скорость тела, — современные физики объединяют вместе и называют одним словом «масса».

Почему эти свойства не объединяемы? Не только ввиду разного физического смысла этих свойств, но хотя бы потому, что у физических величин, количественно описывающих эти свойства, размерность разная: только количество вещества измеряется в килограммах, но даже у современных физиков гравитационная сила измеряется в ньютонах, а работа (энергия) в джоулях.

Задача науки прояснить вопросы, а мы видим, как абсолютно ясный вопрос тщательно запутывается, введением понятия «мера инертности», которое до Теории относительности никому и даром не требовалось и не требуется.

А в «самое знаменитое уравнение в мире» не менее знаменитые современные физики в качестве массы m ставят «эквивалент энергии покоя». Но отсюда следует, что будь они честными людьми (или умными), то (исходя их физического смысла их меры инертности) они обязаны были бы в пресловутой формуле энергии Е=mс2 размерность «массы» давать в джоулях, а не в килограммах. А как иначе, если их «масса» это эквивалент энергии, а не количества вещества?

Но ведь и сама энергия Е в «самом знаменитом уравнении в мире» измеряется в джоулях! И если в уравнении Е=mс2 для m, вместо килограммов количества вещества подставить меру инертности в джоулях, то по размерности «самое знаменитое уравнение» приобретает вид: джоули равны джоулям, умноженным на метр квадрат и деленные на секунду квадрат. Но ведь это же получается не уравнение, а малограмотный бред!

Только руками развести!

И, кстати, такой же идиотский по своей размерности вид получат и все уравнения классической механики и химии. Это к вопросу, почему нормальная физика и продолжает утверждать, что масса это все же количество вещества.

Что получается? Современные «ученые» взяли аналог точного и имеющего физический смысл уравнения кинетической энергии, дающего размерность в джоулях, объявили, что заменили в этом аналоге количество вещества мерой инертности, но чтобы идиотизм замены не бросался в глаза, размерность этой «меры инертности» оставили в килограммах, то есть, оставили размерность количества вещества.

«Видите, Балаганов, что можно сделать из простой швейной машины Зингера? Небольшое приспособление — и получилась прелестная колхозная сноповязалка».

Я, по примеру О. Бендера, тоже хочу обратить внимание публики на «самое знаменитое уравнение в мире»: и эдакие махинации теперь называются наукой?!

Совсем плохо

Возникает вопрос: зачем? Зачем эйнштейнисты сделали эту подтасовку массы «мерой инертности»? Думаю, что не от хорошей жизни – у них просто не было иного выхода. Ведь Эйнштейн доработал уравнение Пуанкаре Е=mс2 своим знаменателем, а при скоростях объекта, равных скорости света, этот знаменатель обращается в нуль, а энергия, согласно доработанного Эйнштейном уравнения Пуанкаре, превращается в бесконечность.

Но ведь требовалось объяснить, за счет чего энергия становится бесконечностью? Квадрат скорости света величина постоянная, значит, до бесконечности растет масса. Но, как и почему из-за увеличения скорости в объекте начнет увеличиваться до бесконечности количество вещества – количество протонов, нейтронов, электронов? Со всей Вселенной сбегаются в этот летящий со скоростью света объект?

Вот и пришлось выдумывать бред про то, что масса это не количество вещества, а некий секундомер, меряющий способности тела без воздействия силы сохранять постоянную скорость килограммами, которые одновременно являются ньютонами и немножко джоулями.

Есть комментаторы, которые тут же начинают кричать: «А ты изучи (как мы, несчастные, изучили) Теорию относительности Эйнштейна, а потом будешь ее критиковать!» Джентльмены, ту писанину, которую вы изучили и предлагаете изучить мне, выбросят в макулатуру, как только государство начнет платить физикам не за писанину, а за результаты их работы, нужные в реальной жизни.

Ну, хорошо, уговорили. Вот читаю преподавателя курса величия Эйнштейна:

«Из последнего уравнения видно, что макроскопическому телу (например, килограммовой гире) практически невозможно придать скорость, близкую к скорости света, так как при этом масса гири, увеличиваясь с ростом ее скорости, стремилась бы к бесконечности. Естественно, возникает вопрос: существуют ли вообще такие частицы, скорости которых равны скорости света?

Забегая немного вперед, скажем: да, существуют. Такой частицей является квант электромагнитного поля, нейтральная (не имеющая электрического заряда) элементарная частица переносчик электромагнитного взаимодействия (а значит, и света) фотон, масса покоя которого равна нулю (tn0 = 0). Ну конечно, скажем мы, уж если бы переносчик света не имел скорости света, дело было бы совсем плохо».

На мой взгляд, скажу я, дело совсем плохо, когда как бы физике учат люди, у которых в мозгу совмещаются понятия «частица» и понятие «масса равна нулю». Если в этой частице нет вещества, то эта частица — это ТО, ЧЕГО НЕТ.

Попробуем образно представить себе эту частицу без вещества — фотон. Фотон не движется, массы нет, значит, ничего нет. Потом крики: смотрите, смотрите – полетел, полетел! Кто полетел? Фотон полетел со скоростью света! То, чего нет, полетело со скоростью света?!

А как себе представить полет того, чего нет? Для того, чтобы что-то полетело, нужно приложить к нему силу. Как приложить силу к тому, чего нет? И к вопросу о частицах. Частица – это кусочек чего-то большего, отсюда кусочек того, чего нет, может быть частицей только чего-то большего, чего тоже нет, не правда ли?

Люди, которые при наличии окружающего нас реального и интереснейшего мира, так увлеченно изучают то большое-большое, чего нет, а потом взахлеб рассказывают другим о свойствах того, чего нет, заслуживают соболезнования. Мне как-то не хочется к ним присоединяться, даже если они все в шоколаде от этого не пыльного занятия.

Остается только воскликнуть: и эти люди, у которых в мозгах со скоростью света летает то, чего нет, запрещают мне считать торию Эйнштейна бредом??

Подтверждение опытом

А как же, — коварно спросите вы, — космические достижения и атомная энергетика? Ведь они все основаны на Теории относительности Эйнштейна! И эта теория блестяще подтверждена практикой!

Сейчас в Интернете много статей на эту тему. Я взял статью некоего О.Х. Деревенского, к ней дается эпиграф: «Теория относительности так надёжно подтверждена опытом, что сегодня сомневаться в этом могут лишь совсем необразованные люди». (Из сборника «Шутки больших учёных»). Как вы поняли, то, что релятивистская физика подтверждена опытом, это анекдот.

Что же касается большой пользы от ТО, то действительно, по теории Эйнштейна космические корабли бороздят просторы Большого театра, а защищаемые от террористов атомные электростанции во всех художественных фильмах из Голливуда тоже построены по теории Эйнштейна. Но в реальной жизни эта теория еще никогда и никому ничего (кроме огромных убытков) не принесла. Помянутый Деревенский в своей работе написал об этом очень много, но поскольку он физик и написал соответственно, то я возьму всего один эпизод, кажущийся мне понятным каждому.

«В 1961 г. группа под руководством Котельникова провела удачную радиолокацию Венеры – не импульсами, а именно узкополосным сигналом. Причём, принцип детектирования эхо-сигнала был основан на выделении его из шумов в очень узкой полосе. А чтобы он в эту полосу попал, требовалось, по релятивистским меркам, компенсировать огромный допплеровский сдвиг, соответствующий удалению Венеры со скоростью более 2 км/с.

Так вот, результат оказался ошеломляющим. Когда компенсация допплеровского сдвига проводилась, никаких эхо-сигналов не обнаружилось. А когда компенсация НЕ проводилась, эхо-сигналы убедительно обнаруживались!    Об этом секрете удачной радиолокации Венеры мало кто знает. Даже за словесную критику ТО можно было не только распрощаться с научной карьерой, но и скоротать остаток жизни в психлечебнице. А тут получился не просто трёп, а убийственный для ТО опытный факт… 

…Вот так и вышло, что специалисты по дальней космической связи, управлявшие автоматическими межпланетными станциями, тоже пребывали в несокрушимой уверенности насчёт того, что линейный эффект Допплера здесь определяется скоростью удаления космического аппарата от наземной антенны, или, наоборот, скоростью его приближения к ней. Так говорит ТО! Какие, мол, сомненья?!

Вот так, под знаменем ТО, и летели аппараты к Венере и к Марсу. А когда долетали они до чужой сферы тяготения и пересекали её границу – радиосвязь с ними немедленно пропадала, и операторам только и оставалось, что помахать им ручкой. Вот так, под знаменем ТО, и потеряли целый ряд советских и американских аппаратов на первых подлётах к Венере и Марсу».

Говоря по-простому, общество затратило огромные деньги на экспедиции к Венере, но из-за Теории относительности эти деньги были выброшены псу под хвост.

Ну, и так далее.

Проблема эфира

Есть еще вопрос – почему физики пошли на этот бред относительности? Оказывается, на рубеже позапрошлого и прошлого веков у физиков-теоретиков возникла проблема. Сторонники и критики ТО рассказывают о ней так (выделено мною, — Ю.М.).

Сторонник: «В 1887 году физика была в тупике: опыт с интерферометром, поставленный Майкельсоном и Морли, не обнаружил тех эффектов, которые должны были бы иметь место в соответствии с тогдашними представлениями в науке. Эти представления таковы: Ньютон в 1687 году постулировал существование абсолютного пространства и абсолютного времени.

Френель в 1820 году выдвинул волновую теорию света, в соответствии с которой распространение световой волны имеет место по отношению к бестелесной среде – эфиру, заполняющей все бесконечное пространство. Этот эфир представлялся межзвездной субстанцией, наподобие тому, как воздух окружает нас в обыденной жизни. При этом он обладал жесткостью наподобие твердого тела и был легче любого газа».

Критик:«Ради исторической справедливости напомним, что вышеупомянутый «жуткий кризис» случился из-за представлений о природе света. Которые были, мол, больно наивными. А особенно – у Лорентца, чья концепция по законченности своей наивности была самой выдающейся.

Всё пространство у него было под завязку заполнено особой субстанцией – эфиром.

Механические напряжения в этой субстанции описывались уравнениями Максвелла. Читаешь Лорентца и изумляешься: становится совершенно понятно, почему уравнения Максвелла именно таковы, каковы они есть. А также – почему в эфире возможны упругие волны. Которыми, как считалось, и был свет. Причём, эта эфирная концепция охватывала и вещество тоже! Лорентц представлял «частички материи» как могущие свободно передвигаться «местные модификации в состоянии эфира». Развив теорию Максвелла на случай присутствия электрических зарядов и выведя законы их взаимодействия и движения, Лорентц объяснил все известные тогда явления в оптике, электродинамике, а также в испускании и поглощении тепла».

Знакомый доктор физико-математических наук объяснил мне это проще. Все открытые и необъясненные в то время явления объяснялись, если принять, что пространство Вселенной заполнено эфиром, причем, эфир должен был иметь свойства твердого тела. Но ведь другие твердые тела перемещаются по Вселенной без сопротивления, не теряют скорости. Как одно твердое тело может перемещаться сквозь другое твердое тело без сопротивления с его стороны?? Вот это физики-теоретики объяснить не могли.

Ну и что? Надо было продолжать эксперименты и искать объяснения этому вопросу. Но в то время физиков уже начали заменять теоретики, а теоретики пошли простым путем – путем голых умствований: они то, что не могли объяснить (эфир), объявили не существующим, а в качестве объяснений уже известных явлений приняли бред Эйнштейна. И так с этим бредом до сих пор и живут, не принося обществу ни малейшей пользы.

А можно было в то время объяснить, как одно твердое тело проникает сквозь другое твердое тело без сопротивления? Уверен, если бы так вопрос и был поставлен, то, со временем, физики его и объяснили бы. Например, так, как объясняю это я.

Проделаем мысленный эксперимент, который легко воспроизвести в натуре. Возьмем две поверхности, скажем, две гладкие доски, на одной из них выполним сферические лунки диаметра, при котором капелька ртути близка к шару, и глубиной, при которой капелька ртути этого диаметра отрывается от объема ртути под действием силы тяжести. Расположим в этих лунках на этой доске капельки ртути. Это будет двухмерная модель эфира. Затем обе доски наклоним и будем спускать по ним лужицы ртути одного размера. Эти лужицы будут моделью элементарных частиц атомов твердого тела. Выступающие из лунок капельки ртути должны, казалось бы, являться препятствием движению лужицы на доске с лунками, казалось бы, и-за них движение лужицы должно тормозиться.

Но на самом деле не будет никакого сопротивления движению этой лужицы. Поскольку силы поверхностного натяжения у фронта лужицы ртути будут подтягивать лужицу вперед (ускорять ее), но силы поверхностного натяжения отрывающихся в лунки капель ртути у заднего края лужицы, будут тормозить ее. Вместе эти силы уравновесят друг друга, а в итоге лужицы на обеих досках будут спускаться по наклонной поверхности с одинаковой скоростью, как бы вовсе без сопротивления.

Точно так же (уравновешивая друг друга) будут действовать и силы, структурирующие частицы эфира в кристаллическую решетку твердого тела.

Я не предлагаю это решение в качестве модели или в качестве единственной модели эфира, просто хочу показать, если эфир состоит из вещества, из которого состоят элементарные частицы (электроны, протоны, нейтроны и те частицы, из которых, возможно, состоят элементарные частицы), то тогда твердые тела будут проходить сквозь эфир без сопротивления, а эфир, тем не менее, будет иметь свойства твердого тела.

В любом случае, не было никакой необходимости отказываться от эфира, вытаскивать из музеев архаические приемы формирования гипотез с помощью постулатов, и превращать явственно бредовую гипотезу в «единственно правильную» теорию.

***

Я знаю, что бесполезно переубеждать в чем-то людей, которых с юности в университете прибило пыльным мешком какого-либо «единственно верного учения». И у меня единственное требование к теоретикам таких учений – за свой счет! Исключительно за свой счет! Как сегодня правоверные марксисты.

А общество может платить только за полезные обществу результаты.

Ю.И. МУХИН

Формула вращательной инерции — GeeksforGeeks

Инерция — это качество тела, которое сопротивляется любой силе, стремящейся сдвинуть его или, если оно движется, изменить величину или направление его скорости. Вращательная инерция определяет то же самое для вращающегося объекта. Это скалярная величина, прямо пропорциональная массе и радиусу вращающегося объекта. В механике вращения функция инерции вращения аналогична массе в линейной механике. Это также зависит от того, как эта масса распределяется вдоль оси вращения. Он используется для вычисления углового момента и для объяснения того, как изменяется вращательное движение при изменении распределения массы.

Формула инерции вращения

Формула инерции вращения вращающегося объекта равна произведению массы на квадрат радиуса его круговой траектории. Он обозначается символом I. Его единица измерения составляет кгм ² , а размерная формула определяется как [M ¹ L ² T ⁰ ].

I = mr ²

Где,

• I — инерция вращения
• m — масса вращающегося объекта
• r радиус окружности

Пример вопроса

Вопрос 1. Рассчитайте инерцию вращения объекта массой 20 кг и радиусом 4 м.

Решение:

Мы имеем,

M = 20

R = 4

Используем формулу, которую мы имеем,

I = MR ²

= 20 × 4

=. 320 кг·м ²

Вопрос 2. Рассчитайте инерцию вращения тела массой 25 кг и радиусом 6 м.

Решение:

Мы имеем,

M = 25

R = 6

Используем формулу, которую мы имеем,

I = MR ²

= 25 × 6

= 900 кг м ²

Вопрос 3. Рассчитайте инерцию вращения тела массой 11 кг и радиусом 4 м.

Решение:

Имеем,

m = 11

r = 4

Используя формулу имеем,

I = MR ²

= 11 × 4 × 4

= 176 кг M ²

Вопрос 4. Рассчитайте массу объекта, если его вращательная инерция составляет 300 кг M ² и. радиус 10 м.

Решение:

У нас есть

I = 300

R = 10

Используем формулу, которую мы имеем,

I = MR ²

=> M = I/R ²

=> m = 300/(10 × 10)

=> m = 300/100

=> m = 3 кг

Вопрос 5. Вычислите массу тела, если инерция его вращения равна 450 кг m ² , а радиус равен 15 м.

Решение:

,

I = 450

R = 15

Используем формулу,

I = MR ²

=> M = I/R ²

=> m = 450/(15 × 15)

=> m = 450/225

=> m = 2 кг

Вопрос 6. Вычислите радиус тела, если его инерция вращения 540 кг m ² и масса 15 кг.

Решение:

,

I = 540

R = 15

Используем формулу, которую мы имеем,

I = MR ²

=> R ² = I/ I/ I/ I/ I/ I/ I/ I/ I/ I/ I/ I/ I/ I/ m

=> r ² = 540/15

=> r ² = 36

=> r = 6 м

Вопрос 7. Вычислите радиус тела, если его инерция вращения равна 972 кг м ² , а масса равна 12 кг.

Решение:

У нас есть

I = 972

R = 12

Используем формулу, которую мы имеем,

I = MR ²

=> R ² = I/ I/ I/ I/ I/ I/ I/ I/ I/ I/ m

=> r ² = 972/12

=> r ² = 81

=> r = 9m

Как рассчитать момент инерции нагрузки

Помимо крутящего момента или скорости, при выборе двигателя следует учитывать еще один фактор.

Вы когда-нибудь задумывались, чем колеса и шины гоночного велосипеда отличаются от горного? Это связано с тем, что в гоночных велосипедах для повышения производительности используются более легкие и тонкие колеса. Более легкие и тонкие колеса уменьшают момент инерции колес; облегчая торговлю вразнос. В гонках, где счет идет на миллисекунды, немного значит очень много.

Что такое «Инерция»?

Инерция происходит от латинского слова iners , означающего праздный или вялый. Инерция определяется как сопротивление любого физического объекта любому изменению его скорости. Чем больше инерция, тем более устойчивым он будет к ускорению или замедлению.

Что такое «инерция нагрузки»?

Инерция нагрузки или момент инерции — это сопротивление любого физического объекта любому изменению его скорости с точки зрения оси вращения.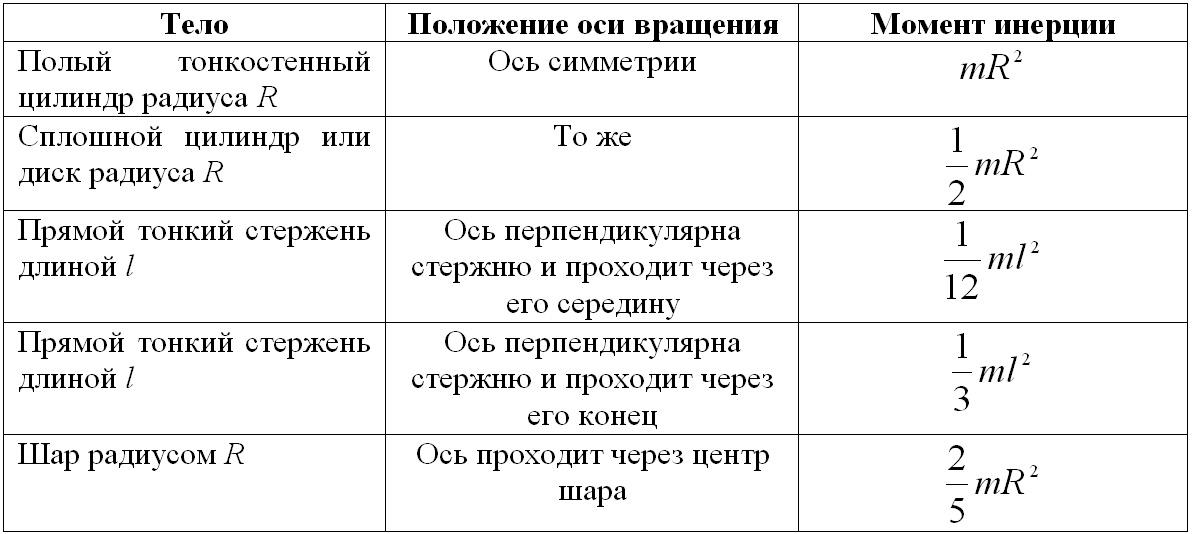 Для вращающейся нагрузки это произведение ее массы на квадрат перпендикулярного расстояния массы от оси. Инерция нагрузки обычно обозначается буквой «J».

Что такое «Допустимая инерция нагрузки» и «Коэффициент инерции»?

Двигатели не могут управлять бесконечной инерцией нагрузки. Производители часто предлагают допустимую инерцию нагрузки или значение коэффициента инерции для двигателей, чтобы помочь с размером двигателя.

Допустимая инерция нагрузки Значения являются ориентировочными, обычно приводимыми для двигателей переменного тока и бесщеточных двигателей (примеры приведены в конце поста). Коэффициент инерции с обычно дается для шаговых или серводвигателей и рассчитывается путем деления общей величины инерции нагрузки (или отраженной инерции нагрузки, если используется редуктор) на инерцию ротора двигателя. Если эти значения превышены, двигатель может пропускать шаги, глохнуть или вибрировать. Двигатели с замкнутым контуром могут работать с большим коэффициентом инерции, чем двигатели с незамкнутым контуром.

 

Пример: рекомендуемые допустимые коэффициенты инерции

Тип двигателя	Размер корпуса (мм)	Типоразмер (NEMA)	Коэффициент инерции
Шаговые двигатели с разомкнутым контуром	20, 28, 35	8, 11, 14	5:1 или меньше
Шаговые двигатели с разомкнутым контуром	42, 50, 56,4, 60, 85	17, 20, 23, 24, 34	10:1 или менее
Шаговые двигатели с замкнутым контуром	—	—	30:1 или менее
Серводвигатели (автоматическая настройка)	—	—	50:1 или менее
Серводвигатели (ручная настройка)	—	—	100:1 или менее

 

СОВЕТ : Если вам необходимо превысить коэффициент инерции нагрузки. ..

Помните, что это безопасная рекомендация, и эти значения могут быть превышены при правильной настройке. Я помню, как разговаривал с кем-то, кто строил игровые автоматы для казино (старые с рычагом). Его команда использовала шаговый двигатель для вращения цилиндров, которые определяли, продолжаете ли вы выполнять свою основную работу или нет. Благодаря правильному профилю движения, медленному разгону и замедлению и повторным испытаниям они смогли использовать двигатель, который превышал эти допустимые значения… намного.

 

Как рассчитать инерцию нагрузки?

Давайте рассмотрим несколько распространенных примеров, чтобы увидеть, как рассчитывается инерция нагрузки. Во-первых, фундаментальное уравнение для инерции (J) показано ниже.

 

Уравнение фундаментальной инерции (Дж)

 

Не беспокойтесь. Существуют упрощенные формы этой формулы. Пять различных упрощенных уравнений для пяти общих нагрузок (объектов) показаны ниже для сплошного цилиндра, полого цилиндра, прямоугольного объекта, прямоугольного объекта со смещенной от центра осью и объекта в линейном движении.

 

Выберите соответствующее уравнение на основе:

• Форма груза (объекта) в движении
• Ось вращения (x или y)
• Подробная информация предоставлена ​​(у вас есть вес груза?)

 

Например, если указан вес и вы рассчитываете объемный цилиндр, вращающийся вокруг своей оси x, используйте первое уравнение ( Jx ) ниже (с массой « м «). Если масса не указана, но известны диаметр, толщина и плотность материала груза, то инерцию груза можно рассчитать по второму уравнению ( Jx) ниже (с плотностью « p «).

 

Inertia of a Cylinder or Disc (as from the x or y axis)

 

 

Inertia of a Hollow Cylinder (as from the x or y axis)

 

 

Инерция прямоугольного объекта (относительно оси x или y)

 

 

Инерция прямоугольного объекта со смещенной от центра осью

Инерция объекта в линейном движении

898

Блок измерения
Блок измерения	.

Единицы инерции обычно используются двумя способами: унций-дюйм² и унций-дюйм² . Первое включает гравитацию, второе — только массу. Теоретически инерция является фактором массы, поэтому она не должна включать гравитацию, однако практически мы не можем легко измерить массу на Земле.

Oriental Motor обычно обеспечивает инерцию в унциях на дюйм². Затем, когда мы вычисляем момент ускорения, мы делим общую инерцию на силу тяжести.

 

Сила тяжести = 386 дюймов/сек²

• унций-дюйм²  = Инерция в зависимости от веса
• унций-в-сек²  = инерция на основе массы

Преобразование унций-дюйм² в унции-дюйм-сек²

 

Для выполнения этих расчетов может потребоваться дополнительная информация, например плотность материала. Это необходимо для расчета веса объекта. Больше можно найти с помощью простого онлайн-поиска.

 

 

Пример: расчет инерции нагрузки

Попробуйте рассчитать инерцию нагрузки для следующего приложения. Для каких частей вам нужно произвести расчет?

 

Вам потребуется сложить все значения инерции нагрузки всех компонентов, приводимых в движение двигателем. Это включает в себя груз, ремень и ролики. Вам нужно будет использовать 2 разных уравнения.

 

 

Из того, что мы узнали в , вот расчет момента нагрузки.

 

 

Работа с большой инерцией нагрузки? Используйте мотор-редуктор

Если вы имеете дело с большой инерцией нагрузки, есть простой способ уменьшить ее в геометрической прогрессии. Инерция нагрузки уменьшается на квадрат передаточного отношения. Полученное значение представляет собой инерцию отраженной нагрузки , который представляет собой инерцию нагрузки на валу двигателя (в отличие от инерции нагрузки на валу редуктора).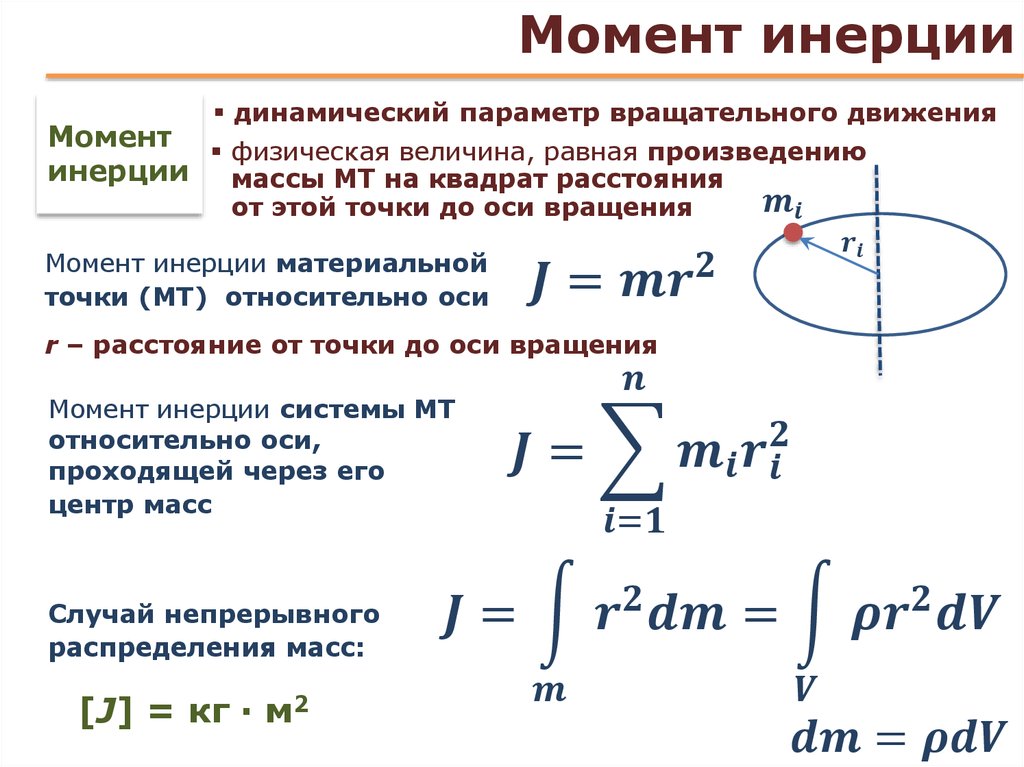

 

 

Если вам интересно узнать больше, вот информационный документ, в котором обсуждается, как использовать редукторы для уменьшения инерции нагрузки. Это специально для шаговых двигателей.

 

 

Где я могу найти «Допустимая инерция нагрузки»?

Теперь, когда вы рассчитали общее значение инерции нагрузки, как найти двигатель, который может с этим справиться?

Вот пример таблицы допустимой инерции нагрузки для бесколлекторного двигателя серии BLE2 мощностью 200/400 Вт (из нашего каталога). Поскольку мы уже рассчитали максимально допустимые значения инерции нагрузки для каждого передаточного числа, вам не нужно этого делать. Старайтесь не превышать эти значения . Двигатели могут продолжать работать, если эти значения превышены, но это не может быть гарантировано.

 

 

Если у вас нет нашего каталога, мы также перечислим Допустимое значение инерции нагрузки на сайте .

 

 

Для шаговых двигателей или серводвигателей допустимые значения инерции нагрузки не публикуются , поэтому используйте рекомендуемые значения коэффициента инерции.

На данный момент это инерция нагрузки. Помните, что инерция нагрузки — это лишь один из трех расчетов, необходимых для правильного определения размера двигателя (не забывайте о крутящем моменте и скорости). В следующем посте «Основы расчета двигателя» я объясню, как инерция нагрузки влияет на другую составляющую крутящего момента — 9.0309 крутящий момент ускорения , который также важен для определения общего требования к крутящему моменту для приложения (и является основной причиной того, почему гоночные велосипеды легче крутят педали, чем обычные велосипеды).

 

Нужно освежить знания? Вот официальный документ по габаритам двигателя (из последнего поста).

 

В следующем посте я объясню, как рассчитать момент ускорения, среднеквадратический момент и скорость.