Индуктивность соленоида
Соленоид —
длинная, тонкая катушка, то есть катушка,
длина которой намного больше, чем её
диаметр (также в дальнейших выкладках
здесь подразумевается, что толщина
обмотки намного меньше, чем диаметр
катушки). При этих условиях и без
использования магнитного материала
плотность магнитного потока 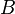 внутри
катушки является фактически постоянной
и (приближенно) равна
внутри
катушки является фактически постоянной
и (приближенно) равна
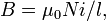
где 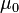 − магнитная
постоянная,
− магнитная
постоянная, 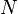 −
число витков,
−
число витков, 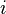
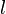 −
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида, получим[16],
что потокосцепление через катушку равно
плотности потока
−
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида, получим[16],
что потокосцепление через катушку равно
плотности потока 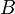 ,
умноженному на площадь поперечного
сечения
,
умноженному на площадь поперечного
сечения 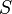 и
число витков
и
число витков 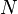 :
: 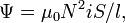
Отсюда следует формула для индуктивности соленоида (без сердечника):
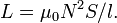
Если
катушка внутри полностью заполнена
магнитным материалом (сердечником), то
индуктивность отличается на
множитель 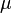 — относительную
магнитную проницаемость[17]сердечника:
— относительную
магнитную проницаемость[17]сердечника:
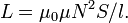
В
случае, когда 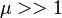
Более точные формулы для соленоида конечного размера
Для однослойного (с очень тонкой намоткой) соленоида конечных размеров (не бесконечно длинного) существуют более точные, хотя и более сложные формулы[18]:
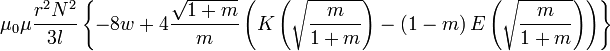
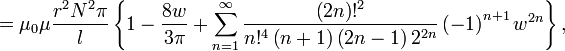
где
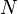 —
количество витков,
—
количество витков,  —
радиус цилиндра,
—
радиус цилиндра,
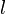 —
длина его образующей,
—
длина его образующей,
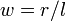 ,
,
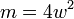 ,
,
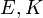
Это дает
для
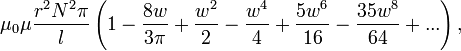
для

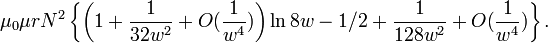
Трансформатор. Энергия магнитного поля. Основы теории Максвелла. Уравнения Максвелла в интегральной форме.
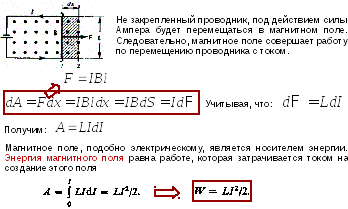


Электрический колебательный контур. Затухающие электромагнитные колебания. Вынужденные электромагнитные колебания. Явление резонанса
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания
Резонансная частота контура определяется так называемой формулой Томсона:
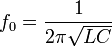
Принцип действия
Пусть
конденсатор ёмкостью C заряжен
до напряжения 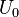 . Энергия,
запасённая в конденсаторе составляет
. Энергия,
запасённая в конденсаторе составляет
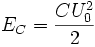
При
соединении конденсатора с катушкой
индуктивности, в цепи потечёт ток 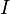
Затем
результирующий ток в цепи будет
возрастать, а энергия из конденсатора
будет переходить в катушку до полного
разряда конденсатора. В этот момент
электрическая энергия конденсатора 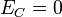
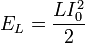 ,
где
,
где 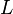 — индуктивность катушки,
— индуктивность катушки, 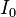 —
максимальное значение тока.
—
максимальное значение тока.
После
этого начнётся перезарядка конденсатора,
то есть заряд конденсатора напряжением
другой полярности. Перезарядка будет
проходить до тех пор, пока магнитная
энергия катушки не перейдёт в электрическую
энергию конденсатора. Конденсатор, в
этом случае, снова будет заряжен до
напряжения 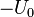
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.
Стоит
заметить, что помимо простого колебательного
контура, есть ещё колебательные контуры
первого, второго и третьего рода, что
учитывают потери и имеют другие
особенности.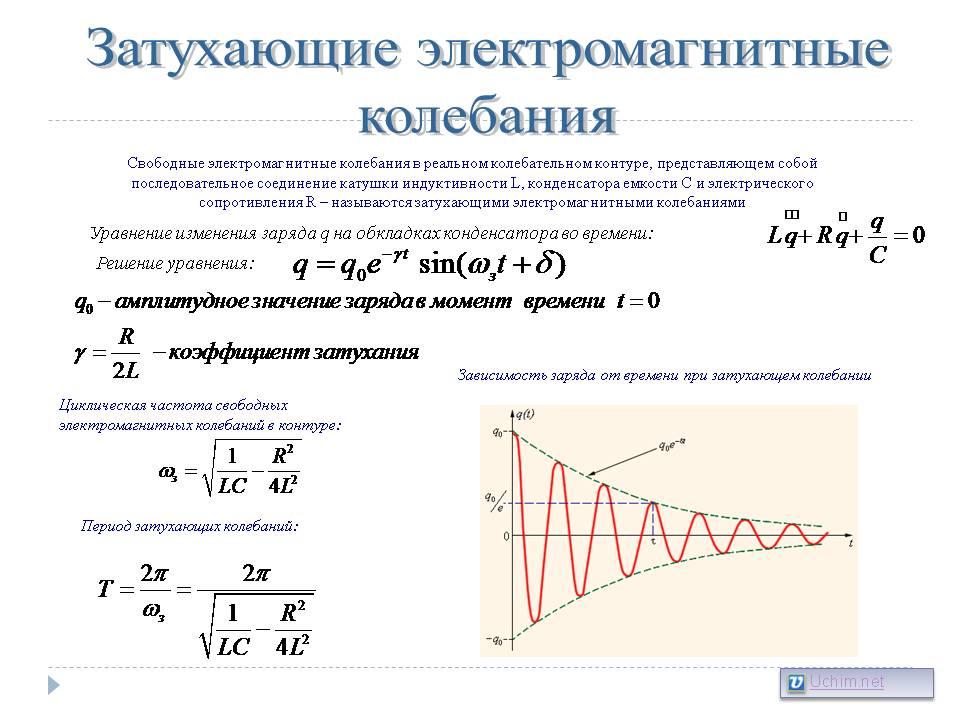
Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Внешним источником ЭДС в электрических цепях являются генераторы переменного тока, работающие на электростанциях.
Принцип действия генератора переменного тока легко показать при рассмотрении вращающейся рамки провода в магнитном поле.
В однородное магнитное поле с индукцией В помещаем прямоугольную рамку, образованную проводниками (abсd).
Пусть плоскость рамки перпендикулярна индукции магнитного поля В и ее площадь равна S.
Магнитный поток в момент времени t0 = 0 будет равен Ф = В*8.
При
равномерном вращении рамки вокруг оси
OO
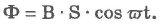
Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную
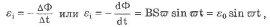
где Е0= ВSw — амплитуда ЭДС.
Если с помощью контактных колец и скользящих по ним щеток соединить концы рамки с электрической цепью, то под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, в электрической цепи возникнут вынужденные гармонические колебания силы тока — переменный ток.
На практике синусоидальная ЭДС возбуждается не путем вращения рамки в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора — неподвижных обмоток, навитых на сердечники из магнитомягкого материала. В этих обмотках находится переменная ЭДС, что позволяет избежать снятия напряжения с помощью контактных колец.
Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.
Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.
Акопов Вачакан Ваграмович /AkopovVachakanVagramovich – учитель физики МОУ СОШ №6, Ставропольский край Курский район,село Полтавское Аннотация: в статье представлен вывод формул индукции поля соленоида, созданного переменным током. Эту формулу можно использовать для углубленного изучения учащимися темы «Магнитное поле» и при решении задач. Ключевые слова: индукция, соленоид, магнитный поток, частота, индуктивность, индуцированное напряжение, мощность переменного тока. При переменном токе соленоид создаёт переменное магнитное поле. При этом, как известно, индуктивность соленоида определяется формулой [1, с.101]: L =  , где (1)гдеU – индуцированное в соленоиде напряжение,n – частота переменного тока,I – сила переменного тока.С другой стороны индуктивность соленоида определяется формулой [2, с.253]: L = , где (1)гдеU – индуцированное в соленоиде напряжение,n – частота переменного тока,I – сила переменного тока.С другой стороны индуктивность соленоида определяется формулой [2, с.253]: L =  , (2)где Ф – магнитный поток соленоида.Приравнивая выражения (1) и (2), получим: Ф = , (2)где Ф – магнитный поток соленоида.Приравнивая выражения (1) и (2), получим: Ф =  . (3)При этом полный магнитный поток соленоида определяется и другой формулой [2, с.242]: Ф =В×S×N . (3)При этом полный магнитный поток соленоида определяется и другой формулой [2, с.242]: Ф =В×S×N  , (4)гдеВ – индукция магнитного поля,N – число витков соленоида,S– площадь поперечного сечения магнитного поля.Приравняв выражения (3) и (4), получим В = , (4)гдеВ – индукция магнитного поля,N – число витков соленоида,S– площадь поперечного сечения магнитного поля.Приравняв выражения (3) и (4), получим В =  . (5)Таким образом, индукция поля соленоида, созданного переменным током, прямо пропорциональна индуцированному в соленоиде напряжению. Как известно, магнитную индукцию поля, созданного постоянным током, текущим по виткам бесконечно длинного соленоида, внутри этого соленоида на его оси определяют по формуле [2, с.232]: В = . (5)Таким образом, индукция поля соленоида, созданного переменным током, прямо пропорциональна индуцированному в соленоиде напряжению. Как известно, магнитную индукцию поля, созданного постоянным током, текущим по виткам бесконечно длинного соленоида, внутри этого соленоида на его оси определяют по формуле [2, с.232]: В =  (в вакууме), (6)гдеn=NI – число ампер-витков соленоида,l – длина соленоида,µо –магнитная постоянная.Единица магнитной индукции (тесла) может быть установлена по формуле (6): [В] = (в вакууме), (6)гдеn=NI – число ампер-витков соленоида,l – длина соленоида,µо –магнитная постоянная.Единица магнитной индукции (тесла) может быть установлена по формуле (6): [В] =  × × = = , (7)С другой стороны единица магнитной индукции (тесла) может быть установлена по формуле (5): [В] = , (7)С другой стороны единица магнитной индукции (тесла) может быть установлена по формуле (5): [В] =  , (8)Перемножив выражения (7) и (8), получим:[В]2 = , (8)Перемножив выражения (7) и (8), получим:[В]2 =  × × = =  = =  , (9)Тогда заменив единицы измерения в выражении (9) физическими величинами, получим формулу для индукции поля соленоида, созданного переменным током:В2 = , (9)Тогда заменив единицы измерения в выражении (9) физическими величинами, получим формулу для индукции поля соленоида, созданного переменным током:В2 =  ,отсюда В = ,отсюда В =  , (10)где V — объём соленоида,Р – мощность переменного тока.Таким образом, индукция магнитного поля соленоида увеличивается при увеличении мощности переменного тока и уменьшается при увеличении объёма соленоида.Задача 1. Магнитная индукция поля внутри соленоида, состоящего из 2000 витков диаметра 2,8см, подключённого к источнику переменного тока с частотой 50Гц, равна 0,72мТл. Каково индуцированное в соленоиде напряжение? , (10)где V — объём соленоида,Р – мощность переменного тока.Таким образом, индукция магнитного поля соленоида увеличивается при увеличении мощности переменного тока и уменьшается при увеличении объёма соленоида.Задача 1. Магнитная индукция поля внутри соленоида, состоящего из 2000 витков диаметра 2,8см, подключённого к источнику переменного тока с частотой 50Гц, равна 0,72мТл. Каково индуцированное в соленоиде напряжение?
|
||
Coil32 — Однослойная катушка
Расчет индуктивности однослойной катушки
Однослойная катушка индуктивности представляет собой провод, свернутый в спираль. Для придания жесткости, провод обычно наматывают на цилиндрический каркас. Поэтому в Coil32 в качестве исходных параметров приняты размеры каркаса и диаметр провода, т.к. их легче измерить практически. В расчетных формулах, однако, используются геометрические параметры самой спирали. Во избежании путаницы на этой страничке справки можно подробнее ознакомиться с этими тонкостями.
Однослойные катушки получили широкое распространение, особенно для конструкций коротковолнового и средневолнового любительских и радиовещательных диапазонов. Основные свойства однослойных катушек — высокая добротность, относительно небольшая собственная емкость, удобство изготовления. Рассмотрим методы расчета такой катушки без промежутка между витками — «виток к витку«…
 Начнем с того, что в конце XIX века Х.А.Лоренц вывел формулу с применением эллиптических интегралов для расчета соленоида. Отличием модели Лоренца от модели Максвелла являлся тот момент, что витки соленоида представлялись не бесконечно тонким круговым проводом, а бесконечно тонкой спиральной проводящей лентой с шириной равной реальной толщине провода, без промежутка между витками. Формула имеет высокую точность при расчете реальной катушки в случае если последняя имеет большое количества витков и имеет намотку виток к витку. В 1909 г. японский физик Х.Нагаока преобразовал формулу Лоренца и привел ее к виду из которого следовал важный вывод — индуктивность соленоида зависит исключительно от формы и размеров катушки. Формула Нагаока имеет следующий вид:
Начнем с того, что в конце XIX века Х.А.Лоренц вывел формулу с применением эллиптических интегралов для расчета соленоида. Отличием модели Лоренца от модели Максвелла являлся тот момент, что витки соленоида представлялись не бесконечно тонким круговым проводом, а бесконечно тонкой спиральной проводящей лентой с шириной равной реальной толщине провода, без промежутка между витками. Формула имеет высокую точность при расчете реальной катушки в случае если последняя имеет большое количества витков и имеет намотку виток к витку. В 1909 г. японский физик Х.Нагаока преобразовал формулу Лоренца и привел ее к виду из которого следовал важный вывод — индуктивность соленоида зависит исключительно от формы и размеров катушки. Формула Нагаока имеет следующий вид:
 |
[2] |
, где
- Ls — индуктивность катушки
- N — число витков катушки
- r — радиус намотки
- l — длина намотки
- kL — коэффициент Нагаока
Важнейшим выводом из анализа этой формулы был тот, что коэффициент Нагаока зависел только от отношения l/D, который был назван форм-фактором катушки. Коэффициент Нагаока вычислялся с применением эллиптических интегралов. Подробнее на этой формуле останавливаться не будем, т.к. Coil32 ее не использует в расчетах. Стоит только отметить, что в случае длинного соленоида формула упрощается до следующего вида:
 |
[3] |
где S — площадь поперечного сечения катушки. Эта формула имеет только академический интерес и не пригодна для расчетов реальных катушек, т.к. справедлива только для бесконечно длинных соленоидов, которых в природе не существует.
Однослойную катушку можно рассчитать численным методом, используя формулу Максвелла или формулу Нагаока для соленоида. Однако современные эмпирические формулы дают очень высокую точность расчетов и вполне достаточны для практических целей.
Обзор и выбор эмпирических формул начнем с самой известной формулы Г.Вилера. Обычно именно эта формула чаще всего используется в различных программах, онлайн калькуляторах, справочниках и статьях, посвященных расчетам индуктивностей.
В оригинале эта формула выглядит так:
L = a2 N2 / ( 9 a + 10 b )
где N — число витков, а a и b — соответственно радиус и длина намотки катушки. Размерности в дюймах. Адаптировав эту формулу для метрической системы (вернее сказать для СГС) и поменяв радиус на диаметр, получаем следующее:
 |
[4] |
, где
- L — индуктивность катушки [мкГн];
- N — число витков катушки;
- D — диаметр намотки [см];
- l — длина намотки [см];
Это самый известный у нас вариант этой формулы. Раньше на сайте С.-Петербуржского университета телекоммуникаций — sut.ru был довольно информативный ресурс — dvo.sut.ru, на котором можно было найти много информации о катушках индуктивности, включая и эту формулу. Теперь это ресурс к сожалению удален. Но удалось обнаружить клон этого ресурса на qrz.ru, на который перекочевала даже старая ошибка (0,5ё1.0) в формуле 2.37. Там можно найти и формулу Нагаока (формула 2.28) и выражение коэффициента Нагаока через формулу Вилера (формула 2.29).
Формула была предложена Вилером в далеком 1928 году, когда еще о компьютерах только мечтали и была очень полезна в то время, т.к. позволяла «в столбик» на бумажке рассчитать практическую катушку. Формула «укоренилась» в массовом сознании радиолюбителей. Однако мало кто знает, что она, как любая эмпирическая формула, имеет ограничения. Эта формула дает погрешность до 1% при l/D > 0,4, т.е если катушка не слишком короткая. Для коротких катушек эта формула не пригодна.
Последовало несколько попыток устранить этот недостаток. В 1985 г. Р.Лундин опубликовал две свои эмпирические формулы, одна — для «длинных», другая — для «коротких» катушек, позволяющие рассчитать коэффициент Нагаока с точностью не менее чем 3ppM (±0.0003%), что несомненно выше точности изготовления или измерения индуктивности катушки. Вот калькулятор, основанный на этих формулах.
В 1982 г., спустя 54 года, с наступлением эры компьютеров, Вилер опубликовал свою «длинную» формулу, которая рассчитывала однослойную катушку с погрешностью не более ±0.1%, как длинную, так и короткую. В дальнейшем эта формула была усовершенствована Р.Розенбаумом, а в последствии Р.Вивером (Robert Weaver — анализ и вывод формулы у него на сайте).
 |
[5] |
где:
- Dk — диаметр намотки
- N — число витков
- k = l/Dk — форм-фактор катушки, отношение длины намотки к ее диаметру
В результате мы имеем формулу, позволяющую рассчитать однослойную катушку с точностью не менее 18.5 ppM (в сравнении с формулой Нагаока), что хуже чем по формулам Лундина, но во-первых вполне достаточно для практических расчетов, во-вторых мы имеем одну более простую формулу вместо двух, рассчитывающую однослойную катушку независимо от ее форм-фактора.
Формула [5] и используется в онлайн-калькуляторе однослойной катушки, старых версиях Coil32, а также во всех версиях программы для Linux и в J2ME приложении для мобильных телефонов.
В основной версии Coil32 для Windows, а также начиная с версии 3.0 для Android, применена более сложная методика расчета однослойной катушки, учитывающая спиральную форму витков и произвольный шаг намотки.
В 1907 году Э.Роза, сравнивая расчеты по методу Максвелла и по методу Лоренца, вывел таблицу поправок, существенно увеличивающих точность расчета по методу Лоренца, особенно если катушка имеет небольшое число витков. Эти поправки стали именоваться «поправки на круглость провода» — Round Wire Corrections. В дальнейшем эти поправки использовались для увеличения точности расчета коэффициента Нагаока и эмпирических формул Лундина и Вивера. В 2008 г. Р.Вивер создал эмпирический алгоритм, позволяющий численным методом рассчитать «поправки на круглость провода» не прибегая к помощи таблиц. Этот алгоритм применяется в Coil32 начиная с версии 8.0, в онлайн-калькуляторе, а также в версиях Coil32 для Андроид и J2ME, для увеличения точности расчета индуктивности однослойных катушек.
Кроме индуктивности, как основного параметра однослойной катушки, программа Coil32 вычисляет и другие параметры:
Этих данных вполне достаточно для создания реалистичной модели катушки в программах схемотехнического моделирования. Например, в популярных RFSim99 или LTSpice IV. В RFSim99 необходимо поставить галочку в чекбоксе «Вкл. физ. модель» и ввести частоту собственного резонанса и добротность. Тип добротности необходимо выбрать третий — Q(f)=Q(F). В LTSpice необходимо задать Rser — это наше сопротивление потерь (r) и Cpar — это собственная емкость катушки Cs.
Кроме того можно рассчитать дополнительные результаты для параллельного колебательного контура на рабочей частоте. Характеристическое сопротивление такого контура равно реактивному сопротивлению катушки на рабочей частоте.
Назад… Вперед…
4.2. Самоиндукция. Индуктивность соленоида
Вокруг
всякого проводника с током существует
магнитное поле. Собственное магнитное
поле контура создает магнитный поток
самоиндукции 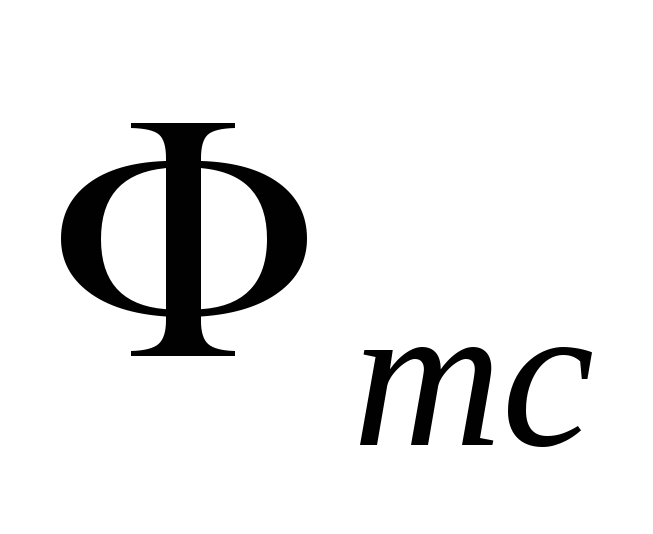 сквозь поверхностьS,
ограниченную этим контуром
сквозь поверхностьS,
ограниченную этим контуром 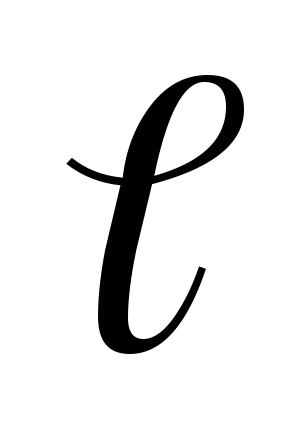 :
:
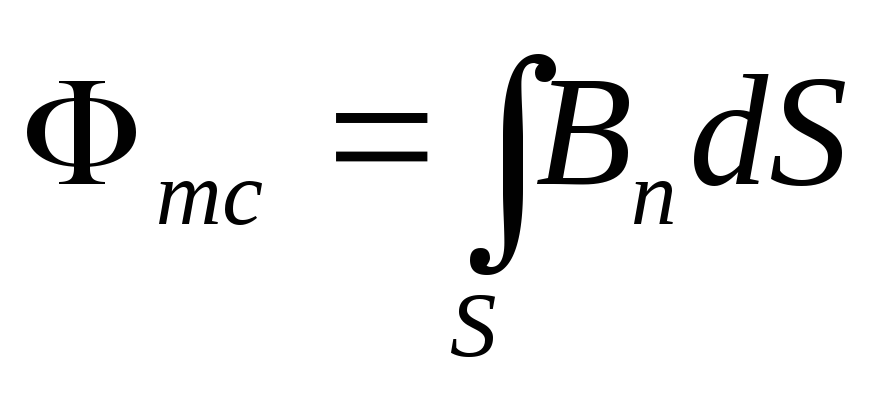 ,
,
где 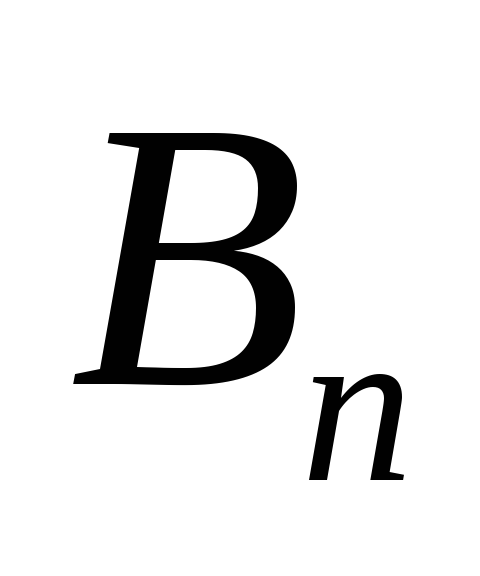 – проекция вектора индукции
– проекция вектора индукции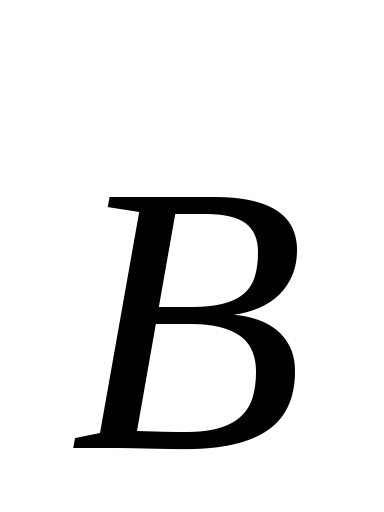 магнитного поля на нормаль к элементу
поверхностиdS.
магнитного поля на нормаль к элементу
поверхностиdS.
По
закону Био- Савара — Лапласа магнитная
индукция 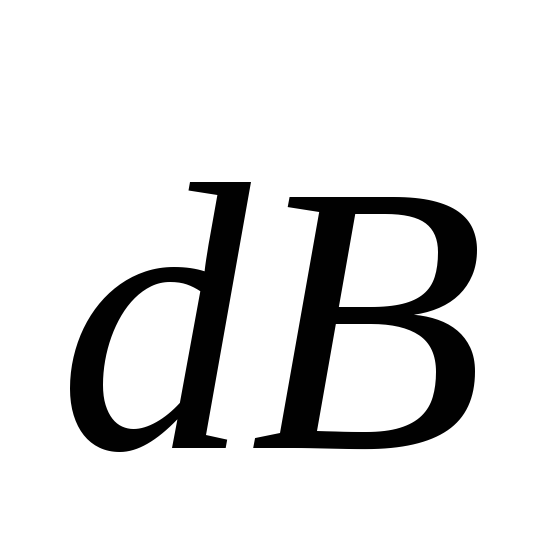 в точке, находящейся на расстоянии
в точке, находящейся на расстоянии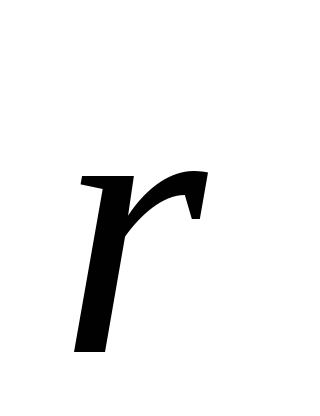 от элемента
от элемента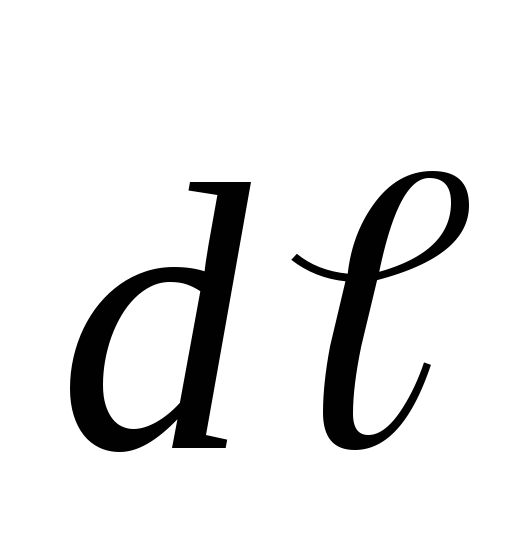 контура равна
контура равна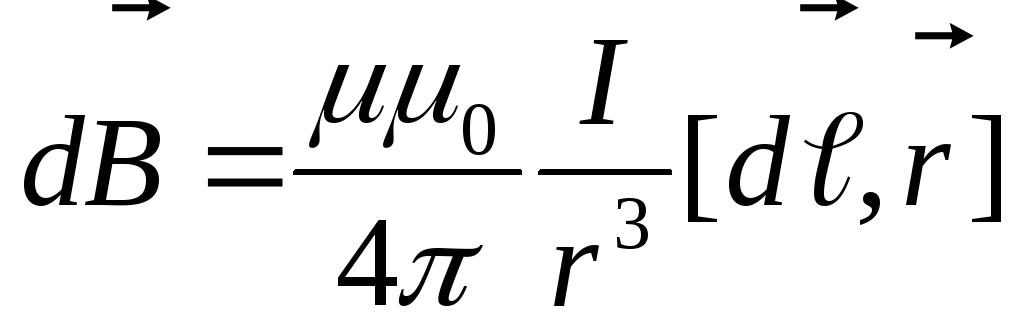 ,
а магнитная индукция, создаваемая всем
контуром
,
а магнитная индукция, создаваемая всем
контуром
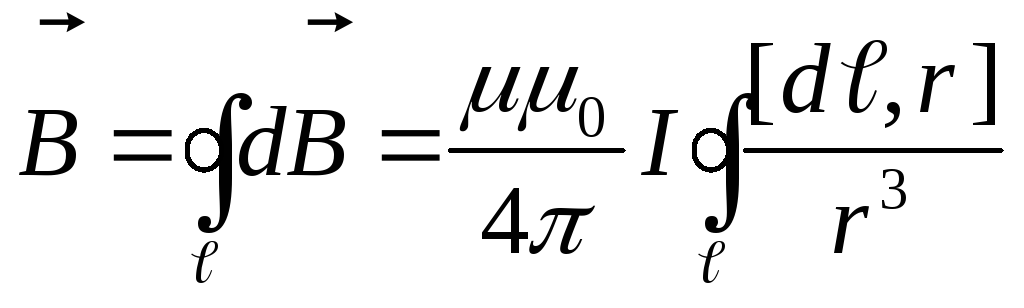 ,
,
тогда 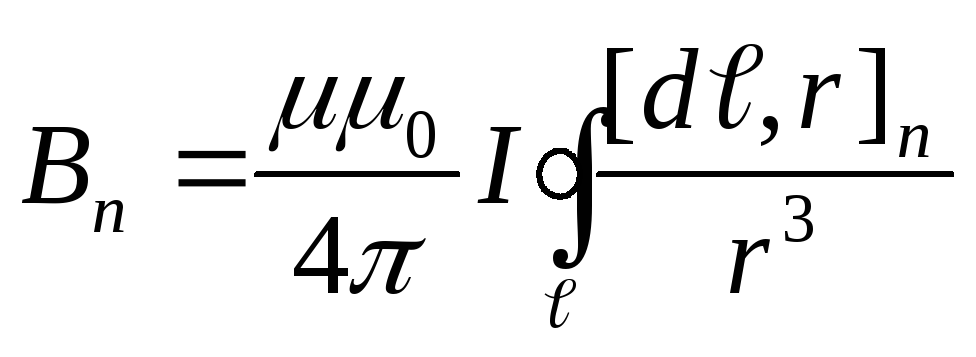 ,
где
,
где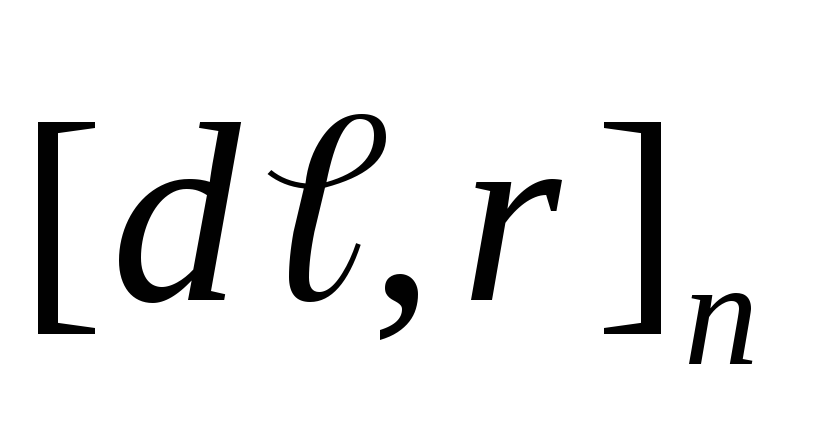 — проекция векторного произведения на
направление нормали к поверхностиdS,
ограниченной контуром
— проекция векторного произведения на
направление нормали к поверхностиdS,
ограниченной контуром 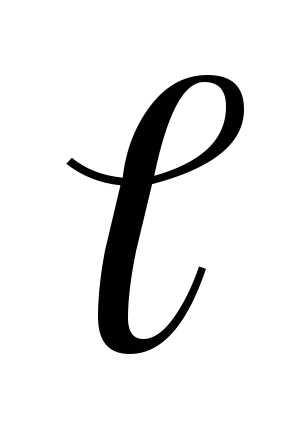 .
Для магнитного потока самоиндукции
имеем:
.
Для магнитного потока самоиндукции
имеем:
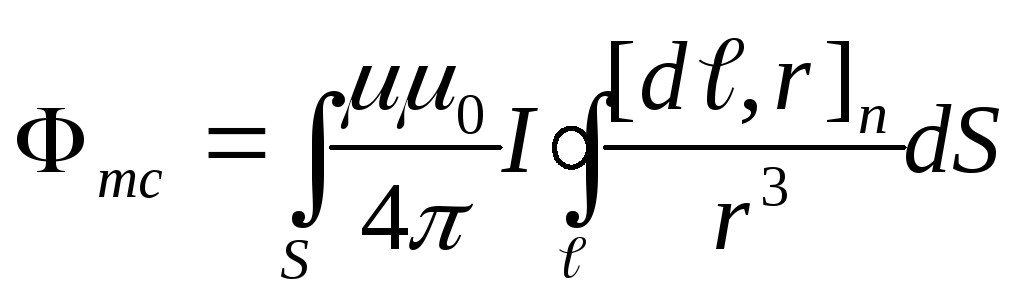 .
.
Обозначим 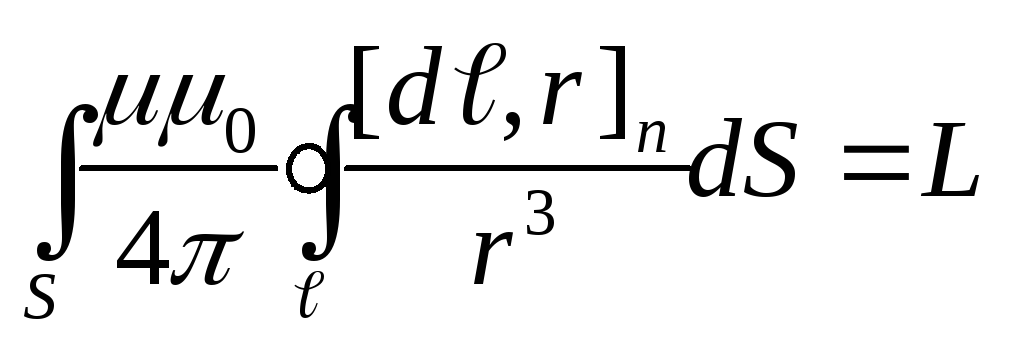 ,
тогда
,
тогда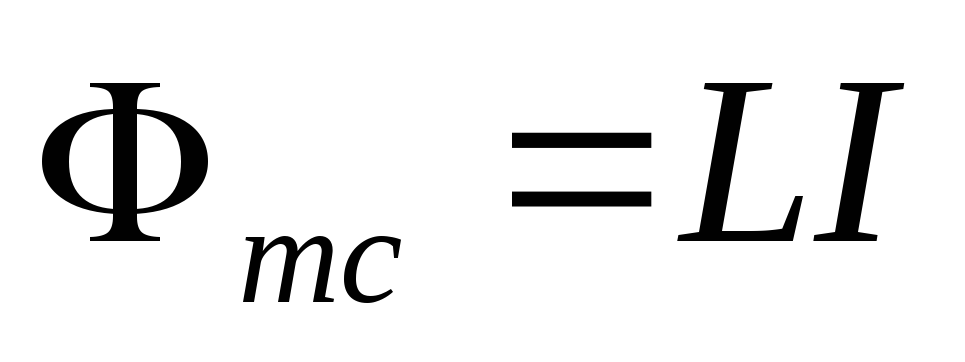 .
ВеличинаL называется индуктивностью контура. Она
зависит от свойств среды (
.
ВеличинаL называется индуктивностью контура. Она
зависит от свойств среды ( 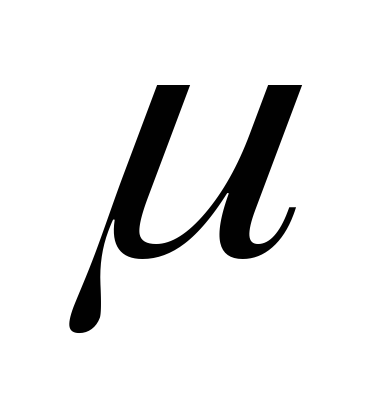 ),
от геометрической формы (S и
),
от геометрической формы (S и 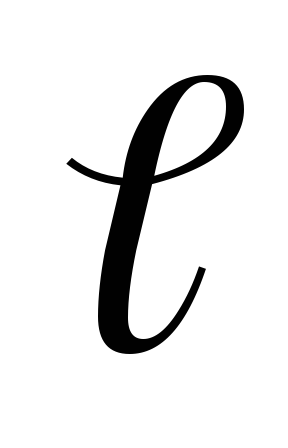 ) и размеров проводника. Индуктивность
равна магнитному потоку самоиндукции,
контура, когда в контуре течет ток
единичной силы.
) и размеров проводника. Индуктивность
равна магнитному потоку самоиндукции,
контура, когда в контуре течет ток
единичной силы.
Единицей
индуктивности в СИ является Гн
(генри), 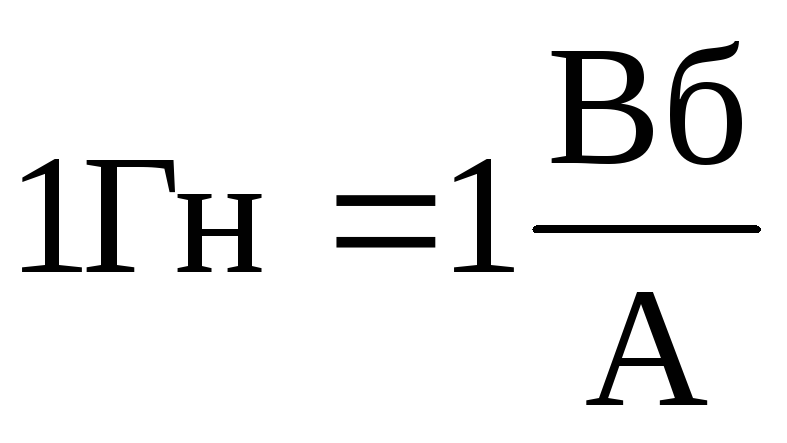 .
.
Самоиндукция – это возникновение ЭДС индукции в результате изменения тока в цепи. ЭДС самоиндукции:
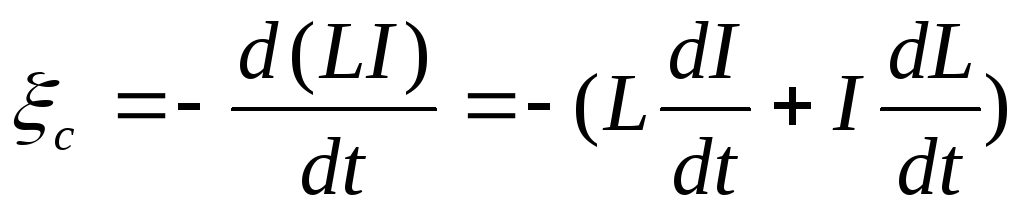 .
.
Если
свойства среды (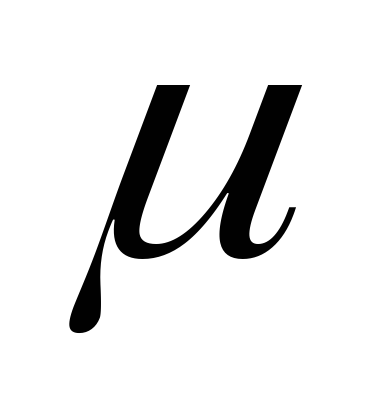 )
и размеры контура (S и
)
и размеры контура (S и 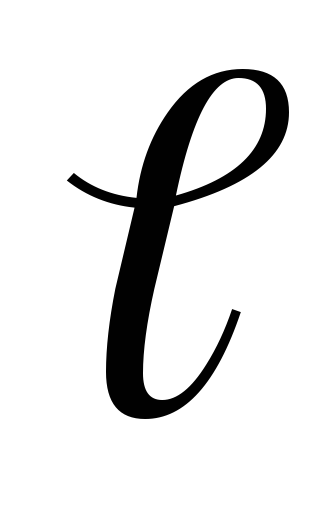 )
остаются неизменными, а среда
неферромагнитная, то
)
остаются неизменными, а среда
неферромагнитная, то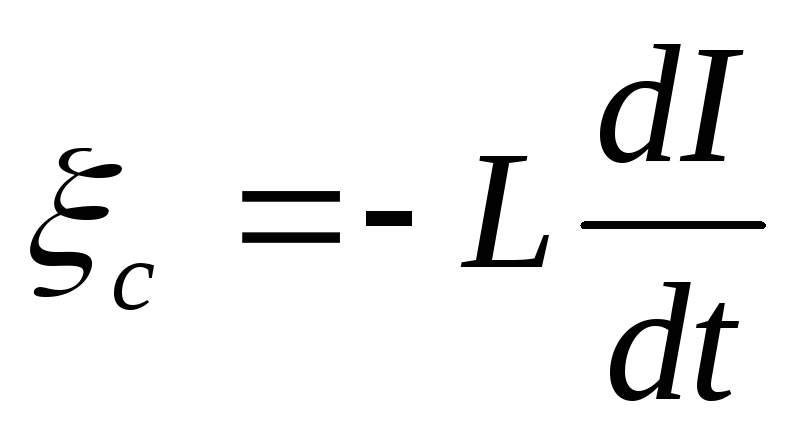 ,
ЭДС самоиндукции пропорциональна
скорости убывания тока в контуре. т. е.
,
ЭДС самоиндукции пропорциональна
скорости убывания тока в контуре. т. е.
Под действием ЭДС самоиндукции в цепи появляется индукционный ток, который по закону Ленца противодействует изменению тока в цепи. Это противодействие будет тем больше, чем больше индуктивность контура. Таким образом, индуктивность контура является мерой его инертности к изменению тока.
Вычислим
индуктивность соленоида бесконечной
длины. При протекании тока I внутри соленоида
возбуждается однородное поле, индукция
которого равна 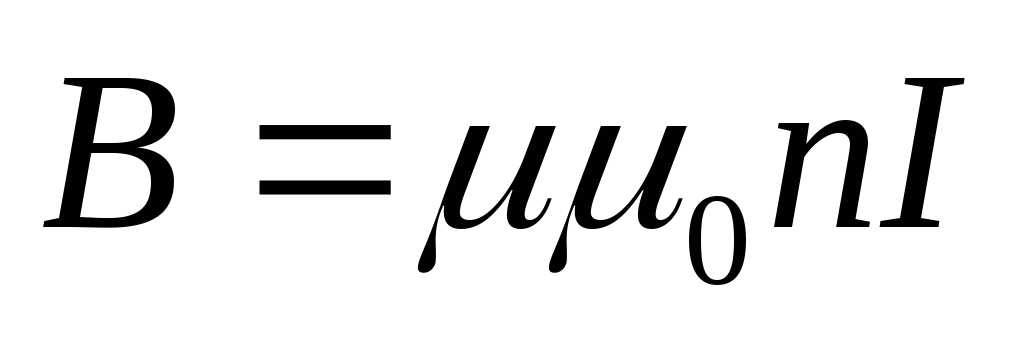 .
Поток через каждый из витков равен
.
Поток через каждый из витков равен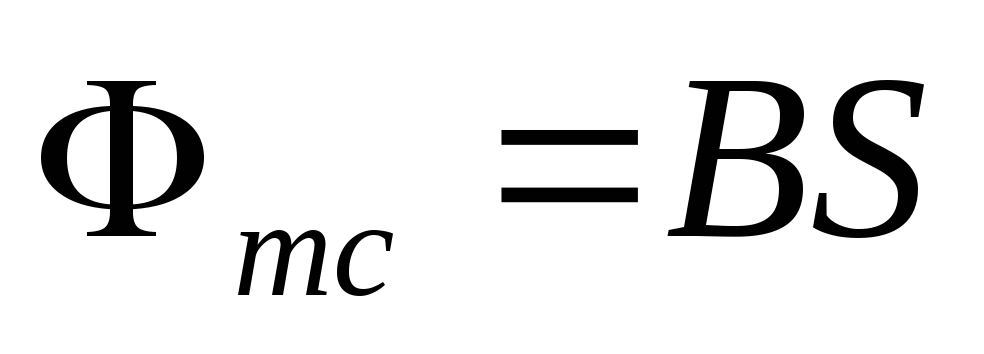 ,
а полный поток, сцепленный с соленоидом,
определяется выражением:
,
а полный поток, сцепленный с соленоидом,
определяется выражением:
 ,
,
где 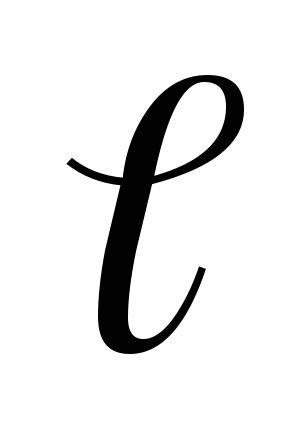 — длина соленоида (которая предполагается
очень большой),S — площадь поперечного сечения, n — число витков на
единицу длины, полное число витков
— длина соленоида (которая предполагается
очень большой),S — площадь поперечного сечения, n — число витков на
единицу длины, полное число витков 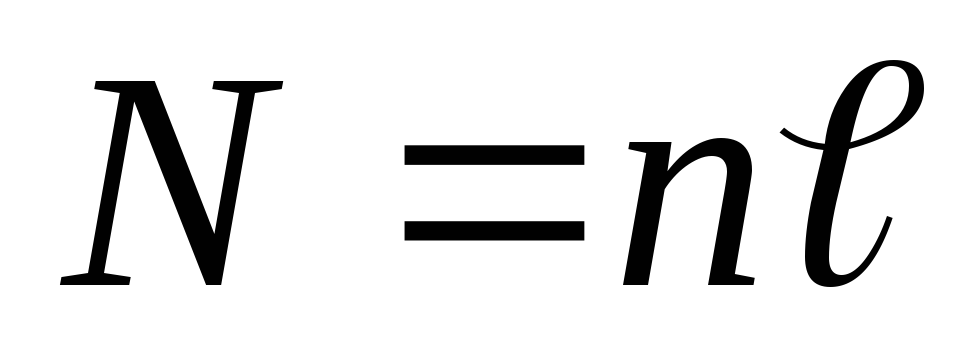 . Известно, что
. Известно, что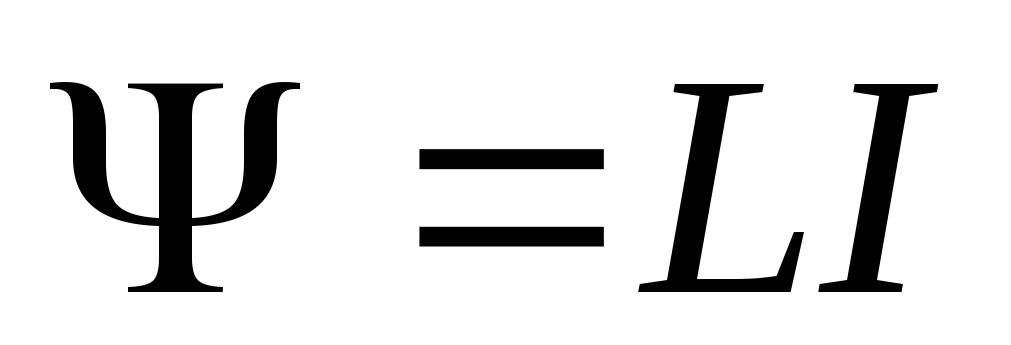 ,
поэтому
,
поэтому
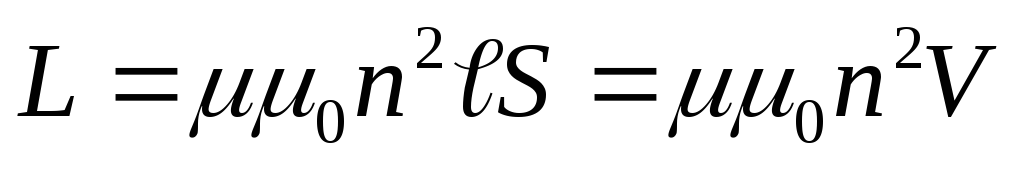 ,
,
где 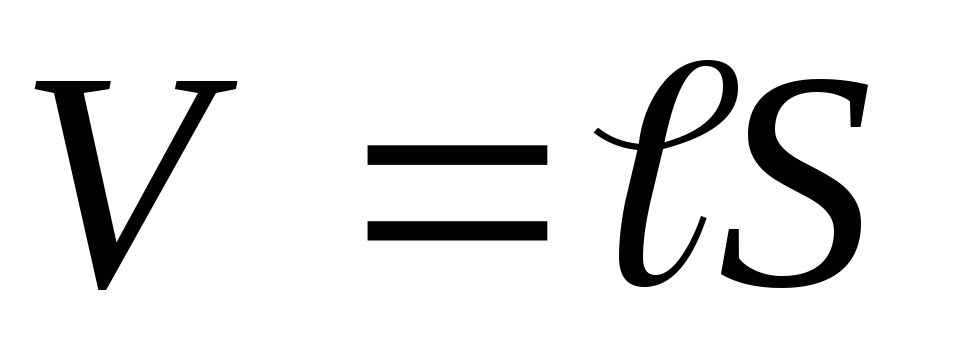 — объем соленоида.
— объем соленоида.
4.3. Токи фуко
Индукционные токи могут возбуждаться в сплошных массивных проводниках. В этом случае их называют токами Фуко или вихревыми токами. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко могут быть очень большими.
В соответствии с правилом Ленца токи Фуко выбирают внутри проводника такие пути и направления, чтобы своим действием возможно сильнее противиться причине, которая их вызывает. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем.
Токи Фуко, возникающие в проводах, по которым течет переменный ток, направлены так, что ослабляют ток внутри провода и усиливают вблизи поверхности. В результате быстропеременный ток оказывается распределенным по сечению провода неравномерно – он как бы вытесняется на поверхность проводника. Это скин-эффект или поверхностный эффект. Из-за скин-эффекта внутренняя часть проводников в высокочастотных линиях оказывается бесполезной и проводники делают в виде трубок.
лабораторная работа 49
Цель работы - определение индуктивности соленоида по его сопротивлению переменному току.
Приборы и принадлежности: исследуемый соленоид, звуковой генератор, электронный осциллограф, миллиамперметр переменного тока, соединительные провода.
Явление самоиндукции. Индуктивность
Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий проводящий контур. В частности, если электрический ток течет в проводящем контуре, то он создает пронизывающий этот контур магнитный поток Ф.
При изменении силы тока I в любом контуре изменяется и магнитный поток Ф, вследствие этого в контуре возникает электродвижущая сила (ЭДС) индукции, которая вызывает дополнительный ток (рис. 1, где 1 - проводящий замкнутый контур, 2 — силовые линии магнитного поля, создаваемого током контура). Это явление называется самоиндукцией, а дополнительный ток, вызываемый ЭДС самоиндукции, – экстратоком самоиндукции.
Явление самоиндукции наблюдается в любой замкнутой электрической цепи, в которой протекает элетрический ток, при замыкании или размыкании этой цепи.
Рассмотрим, от чего зависит величина ЭДС εs самоиндукции. Магнитный поток Ф, пронизывающий замкнутый проводящий контур, пропорционален магнитной индукции В магнитного поля, создаваемого током, протекающим в контуре, а индукция В пропорциональна силе тока.
Рис. 1
Тогда магнитный поток Ф пропорционален силе тока, т.е.
Ф = L · I, (1)
где L — индуктивность контура, Гн (Генри).
Из (1) получим
L = Ф/I . (2)
Индуктивностью контура L называется скалярная физическая величина, равная отношению магнитного потока Ф, пронизывающего данный контур, к величине силы тока, текущего в контуре.
Генри — это индуктивность такого контура, в котором при силе тока в 1А возникает магнитный поток 1Вб, т.е. 1 Гн = 1.
Согласно закону электромагнитной индукции
. (3)
Подставляя (1) в (3), получим ЭДС самоиндукции:
. (4)
Формула (4) справедлива при L=const.
Опыт показывает, что при увеличении индуктивности L в электрической цепи сила тока в цепи увеличивается постепенно (см. рис. 2), а при уменьшении L сила тока уменьшается так же медленно (рис. 3).
Сила тока в электрической цепи при замыкании изменяется по закону , а при размыкании – по закону .
Кривые изменения силы тока показаны на рис. 2 и 3.
Рис. 2 Рис.3
Индуктивность контура зависит от формы, размеров и деформации контура, от магнитного состояния среды, в которой находится контур, а также от других факторов.
Найдем индуктивность соленоида. Соленоид — это цилиндрическая трубка, изготовленная из немагнитного непроводящего материала, на которую плотно, виток к витку, намотана тонкая металлическая проводящая проволока. На рис. 4 показан разрез соленоида вдоль цилиндрической трубки по диаметру (1 — силовые линии магнитного поля).
Рис. 4
Длина l соленоида намного
больше, чем диаметр d,
т.е.
l>> d. Если l< d, то соленоид можно рассматривать как
короткую катушку.
Диаметр тонкой проволоки намного меньше, чем диаметр соленоида. Для увеличения индуктивности внутрь соленоида помещают ферромагнитный сердечник с магнитной проницаемостью μ. Если l>>d, то при протекании тока внутри соленоида возбуждается однородное магнитное поле, индукция которого определяется формулой
В=μо μnI, (5)
где μо = 4π·10-7 Гн/м – магнитная постоянная; n = N/l – число витков единицы длины соленоида; N – число витков соленоида.
Вне соленоида магнитное поле практически равно нулю. Поскольку соленоид имеет N витков, то полный магнитный поток ψ (потокосцепление), пронизывающий поперечное сечение S соленоида, равен
Ψ = NФ = NВS, (6)
где Ф = BS – поток, пронизывающий один виток соленоида.
Подставляя (5) в (6) и с учётом того, что N = nl, получим
Ψ = μо μn2 lSI . (7)
С другой стороны,
Ψ = LI . (8)
Сравнивая (7) и (8), получим
L = μо μn2lS = μо μS. (9)
Площадь сечения соленоида равна
. (10)
С учётом (10) формула (9) запишется в виде
L = μо μ. (11)
Определить индуктивность соленоида можно, подключив соленоид в электрическую цепь переменного тока с частотой ω. Тогда полное сопротивление (импеданс) определится формулой
, (12)
где R – активное сопротивление, Ом; = хL – индуктивное сопротивление; = хс – ёмкостное сопротивление конденсатора с
ёмкостью С.
Если в электрической цепи отсутствует конденсатор, т.е. электроёмкость цепи мала, то хс<< хL и формула (12) будет иметь вид
. (13)
Тогда закон Ома для переменного тока запишется в виде
, (14)
где Im , Um – амплитудные значения силы тока и напряжения.
Так как ω = 2πν, где ν – частота колебаний переменного тока, то (14) примет вид
. (15)
Из (15) получим рабочую формулу для определения индуктивности:
. (16)
Ход работы
Для выполнения работы собрать цепь по схеме рис. 5.
1. Установить на звуковом генераторе частоту колебаний, указанную преподавателем.
2. Измерить с помощью осциллографа амплитуду напряжения Um и частоту .
3. С помощью миллиамперметра определить действующее значение силы тока в цепи ; пользуясь соотношением и решая его относительно Ie, определить амплитуду тока в цепи.
Рис. 5
4. Данные занести в таблицу.
Таблица
|
ν, Гц |
Ie, мА |
Im, мА |
Um, В |
R, Ом |
N |
d, м |
l, м |
L, Гн |
Lпров, Гн |
ΔL=L-Lпров, Гн |
|
|
|
|
|
|
|
|
|
|
|
|
6. По формуле (16) рассчитать индуктивность соленоида.
7. По формуле (11) рассчитать проверочное значение индуктивности соленоида, исходя из его геометрии и числа витков.
Справочные данные: активное сопротивление соленоида
R = 56 Ом; длина
соленоида l = 40 см; диаметр соленоида
d = 2 см;
число витков соленоида N = 2000.
Рекомендуемая частота переменного тока .
Вопросы для допуска к работе
1. Сформулируйте цель работы.
2. Дайте определение индуктивности?
3. Какова единица измерения индуктивности?
4. Запишите рабочую формулу для определения индуктивности соленоида.
Вопросы для защиты работы
1. Получите формулу для определения индуктивности соленоида, исходя из его геометрических размеров и числа витков.
2. Что называется импедансом?
3. Как связаны между собой максимальное и действующее значения силы тока и напряжения в цепи переменного тока?
4. Выведите рабочую формулу индуктивности соленоида.
5. Опишите явление самоиндукции.
6. Каков физический смысл индуктивности?
Определение индуктивности соленоида Цель работы
Лабораторная работа № 15
Изучить явления самоиндукции, понятие индуктивности и методы измерения индуктивности соленоида.
Краткое теоретическое введение
1. Индуктивность контура. Явление самоиндукции.
Вокруг любого проводника с током I существует магнитное поле.
Собственное магнитное поле контура с
током создает магнитный поток самоиндукции 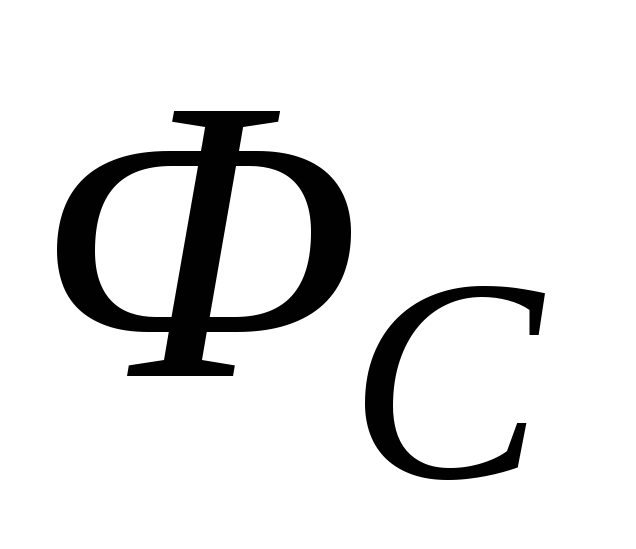 через
воображаемую поверхностьS,
ограниченную этим контуром:
через
воображаемую поверхностьS,
ограниченную этим контуром:
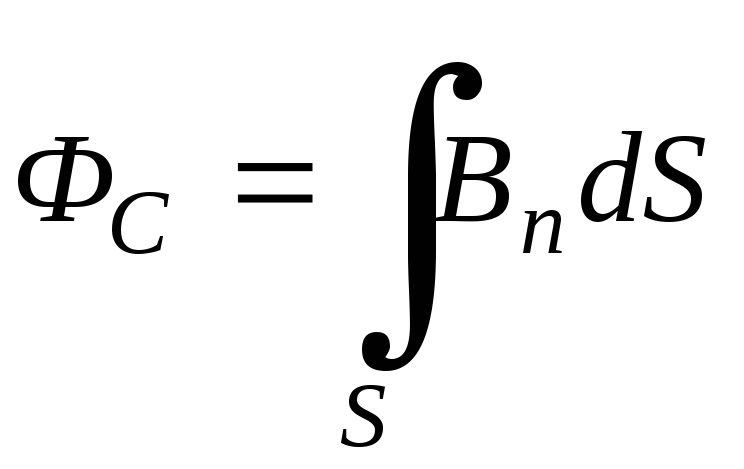 ,
(1)
,
(1)
где 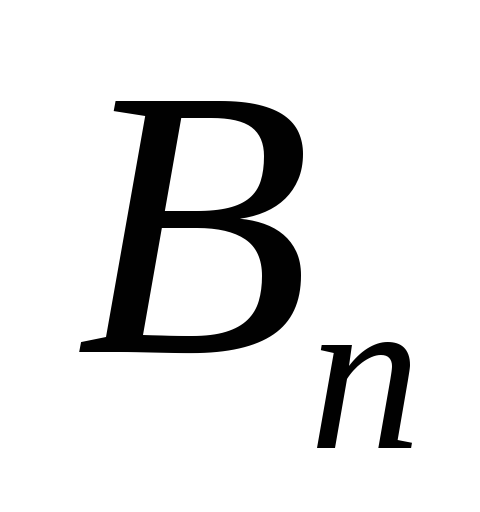 —
проекция вектора индукции
—
проекция вектора индукции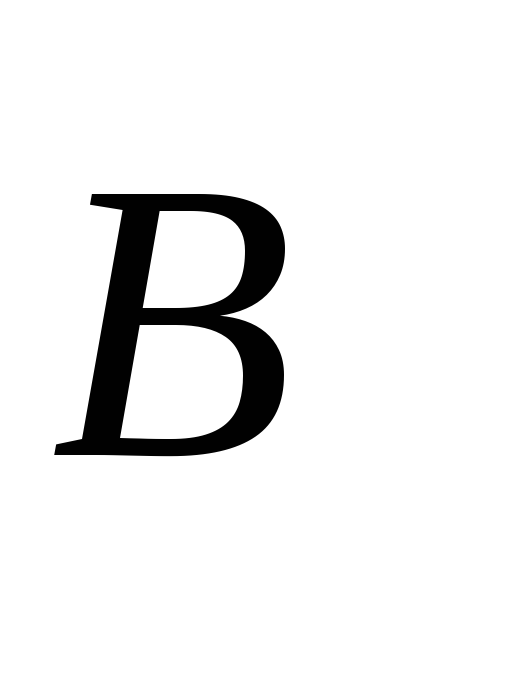
 магнитного поля токаI на нормаль к элементу поверхностиdS.
магнитного поля токаI на нормаль к элементу поверхностиdS.
Из закона Био-Савара-Лапласа и принципа суперпозиции следует, что эта проекция равна
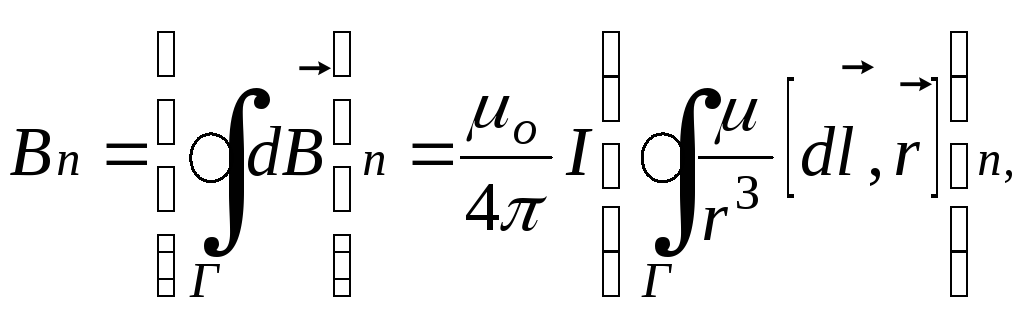
где  — вектор индукции магнитного поля,
созданного элементом
— вектор индукции магнитного поля,
созданного элементом  замкнутого контураГ с токомIв точке, местоположение которой
относительно
замкнутого контураГ с токомIв точке, местоположение которой
относительно определяется
радиус — вектором
определяется
радиус — вектором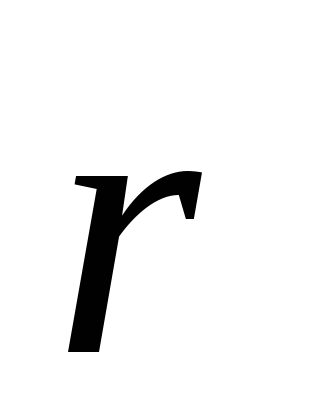 .
.
Подставляя выражение для 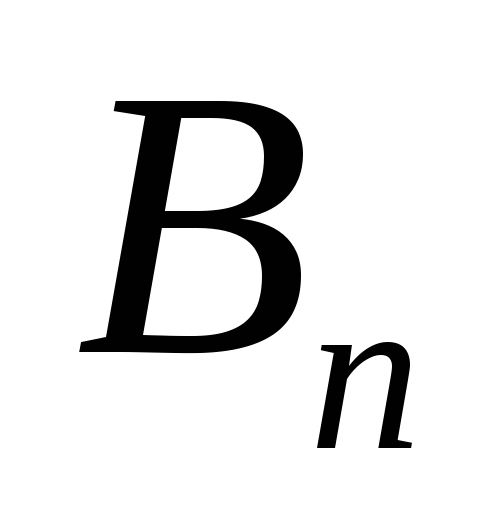 в формулу (1) и вынося из-под знака
интеграла постоянные, получим
в формулу (1) и вынося из-под знака
интеграла постоянные, получим
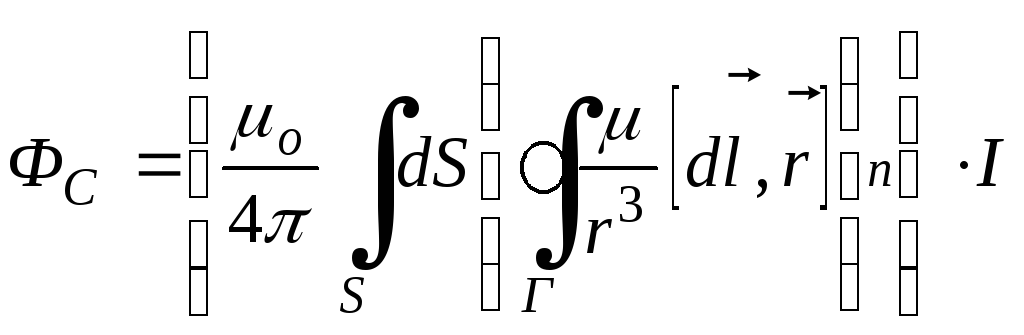 (2)
(2)
или
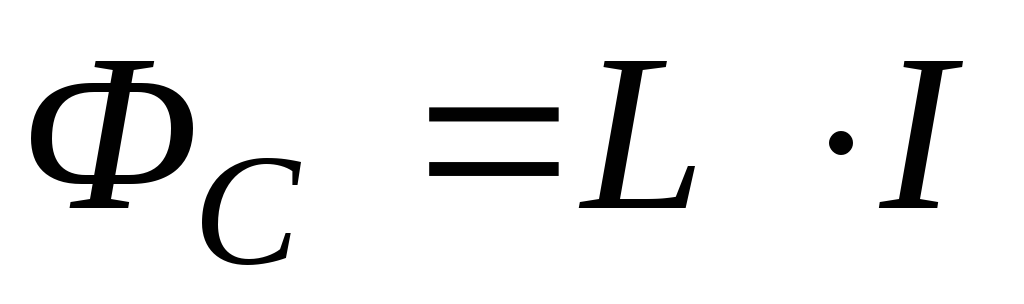 .
.
Коэффициент пропорциональности 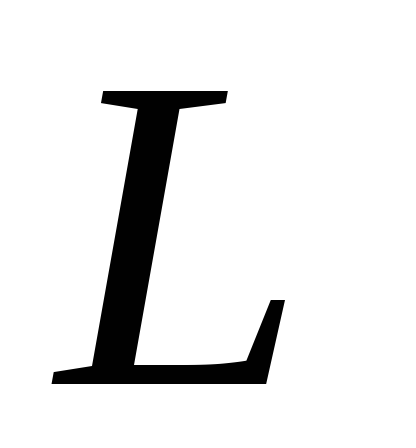 между собственным потоком вектора
магнитной индукции
между собственным потоком вектора
магнитной индукции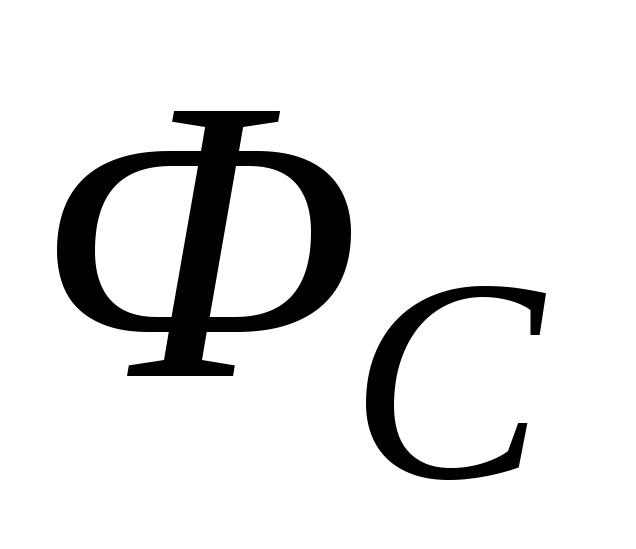 через поверхность, ограниченную контуром,
и силой тока
через поверхность, ограниченную контуром,
и силой тока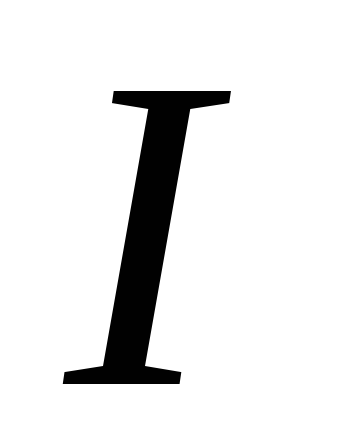 в этом контуре называется индуктивностью
контура (коэффициентом самоиндукции).
в этом контуре называется индуктивностью
контура (коэффициентом самоиндукции).
Из формулы (2) следует, что индуктивность
контура зависит только от геометрических
размеров, формы контура и магнитной
проницаемости  той среды, в которой он находится.
той среды, в которой он находится.
Единица индуктивности в СИ называется
Генри (Г): 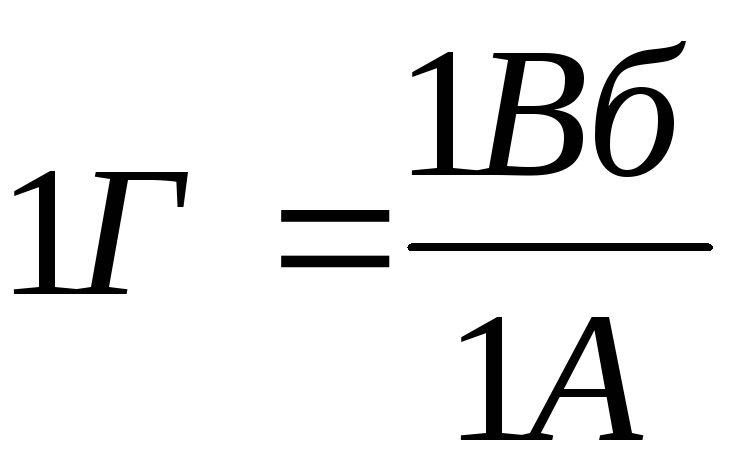
Для бесконечно длинного соленоида, витки которого плотно прилегают друг к другу и сделаны из проводника с очень малым поперечным сечением, индуктивность выражается следующей формулой:
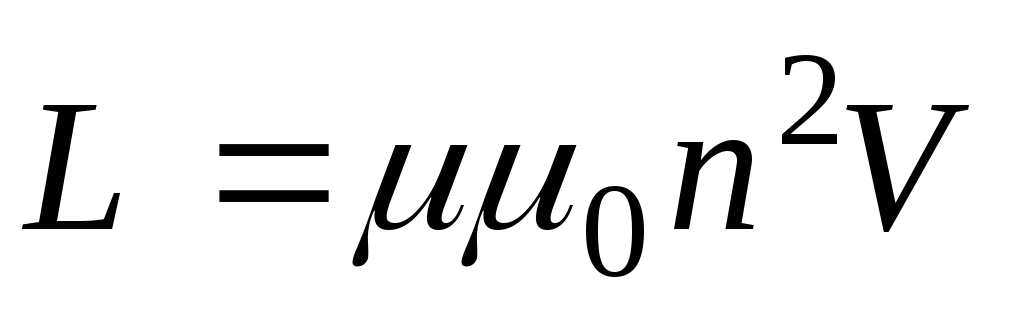 , (3)
, (3)
где 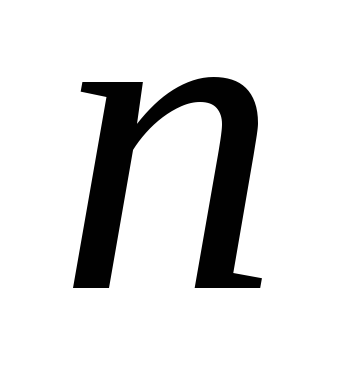 — плотность намотки витков соленоида,
— плотность намотки витков соленоида, — объем соленоида,
— объем соленоида, — магнитная проницаемость вещества
сердечника.
— магнитная проницаемость вещества
сердечника.
Если сила тока, протекающего по контуру,
изменяется со временем, то в соответствии
с законом Фарадея, в контуре наводится
ЭДС самоиндукции 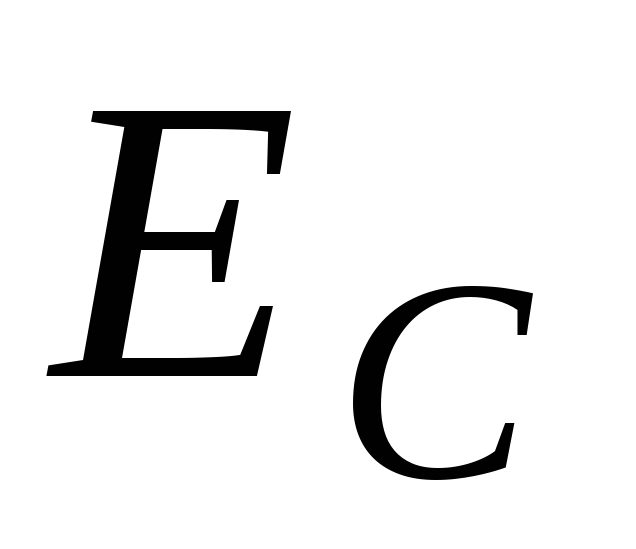
 :
:
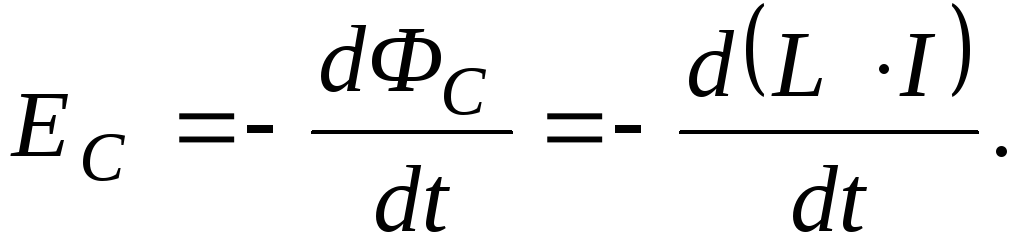
Если контур с током не деформируется и
магнитная проницаемость среды  не изменяется (нет ферромагнетиков в
магнитном поле контура), то
не изменяется (нет ферромагнетиков в
магнитном поле контура), то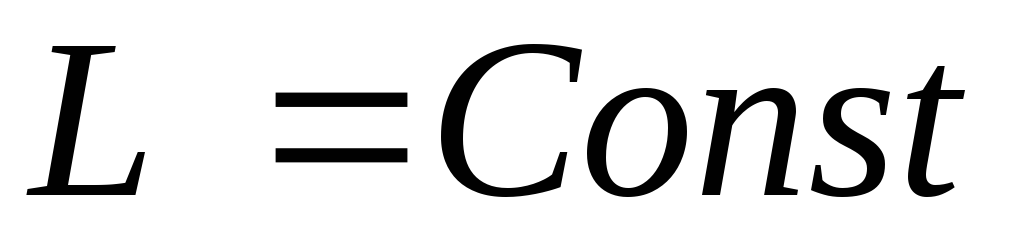 и
и
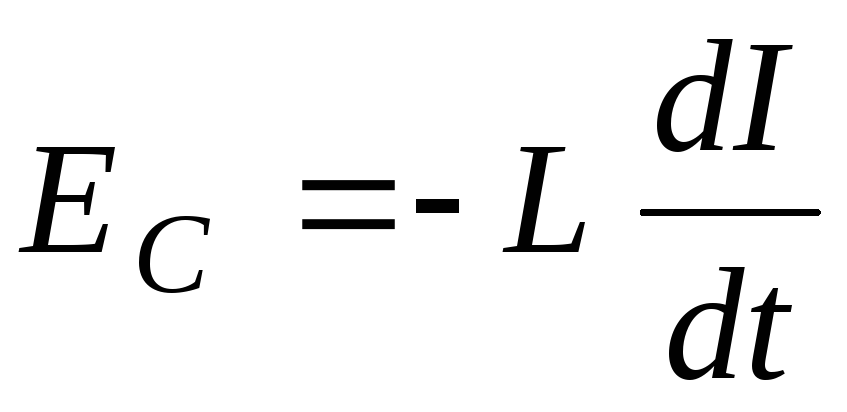 . (4)
. (4)
По правилу Ленца ЭДС самоиндукции противодействует изменению тока в контуре, замедляя как его возрастание, так и убывание.
2. Закон изменения тока в цепи при подключении и отключении источника, его применение для определения индуктивности.
Найдем изменение тока в цепи, индуктивность
которой равна 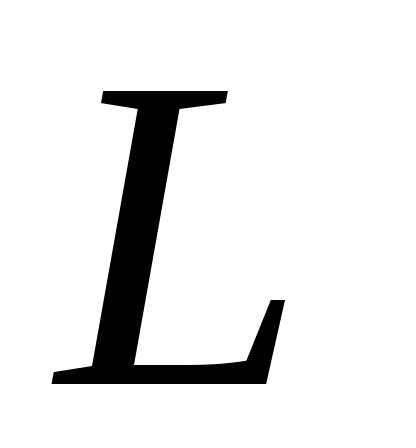 ,
а активное сопротивление —
,
а активное сопротивление — .
.
Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.
Из закона Ома для замкнутой цепи, в
которой действует источник ЭДС  ,
а общее активное сопротивление
,
а общее активное сопротивление ,
сила тока равна
,
сила тока равна
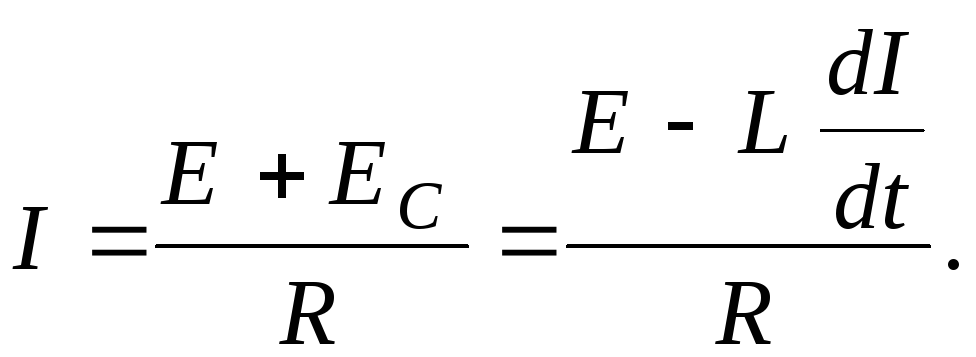
Для нахождения зависимости силы тока от времени разделим переменные:
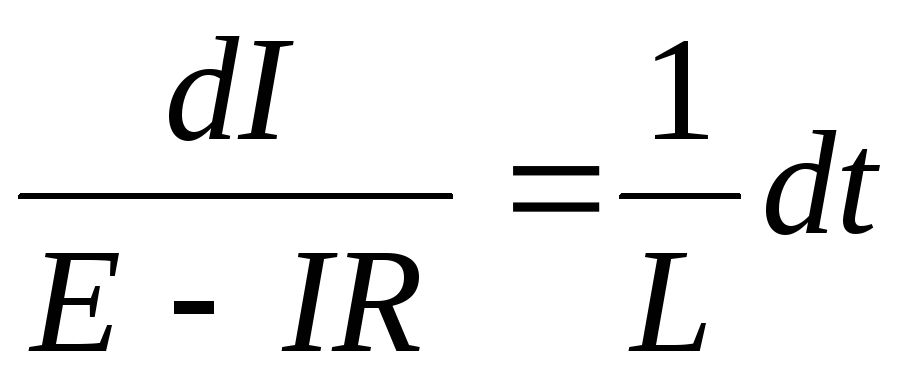 .
.
Полагая 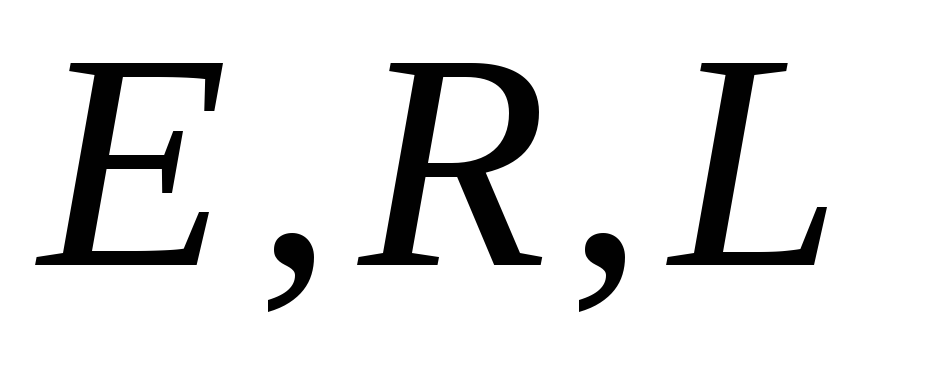 постоянными интегрируя, получаем:
постоянными интегрируя, получаем:
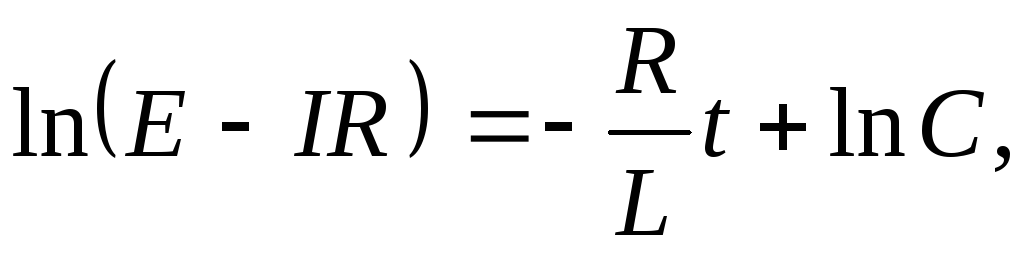
где  — постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
— постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
Пусть в момент времени 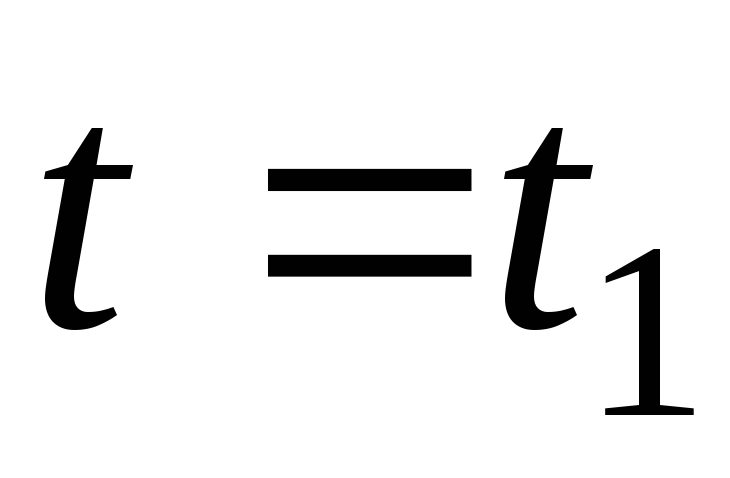 сила тока
сила тока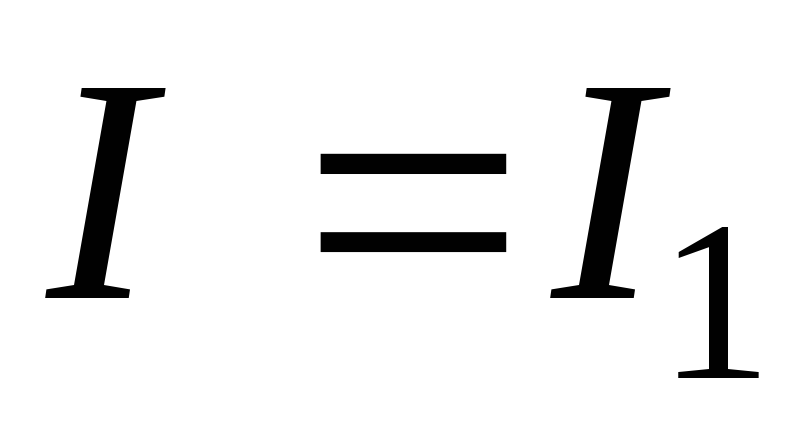 .
Тогда
.
Тогда
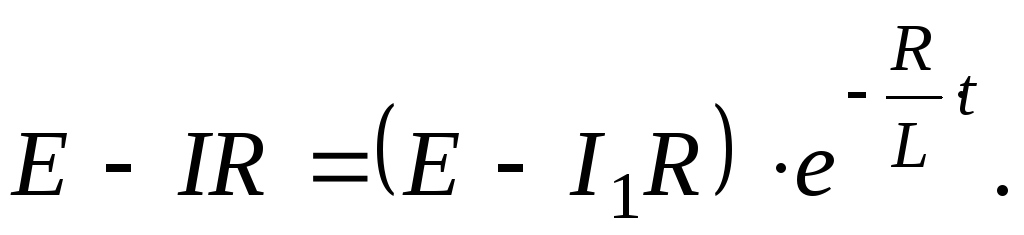
Выразив силу тока, получим
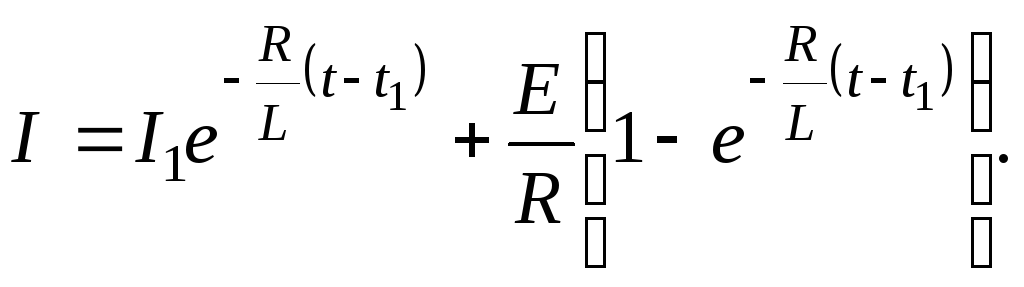 (5)
(5)
Из этой общей формулы можно получить
зависимость силы тока от времени при
замыкании цепи. В этом случае начальный
ток равен нулю 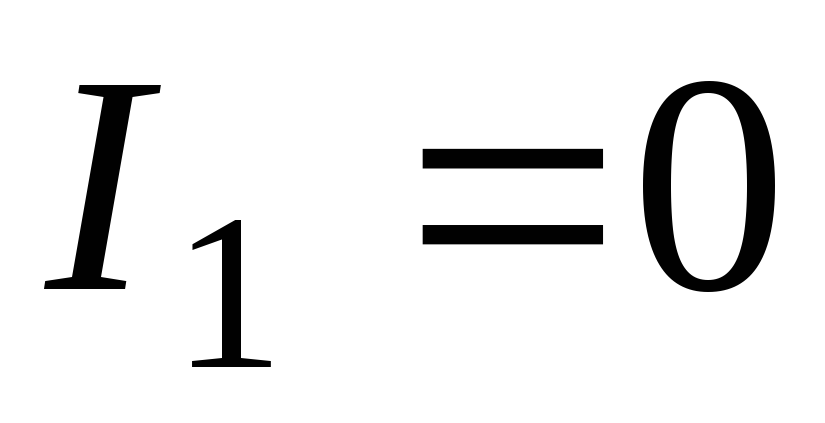 и выражение (5) приобретает вид:
и выражение (5) приобретает вид:
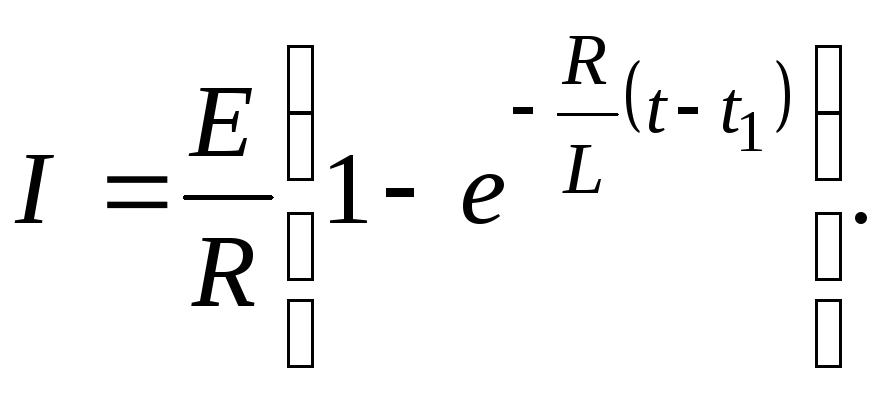 (6)
(6)
Из этой формулы видно, что сила тока при
замыкании цепи постепенно увеличивается,
стремясь к 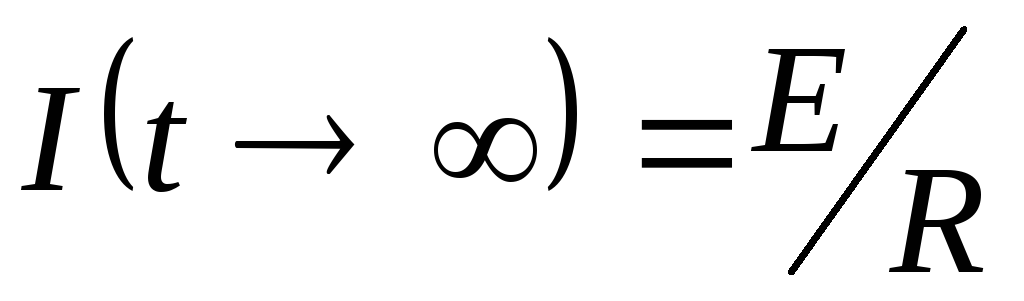 ,
соответствующей величине постоянного
тока (Рис. 1). Нарастание тока происходит
тем медленнее, чем меньше отношение
,
соответствующей величине постоянного
тока (Рис. 1). Нарастание тока происходит
тем медленнее, чем меньше отношение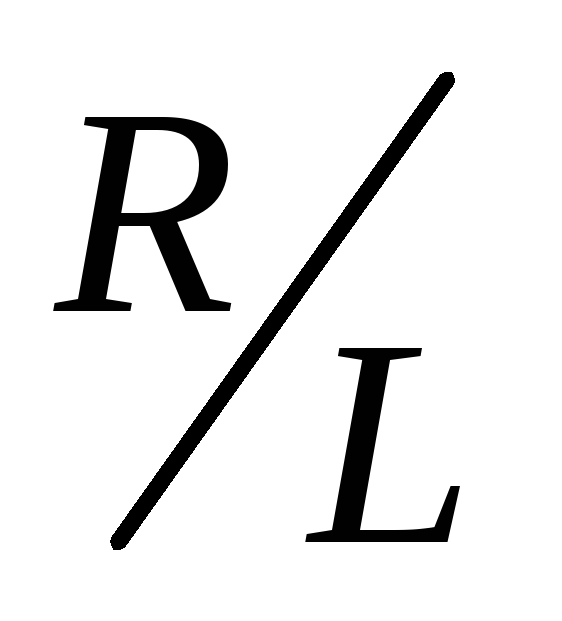 в показателе степени экспоненты или
больше обратное отношение
в показателе степени экспоненты или
больше обратное отношение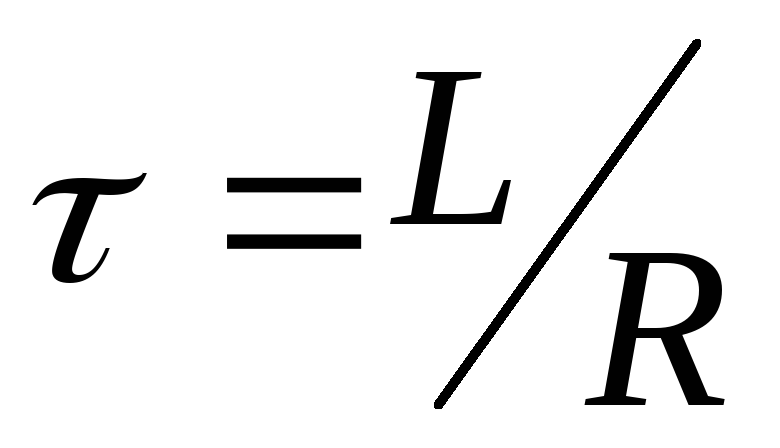 ,
физический смысл которого обсуждается
ниже.
,
физический смысл которого обсуждается
ниже.
Если же в момент времени 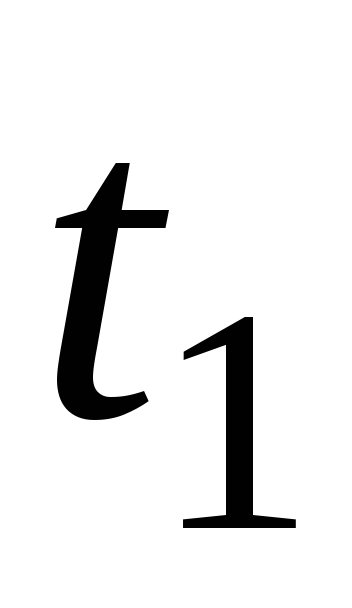 при силе тока
при силе тока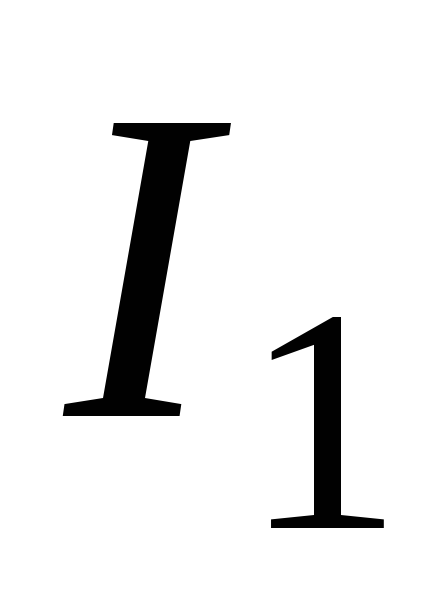 источник ЭДС отключить (
источник ЭДС отключить (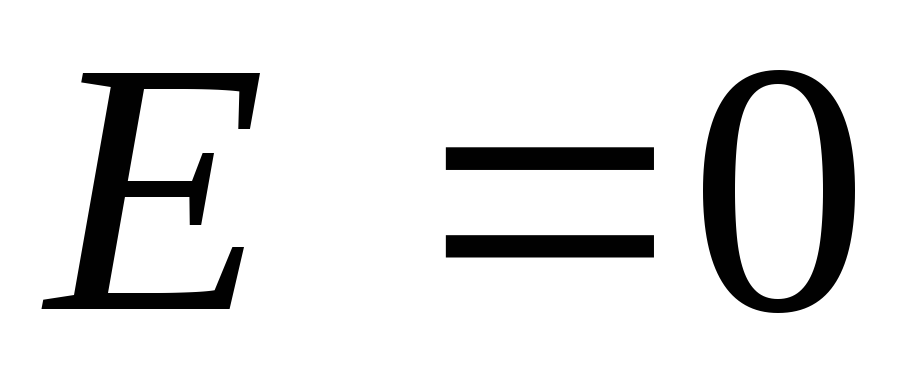 )
сохранив замкнутость цепи, то из формулы
(5) получим следующую зависимость силы
тока от времени:
)
сохранив замкнутость цепи, то из формулы
(5) получим следующую зависимость силы
тока от времени:
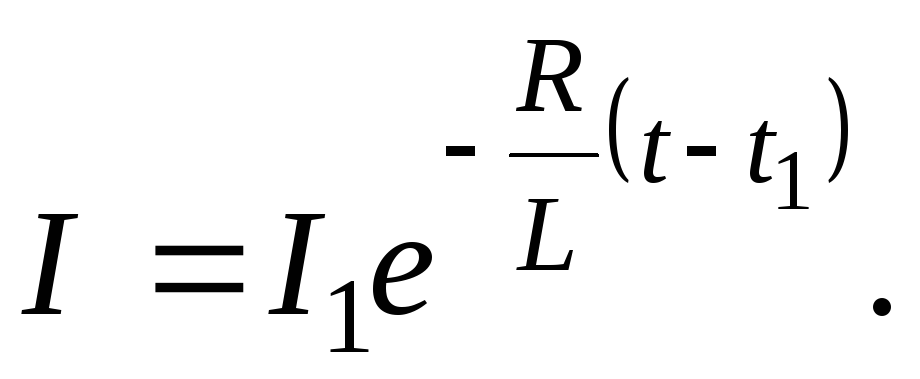 (7)
(7)
В этом случае сила тока в цепи постепенно
уменьшается от начального значения 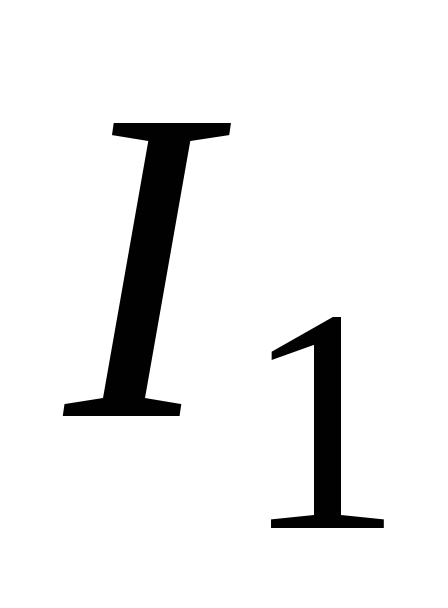 ,
стремясь к нулю. При этом за время
,
стремясь к нулю. При этом за время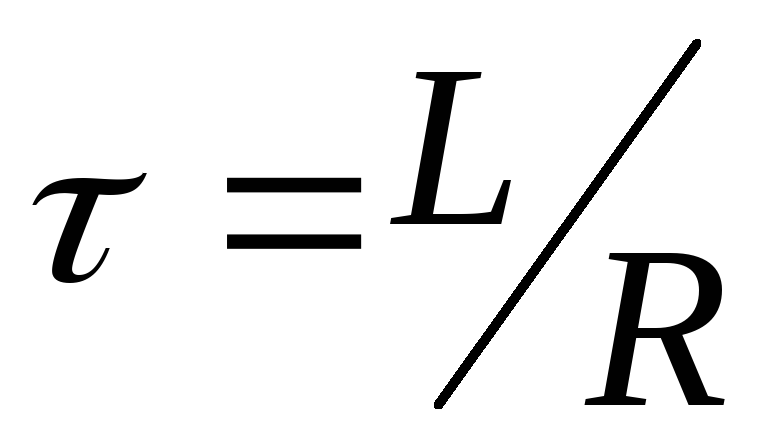 (время релаксации) сила тока
изменяется в
(время релаксации) сила тока
изменяется в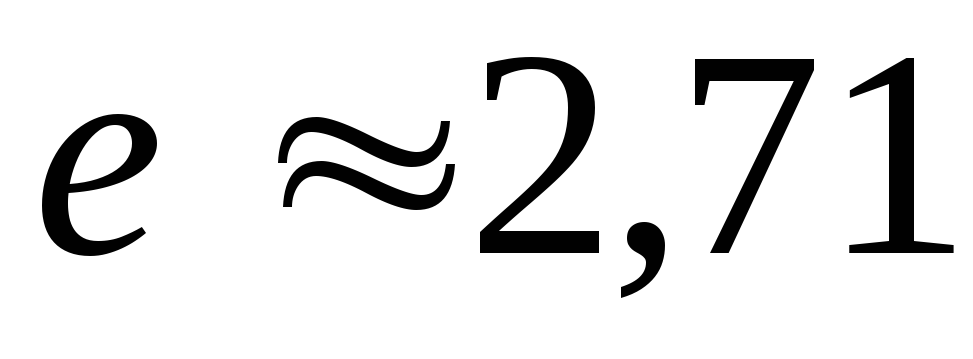 раз.
раз.

Рис. 1
Следует заметить, что в опыте удобнее
снимать вместо зависимости силы тока
в цепи от времени 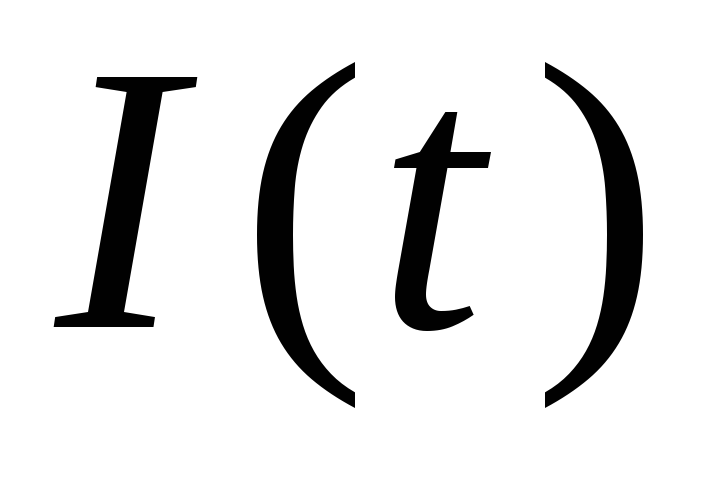 зависимость напряжения на некотором
известном активном сопротивлении
зависимость напряжения на некотором
известном активном сопротивлении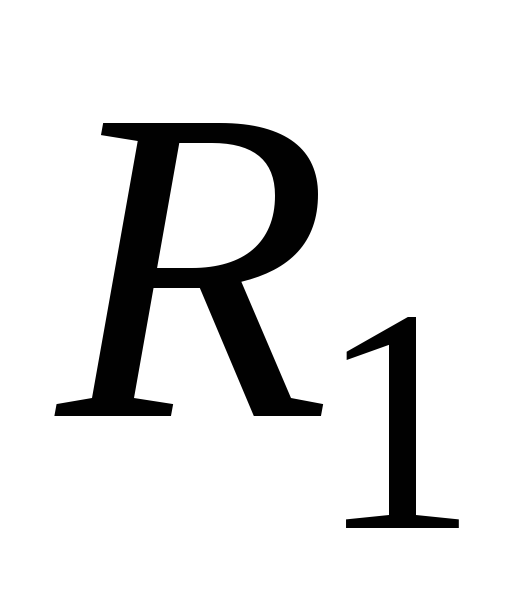 ,
последовательно включенном в цепь, от
времени
,
последовательно включенном в цепь, от
времени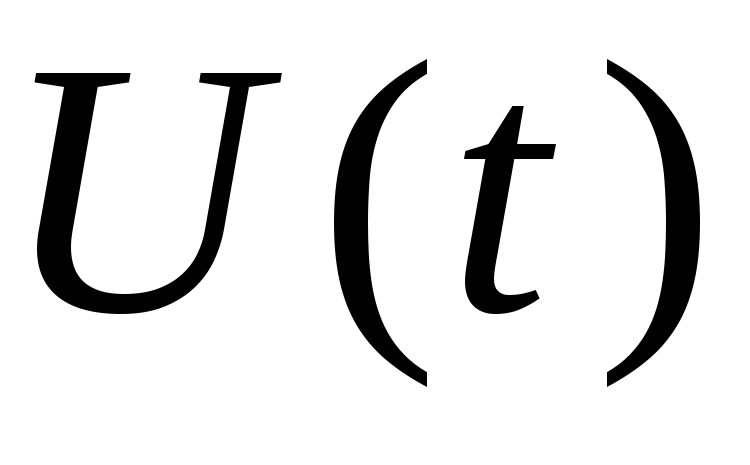 .
Напряжение в этом случае будет
пропорционально силе тока.
.
Напряжение в этом случае будет
пропорционально силе тока.
Из сказанного ясно, что, измерив силу
токов (или напряжения) в некоторые
моменты времени 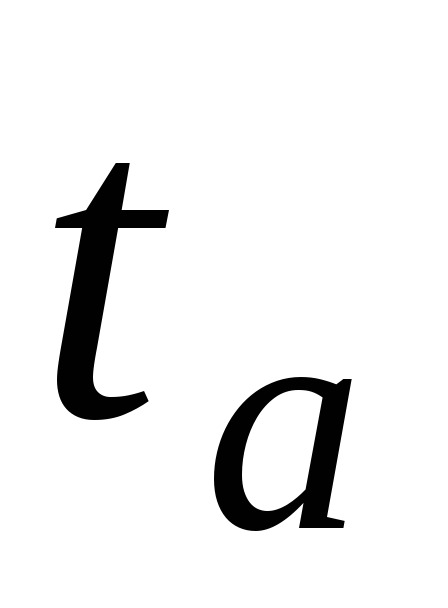 ,
,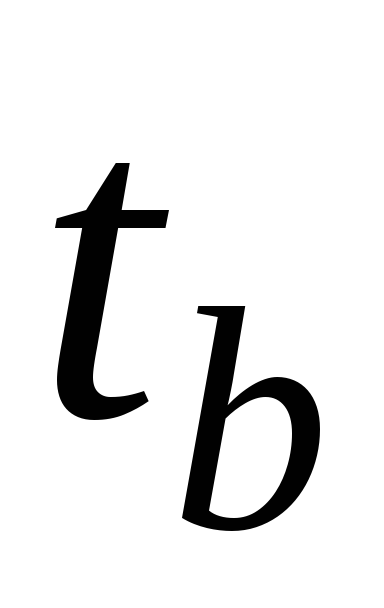 и зная, кроме того, величину общего
активного сопротивления контура
и зная, кроме того, величину общего
активного сопротивления контура ,
можно с помощью зависимостей (6) или (7)
определить индуктивность контура
,
можно с помощью зависимостей (6) или (7)
определить индуктивность контура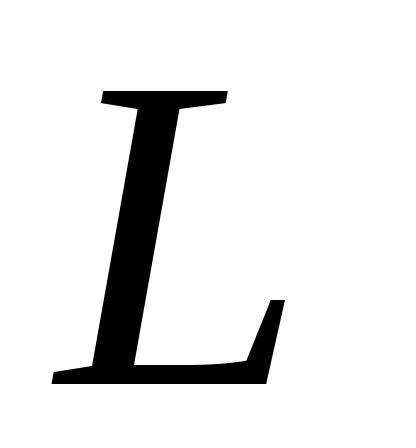 .
.
Особенно просто, зная активное
сопротивление цепи  ,
определить её индуктивность, измерив,
время релаксации:
,
определить её индуктивность, измерив,
время релаксации:
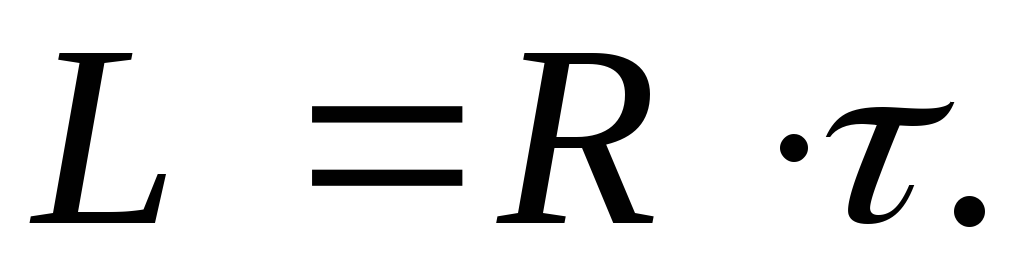 (8)
(8)
3. Вынужденные электромагнитные колебания в контуре, их применение для измерения индуктивности.
Рассмотрим контур, состоящий из
последовательно соединенных конденсатора
емкостью  ,
активного сопротивления
,
активного сопротивления и соленоида индуктивностью
и соленоида индуктивностью 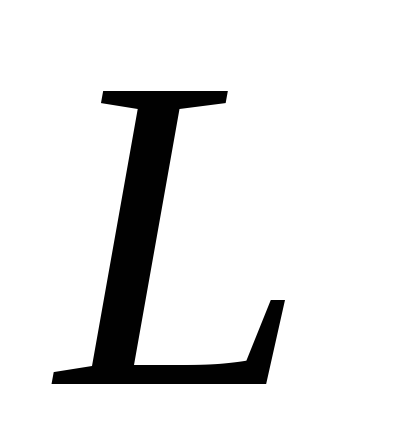 .
.
Д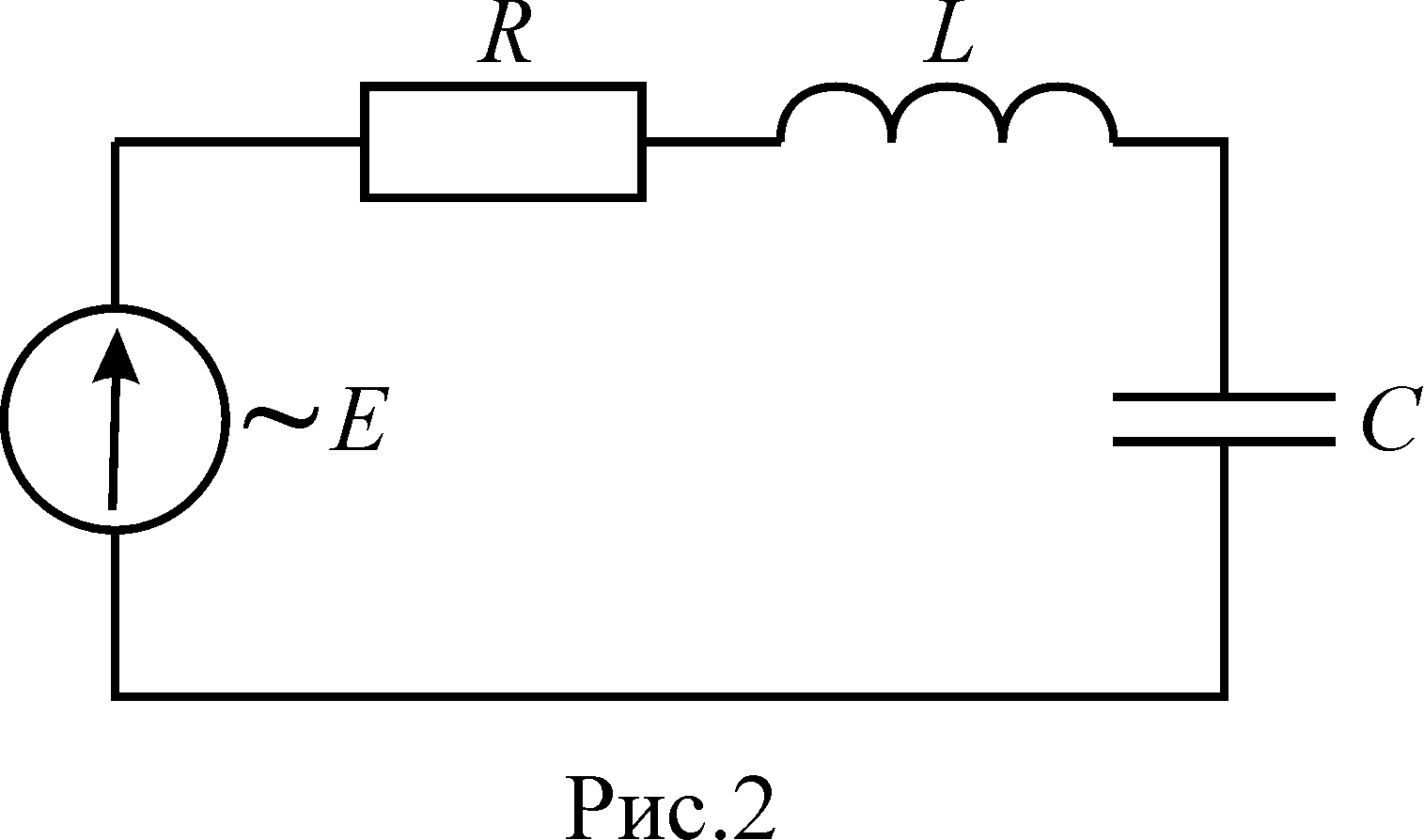 ля
получения незатухающих электромагнитных
колебаний необходимо включить в контур
источник тока с периодически изменяющейся
ЭДС (Рис.2).
ля
получения незатухающих электромагнитных
колебаний необходимо включить в контур
источник тока с периодически изменяющейся
ЭДС (Рис.2).
В этом случае колебания в контуре являются вынужденными.
Пусть, внешняя ЭДС изменяется по гармоническому закону
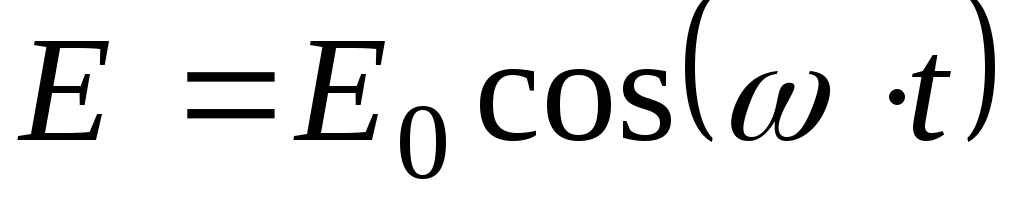 .
.
Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний
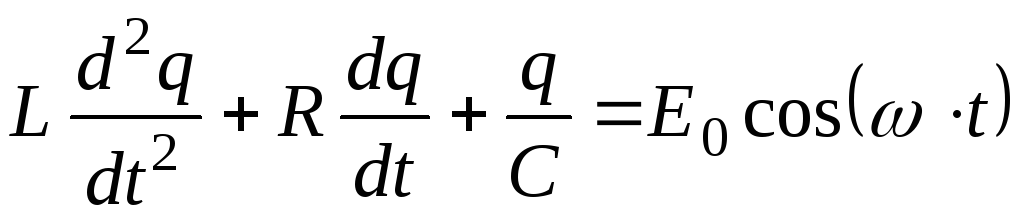
и, решив это уравнение, получить для установившихся вынужденных колебаний следующую связь амплитудных значений силы тока и внешней ЭДС:
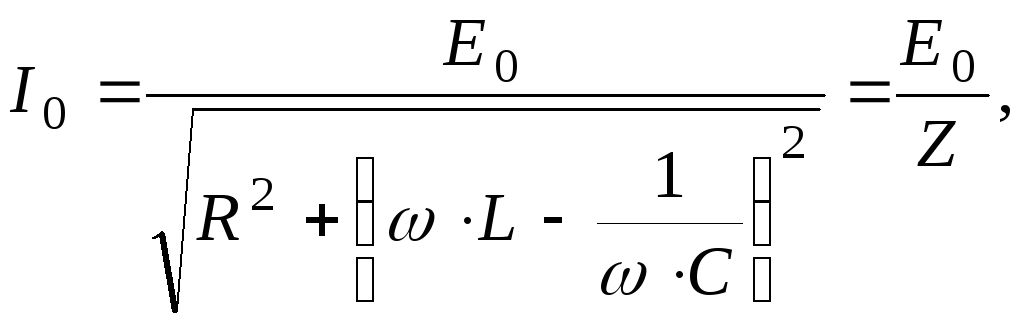 (9)
(9)
где величина 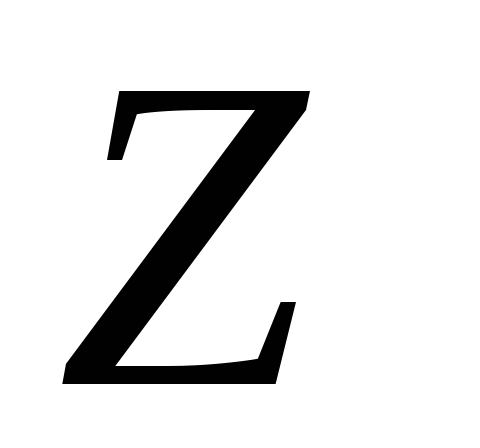 называется полным сопротивлением
электрической цепи переменного тока.
называется полным сопротивлением
электрической цепи переменного тока.
В нее входят активное сопротивление контура,емкостное сопротивление
контура,емкостное сопротивление 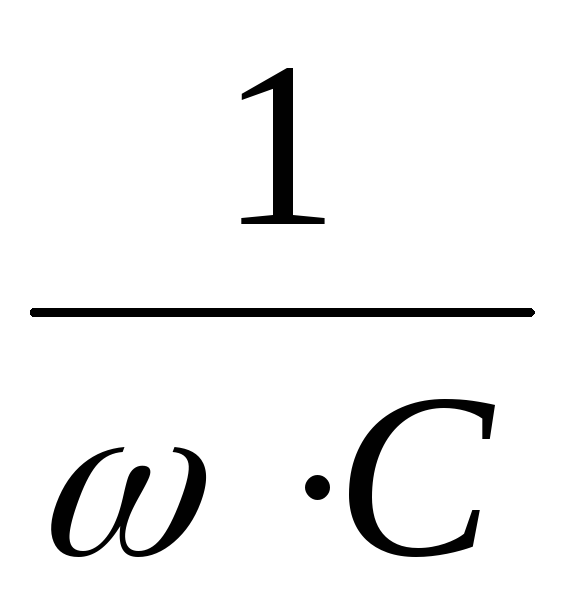 ииндуктивное сопротивление
ииндуктивное сопротивление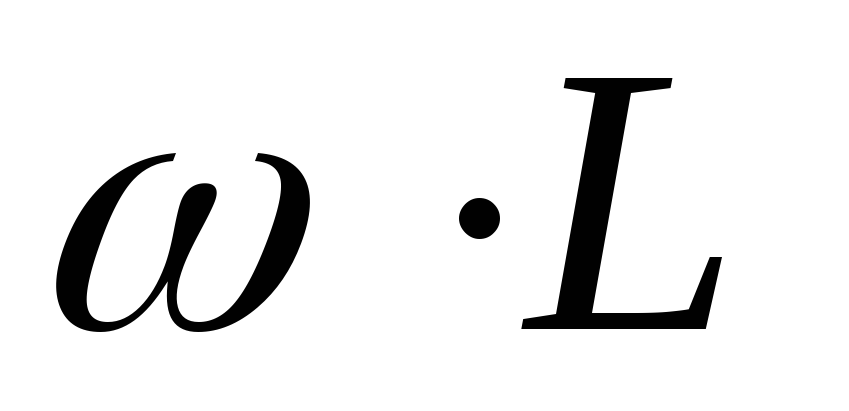 .
.
Если электрическая емкость контура
стремится к бесконечности  ,
то есть емкостное сопротивление к нулю,
то формула (9) упрощается:
,
то есть емкостное сопротивление к нулю,
то формула (9) упрощается:
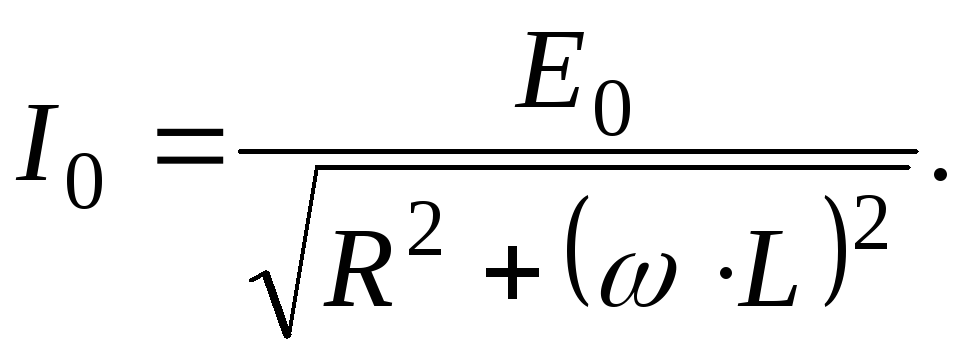 (10)
(10)
Используя это выражение, получим рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении Rсвязана с амплитудой силы тока в цепи формулой
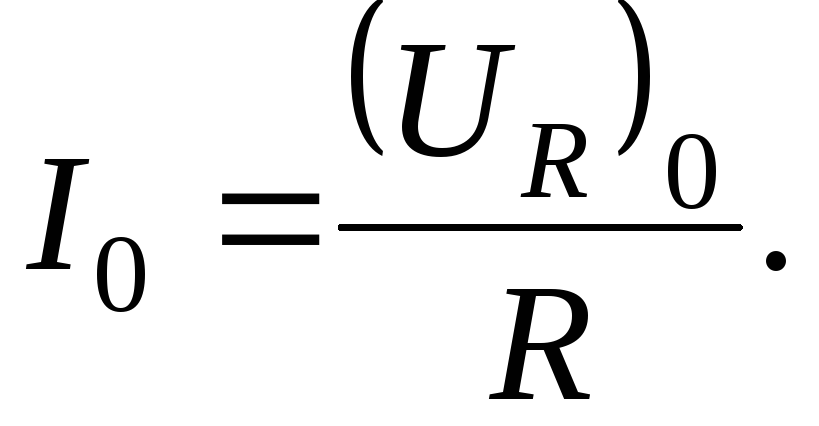 (11)
(11)
Из выражений (10) и (11) получим
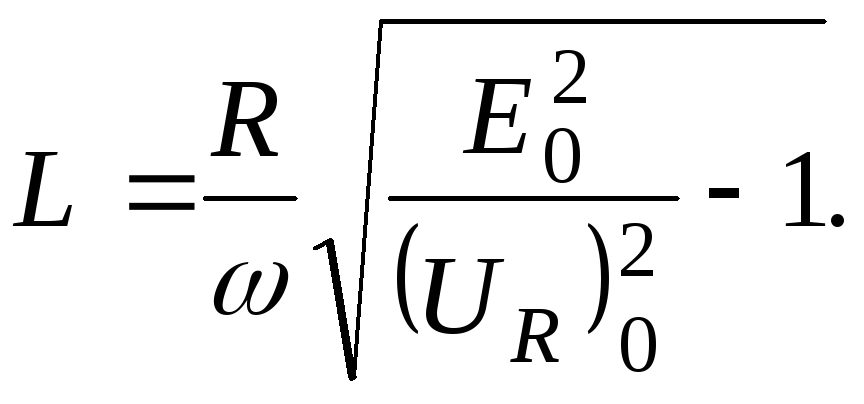 (12)
(12)
Лабораторная работа № 32 определение индуктивности катушки Цель работы:
15
Ознакомиться с явлениями электромагнитной индукции и самоиндукции.
Определить индуктивность катушки методом амперметра и вольтметра.
Исследовать влияние ферромагнитного сердечника на индуктивность катушки.
Теоретическое введение
Магнитным потоком через бесконечно малую площадку dS называется скалярная величина, равная:
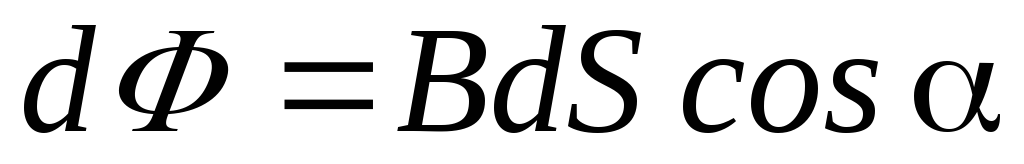 , (1)
, (1)
где B– индукция
магнитного поля, α – угол между вектором
магнитной индукции и нормалью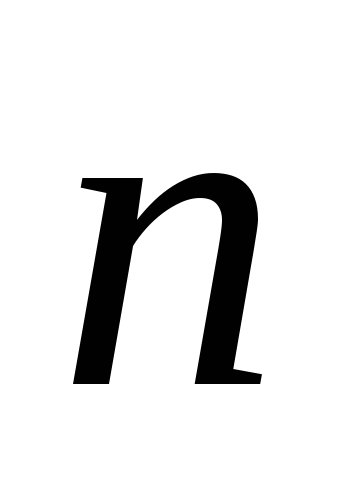 к площадкеdS (рис. 1). Магнитный потокΦ через
произвольную поверхностьS равен:
к площадкеdS (рис. 1). Магнитный потокΦ через
произвольную поверхностьS равен:
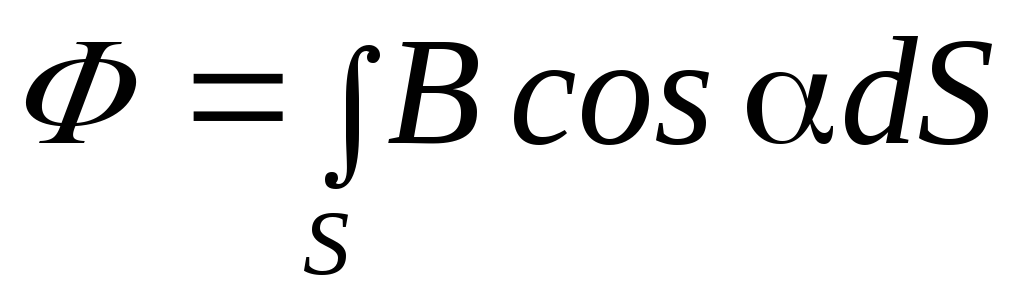 , (2)
, (2)
а в случае однородного поля и плоской площадки:
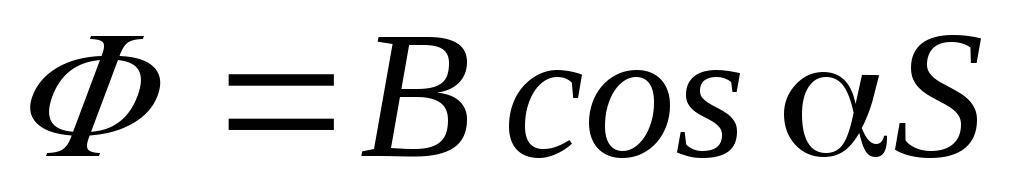 . (3)
. (3)
И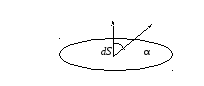 з
формулы (3) видно, что изменить магнитный
поток можно, изменяяВ, S или α как по отдельности, так и вместе.
з
формулы (3) видно, что изменить магнитный
поток можно, изменяяВ, S или α как по отдельности, так и вместе.
Рисунок 1 — Площадка dS в магнитном поле
В 1834 г. М. Фарадей открыл явление электромагнитной индукции, заключающееся в следующем: при любом изменении магнитного потока, пронизывающего замкнутый проводящий контур, в нём возникает ЭДС (ЭДС индукции)Εiи протекает индукционный ток. Согласнозакону Фарадея(закону электромагнитной индукции), ЭДС индукцииΕi существует только в те промежутки времени, когда магнитный поток изменяется, и равна (с обратным знаком) скорости изменения магнитного потока:
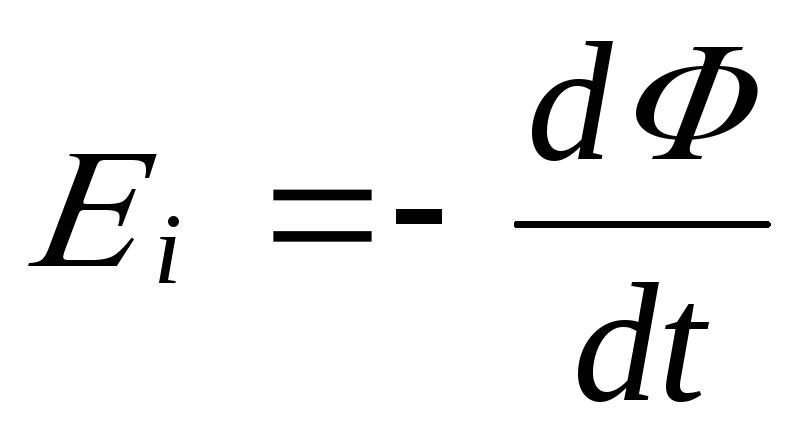 , (4)
, (4)
где dΦ/dt– cкорость изменения магнитного потока.
Знак минус показывает, что если Φ возрастает, то естьdΦ/dt> 0, тоΕi < 0 и наоборот. Этот знак выражаетправило Ленца, определяющее направление индукционного тока: индукционный ток имеет такое направление, что своим магнитным полем противодействует изменению магнитного потока, вызывающему этот ток. Правило Ленца согласуется с законом сохранения энергии.
Электрический ток, текущий в замкнутом контуре (витке), создаёт вокруг себя магнитное поле, пронизывающее сам этот контур. Сцеплённый с контуром магнитный поток пропорционален силе тока, то есть:
Φ ~ I(5)
Отношение магнитного потока, сцеплённого с контуром, к силе тока, создающего этот магнитный поток, называется индуктивностью контура. Это – статическое определение индуктивности:
L = 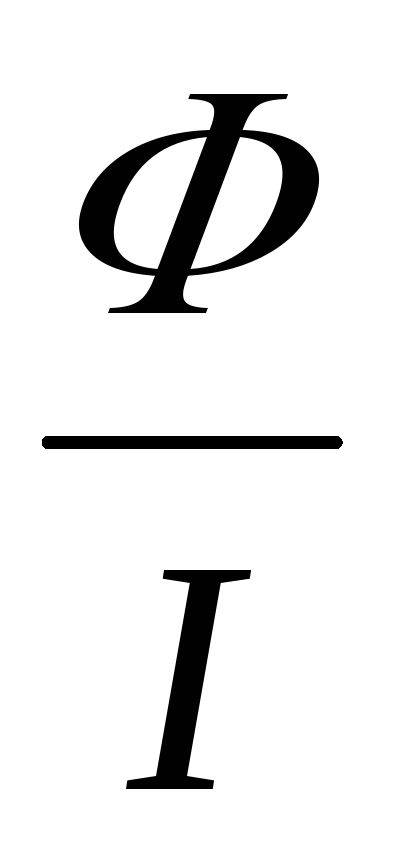 .
(6)
.
(6)
Если контур состоит из Nвитков, намотанных на один каркас, то такой контур называют индуктивной катушкой и вводят понятиепотокосцепления Ψ:
Ψ = Φ∙N , (7)
где под Φ понимают магнитный поток через один виток. В этом случае индуктивность контура определяется соотношением:
L = 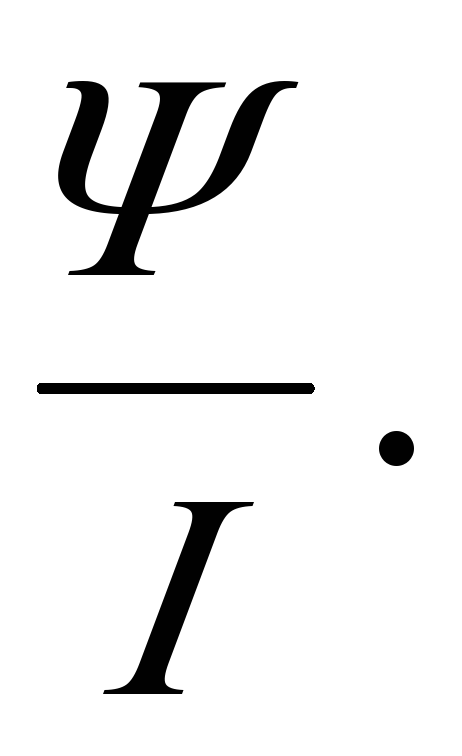 (8)
(8)
Индуктивность измеряется в генри (Гн = Вб/А = В∙с/А = Ом∙с).
Так как внутри катушки магнитное поле направлено вдоль её оси, то есть перпендикулярно плоскости витков, формула (3) принимает вид:
Φ = B∙S . (9)
Как известно, индукция магнитного поля связана с напряжённостью:
В = μμоН , (10)
где μ– магнитная проницаемость среды (сердечника, помещённого в катушку),μо = 4π∙10-7Гн/м – магнитная постоянная. Напряжённость магнитного поля внутри длинной катушки – соленоида (l >>d) равна:
Н = I∙n , (11)
где n = N/l– число витков на единицу длины,l – длина соленоида,d– его диаметр.
Решая совместно (7), (8), (9), (10), (11) получим формулу для индуктивности длинного соленоида:
L = μoμn2V ,(12)
где V = l∙S = l∙πd2/4 – объём магнитного поля внутри соленоида.
Если соленоид включить в цепь постоянного тока и измерить силу тока Iв цепи и напряжениеU, приложенное к соленоиду, то по закону Ома для постоянного тока можно найти сопротивлениеR проволоки, из которой он изготовлен. Это сопротивление называетсяактивнымилиомическим:
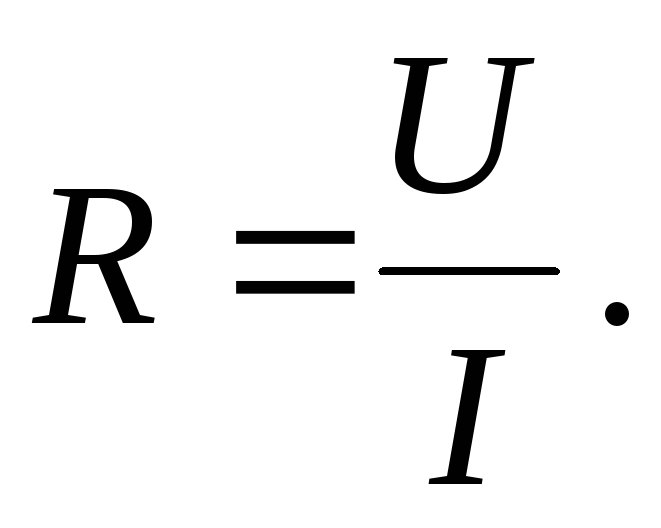 (13)
(13)
При включении соленоида в цепь переменного тока магнитный поток, пронизывающий витки катушки, изменяется. Это по закону Фарадея приводит к возникновению в катушке ЭДС индукции (в данном случае называемой ЭДС самоиндукции) Εsi. В результате возникает индукционный ток, по правилу Ленца направленный против «основного» тока в катушке, если он («основной» ток) возрастает, и в том же направлении, если он убывает. Таким образом, при включении соленоида в цепь переменного тока индукционный ток препятствует возрастанию и убыванию «основного» тока. В результате в цепи переменного тока сопротивление катушки больше, чем в цепи постоянного тока, и закон Ома для действующих значений токаI и напряжения U записывается в виде:
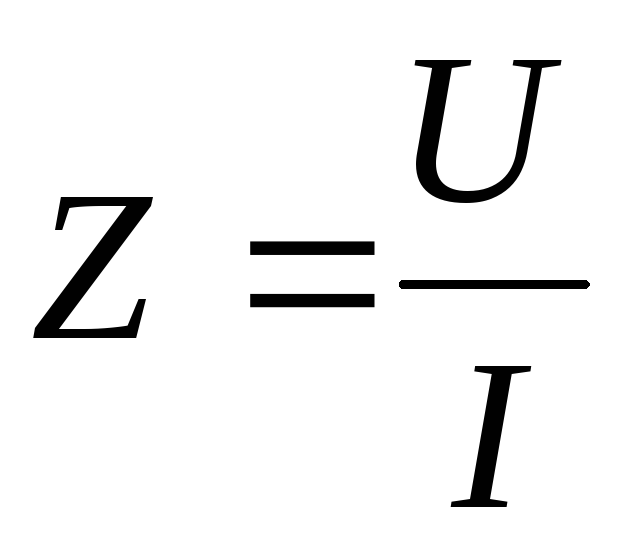 , (14)
, (14)
где Z – полное сопротивление цепи, определяемое формулой:
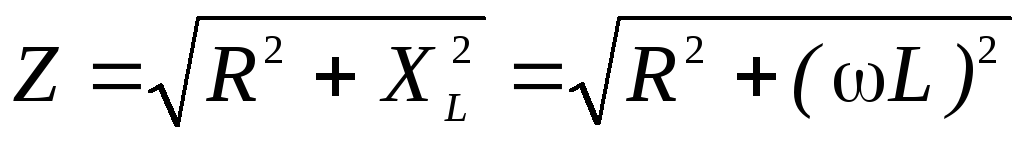 , (15)
, (15)
где ω = 2πf – циклическая частота,f– частота переменного тока (в нашем случаеf = 50,0 Гц),XL=ωL– так называемоеиндуктивное сопротивление.
Закон Фарадея для ЭДС самоиндукции можно записать в виде:
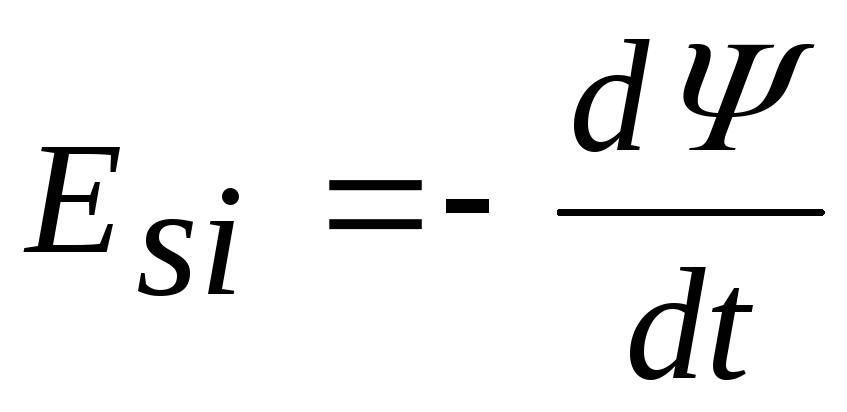 , (16)
, (16)
или, используя (8), Еsi = —d(LI)/dt. В случае, когдаL не зависит от силы токаI, формула ЭДС самоиндукции принимает вид:
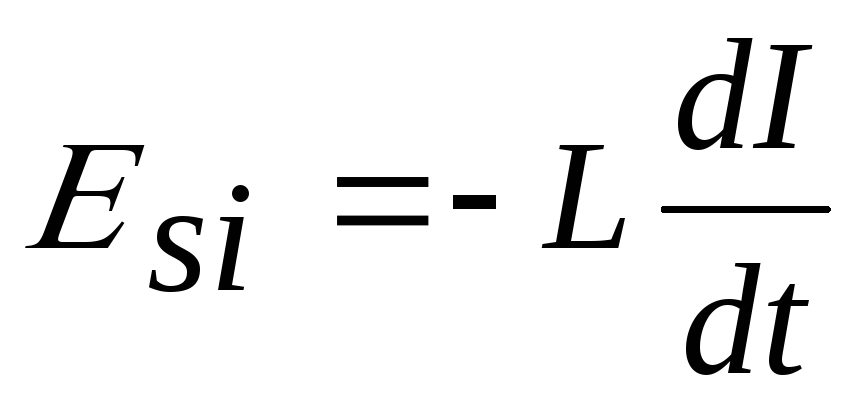 . (17)
. (17)
На основании формулы (17) можно дать динамическое определение индуктивности: величина, равная модулю отношения ЭДС самоиндукции Еsi,возникающей в контуре, к скорости изменения силы токаdI/dtв нём, называется индуктивностью контура:
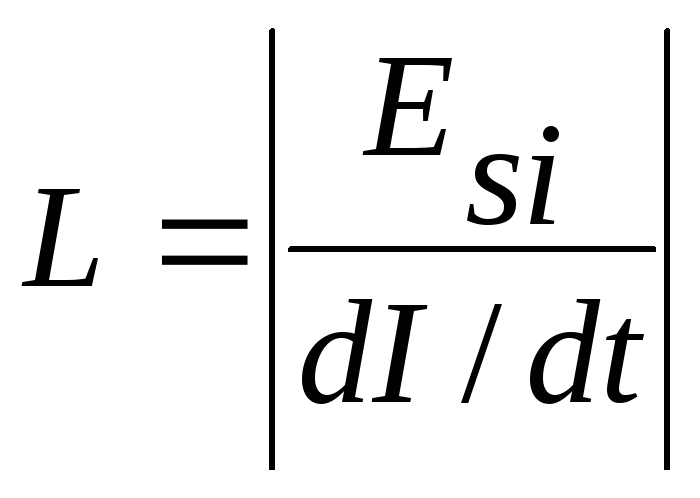 . (18)
. (18)
Индуктивность статическая равна динамической, если она не зависит от силы тока. Это возможно, если в катушке нет сердечника из ферромагнитного материала.
При наличии такого сердечника его магнитная проницаемость μ является сложной функцией напряжённости магнитного поляН(рис. 2), которая зависит от силы токаI(см. формулу (11)), и поэтому индуктивность является сложной функциейI.
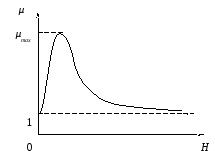
Рисунок 2 — Зависимость магнитной проницаемости μ ферромагнетика от напряжённости H магнитного поля (кривая Столетова)
Из формулы (15) следует формула для расчёта индуктивности:
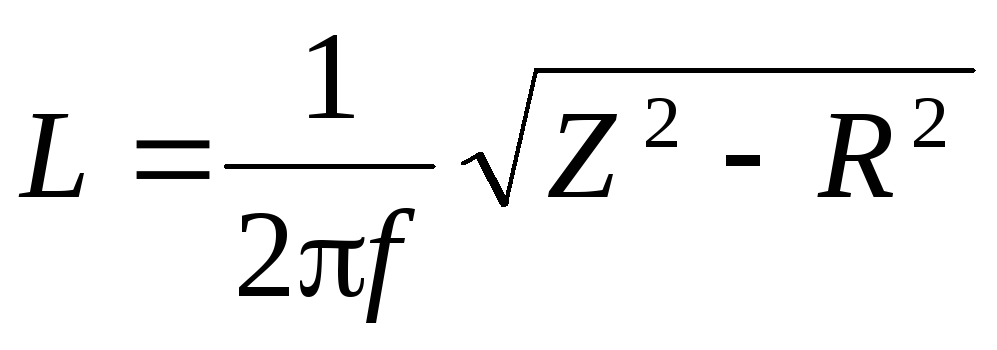 . (19)
. (19)


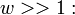
 , (1) Учитывая, что S =
, (1) Учитывая, что S =  , (2) и, используя выражения (1) и (2), найдём
, (2) и, используя выражения (1) и (2), найдём  . (3)
. (3) = 0,278 В.
= 0,278 В. . (3)
. (3) витков
витков .Подставляя исходные данные, получим:
.Подставляя исходные данные, получим: 