По какой формуле найти ёмкость (объем) конденсаторов
Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.

Конденсаторы
Расчёт конденсаторов
Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:
C=q/U, где:
- C – ёмкость,
- q – заряд одной из обкладок элемента,
- U – разность потенциалов между обкладками.
В электротехнике вместо понятия “разность потенциалов между обкладками” используется “напряжение на конденсаторе”.
Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:
С=Co*ε, где:
- С – реальная ёмкость,
- Со – идеальная, при условии, что между пластинами вакуум или воздух,
- ε – диэлектрическая проницаемость материала между ними.
Например, если в качестве диэлектрика используется слюда, “ε” которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.
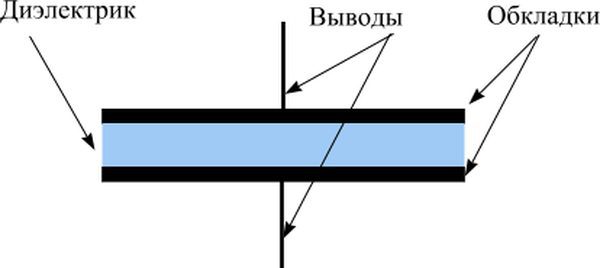
Устройство конденсатора
Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).
Расчет плоской конструкции
Если нужно рассчитать плоский конденсатор, то необходимо учесть площадь обкладок и расстояние между ними. Это отражено в формуле, по которой рассчитывается ёмкость плоского конденсатора:
C=ε/d, где:
- ε – диэлектрическая проницаемость изолирующего материала,
- d – расстояние между пластинами.
Расчет конструкции цилиндрической формы
Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.
Вычисляются параметры такого устройства по формуле:
C=(2π*l*R*ε)/d, где:
- l – длина устройства,
- R – радиус цилиндра,
- ε – диэлектрическая проницаемость изолятора,
- d – его толщина.
Расчёт сферической конструкции
Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:
C=(4π*l*R1*R2*ε)/(R2-R1), где:
- R1 – радиус внутренней сферы,
- R2 – радиус внешней сферы,
- ε – диэлектрическая проницаемость.
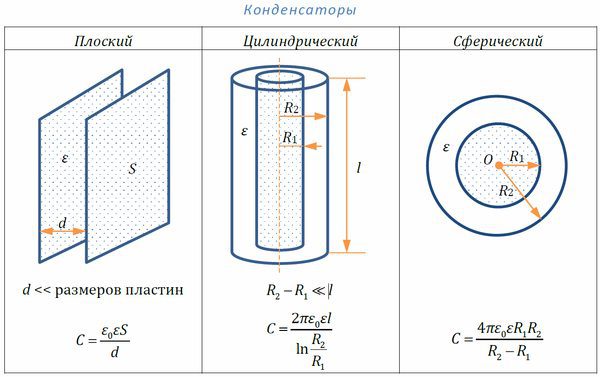
Формулы ёмкости конденсаторов различной формы
Ёмкость одиночного проводника
Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:
C=Q/φ, где:
- Q – заряд,
- φ – потенциал проводника.
Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.
Способы соединения элементов
Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.
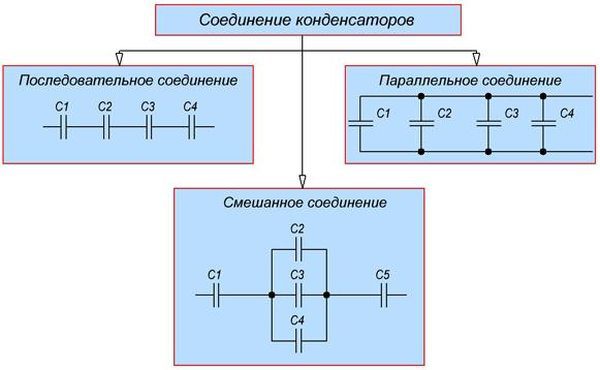
Соединение конденсаторов
Параллельное соединение
Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.
При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:
C=C1+C2+…Cn,
где C1-Cn – параметры деталей, участвующих в параллельном соединении.
Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.
Последовательное соединение
Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.
При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.
Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.
Рассчитываются эти параметры следующим образом:
- Допустимое напряжение:
Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;
- Общая ёмкость:
1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.
Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).
Смешанное соединение
Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:
- определяются группы элементов, соединённые параллельно;
- для каждой группы в отдельности рассчитывается эквивалентные значения;
- рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
- получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.
Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.
Видео
Оцените статью:Расчет параметров конденсатора онлайн
Не знаю как Вам, а мне никогда не нравилось работать и вычислять ёмкости конденсаторов. Больше всего раздражало наличие в исходных данных, ёмкостей в разных номиналах, в пикофарадах, в нанофарадах, микрофарадах. Их приходилось переводить в Фарады, что влекло за собой глупейшие ошибки в расчетах.
Конденсатор — в принципе это любая конструкция, которая может сохранять накопленный электрический потенциал. Если же эта конструкция, не только хранит электроэнергию, но и генерирует её, то это уже источник электропитания и никак не конденсатор.
Конструкция конденсаторов может быть любой, но чаще всего в практике используется плоский конденсатор, состоящий из двух проводящих пластин, между которыми находится какой либо диэлектрик. Это связано с тем, что расчет ёмкости такого конденсатора ведется по известной формуле и простотой его создания. Свернув такой плоский конденсатор в рулон, мы получаем, что при фактическом скромном размере «рулона», там находится плоский конденсатор, длиной в десятки сантиметров и обладающий повышенной ёмкостью.
Емкости конденсаторов некоторых форм известны, и мы дальше их рассмотрим.
Но хотелось бы заметить, что на наш взгляд, потенциал развития конденсаторов до конца не завершен. Ведь форма конструкции какого либо конденсатора может быть любая, материалы из которого сделаны обкладки или диэлектрический слой тоже могут быть любыми в пределах таблицы Менделеева. Единственная сложность, это невозможность теоретически просчитать потенциальную ёмкость, новосозданного (другой конструкции) конденсатора. Это усложняет нахождение самой лучшей конструкции конденсатора.
Есть хорошая книга по рассмотрению электрической ёмкости различных фигур. Для любопытных рекомендую поискать на просторах Интернета: Расчет электрической ёмкости в авторстве Ю.Я.Иоселль 1981 года
Данный бот рассчитывает параметры типовых форм конденсаторов. Отличие от других калькуляторов, присутствующих в интернете, это возможность задавать параметры, которые Вам известны, для того что бы рассчитать остальные.
И последнее нововведение, которое вы можете использовать. Вам не обязательно придется переводить заданные данные в метры, фарады и т.д. Достаточно обозначить размерность данных.
Например, если ёмкость известна и равно 100 пикофарад, то боту можно так и написать
Результат, тоже будет выдан оптимально визуальному восприятию пользователя.
Это стало возможно с созданием бота Система единиц измерения онлайн
Плоский конденсатор. Параметры
| Полученные характеристики плоского конденсатора |
Ёмкость такого сооружения определяется следующей формулой.
где ε0 = 8,85.10-12 Ф/м — абсолютная диэлектрическая проницаемость
Если же конденсатор состоит не из пары пластин, а каого то n-ого количества плоских пластин то ёмкость такого «слоёного» конденсатора составит
Еще интереснее выглядит формуа такого «слоёного» конденсатора, если в слоях находятся разные диэлектрики , разной толщины d
S- площадь одной из обкладок конденсатора ( предполагаем что другая обкладка имеет такую же площадь)
d- расстояние между обкладками
С- ёмкость конденсатора
Рассмотрим примеры
Задача: Ёмкость плоского конденсатора 350 нанофарад, расстояние между обкладками 1 миллиметр, и заполнено воздухом. Определить какова площадь обкладок?
Сообщаем боту что нам известно: C=350нФ, d=1мм. Так как у воздуха диэлектрическая проницаемость 1.00059 то e=1.00059. Поле площадь очистим, так именно его мы будем определять
Получаем вот такой ответ
| Полученные характеристики плоского конденсатора |
|
d = 1 милиметр |
Ответ, площадь обкладок конденсатора при таких значениях должна составлять почти 40 квадратных метров.
Цилиндрический КОНДЕНСАТОР
| Полученные характеристики цилиндрического конденсатора |
Цилиндрический конденсатор представляет в простейшем случае две трубки разного диаметра вложенных друг в друга. разделенных диэлетриком
Иногда может получится так, что ёмкость цилиндрического конденсатора станет отрицательной величиной. Ничего страшного, это лишь говорит о том что Вы перепутали радиусы внешней и внутренней оболочки местами.
- Расчет понижающего конденсатора >>
Конденсаторы и емкость. Формулы конденсатора
Одним из важнейших компонентов электрических цепей является конденсатор. В общем виде, конденсатор представляет из себя две пластины проводящего материала, между которыми заключен диэлектрик. При подключении конденсатора к источнику напряжения, на пластинах конденсатора появляется заряд +Q на верхней и –Q на нижней. Сила тока протекающего через конденсатор во время зарядки описывается формулой:
I= C * (dV/dt)
Решая данное уравнение относительно V, можно вычислить значение напряжения в момент времени t.
Как видно из уравнения, сила тока протекающего через конденсатор пропорциональна изменению напряжения во времени. При отключении источника питания от конденсатора, заряд а его пластинах будет равен:
Q=C*V
Где, С – Емкость конденсатора в Фарадах, V — напряжение в Вольтах.
Емкость конденсатора напрямую зависит от его конструктивных параметров. Емкость плоского конденсатора площадь пластин которого S с расстоянием d между ними
описывается формулой:
C=(E0 * E * S)/d
Где, E — Диэлектрическая проницаемость среды между пластинами, E0 — Электрическая постоянная.
На схемах, конденсатор обозначается следующими символами:

Промышленностью выпускаются как полярные так и неполярные конденсаторы. При включении полярных конденсаторов следует соблюдать полярность включения выводов. Зачастую отрицательный вывод конденсатора помечен специальным образом, чаще всего непосредственно на корпусе конденсатора. Внешний вид такого конденсатора представлен на следующем рисунке:
Внешний вид керамического конденсатора (неполярного) представлен на следующем изображении:

Последовательное и параллельное включение
Конденсаторы,как и резисторы, можно объединять между собой последовательным и параллельным соединением.

При последовательном соединении, общая емкость будет равна:
(1/Cобщ) = 1/C1+1/C2+1/C3
При параллельном, формула емкости запишется следующим образом:
Собщ=C1+C2+C3
Энергия запасенная в конденсаторе
Количество энергии запасенной конденсатором можно вычислить согласно следующей формуле:
РАДИО ВСЕМ, №12, 1926 год. Расчет емкости конденсаторов
РАДИО ВСЕМ, №12, 1926 год. Расчет емкости конденсаторов«Радио Всем», №12, декабрь 1926 год, стр. 20-21
Расчет емкости конденсаторов
М. А. Нюренберг.
Почти во всех случаях радиолюбительской практики приходится иметь дело с конденсаторами — постоянной и переменной емкости и их расчету мы посвящаем эту статью.
Конденсатор постоянной емкости.
Простейший конденсатор постоянной емкости (черт. 1) представляет собой две металлические обкладки, разделенные друг от друга каким-либо диэлектриком (воздухом, слюдой и пр.). Емкость такого конденсатора зависит от площади металлической обкладки; расстояния между обкладками (толщины диэлектрика) и свойств того диэлектрика, который применен в конденсаторе.
Черт. 1.
Емкость такого конденсатора определяется формулой:
где
C — емкость конденсатора в см.
S — плошадь одной обкладки в кв. см.
d — расстояние между обкладками в см.
ε — диэлектрическая постоянная (величины ε для различных диэлектриков приводятся ниже в таблице):
| Диэлектрик | ε = | Диэлектрик | ε = |
| Пустота…… | 1 | Бумага (сухая).. | 1,8—2,6 |
| Воздух…… | 1,0006 | Каучук…… | 2,0—3,5 |
| Керосин…… | 2 | Парафин…… | 1,8—2,3 |
| Эбонит…… | 2—3 | Сера…… | 3,6—4,8 |
| Маслян. бумага.. | 2 | Целлюлоид…… | 4 |
| Шеллак…… | 3,0—3,8 | Сургуч…… | 4 |
| Стекло…… | 5—10 | Вода (химич. чистая)…… |
81 |
| Слюда…… | 5—8 |
Конденсаторы, состоящие из двух обкладок, имеют очень незначительную емкость и потому применяются очень редко — в специальных схемах для коротких волн. Обычно применяются конденсаторы, состоящие из нескольких обкладок, емкость которых может быть очень велика (черт.2).
Черт. 2.
Емкость таких конденсаторов зависит, кроме всего указанного ранее (для случая конденсатора с двумя обкладками), также от числа обкладок. Прибавляя к описанному ранее конденсатору одну, две, три и т. д. обкладок, мы будем увеличивать емкость конденсатора в 2, 3, 4 и т. д. раза.
Подсчитать емкость плоского конденсатора можно по номограмме черт. 3. В этой номограмме: dmm — толщина диэлектрика в мм. Fсм2 — площадь одной обкладки в кв. см., Cсм — емкость в см., n — общее число обкладок. Диэлектрическая постоянная ε — принята равной единице (воздух), Z — вспомогательная прямая. Способ пользования этой номограммой тот же, что номограммой для расчета самоиндукций (см. № 8 «Радио Всем»1) и мы на его описании останавливаться не будем. Последовательность соединения точек следующая: F — n — Z — d — C.
Черт. 2.
(увеличенное изображение)
В таблице II приведены значения емкости конденсатора в зависимости от числа обкладок и толщины диэлектрика при площади обкладки равной 1 кв. сантиметру. Для расчета емкости следует величину, взятую из таблицы, умножить на площадь обкладки в кв. см., например: нужно определить емкость конденсатора: число обкладок 5, толщина слюды 0,01 см., площадь каждой обкладки = 16 кв. см. По таблице находим, что емкость при площади, равной 1 кв. см. будет равна 191 см. Следовательно, полная емкость будет равна:
С = 191 × 16 = 3056 см.| d (см.) | Число пластин | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 0,005 | 31,9 | 63,8 | 95,7 | 127 | 159 | 191 | 223 | 255 | 287 | 319 | 351 | Пара- фин ε = 2. |
| 0,01 | 15,9 | 31,9 | 47,8 | 63,7 | 79,6 | 95,5 | 111 | 127 | 143 | 159 | 175 | |
| 0,03 | 5,3 | 10,6 | 15,9 | 21,2 | 26,5 | 31,9 | 37,2 | 42,5 | 47,8 | 53,2 | 58,5 | |
| 0,05 | 3,2 | 6,4 | 9,5 | 12,7 | 15,9 | 19,1 | 22,3 | 25,5 | 28,7 | 31,9 | 35,1 | |
| 0,08 | 1,99 | 3,98 | 5,96 | 7,95 | 9,95 | 11,9 | 13,9 | 15,9 | 17,9 | 19,9 | 21,8 | |
| 0,1 | 1,59 | 3,19 | 4,78 | 6,37 | 7,96 | 9,55 | 11,1 | 12,7 | 14,3 | 15,9 | 17,5 | |
| 0,005 | 95,6 | 191 | 287 | 381 | 477 | 572 | 669 | 765 | 860 | 956 | 1050 | Слюда ε = 6. |
| 0,01 | 47,7 | 95,6 | 143 | 191 | 239 | 286 | 333 | 381 | 428 | 476 | 524 | |
| 0,03 | 15,9 | 31,8 | 47,7 | 63,5 | 79,4 | 95,5 | 111 | 127 | 143 | 159 | 175 | |
| 0,05 | 9,6 | 19,2 | 28,7 | 38,1 | 47,7 | 57,2 | 66,9 | 76,5 | 86,0 | 95,6 | 105 | |
| 0,08 | 5,9 | 11,9 | 17,9 | 23,9 | 29,9 | 35,7 | 41,7 | 47,7 | 53,7 | 59,7 | 65,4 | |
| 0,1 | 4,7 | 9,5 | 14,3 | 19,1 | 23,9 | 28,6 | 33,3 | 38,1 | 42,8 | 47,6 | 52,4 | |
Формула для расчета емкости конденсатора, состоящего из нескольких обкладок, имеет следующий вид:
C = ε·S (n — 1) 12,5d Все обозначенные те же, что и в ранее приведенной формуле.
n — общее число обкладок (положительных и отрицательных).
Конденсатор переменной емкости.
Расчет конденсатора переменной емкости заключается в подсчете его максимальной емкости (при вдвинутых подвижных пластинах) и ничем не отличается от расчета плоского постоянного конденсатора. Начальная емкость (при выдвинутых подвижных пластинах) подсчету не поддается и обычно определяется экспериментальным путем.
Черт. 4.
При расчете конденсатора переменной емкости следует за площадь пластины принимать лишь ту площадь, которая взаимно перекрывается пластинами (подвижной и неподвижной). На черт. 4 эта площадь заштрихована.
Формула для расчета емкости переменного конденсатора, пластины которого имеют полукруглую форму, следующая:
C = ε (r12 — r22) (n — 1) 8d где r1 — радиус подвижной пластины в см.
r2 — внутренний радиус неподвижной пластины в см. (см. черт. 4).Остальные обозначения те же, что в ранее приведенных формулах.
Расчет емкости квадратичного конденсатора описан в № 11 «Радио Всем», где также описаны графики емкости конденсаторов, почему на этом вопросе мы останавливаться не будем.
Соединение конденсаторов.
При параллельном соединении нескольких конденсаторов (черт. 5) емкость всей группы будет равна сумме емкостей отдельных конденсаторов, т. е.
C = C1 + C2 + C3 +…Черт. 5.
При последовательном соединении нескольких конденсаторов (черт.6) общая емкость группы будет меньше емкости любого из включенных в группу конденсаторов. Для двух последовательно включенных конденсаторов общую емкость легко подсчитать по номограмме черт. 7, где C1 и C2 — емкости отдельных конденсаторов, а C — общая емкость этих конденсаторов, включенных последовательно. Простым соединением помощью линейки C1 и C2 определяется в точке пересечения общая емкость C. Очевидно, что, пользуясь этой номограммой, можно определить емкость нескольких, последовательно включенных конденсаторов. Для этого последовательно определяются значения C при двух конденсаторах C1 и C2; полученное значение C для двух конденсаторов соединяется с третьим конденсатором C3 и т. д.
Черт. 6.
Формула для последовательно соединенных конденсаторов имеет вид:
1 = 1 + 1 + 1 + … C C1 C2 C3 где C — общая емкость группы
C1, C2, C3 … — емкости отдельных конденсаторов.Дпя двух конденсаторов формула имеет вид:
Черт. 7.
(увеличенное изображение)
Этой статьей мы заканчиваем первый цикл статей, посвященных расчетам деталей и в следующих номерах журнала перейдем к расчетам антенн и приемников.
1) Пример работы с номограммой приведен не в №8, а в №7 «Радио Всем» за 1926 год. (примечание составителя).

