Электроёмкость конденсатора: формулы и история
Электроемкость конденсатора – физическая величина, характеризующая процесс заряда проводников, разделенных слоем диэлектрика. Используется многочисленными математическими расчетами, маркируется на корпусе изделия.
Формулы
Электроемкость конденсатора принято выражать через запасаемый заряд q при приложенном напряжении U подобным образом:
C = q/U.
Происхождение формулы – загадка. Известно только: из теоремы Гаусса по напряженности электрического поля найдем электроемкость конденсатора. Кто провел расчет, нигде не говорится. Физическая величина фарад изначально в системе СГС отсутствовала, в 1861 году ввела специальная комиссия, сформированная физиками.
По отдельным сведениям, впервые электроемкость конденсатора определил введший термины в обиход. Подразумеваем Алессандро Вольту. Поздние 70-е (XVIII века) ученый уделил исследованиям вопроса, установил: электроемкость можно выразить через накапливаемый заряд, приложенное к электродам напряжение.
Вдобавок удаётся часто встретить формулу электроемкости плоского конденсатора:
Авторы избегают судить, кто занимался расчетами выражения. Рассуждая логически, мало кого интересовала электроемкость плоского конденсатора до появления на свет изобретения Полака. Лейденские банки по-другому распределяют заряд. Рассуждения приводят к началу XX века. Возможно, вопросом занимались Тесла, Герц. С меньшей вероятностью – Попов.
Фамилии названы по критериям заинтересованности переменным током. Тесла изучал вопросы безопасности электричества, передачи на расстояние, конструировал двигатели. Герц и Попов исследовали антенны, заведомо настраиваются на некую длину волны, которую проще получить, применяя колебательный контур. Следовательно, ученые обязаны иметь представление об электроемкости конденсатора, катушках индуктивности.
Джеймс Максвелл, лорд Кельвин, Вильгельм Вебер много внимания уделяли совершенствованию единых систем измерения физических величин. Вероятно, кто-то приложил руку к исследованию конденсаторов. Ясно одно – в мировой истории естественных наук масса белых пятен, когда дело касается русскоязычных источников. Портал ВашТехник одним из первых начнёт публиковать новейшие исследования в области правильного понимания произошедших событий.
История
Нетерпеливым читателям докладываем: Алессандро Вольта ввел собственно термин емкости. Неизвестно точно, употреблял ли кто раньше, но в своей работе итальянский ученый, называя электрофорус конденсатором, одновременно применяет к нему термин емкости. Как сосуду, куда можно «налить» заряд из емкости. Конденсатором зовет за схожесть процесса с осаждением паров: понемногу наберем произвольное количество электричества. По большому счету, это верно.
Термин конденсатор
Исторически первым конденсатором считают лейденскую банку. Поныне ходят споры, кто изобрел прибор, поскольку оба ученых, увлеченных событиями, избегали ведения аккуратных записей. Бесспорно одно – электроемкость прибора измерить было нельзя, отсутствовало соответствующее понятие «электроемкость конденсатора».

Скрин печатного варианта трактата Вольты, 1782 год
Придумавший термин бессилен произнести слово раньше, нежели Алессандро Вольта в 1782 году, докладывая Королевскому Научному обществу изыскания в области электростатики, чтобы понять, откуда берется электричество. Известно, в течение следующих пяти лет Луиджи Гальвани откроет «животное электричество», приведшее Вольту прямиком к созданию первого элемента питания. Докладывая обществу, молодой ученый лишен упомянутых знаний, светило пытается понять, откуда появляется заряд. Рассуждает приблизительно так: «К настоящему времени немало свидетельств существования атмосферного электричества. Люди бессильны найти следы присутствия. Вероятно, означает: созданные электроскопы слишком слабы, неспособны уловить столь тонкую материю. Следовательно, требуется найти способ забрать из воздуха флюиды».
Выполняя сказанное, Алессандро Вольта предлагает приспособление, называемое электрофорусом (не путать с электрофорной машиной). Прибор захватывает флюиды атмосферного проводника (воздуха). Принцип служения Вольте напоминает процесс конденсации: собирает электричество.
Электрофорус
Запад электрофорус называет генератором емкостного типа. Указанное выше позволяет полагать: подобное определение прилепилось благодаря написанному Английскому Королевскому обществу Вольтой. Устройство придумано другим человеком – шведским физиком Джоном Кларком Вилке. Случилось двумя десятилетиями ранее – 1762 год.
Ныне считается, популярность прибору придал Вольта, называя любимца вечным генератором электричества. Тоже по сути правильно, тереть резину можно тысячелетиями. Больше «конденсатор» напоминает (см. рис.) здоровенную печать. Сверху, помимо основной центральной ручки, стоит боковая – снятия отрицательного потенциала. Видим три слоя:
- Подложка необязательна, на нее наклеивается резина.
- Тонкий слой резины служит телом электризации трением.
- Сверху – тонкий лист металла, снабженный двумя рукоятками, одна (центральная) изолирована.

Внешний вид электрофоруса
Начав работы, нужно убрать «печать», натереть резину шерстью. Затем гладкий диск ставится обратно. Площадь соприкосновения с резиной невелика из-за присутствующих шероховатостей, положительный заряд приобретается нескоро. Нужно выждать. Оператор на короткий миг заземляет крышку боковой ручкой, снимая отрицательный заряд, снизу остается положительный. Прикасаясь одной рукой к металлу, можно слышать хорошо различимый треск. Резина после поднятия крышки несет избыток электронов, позволяющий повторить опыт несколько раз (верится с трудом, некоторые источники говорят о сотне повторений).
Разнимая тела, резким движением потянув изолирующую рукоятку, оператор получает статическое электричество. Изобретение революционное, примечательно, появилось в считанные годы после отмены закона охоты на ведьм. По заявлению Вольты, круг резины делается по возможности тонким, в пределах 50-й доли дюйма. Удается получить наилучший результат. Лист металла фактически становится пластиной. В противном случае долго придётся ждать наполнения объема проводника. В простонародье «конденсатор» называют резиновым пирогом. Пирогом, покрытым металлической начинкой.
Действительно ли электрофорус является неисчерпаемым источником энергии? В идеальных условиях, хотя верится с трудом. Отрицательный заряд резины поляризует металлическую пластину, создавая некий потенциал. Вытесненные на внешнюю поверхность электроны снимаются прикосновением заземлителя. Остается разнять составные части электрофоруса. Уничтожив положительный заряд прикосновением, услышав звук проскочившей искры, можно заново начинать опыт.
Электрофорус действительно напоминает конденсатор. После снятия лишнего отрицательного заряда превращается фактически в упомянутый прибор. Долго храниться конденсатор не может, поскольку электроны с резины понемногу будут стекать на металл. Устройство разрядится. Фактически резина, металл отделены друг от друга воздухом, служащим диэлектриком. Вместо резины используем различные полимеры, например, Тефлон.
Осталось заметить: во времена Вольты не знали методов избавления резины от статического заряда. «Обкладка» конденсатора могла долгое время хранить груз электронов. Вольта предлагает для разрядки поместить образец под солнечные лучи, либо поводить рядом горящей свечой. Через ионизированное пламя электроны покидают конденсатор. Сегодня понятно, достаточно вымыть резину, чтобы следов не осталось статического напряжения. Для работы потребуется вновь высушить.
Лейденская банка
Считается, что Феликс Савари обнаружил колебания резонансного контура. Разряжая лейденскую банку через витую нить меди, наблюдал беспорядочное снование стрелки компаса. 1826 год, когда Англия, Франция, Германия, частично Италия лихорадочно исследовали новое явление, привнесенное в научный мир Эрстедом.
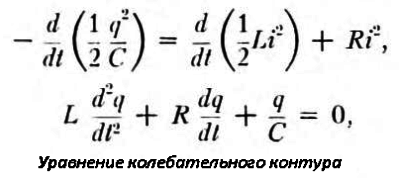
Историю создания лейденской банки можно прочитать в соответствующем обзоре. Следует сказать, никто не пытался толком понять, какова электроемкость конденсатора. Не нужно по очевидным соображениям: лейденскую банку преимущественно использовали научные круги, решая специфические задачи. Опыт Феликса Савари надолго остался без внимания…
В 1842 году колебательным контуром, электроемкостью конденсатора занялся наш старый знакомый, сэр Джозеф Генри, изобретатель электромагнитного реле, любитель телеграфа. Изложил письменно после опробования заметок Савари практикой:
«Аномалия, остающаяся столь долго без объяснения, которая на первый взгляд представляется существующей наперекор нашей теории электричества и магнетизма, после тщательного изучения мною отнесена к доселе неизведанным явлениям. Разряд происходит странно (вразрез теории Франклина), ощущение, что, выходя из банки, флюид начинает странствовать взад-вперед. Увиденное принуждает признать: процесс начинается нормальным образом, затем происходит несколько смен направлений, каждый раз амплитуда становится меньше, пока движения затухнут вовсе. Судя по всему, феномен сегодня не может быть объяснен, физики встречались с ним (Савари), но оказались бессильны».
Очевидно, ученого совершенно не интересует электроемкость конденсатора – мысли поглощены аномалией, которую хотелось бы разведать. Пятью годами позже, ознакомившийся с отчетом Генри физик Гельмгольц на встрече Физического общества Берлина, говорит:
«Проводя электролиз, заметил необычные колебания. Такое ощущение, процесс колебаний продолжается, пока само vis viva не исчезнет навсегда, поглощенное суммарным сопротивлением цепи. Создается впечатление, по контуру текут два тока противоположных направлений, верх берет то один, то другой».
Конец спорам положил знаменитый Вильям Томсон, нареченный лорд Кельвин. Математически исследовав процесс, заявил: в цепи очевидно присутствуют две вещи: электроемкость конденсатора и индуктивность свернутой медной проволоки. Работа On Transient Electric Currents стала классической. Хотя лорд Томсон зовет индуктивность электродинамической емкостью, смысл формулы однозначный. Ученый первым заявил: энергия передается меж конденсатором и катушкой индуктивности, постепенно затухая на активном сопротивлении цепи.
Формула, приведенная на рисунке, дана в современных величинах, обозначения стандартные. С – электроемкость конденсатора, L – индуктивность катушки, q – величина заряда, I – ток цепи. Прочие символы относятся к операциям дифференцирования. Термин индуктивность введен намного позже – в 1886 году Оливером Хэвисайдом. Формула резонансной частоты, зависящей от электроемкости конденсатора и индуктивности катушки, выведена Джеймсом Максвеллом в 1868 году.
Урок 28. электрическая ёмкость. конденсатор — Физика — 10 класс
Физика, 10 класс
Урок 28. Электрическая ёмкость. Конденсатор
Перечень вопросов, рассматриваемых на уроке:
- Электрическая ёмкость
- Плоский конденсатор
- Энергия конденсатора
Глоссарий по теме:
Конденсатор – устройство для накопления электрического заряда.
Электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Под зарядом конденсатора понимают модуль заряда одной из его обкладок.
Последовательное соединение – электрическая цепь не имеет разветвлений. Все элементы цепи включают поочередно друг за другом. При параллельном соединении концы каждого элемента присоединены к одной и той же паре точек.
Смешанное соединение — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Энергия конденсатора прямо пропорциональна квадрату напряжённости электрического поля внутри его: 
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения.
Основная и дополнительная литература по теме:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 321-330.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 97-100.
Теоретический материал для самостоятельного изучения
Конденсатор при переводе с латиницы означает, то что уплотняет, сгущает – устройство, предназначенное для накопления зарядов энергии электрического поля. Конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга. Главной характеристикой этого прибора, является его электроёмкость, которая зависит от площади его пластин, расстояния между ними и свойств диэлектрика.
Заряд конденсатора определяется – модулем заряда на любой одной из её обкладок. Заряд конденсатора прямо пропорционален напряжению между обкладками конденсатора. Коэффициент пропорциональности С называется электрической ёмкостью, электроёмкостью или просто ёмкостью конденсатора.

Электрической ёмкостью конденсатора называется физическая величина, которая численно равна отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Чем больше площадь проводников и чем меньше пространство заполняющего диэлектриком, тем больше увеличивается ёмкость обкладок конденсатора.

Измеряется электрическая ёмкость в Международной системе СИ в Фарадах. Эта единица имеет своё название в честь английского физика экспериментатора Майкла Фарадея который внёс большой вклад в развитие теории электромагнетизма. Один Фарад равен ёмкости такого конденсатора, между пластинами которого возникает напряжение, равное одному Вольту, при сообщении заряда в один Кулон.
Электрическая ёмкость конденсаторов определяется их конструкцией, самыми простыми из них являются плоские конденсаторы.
Чем больше площадь взаимного перекрытия обкладок и чем меньше расстояние между ними, тем значительнее будет увеличение ёмкости обкладок конденсатора. При заполнении в пространство между обкладками стеклянной пластины, электрическая ёмкость конденсатора значительно увеличивается, получается, что она зависит от свойств используемого диэлектрика.
Электрическая ёмкость плоского конденсатора зависит от площади его обкладок, расстояния между ними, диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками и определяется по формуле:
 где
где  – электрическая постоянная.
– электрическая постоянная.
Для того чтобы получить необходимую определённую ёмкость, берут несколько конденсаторов и собирают их в батарею применяя при этом параллельное, последовательное или смешанное соединения.
Параллельное соединение:
q = q1 + q2 + q3
u = u1 = u2 = u3
с = с1+с2+с3
с = n∙с
Последовательное соединение:
q = q1 = q2 = q3
u = u1 + u2 + u3


Энергия конденсатора равна половине произведения заряда конденсатора напряжённости поля и расстояния между пластинами конденсатора: u = Еd

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин, это поле совершает положительную работу. При этом энергия электрического поля уменьшается:

Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения:

Примеры и разбор решения заданий:
1. Плоский конденсатор, расстояние между пластинами которого равно 3 мм, заряжен до напряжения 150 В и отключен от источника питания. Разность потенциалов между пластинами возросла до 300 В.
- Во сколько раз увеличилась разность потенциалов между пластинами?
- Какое расстояние между пластинами конденсатора стало после того, как пластины были раздвинуты?
- Во сколько раз изменилось расстояние между пластинами.
Решение:
Электрическая ёмкость конденсатора определяется по формуле:

1.По условию разность потенциалов увеличилось в два раза. U1 = 150В→ U2 = 300В.
2.По условию d = 3 мм, если разность потенциалов увеличилось в два раза, по формуле соответственно и расстояние между пластинами увеличилось в два раза, и d =2·3 мм = 6 мм.
3.Расстояние между пластинами увеличилось в два раза.
Ответ:
1. 2
2. 6мм
3. 2
2. Конденсатор электроёмкостью 20 мкФ имеет заряд 4 мкКл. Чему равна энергия заряженного конденсатора?
Дано: С = 20 мкФ = 20 · 10-6 Ф, q = 4 мкКл = 4·10-6 Кл.
Найти: W.
Решение:
Энергия заряженного конденсатора W через заряд q и электрическую ёмкость С определяется по формуле:


Ответ: W = 0,4 мкДж.
Электроемкость конденсатора, теория и примеры
Одним их важнейших параметров, при помощи которого характеризуют конденсатор, является его электроёмкость (C). Физическая величина C, равная:
называется емкостью конденсатора. Где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Для конденсаторов с одинаковым устройством и при равных зарядах на его обкладках разность потенциалов воздушного конденсатора будет в раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Значит емкость конденсатора с диэлектриком (C) в раз больше, чем электроемкость воздушного конденсатора ():
где – диэлектрическая проницаемость диэлектрика.
Единицей емкости конденсатора считают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) является фарад (Ф).
Электроемкость плоского конденсатора
Поле между обкладками плоского конденсатора в большинстве случаев считают однородным. Однородность нарушается только около краев. При расчете емкости плоского конденсатора данными краевыми эффектами обычно пренебрегают. Это возможно, если расстояние между пластинами мало в сравнении с их линейными размерами. В таком случае емкость плоского конденсатора вычисляют как:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Электрическая емкость цилиндрического конденсатора
Конструкция цилиндрического конденсатора включает две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость такого конденсатора находят как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач
Лекция по физике для 10-го физико-математического профильного класса «Электрическая емкость проводника. Единица электроемкости. Конденсатор. Емкость плоского конденсатора. Соединения конденсаторов. Энергия, накопленная в конденсаторе. Применение конденсаторов»
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели и задачи: сформировать представление об электроёмкости вообще и конденсатора в частности, ввести единицу измерения электроёмкости, рассмотреть зависимость ёмкости конденсатора от его геометрической конструкции, соединения конденсаторов, типы конденсаторов и их применение, обратив особое внимание на использование конденсатора в качестве накопителя энергии и выяснив формулы для энергии конденсатора.
УМК: Конденсатор, электрометр, пластина из диэлектрика, набор конденсаторов, проектор, компьютер.
Домашнее задание задано по учебнику Мякишева А.В. для профильных 10-11 классов “Электродинамика” 2011 г., задачи заданы по сборнику Гольдфарба Н.И. с целью ознакомления учащихся с примерами решения задач по данной теме (учащиеся их оформляют в тетради для домашних работ и следующий урок – семинар, посвящён именно решению задач по теме).
Ход урока
рис.1.
На демонстрационном столе собрана установка (см. рис.1).
Если корпус электрометра соединить с землей, то он измеряет напряжение. Зарядим шарик (малый), сообщая ему заряд от разрядника. Видим, что с ростом заряда, растет напряжение между ним и землей. После того как опыт повторили 3-4 раза заряд и напряжение перестают расти.
Следовательно шарик вмещает в себе определенное кол-во зарядов. Если заменить малый шар на большой, то видно, что он вмещает большее количество зарядов.
Электрическая ёмкость С уединённого проводника — это отношение заряда проводника к его потенциалу.
Электроёмкость не зависит от величины заряда и напряжения на проводнике, а характеризует его электрические свойства и определяется размерами и формой проводника.
1Рассмотрим электроёмкость уединённого шара:
Единица электроёмкости : [C] = 1 Ф (фарад) – это электроёмкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1 Кл.
Конденсатор – устройство для накопления заряда и энергии. Конденсатор представляет собой два проводника, разделённых тонким слоем диэлектрика. Проводники называют обкладками конденсатора.
На демонстрационном столе установка (см. рис.2)
рис.2
Демонстрируется Приложение 1 (ВИДЕО об устройстве конденсаторов)
Электроемкость конденсатора зависит:
1. От величины заряда C q (одной из обкладок)
2. От напряжения между пластинами
Электроёмкость конденсатора определяется формулой:
Различают конденсаторы также по форме: плоские и сферические. (см. рис.3)
рис.3.
Также конденсаторы различают по диэлектрику:
— Электролитические
— Воздушные
— Слюдяные
— Бумажные. (см. рис.4)
рис.4
Далее учащимся по партам передаются конденсаторы разные по форме, демонстрируются также конденсаторы переменной ёмкости. (см. рис.5).
рис.5
Электрическое поле плоского конденсатора (см.рис.6)
рис.6
Электроемкость плоского конденсатора зависит от геометрических размеров
C S (площадь пластины)
(диэлектрическая проницаемость)
C (расстояние между пластинами)
Рассмотрим энергию заряженного конденсатора.
Т.к. энергия однородного поля равна Wp = Eqd, то для одной пластины Wp = Eqd/2.
Пример 1. Если расстояние между пластинами уменьшили в 2 раза, как изменились емкость, напряжение, напряженность, энергия поля?
Если конденсатор отключен от источника напряжения, то q = const!
| Емкость |
|
Увеличилась |
| Напряжение |
|
уменьшилось |
| Напряженность |
|
Не изменилась |
| Энергия электрического поля |
|
Уменьшилась |
Пример 2. Как изменятся емкость, заряд, напряженность и энергия поля при удалении диэлектрика с ??
Если конденсатор не отключен от источника напряжения, то U = const!
| Емкость |
|
уменьшилась |
| Заряд |
|
уменьшился |
| Напряженность |
|
Не изменилась |
| Энергия электрического поля |
|
уменьшилась |
Соединения конденсаторов:
1) Последовательное (см. рис.7)
q1 = q2
U = U1 + U2
рис.7
2) Параллельное (см. рис.8)
U = U1 = U2
q = q1 + q2
CU = C1U + C2U —> C = C1 + C2
рис.8
Рассмотрим свойства и применение конденсаторов.
Конденсатор – накопитель электроэнергии. Как видно из формулы конденсатор способен хранить электрические заряды тем больше, чем больше его емкость. Если необходимо получить электрический ток большой мощности (N = I2 R), то выгодно иметь большую силу тока, а (I = Q/t), т.е. имея большой заряд, протекающий по проводнику за очень малое время, получаем большую мощность. Конденсатор большой емкости при разрядке дает большую мощность. Пример: фотовспышка
конденсатор – измеритель времени. При зарядке и разрядке конденсатора время этих процессов зависит от емкости конденсатора пропорционально. Это свойство можно использовать для отсчета времени. Например: часы, реле времени ….
Конденсатор в переменном токе. В цепях переменного тока конденсатор периодически перезаряжается, поэтому по подводящим к нему проводникам постоянно проходит ток, а в цепи постоянного тока конденсатор, зарядившись, ток не пропускает. Поэтому конденсатор можно использовать как фильтр для переменного тока. Пример: выпрямители.
Конденсатор и частота переменного тока. В зависимости от частоты переменного тока конденсатор быстро или медленно перезаряжается , при этом оказывая разное сопротивление переменному току. Это используют в частотных фильтрах переменного тока. Например: приемный контур радиоприемника, телевизора, генераторы переменных сигналов….
Демонстрируется Приложение 2 (ВИДЕО о применении конденсаторов).
Электроемкость конденсатора: формулы и история
Электрический конденсатор является пассивным прибором, который способен накапливать и сохранять электрическую энергию. Он состоит из двух проводящих пластин, разделенных диэлектрическим материалом. Приложение электрических потенциалов различного знака к проводящим пластинам приводит к приобретению ими заряда, который на одной пластине является положительным, а на другой отрицательным. При этом суммарный заряд равен нулю.
В данной статье рассмотрены вопросы истории и определение электроемкости конденсатора.
История изобретения

В октябре 1745 года немецкий ученый Эвальд Георг фон Клейст заметил, что электрический заряд может быть запасен, если соединить с помощью кабеля электростатический генератор и некоторый объем воды, находящийся в стеклянном сосуде. В этом эксперименте рука фон Клейста и вода являлись проводниками, а стеклянный сосуд — электрическим изолятором. После того как ученый коснулся металлической проволоки рукой, произошел мощный разряд, который был намного сильнее, чем разряд электростатического генератора. В результате фон Клейст сделал вывод о существовании запасенной электрической энергии.
В 1746 году голландский физик Питер ван Мушенбрук изобрел конденсатор, который назвал лейденской бутылкой в честь Лейденского университета, в котором работал ученый. Затем Даниэль Гралат увеличил электроемкость конденсатора, соединив несколько лейденских бутылок.
В 1749 году Бенджамин Франклин исследовал лейденский конденсатор и пришел к выводу, что электрический заряд запасается не в воде, как полагали до этого, а на границе воды и стекла. Благодаря открытию Франклина, лейденские бутылки стали изготавливать, покрывая внутреннюю и внешнюю поверхность стеклянных сосудов металлическими пластинами.

Развитие индустрии
Термин «конденсатор» ввел в употребление Алессандро Вольта в 1782 году. Изначально для изготовления изоляторов электрических конденсаторов использовали такие материалы, как стекло, фарфор, слюду и обычную бумагу. Так, радиотехник Гульельмо Маркони использовал для своих аппаратов-передатчиков фарфоровые конденсаторы, а для приемников — небольшие конденсаторы с изолятором слюды, которые были изобретены в 1909 году — до Второй мировой войны в США именно они были наиболее распространенными.
Первый электролитический конденсатор был изобретен в 1896 году и представлял собой электролит с алюминиевыми электродами. Бурное развитие электроники началось только после изобретения в 1950 году танталового миниатюрного конденсатора с твердым электролитом.
Во время Второй мировой войны в результате развития химии пластмасс стали появляться конденсаторы, в которых роль изолятора была отведена тонким полимерным пленкам.
Наконец, в 50-60 годах развивается индустрия суперконденсаторов, которые обладают несколькими рабочими проводящими поверхностями, благодаря чему электроемкость конденсаторов повышается на 3 порядка в сравнении с ее значением для обычных конденсаторов.

Понятие об электроемкости конденсатора
Электрический заряд, запасенный в пластине конденсатора, пропорционален напряжению электрического поля, которое существует между пластинами прибора. При этом коэффициент пропорциональности называется электроемкостью плоского конденсатора. В СИ (международная система единиц) электроемкость, как физическая величина, измеряется в фарадах. Один фарад — это такая электроемкость конденсатора, напряжение между пластинами которого равно 1 вольт при запасенном заряде в 1 кулон.
Электроемкость в 1 фарад является огромной, и на практике в электротехнике и электронике обычно пользуются конденсаторы с емкостями порядка пикофарада, нанофарада и микрофарада. Исключением являются только суперконденсаторы, которые состоят из активированного угля, благодаря чему увеличивается рабочая площадь прибора. Они могут достигать емкостей в тысячи фарадов и используются для питания прототипов электромобилей.
Таким образом, электроемкость конденсатора равна: C = Q1/(V1-V2). Здесь C — электроемкость, Q1 — электрический заряд, запасенный в одной пластине конденсатора, V1-V2 — разница между электрическими потенциалами пластин.
Формула для емкости плоского конденсатора имеет вид: C = e0eS/d. Здесь e0 и e — универсальная диэлектрическая постоянная и диэлектрическая постоянная материала изолятора S — площадь пластин, d — расстояние между пластинами. Эта формула позволяет понять, как изменится электроемкость конденсатора, если изменить материал изолятора, расстояние между пластинами или их площадь.

Виды используемых диэлектриков
Для изготовления конденсаторов используют различные типы диэлектриков. Наиболее популярными являются следующие:
- Воздух. Эти конденсаторы представляют собой две пластины из проводящего материала, которые разделены прослойкой воздуха и помещены в стеклянный корпус. Электроемкость воздушных конденсаторов невелика. Обычно они используются в радиотехнике.
- Слюда. Свойства слюды (способность разделяться на тонкие пластины и выдерживать высокие температуры) являются подходящими для ее использования в качестве изоляторов в конденсаторах.
- Бумага. Для защиты от намокания используют парафинированную или лакированную бумагу.
Запасенная энергия

По мере того, как увеличивается разность потенциалов между пластинами конденсатора, прибор запасает электрическую энергию благодаря присутствию внутри него электрического поля. Если разность потенциалов между пластинами уменьшается, то конденсатор разряжается, отдавая энергию в электрическую цепь.
Математически электрическую энергию, которая запасена в конденсаторе произвольного типа, можно выразить следующей формулой: E = ½C(V2-V1)2, где V2 и V1 — конечное и начальное напряжение между пластинами.
Заряд и разряд
Если конденсатор подсоединить в электрическую цепь с резистором и каким-либо источником электрического тока, тогда по цепи пойдет ток, и конденсатор начнет заряжаться. Как только он будет полностью заряжен, электрический ток в цепи прекратится.
Если заряженный конденсатор подсоединить параллельно резистору, то от одной пластины к другой через резистор потечет ток, который будет продолжаться до тех пор, пока прибор полностью не разрядится. В данном случае направление тока разряда будет противоположно направлению течения электрического тока, когда прибор заряжался.
Заряд и разряд конденсатора подчиняется экспоненциальной зависимости от времени. Например, напряжение между пластинами конденсатора при его разряде изменяется согласно следующей формуле: V(t) = Vie-t/(RC), где Vi — начальное напряжение на конденсаторе, R — электрическое сопротивление в цепи, t — время разряда.
Объединение в электрической цепи

Чтобы определить электроемкость конденсаторов, которые имеются в электрической цепи, следует вспомнить, что они могут объединяться двумя различными способами:
- Последовательное соединение: 1/Cs = 1/C1+1/C2+…+1/Cn.
- Параллельное соединение: Cs = C1+C2+…+Cn.
Cs — суммарная емкость n конденсаторов. Суммарная электроемкость конденсаторов определяется по формулам, аналогичным математическим выражениям для суммарного электрического сопротивления, только формула для последовательного соединения приборов справедлива для параллельного соединения резисторов и наоборот.
Электроёмкость плоского конденсатора | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Плоским конденсатором обычно называют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Простота конструкции такого конденсатора позволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.
| Рис. 4.71. Плоский конденсатор на электрометре |
Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электрометра, а вторая — к его металлическому корпусу (рис. 4.71). При таком соединении электрометр будет измерять разность потенциалов между пластинами, которые образуют плоский конденсатор из двух пластин. Проводя исследования, необходимо помнить, что
при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам разноименные заряды и отметим отклонение стрелки электрометра. Приближая пластины друг к другу (уменьшая расстояние между ними), заметим уменьшение разности потенциалов. Таким образом, при уменьшении расстояния между пластинами конденсатора его электроемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельством уменьшения электроемкости.
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
C ~ 1 / d,
где d — расстояние между обкладками.
| Рис. 4.72. График зависимости емкости плоского конденсатора от расстояния между пластинами |
| Рис. 4.73. При расчетах емкости плоских конденсаторов учитывают площадь перекрытия пластин |
Эту зависимость можно изобразить графиком обратной пропорциональной зависимости (рис. 4.72).
Будем смещать пластины одну относительно другой в параллельных плоскостях, не изменяя расстояния между ними.
При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об уменьшении электроемкости.
Увеличение площади перекрытия пластан приведет к увеличению емкости.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
C ~ S,
где S — площадь пластин.
| Рис. 4.74. График зависимости емкости плоского конденсатора от площади его пластин |
Эту зависимость можно представить графиком прямой пропорциональной зависимости (рис. 4.74).
Возвратив пластины в начальное положение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости конденсатора. Если между пластинами поместить другой диэлектрик, то изменение электроемкости будет иным.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
C ~ ε,
где ε — диэлектрическая проницаемость диэлектрика. Материал с сайта http://worldofschool.ru
| Рис. 4.75. График зависимости емкости плоского конденсатора от диэлектрической проницаемости диэлектрика |
Такая зависимость показана на графике рис. 4.75.
Результаты опытов можно обобщить в виде формулы ёмкости плоского конденсатора:
C = εε0S / d,
где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая проницаемость диэлектрика; ε0 — электрическая постоянная.
Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.
На этой странице материал по темам:Физика 10 класс . рассчитать площадь и электроемкость плоского конденсатора.
Решение задач по теме электроемкость плоского конденсатора
График зависимости электроемкости плоского конденсатора от площади его пластин
Заключение по электроемкости
Теория плоских конденсаторов
Какое строение плоского конденсатора?
По изменению какой величины в опыте можно делать заключение об изменении электроемкости?
В какой последовательности проводится опыт, в котором устанавливалась зависимость электроемкости конденсатора от его параметров?
Как зависит электроемкость плоского конденсатора от активной площади пластин?
Как зависит электроемкость плоского конденсатора от расстояния между пластинами?
Как влияет диэлектрик на электроемкость конденсатора?
3 Конденсаторы. Расчет электроемкостей конденсаторов
Конденсаторы – это приборы, обладающие
большой электроемкостью, которые
способны накапливать большие заряды.
Простейший конденсатор состоит из двух
проводников (обкладок), расположенных
на малом расстоянии друг от друга.
Практически очень важно, чтобы
электрическое поле было сосредоточено
внутри конденсатора. Для этого заряды
на обкладках должны быть одинаковы по
модулю и противоположны по знаку ( и
и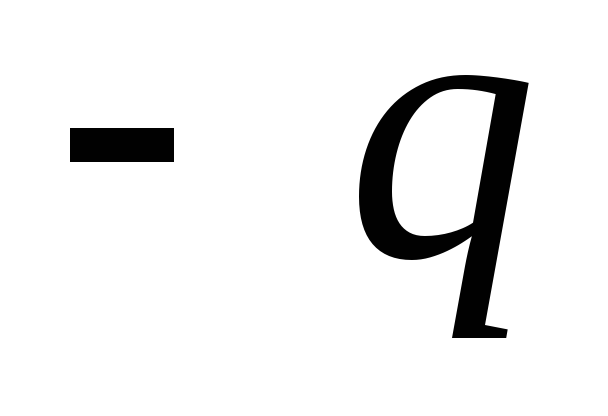 ).
).
Электроемкостью конденсатора называют
величину  ,
пропорциональную заряду
,
пропорциональную заряду конденсатора, и обратно пропорциональную
разности потенциалов между обкладками:
конденсатора, и обратно пропорциональную
разности потенциалов между обкладками:
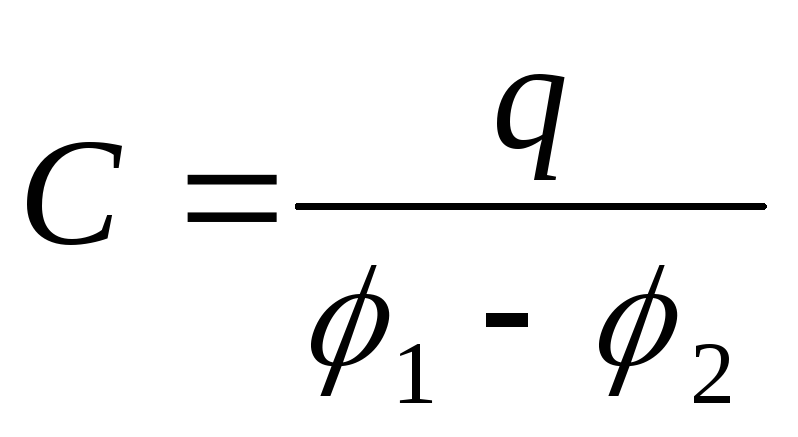 (2.7)
(2.7)
Разность потенциалов 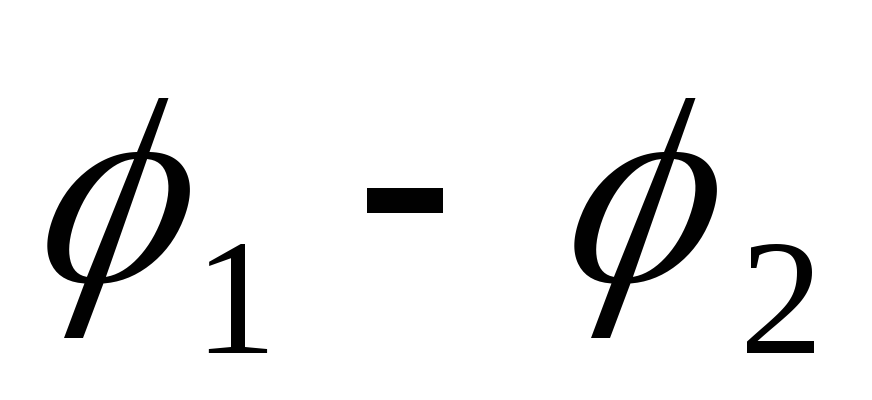 называют напряжением и обозначают
называют напряжением и обозначают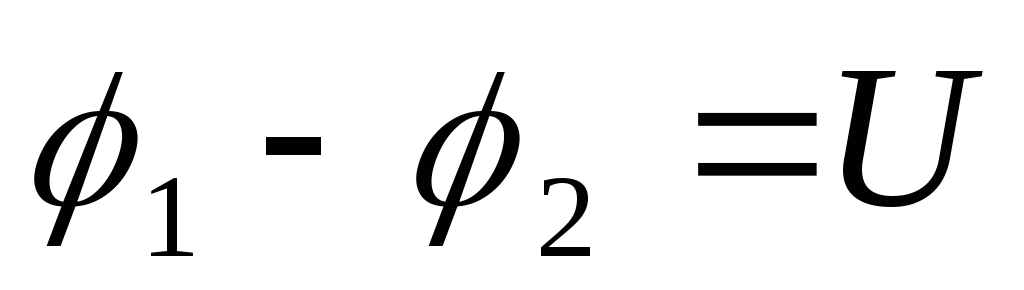 .
Поэтому формулу (2.7) можно представить
в виде:
.
Поэтому формулу (2.7) можно представить
в виде:
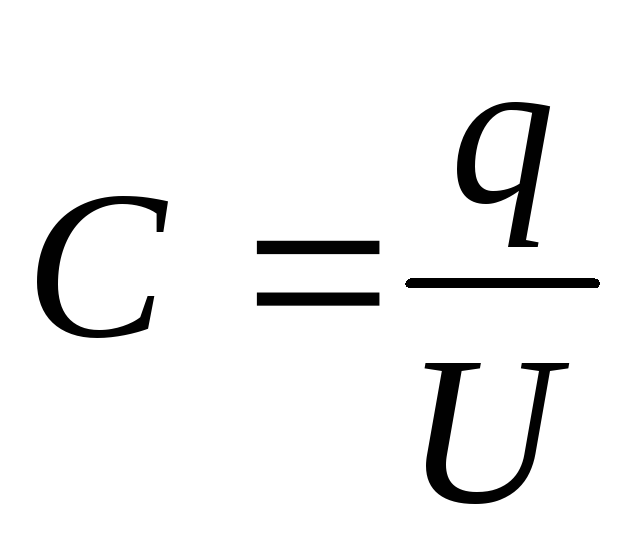 (2.8)
(2.8)
Размерность емкости конденсатора 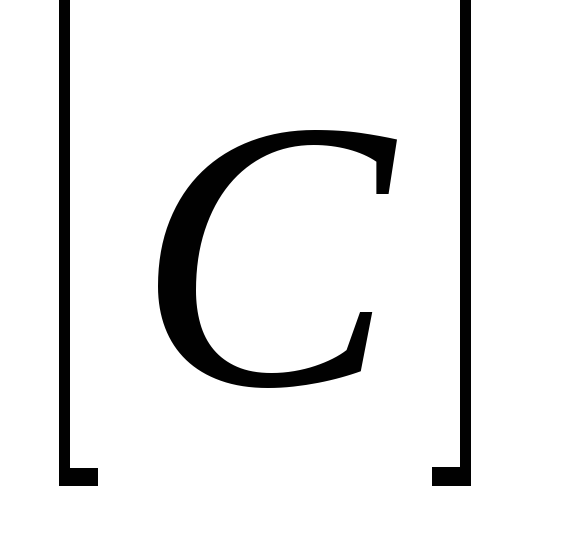 = ФАРАД.
= ФАРАД.
Емкость конденсатора зависит от размеров и формы обкладок, от расстояния между ними и от диэлектрика, заполняющего конденсатор.
Примеры вычисления электроемкостей различных конденсаторов
1 Электроемкость плоского конденсатора(рис. 4)
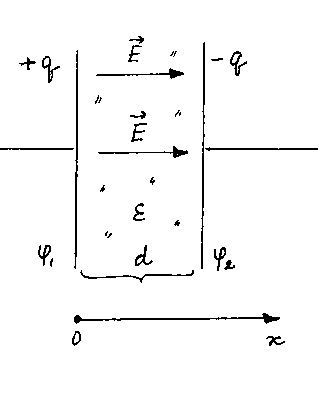
Рис. 4
Пусть  — площадь обкладок,
— площадь обкладок, —
расстояние между обкладками, зазор
между обкладками заполнен диэлектриком
с проницаемостью
—
расстояние между обкладками, зазор
между обкладками заполнен диэлектриком
с проницаемостью .
Если
.
Если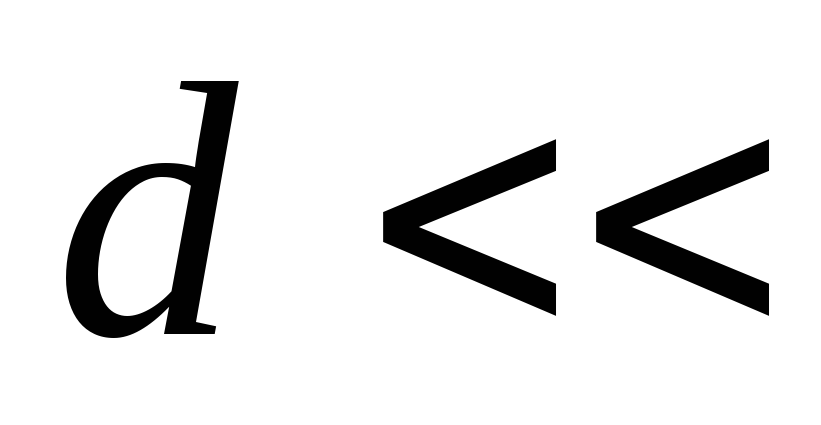 линейных размеров обкладок, можно
пренебречь краевыми эффектами и считать
электрическое поле
линейных размеров обкладок, можно
пренебречь краевыми эффектами и считать
электрическое поле внутри конденсатора практически
однородным, а заряд
внутри конденсатора практически
однородным, а заряд распределенным по пластинам равномерно
с поверхностной плотностью
распределенным по пластинам равномерно
с поверхностной плотностью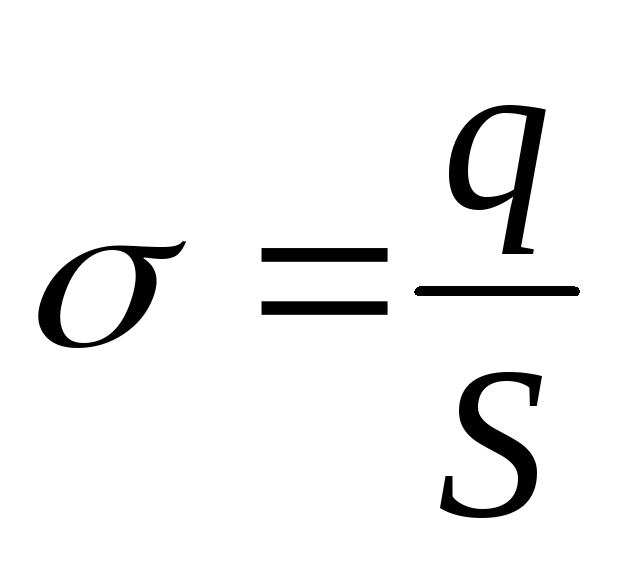 .
.
Напряженность поля в конденсаторе:
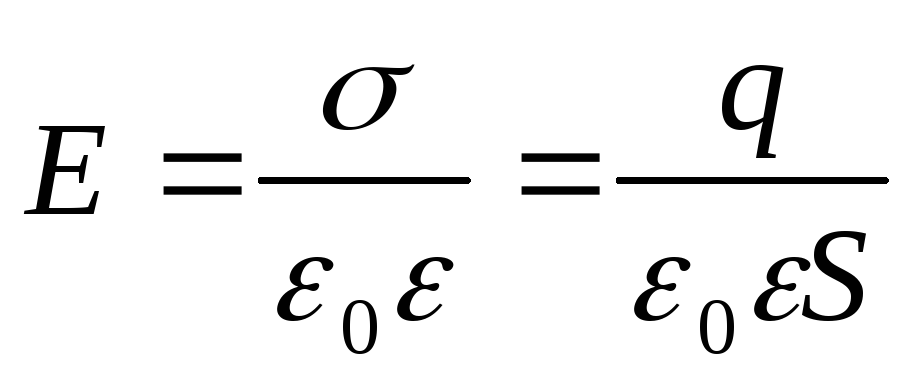
Напряжение между обкладками:
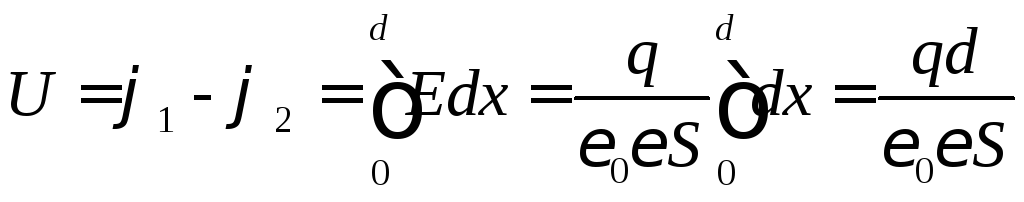 .
.
Отсюда емкость плоского конденсатора равна:
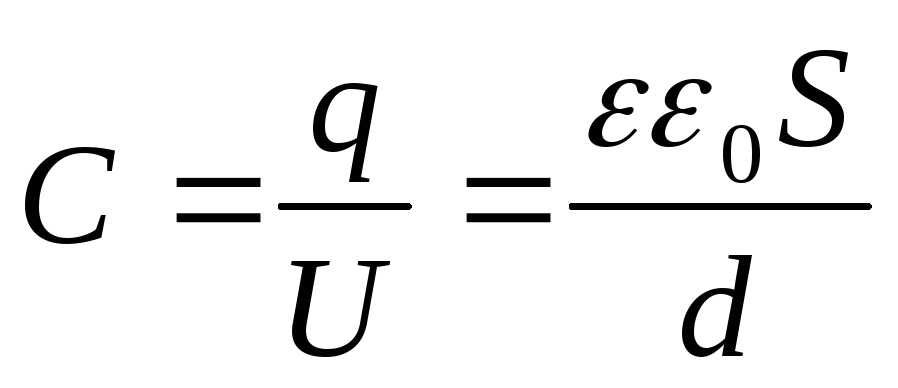 (2.9)
(2.9)
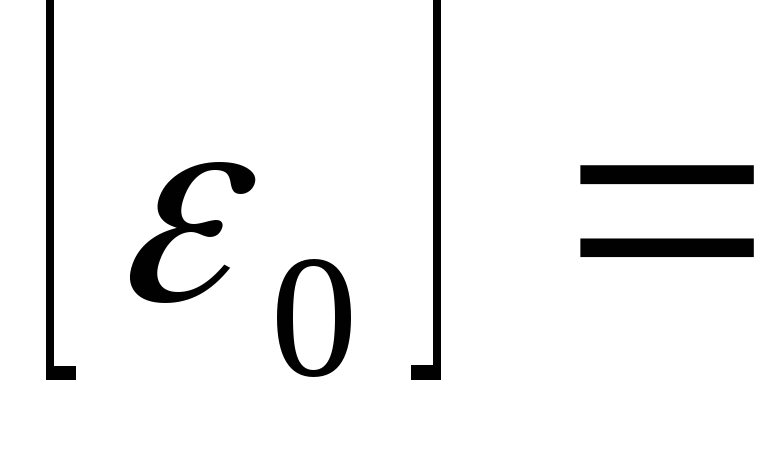 Ф/м
Ф/м
2 Электроемкость цилиндрического конденсатора(рис. 5)
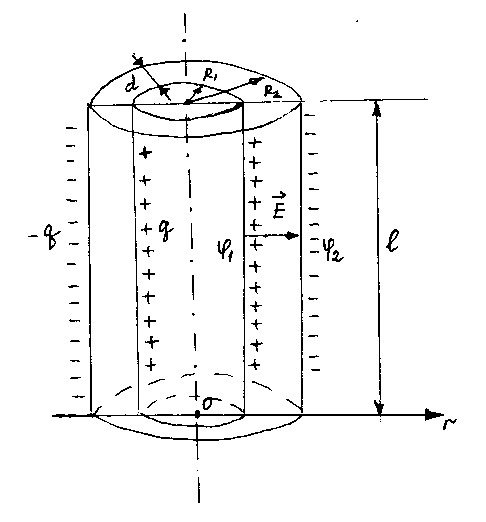
Рис. 5
Пусть  ,
,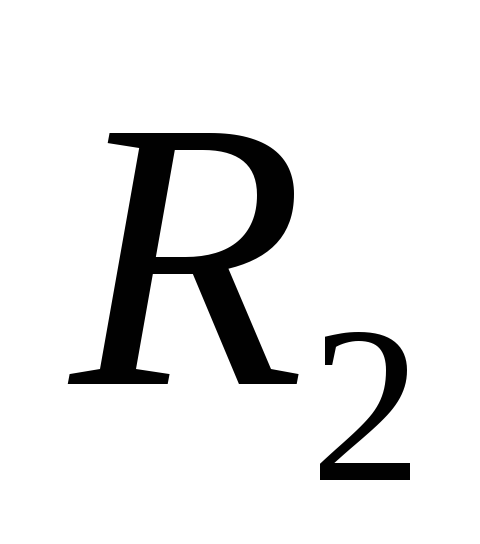 — радиусы внутренней и внешней
цилиндрических обкладок,
— радиусы внутренней и внешней
цилиндрических обкладок,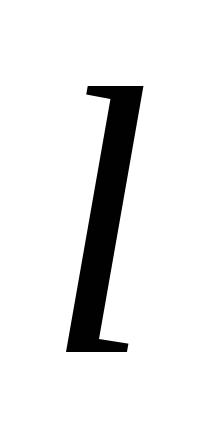 — длина конденсатора,
— длина конденсатора, —
зазор между обкладками.
—
зазор между обкладками.
Если 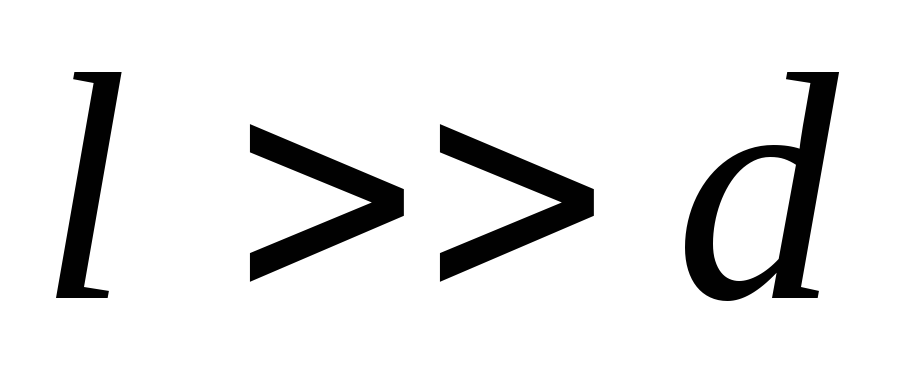 ,
то рассеянием поля вблизи краев обкладок
можно пренебречь и вычислить поле в
зазоре по формуле
,
то рассеянием поля вблизи краев обкладок
можно пренебречь и вычислить поле в
зазоре по формуле
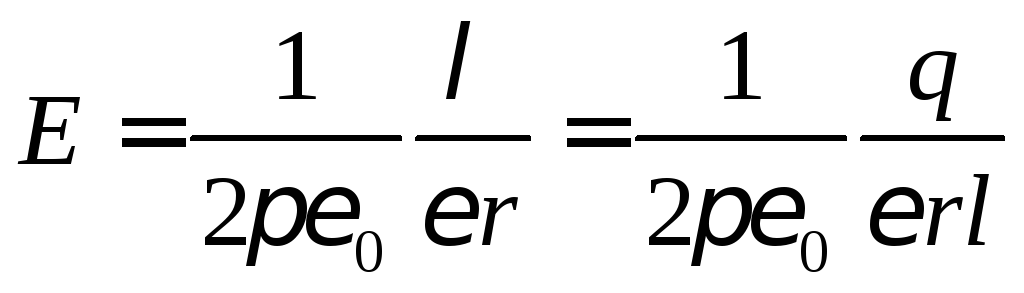 .
.
(см. 1.24 и 1.13).
Напряжение между обкладками
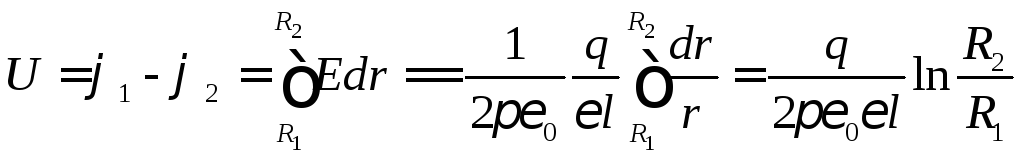 .
.
Следовательно, емкость цилиндрического конденсатора равна
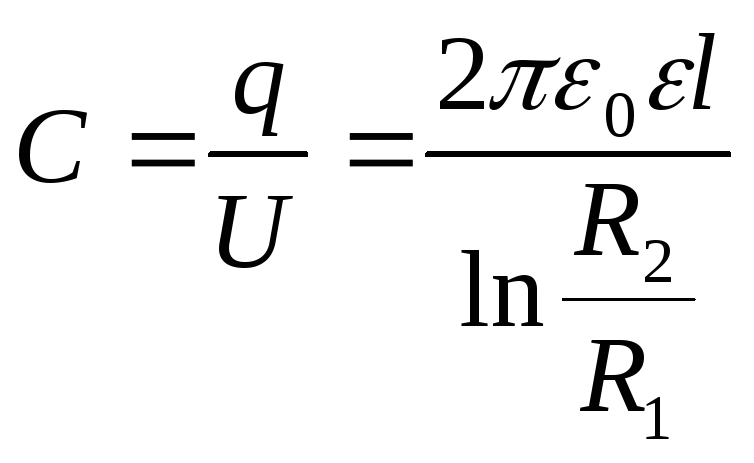 . (2.10)
. (2.10)
Предположив, что 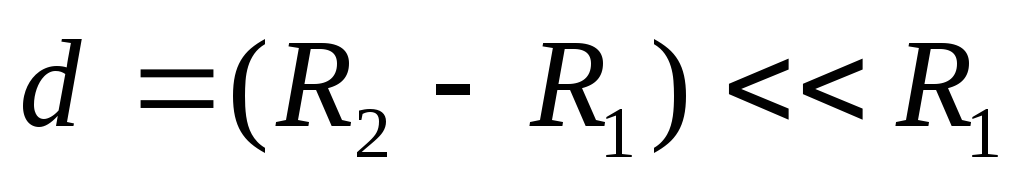 ,
преобразуем
,
преобразуем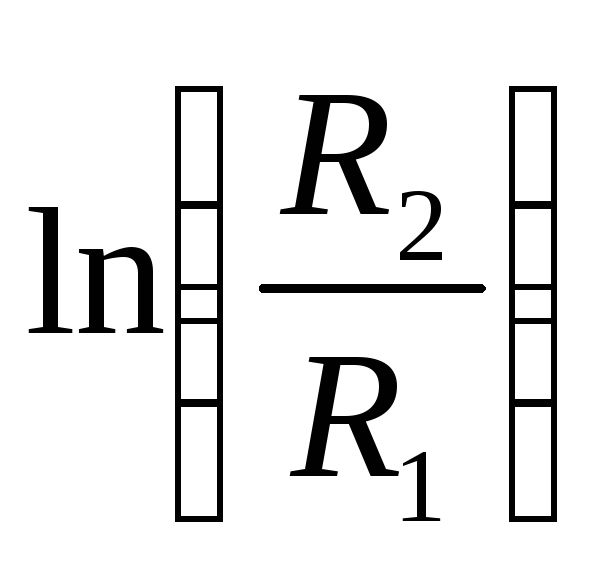 по формуле
по формуле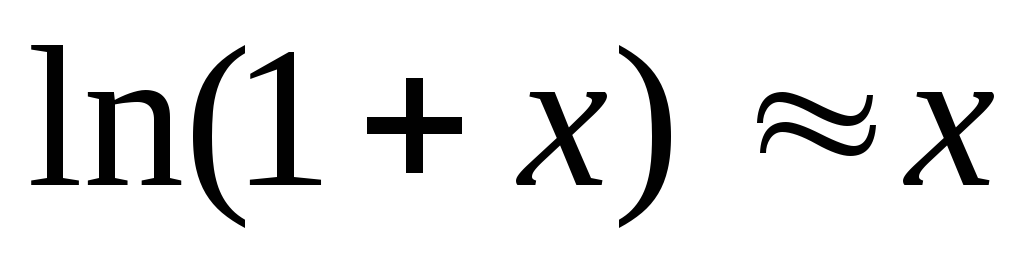 ,
справедливой для
,
справедливой для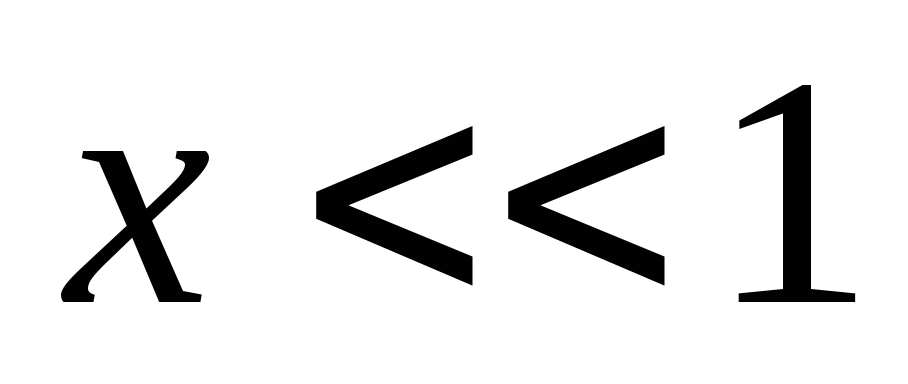 :
:
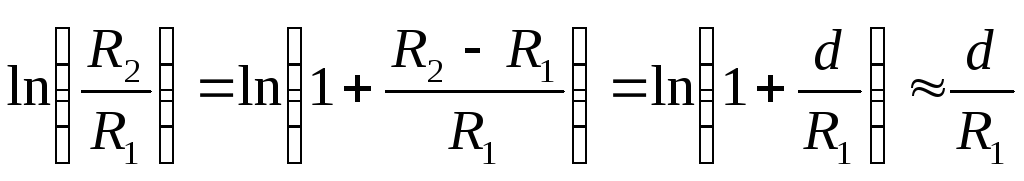
Подставив в (2.10) и учтя, что 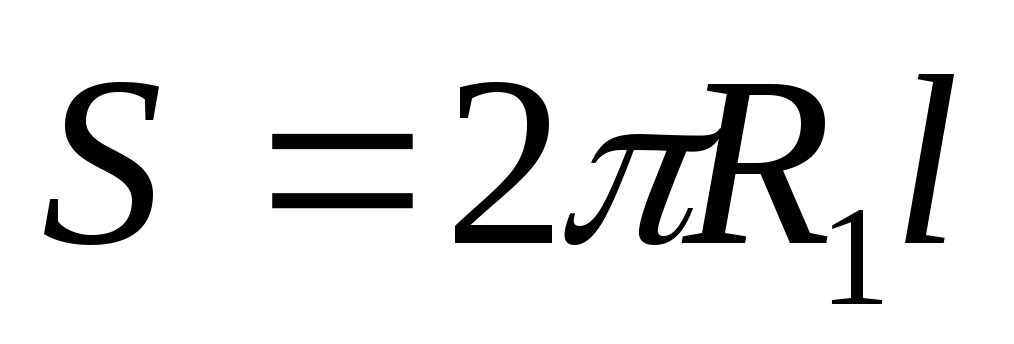 —
площадь обкладки, получим
—
площадь обкладки, получим
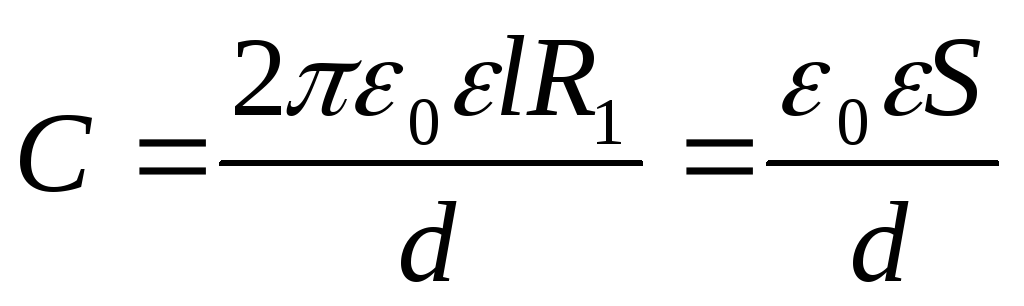 ,
,
Что совпадает с формулой (2.9) для емкости плоского конденсатора.
3 Электроемкость сферического конденсатора (рис. 6)
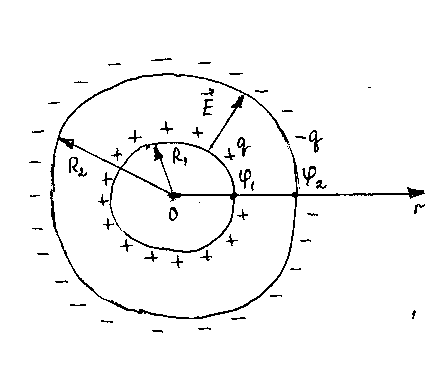
Рис. 6
Пусть  ,
,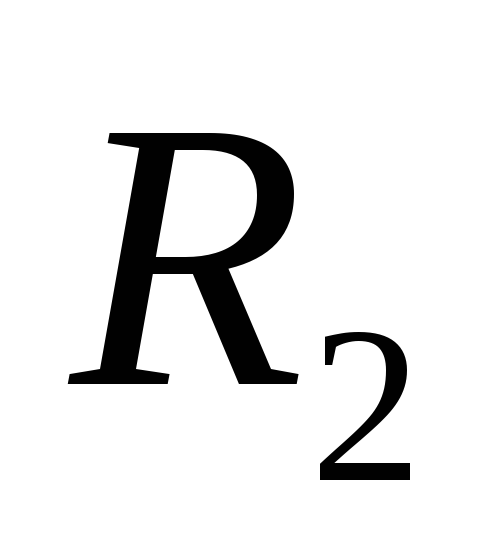 — радиусы внутренней и внешней сферических
обкладок,-
зазор между обкладками. Если заряд
конденсатора
— радиусы внутренней и внешней сферических
обкладок,-
зазор между обкладками. Если заряд
конденсатора ,
то напряженность поля между обкладками
(
,
то напряженность поля между обкладками
(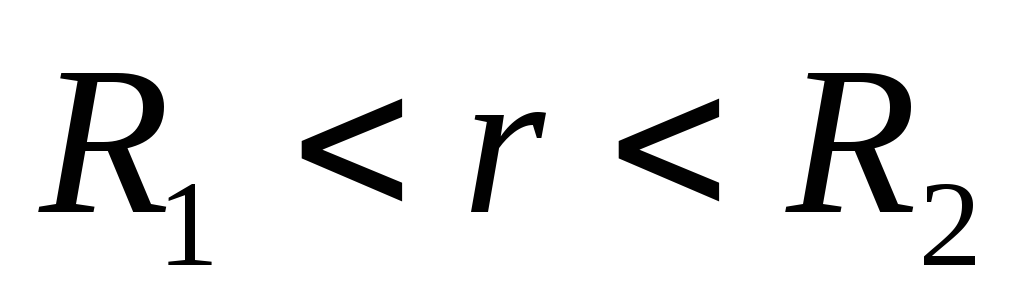 )
определяется по теореме Гаусса:
)
определяется по теореме Гаусса:
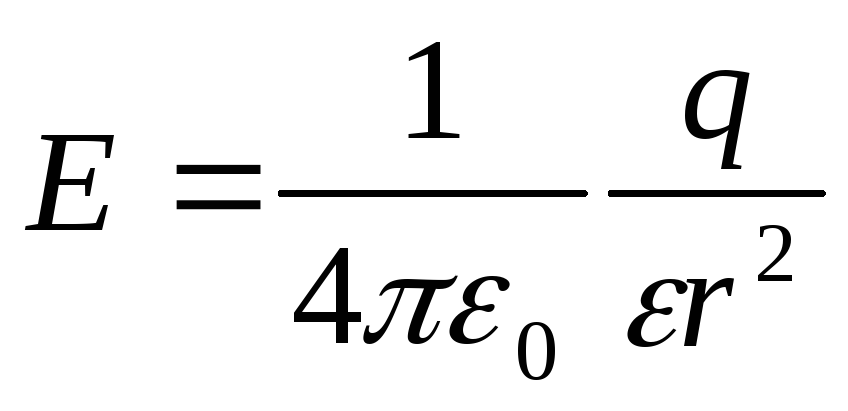
Напряжение на конденсаторе
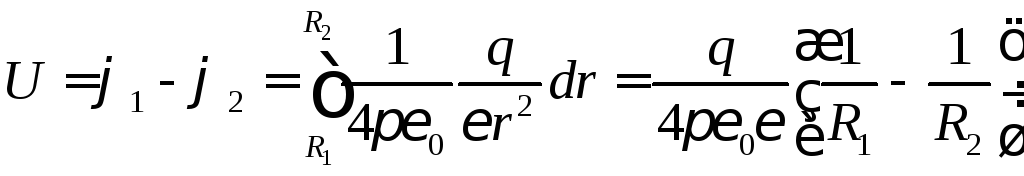
Отсюда следует, что емкость сферического конденсатора
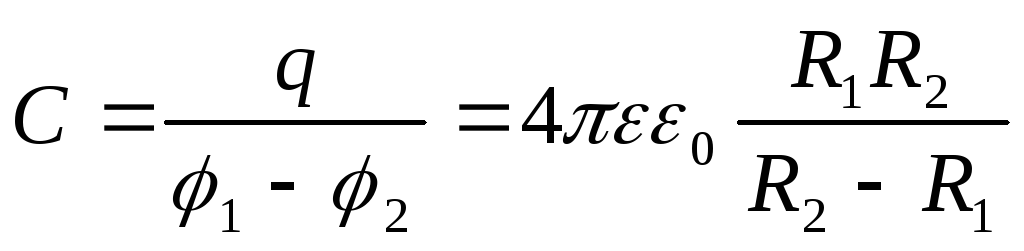 (2.11)
(2.11)
Если 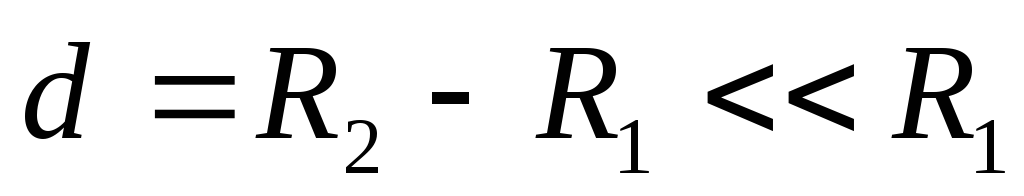 ,
то
,
то
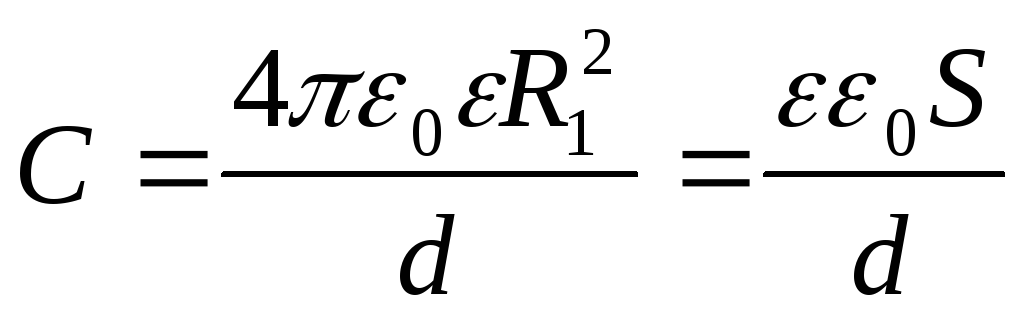 ,
совпадает с формулой (2.9)
,
совпадает с формулой (2.9)
Соединение конденсаторов
1 Параллельное соединение конденсаторов (рис. 7)
Напряжение на конденсаторах одинаково
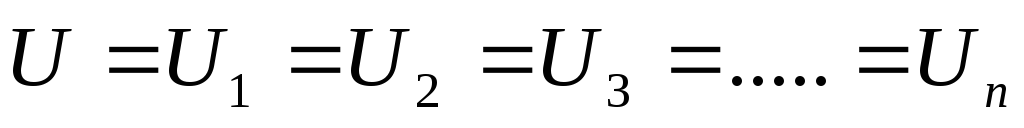 ,
,
заряд различен 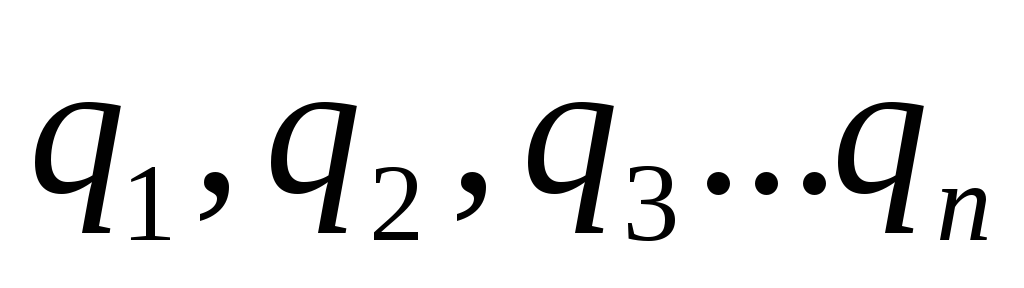 .
.
Общий заряд  всей батареи равен
всей батареи равен
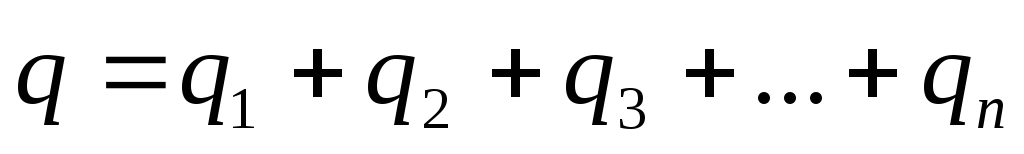
Емкость батареи
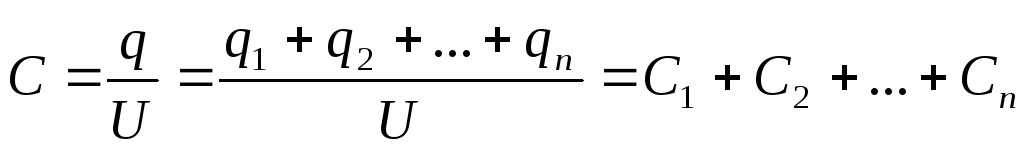
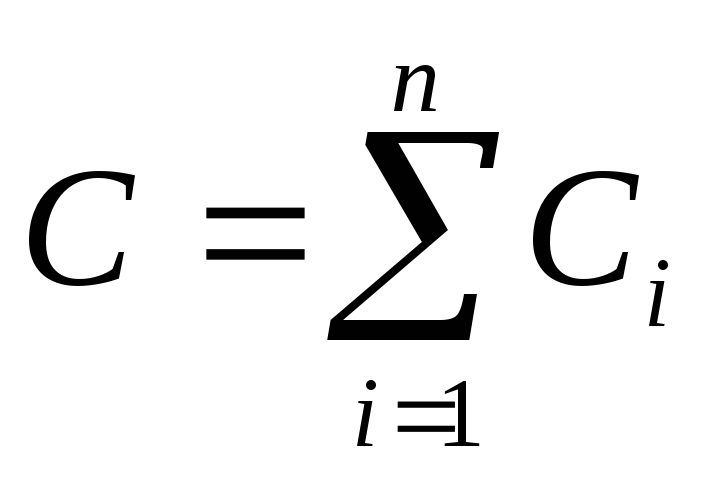 (2.12)
(2.12)
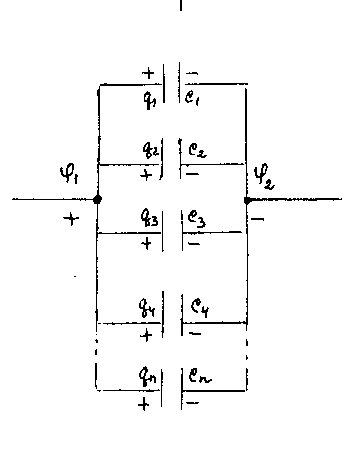
Рис. 7
Таким образом, при параллельном соединении конденсаторов емкости складываются.
2. Последовательное соединение(рис. 8)
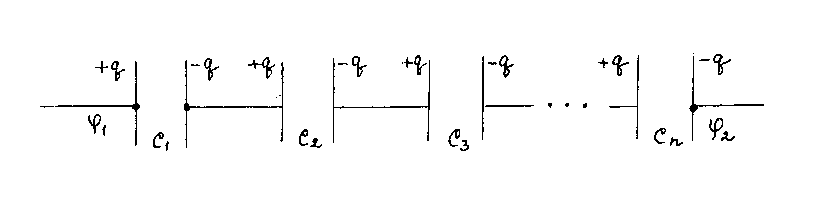
Рис. 8
Напряжение на батарее
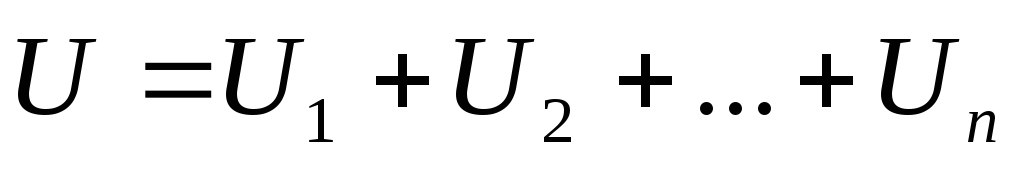
Заряд на конденсаторах одинаков
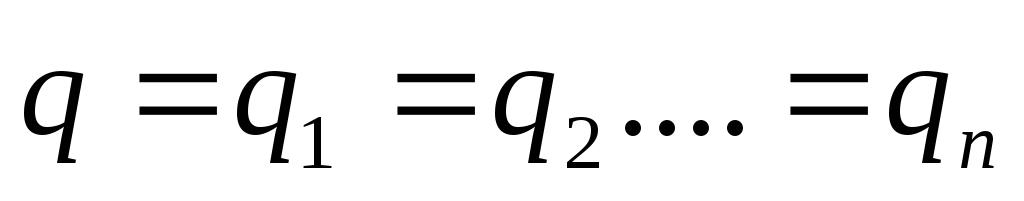
Поэтому напряжение на каждом из конденсаторов:
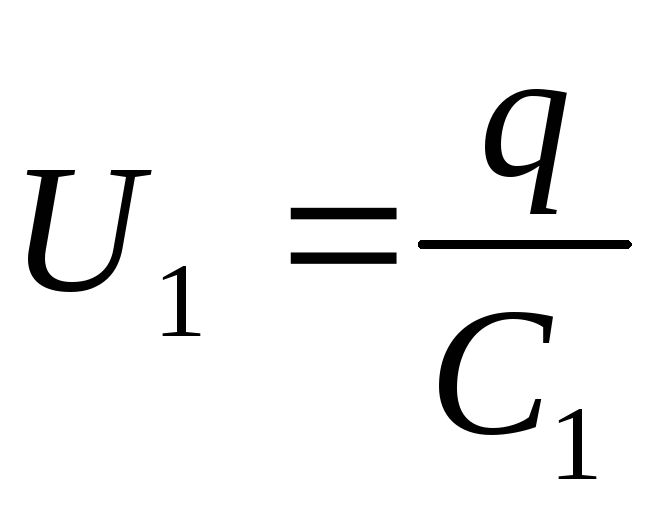 ;
;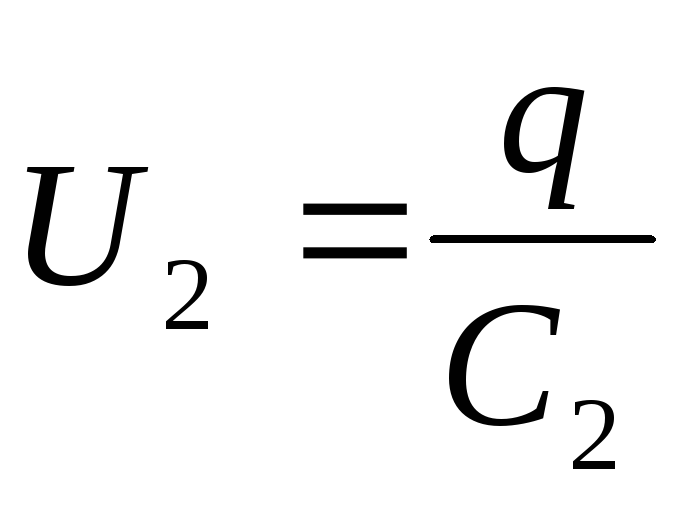 ;….
;….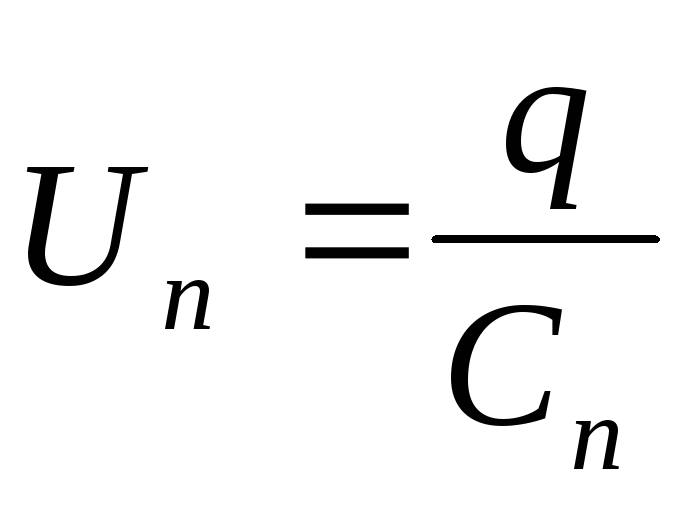
Отсюда
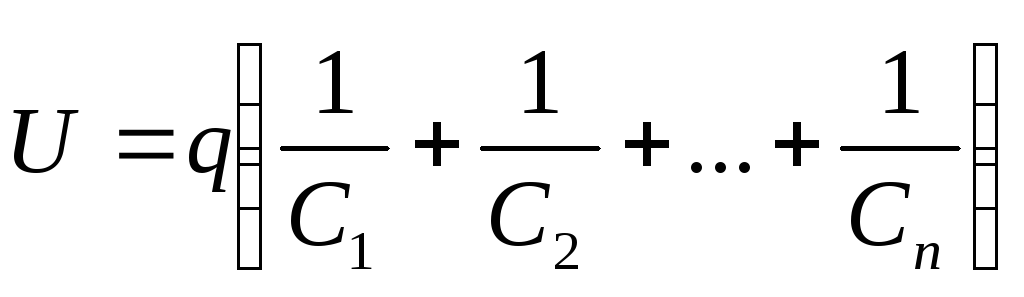 ,
или
,
или
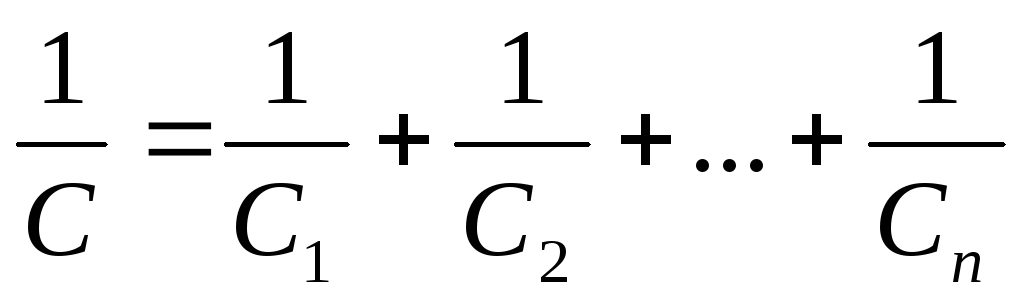
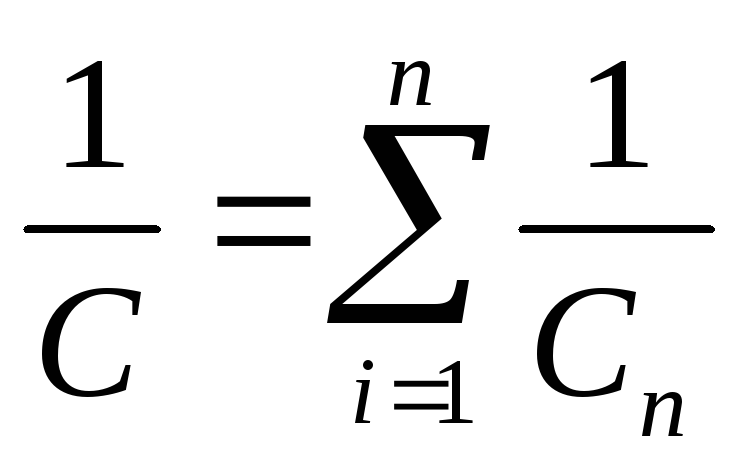 (2.13)
(2.13)
При последовательном соединении конденсаторов складываются величины, обратные емкости.
Задачи
1. На два последовательно соединенных
конденсатора, имеющих емкости  =100
пФ и
=100
пФ и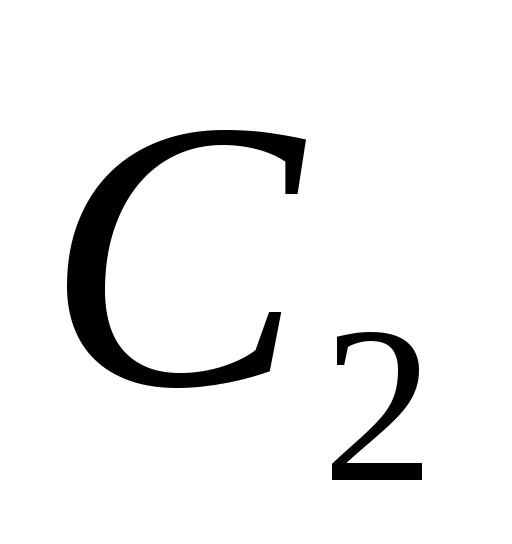 =200
пФ, подано постоянное напряжение
=200
пФ, подано постоянное напряжение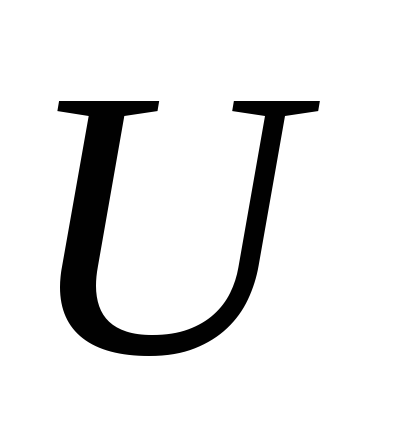 =300
В. Определить напряжения
=300
В. Определить напряжения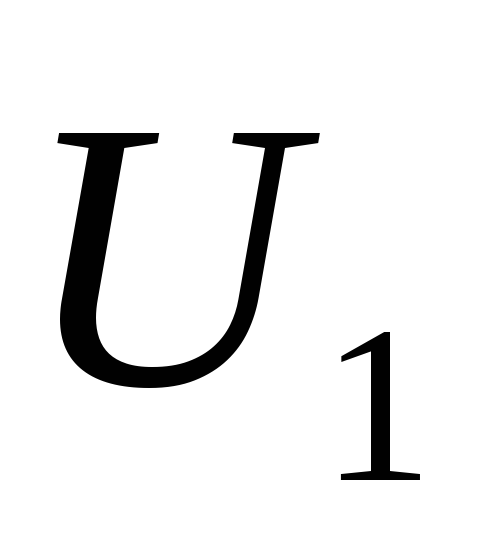 и
и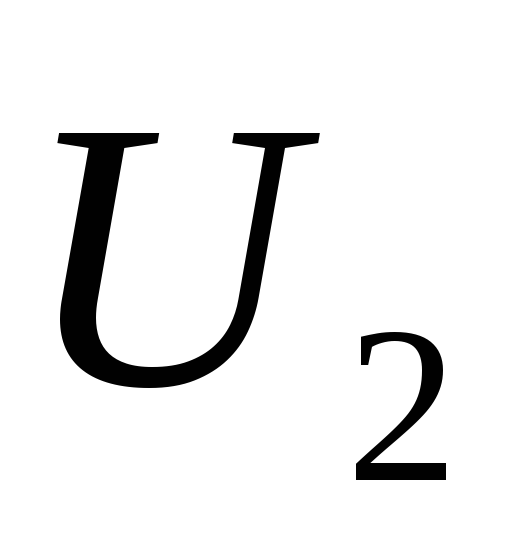 на конденсаторах и заряд
на конденсаторах и заряд на
их обкладках.
на
их обкладках.
Решение:

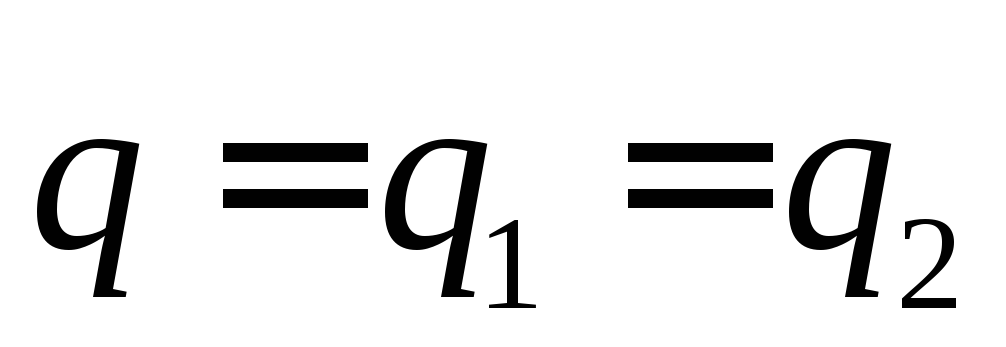
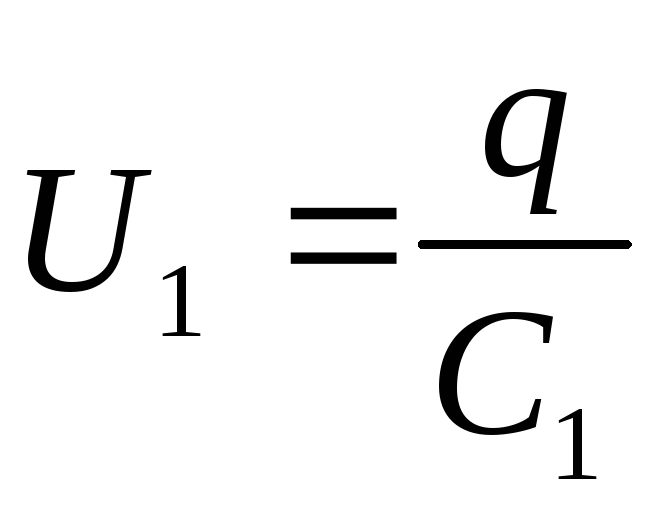 ,
,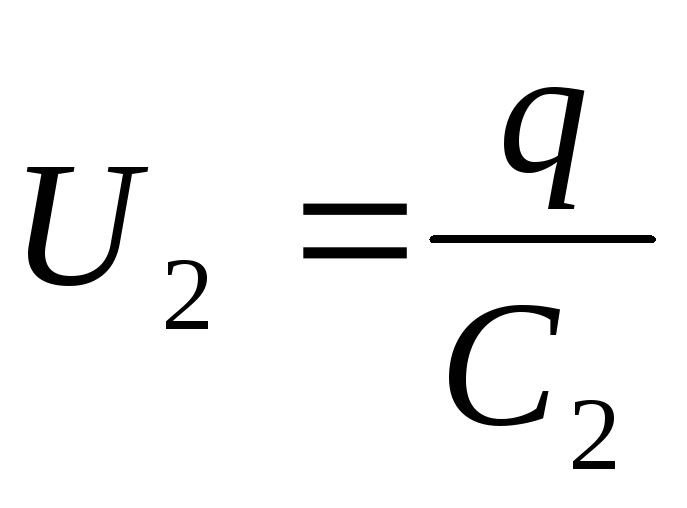
Отсюда следует равенство
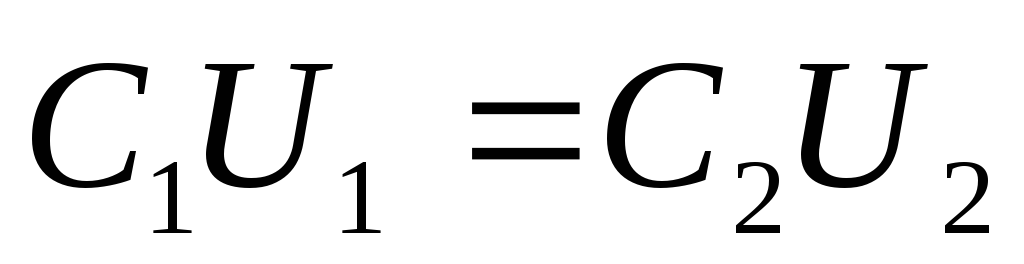
Кроме того,
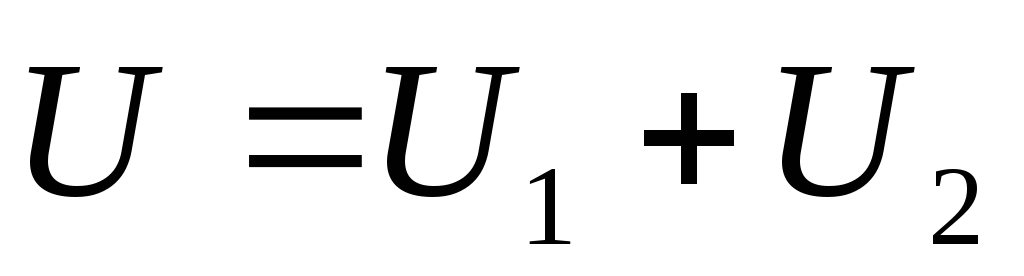
Отсюда получим, что
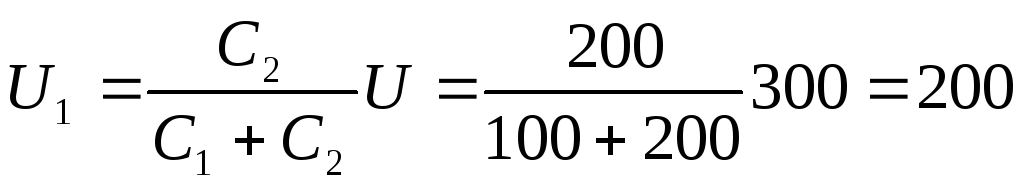 В
В
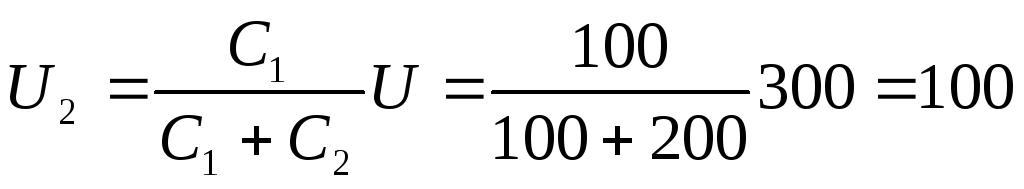 В
В
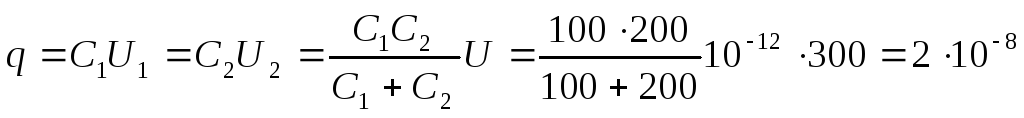 Кл
Кл


