Электрический потенциал | это… Что такое Электрический потенциал?
У этого термина существуют и другие значения, см. Потенциал.
Электри́ческий потенциа́л[1] — временна́я компонента четырёхмерного электромагнитного потенциала, называемый также иногда скалярным потенциалом (скалярным — в трёхмерном смысле; инвариантом группы Лоренца он не является, то есть, не является неизменным при смене системы отсчёта).
Через электрический потенциал (но в общем случае не через него один[2]) выражается напряжённость электрического поля:
где — оператор градиента (набла), а — векторный потенциал, через который выражается (также) магнитное поле.
В частном случае постоянных или пренебрежимо медленно[3] меняющихся со временем электрического и магнитного полей (случай электростатики), электрический потенциал носит название электростатического потенциала, а формула для напряжённости электрического поля (называемого в этом случае электростатическим) упрощается, так как второй член (производная по времени) равен нулю (или достаточно мал по сравнению с первым — и его можно приравнять нулю в рамках принятого приближения):
В этом случае, как нетрудно увидеть, пропадает (отсутствует) вихревое электрическое поле[4], поле — потенциально, а отсюда следует возможность определить электростатический потенциал через работу, совершаемую электрическим полем, так как она в этом случае полностью определяется разностью потенциалов в начальной и конечной точке[5].
- ↑ В этой статье предмет рассмотрен с точки зрения классической электродинамики. В квантовой электродинамике, так как она сложилась уже после переформулировки электродинамики в лоренц-ковариантной (четырёхмерной) форме, электрический потенциал отдельно не играет в целом слишком существенной роли, обычно рассмариваясь всего лишь как компонента четырёхмерного потенциала. Тем не менее, при необходимости рассмотренные в этой статье определения могут применяться и в квантовой электродинамике, хотя чаще можно видеть упоминание его просто как «нулевой компоненты электромагнитного потенциала». В квантовой теории атома можно встретить нередко также электростатический потенциал; обсуждение причин и контекста этих упоминаний выходят за рамки данной статьи, однако заметим, что в этом случае обычно речь идёт о самом обычном классическом кулоновском потенциале.
- ↑ ещё в выражение входит и векторный потенциал .
- ↑ «Пренебрежимо медленно» означает здесь, например, то, что вихревым электрическим полем, порождаемым изменением магнитного поля — и векторного потенциала — можно пренебречь по сравнению с полем, вычисленным по формуле без производной по времени от векторного потенциала.

- ↑ То, что вихревое поле присутствует в общем случае, нетрудно увидеть прямо из уравнений Максвелла.
- ↑ В общем — не электростатическом — случае в работу очевидно войдёт ещё слагаемое от второго члена в формуле электрического поля, что сделает определение электрического потенциала в этом случае через работу несколько затруднительным и искусственным; впрочем, конструктивный путь может состоять в определении сначала для частного — электростатического — случая, а затем — в прямом обобщении определения. Очевидно, исторически во многом всё происходило именно так.
Электростатический потенциал из-за точечного заряда Калькулятор
✖Заряд — это фундаментальное свойство форм материи, проявляющих электростатическое притяжение или отталкивание в присутствии другой материи.ⓘ Обвинение [q] | абкулоновАмпер-часАмпер-минутаАмпер-секундаКулонэлементарному зарядуЭМУ заряженностиESU заряженностиФарадейФранклинкилокулонМегакулонмикрокулонМиллиампер-часМилликулонНанокулонПико кулонстаткулон | +10% -10% | |
✖Расстояние между зарядами определяется как расстояние между двумя электрическими зарядами и зависит от полярности зарядов. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Электростатический потенциал – это мера потенциальной энергии на единицу заряда. |
AbvoltАттовольтсантивольтДецивольтДекавольтEMU электрического потенциалаESU электрического потенциалаФемтовольтГигавольтГектовольткиловольтМегавольтмикровольтмилливольтНановольтпетавольтпиковольтПланка напряженияStatvoltТеравольтвольтВатт / АмперЙоктовольтЦептовольт |
⎘ копия |
👎
Формула
сбросить
👍
Электростатический потенциал из-за точечного заряда Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Обвинение: 0.3 Кулон —> 0.3 Кулон Конверсия не требуется
Разделение между обвинениями: 2000 Миллиметр —> 2 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
1348132768.845 вольт —> Конверсия не требуется
< 10+ Электростатика Калькуляторы
Электростатический потенциал из-за точечного заряда формула
Электростатический потенциал = [Coulomb]*Обвинение/Разделение между обвинениями
Vₑ = [Coulomb]*q/rqs
Что такое электростатический потенциал?
Электростатический потенциал объем работы, необходимо, чтобы переместить блок электрического заряда от опорной точки к определенной точке в электрическом поле, не вызывая ускорение.
Разница между электрическим полем и электрическим потенциалом
Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для любого положения в пространстве. Поскольку оно происходит от силы, это векторное поле. Электрический потенциал — это электрическая потенциальная энергия пробного заряда, деленная на его заряд для любого положения в пространстве. Поскольку оно получено из энергии, это скалярное поле.
Share
Copied!
Электрическая потенциальная энергия: разность потенциалов
Цели обучения
К концу этого раздела вы сможете:
- Давать определение электрического потенциала и электрической потенциальной энергии.
- Опишите взаимосвязь между разностью потенциалов и электрической потенциальной энергией.
- Объясните электрон-вольт и его использование в субмикроскопическом процессе.

- Определить электрическую потенциальную энергию, зная разность потенциалов и величину заряда.
Рис. 1. Заряд, ускоренный электрическим полем, аналогичен массе, спускающейся с холма. В обоих случаях потенциальная энергия переходит в другую форму. Работа совершается силой, но поскольку эта сила консервативна, мы можем написать Вт = –ΔPE.
Когда свободный положительный заряд q ускоряется электрическим полем, как показано на рис. 1, он получает кинетическую энергию. Этот процесс аналогичен ускорению объекта гравитационным полем. Это похоже на то, как будто заряд спускается с электрического холма, где его электрическая потенциальная энергия преобразуется в кинетическую энергию. Исследуем работу, совершенную над зарядом 9.0017 q
Электростатическая или кулоновская сила является консервативной, что означает, что работа, совершенная над q , не зависит от пройденного пути. Это в точности аналогично гравитационной силе в отсутствие диссипативных сил, таких как трение. Когда сила консервативна, можно определить потенциальную энергию, связанную с силой, и обычно легче иметь дело с потенциальной энергией (поскольку она зависит только от положения), чем напрямую вычислять работу.
Это в точности аналогично гравитационной силе в отсутствие диссипативных сил, таких как трение. Когда сила консервативна, можно определить потенциальную энергию, связанную с силой, и обычно легче иметь дело с потенциальной энергией (поскольку она зависит только от положения), чем напрямую вычислять работу.
Мы используем буквы PE для обозначения потенциальной электрической энергии, которая измеряется в джоулях (Дж). Изменение потенциальной энергии ΔPE имеет решающее значение, поскольку работа, совершаемая консервативной силой, равна отрицательной величине изменения потенциальной энергии; то есть Вт = –ΔPE. Например, работа Вт , совершаемая для ускорения положительного заряда из состояния покоя, положительна и является результатом потери PE или отрицательного ΔPE. Перед ΔPE должен стоять знак минус, чтобы W было положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и рассчитав работу, необходимую для перемещения заряда в другую точку.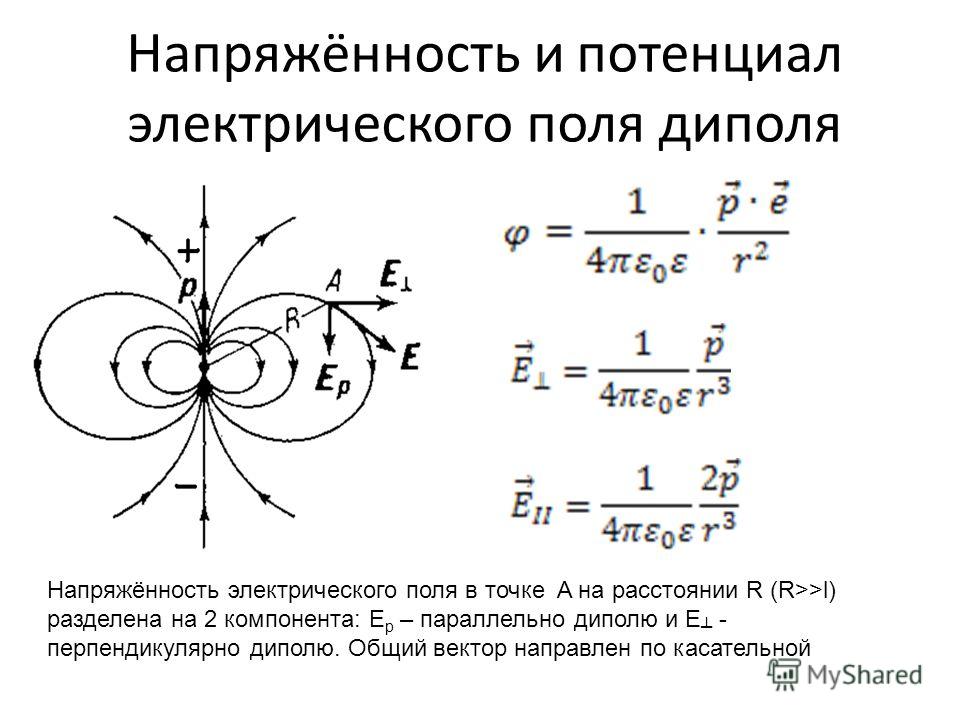
Потенциальная энергия
Вт = –ΔPE. Например, работа Вт , совершаемая для ускорения положительного заряда из состояния покоя, положительна и является результатом потери PE или отрицательного ΔPE. Перед ΔPE должен стоять знак минус, чтобы W было положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и рассчитав работу, необходимую для перемещения заряда в другую точку.
Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны. Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное представление об энергии и преобразовании энергии без необходимости иметь дело с силой напрямую. Например, гораздо чаще используется понятие напряжения (связанное с потенциальной электрической энергией), чем непосредственное рассмотрение кулоновской силы.
Прямой расчет работы, как правило, затруднен, поскольку W = Fd cos θ , а направление и величина F могут быть сложными для нескольких зарядов, для объектов необычной формы и на произвольных путях. Но мы знаем, что, поскольку F = qE , работа и, следовательно, ΔPE пропорциональны пробному заряду q. Чтобы иметь физическую величину, независимую от пробного заряда, мы определяем электрический потенциал V (или просто потенциал, поскольку понимается электричество) как потенциальная энергия на единицу заряда [латекс]V=\frac{\text{PE}}{q}\\[/latex].
Но мы знаем, что, поскольку F = qE , работа и, следовательно, ΔPE пропорциональны пробному заряду q. Чтобы иметь физическую величину, независимую от пробного заряда, мы определяем электрический потенциал V (или просто потенциал, поскольку понимается электричество) как потенциальная энергия на единицу заряда [латекс]V=\frac{\text{PE}}{q}\\[/latex].
Электрический потенциал
Это электрическая потенциальная энергия на единицу заряда.
[латекс]\displaystyle{V}=\frac{\text{PE}}{q}\\[/latex]
Поскольку PE пропорционально q , зависимость от q отменяет. Таким образом, V не зависит от q . Изменение потенциальной энергии ΔPE имеет решающее значение, поэтому нас интересует разность потенциалов или разность потенциалов Δ V между двумя точками, где
[латекс] \ displaystyle \ Delta {V} = V _ {\ text {B }}-V_{\text{A}}=\frac{\Delta{\text{PE}}}{q}\\[/latex]
Разность потенциалов между точками A и B, В B − В A , таким образом, определяется как изменение потенциальной энергии заряда q перемещены из A в B, разделенные на заряд. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.
Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.
[latex]1\text{V}=1\frac{\text{J}}{\text{C}}\\[/latex]
Разность потенциалов
Разность потенциалов между точками A и B, V B – V A , определяется как изменение потенциальной энергии заряда q , перемещенного из A в B, деленное на заряд. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.
[латекс]\displaystyle{1}\text{V}=1\frac{\text{J}}{\text{C}}\\[/latex]
Знакомый термин напряжение является общим название разности потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, подразумевается разность потенциалов между двумя точками. Например, у каждой батареи есть две клеммы, а ее напряжение — это разность потенциалов между ними. Более того, точка, которую вы выбираете как ноль вольт, является произвольной. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный нуль, например, уровень моря или, возможно, пол лекционного зала.
Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный нуль, например, уровень моря или, возможно, пол лекционного зала.
Таким образом, связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением [латекс]\Delta{V}=\frac{\Delta\text{PE}}{q}\\[/latex] и ΔPE = q Δ V .
Разность потенциалов и электрическая потенциальная энергия
Отношение между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением
[латекс]\Delta{V}=\frac{\Delta\text{PE}}{q }\\[/латекс] и ΔPE = q Δ В
Второе уравнение эквивалентно первому.
Напряжение — это не то же самое, что энергия. Напряжение – это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), однако один из них хранит гораздо больше энергии, чем другой, поскольку ΔPE = q Δ В . Автомобильный аккумулятор может передавать больше заряда, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами на 12 В.
Автомобильный аккумулятор может передавать больше заряда, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами на 12 В.
Пример 1. Вычисление энергии
Предположим, у вас есть мотоциклетная батарея на 12,0 В, которая может заряжать 5000 Кл, и автомобильная батарея на 12,0 В, которая может заряжать 60 000 Кл. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда соответствует трем значащим цифрам.)
Стратегия
Если мы говорим, что у нас есть батарея на 12,0 В, это означает, что ее клеммы имеют разность потенциалов 12,0 В. Когда такая батарея перемещает заряд, она проводит заряд через разность потенциалов 12,0 В, и заряду сообщается изменение потенциальной энергии, равное ΔPE = q Δ V .
Итак, чтобы найти выходную энергию, мы умножаем перемещенный заряд на разность потенциалов.
Решение
Для аккумуляторной батареи мотоцикла q = 5000 C и Δ В = 12,0 В. Полная энергия, отдаваемая аккумуляторной батареей мотоцикла, составляет
[латекс]\begin{array}{lll}\Delta\ text{PE}_{\text{цикл}}&=&\left(5000\text{C}\right)\left(12. 4\text{J}\end{массив}\ \[/латекс] 95\text{ J}\end{array}\\[/latex]
4\text{J}\end{массив}\ \[/латекс] 95\text{ J}\end{array}\\[/latex]
Обсуждение
Хотя напряжение и энергия связаны, это не одно и то же. Напряжения батарей идентичны, но энергия, выдаваемая каждой из них, совершенно разная. Учтите также, что по мере разрядки аккумулятора часть его энергии расходуется внутри, и напряжение на его клеммах падает, например, когда фары тускнеют из-за низкого заряда автомобильного аккумулятора. Энергия, поставляемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.
Обратите внимание, что энергии, рассчитанные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для батареи отрицательно, так как она теряет энергию. Эти батареи, как и многие электрические системы, на самом деле перемещают отрицательный заряд, в частности электроны. Батареи отталкивают электроны от своих отрицательных клемм (A) через любую задействованную схему и притягивают их к своим положительным клеммам (B), как показано на рисунке 2. Изменение потенциала составляет Δ В = В B – V A = +12 В, а заряд q отрицательный, так что ΔPE = q Δ В отрицательный, что означает, что потенциальная энергия батареи уменьшилась, когда 9017 q переместился из точки A в точку B.
Изменение потенциала составляет Δ В = В B – V A = +12 В, а заряд q отрицательный, так что ΔPE = q Δ В отрицательный, что означает, что потенциальная энергия батареи уменьшилась, когда 9017 q переместился из точки A в точку B.
Рисунок 2. Аккумулятор перемещает отрицательный заряд с отрицательной клеммы через фару на положительную клемму. Соответствующие комбинации химических веществ в батарее разделяют заряды так, что на отрицательной клемме появляется избыток отрицательного заряда, который отталкивается ею и притягивается к избыточному положительному заряду на другой клемме. С точки зрения потенциала, положительная клемма находится под более высоким напряжением, чем отрицательная. Внутри батареи движутся как положительные, так и отрицательные заряды.
Пример 2. Сколько электронов проходит через фару каждую секунду?
Когда автомобильный аккумулятор на 12,0 В питает одну фару мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?
Стратегия
Чтобы найти количество электронов, мы должны сначала найти заряд, который переместился за 1,00 с. Перемещенный заряд связан с напряжением и энергией через уравнение ΔPE = q Δ V . Лампа мощностью 30,0 Вт потребляет 30,0 Дж в секунду. Поскольку батарея теряет энергию, мы имеем ΔPE = –30,0 Дж, и, поскольку электроны движутся от отрицательного вывода к положительному, мы видим, что Δ В = +12,0 В.
Перемещенный заряд связан с напряжением и энергией через уравнение ΔPE = q Δ V . Лампа мощностью 30,0 Вт потребляет 30,0 Дж в секунду. Поскольку батарея теряет энергию, мы имеем ΔPE = –30,0 Дж, и, поскольку электроны движутся от отрицательного вывода к положительному, мы видим, что Δ В = +12,0 В.
Решение
Чтобы найти заряд q перемещений, решаем уравнение ΔPE = q Δ V : V}}\\[/латекс].
Вводя значения для ΔPE и Δ V , получаем
[latex]q=\frac{-30.0\text{ J}}{+12.0\text{ V}}=\frac{-30.0\text { J}}{+12.0\text{ J/C}}-2.50\text{ C}\\[/latex]
Число электронов n e равно общему заряду, деленному на заряд, приходящийся на один электрон. то есть 9{19}\text{ электроны}\\[/latex]
Обсуждение
Это очень большое число. Неудивительно, что мы обычно не наблюдаем отдельных электронов, когда их так много в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих случаях были отрицательными. Положительный заряд, движущийся в направлении, противоположном направлению отрицательного заряда, часто производит идентичные эффекты; это затрудняет определение того, что движется или движутся ли оба.
Положительный заряд, движущийся в направлении, противоположном направлению отрицательного заряда, часто производит идентичные эффекты; это затрудняет определение того, что движется или движутся ли оба.
The Electron Volt
Рис. 3. Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя металлическими пластинами. Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны с энергией 5000 эВ.
Энергия, приходящаяся на электрон, очень мала в макроскопических ситуациях, таких как в предыдущем примере, — крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на одну частицу (электрон, протон или ион), может иметь большое значение. Например, даже крошечной доли джоуля может быть достаточно для того, чтобы эти частицы разрушили органические молекулы и нанесли вред живым тканям. Частица может нанести ущерб при прямом столкновении или создать вредное рентгеновское излучение, которое также может нанести ущерб. Полезно иметь единицу энергии, связанную с субмикроскопическими эффектами. На рисунке 3 показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как в телевизионной трубке старой модели или в осциллографе. Электрон получает кинетическую энергию, которая затем преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что нисходящий для электрона восходящий для положительного заряда.) Поскольку энергия связана с напряжением соотношением ΔPE = 9{-19}\text{ J}\end{array}\\[/latex]
Полезно иметь единицу энергии, связанную с субмикроскопическими эффектами. На рисунке 3 показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как в телевизионной трубке старой модели или в осциллографе. Электрон получает кинетическую энергию, которая затем преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что нисходящий для электрона восходящий для положительного заряда.) Поскольку энергия связана с напряжением соотношением ΔPE = 9{-19}\text{ J}\end{array}\\[/latex]
Электрон, ускоренный разностью потенциалов в 1 В, получает энергию 1 эВ. Отсюда следует, что электрон, ускоренный через 50 В, получает энергию 50 эВ. Разность потенциалов 100 000 В (100 кВ) даст электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получит энергию 200 эВ. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.
Установление соединений: единицы энергии
Электрон-вольт (эВ) является наиболее распространенной единицей энергии для субмикроскопических процессов. Это будет особенно заметно в главах, посвященных современной физике. Энергия настолько важна для очень многих предметов, что существует тенденция определять специальную единицу измерения энергии для каждой основной темы. Есть, например, калории для пищевой энергии, киловатт-часы для электрической энергии и термы для энергии природного газа.
Электрон-вольт обычно используется в субмикроскопических процессах — химические валентные энергии, молекулярные и ядерные энергии связи входят в число величин, часто выражаемых в электрон-вольтах. Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, ему придается энергия 30 кэВ (30 000 эВ), и он может разбить до 6000 таких молекул (30 000 эВ ÷ 5 эВ на молекулу = 6000 молекул).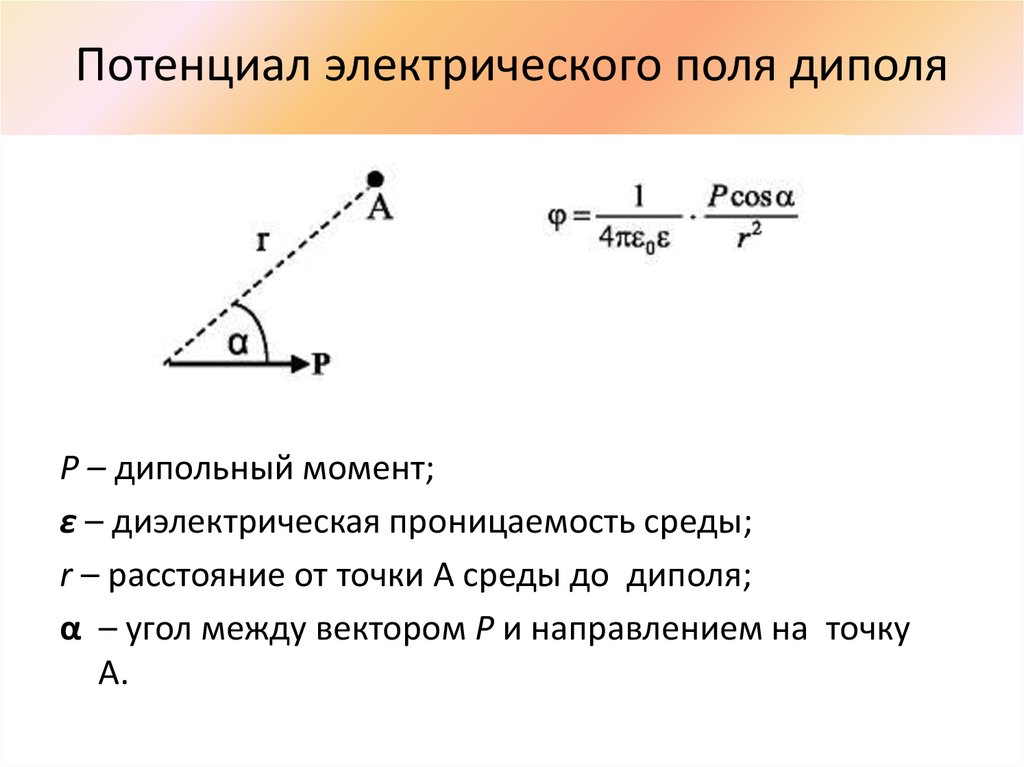 ). Энергия ядерного распада составляет порядка 1 МэВ (1 000 000 эВ) на событие и, таким образом, может привести к значительным биологическим повреждениям.
). Энергия ядерного распада составляет порядка 1 МэВ (1 000 000 эВ) на событие и, таким образом, может привести к значительным биологическим повреждениям.
Сохранение энергии
Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия является константой.
Механическая энергия представляет собой сумму кинетической энергии и потенциальной энергии системы; то есть KE+PE = константа. Потеря PE заряженной частицы становится увеличением ее KE. Здесь РЕ — электрическая потенциальная энергия. Сохранение энергии выражается в виде уравнения: KE + PE = константа или KE i + PE i = KE f + PE f , где i и f обозначают начальное и конечное условия. Как мы уже много раз убеждались, рассмотрение энергии может дать нам понимание и облегчить решение проблем.
Пример 3. Электрическая потенциальная энергия, преобразованная в кинетическую энергию
Рассчитайте конечную скорость свободного электрона, ускоренного из состояния покоя при разности потенциалов 100 В. (Предположим, что это численное значение имеет точность до трех значащих цифр.) 96\text{ м/с}\end{array}\\[/latex]
Обсуждение
Обратите внимание, что и заряд, и начальное напряжение отрицательны, как на рисунке 3. Из обсуждений в разделе Электрический заряд и электрическое поле Мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой гравитации. Большая конечная скорость подтверждает, что гравитационной силой здесь действительно можно пренебречь. Большая скорость также указывает на то, насколько легко ускорять электроны при малых напряжениях из-за их очень малой массы. Напряжения, намного превышающие 100 В в этой задаче, обычно используются в электронных пушках. Эти более высокие напряжения создают настолько большие скорости электронов, что необходимо учитывать релятивистские эффекты.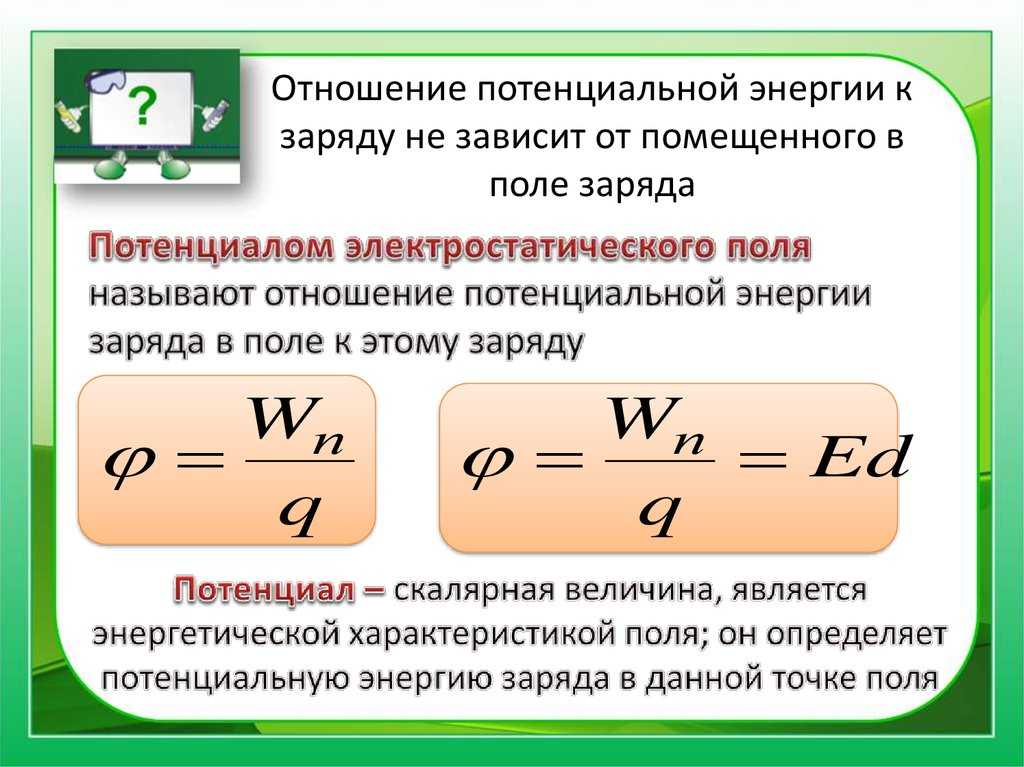 Вот почему в этом примере рассматривается (точно) низкое напряжение.
Вот почему в этом примере рассматривается (точно) низкое напряжение.
Резюме раздела
- Электрический потенциал – это потенциальная энергия на единицу заряда.
- Разность потенциалов между точками A и B, В B − В A , определяемая как изменение потенциальной энергии заряда q , перемещаемого из A в B, равна изменению потенциальная энергия, деленная на заряд. Разность потенциалов обычно называют напряжением, обозначаемым символом Δ В : [латекс]\Delta V=\frac{\Delta\text{PE}}{q}\\[/ латекс] и ΔPE = 9{\text{-19}}\text{J.}\end{массив}\\[/латекс]
- Механическая энергия есть сумма кинетической энергии и потенциальной энергии системы, то есть КЕ + РЕ. Эта сумма является константой.
Концептуальные вопросы
- Напряжение — обычное слово для обозначения разности потенциалов. Какой термин является более описательным, напряжение или разность потенциалов?
- Если напряжение между двумя точками равно нулю, можно ли перемещать между ними пробный заряд, совершая нулевую чистую работу? Обязательно ли это можно сделать без приложения силы? Объяснять.

- Какая связь между напряжением и энергией? Точнее, какова связь между разностью потенциалов и электрической потенциальной энергией?
- Напряжения всегда измеряются между двумя точками. Почему?
- Как связаны между собой единицы измерения вольт и электрон-вольт? Чем они отличаются?
Задачи и упражнения
- Найдите отношение скоростей электрона и отрицательного иона водорода (с дополнительным электроном), ускоренных при одинаковом напряжении, при нерелятивистских конечных скоростях. Примем массу иона водорода равной 1,67 × 10 −27 кг.
- В вакуумной трубке используется ускоряющее напряжение 40 кВ для ускорения электронов, которые ударяются о медную пластину и производят рентгеновское излучение. Нерелятивистски, какова была бы максимальная скорость этих электронов?
- Голое ядро гелия имеет два положительных заряда и массу 6,64 × 10 −27 кг. (a) Рассчитайте его кинетическую энергию в джоулях при 2,00% скорости света.
 б) Сколько это в электрон-вольтах? в) Какое напряжение потребуется для получения этой энергии?
б) Сколько это в электрон-вольтах? в) Какое напряжение потребуется для получения этой энергии? - Интегрированные концепции. Однозарядные ионы газа ускоряются из состояния покоя напряжением 13,0 В. При какой температуре средняя кинетическая энергия молекул газа будет такой же, как у этих ионов?
- Интегрированные концепции. Считается, что температура вблизи центра Солнца составляет 15 миллионов градусов Цельсия (1,5 × 10 7 ºC). При каком напряжении должен быть ускорен однозарядный ион, чтобы его энергия равнялась средней кинетической энергии ионов при данной температуре?
- Интегрированные концепции. (a) Какова средняя выходная мощность сердечного дефибриллятора, который рассеивает 400 Дж энергии за 10,0 мс? (b) Почему дефибриллятор, учитывая большую выходную мощность, не вызывает серьезных ожогов?
- Интегрированные концепции. Молния ударяет в дерево, перемещая заряд 20,0 Кл через разность потенциалов 1,00 × 10 2 МВ.
 а) Какая энергия была рассеяна? б) Какую массу воды можно поднять с 15°С до температуры кипения и затем вскипятить с помощью этой энергии? в) Обсудите ущерб, который может нанести дереву расширение кипящего пара.
а) Какая энергия была рассеяна? б) Какую массу воды можно поднять с 15°С до температуры кипения и затем вскипятить с помощью этой энергии? в) Обсудите ущерб, который может нанести дереву расширение кипящего пара. - Интегрированные концепции. Подогреватель бутылочек с питанием от батареи 12,0 В нагревает 50,0 г стекла, 2,50 × 10 2 г детской смеси и 2,00 × 10 2 г алюминия с 20,0 °C до 90,0 °C. а) Какой заряд переносится батареей? б) Сколько электронов течет в секунду, если для нагревания формулы требуется 5,00 мин? (Подсказка: предположим, что удельная теплоемкость детского питания примерно такая же, как удельная теплоемкость воды.)
- Интегрированные концепции. В автомобиле с батарейным питанием используется система 12,0 В. Найти заряд, который должны иметь аккумуляторы, чтобы разогнать автомобиль массой 750 кг из состояния покоя до 25,0 м/с, заставить его подняться на высоту 2,00 × 10 холм высотой 2 м, а затем заставить его двигаться с постоянной скоростью 25,0 м/с, прилагая силу 5,00 × 10 2 Н в течение часа.

- Интегрированные концепции. Вероятность синтеза значительно возрастает, когда соответствующие ядра сближаются, но необходимо преодолеть взаимное кулоновское отталкивание. Это можно сделать, используя кинетическую энергию высокотемпературных ионов газа или ускоряя ядра навстречу друг другу. (а) Рассчитайте потенциальную энергию двух однозарядных ядер, разделенных расстоянием 1,00 × 10 −12 м, найдя напряжение одного на этом расстоянии и умножив его на заряд другого. б) При какой температуре атомы газа будут иметь среднюю кинетическую энергию, равную этой необходимой электрической потенциальной энергии?
- Необоснованные результаты. (a) Найдите напряжение вблизи металлического шара диаметром 10,0 см, на котором имеется 8,00 Кл избыточного положительного заряда. б) Что неразумного в этом результате? (c) Какие предположения ответственны?
- Создайте свою собственную задачу. Рассмотрите аккумулятор, используемый для питания сотового телефона.
 Составьте задачу, в которой вы определяете энергию, которая должна быть предоставлена батареей, а затем вычисляете количество заряда, которое она должна быть в состоянии переместить, чтобы обеспечить эту энергию. Среди вещей, которые следует учитывать, — потребности в энергии и напряжение батареи. Возможно, вам придется заглянуть вперед, чтобы интерпретировать характеристики батареи производителя в ампер-часах как энергию в джоулях.
Составьте задачу, в которой вы определяете энергию, которая должна быть предоставлена батареей, а затем вычисляете количество заряда, которое она должна быть в состоянии переместить, чтобы обеспечить эту энергию. Среди вещей, которые следует учитывать, — потребности в энергии и напряжение батареи. Возможно, вам придется заглянуть вперед, чтобы интерпретировать характеристики батареи производителя в ампер-часах как энергию в джоулях.
Глоссарий
электрический потенциал: потенциальная энергия на единицу заряда
разность потенциалов (или напряжение): изменение потенциальной энергии заряда, перемещаемого из одной точки в другую, деленное на заряд; единицами разности потенциалов являются джоули на кулон, известные как вольт
электрон-вольт: энергия, переданная основному заряду, ускоренному за счет разности потенциалов в один вольт
механическая энергия: сумма кинетической энергии и потенциальной энергии система; эта сумма является константой
Избранные решения задач и упражнений
1. 42,8
42,8
4. 1,00 × 10 5 K
6. (a) 4 × 10 4 Вт; (b) Дефибриллятор не вызывает серьезных ожогов, потому что кожа хорошо проводит электричество при высоких напряжениях, подобных тем, которые используются в дефибрилляторах. Используемый гель способствует передаче энергии в тело, и кожа не поглощает энергию, а пропускает ее к сердцу.
8. (а) 7,40 × 10 3 С; (б) 1,54 × 10 20 электронов в секунду
9. 3,89 × 10 6 C
11. (а) 1,44 × 10 12 В; (b) Это напряжение очень велико. Сфера диаметром 10,0 см никогда не сможет поддерживать такое напряжение; он будет разряжаться; (c) Заряд в 8,00 Кл больше заряда, чем может разумно накопиться на сфере такого размера.
Электростатический потенциал — объяснение, формула, пример и часто задаваемые вопросы
После понимания электрического поля становится важным понять, как электрическое поле влияет на заряд источника. Электростатический потенциал или электрический потенциал играет жизненно важную роль в электростатике. Электростатический потенциал — это количество работы, необходимой для перемещения точечного заряда из контрольной точки в определенное положение против действия электрического поля. Понятие электрического потенциала используется для демонстрации действия электрического поля исходного заряда с точки зрения положения в пределах электрического поля. В этой статье мы рассмотрим формулу электрического потенциала и подробную информацию об уравнении разности электрических потенциалов.
Электростатический потенциал — это количество работы, необходимой для перемещения точечного заряда из контрольной точки в определенное положение против действия электрического поля. Понятие электрического потенциала используется для демонстрации действия электрического поля исходного заряда с точки зрения положения в пределах электрического поля. В этой статье мы рассмотрим формулу электрического потенциала и подробную информацию об уравнении разности электрических потенциалов.
Формула разности потенциалов
Чтобы понять формулу разности потенциалов, мы должны знать такие понятия, как электростатическая потенциальная энергия. Прежде чем перейти к формуле разности потенциалов, давайте взглянем на понятие потенциальной энергии или электрической потенциальной энергии.
Формула электрической потенциальной энергии
Всякий раз, когда объект или частица помещаются в определенное положение или конфигурацию, внешняя работа, совершаемая над объектом, сохраняется в виде потенциальной энергии. Следовательно, в общем случае потенциальная энергия является формой запасенной энергии. Если работа, необходимая для изменения положения или конфигурации объекта, больше, то и потенциальная энергия, запасенная в объекте, также будет больше. Величина потенциальной энергии прямо пропорциональна внешней работе, совершенной над телом.
Следовательно, в общем случае потенциальная энергия является формой запасенной энергии. Если работа, необходимая для изменения положения или конфигурации объекта, больше, то и потенциальная энергия, запасенная в объекте, также будет больше. Величина потенциальной энергии прямо пропорциональна внешней работе, совершенной над телом.
Рассмотрим пример, предположим, что объект массой m находится на земле. Чтобы переместить объект от земли на высоту h, нужно приложить внешнюю силу, равную mg. Тогда работа, совершаемая для подъема тела с уровня земли на высоту h, будет равна mgh и называется потенциальной энергией гравитации. Таким образом, работа, совершаемая над объектом из одной точки в другую, будет равна разнице объективных потенциальных энергий.
Итак, что такое электрическая потенциальная энергия? Электростатическая потенциальная энергия почти аналогична гравитационной потенциальной энергии. Мы обсуждаем формулу потенциальной электрической энергии, относящуюся к концепции гравитационной потенциальной энергии. Когда электрический заряд подвергается внешнему электрическому полю, внешняя работа, совершаемая над электрическим зарядом, сохраняется в виде потенциальной электрической энергии или потенциальной электростатической энергии. Поэтому электрическая потенциальная энергия определяется как внешняя работа, совершаемая агентом по переводу заряда или системы зарядов из бесконечности в требуемое положение без ускорения заряда.
Когда электрический заряд подвергается внешнему электрическому полю, внешняя работа, совершаемая над электрическим зарядом, сохраняется в виде потенциальной электрической энергии или потенциальной электростатической энергии. Поэтому электрическая потенциальная энергия определяется как внешняя работа, совершаемая агентом по переводу заряда или системы зарядов из бесконечности в требуемое положение без ускорения заряда.
Рассмотрим положительный заряд q, помещенный во внешнее электрическое поле, пусть пробный заряд + \[q_{0}\] помещен в точку A (скажем). Из-за электрического поля вокруг заряда +q пробный заряд + \[q_{0}\] будет испытывать электростатическую силу \[F_{e}\], направленную от заряда (или наружу). Поскольку оба заряда имеют одинаковую природу, прилагаемая сила будет отталкивающей, т.е. \[F_{ext} = -F_{e}\]
Пусть потенциальная энергия заряда + \[q_{0}\] при точка А — UA и смещена на расстояние dr в сторону заряда +q. Величина внешней силы, действующей на пробный заряд, будет равна электростатической силе. 9{B} F_{e} . dr …(3)\]
9{B} F_{e} . dr …(3)\]
Следовательно, полная потенциальная энергия, запасенная в заряде, равна разности потенциальных энергий в точках A и B соответственно. Итак, формулу электростатической потенциальной энергии можно вывести, рассчитав разность потенциалов в двух точках.
Что такое разность электростатических потенциалов?
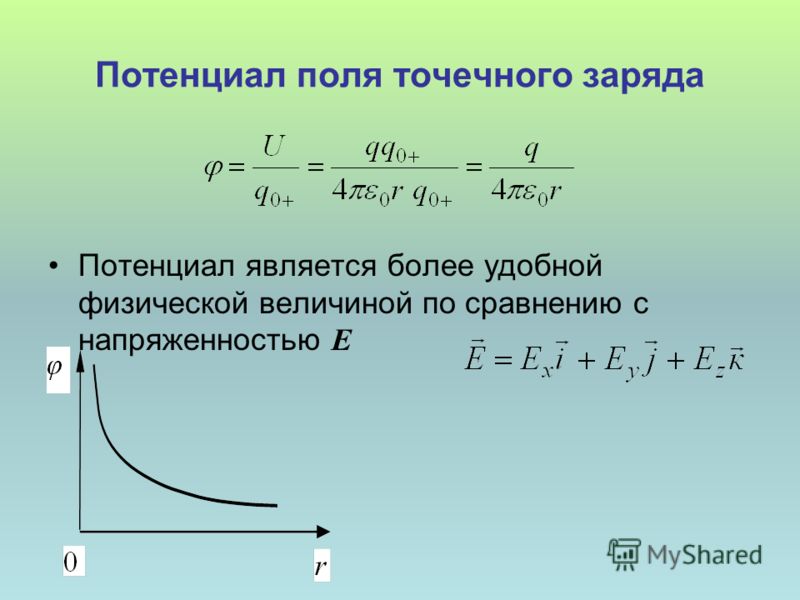
Теперь давайте посмотрим, что такое электростатический потенциал и формулы разности электрических потенциалов. Электростатический потенциал определяется как электрическая потенциальная энергия на единицу заряда. Внешняя работа, совершаемая на единицу заряда, равна изменению потенциала точечного заряда. Рассмотрим электрический заряд q, и если мы хотим переместить заряд из точки A в точку B, а внешняя работа, совершенная для перемещения заряда из точки A в точку B, равна W AB , тогда электростатический потенциал определяется как:
\[\Стрелка вправо \Delta V = V_{A} — V_{B} = \frac{W_{AB}}{q} …. (1)\]
(1)\]
Где,
\[W_{AB}\] − Внешняя работа, совершаемая при переносе заряда из точки A в B.
Уравнение (1) известно как уравнение разности электрических потенциалов или уравнение электростатического потенциала. Если начальное положение заряда находится в бесконечности, мы знаем, что потенциал на бесконечности будет равен нулю, поэтому мы пишем
\[\Стрелка вправо \Delta V = V_{\infty} — V_{B} = \frac{W_{ \infty B}}{q}\]
\[\Rightarrow V_{B} = \frac{W_{\infty B}}{q} … (2)\]
Уравнение (2) известно как уравнение электрического потенциала. Поэтому электростатический потенциал определяется как полная внешняя работа, совершаемая для перевода точечного заряда из бесконечности в требуемое положение.
Пример
1. Рассчитайте электростатический потенциал точечного заряда, расположенного на расстоянии r.
Ответ: Электрический потенциал в точке в электрическом поле определяется как количество внешней работы, совершаемой при перемещении единичного положительного заряда из бесконечности в эту точку по любому пути (т. е. независимо от пути), когда электростатические силы применяемый.
е. независимо от пути), когда электростатические силы применяемый.
Предположим, что положительный заряд помещен в точку P в заданном внешнем электрическом поле. Заряд, помещенный в эту точку, будет оказывать внешнее воздействие из-за наличия электрического поля. Электрический потенциал в любой точке на расстоянии r от положительного заряда +q определяется как:
\[\Rightarrow V\frac{kq}{r} …(1)\]
Где,
K — постоянная Кулона и равна \[ \frac{1}{4\pi \epsilon \theta}\]
r — вектор положения.
Когда внешняя работа совершается при перемещении заряда в 1 кулон из бесконечности в определенную точку за счет электрического поля, противодействующего электростатической силе, то говорят, что она составляет 1 вольт электростатического потенциала в точке.
Важность электростатического потенциала
Интернет переполнен ресурсами на тему электростатического потенциала, но их подлинность и надежность остаются сомнительными.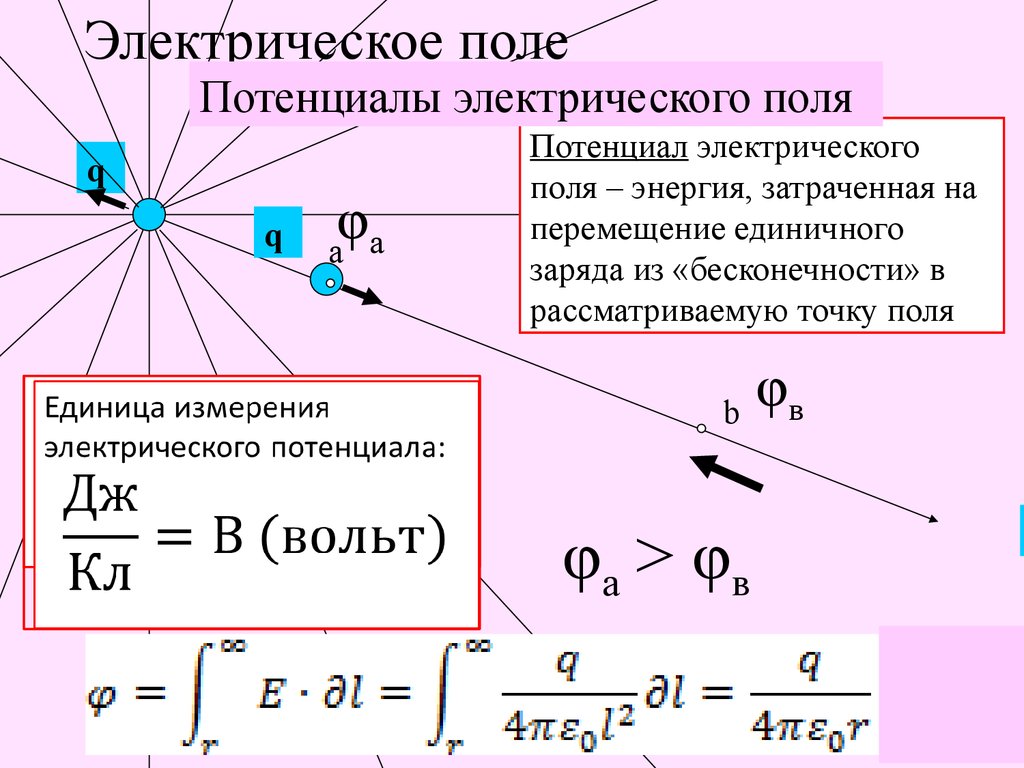 Чтобы помочь учащимся справиться с этой проблемой, Веданту представила свой Электростатический потенциал.
Чтобы помочь учащимся справиться с этой проблемой, Веданту представила свой Электростатический потенциал.
Контент, доступный для вас, разработан под руководством экспертов в области физики, которые имеют многолетний опыт работы в сфере образования. Весь контент, доступный на веб-странице, создан после тщательного анализа работ различных экзаменов за предыдущий год.
Этот контент предоставляется вам бесплатно, и в прошлом на него ссылались многие топперы. Это подчеркивает тот факт, насколько полезны эти учебные материалы.
Вы можете получить доступ ко многим другим бесплатным учебным материалам для различных экзаменов на веб-сайте Vedantu.
Заключение
Прочитав эту статью, вы поняли значение электростатического потенциала и связанных с ним понятий, таких как его формулы, проделанная работа и многое другое. Можно видеть, как эти объекты меняются с расстоянием. Можно также в некоторой степени использовать аналогию с электрическим потенциалом, чтобы понять эту концепцию.



 ⓘ Разделение между обвинениями [rcharges]
ⓘ Разделение между обвинениями [rcharges]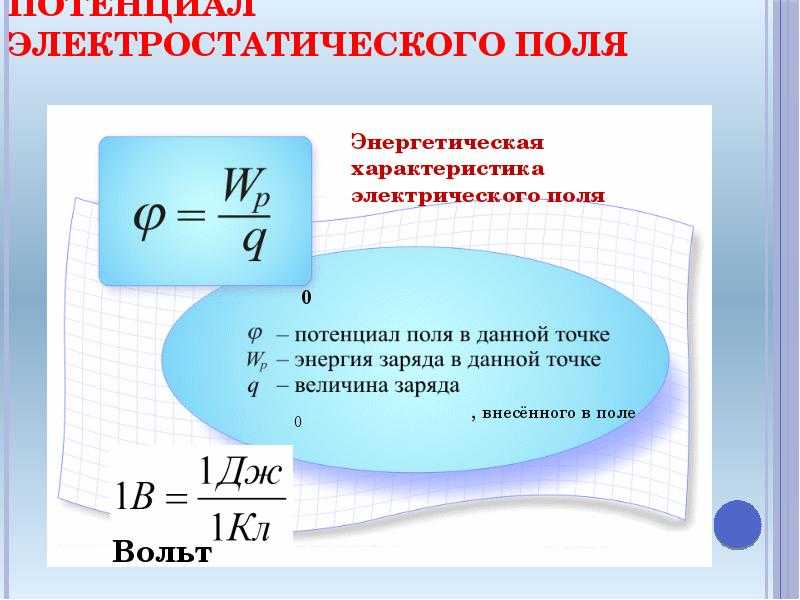 ⓘ Электростатический потенциал из-за точечного заряда [Vₑ]
ⓘ Электростатический потенциал из-за точечного заряда [Vₑ]


 б) Сколько это в электрон-вольтах? в) Какое напряжение потребуется для получения этой энергии?
б) Сколько это в электрон-вольтах? в) Какое напряжение потребуется для получения этой энергии? а) Какая энергия была рассеяна? б) Какую массу воды можно поднять с 15°С до температуры кипения и затем вскипятить с помощью этой энергии? в) Обсудите ущерб, который может нанести дереву расширение кипящего пара.
а) Какая энергия была рассеяна? б) Какую массу воды можно поднять с 15°С до температуры кипения и затем вскипятить с помощью этой энергии? в) Обсудите ущерб, который может нанести дереву расширение кипящего пара.
 Составьте задачу, в которой вы определяете энергию, которая должна быть предоставлена батареей, а затем вычисляете количество заряда, которое она должна быть в состоянии переместить, чтобы обеспечить эту энергию. Среди вещей, которые следует учитывать, — потребности в энергии и напряжение батареи. Возможно, вам придется заглянуть вперед, чтобы интерпретировать характеристики батареи производителя в ампер-часах как энергию в джоулях.
Составьте задачу, в которой вы определяете энергию, которая должна быть предоставлена батареей, а затем вычисляете количество заряда, которое она должна быть в состоянии переместить, чтобы обеспечить эту энергию. Среди вещей, которые следует учитывать, — потребности в энергии и напряжение батареи. Возможно, вам придется заглянуть вперед, чтобы интерпретировать характеристики батареи производителя в ампер-часах как энергию в джоулях.