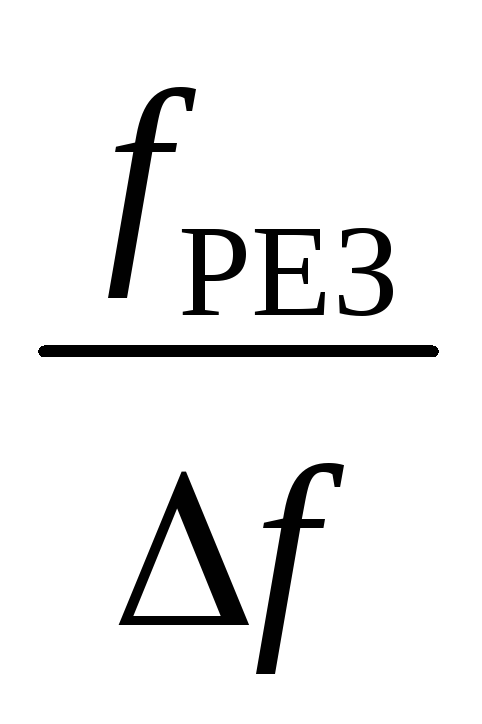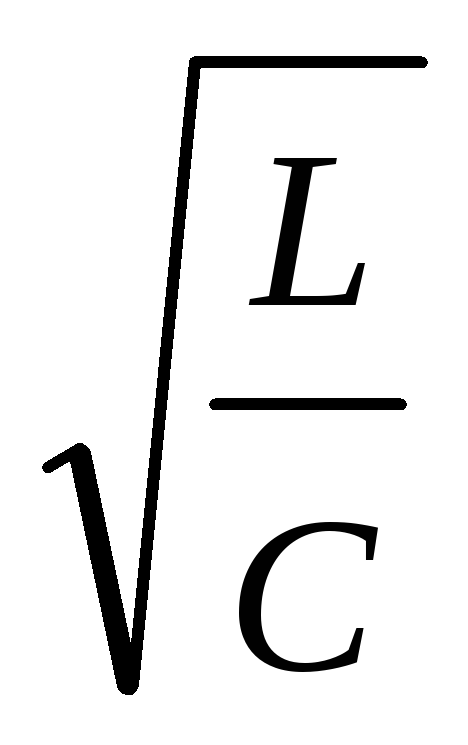Добротность контура | Шаг за шагом

С течением времени амплитуды напряжения и тока в контуре уменьшаются — электромагнитные  колебания  затухают,   подобно тому, как затухают колебания маятника или струны (рис. 48, 49).

Затухание электромагнитных колебаний в контуре связано с тем, что всякий раз при «перекачивании» энергии из конденсатора в катушку и обратно часть этой энергии безвозвратно теряется. Основные потери энергии в контуре — это потери в проводе катушки, в соединительных проводах, в изоляции проводов, потери в диэлектрике конденсатора и каркасе катушки, а также на излучение электромагнитных волн.

Таким образом, если мы хотим нарисовать реальную схему контура, то, помимо контурной катушки _Lк и конденсатора С_к, мы должны включить в нее и сопротивления, которые будут характеризовать потери энергии (лист 76). В действительности никаких сопротивлений (имеется в виду отдельная деталь) в контуре, конечно, нет. Но потери энергии в катушке, конденсаторе и т. д. существуют реально. Для того чтобы не забывать об этом, мы и рисуем на схеме не только катушку L

к и конденсатор С_к, но и условные сопротивления, которые отображают фактически существующие потери энергии.

Основные виды потерь — потери в катушке, потери на излучение и другие — условно характеризуются сопротивлением R_к, включенным последовательно, с L_к и С_к (лист 76, упрощенные схемы). Во время колебаний по сопротивлению R_к проходит весь контурный ток и, чем больше R_к, тем больше энергии на нем теряется.

Для учета некоторых видов потерь (потери в конденсаторе, в каркасе и др.) иногда приходится считать, что в контуре имеется еще одно сопротивление R_ш, шунтирующее (лист 32) конденсатор С_к или катушку L_к. Во время разряда конденсатора ток разветвляется: часть его проходит через катушку и создает там запасы энергии в виде магнитного поля. Другая часть разрядного тока проходит через сопротивление R_ш и создает там безвозвратные потери энергии. Чем меньше тем больший ток через него проходит, тем больше энергии теряется на этом сопротивлении.

Таким образом, для того чтобы уменьшить потери в контуре, нужно стремиться к тому,чтобы сопротивление R_к было как можно меньше, а сопротивление R_ш как можно больше (рис 50, 51). Сопротивления R_к и R_ш на схемах радиоаппаратуры не изображаются, так как они не представляют собой самостоятельных деталей. Однако эти сопротивления реально существуют и, потребляя энергию, приводят к затуханию колебаний.

Для характеристики затухания колебаний существует специальная величина,  называемая добротностью  (лист 77).

Добротность обозначается буквой «Q» и представляет собой относительное число, показывающее, во сколько раз энергия, запасаемая в конденсаторе или катушке за четверть периода, больше, чем энергия, теряемая на сопротивлениях R_к и R_ш за то же время. Совершенно очевидно, что, чем выше добротность Q, тем медленнее будут затухать колебания в контуре (лист 78). Добротность реальных колебательных контуров обычно лежит в пределах от 30 (в контуре каждый раз теряется одна тридцатая часть, то есть около 3 % перекачиваемой энергии) до 300 (потери около 0,3% от запасенной энергии). Добротность специальных колебательных систем (кварцевые пластины, объемные резонаторы) достигает нескольких десятков и даже сотен тысяч.

Ухудшить добротность контура (иногда возникает и такая необходимость) можно очень просто: достаточно увеличить потери в контуре, увеличив Rк или уменьшив R_ш. Для этого можно, например, включить в контур обычные сопротивления.

7.5. Добротность. Влияние добротности на резонансные кривые последовательного контура r ,l, с

Любой резонансный контур, в том числе и последовательный принято характеризовать добротностью Q и характеристическим сопротивлением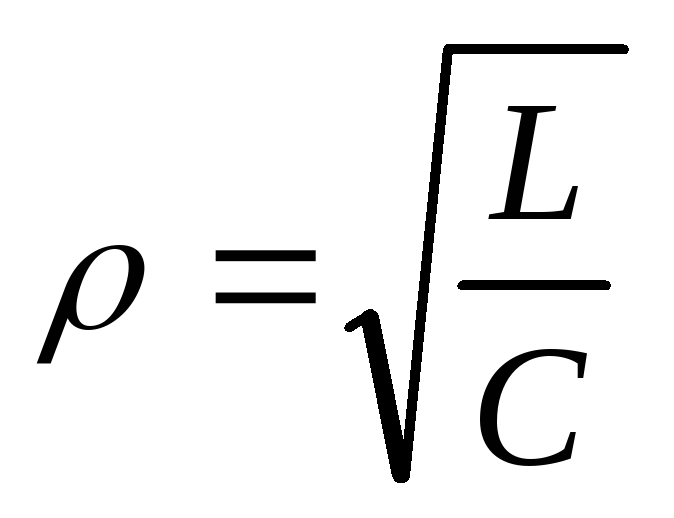

.

Напомним, что в данном случае будем рассматривать определение добротности контура при изменении частоты источника питания.

При резонансе .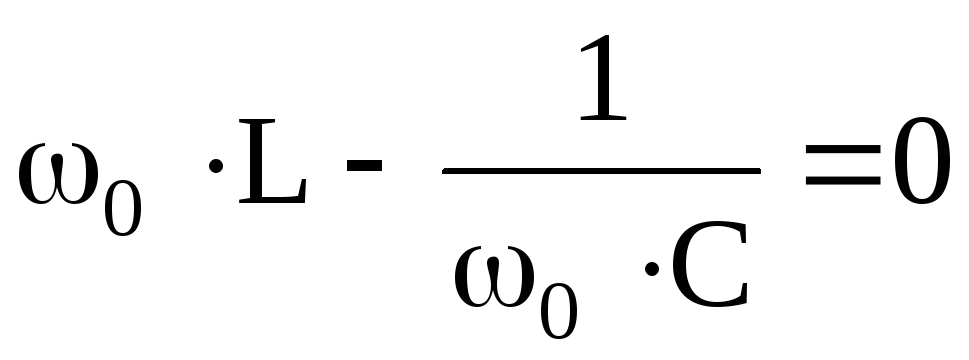

Добротность контура определяет кратность превышения напряжения на зажимах индуктивного или емкостного элемента сопротивления при резонансе над напряжением всей цепи U = U_R.

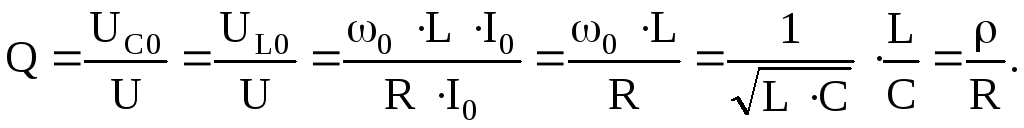
В электротехнических и радиотехнических установках добротности могут быть любого порядка, вплоть до десятков тысяч. При больших добротностях (50–500) U_L0 >> U_R, U_R = U_ВХ = U, т. е. напряжение на индуктивности (или на емкости) во много раз больше приложенного напряжения.

Выясним влияние добротности на резонансные кривые при последовательном соединении

R, L, С. Ток в цепи равен

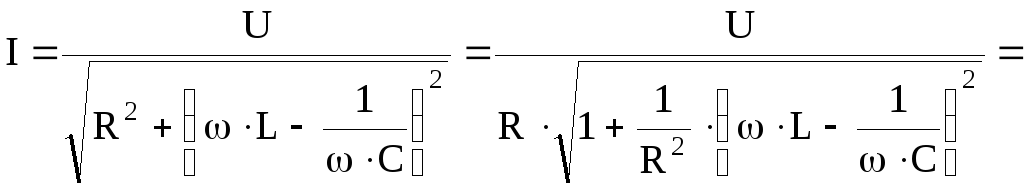
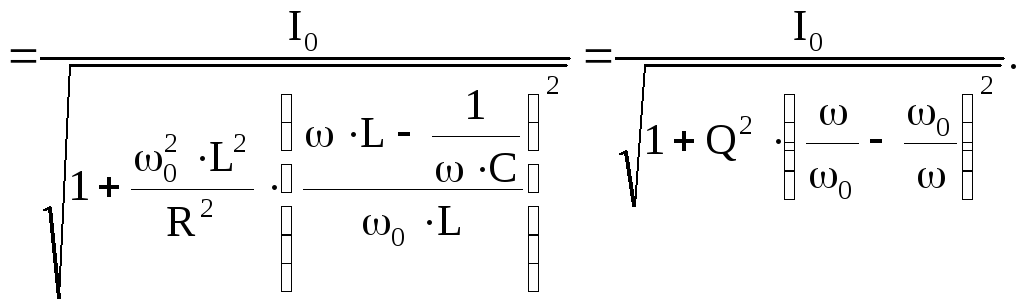
Относительное значение тока: 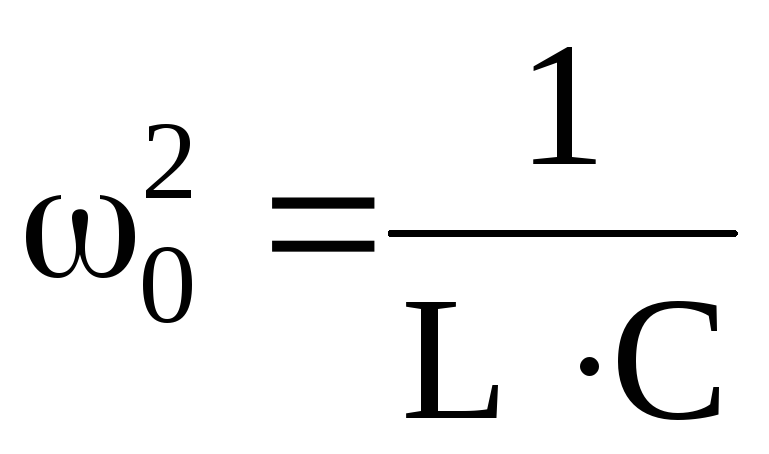, т.е..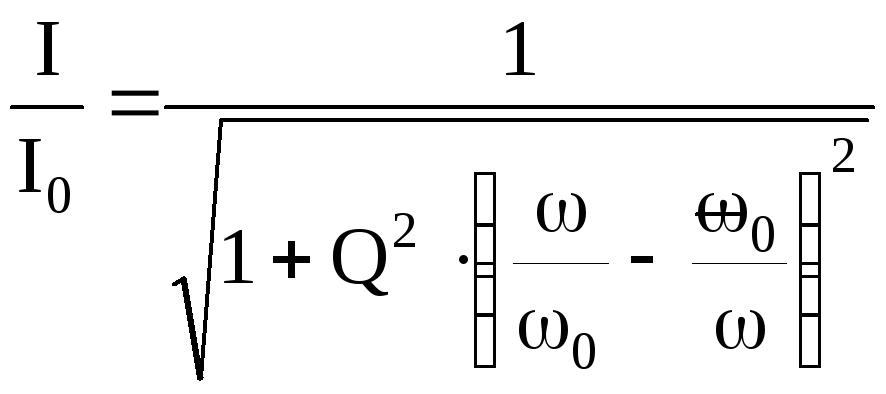

Пои выводе этой формулы учитывалось, что .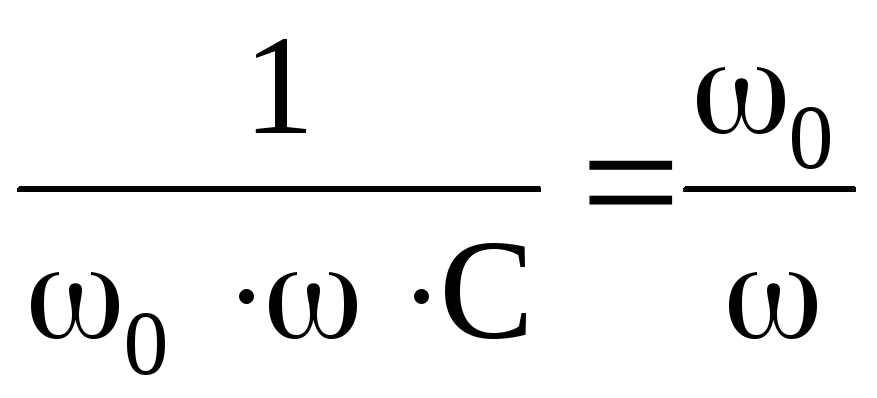

Иногда вводят понятие относительной частоты .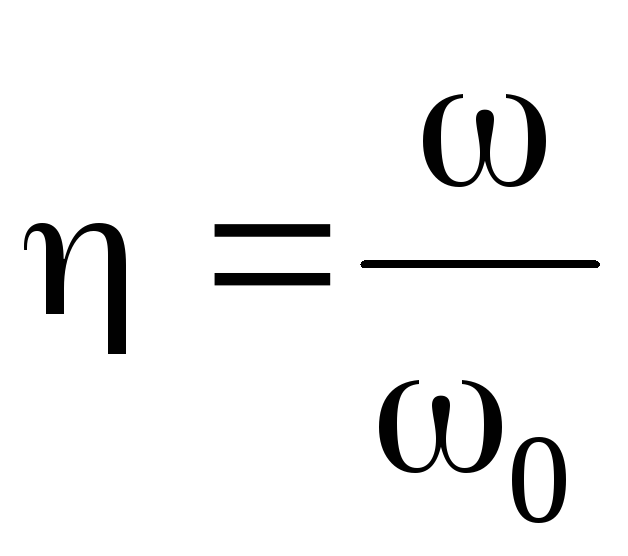

Тогда предыдущая формула запишется так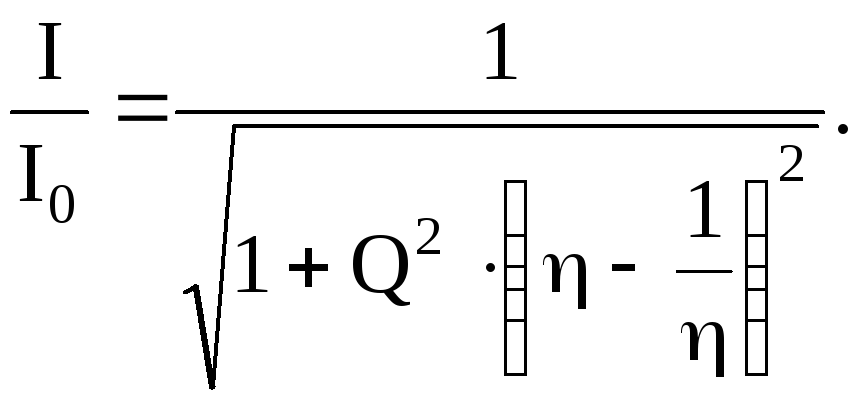

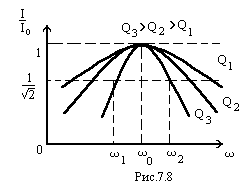
Построим резонансные кривые в относительных (по току) единицах (рис. 7.8) для трех добротностей. Рассматривая три резонансные кривые, видим, что чем больше добротность, тем острее получается резонансная кривая. Полоса пропускания контура определяется разностью частот, которые получатся при пересечении резонансной кривой горизонтальной линией на уровне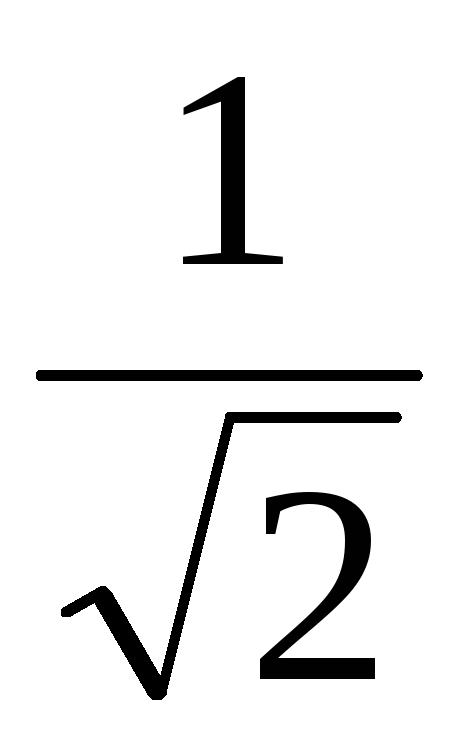

.

Из рис. 7.8 видно, что чем меньше добротность, тем шире полоса пропускания. В радиоприемниках колебательные контуры имеют большие добротности (500–1000), поэтому эти контуры обладают достаточно узкими полосами пропускания, что способствует избирательному радиоприему только одной станции.

7.6. Определение добротности по резонансной кривой

На практике резонансные частотные характеристики реальных контуров можно получать, изменяя частоту генератора в определенных пределах и снимая показания вольтаметра, подключенного параллельно резистору (см. рис. 7.9 а). Строят экспериментальную резонансную кривую и по этой кривой определяют полосу пропускания. Выведем соответствующую формулу для расчета добротности по резонансной кривой, снятой экспериментально.

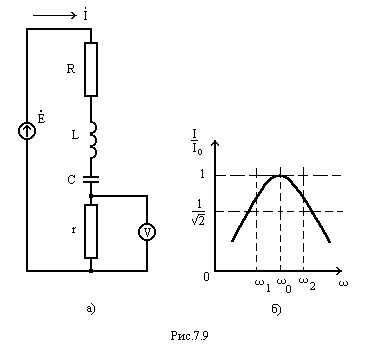
Из рис. 7.9 б следует:

.

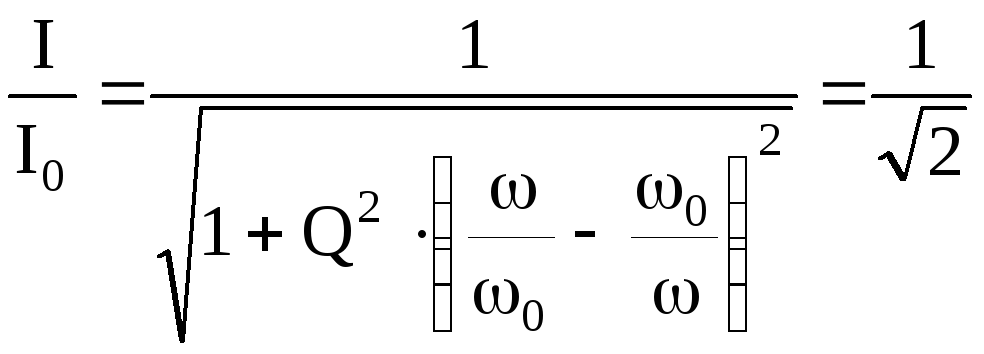В этом равенстве знаменатели равны, поэтому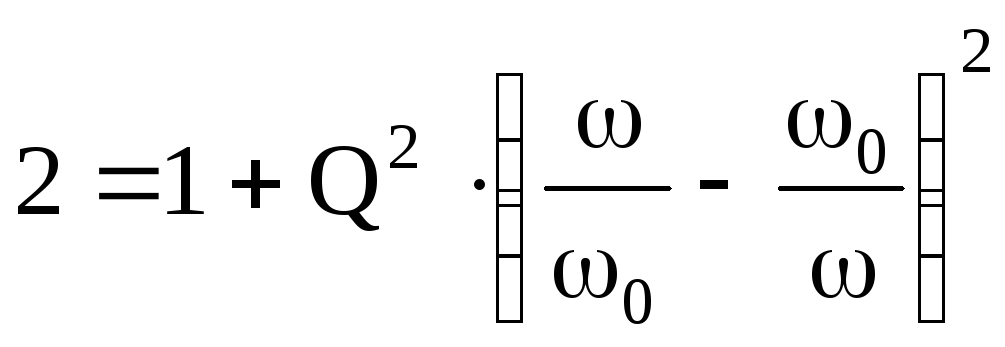

Отсюда .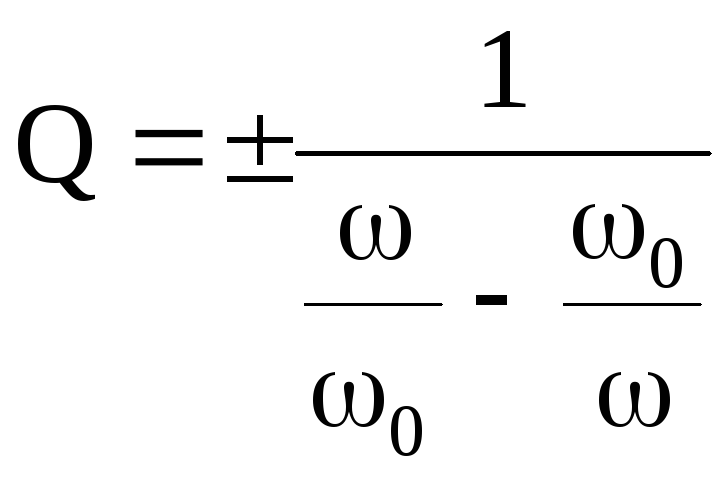

Запишем дважды: при

итакие выражения;.

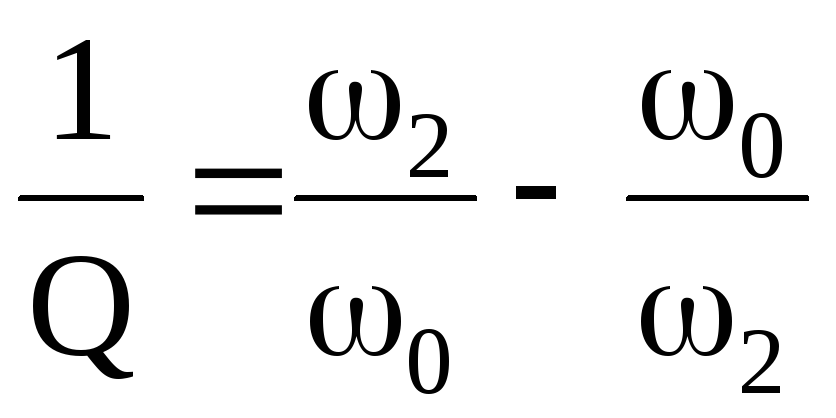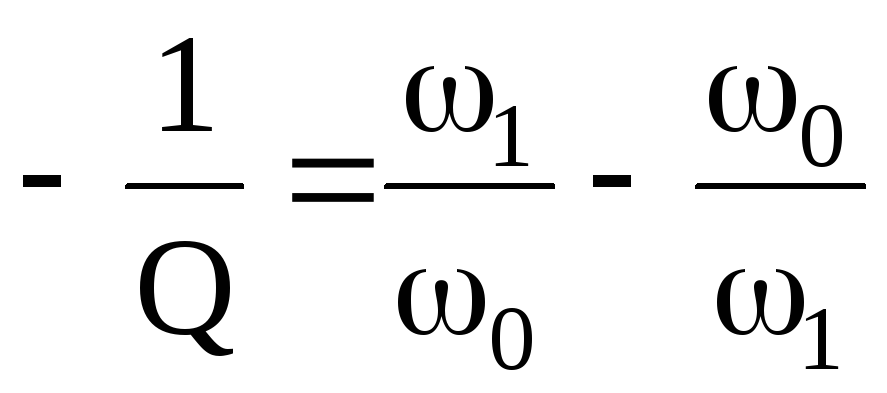После сложения последних выражений получим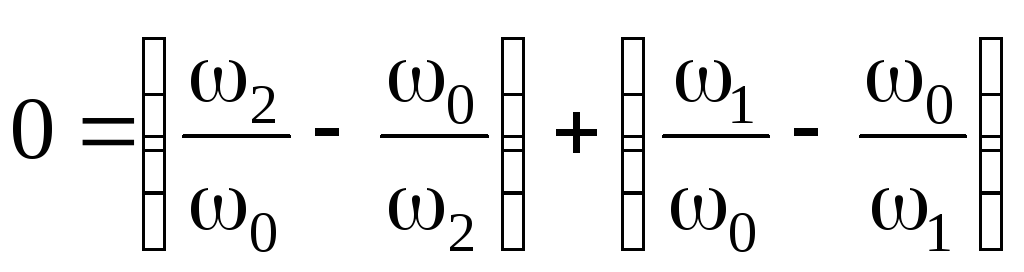

или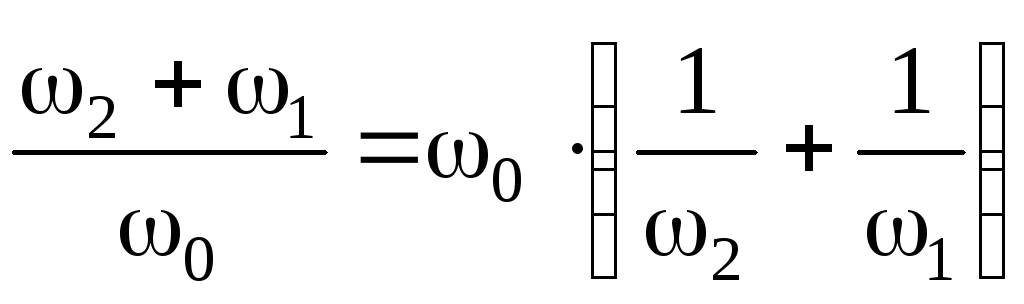

Отсюда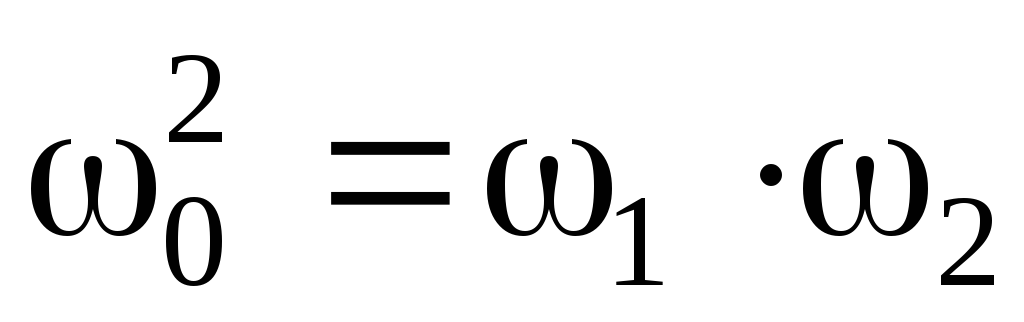

И далее .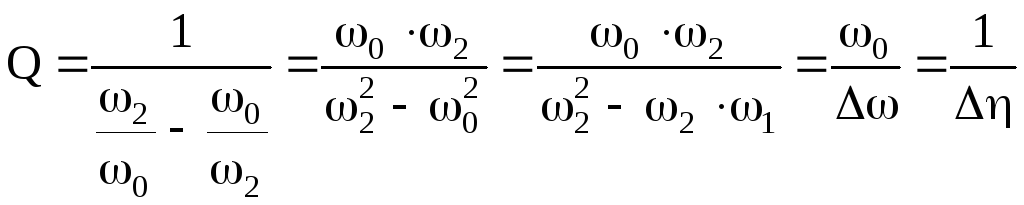

Очень важно: добротность обратно пропорциональна .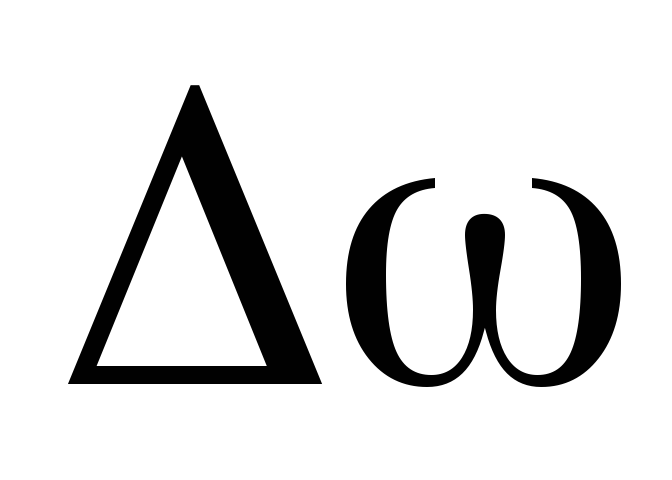

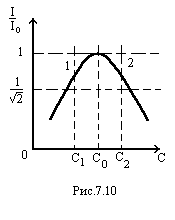
Для последовательного контура R, L, С построена резонансная кривая тока при изменении

емкости С (рис. 7.10).

Пользуясь этой кривой, определим добротность контура. Выражение для тока

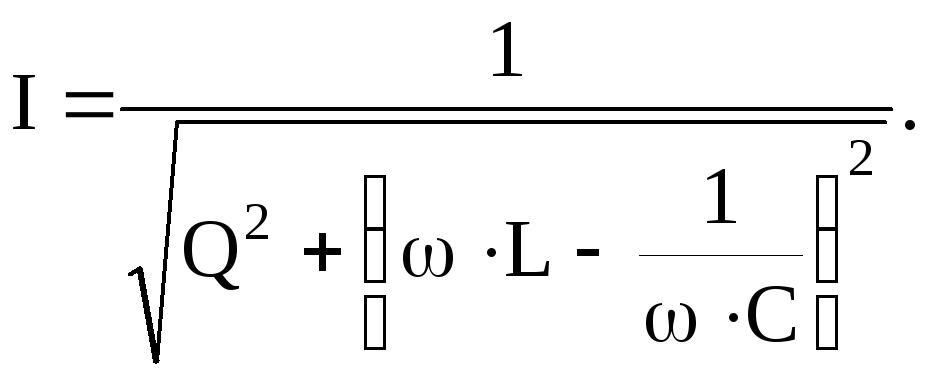
Выполним ряд преобразований последней формулы

;

.

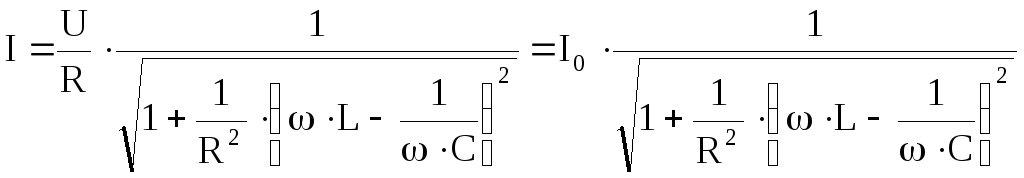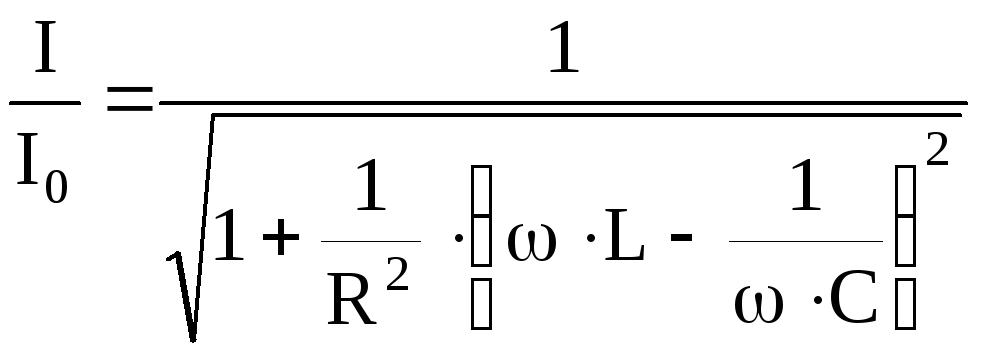Проведем горизонтальную прямую на уровне .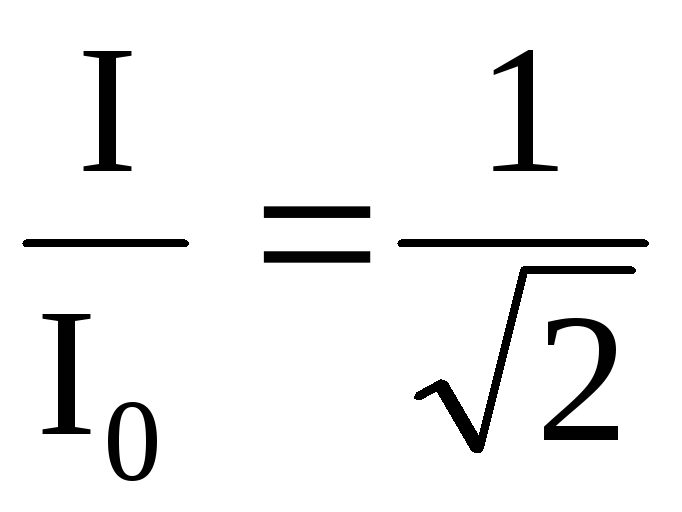

Отметим значения емкости C₁ и С₂.

Далее сделаем ряд очевидных выкладок. Выразим добротность Q через значения

емкости С₁ и С₂. Запишем

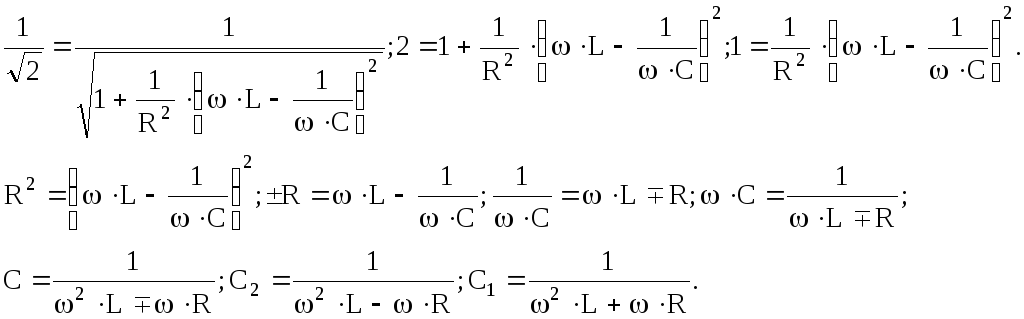
Найдем сумму и разность емкостей

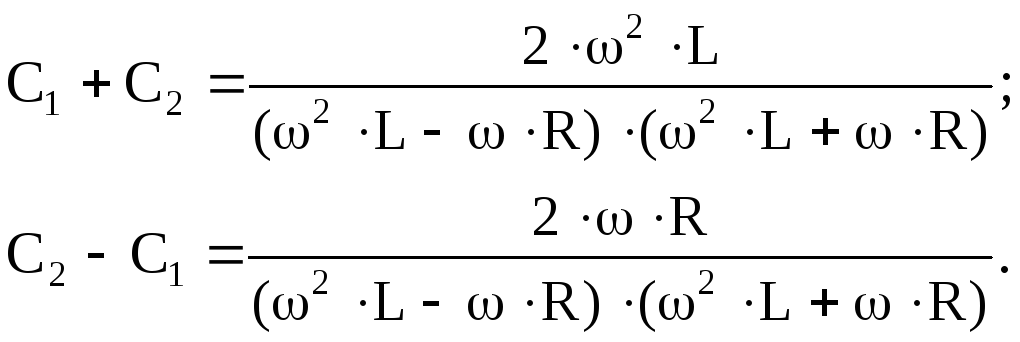
Запишем отношение .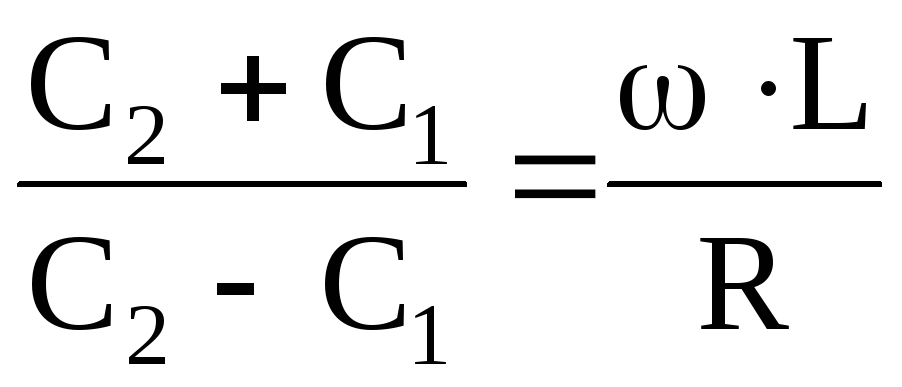

Напомним, что добротность контура определяется превышением напряжения на индуктивном (или емкостном) сопротивлении при резонансе над напряжением всей цепи (или напряжением на активном сопротивлении), т. е.

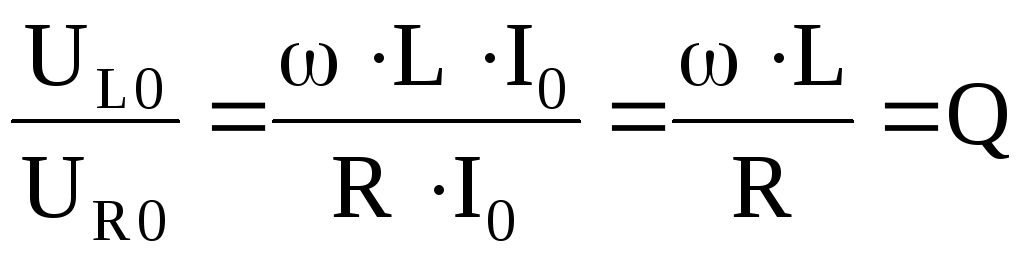
Таким образом,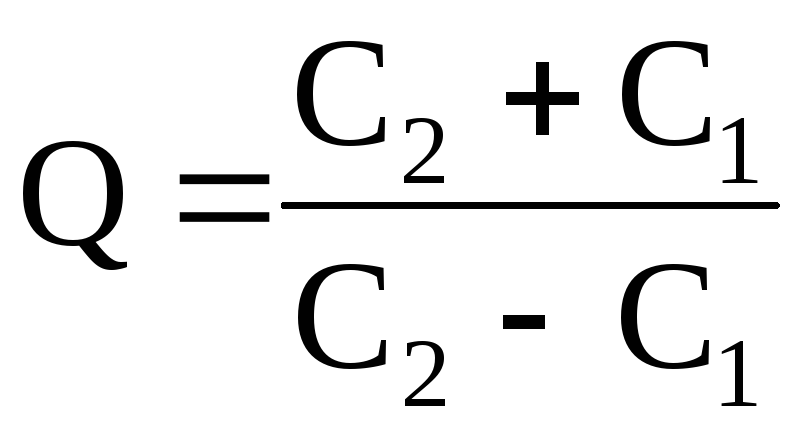

Кроме этого результата, представляется возможным получить значения параметров катушки индуктивности (L и R)

.

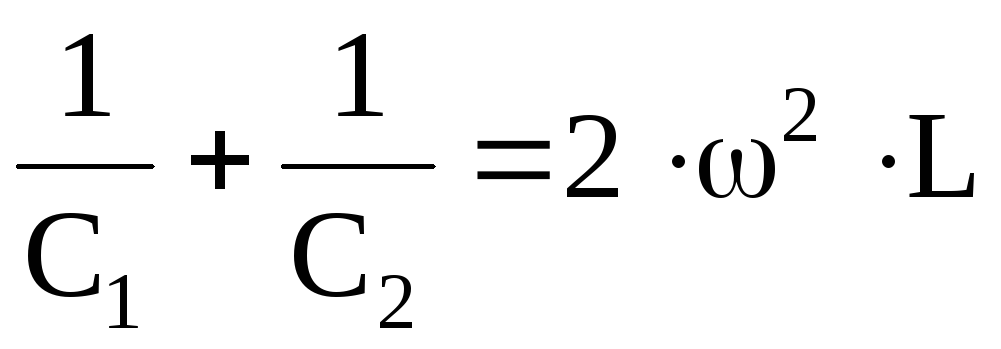Откуда ;.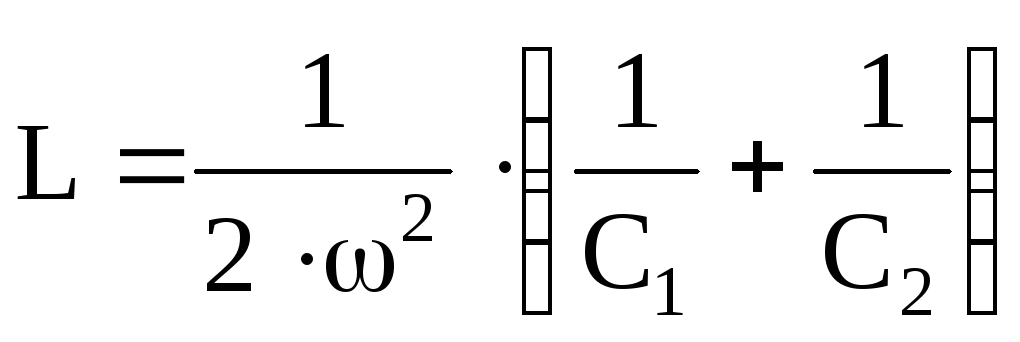

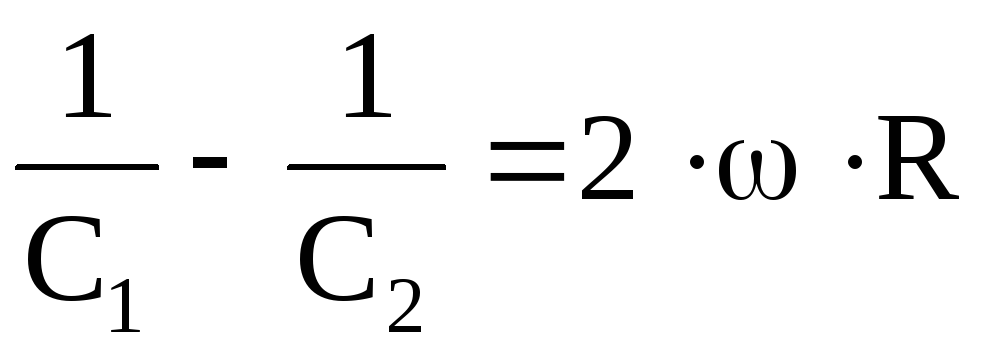Откуда .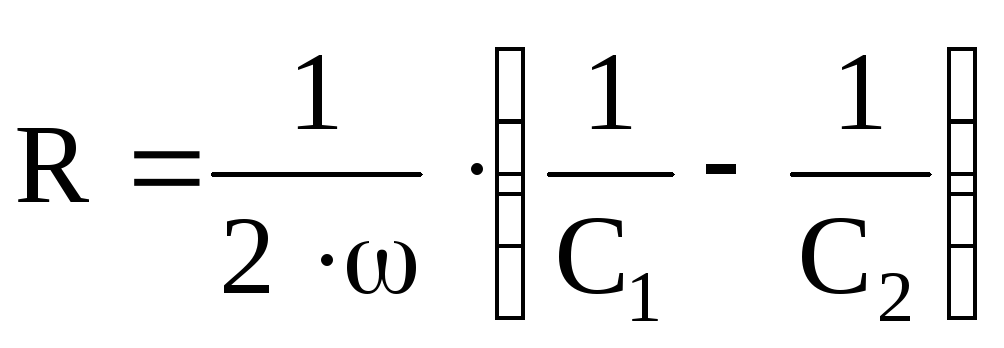

Величина емкости С₀, при которой наступает резонанс, определится так:

; ;;.

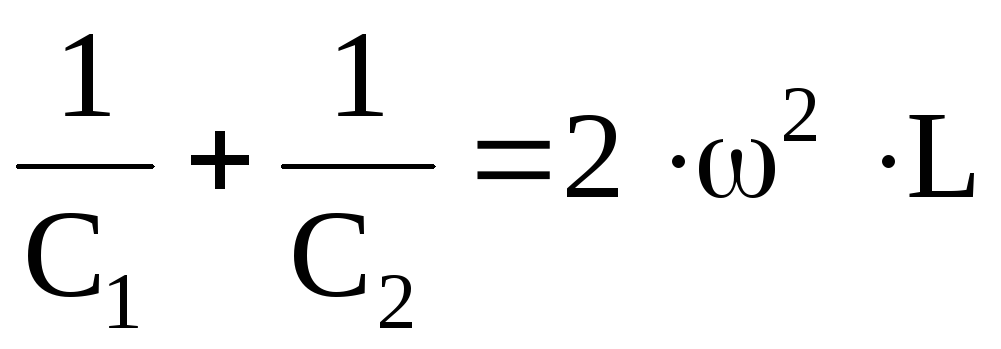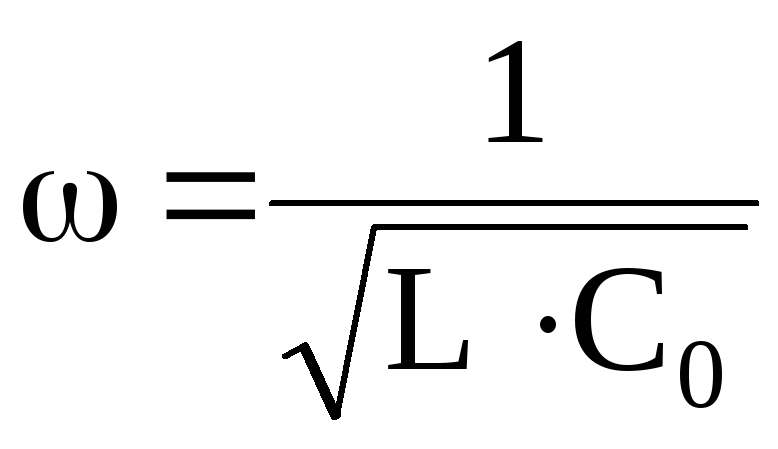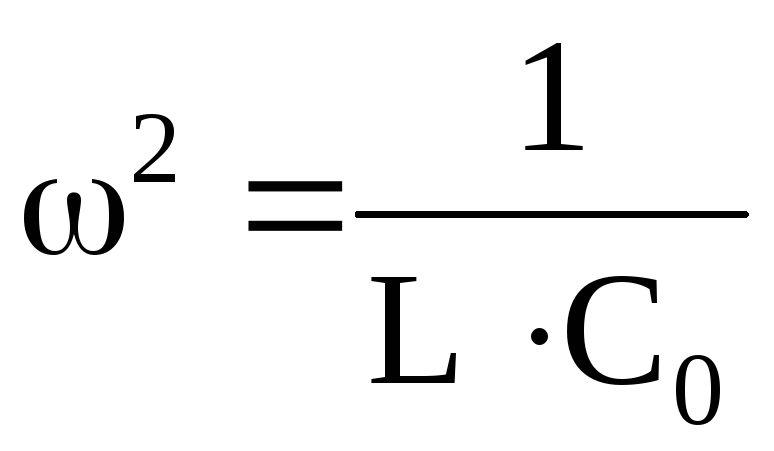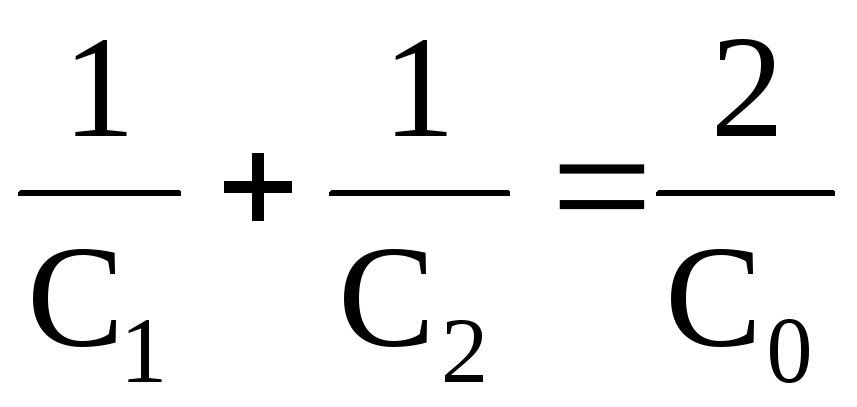Откуда .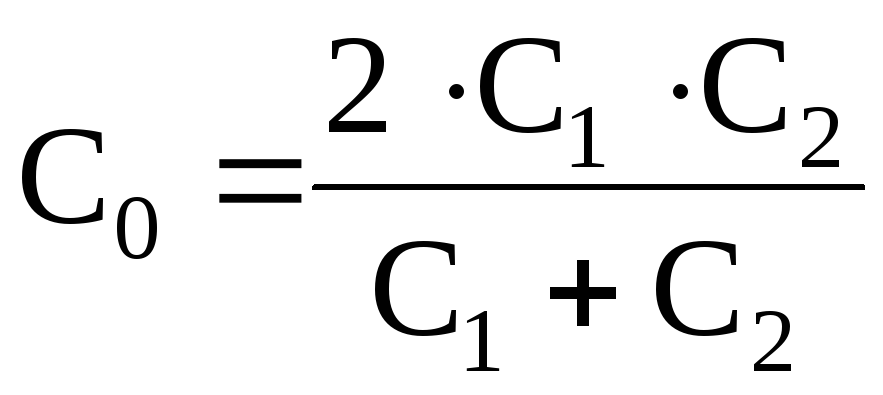

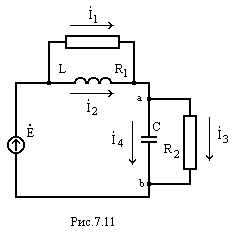
Резонанс напряжений может наблюдаться в схеме, показанной на рис. 7.11.

Входное сопротивление такой схемы

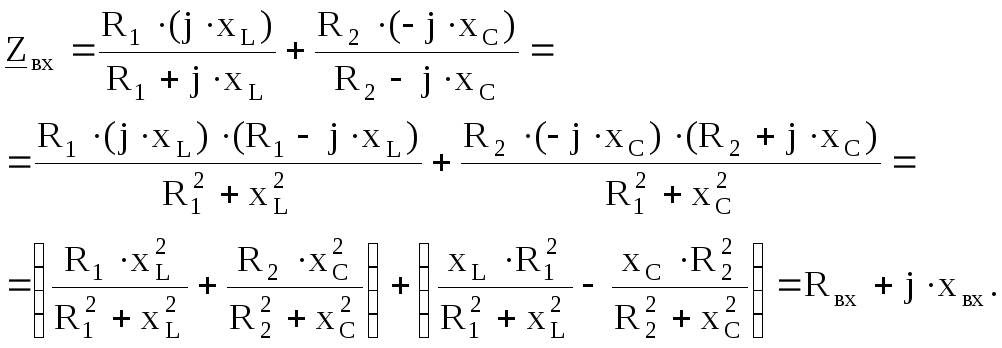
При резонансе реактивная составляющая входного сопротивления должна быть равна нулю, т. е.

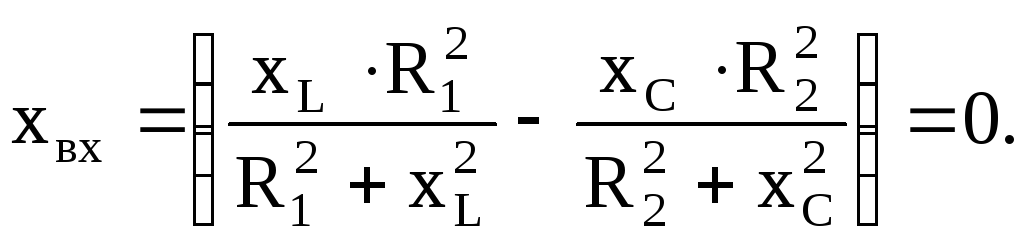
Резонансная частота, добротность последовательного контура

⇐ ПредыдущаяСтр 3 из 7Следующая ⇒

Выведем формулу резонансной частоты:

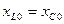
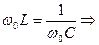
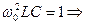
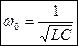
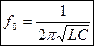
Вывод: резонанс напряжений наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура .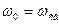

Настроить контур в резонанс можно:

1) изменяя L или C, при этом подгоняем частоту собственных колебаний под частоту питающего напряжения;

2) можно изменять частоту питания, подгоняя её под частоту собственных колебаний контура.

Т. к. 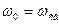, то можно записать, что .

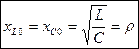Сопротивление катушки и конденсатора на резонансной частоте равно характеристическому сопротивлению контура.

Формула добротности:

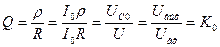
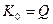
Вывод:добротность в последовательном контуре показывает, во сколько раз напряжение на выходе больше, чем на входе в момент резонанса.

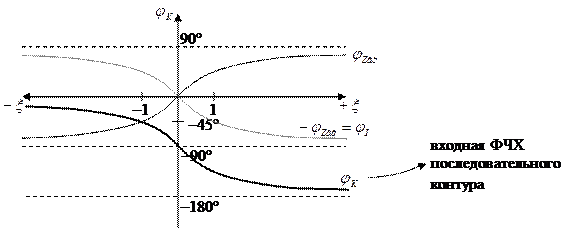
Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной

Расстройка — отклонение частоты от резонансной. Различают:

1) Абсолютная расстройка — разность текущей частоты и резонансной:

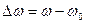
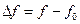
Расстройка может и положительной и отрицательной.

2) Относительная расстройка — отношение абсолютной расстройки к резонансной частоте:

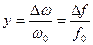
3) Обобщённая расстройка — отношение реактивного сопротивления x к резистивному:

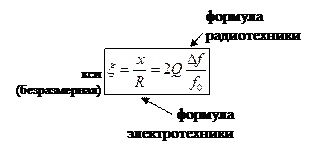
Обычно входные характеристики строят от расстройки.

 

Входные АЧХ и ФЧХ последовательного контура

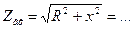, где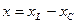

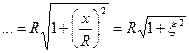
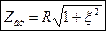— формула входной АЧХ последовательного контура

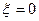
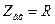
(на резонансной частоте все расстройки равны 0)

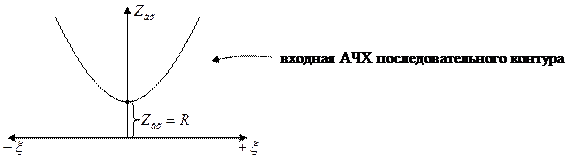
Вывод: на резонансной частоте сопротивление последовательного контура имеет наименьшее значение 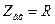. По мере увеличения расстройки сопротивление контура возрастает.

ФЧХ:

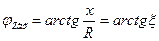
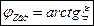— формула входной ФЧХ последовательного контура

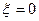
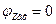
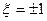
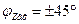
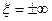
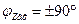
Вывод: на резонансной частоте последовательный контур имеет чисто активное сопротивление: 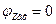. На частотах меньше резонансной характер сопротивления активно-емкостной, т. к. 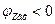. На частотах больше резонансной характер сопротивления активно-индуктивный: .

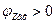Передаточные АЧХ и ФЧХ последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы

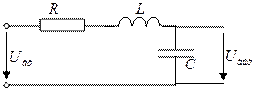
Обычно спектр частот радиосигнала составляет 2-3% от несущей частоты, поэтому можно приблизительно считать

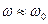
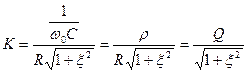
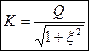— передаточная АЧХ последовательного контура в абсолютных координатах

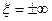
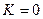
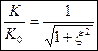
Вывод: на резонансной частоте коэффициент передачи последовательного контура максимальный: .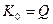

ФЧХ:

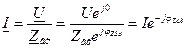
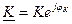
На выходе стоит конденсатор, поэтому напряжение выхода отстаёт от тока на 90°. Угол 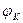практически равен углу выходного напряжения, поэтому характеристику 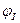сдвигаем на 90° вниз:

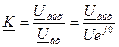
Передаточная ФЧХ имеет линейный участок при расстройках от до .

 

Прохождение через колебательный контур сигналов негармонической формы. Избирательные свойства последовательного контура

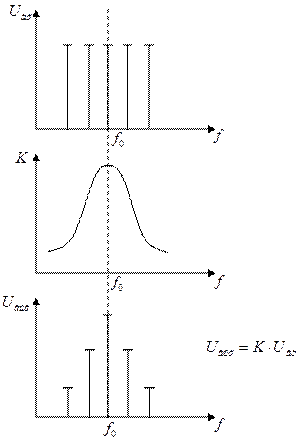
Избирательность — способность цепи различать сигналы по частоте. Подадим на последовательный контур сигнал, который состоит из 5 гармоник одинаковой амплитуды.

На выходе амплитуда сигнала не резонансной частоте будет максимальной, т. к. 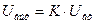, и на этой частоте самый большой коэффициент передачи.

Вывод: последовательный контур обладает избирательностью по напряжению. Он выделяет сигнал резонансной частоты.

 

Полоса пропускания контура — область частот, на границах которой модуль комплексного коэффициента передач уменьшается в 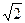раз по сравнению с резонансным.

На уровне полосы пропускания коэффициент обозначается :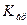

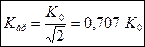
Нарисуем передаточную характеристику :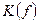

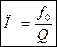
Вывод: чем выше добротность, тем уже полоса пропускания контура.

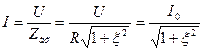
1)

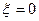
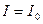
2)

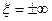
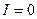
Кривые тока и напряжения такого вида называются резонансными.

Примечание:

При малых расстройках напряжение на катушке и конденсаторе можно рассчитать по формуле:

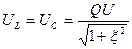
Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность

Контур называется параллельным, если катушка, конденсатор и источник соединены параллельно.

В параллельном контуре может возникнуть резонанс токов, когда напряжение и ток на входе совпадают по фазе: .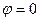

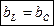— условие резонанса токов

Проводимость индуктивная равна проводимости емкостной.

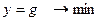
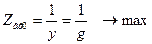
При резонансе токов сопротивление параллельного контура максимально.

 

Свойства цепи при резонансе токов:

1. Ток в момент резонанса:

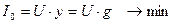
При резонансе токов общий ток минимальный.

2. На практике ,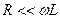

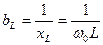
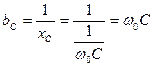
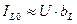
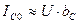
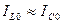
При резонансе токов токи ветвей приблизительно равны.

3. Построим векторную диаграмму для резонанса токов:

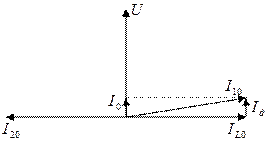
Если бы (контур идеальный), то токи , и общий ток был бы равен 0, но т. к. есть небольшое , то существует активная составляющая тока (маленькая) и общий ток равен этой активной составляющей.

4. Выведем формулу резонансной частоты. Для этого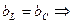

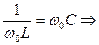
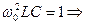
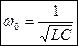
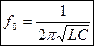
Вывод: резонанс токов наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура.

Получить резонанс токов можно, изменяя L или C, или частоту питающего напряжения.

5. Энергетический процесс при резонансе токов такой же, как и при резонансе напряжений:

 

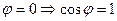
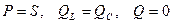
Рассчитаем токи в момент резонанса:

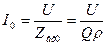
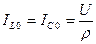
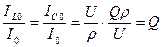
Вывод: добротность в параллельном контуре показывает, во сколько раз токи ветвей больше общего тока в момент резонанса, поэтому это явление и называется резонанс тока.

 



6. Добротность и полоса пропускания резонансной цепи | 6. Резонанс | Часть2

6. Добротность и полоса пропускания резонансной цепи

Добротность и полоса пропускания резонансной цепи

Добротность (Q) резонансной цепи характеризует ее качество. Более высокое значение этого показателя соответствует более узкой полосе пропускания (что весьма желательно для многих схем). Если говорить проще, то добротность представляет собой отношение энергии, накопленной в реактивном сопротивлении цепи, к энергии, рассеиваемой активным сопротивлением этой цепи:

 

 

Данная формула применима к последовательным резонансным цепям, а также к параллельным резонансным цепям, если сопротивление в них включено последовательно с катушкой индуктивности. Действительно, в практических схемах нас часто беспокоит сопротивление катушки индуктивности, которое ограничивает добротность. Заметьте: Некоторые учебники в формуле «Q» для параллельных резонансных схем меняют местами X и R. Это верно для большого значения R, включенного параллельно с C и L. Наша формула верна для небольшого значения R, включенного последовательно с L.

Практическое применение добротности (Q) заключается в том, что напряжение на L или С в последовательной резонансной цепи в Q раз больше общего приложенного напряжения. В параллельной резонансной цепи ток через L или С в Q раз больше общего приложенного тока.

 

Последовательные резонансные цепи.

 

Резонанс последовательной LC цепи выражается в том, что полный импеданс этой цепи становится наименьшим и равным активному сопротивлению  (которое имеет сравнительно небольшую величину), а ток становится максимальным. Условием резонанса является равенство индуктивного и емкостного сопротивлений X_L = X_C. Когда частота генератора больше частоты контура, индуктивное сопротивление преобладает над емкостным и контур представляет для генератора сопротивление индуктивного характера. Если частота генератора меньше частоты контура, то емкостное сопротивление больше индуктивного и контур для генератора является сопротивлением емкостного характера.

 

 

Ток при резонансе имеет максимальное значение, а импеданс — минимальное. Величина тока определяется величиной сопротивления. На частоте, выше или ниже резонансной, импеданс увеличивается.

 

 

Пиковое значение тока при резонансе можно изменить путем подбора величины последовательного резистора, которая, в свою очередь, изменяет добротность. Все эти значения оказывают влияние на ширину полосы пропускания. Контур с низким сопротивлением и высокой добротностью имеет более узкую полосу пропускания, чем контур с высоким сопротивлением и низкой добротностью. Зависимость полосы пропускания контура от его резонансной частоты и добротности определяется следующей простой формулой:

 

 

 

Ширина полосы пропускания обычно определяется на уровне 0,707 от максимальной амплитуды тока. Уровню 0,707 соответствуют точки половинной мощности, равные P = I²R, (0,707)² = (0,5)

 

 

           Ппр = Δf = fв-fн = fc/Q 
           Где: fв = верхняя граница полосы пропускания,  
fн = нижняя граница полосы пропускания 
 
           fн = fc - Δf/2 
           fв = fc + Δf/2
           Где:  fc = резонансная частота

 

На представленном выше графике 100% тока — это 50мА. Уровню 70,7% соответствует величина тока 0,707(50мА) = 35,4 мА. Верхняя и нижняя границы полосы пропускания составляют 355 и 291 Гц соответственно. Ширина полосы пропускания равна 64 Гц, а точки половинной мощности составляют ± 32 Гц от центра резонансной частоты:

 

           Ппр = Δf = fв-fн = 355-291 = 64 
           fн = fc - Δf/2 = 323-32 = 291 
           fв = fc + Δf/2 = 323+32 = 355 

 

Поскольку П_пр = f_c/Q:

 

           Q = fc/Ппр = (323 Гц)/(64 Гц) = 5

 

Параллельные резонансные цепи

 

Резонанс параллельной LC цепи выражается в том, что полный импеданс этой цепи (между точками разветвления) становится максимальным, а ток принимает минимальное значение. Условием резонанса, как и в последовательной LC цепи,  является равенство индуктивного и емкостного сопротивлений X_L = X_C. Когда частота генератора больше частоты контура, емкостное сопротивление преобладает над индуктивным и контур представляет для генератора сопротивление емкостного характера. Если частота генератора меньше частоты контура, то индуктивное сопротивление больше емкостного и контур для генератора является сопротивлением индуктивного характера.

 

 

Импеданс при резонансе имеет максимальное значение, но на частотах, выше или ниже резонансной, он уменьшается. Поскольку напряжение пропорционально импедансу (U = IZ), при резонансе оно также имеет максимальное значение.

 

 

Низкая добротность (Q), обусловленная высоким сопротивлением (последовательно с катушкой индуктивности), производит низкий пик с широкой полосой пропускания. И наоборот, высокая добротность, обусловленная низким сопротивлением, производит высокий пик с узкой полосой пропускания. Высокая добротность достигается применением катушек индуктивности имеющих большой диаметр и малое сопротивление провода.

 

 

Ширина полосы пропускания кривой параллельного резонанса измеряется между точками половинной мощности. Поскольку мощность пропорциональна U², этим точкам соответствует уровень 70,7% от максимальной амплитуды напряжения ^{((0,707)2 = 0,5). Так как напряжение пропорционально импедансу, мы можем воспользоваться графиком импеданса.}

 

 

На представленном выше графике 100% сопротивления — это 500 Ом. Уровню 70,7% соответствует величина сопротивления 0,707(500) = 354 Ом. Верхняя и нижняя границы полосы пропускания составляют 343 и 281 Гц соответственно. Ширина полосы пропускания равна 62 Гц, а точки половинной мощности составляют ± 31 Гц от центра резонансной частоты:

 

           Ппр = Δf = fв-fн  = 343-281 = 62 
           fн = fc - Δf/2 = 312-31 = 281 
           fв = fc + Δf/2 = 312+31 = 343 

           Q = fc/Ппр = (312 Гц)/(62 Гц) = 5

Борьба за добротность | Шаг за шагом

Повышения добротности (как правило, нам нужны контуры с высокой добротностью) — довольно сложная задача, которая в основном решается путем уменьшения потерь в контурной катушке.

Индуктивность контурных катушек, применяемых на коротких и ультракоротких волнах (лист 81), очень мала и составляет единицы и даже десятые доли микрогенри (лист 66). Катушки такой маленькой индуктивности содержат лишь несколько витков сравнительно толстого (диаметр 0,6-1,2 мм) медного провода, как правило, без всякой изоляции или покрытого тонким слоем эмали (провод ПЭ, лист 79). Диаметр провода в миллиметрах указан в его названии цифрой, которая следует сразу же после букв, определяющих марку провода.

Для уменьшения потерь в таких катушках иногда применяют провод, покрытый тонким, толщиной в несколько микрон, слоем серебра. Дело в том, что при прохождении переменного тока по проводнику наблюдается интересное явление, получившее название поверхностного эффекта (лист 80) или скин-эффекта («скин» в переводе на русский язык значит «кожа»). Сущность этого явления состоит в том, что переменный ток не распределяется равномерно по всему проводнику, а проходит лишь по наружному его слою. Чем выше частота, тем сильнее проявляется поверхностный эффект, тем тоньше наружный слой проводника, по которому проходит ток. Поэтому для уменьшения потерь в высокочастотных катушках их не нужно целиком делать из серебряного провода (серебро, как известно, лучше всех других металлов пропускает ток, то есть обладает наименьшим удельным сопротивлением — лист 16), а достаточно применить посеребренный провод.

Катушки КВ и УКВ контуров выполняют на керамических или полистироловых каркасах, причем шаг намотки часто в полтора-два раза превышает диаметр провода, то есть между соседними витками имеются значительные просветы. Это, между прочим, и хорошо и плохо. Хорошо потому, что, сближая либо раздвигая соседние витки, можно подгонять индуктивность катушки, а плохо потому, что при недостаточно тугой намотке или недостаточно жестком каркасе витки сместятся и индуктивность катушки изменится.

Индуктивность катушек, применяемых в колебательных контурах на длинных и средних волнах (лист 82), составляет сотни и тысячи микрогенри. Такие катушки обычно содержат несколько десятков и даже сотен витков и выполняются из тонкого (диаметром 0,1-0,2 мм) медного провода. Чаще всего используют провод марки ПЭ — провод эмалированный или ПЭШО — провод эмалированный в шелковой оплетке. Намотку производят на каркасах из картона, эбонита, полистирола и других изоляционных материалов, причем всю обмотку часто делят на несколько секций, что позволяет несколько снизить потери. В ряде фабричных приемников, особенно старых выпусков, широко применялась намотка «Универсаль», выполняемая на специальных станках. Намотка «Универсаль» характеризуется тем, что провод укладывается ровными рядами, несколько «перекрещенными», то есть повернутыми один относительно другого. В настоящее время намотка «Универсаль» применяется редко — вместо нее производят намотку «внавал», укладывая провод между двумя щечками.

Раньше для намотки ДВ и СВ катушек широко применялся провод литцентрат (ЛЭШО — литцентрат эмалированный в шелковой оплетке), состоящий из нескольких тонких (диаметром 0,05-0,07 мм), изолированных друг от друга медных проводов. Общая поверхность всех этих проводов получается довольно большой, и поэтому на высоких частотах сопротивление литцентрата оказывается несколько меньше, чем у обычного провода такого же диаметра. Следует отметить, что в случае применения литцентрата необходимо тщательно зачищать и пропаивать все его проводники. Одна непропаянная жилка может во много раз ухудшить добротность катушки.

Несмотря на то что литцентрат позволяет заметно уменьшить потери в катушке, в настоящее время он почти не применяется. Уменьшение потерь в катушке получают более эффективным и в то же время более простым и дешевым способом — путем применения ферромагнитных сердечников (лист 83).

Как уже говорилось, ферромагнитный сердечник резко увеличивает индуктивность катушки. Поэтому, если изготовить две катушки с одинаковой индуктивностью — одну из них с сердечником, а другую без него, то у катушки с сердечником будет намного меньше витков, и поэтому сопротивление ее тоже будет меньше (сопротивление проводника зависит от его длины: чем длиннее проводник, тем больше его сопротивление).

Для катушек, по которым течет переменный ток, нельзя использовать сердечник из целого куска стали, так как изменяющееся магнитное поле катушки наведет в таком сердечнике вихревой ток, потеряв на это большую часть энергии. Таким образом, сердечник, с помощью которого мы хотели уменьшить потери в катушке, сам становится источником потерь, которые возрастают с увеличением частоты переменного тока в контуре.

Для борьбы с этим видом потерь сердечники низкочастотных катушек (то есть катушек, по которым проходит ток низкой частоты) собирают из отдельных, изолированных друг от друга пластин. Ток, наведенный в каждой такой пластине, создает свое магнитное поле, которое… ослабляет токи в соседних пластинах. В результате токи в пластинах сердечника оказываются очень слабыми, и он «отбирает» у катушки мало энергии. Чем тоньше пластины, из которых собран сердечник, тем меньше потери в нем.

В высокочастотных катушках собирать сердечник из тонких пластин уже оказывается недостаточным. Сердечники для этих катушек прессуют из ферромагнитного порошка, смешанного со специальными связующими веществами (бакелитовый лак, полистирол и др.). Связующее вещество обволакивает отдельные крупинки ферромагнитного порошка и изолирует их друг от друга. Спрессованные подобным образом ферромагнитные порошки плохо проводят электрический ток, и поэтому они получили название магнитодиэлектриков.

Для изготовления сердечников высокочастотных катушек чаще всего используются следующие магнитодиэлектрики: магнетит, альсифер, карбонильное железо и ферриты. Наиболее широко в последнее время используются ферриты, большинство которых увеличивает индуктивность катушки намного сильней, чем другие магнитодиэлектрики. Обычно сердечник выполняют в виде стержня с резьбой, который ввинчивается в каркас катушки. Выпускаются также сердечники типа СБ (сердечник броневой), имеющие форму закрытой чашки (горшка), внутрь которой вставляется сама катушка (лист 83). В горшкообразном сердечнике также имеется подвижной стерженек, снабженный резьбой. Применение ввинчивающихся сердечников имеет одно большое достоинство: перемещая такой сердечник внутри катушки, можно в значительных пределах менять ее индуктивность, а это часто бывает очень важно.

Применение сердечников из магнитодиэлектриков позволяет в несколько раз уменьшить сопротивление потерь R_к и, следовательно, повысить добротность контура Q. Другие пути уменьшения потерь — это применение в качестве С_к керамических, слюдяных и воздушных конденсаторов, обладающих малыми потерями; монтаж высокочастотных цепей короткими проводами; использование для каркаса катушки материала с малыми потерями, а также ряд других мер. В любительских условиях не всегда имеется возможность да и не всегда есть смысл принимать все возможные меры для уменьшения потерь, и поэтому часто приходится мириться с несколько пониженной добротностью контуров.

Добротность Q контура зависит не только от потерь в нем, но и от соотношения между индуктивностью L_к и емкостью С_к; чем больше L_к и чем меньше С_к, тем выше добротность. С другой стороны, из формулы для определения _f0 (рис. 47, лист 73) видно, что одну и ту же частоту собственных колебаний можно получить при различных соотношениях L_к и С_к. Иными словами, если емкость С_к уменьшить, например, в 10 раз и во столько же раз увеличить индуктивность L_к, то произведение L_кС_к останется неизменным, а значит, не изменится и частота f₀.

Из всего этого можно сделать простой вывод: если хочешь повысить добротность контура, уменьшай его емкость и увеличивай индуктивность (в одно и то же число раз, иначе изменится частота!).

Если посмотреть на схему самых различных приемников и передатчиков, то можно увидеть, что в контурах почти всегда используются конденсаторы, емкость которых не превышает нескольких сотен пикофарад. А ведь если бы соотношение между L_к и С_к не влияло на величину добротности, то мы, пожалуй, еще подумали, каким путем легче построить контур — применяя громоздкую катушку большой индуктивности и конденсатор малой емкости или же используя конденсатор емкостью в несколько микрофарад и простейшую катушку, содержащую всего два-три витка.

В заключение необходимо отметить, что в погоне за высокой добротностью нельзя беспредельно увеличивать индуктивность и уменьшать емкость контура. Здесь существует ряд ограничений, разбирать которые мы не имеем возможности, так как это отвлечет нас от основной задачи.

Итак, мы выяснили, что в контуре, состоящем из конденсатора и катушки, могут возникнуть собственныеэлектромагнитные колебания и что постепенно эти колебания затухают. Чем меньше потери энергии в контуре, то есть чем выше его добротность, тем медленнее затухают в нем собственные колебания.

Расчет добротности контура

8. По резонансным кривым, снятым экспериментально, определите частоты f₁ и f₂, соответствующие границам полосы пропускания контура и их разность f  f₂  f₁. Результаты измерений занесите в табл. 2.

Таблица 2

Сопротивление контура, Ом	R1	R2
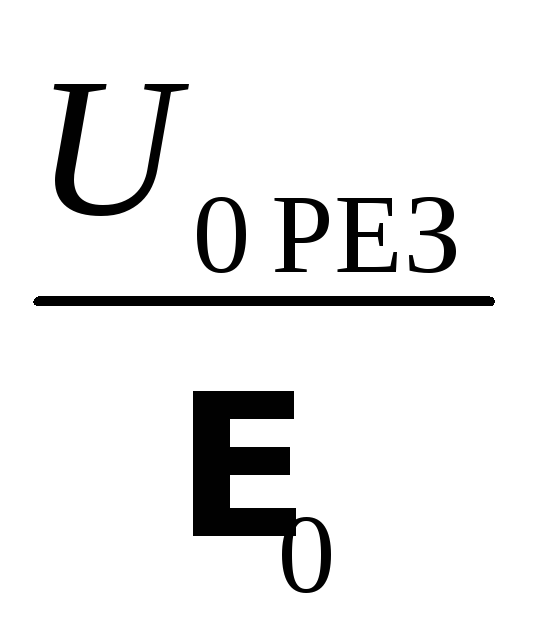
U0 РЕЗ, В
0,7U0 РЕЗ, В
fРЕЗ, МГц
f1, МГц
f2, МГц
f, МГц
Q1
E0, В
Q2
QСР(Q1  Q2)/2
QТЕОРQ

9. Вычислите значения добротности Q₁ и Q₂ по формулам (10) и (12) для различных значений сопротивлений контура. Результаты занесите в табл. 2.

10. Определите среднее арифметическое значение добротности при различных фиксированных значениях сопротивлений контура:

Q_СР  (Q₁  Q₂)/2.

11. Оцените относительную погрешность определения добротности по косвенным измерениям:

Q₁     ,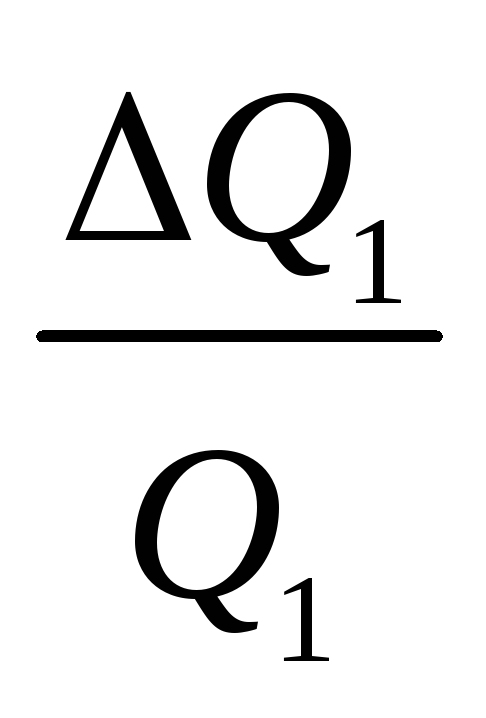

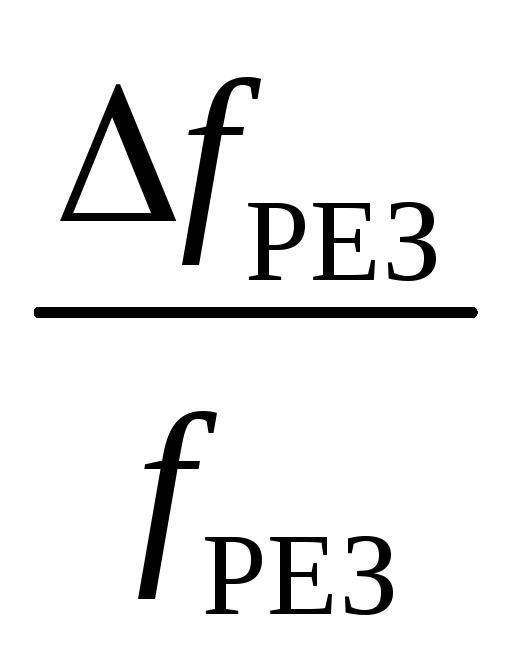
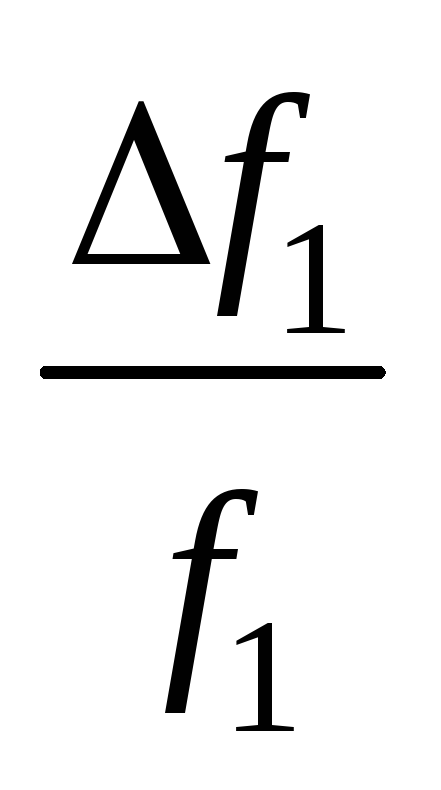
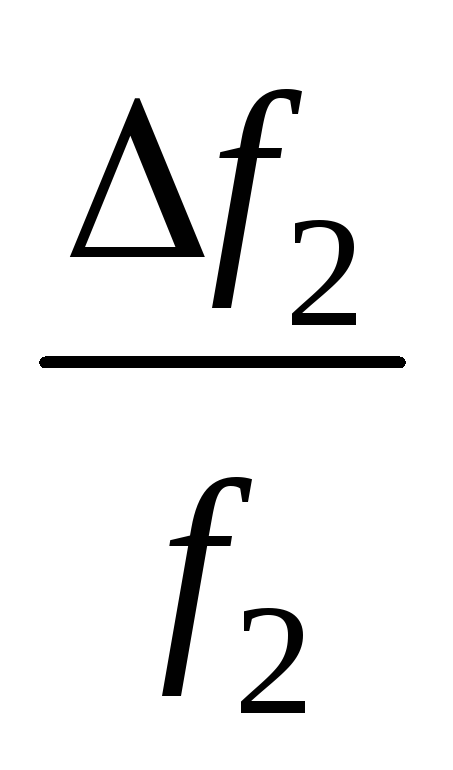Q₂   ,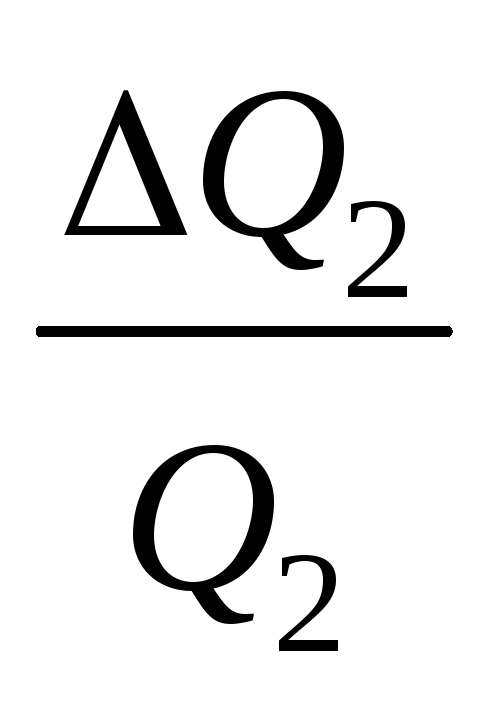

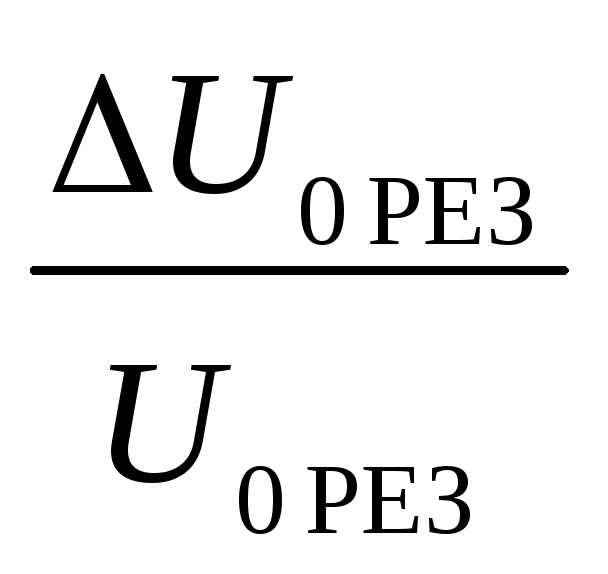
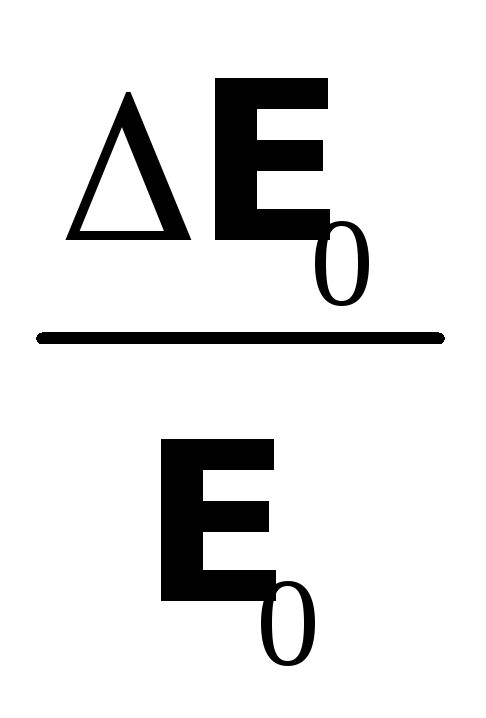где f_РЕЗ, f₁, f₂, U_{0 РЕЗ}, E₀ – ошибки в определении соответствующих значений f_РЕЗ, f₁, f₂, U_{0 РЕЗ}, E₀.

Вычислите теоретическое значение добротности контура по формуле (9) и сравните его с результатами расчета по формулам (10) и (12). Объясните возможные причины расхождения результатов измерений и расчета.

Контрольные вопросы

1. Какие колебания называются вынужденными?

2. В чем заключается явление резонанса?

3. От чего зависит добротность контура?

4. Перечислите методы определения добротности контура.

5. Дайте определение полосы пропускания контура.

6. Чему равна частота вынуждающей э. д. с. в момент резонанса?

7. Каким образом снимается резонансная кривая в данной работе?

Список литературы

3. Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.

4. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

Работа 129

Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа

Цель работы. Изучение с помощью электронного осциллографа электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление; изучение условий возникновения затухающих колебаний в контуре; расчет основных физических величин, характеризующих эти колебания.

Введение

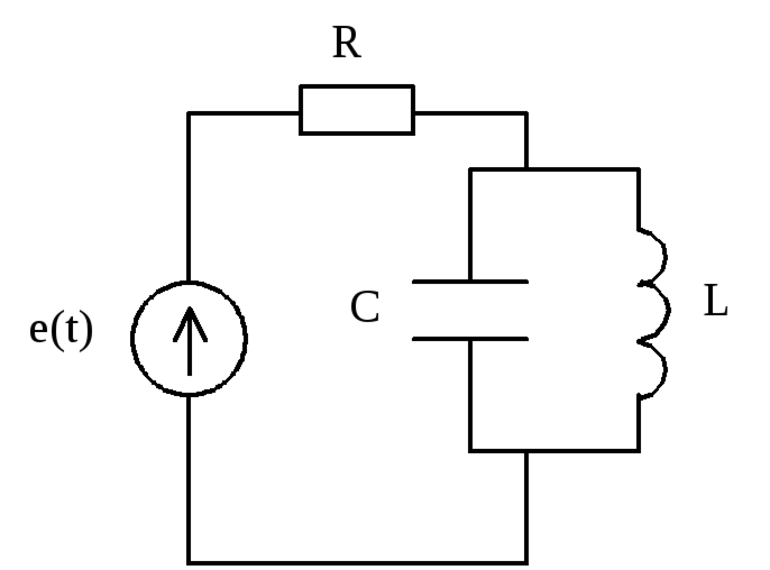
На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, содержащего последовательно соединённые конденсатор емкостью C, катушку индуктивностью L и активное сопротивление R.

Е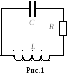сли в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э.д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.

Исследуем характер колебаний, возникающих в идеализированном колебательном контуре в отсутствие сопротивления R  0 при сообщении конденсатору заряда q₀.

Вначале энергия электрического поля конденсатора емкостью C равна:

W_C q₀²/2C  CU₀²/2,

где U₀  q₀/С – максимальная разность потенциалов на обкладках конденсатора. Под действием электрического поля начинается движение зарядов и конденсатор разряжается. В контуре возникает электрический ток:

I(t)   dq(t)/dt, (1)

где dq(t) – изменение заряда на обкладках конденсатора. Знак минус показывает, что возникновение тока сопровождается уменьшением заряда на обкладках конденсатора (dq < 0).

Энергия электрического поля конденсатора уменьшается, переходя в энергию магнитного поля, создаваемого током в катушке. Возрастание тока (dI > 0) в катушке индуктивностью L приводит к появлению в ней электродвижущей силы (э. д. с.) самоиндукции Et), препятствующей изменению тока (E < 0):

E(t)  – L(dI/dt).

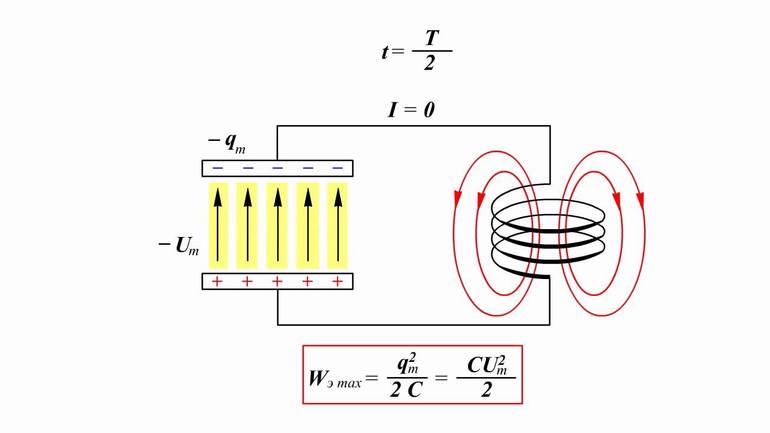
При полном разряде конденсатора его электрическое поле исчезает, а ток в контуре, наоборот, достигает максимального значения I₀. Максимального значения достигает и энергия магнитного поля в катушке:

W_L  LI₀²/2.

С этого момента начинается перезарядка конденсатора под действием э. д. с. самоиндукции. Ток в контуре начинает убывать, вследствие чего э. д. с. самоиндукции изменяет знак, препятствуя убыванию тока. Энергия магнитного поля катушки уменьшается, а энергия электрического поля конденсатора растет, стремясь к максимальному значению, которому соответствует полная перезарядка конденсатора. В тот момент времени мгновенные значения электрического тока и энергии магнитного поля обращаются в нуль. Далее процесс повторяется в обратном порядке. В контуре устанавливаются незатухающие электромагнитные колебания.

Интервал времени между двумя последовательными максимальными значениями колеблющейся величины называется периодом колебаний T.

Заметим, что описанные выше колебания происходили бы бесконечно долго лишь при отсутствии испускания таким контуром электромагнитного излучения.

Если колебательный контур содержит активное сопротивление R, то при протекании по нему тока часть общей энергии контура W выделяется в виде тепла:

Q = W_R  I²Rt.

При этом уменьшаются с течением времени амплитудные значения тока в контуре и разности потенциалов на обкладках конденсатора. Колебания затухают.

Временная зависимость разности потенциалов на обкладках конденсатора U(t)  ₁ ₂ наблюдается в данной работе на экране осциллографа. Эту зависимость можно получить теоретическим путем, используя закон Ома для участка цепи, содержащей э. д. с. Для мгновенных значений токов и напряжений в таком контуре закон Ома запишется в виде:

IR  ₁ – ₂  E  U – L(dI/dt). (2)

Преобразуем это уравнение, используя формулу (1) и соотношение q  CU. Тогда уравнение (2) примет вид:

LC(d²U/dt²)  RC(dU/dt)  U  0. (3)

Разделив обе части уравнения (3) на LC и введя обозначения

R/2L = , 1/LC  ₀²,

где ₀ называется собственной циклической (круговой) частотой контура, а  – коэффициентом затухания, получим дифференциальное уравнение:

d²U/dt²  2(dU/dt)  ₀²U  0, (4)

решение которого дает искомую зависимость U(t).

Следует отметить, что аналогичные дифференциальные уравнения могут быть получены для различного рода механических, электромеханических и других колебательных систем, в которых отсутствуют внешние вынуждающие воздействия, а силы сопротивления при малых скоростях движения (скоростях изменения параметра системы, совершающей колебания) линейно зависят от скорости.

При этом энергия, внесенная в сиcтему извне, непрерывно уменьшается в процессе колебаний, переходя, в конечном счете, в тепловую энергию. Уравнение (4) есть линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Для частного случая, когда  < ₀, его решение имеет вид:

U(t)  U₀e^βtcos(t  ₀), (5)

где ₀ – начальная фаза колебаний;  – циклическая частота затухающих колебаний:

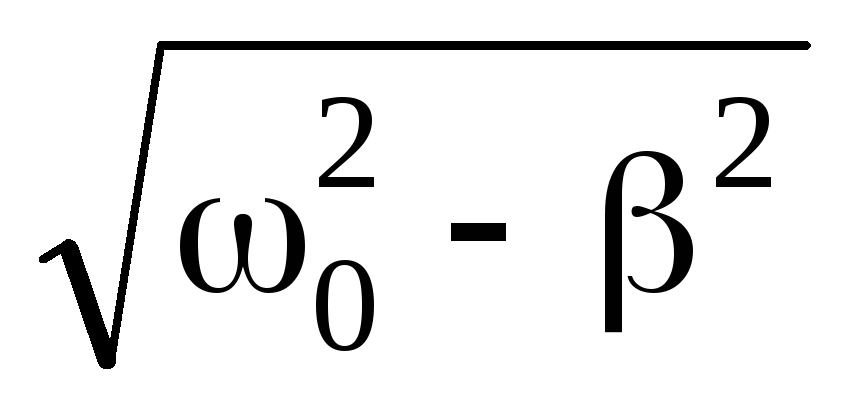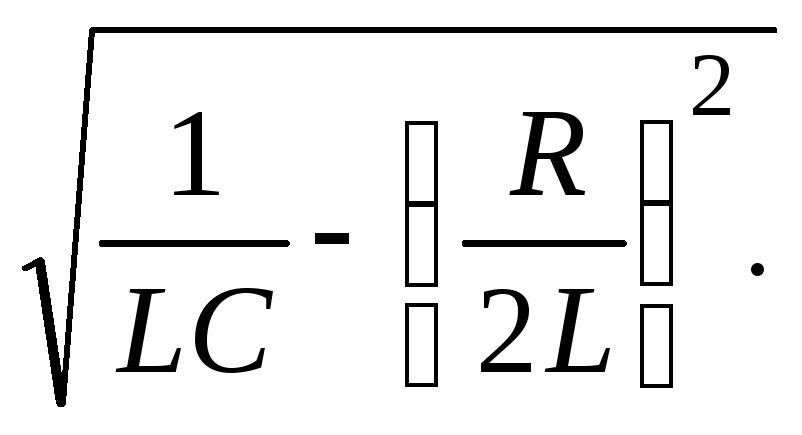= (6)

На рис. 2 приведены примеры графиков зависимости U(t) для различных типов колебаний в контуре.

Выражение (5) описывает затухающий колебательный процесс (рис. 2б) с периодом колебаний

T 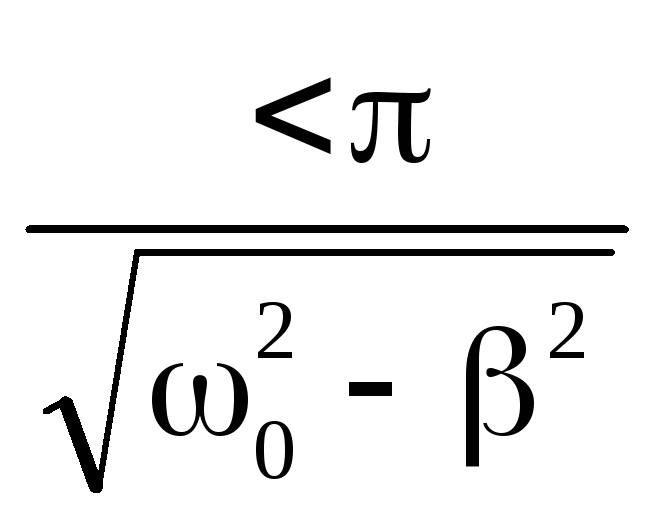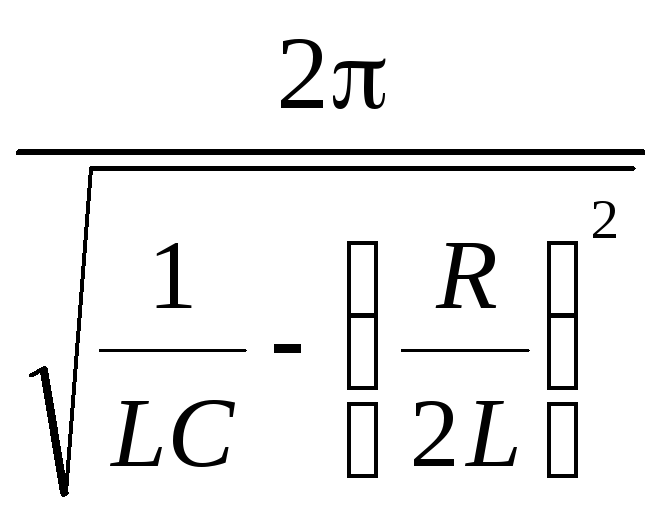 . (7)

Амплитудой затухающих колебаний называют величину

A(t)  U₀e^t, (8)

где U₀ – максимально возможное значение амплитуды напряжения:

U₀  A(t  0).

Вообще говоря, при  0 разность потенциалов U(t) не является строго периодической функцией времени: U(t)U(t  T). Периодом колебаний в этом случае принято считать минимальные промежутки времени между наибольшими значениями напряжения одного знака.

Как следует из формул (5) и (8), изменение амплитуды колебаний зависит от величины коэффициента затухания . Согласно (8) коэффициент затухания есть физическая величина, обратная времени , в течение которого амплитуда колебаний уменьшается в е раз:

U₀/A()  e при t    1/.

Таким образом, характер колебательного процесса определяется соотношениями между электрическими параметрами контура R, L и C. Так, при   0 в контуре устанавливаются свободные незатухающие гармонические (колеблющаяся величина изменяется со временем по закону синуса или косинуса) колебания (рис. 2а):

U(t)  U₀cos(₀t  ₀)

с периодом T₀  2/₀  2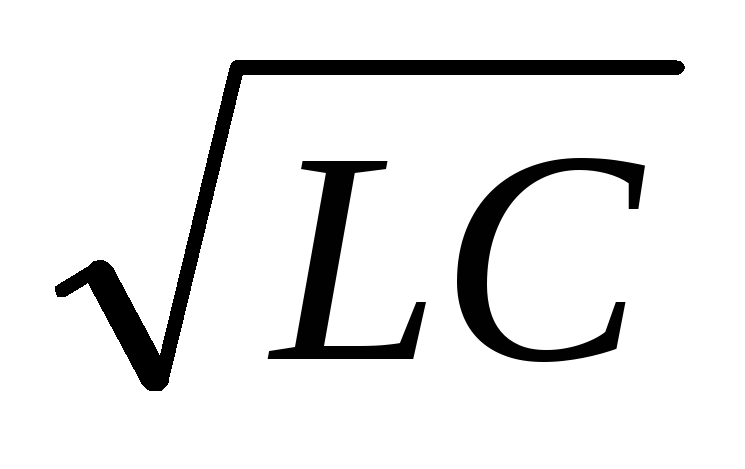(формула У.Томсона).

При критическом сопротивлении (см. формулы (6) и (7))

R  R_КР  2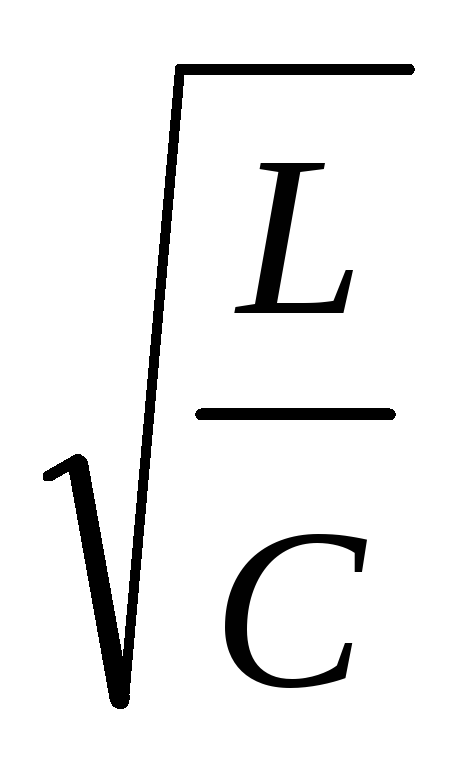

  ₀, и период колебаний становится бесконечным. В контуре возникает апериодический процесс, когда напряжение на конденсаторе постепенно уменьшается, не совершая при этом колебаний (рис. 2в).

При R < R_КР (т. е. при  < ₀) в контуре реализуется затухающий колебательный процесс (рис. 2б).

При R > R_КР (  ₀) циклическая частота  и период колебаний Т становятся мнимыми величинами. Это соответствует апериодическому процессу разряда конденсатора на большое активное сопротивление (рис. 2г).

Для характеристики затухающих колебаний наряду с коэффициентом затухания  используются и другие параметры: логарифмический декремент  и добротность контура Q.

Логарифмический декремент вводится как натуральный логарифм отношения амплитуд колебаний, разделенных во времени на период Т (рис. 2):

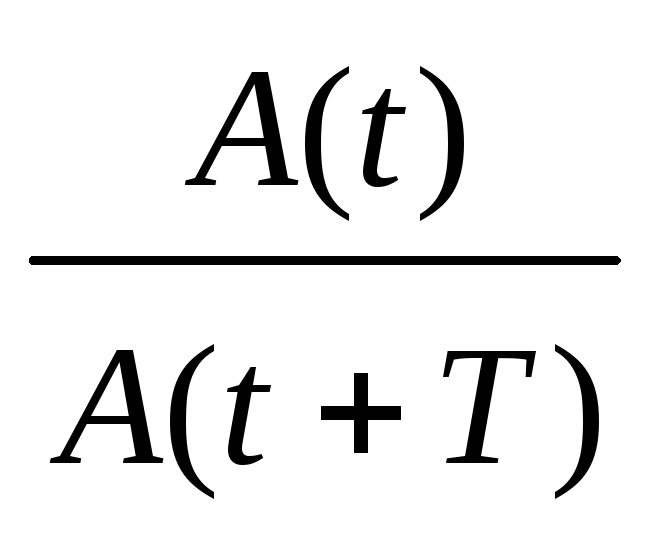  ln ln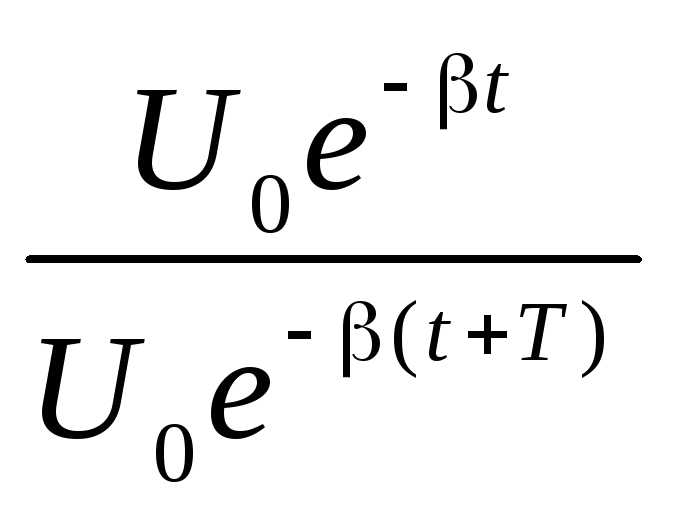 T  T/  1/N, (9)

т.е. он равен величине, обратной числу колебаний (периодов), за которое амплитуда уменьшается в е раз (N  ).

Из соотношения между  и 

  T  RT/(2L) (10)

при малых затуханиях (  ₀): T  T₀  2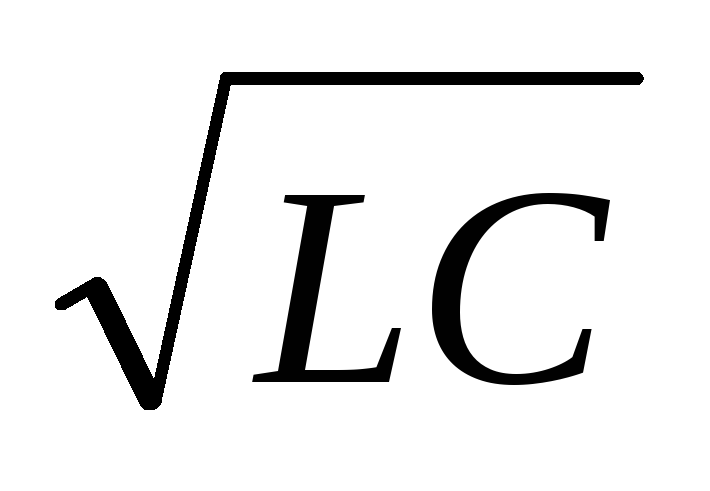можно, зная , определить коэффициент затухания :

  /T₀  /(2 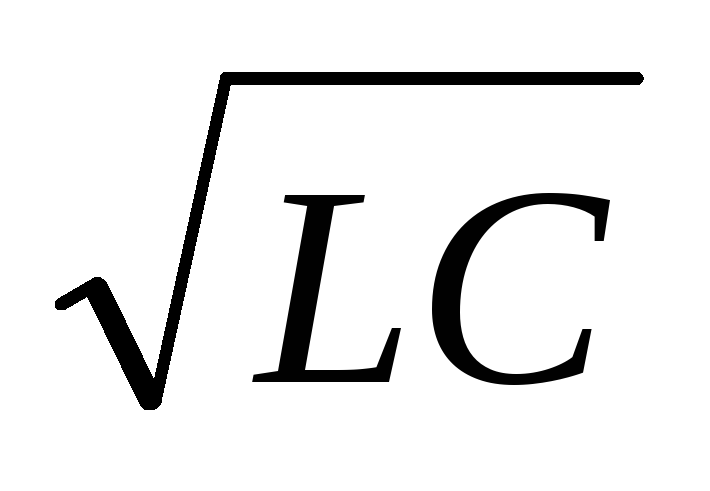

Добротность контура Q – важный параметр, характеризующий быстроту потери энергии, запасенной в контуре. Добротность контура показывает, во сколько раз амплитуда вынужденных колебаний напряжения на конденсаторе при резонансе превышает амплитуду внешней прикладываемой электродвижущей силы, и определяется формулой:

Q  ₀/2.

Для колебаний при малых  частота затухающих колебаний ω приблизительно равна собственной частоте колебаний ₀ (см. формулу (6)) и тогда, учитывая формулу (9), величина добротности:

Q  ₀/2 ≈ /2 = 2/2βT  /. (12)

Для колебательного контура:

R/2L, и ₀  1/.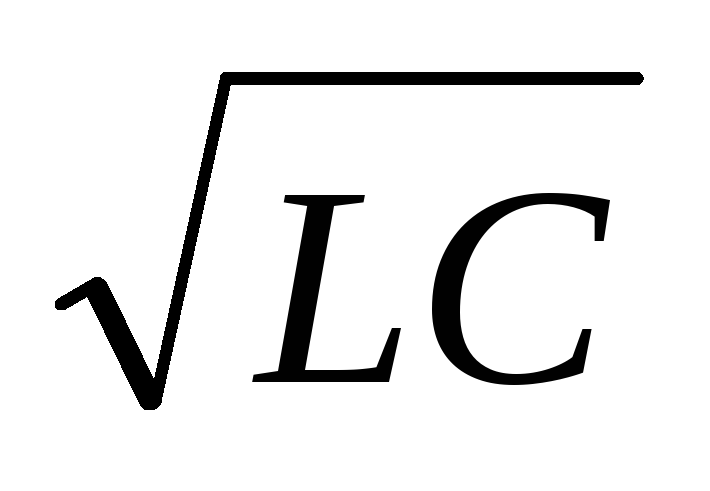

Добротность в этом случае:

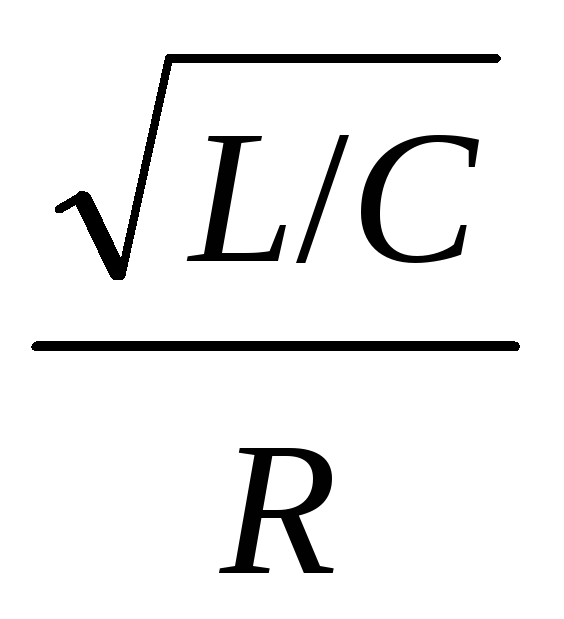
Q  ₀/2   /R. (13)

Физическую величину 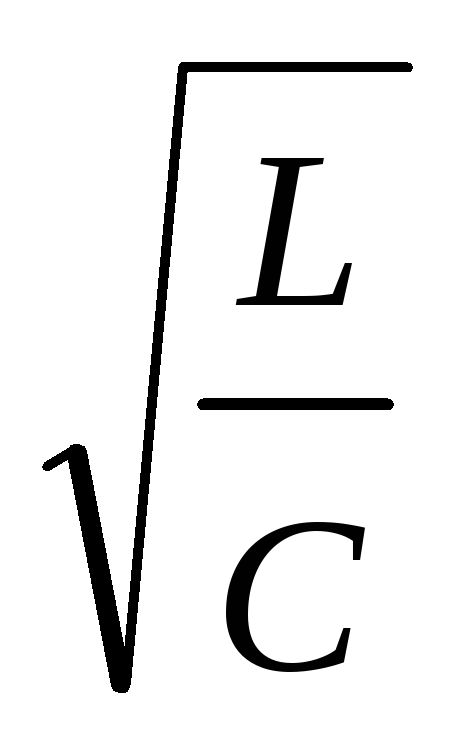  называют волновым или характеристическим сопротивлением колебательного контура.

Из соотношения (13) следует, что контур, имеющий большое активное сопротивление, обладает малой добротностью и интенсивно теряет электромагнитную энергию, колебания быстро затухают.

Все рассмотренные процессы относятся к колебательному контуру с сосредоточенными параметрами R, L и C. В реальных колебательных контурах нельзя выделить ни одного участка цепи, не обладающего активным сопротивлением, индуктивностью и емкостью, т. е. параметры R, L и С не являются сосредоточенными, а распределены по участкам цепи, что усложняет анализ колебательных процессов. При этом также необходимо учитывать входные электрические параметры измерительных приборов.

Колебательный контур ℹ️ схема идеальной цепи, функции, формула Томсона, расчет добротности, частоты, периода и других параметров, уравнение, описывающее процессы

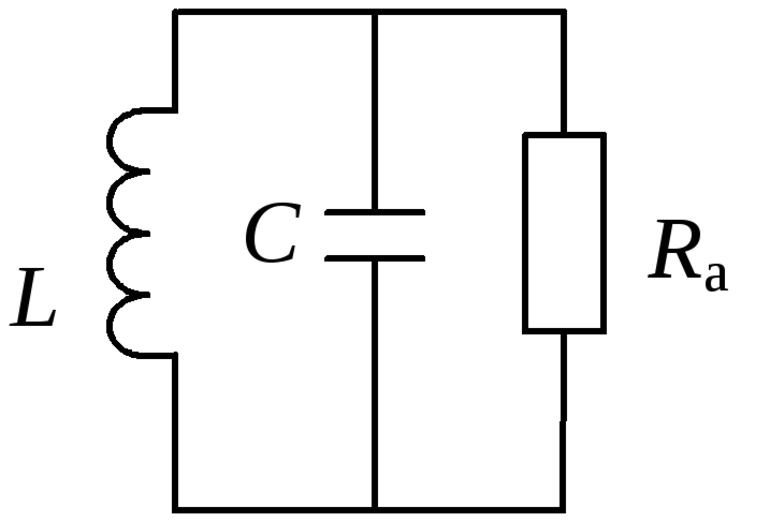
Общие сведения

Колебательным контуром называется электрическая цепь, состоящая из конденсатора и катушки индуктивности, применяемой для генерации свободных электромагнитных колебаний в радиоприемниках и радиопередатчиках. Это устройство используется в качестве различных фильтров (полосовых и режекторных). Для подстройки сигналов в сторону увеличения или уменьшения амплитуды используется этот радиоэлемент. Основная функция контура — фильтрация частот.

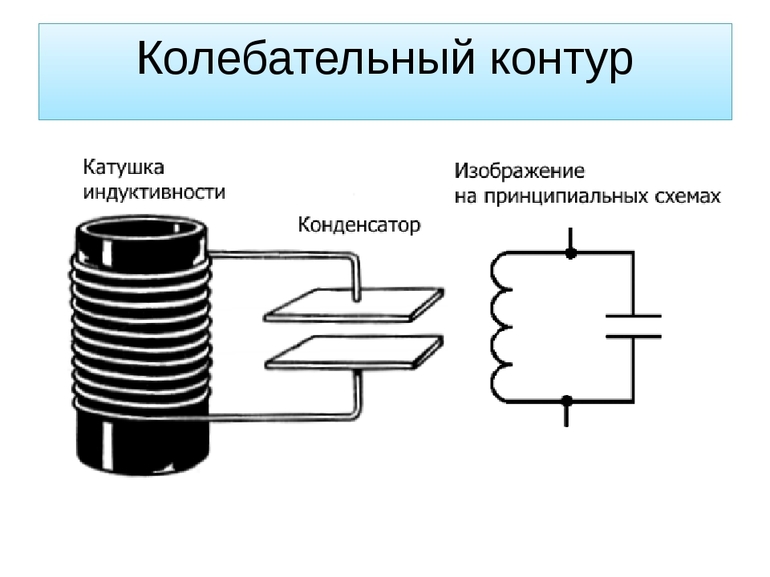
Широкое распространение устройство получило в военной сфере. В радиолокационных станциях применяются фильтры шумоподавления. Противник использует различные постановщики помех, блокирующие обнаружение цели. В состав техники входит специальное устройство, состоящее из обыкновенных контуров, но с сердечником из специального сплава. Помехи «фильтруются», и оператор радиолокационной станции получает полную картину воздушной обстановки.

Устройство можно применять и для автоматизации. Например, в состав самолетов включен блок для регулировки частоты. Основными его элементами являются два контура, которые настроены только на две частоты — 760 и 840 Гц. На них приходит напряжение с частотой 790 Гц от специального генератора. Последний издает всего 395 Гц. Если частота отклоняется от номинального значения в меньшую сторону, то реактивное сопротивление одного из контуров уменьшается.

После этого активируется электроника блока, и выдается сигнал на увеличение оборотов генератора. Когда величина частоты превышает номинальное значение, реактивное сопротивление другого контура увеличивается. В результате этого срабатывает автоматика, и поступает другой тип сигнала на уменьшение оборотов генератора.

Виды и особенности

Схемы колебательных контуров бывают двух видов: последовательными и параллельными. Они отличаются типом соединения элементов емкости и индуктивности. В первом случае они соединены последовательно, а во втором — параллельно. Для работы необходима постоянная электрическая энергия, в противном случае происходит ее затухание, поскольку часть уходит на генерацию электромагнитного поля и нагрев провода обмотки катушки индуктивности. Контур также может быть открытым и закрытым. Открытый выпускается без специальной защитной крышки.

При решении задач по физике можно встретить интересное понятие — идеальный колебательный контур. Если в задании встречается такой термин, то это говорит о том, что энергия остается в системе, а не уходит на описанные выше процессы.

Устройство постоянно генерирует электромагнитные колебания, то есть является подобием вечного двигателя, однако такого не может быть вообще. На практике при расчете параметров учитываются затухания — постепенные уменьшения амплитуды электромагнитной волны.

Последовательное соединение

Последовательный контур — простейшая резонансно-колебательная система. Он состоит из двух элементов, подсоединенных последовательно. Через них при подключении переменного напряжения будет протекать ток переменной составляющей. Его величина определяется по закону Ома: i = U / Zlc. В этой формуле Zlc является суммой реактивных сопротивлений катушки индуктивности (Xl) и конденсатора (Xc).

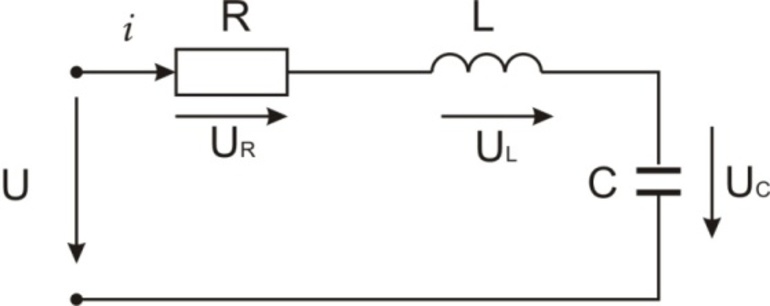
Величины определяются по формулам Xl = wL и Xc = 1 / (wC). Параметр w — угловая частота, которую можно найти по такому соотношению через частоту переменного тока и число Pi: w = 2 * Pi * f. Из соотношений можно сделать вывод, что реактивное сопротивление на индуктивности растет с увеличением f, а для емкости — уменьшается. В первом случае тип зависимости называется прямо пропорциональным, а во втором — обратно пропорциональным.

При определенном значении частоты сопротивления двух элементов равны по модулю друг другу. Следовательно, это явление называется резонансом колебательной системы. Частоту w при таком условии называют собственной резонансной частотой контура. Рассчитать ее довольно просто, поскольку следует приравнять две формулы для получения уравнения: wL = 1 / (wC). Далее нужно выразить значение f: f = [(1 / (L * C))^(½)] / 2Pi. Последнее соотношение называется формулой Томсона.

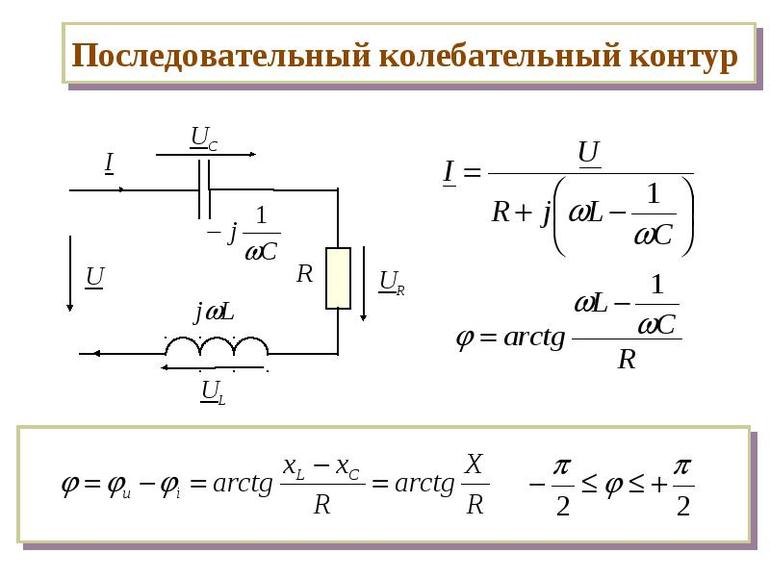
Когда контур подключается к цепи генератора (источника) переменного напряжения с активным сопротивлением R, полный импеданс цепи (Z) определяется с помощью соотношения Z = [R² + Zlc²]^(½). Если происходит резонанс, то Z = R, а реактивная составляющая исчезает.

У контура существуют еще две важные характеристики: добротность (Q) и характеристическое сопротивление (р). Последней называется величина сопротивления реактивного типа при резонансе. Вычисляется она по формуле р = (L * C)^(½) и показывает количество энергии катушки и конденсатора, которое было запасено. Для емкости значение определяется по соотношению Wс = (C * U²) / 2, а для индуктивности — Wl = (L * I²) / 2.

Отношение величины энергии, которая была запасена конденсатором и катушкой, к показателю потерь называется добротностью колебательного контура (Q). Параметр определяет амплитуду и ширину АЧХ резонанса и показывает превышение энергии запаса над потерями за одно колебание. При этом учитывается реактивная нагрузка R. Характеристика определяется по формуле Q = (1 / R) * [(L / C)^(½)].

В некоторых случаях описывать добротность можно другим тождеством: Q = p / R. Современные устройства выполняются на дискретных катушках, а их Q колеблется от нескольких единиц до сотен. Системы, построенные на принципе пьезоэлектронных устройств (кварцевые резонаторы), имеют высокий показатель Q. Его значение может достигать 1 тыс. и больше. Затухание контура (d) — характеристика, которая является обратной добротности. Она определяется по такому соотношению: d = 1 / Q.

Параллельный контур

Контур параллельного типа состоит также из конденсатора и катушки. Отличие заключается в том, что эти два элемента соединены параллельно между собой. Этот тип устройства применяется чаще, чем последовательный контур. Чтобы найти общее сопротивление индуктивного характера, нельзя просто сложить значения Xl и Xc. Складываются только проводимости двух элементов.

Из курса физики известно, что проводимость — величина, обратная сопротивлению, то есть Xc = 1 / Gc и Xl = 1 / Gl. Следовательно, формулы для параллельного соединения имеют такой вид:

1. Gl = 1 / wL.
2. Gc = wC.
3. Q = R * [(С / L)^(½)].

Для примера необходимо рассмотреть электрическую цепь, состоящую из генератора переменного тока и параллельного контура. В какой-то момент времени их частоты будут совпадать. Кроме того, проводимости двух элементов равны по модулю между собой. В результате этого происходит явление резонанса токов.

В цепи будет только активное сопротивление Rэкв, которое называют в радиотехнике эквивалентным. Оно вычисляется по формуле Rэкв = Q * p. Если частота не соответствует резонансной, то в устройстве происходят другие процессы: на низких наблюдается уменьшение индуктивного сопротивления, а на высоких — емкостного.

Во время работы контура за период колебаний два раза происходит обмен энергией между катушкой и конденсатором. В радиоэлементе протекает ток, по силе превосходящий внешний в Q раз.

Принцип работы

Принцип работы контура состоит в поочередном обмене электрической энергией между элементами емкости и индуктивности. Происходит превращение емкостной в индуктивную и обратно. Процессы следует рассмотреть подробнее. Для этого нужно зарядить конденсатор до величины напряжения Uc. Энергия будет определяться по формуле Wс = (C * U²) / 2. Если к конденсатору подсоединить катушку индуктивности, то это вызовет в ней ЭДС самоиндукции.

При этом энергия электромагнитного поля станет рассчитываться по такому соотношению: Wl = (L * I²) / 2. Из-за нее будет постепенно уменьшаться ток в электрической цепи контура. Векторы токов конденсатора и катушки направлены в разные стороны. Следовательно, они компенсируют друг друга по I закону Кирхгофа и не выходят за пределы системы.

При постоянной работе генератора (источника питания) результирующий ток в системе начнет возрастать. Энергия Wc будет полностью переходить в катушку, пока не разрядится полностью конденсатор (Wc = 0). Далее в ней появляется электромагнитное поле за счет ЭДС самоиндукции, и обкладки конденсатора будут снова заряжаться до тех пор, пока Wl не будет равна 0. Такая особенность обмена энергиями порождает колебания. Их длительность зависит от коэффициента затухания контура.

Величина сопротивления для параллельного колебательного контура на частоте резонанса стремится к бесконечности, а последовательного — к 0. Последний и применяется в качестве фильтра благодаря такой особенности.

Расстройка устройства

Расстройка — это настройка контура на частоту, отличную от резонансной. Последняя наступает в том случае, когда характеристики частот радиодетали и генератора совпадают. В некоторых устройствах этого необходимо избегать. Чтобы получить резонанс, нужно воспользоваться одним из трех методов изменения характеристик:

• частоты генератора;
• индуктивности;
• емкости.

Два последних метода можно делать одновременно для достижения лучшего эффекта. Расстройки классифицируются на три вида: абсолютную, обобщенную и относительную. Первой называется разность между частотами контура и резонанса. Обобщенная вычисляется при помощи отношения реактивного сопротивления к активному. Относительная выражается в виде отношения абсолютной расстройки к резонансной частоте.

Кроме того, расстройка бывает положительной и отрицательной. В первом случае необходимо, чтобы частота генератора была больше частоты контура. Для отрицательной должно соблюдаться другое условие: частота генератора меньше, чем у контура.

В некоторых случаях необходимо убрать резонансную частоту. Выполняется такая операция при помощи изменения необходимых характеристик электроцепи «контур — генератор». Очень часто в контуре применяются конденсаторы с переменной емкостью, позволяющие настраивать его. Настройка конденсатора происходит благодаря изменению расстояния между его обкладками. Этот принцип очень удобен, поскольку для изменения индуктивности катушки необходим сердечник, который будет выкручиваться.

Однако существуют радиоэлементы и такого типа. В них емкость является постоянной величиной, а индуктивность изменяется с помощью сердечника. Конструктивная особенность последнего представляет обыкновенный ферритовый болт, который вкручивается в пластиковый корпус. На последний наматывается провод.

Пример решения

Для устройства нужно произвести расчет контура с частотой резонанса 1 МГц. Можно воспользоваться описанными формулами, однако радиолюбители произвели некоторые вычисления и предложили более упрощенный вариант: L = (159,1 / f)^2 / C. Для контура можно взять приближенное значение емкости плоского конденсатора, равное 1000 пкФ. На корпусе указывается этот параметр.

Кроме того, маркировка может содержать напряжение, на которое он рассчитан. Подставив все значения в формулу, можно узнать индуктивность: L = (159,1 / 1)^2 / 1000 = 25 (мкГн). После этого следует вычислить количество витков N катушки с диаметром каркаса D по такому соотношению: N = 32 * [L / D]^(½). Если предположить, что D = 5 мм (можно взять со старых контуров), то N = 32 * [25 / 5]^(½) = 72 (витка). Однако за основу можно взять катушку с подстроечным ферритовым сердечником со следующими параметрами:

• длина — 13—15 мм;
• диаметр — 2,3—3,2 мм.

Можно воспользоваться таким соотношением: N = 8,5 * L^(½) = 8,5 * 25^(½) = 43 (витка). Провод следует брать 0,1 мм в диаметре. Это показатель измеряется при помощи штангенциркуля.

Таким образом, колебательный контур является простейшей системой для генерации электромагнитных колебаний, затухание которых зависит от частоты резонанса и добротности радиоэлемента.