Добротность — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 сентября 2017; проверки требуют 6 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 сентября 2017; проверки требуют 6 правок.Добро́тность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом Q{\displaystyle Q} (В русской литературе Д) от англ. quality factor.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая формула для добротности любой колебательной системы:
- Q=ω0WPd=2πf0WPd{\displaystyle Q={\frac {\omega _{0}W}{P_{d}}}={\frac {2\pi f_{0}W}{P_{d}}}},
где:
- ω0{\displaystyle \omega _{0}} — резонансная круговая частота колебаний
- f0{\displaystyle f_{0}} — резонансная частота колебаний
- W{\displaystyle W} — энергия, запасённая в колебательной системе
- Pd{\displaystyle P_{d}} — рассеиваемая мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.
Для последовательного колебательного контура в RLC-цепях, в котором все три элемента включены последовательно:
- Q=1RLC=ω0LR,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}}={\frac {\omega _{0}L}{R}},}
где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно, а ω0{\displaystyle \omega _{0}} — частота резонанса. Выражение L/C{\displaystyle {\sqrt {L/C}}} часто называют характеристическим или волновым сопротивлением колебательного контура. Таким образом, добротность в колебательном контуре равна отношению волнового сопротивления к активному.
Для параллельного контура, в котором индуктивность, ёмкость и сопротивление включены параллельно:
- Q=RCL=Rω0L{\displaystyle Q=R{\sqrt {\frac {C}{L}}}={\frac {R}{\omega _{0}L}}}
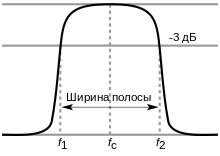 Формулировка частотного отклика или ширины полосы пропускания колебательной системы
Формулировка частотного отклика или ширины полосы пропускания колебательной системы 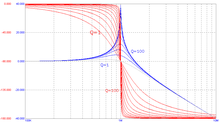 ЛАФЧХ колебательных звеньев с разной добротностью
ЛАФЧХ колебательных звеньев с разной добротностьюВ данном случае R является входным сопротивлением параллельного контура. Однако практически для электрической цепи гораздо проще измерить ток или напряжение, чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды колебаний, ширина полосы частот на АЧХ определяется на высоте 1/2{\displaystyle 1/{\sqrt {2}}} от высоты максимума (примерно −3 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой Δω{\displaystyle \Delta \omega } по уровню 1/2{\displaystyle 1/{\sqrt {2}}} с круговой частотой резонанса ω0=2πf0:{\displaystyle \omega _{0}=2\pi f_{0}:}
Q=ω0Δω=πδ=πNe,{\displaystyle Q={\frac {\omega _{0}}{\Delta \omega }}={\frac {\pi }{\delta }}=\pi N_{e},}
где δ — логарифмический декремент затухания, равный отношению полуширины резонансной кривой к частоте резонанса, Ne{\displaystyle N_{e}} — число колебаний за время релаксации.
Для измерения электрической добротности на частотах до десятков — сотен мегагерц применяют измеритель добротности или измеритель иммитанса (косвенным способом), в диапазоне СВЧ применяются специальные методы.
Измеритель добротности
Что такое добротность колебательного контура?как измерить добротность в радиолюбительских условиях.
«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы, который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания» — авторитетно учит нас Википедия.
Да уж. Напустили тумана ироды — без поллитры не разберёшься. А ведь придётся, раз впряглись.
Для начала возьмём ёжика. Хорошее животное! Хотя выдающимся умом не обладает, но думаю, что и оно в курсе, что
«quality factor» — это показатель качества колебательного контура и в первую очередь, конструктивного качества катушки индуктивности.
Теперь возьмём женщину в теле — добротную женщину. Таких женщин рисовали художники 18-го, 19-го веков, а поэты писали: «Её
выпуклости меня восхищают, её впуклости сводят с ума».
Так вот. К чему это я?
А к тому, что для получения в сухом остатке высокодобротного колебательного контура, придётся поискать в загашнике и высококачественный
конденсатор с низким током утечки, и катушку индуктивности — крепкую, добротную и красивую, словно выпавшую из картины
венецианского мастера в Пушкинском музее.
Приведём эквивалентную схему колебательного контура.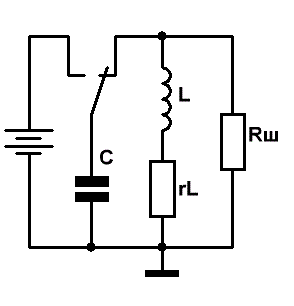
Здесь L
rL — сопротивление катушки, эквивалентное потерям электрической энергии в проводе катушки индуктивности,
Rш — сумма сопротивлений, обусловленных потерями в изоляции провода, каркасе, экране, сердечнике катушки индуктивности, а также потерями, вызванные наличием токов утечки в конденсаторе.
Рис.1
При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.
По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо учитывать и суммировать со значением основной ёмкости С.
Теперь давайте разберёмся, что такое «скорость затухания собственных колебаний в системе» и, каким боком она связана с добротностью.
 Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).
Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).
Конденсатор С зарядится до уровня, равного напряжению питания.
Теперь перещёлкнем переключатель в правое по схеме положение.
Благодаря энергии, запасённой в конденсаторе, в образовавшейся LC-цепи возникнут свободные колебания на частоте резонанса
колебательного контура, равной fо= 1/2π√LС.
Поскольку у нас ни с какой стороны не вечный двигатель — свободные колебания затухают, причём скорость затухания зависит от потерь
в конденсаторе и катушке индуктивности: чем они меньше, тем медленнее затухание.
Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность колебательного контура, генератор сигналов в этом случае не нужен.
Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.
Вспоминаем дальше: «Добротность является тем параметром колебательной системы, который определяет ширину резонанса».
Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.
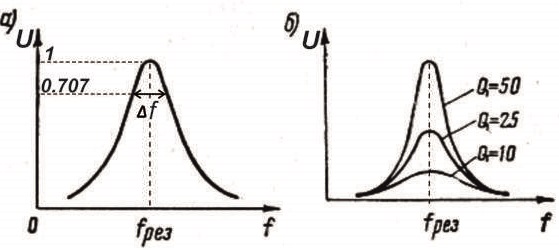 По частотной характеристике условно определяется полоса пропускания контура Δf.
По частотной характеристике условно определяется полоса пропускания контура Δf.
При этом сделано допущение, что напряжение внутри этой полосы имеет право снижаться до уровня 0,707 от максимального.
Исходя из этого, формула для определения добротности приобретает следующий вид:
Q = f рез/Δf .
Рис.2
Из формулы естественным образом вытекает, что чем выше добротность — тем уже полоса пропускания резонансного контура, соответственно, чем ниже — тем шире.
А как измерить добротность контура
1. Если речь идёт о низких (звуковых) частотах, то тут всё просто.
В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления)
к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не
вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления
катушки.
А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую
манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт
добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих
существенных потерь в работу колебательного контура.
2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к
тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными
методами, как в случае НЧ обойтись не удастся.
Рискну сделать осторожное предположение, что в радиолюбительской лаборатории у нас затерялся высокочастотный генератор с 50-омным
выходом и такой же высокочастотный осциллограф, или, на худой конец, измеритель ВЧ напряжений.
В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с контуром.
Спаяем пару резисторов.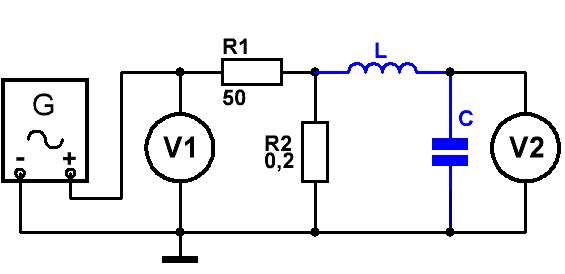
Добротность измеряется при настройке генератора сигналов на частоту резонанса контура, соответствующую максимальному выходному
напряжению.
Добротность Q рассчитывается как отношение выходного напряжения на резонансном контуре к напряжению, поданному на него.
В нашем случае Q = 250 x V2/V1 .
Рис.3
Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать это значение как минимум на порядок.
Все наши рассуждения и формулы корректны для ненагруженных параллельных колебательных контуров, то есть для случаев, когда на выходе
отсутствует реальная нагрузка.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность.
Эквивалентная добротность Q параллельного колебательного контура с учётом этих потерь вычисляется по следующей формуле:
Q = Q0x Rш/(Rш+Rо) , где
Q0 — добротность ненагруженного контура,
Rш — шунтирующее сопротивление, равное R(источника) ll R(нагрузки),
Rо — эквивалентное сопротивление ненагруженного контура, равное сопротивлению контура на резонансной частоте,
значение которого можно посчитать на той же странице ссылка на страницу во 2-ой таблице.
А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.

Добротность колебательной системы — это… Что такое Добротность колебательной системы?
- Добротность колебательной системы
- отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания. Добротность характеризует качество колебательной системы (См. Колебательные системы), т.к. чем больше Д. к. с., тем меньше потери энергии в системе за одно колебание. Д. к. с. Q связана с логарифмическим Декрементом затухания δ; при малых декрементах затухания Q ≈ π/δ. В колебательном контуре с индуктивностью L, ёмкостью C и омическим сопротивлением R Д. к. с.

где ω — собственная частота контура. В механической системе с массой m, жёсткостью k и коэффициентом трения b Д. к. с.
 Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний (См. Вынужденные колебания) при Резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты. На этом свойстве основан метод измерения Д. к. с. Величина добротности характеризует также и избирательность колебательной системы; чем больше добротность, тем у́же полоса частот внешней силы, которая может вызвать интенсивные колебания системы. Экспериментально Д. к. с. обычно находят как отношение частоты собственных колебаний к полосе пропускания системы, т. е. Q = ω/Δω. Численные значения Д. к. с.: для радиочастотного колебательного контура 30—100; для камертона 10000; для пластинки пьезокварца 100000; для объёмного резонатора СВЧ колебаний 100—100000.
Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний (См. Вынужденные колебания) при Резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты. На этом свойстве основан метод измерения Д. к. с. Величина добротности характеризует также и избирательность колебательной системы; чем больше добротность, тем у́же полоса частот внешней силы, которая может вызвать интенсивные колебания системы. Экспериментально Д. к. с. обычно находят как отношение частоты собственных колебаний к полосе пропускания системы, т. е. Q = ω/Δω. Численные значения Д. к. с.: для радиочастотного колебательного контура 30—100; для камертона 10000; для пластинки пьезокварца 100000; для объёмного резонатора СВЧ колебаний 100—100000.Лит.: Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964; Горелик Г. С., Колебания и волны, 2 изд., М., 1959.
В. Н. Парыгин.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Добротности измеритель
- Добруджа
Смотреть что такое «Добротность колебательной системы» в других словарях:
ДОБРОТНОСТЬ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ — характеристика резонансных свойств системы, показывающая, во сколько раз амплитуда вынужденных колебаний при резонансе превышает амплитуду при его отсутствии. Чем выше добротность колебательной системы, тем меньше потери энергии в ней за период.… … Большой Энциклопедический словарь
добротность колебательной системы — характеристика резонансных свойств системы, показывающая, во сколько раз амплитуда вынужденных колебаний при резонансе превышает амплитуду при его отсутствии. Чем выше добротность колебательной системы, тем меньше потери энергии в ней за период.… … Энциклопедический словарь
ДОБРОТНОСТЬ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ — характеристика резонансных свойств системы, показывающая, во сколько раз амплитуда вынужденных колебаний при резонансе превышает амплитуду при его отсутствии. Чем выше Д. к. с., тем меньше потери энергии в ней за период. Добротность колебат.… … Естествознание. Энциклопедический словарь
ДОБРОТНОСТЬ — величина, характеризующая резонансные свойства линейной колебат. системы; численно равна отношению резонансной частоты со к ширине резонансной кривой Dw на уровне убывания амплитуды в ?2 раза: Q=w/Dw. Принято также выражать Д. колебат. системы… … Физическая энциклопедия
ДОБРОТНОСТЬ — колебательной системы, характеристика резонансных свойств системы, показывающая, во сколько раз амплитуда вынужденных колебаний при резонансе превышает их амплитуду вдали от резонанса. Чем выше добротность системы, тем меньше потери энергии в ней … Современная энциклопедия
Добротность — колебательной системы, характеристика резонансных свойств системы, показывающая, во сколько раз амплитуда вынужденных колебаний при резонансе превышает их амплитуду вдали от резонанса. Чем выше добротность системы, тем меньше потери энергии в ней … Иллюстрированный энциклопедический словарь
Добротность — Добротность характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Добротность обратно пропорциональна скорости… … Википедия
добротность — 1. Количественная характеристика потерь колебательной системы при резонансе, равная где Wк полный запас энергии колебаний при резонансе; Wп потери энергии за период [Физический энциклопедический словарь] 2. Количественная мера потерь… … Справочник технического переводчика
добротность — 3.17 добротность (Q factor): Величина, характеризующая степень остроты резонанса или избирательность по частоте колебательной механической системы с одной степенью свободы и обратная удвоенному коэффициенту демпфирования. Источник … Словарь-справочник терминов нормативно-технической документации
ненагруженная добротность — Собственная добротность колебательной системы. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики электросвязь, основные понятия EN unloaded Q … Справочник технического переводчика
3. ДОБРОТНОСТЬ

39
3.1.Добротность колебательной системы
Добротность произвольной колебательной системы есть безразмерная величина Q, определяемая формулой
где ω − частота колебаний; W – запасенная системой энергия; Р – усредненная по времени мощность потерь. Из определения (3.1) получается, в частности, известная формула
для добротности последовательного контура на его резонансной частоте. Если колебательная система совершает свободные колебания, то их амплитуда убывает во времени. Для описания затухающих гармонических
колебаний удобно использовать комплексную частоту
ω = ω′−iω″. | (3.3) |
В этом случае зависимость от времени вещественной колеблющейся величины A(t) (ток, напряжение, деформация и т. д.) описывается формулой
A(t) = Re [A0e– i ωt ] = |A0|e– ω″t cos(ω′t – arg A0) , | (3.4) |
где A0 = |A0| ei arg A0 − комплексная амплитуда колебаний (начальная). Очевидно, что в случае затухающих колебаний частота ω в формуле (3.1) должна быть заменена на ω′.
Установим связь добротности Q с вещественной и мнимой частью комплексной частоты. Как известно, энергия, запасенная любой колебательной системой, пропорциональна квадрату модуля амплитуды колебаний. Поэтому, используя формулу (3.4), запасенную энергию можно записать в виде
W = α|A0|2e –2ω″t, | (3.5) |
где коэффициент α − константа, зависящая только от типа и параметров колебательной системы*.
*Например, в случае колебательного контура, когда A(t) есть ток, коэффициент
α=L/2, где L – индуктивность.

40 |
|
Мощность потерь связана с запасенной энергией соотношением |
|
P = −dW/dt. | (3.6) |
Подставляя (3.5) и (3.6) в определение (3.1), получаем искомое соотношение
Q = ω′/(2ω″). | (3.7) |
Колебательные системы обычно подключают к внешним нагрузкам. | |
В этом случае мощность потерь |
|
P = P0 +Ре, | (3.8) |
где P0 – мощность потерь внутри колебательной системы; Ре – мощность по- | |
терь во внешней нагрузке. Тогда формулу (3.1) можно записать в виде |
|
Q−1 = Q0−1 + Qe−1, | (3.9) |
где величину |
|
Q0 = ωW⁄P0 | (3.10) |
называют собственной добротностью колебательной системы, а величину
называют внешней добротностью. Собственная добротность Q0 характеризует свойства уединенной колебательной системы, а внешняя добротность Qe характеризует величину связи колебательной системы с внешним окружением. Величину Q, описываемую формулой (3.9), называют нагруженной добротностью.
Формула (3.1) есть общее определение добротности, применимое к любой колебательной системе на любой частоте. Однако в некоторых случаях приходится иметь дело с двухполюсником, являющимся «черным ящиком», о котором известно только то, что его входное комплексное сопротивление описывается функцией
Zвх(ω) = R−iX, | (3.12) |
а обратная ему величина – входная комплексная проводимость − функцией
Yвх(ω) = G −iB. | (3.13) |
Величину X(ω) называют реактивным сопротивлением, а величину B(ω) − реактивной проводимостью. Обе эти величины называют реактансами.
Знак перед мнимой единицей i в формулах (3.12), (3.13) выбран в соответствии со знаком в формуле (1.1).
41
Реактансы могут на некоторых частотах обращаться в нуль. Если на частоте ω0 обращается в нуль X, то двухполюсник на этой частоте проявляет свойства последовательного колебательного контура, если же в нуль обращается B, то − параллельного.
Добротность двухполюсника на резонансной частоте ω0 определяют формулой
| Q =x/R |
|
| (3.14) | ||
для случая последовательного резонанса и формулой |
| |||||
| Q = b/G |
|
| (3.15) | ||
для случая параллельного резонанса, где величина |
| |||||
x = | ω0 | dX (ω) |
| ω=ω0 | (3.16) | |
| ||||||
| ||||||
| 2 dω |
|
|
| ||
называется параметром крутизны реактивного сопротивления, а величина
b = | ω0 | dB(ω) |
| ω=ω0 | (3.17) | |
| ||||||
| ||||||
| 2 dω |
|
|
| ||
называется параметром крутизны реактивной проводимости. Формулы (3.14)–(3.15) получаются из формулы (3.7) и резонансных
условий Z(ω′−iω″) = 0 и Y(ω′−iω″) = 0. Не трудно убедиться, что для последовательного колебательного контура с входным сопротивлением
Zвх(ω) = R −iωL +i/(ωC) | (3.18) |
и для параллельного колебательного контура с входной проводимостью
Yвх(ω) = 1/R −iωC +i/(ωL) | (3.19) |
выражения (3.14) и (3.15) дают правильную формулу (3.2) и потому согласуются с общим определением (3.1).
Термин «добротность» используется не только для описания колебательных систем, но и для описания линий передачи. Добротностью линии передачи называют добротность резонатора СВЧ, образованного из отрезка линии передачи.
Добротность линии передачи Q в случае гармонических колебаний с вещественной частотой ω связана с волновым числом kz бегущей волны формулой
Q = kz′/(2kz″). | (3.20) |
42
Для доказательства этой формулы рассмотрим отрезок линии длиною l. За период колебания Т фронты прямой и обратной волны пройдут путь vT, дважды претерпевая отражения на концах, и возвратятся на исходное место. Этот путь будет равен 2l. Поэтому имеем
2l = ωТ/kz′. | (3.21) |
Пройдя расстояние 2l, амплитуды бегущих волн станут |
|
A(z, t+T) = A(z, t)e−kz″2l = A0e−k z″2l. | (3.22) |
Из формул (3.21), (3.22) получаем закон убывания запасенной энергии
W(t) = W0 e−2ωt kz″⁄ kz′. | (3.23) |
Подставляя (3.23) и (3.6) в определение (3.1), получаем формулу (3.20). Мощность потерь в линии передачи
где Pd – мощность потерь в диэлектрическом заполнении линии, а Pc – мощность потерь в проводниках линии передачи. Тогда, согласно (3.1), обратную величину добротности линии можно представить в виде суммы
Q−1 = Qd−1 + Qc−1, | (3.25) |
где величину |
|
Qd = ωW⁄Pd | (3.26) |
называют добротностью диэлектрического заполнения линии, а величину
называют добротностью проводников линии.
Добротность Qd есть усредненная характеристика материалов, заполняющих линию передачи. В однородной линии величина Qd не зависит ни от конструкции, ни от размеров линии, а зависит только от тангенсов угла диэлектрических и магнитных потерь. В случае, когда однородное диэлектри-
ческое заполнение не является магнитным, имеет место равенство |
|
Qd = εr′ ⁄εr″. | (3.28) |
Равенство (3.28) получается из формул (1.20), (1.38) и (3.20) и предположения о малости тангенса угла диэлектрических потерь.
Добротность — это… Что такое Добротность?
Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая формула для добротности любой колебательной системы:
,
где:
- — резонансная частота колебаний
- — энергия, запасённая в колебательной системе
- — рассеиваемая мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.
Для Колебательного контура в RLC цепях:
- ,
где , и — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.
Для электрической цепи гораздо проще измерить амплитуду (ток или напряжение), чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды осцилляции, полоса на АЧХ будет от пика (примерно −3 дБ, а 1/2 это −6 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой по уровню с круговой частотой резонанса :
,
где: — коэффициент затухания, равный полуширине резонансной кривой, — число колебаний за время релаксации.
Метрологические аспекты
Для измерения электрической добротности на частотах до десятков — сотен мегагерц применяют измеритель добротности или измеритель иммитанса (косвенным способом), в диапазоне СВЧ применяются специальные методы.
Ссылки
Литература
См. также
Измеритель добротности
Методы определения добротности
Пользуясь определением добротности, можно показать, что
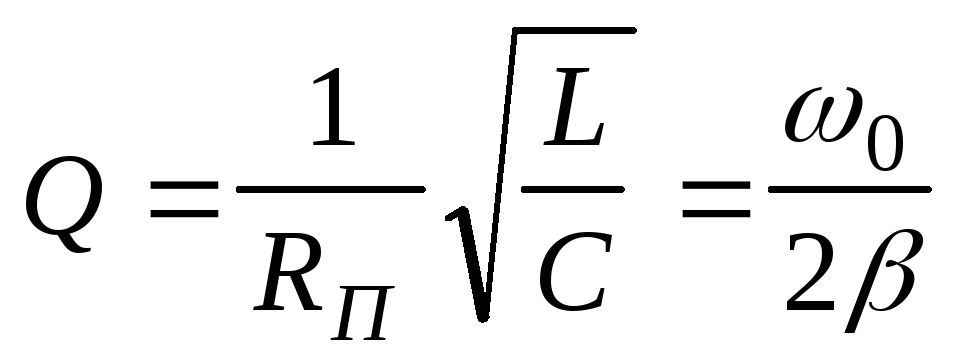 ,
(9)
,
(9)
RП = r + R + RL,
где RП – полное сопротивление цепи; r – внутреннее сопротивление источника тока; R – сопротивление, включенное в контур; RL – активное сопротивление катушки индуктивности.
1. Расчет теоретического значения добротности. Добротность контура Qтеор можно рассчитать по формуле (9), зная параметры электрической цепи RП, L и C.
2. Определение добротности по измерениям резонансного напряжения U0рез и амплитуды вынуждающей ЭДС 0. Соотношение (8) при малых коэффициентах затухания принимает вид
 ,
,
откуда
 .
(10)
.
(10)
3. Определение
добротности по ширине резонансной
кривой. Шириной резонансной кривой называется
разность частот, при которых достигается
эффективное значение резонансного
напряжения на конденсаторе, равное (см.
рис. 3)  .
.
Разность этих частот = 2 – 1 является полосой пропускания контура.
Энергия, запасенная в контуре при резонансе, на границах полосы пропускания уменьшается в два раза.
Пользуясь соотношениями (9) и (10) и преобразуя уравнение (5), получаем, что с достаточной степенью точности
 .
(11)
.
(11)
Таким образом, зная и рез, можно вычислить добротность контура.
Расчет добротности
этим методом производится с помощью
полученной экспериментально резонансной
кривой в координатах U0 , .
По ней определяются для 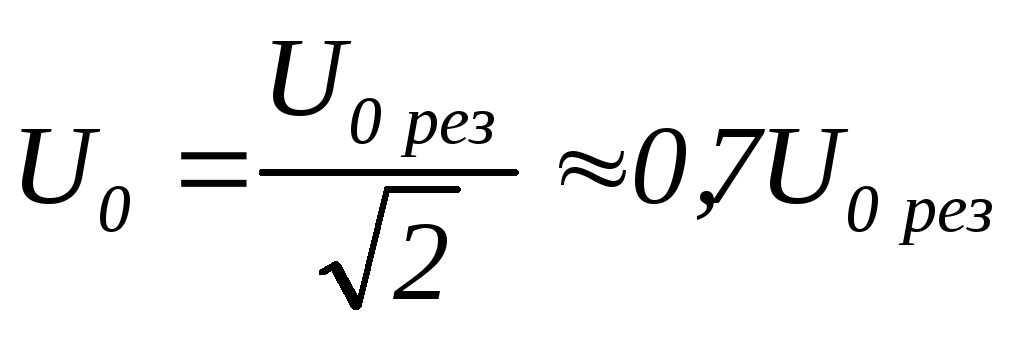 значения 1 и 2 слева и справа от рез.
значения 1 и 2 слева и справа от рез.
Вместо рез и циклических частот 1 и 2 используются соответствующие частоты генератора
 .
(12)
.
(12)
Метод измерения и описание аппаратуры
Для выполнения работы используется простейший колебательный контур из последовательно соединенных катушки индуктивности L, конденсатора C и сопротивления R. Резонансные кривые снимают при различных сопротивлениях, включенных в контур. Наблюдение за изменением амплитуды колебаний на конденсаторе производится с помощью электронного осциллографа. Для этого сигнал с конденсатора подается на вход осциллографа, и при изменении частоты генератора измеряется амплитуда напряжения. При этом диапазон частот выбирается достаточно широким в обе стороны по отношению к резонансной частоте. Резонансная частота соответствует наибольшей амплитуде измеряемого напряжения при заданном сопротивлении контура. Определение добротности контура производится двумя из вышеописанных способов: по ширине резонансной кривой и по отношению резонансного напряжения к амплитуде вынуждающей ЭДС. Полученные результаты позволяют вычислить омическое сопротивление контура и оценить значение внутреннего сопротивления генератора.
Порядок выполнения работы
Включите генератор синусоидальных колебаний и электронный осциллограф и соберите схему для измерений в соответствии с указаниями на стенде.
Рассчитайте собственную частоту контура по формуле
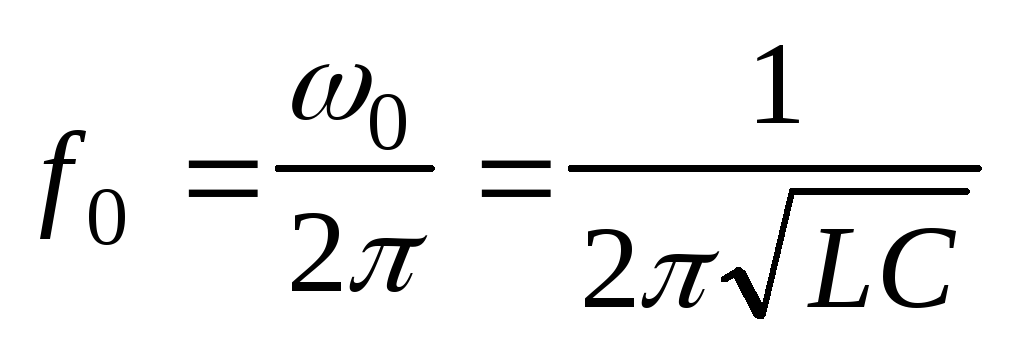 .
.
Параметры L, C, RL, r контура даны на стенде. Значения L, C и f0 запишите в табл. 1.
Определите по осциллографу амплитуды вынужденных колебаний напряжения U0, снимаемого с конденсатора в делениях масштабной сетки на экране осциллографа, при фиксированных значениях частоты F генератора в выбранном диапазоне частот при R1. Полученные данные занесите в табл. 1.
Повторите опыт (пункт 3) при другом сопротивлении R2, включенном в контур.
Не изменяя настройки генератора определите амплитуду колебаний ЭДС генератора, соответствующую резонансной частоте, полученной экспериментально в п. 3,4. Для этого установите на генераторе резонансную частоту, выход генератора подключите непосредственно к входу электронного осциллографа с помощью переключателя на стенде, и зафиксируйте амплитуду сигнала 0. Результат занесите в табл. 1 и табл. 2.
По данным табл. 1 постройте резонансные кривые при различных сопротивлениях контура R1 и R2.
На каждой резонансной кривой отметьте уровень, соответствующий 0,7U0 рез.
Таблица 1
№ | Частота | U0, В | |
п/п | F, МГц | R1 = … Ом | R2 = … Ом |
1 2 … 11 | |||
С = … Ф; f0 = … КГц;
L = … Гн; 0 = … В.
Добротность Википедия
Добро́тность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом Q{\displaystyle Q} (В русской литературе Д) от англ. quality factor.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Теория[ | ]
Общая формула для добротности любой колебательной системы:
- Q=ω0WPd=2πf0WPd{\displaystyle Q={\frac {\omega _{0}W}{P_{d}}}={\frac {2\pi f_{0}W}{P_{d}}}},
где:
- ω0{\displaystyle \omega _{0}} — резонансная круговая частота колебаний
- f0{\displaystyle f_{0}} — резонансная частота колебаний
- W{\displaystyle W} — энергия, запасённая в колебательной системе
- Pd{\displaystyle P_{d}} — рассеиваемая мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.
Для последовательного колебательного контура в RLC-цепях, в котором все три элемента включены последовательно:
- Q=1RLC=ω0LR,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}}={\frac {\omega _{0}L}{R}},}
где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно, а ω0{\displaystyle \omega _{0}} — частота резонанса. Выражение L/C{\displaystyle {\sqrt {L/C}}} часто называют характеристическим или волновым сопротивлением колебательного контура. Таким образом, добротность в колебательном контуре равна отношению во


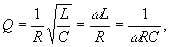
 Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний (См. Вынужденные колебания) при Резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты. На этом свойстве основан метод измерения Д. к. с. Величина добротности характеризует также и избирательность колебательной системы; чем больше добротность, тем у́же полоса частот внешней силы, которая может вызвать интенсивные колебания системы. Экспериментально Д. к. с. обычно находят как отношение частоты собственных колебаний к полосе пропускания системы, т. е. Q = ω/Δω. Численные значения Д. к. с.: для радиочастотного колебательного контура 30—100; для камертона 10000; для пластинки пьезокварца 100000; для объёмного резонатора СВЧ колебаний 100—100000.
Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний (См. Вынужденные колебания) при Резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты. На этом свойстве основан метод измерения Д. к. с. Величина добротности характеризует также и избирательность колебательной системы; чем больше добротность, тем у́же полоса частот внешней силы, которая может вызвать интенсивные колебания системы. Экспериментально Д. к. с. обычно находят как отношение частоты собственных колебаний к полосе пропускания системы, т. е. Q = ω/Δω. Численные значения Д. к. с.: для радиочастотного колебательного контура 30—100; для камертона 10000; для пластинки пьезокварца 100000; для объёмного резонатора СВЧ колебаний 100—100000.