Активное сопротивление. Действующие значения силы тока и напряжения

«Не стыдно не знать, стыдно не учиться».

Задача 1. В колебательном контуре напряжение на зажимах изменяется по закону  . Найдите действующие значения силы тока и напряжения, если активное сопротивление цепи равно 50 Ом.

ДАНО:	РЕШЕНИЕ Запишем общее уравнение гармонических колебаний напряжения Исходя из заданного по условию задачи уравнения можно определить, что амплитудное напряжение равно Из закона Ома для участка цепи Тогда действующие значения напряжения и силы тока равны

Ответ: U_д = 70,7 В; I_д = 1,4 А.

Задача 2. В цепь параллельно включены катушка с индуктивностью 30 мГн и конденсатор с ёмкостью 50 мкФ. Действующее значение силы тока равно 10 А. Запишете уравнения, описывающие колебания тока и напряжения, а также найдите активное сопротивление цепи.

ДАНО:	СИ	РЕШЕНИЕ Уравнения гармонических колебаний для напряжения и силы тока имеют вид Циклическая частота колебательного контура определяется по формуле Действующие значения напряжения и силы тока рассчитываются по выражениям Тогда амплитудное значение силы тока равно Амплитудное значение напряжения можно рассчитать по формуле С учетом рассчитанных значений уравнения гармонических колебаний примут вид Активное сопротивление цепи определяется по формуле

Задача 3. Действующее значение напряжения в цепи с колебательным контуром  составляет 50 В. Известно, что в некоторый момент времени t = 2 мс ток в цепи равен 2 А. Найдите индуктивность катушки, если ёмкость конденсатора равна 80 нФ,а активное сопротивление цепи равно 20 Ом. Сдвиг фаз равен нулю.

ДАНО:	СИ	РЕШЕНИЕ Запишем уравнения, описывающие колебания тока и напряжения в общем виде Из закона Ома для участка цепи Действующие значения напряжения и силы тока рассчитываются по формулам Тогда амплитудные значения напряжения и силы тока равны Циклическая частота колебательного контура определяется по формуле С учётом рассчитанного значения амплитудной силы тока и формулы для расчёта циклической частоты колебательного контура уравнение гармонических колебаний силы тока примет вид Т.к. по истечении 2 мс сила тока равна 2А, то

Ответ: 53 Гн.

Задача 4. Активное сопротивление колебательного контура равно 35 Ом, а частота колебаний равна 25 кГц. Найдите ёмкость конденсатора и индуктивность катушки.

ДАНО:	СИ	РЕШЕНИЕ Максимальная электрическая энергия колебательного контура Максимальная магнитная энергия колебательного контура Когда электрическая энергия максимальна, магнитная энергия равна нулю и наоборот, когда магнитная энергия максимальна, электрическая энергия равна нулю. Поэтому, оба выражения для максимальной энергии соответствуют полной энергии контура. В общем случае в контуре с активным сопротивлением происходят потери энергии. Однако, в течение одного колебания эти потери ничтожно малы, поэтому можно приравнять максимальную электрическую и максимальную магнитную энергию. Частота колебательного контура определяется по формуле Преобразуем данное выражение Активное сопротивление определяется по формуле Из равенства максимальной электрической энергии и максимальной магнитной энергии получаем Получаем систему состоящую из двух уравнений Из первого уравнения получаем Из второго уравнения

Ответ: L = 2,2×10^–4 Гн; C = 1,7×10^–7 Ф.

Переменный электрический ток. Активное сопротивление. Действующие значения силы тока и напряжения

Переменный электрический ток. Активное сопротивление. Действующие значения силы тока и напряжения

Цели урока:

Образовательная: сформировать у учащихся представление о переменном токе. Рассмотреть основные особенности активного сопротивления. Раскрыть основные понятия темы.

Развивающая: развивать у учащихся умение применять полученные знания о переменном токе в практическом применении в быту, технике и на производственной практике; развивать интерес к знаниям, способность анализировать, обобщать, выделять главное.

Воспитательная: привить уважение к науке. Воспитывать у учащихся чувство требовательности к себе, дисциплинированность. Расширить рамки окружающего мира учащихся.

ХОД УРОКА

1.Организационный момент (объявление темы, задач и целей урока, психологическая подготовка учащихся к уроку).

Этот урок посвящён вынужденным электромагнитным колебаниям и переменному электрическому току. Вы узнаете,

— каким образом можно получить переменную ЭДС;

— какие соотношения существуют между силой тока и напряжением в цепях переменного тока;

— в чём разница между действующими и амплитудными значениями силы тока и напряжения.

2.Актуализация опорных знаний

1) Вопросы для фронтального опроса:

• Какие колебания называются электромагнитными?

• В каком устройстве создаются электромагнитные колебания?

• Из каких частей состоит колебательный контур?

• От каких величин зависит частота и период колебаний в контуре?

• Как будут меняться колебания в реальном контуре с течением времени?

3.Объяснение нового материала

1) Переменный ток

В электростатических машинах, гальванических элементах, аккумуляторах ЭДС с течением времени не меняла своего направления. В такой цепи ток шёл всё время, не меняя ни величины, ни направления и поэтому назывался постоянным.

Электрическая энергия обладает неоспоримым преимуществом перед всеми другими видами энергии. Её можно передавать по проводам на огромные расстояния со сравнительно малыми потерями и удобно распределять между потребителями. Главное же в том, что эту энергию с помощью достаточно простых устройств легко превратить в любые другие формы: механическую, внутреннюю, энергию света и т.д. На практике можно увидеть множество различных устройств, в которых электрическая энергия превращается в другие виды энергии. Примерами такого оборудования являются: картофелечистка, электромясорубка, хлеборезка… (слайд 4)

Всё это оборудование и многое другое включается в цепь, в которой протекает переменный электрический ток.

Переменный ток генерируется на электростанциях. Происходит рождение переменной ЭДС, которая многократно и непрерывно меняет свою величину и направление. Это происходит в генераторах – это машины, в которых ЭДС возникает в результате явления электромагнитной индукции.

Переменный ток имеет преимущество перед постоянным: напряжение и силу тока можно в очень широких пределах преобразовывать, трансформировать почти без потерь энергии.

Так что же представляет собой переменный электрический ток? (слайд 5) Электрический ток, изменяющийся во времени, называют переменным.

Переменный электрический ток вырабатывается в генераторах переменного тока, принцип работы которых основан на законе электромагнитной индукции. Вращение генератора осуществляется механическим двигателем, использующим тепловую, гидравлическую или атомную энергию.

Простейшей моделью такого генератора служит проволочный виток, который вращается в однородном магнитном поле.

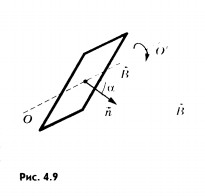
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции: Ф = BS cos α

При равномерном вращении рамки угол а увеличивается прямо пропорционально времени: α = ωt,

где 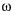— угловая скорость вращения рамки.

Поток магнитной индукции меняется по гармоническому закону: Ф = BS cos ωt

Здесь величина ω играет уже роль циклической частоты.

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «-» скорости изменения потока магнитной индукции, т. е. производной потока магнитной индукции по времени:

Ф = B∙S∙cos α = B∙S∙cos ωt

e = – Ф = – B∙S∙(cos ωt) = B∙S∙ω∙sin ωt = ε_m∙sin ωt,

где ε_m = B∙S∙ω – амплитуда ЭДС индукции.

Если к рамке подключить колебательный контур,  то угловая скорость ω вращения рамки определит  частоту ω колебаний значений ЭДС, напряжения на paзличныx участках цепи и силы тока.

Мы будем изучать в дальнейшем вынужденные электрические колебания, происходящие в цепях под действием напряжения, меняющегося с циклической частотой ω по закону синуса или косинуса:

u =  U_m ∙ sin ωt или u =  U_m cos ωt

где U_m— амплитуда напряжения, т. е. максимальное по модулю значение напряжения.

Если напряжение меняется с циклической частотой ω, то и сила тока в цепи будет меняться с той же частотой. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока і в любой момент времени (мгновенное значение силы тока) определяется по формуле:

i= I_m∙sin (ωt + φ_c)

Здесь I_m — амплитуда силы тока, т. е. максимальное по модулю значение силы тока, а φ_c — разность (сдвиг) фаз между колебаниями силы тока и напряжения. В промышленных цепях переменного тока сила тока и напряжение меняются гармонически с частотой v = 50 Гц. Переменное напряжение на концах цепи создается генераторами на электростанциях.

Рассмотрим принцип действия генератора: возьмем рамку, состоящую из n витков, и соединим ее с гальванометром с помощью колец и скользящих по ним контактов (щеток). Когда рамка вращается в магнитном поле постоянного магнита, то стрелка гальванометра совершает колебания около положения равновесия. Это означает, что в цепи появился переменный ток. Этот опыт моделирует работу генератора переменного тока. Конструкция и действие реального генератора, используемого в промышленности, значительно сложнее.

2) Активное сопротивление

Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R. Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.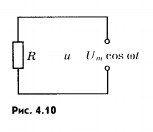

Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от  генератора.

Эта энергия превращается во внутреннюю энергию проводников — они  нагреваются.   Будем  считать, что напряжение на зажимах цепи меняется по гармоническому закону: u =  U_m sin ωt

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:

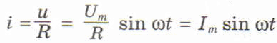
Из этой формулы следует, что колебания силы тока на резисторе совпадают по фазе с колебаниями напряжения. Амплитуда силы тока определяется равенством

Мощность в цепи с резистором

В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найти среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

P = I²R.

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным. Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой P = i²R

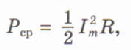
Среднее значение мощности за период

График зависимости мгновенной мощности от времени изображен на рисунке

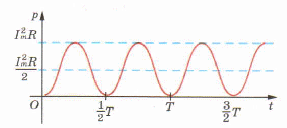
График изменения мгновенной мощности с течением времени

Несмотря на то что мощность переменного тока непрерывно меняется, ее среднее значение за любой период одинаково.

Приравниваем выражения для средней мощности переменного тока и мощности постоянного тока:

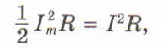
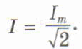
Выразим силу тока I: Эту величину называют действующим значением силы переменного тока.

Действующее значение силы переменного тока равно силе такого постоянного тока, который выделяет в проводнике ту же мощность, что и переменный ток за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока: — эту величину называют действующим значением напряжения переменного тока.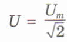

Действующее значение напряжения в осветительной сети равно 220 В, а амплитудное значение напряжения при этом составляет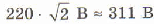

С учетом предыдущих формул можно выразить среднюю мощность переменного тока: Р_ср = IU

Амперметры и вольтметры переменного тока обычно градуируют по действующим значениям силы тока и напряжения.

4.Закрепление и обобщение нового материала.

Итак, что же сегодня мы с вами выяснили на уроке:

— что представляет собой переменный электрический ток переменный электрический ток?

— на каком явлении основано получение переменной ЭДС в цепи?

— чему равна разность фаз колебаний силы тока и напряжения на активном сопротивлении?

— как соотносятся действующие значения переменного тока и напряжения со значениями постоянного тока и напряжения?

— как определяется мощность в цепи переменного тока?

Решение задачи:

5.Подведение итогов урока. (Выставление оценок и их комментарий)

6.Задание на дом: § 31, 32; Г.Я.Мякишев, Б.Б.Буховцев «Физика – 11», упр.4(№5)

действующие значения силы тока и напряжения

 

Рассмотрим следующую цепь.

рисунок

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Активное сопротивление

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = Um*cos(ω*t).

Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.

I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).

Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.

 Действующее значение силы тока

Амплитуда силы тока определяется по следующей формуле:

Im = Um/R.

Среднее значение квадрата силы тока за период вычисляется по следующей формуле:

i^2 = (Im)^2/2.

Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока. 

Для обозначения действующего значения силы тока используется буква I. То есть в виде формулы это будет выглядеть следующим образом:

I = √(i^2) = Im/√2.

Действующее значение силы переменного тока будет равно силе такого постоянного тока, при котором за одинаковый промежуток времени в рассматриваемом проводнике будет выделяться столько же теплоты, сколько и при переменном токе. Для определения действующего значения напряжения используется следующая формула.

U = √(u^2) = Um/√2.

Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:

I = U/R.

Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения. 

Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

Для вычисления средней мощности используется следующая формула:

P = (I^2)*R = U*I.

Нужна помощь в учебе?

Предыдущая тема: Переменный электрический ток: формулы и примеры
Следующая тема:&nbsp&nbsp&nbspКонденсатор в цепи переменного тока: изменение силы тока в цепи

Все неприличные комментарии будут удаляться.

Действующие значения силы тока и напряжения.

Презентация по физике

Переменный электрический ток. Активное сопротивление. Действующие значения силы тока и напряжения.

Выполняли ученицы 11 «А» класса Радукан Яна, Иванова Алина.

Переменный электрический ток

• Как известно, ток (электрический) бывает переменным и постоянным.Переме́нный ток (англ. alternating current — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению.В настоящее время очень широко используется переменный электрический ток. Его можно получить с помощью электрогенераторов переменного тока с применением эффекта электромагнитной индукции. На рисунке изображена примитивная установка для выработки переменного тока.

• Принцип действия установки прост. Проволочная рамка вращается в однородном магнитном поле с постоянной скоростью. Своими концами рамка закреплена на кольцах, вращающихся вместе с ней. К кольцам плотно прилегают пружины, выполняющие роль контактов. Через поверхность рамки непрерывно будет протекать изменяющийся магнитный поток, но поток, создаваемый электромагнитом, останется постоянным. В связи с этим в рамке возникнет ЭДС индукции.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

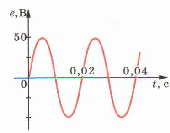
Ф = BScoswt «

Переменный ток в осветительной сети квартиры, применяемый па заводах и фабриках и т. д., представляет собой не что иное, как вынужденные электромагнитные колебания. Данные колебания напряжения легко обнаружить с помощью осциллографа.(рис. 4.8)

Стандартная частота промышленного переменного тока равна 50 Гц. Это означает, что на протяжении 1 с ток 50 раз идет в одну сторону и 50 раз — в противоположную. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц. Если напряжение на концах цепи меняется по гармоническому закону, то и напряженность электрического поля внутри проводников будет также меняться гармонически.

Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока. Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла а между нормалью к рамке и вектором магнитной индукции (рис. 4.9):

Ф = BScos а

При равномерном вращении рамки угол а увеличивается прямо пропорционально времени: а=2Пnt , где n – частота вращения.Поэтому поток магнитной индукции меняется гармонически :

Ф = BS cos 2Пnt , Здесь 2Пn число колебаний магнитного потока за 2П с. Это ЦИКЛИЧЕСКАЯ ЧАСТОТА колебаний w=2Пn = Ф = BScoswt

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «-» скорости изменения потока магнитной индукции, т. е. производной потока магнитной индукции по времени:

Если к рамке подключить колебательный контур,  то угловая скорость w вращения рамки определит  частоту w колебаний значений ЭДС, напряжения на paзличныx участках цепи и силы тока.

Если напряжение меняется с циклической частотой , то и сила тока в цепи будет меняться с той же частотой. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока і в любой момент времени (мгновенное значение силы тока) определяется по формуле

Здесь I m — амплитуда силы тока, т. е. максимальное по модулю значение силы тока, а — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Активное сопротивление .

Действующие значения силы тока и напряжения.

Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.

Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от  генератора. Эта энергия превращается во внутреннюю энергию проводников — они  нагреваются.   Будем  считать, что напряжение на зажимах цепи меняется по гармоническому закону:

u = U m cos w t

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома :

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найти среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой :

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения (рис. 4.17), а амплитуда силы тока определяется равенством

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение

Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой :

P = i 2 R. (4.19)  

Средняя мощность

равна первому члену в формуле (4.20)

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем закон Ома для участка цепи переменного тока с резистором

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:

P = I 2 R = UI.

Конденсатор в цепи переменного тока

Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком.

Пусть у нас имеются источники постоянного и переменного напряжений, причем постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 4.13), соединенных последовательно. При включении постоянного напряжения (переключатель повернут влево, цепь подключена к точкам АА’) лампа не светится. Но при включении переменного напряжения (переключатель повернут вправо, цепь подключена к точкам ВВ’) лампа загорается, если емкость конденсатора достаточно велика.

Переменный же ток может идти по цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.

Как же переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Все дело в том, что происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.

Сила тока, представляющая собой производную заряда по времени , равна:

Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь (рис. 4.14).

Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на

(рис. 4.15).

Напряжение на конденсаторе

Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.

Амплитуда силы тока равна:

I m = U m C

(4.29)

Если ввести обозначение :

В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение X c . С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим :

C

Величину X c , обратную произведению

циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением .

Сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания  напряжения на

Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.

КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта.

Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока.

Соберем цепь из катушки с большой индуктивностью и электрической лампы накаливания (рис. 4.16). С помощью переключателя можно подключить эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть равны.

Объясняется это различие явлением самоиндукции.

Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.

Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.

Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (рис. 4.17). Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.

i

k

=

—

Из равенства

следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции е і ) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: е і = -u.

Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля

При изменении силы тока по гармоническому закону :

t

i =  I m   sin

ЭДС самоиндукции равна:

порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля

e і = — L i ‘ = — L

l m cos

t.

Так как u = -е і , то напряжение на концах катушки оказывается равным

создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на

Индуктивное сопротивление зависит от частоты

что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на (рис. 4.18)

Постоянный ток вообще «не замечает» индуктивности катушки. При = 0

индуктивное сопротивление равно нулю (X L = 0).

Амплитуда силы тока в катушке равна:

Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.

Катушка индуктивности оказывает сопротивление переменному току.

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим:

Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.

Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на

Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Согласно формуле (4.35) действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.

Спасибо за внимание!

Источники:https://vk.com/away.php?to=http%3A%2F%2Fselectelement.ru%2Fbasic-concepts%2Felectric-ac.php&cc_key= https://vk.com/away.php?to=https%3A%2F%2Fsites.google.com%2Fsite%2Fopatpofizike%2Fteoria%2Fteoria-11-klass%2Feds-zakon-oma-dla-polnoj-cepi%2Fperemennyj-elektriceskij-tok-aktivnoe-induktivnoe-eemkostnoe-soprotivlenia&cc_

Действующие значения силы тока и напряжения

Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.

Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:

Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.

Действующие значения периодических и синусоидальных токов

Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока. В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу:

Для колебаний более сложной формы тем же способом будем получать иные формулы. Например, пилообразный ток имеет действующее значение, определяемое по формуле: