амплитудное значение напряжение | Электрознайка. Домашний Электромастер.

Действующее значение синусоидального
переменного напряжения – тока.

data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.

Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax .  Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой   Т.
Количество периодов переменного тока за 1 секунду, есть частота  f.
Частота переменного тока f измеряется в герцах .

f = 1 / T.

Например.
Частота в нашей электрической сети 50 Гц.  Период этих колебаний будет равен:

T = 1 / f = 1 / 50 = 0,02 сек.

Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.

Umax = Ua и Imax = Ia

За один период напряжение принимает эти значения два раза: + Ua  и  — Ua .

♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного

напряжения Uд и тока Iд.

Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.

♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.
Следовательно действующее (или эффективное) значение переменного тока будет равно:

Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока

Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения

На все эти теоретические размышления можно посмотреть иначе!

   ♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.
После выпрямительных диодов оно принимает вид как на рисунке 2.

Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.

    ♦На рисунке приняты обозначения:

Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение  Ua примем за единицу.

Из формулы приведенной выше Uд = 1 / 1,41 = 0,707

 — действующее напряжение равно 0,707 от амплитудного значения        Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах.

P = Ua х Ia = Uд х Iд = U х I

♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт.
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.

Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.

data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>

Параметры переменного напряжения | Практическая электроника

Как вы помните из предыдущей статьи, переменное напряжение – это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср – это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

среднее значение напряжения за период

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком “минус”. А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр – это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

меандр

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая “пробивает пол” берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

выпрямленное переменное напряжение после диодного моста

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже  простым графиком не отделаешься. Среднеквадратичное значение –  это значение постоянного напряжения, который, проходя через  нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение  обозначается так:

RMS (rms) – root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 – это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS – как вы уже знаете – это среднеквадратическое значение. А что за буква “T” впереди? Думаю, вы помните, как раньше была мода на одно словечко: “тру”. “Она вся такая тру…”, “Ты тру или не тру?” и тд. Тру (true) – с англ. правильный, верный.

Так вот, T-RMS  расшифровывается как True RMS –  “правильное среднеквадратическое значение”. Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип “T-RMS”.

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал “пол” или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов – это двуполярный меандр, ну тот есть тот, который “пробивает пол”.

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

• Сред.  – средневыпрямленное значение сигнала. Это и есть площадь под кривой
• СКЗ – среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
• Пик. – амплитудное значение сигнала
• Пик-пик. – размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее  и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

Прописные истины для новичков. — Начинающим — Теория

Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.

Закон Ома.

Основным законом, которым руководствуются радиолюбители — является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm,  1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.
Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.
I = U/R, где R — электрическое сопротивление проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать  U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.

Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля — Ленца. Звучит так;

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.

Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.
В центре искомые величины, а в секторах с соответствующими цветами — варианты решений в зависимости от известных величин.

Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье — треугольник Ома.
Выглядит она следующим образом:

В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

• — ЭДС цепи,
• I — сила тока в цепи,
• R — сопротивление всех элементов цепи,
• r — внутреннее сопротивление источника питания.

Закон Ома для полной цепи звучит так — Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Электрические измерения.

Нарисуем простейшую электрическую цепь, состоящую из батареи «В» и нагрузки «R», и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.

Что бы измерить протекающий в цепи ток, необходимо в разрыв источника питания и нагрузки включить измерительный прибор (амперметр).
Для того, что бы на измеряемую цепь было как можно меньше влияний и для повышения точности измерения, амперметры изготавливают с очень малым внутренним сопротивлением, то есть если включить амперметр в разрыв проверяемой цепи, то он практически не добавит к измеряемой цепи дополнительного сопротивления, и протекающий по цепи ток практически не изменится, или уменьшится на очень незначительную величину не оказывающую значительного влияния на конечный результат измерения.
Поэтому категорически нельзя измерять «ток приходящий на нагрузку» путём подключения амперметра параллельно нагрузке, или непосредственно у источника питания (без нагрузки) и таким образом попытаться замерить выходной ток выдаваемый источником питания или осветительной сетью.
Это равносильно тому, что подключить параллельно нагрузке или источнику питания обычный провод. Попросту сказать — закоротить цепь.
Если источник питания обладает хорошей мощностью — будет очень сильный Б А Х !!! Последствия могут быть самыми разными, от выхода из строя измерительного прибора (амперметра), что обычно и случается, и до выбитых пробок (АЗС) в квартире и обесточивания помещения и возможного поражения током.

Для измерения напряжения на нагрузке необходимо, что бы подключаемый к ней вольтметр не шунтировал нагрузку и не оказывал заметного влияния на результат измерения. Для этого вольтметры изготавливают с очень высоким входным сопротивлением и их наоборот подключают параллельно измеряемой цепи. Благодаря высокому входному сопротивлению вольтметра — сопротивление измеряемой цепи практически не изменяется, или изменяется очень не значительно, не оказывая заметного влияния на результат измерения.

На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.

Постоянный и переменный ток.

Кратко напомню — постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.
Переменный ток (AC) — это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению.

На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.

Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Возникает вопрос, как же его измерять? Для его измерения и введено понятие — «Действующее (или эффективное) значение» переменного тока.

Что же такое действующее (или эффективное) и амплитудное значение переменного тока?
Как Вам попроще объяснить, чтобы было понятно.
Действующее (эффективное) значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время, выделяет такое же количество энергии.
То есть если к какой либо активной нагрузке (нагревательный элемент, лампа накаливания, резистор и т.д.) подключить переменный ток, который за определённый промежуток времени (например 10 секунд) выделит на активной нагрузке то-же количество энергии, тепла на нагревательном элементе, резисторе, или разогреет спираль лампы накаливания до точно такой же светоотдачи, что и постоянный ток какой-то определённой величины за тот же промежуток времени (тоже 10 секунд) — то тогда действующее (эффективное) значение такого переменного тока будет равняться величине постоянного тока.

Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.

Что такое «Амплитудное значение» переменного тока?
Если объяснять попроще, то это самое максимальное значение (величина) синусоидального тока на самом пике (максимуме) синусоиды.
Амплитудное значение переменного тока можно измерить электронно — лучевым осциллографом, так как все осциллографы откалиброваны на измерение амплитудных значений.

Поскольку действующее значение переменного синусоидального тока пропорционально квадратному корню из площади, то оно получается в 1,41 раза меньше его амплитудного значения.
Проще говоря — если измерить величину переменного тока (напряжения) электроизмерительными приборами, отградуированными для измерения переменного синусоидального тока (напряжения), то есть например замерить величину переменного напряжения на вторичной обмотке трансформатора, — то амплитудное значение напряжения на этой обмотке будет соответственно в 1,41 раз больше замеренного.
Это справедливо только для переменного синусоидального тока (напряжения).

Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.

Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).

Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.

Для действующего значения переменного синусоидального напряжения (тока) — справедливы формулы для расчётов сопротивлений, мощности, действующих токов и напряжений — приведённые выше в Законе Ома для постоянного тока.

Ответим на вопросы в начале статьи;

Как рассчитать шунт для амперметра?
Большинство отечественных измерительных головок для амперметров, рассчитываются на полное отклонение при подведении к ним напряжения в 75 мВ (0,075 вольта). У них на шкале имеется надпись «НШ — 75 мВ», или «Наружный шунт 75 мв», или что-то подобное.
Нам стало известно две величины, а именно — необходимый нам ток полного отклонения и напряжение полного отклонения измерительной головки.
Например, нам нужно рассчитать шунт на 20 ампер. По Закону Ома 0,075 делим на 20 = 0,00375 Ом.
Изготовить такой шунт можно из медной проволоки, посмотрев её удельное сопротивление по таблице ЗДЕСЬ . Только необходимо брать проволоку, диаметром желательно не менее 1,5 мм, так как шунт при большом токе будет греться, и показания прибора будет изменяться (при нагреве проволоки увеличится её внутреннее сопротивление).

Почему из 12 вольт переменного напряжения, стало около 16 вольт постоянного — надеюсь Вам стало понятно. У переменного напряжения 12 вольт (действующее его значение) — амплитудное значение будет в 1,41 раз больше, то есть 16,92 вольта, минус около вольта падение напряжения на диодах. В итоге получается около 16 вольт — до которых и заряжаются электролитические конденсаторы фильтра.

Как правильно измерить мощность УНЧ?
Давайте для начала вспомним теорию.
Выходная мощность усилителей НЧ измеряется на синусоидальном сигнале. У идеального двухтактного выходного каскада, максимальное амплитудное значение синусоидального сигнала на выходе может приблизиться к величине равной половине напряжения источника питания.
У каскада по мостовой схеме, выходное напряжение может приблизиться к величине напряжения источника питания.
Говоря другими словами, у автомобильной магнитолы при напряжении питания 13,5 вольт, для двухтактного выходного каскада максимальное выходное напряжение (синус) будет 6,5 вольт, а его действующее значение 4,6 вольта, для мостовой схемы соответственно 13 В. и 9,2 вольта.
Возьмём минимальную нагрузку для этих усилителей 2 Ома, соответственно максимальная выходная мощность (исходя из Закона Джоуля — Ленца) для первой магнитолы, которую она выдаст теоретически — будет 10,6 ватта, для второй — 42,3 ватта (это для нагрузки 2 Ома). На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность.

В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными «цешками» или бытовыми «цифровиками», так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.
Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт — это развод, рекламный ход и т.д., если только для питания этого усилителя не применяется повышающий преобразователь.

 

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мс =0,001сек =10^-3сек.

1 мкс=0,001 мс = 0,000001сек =10^-6сек.

1000 мкс = 1 мс.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10³ Гц = 1 кГц;

1000 000 Гц = 10⁶ Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10⁹ Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

Тогда,

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в тече­ние одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его ко­нец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.

Итак,

?= 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Переменное напряжение и его значения — Help for engineer

Переменное напряжение и его значения

Все мы знаем, что дома в розетках у нас напряжение 220В. Но не каждый знает, какое именно это напряжение. Давайте же разберемся с этой ситуацией.

Для упрощения рассматриваемого примера будем считать, что вид напряжения – синусоида, то есть переменное напряжение (с определенной периодичностью меняет значение с положительного на отрицательное).

Рисунок 1 – Вид переменного напряжения

На рисунке 1 изображен вид идеального синусоидального напряжения одного периода Т. Есть несколько значений напряжения, о которых обычно говорят и используют, рассмотрим:

Амплитудное значение напряжения (Um) – это максимальное, мгновенное значение напряжения, то есть амплитуда синусоиды.

Теперь правильнее будет говорить о токе.

Действующее значение переменного тока — это величина постоянного тока, который может выполнить ту же самую работу (нагрев).

Действующее значение напряжения (U) обозначают латинской буквой без индекса, в литературе может еще использоваться термин – эффективное значение напряжения.

Для периодически изменяющегося сигнала за период Т, величина действующего напряжения находится:

Приведем формулу к простому виду, приняв за изменяющийся сигнал синусоиду. Между рассмотренными выше двумя параметрами существует зависимость, которая выражается формулой:

То есть амплитудное значение в 1,414 раза больше действующего.

Вернемся к домашним розеткам с напряжением 220В. Это действующее значение напряжения, которое можно измерить тестером. Определим его амплитудное значение напряжения:

Среднее значение синусоидального тока, напряжения будет равно нулю. Поэтому если говорят о среднем значении переменного тока, то подразумевают рассматривание его в пол периода.

Недостаточно прав для комментирования

амплитудное, среднее, среднеквадратическое и средневыпрямленное значение.

Уровень переменного напряжения можно определить по амплитудному, среднеквадратическому, среднему или средневыпрямленному значениям. Амплитуда(пиковое значение) Um-наибольшее мгновенное значение напряжения за интервал наблюдения или за период. Измеряемые на практике напряжения могут иметь различный вид, например, форму импульсов, синусоидального или несинусоидального колебаний- суммы синусоиды с постоянной составляющей и т.д. При разнополярных несимметричных кривых формы напряжения различают два амплитудных значения: положительное Um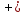 и отрицательное Um.

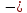Среднее квадратическое значение напряжения есть корень квадратный из среднего квадрата его мгновенного значения за время измерения(за период):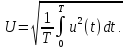

Если периодический сигнал несинусоидален, то квадрат среднего квадратического значения равен сумме квадратов постоянной составляющей и средних квадратических значений гармоник :

= +++ …

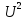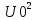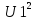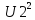Среднее значение(постоянная составляющая) напряжения равно среднему арифметическому всех мгновенных значений за период :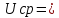

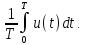
Средневыпрямленное напряжение определяется как среднее арифметическое абсолютных мгновенных значений за период :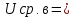

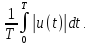
Для напряжения одной полярности среднее и средневыпрямленное значения равны. Для разнополярных напряжений эти значения могут существенно отличаться. Так, для гармонического напряжения .

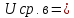
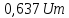Чаще измеряют среднее квадратическое изменение напряжения, так как этот параметр связан с мощностью, нагревом, потерями. Однако проще измерить амплитудное или средневыпрямленное значение и произвести пересчёт с применением коэф. Амплитуды Ка и формы Кф : Ка = , Ка =.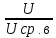

В частности, для синусоидальной (гармонической) формы переменного напряжения : Ка = 1,41; Кф = 1,11.

Значения этих коэффициентов для наиболее употребляемых видов сигналов и соотношения между ними даны в табл., где все напряжения для упрощения обозначены буквой .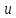

2 Преобразователи пикового значения: с открытым и закрытым входами: схемы, принцип действия.

Преобразователи пикового значения. Особенность преобразо­вателя этого вида заключается в том, что напряжение на его вы­ходе непосредственно соответствует пиковому (амплитудному) значению напряжения, поданного на вход преобразователя. Он должен содержать элемент, запоминающий пиковое значение напряжения. Обычно это конденсатор, заряжаемый через диод до пи­кового значения.

Необходимо подчеркнуть, что преобразователи пикового зна­чения, которые в дальнейшем для кратности будем называть пи­ковыми, — самые широкополосные преобразователи напряжения переменного тока в напряжение постоянного тока.

Пиковый (амплитудный) детектор — это детектор, напряжение на выходе которого непосредственно соответствует измеряемому пиковому (амплитудному) значению напряжения. Пиковый детектор должен содержать элемент, запоминающий пиковое значение напряжения. Таким элементом обычно служит конденсатор, заряжаемый через диод до пикового значения.

Пиковые детекторы

При измерении напряжений, не содержащих постоянной составляющей, детекторы с открытым и закрытым входом дают одинаковые результаты: напряжения на конденсаторах С в обоих случаях весьма близки к U_м и показания обоих вольтметров пропорциональны амплитуде измеряемого напряжения.

Если ко входу (рис. а), подводится напряжение u_х = U_о + U^′_мsinωt, в котором содержатся и постоянная и переменная составляющие, то прибор будет измерять пиковое значение U_м =U_о + U^′_м. В случае подачи пульсирующего напряжения на вход детектора с закрытым входом вольтметр измеряет пиковое значение U^′_м напряжения без постоянной составляющей.

ФИЗИКА

Министерство сельского хозяйства Российской федерации

ФГБОУ ВПО «Оренбургский государственный аграрный университет»

Институт управления рисками и комплексной безопасности

Кафедра «Автоматизированные системы обработки информации и управления»

Реферат

на тему:

«Переменный ток»

Выполнил: студент 21ИВТ

Туканова Д.

Проверил: к.ф.-м.н., доцент

Каррыев А.Н.

Оренбург 2014

План

1. Переменный ток, текущий через резистор.

2. Переменный ток, текущий через индуктивность.

3. Переменный ток, текущий через конденсатор.

4. Цепь переменного тока, содержащая активное и реактивное сопротивления (нагрузки).

5. Мощность, выделяемая в цепи переменного тока. Действующие значения тока и напряжения.

6. Использованная литература

Переменный ток, текущий через резистор.

При выполнении условия квазистационарности ток через резистор опреде­ляется законом Ома:

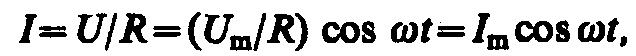
где амплитуда силы тока I_m= U_m/R.

Для наглядного изображения соотношений между переменными токами и напряже­ниями воспользуемся методом векторных диаграмм. На рис. 213, б дана векторная диаграмма амплитудных значений тока I_m и напряжения U_m на резисторе (сдвиг фаз между I_m и U_m равен нулю).

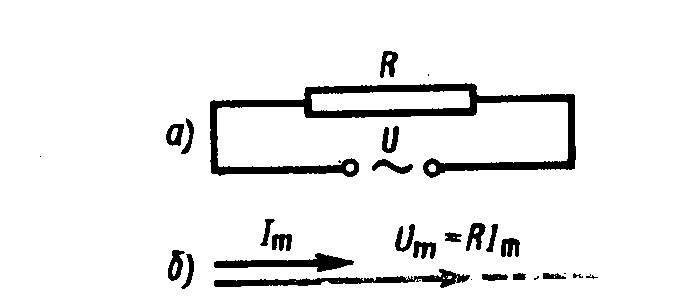
Переменный ток, текущий через индуктивность.

Если в цепи приложено переменное напряжение, то в ней потечет переменный ток, в результате чего возникнет э.д.с. самоиндукции 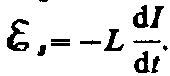. Тогда закон Ома для рассматриваемого участка цепи имеет вид

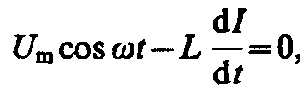
откуда

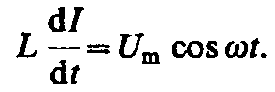
Так как внешнее напряжение приложено к катушке индуктивности, то

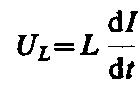
есть падение напряжения на катушке. Из уравнения выше следует, что

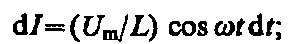
после интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим

где I_m= U_m/(L). Величина

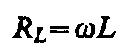
называется реактивным индуктивным сопротивлением (или индуктивным сопротивлени­ем). Из выражения 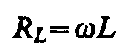вытекает, что для постоянного тока ( = 0) катушка индук­тивности не имеет сопротивления. Подстановка значения U_m=LI_m в выражение 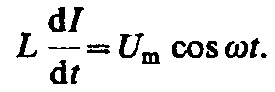с учетом 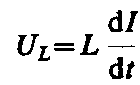приводит к следующему значению падения напряжения на катушке индуктивности:

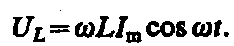
Сравнение выражени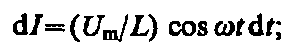й и 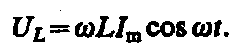приводит к выводу, что падение напряжения U_L опережает по фазе ток I, текущий через катушку, на /2, что и показано на векторной диаграмме (рис. б).

Переменный ток, текущий через конденсатор.

Если переменное напряжение приложено к конденсатору, то он все время перезаряжается, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренеб­речь, то

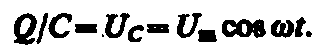
Сила тока

где

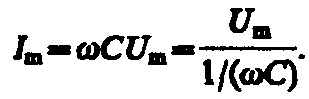
Величина

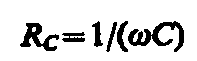
называется реактивным емкостным сопротивлением (или емкостным сопротивлением). Для постоянного тока ( = 0) R_С = , т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе

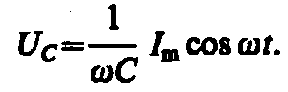
Сравнение выражений выше приводит к выводу, что падение напряжения U_С отстает по фазе от текущего через конденсатор тока I на /2.

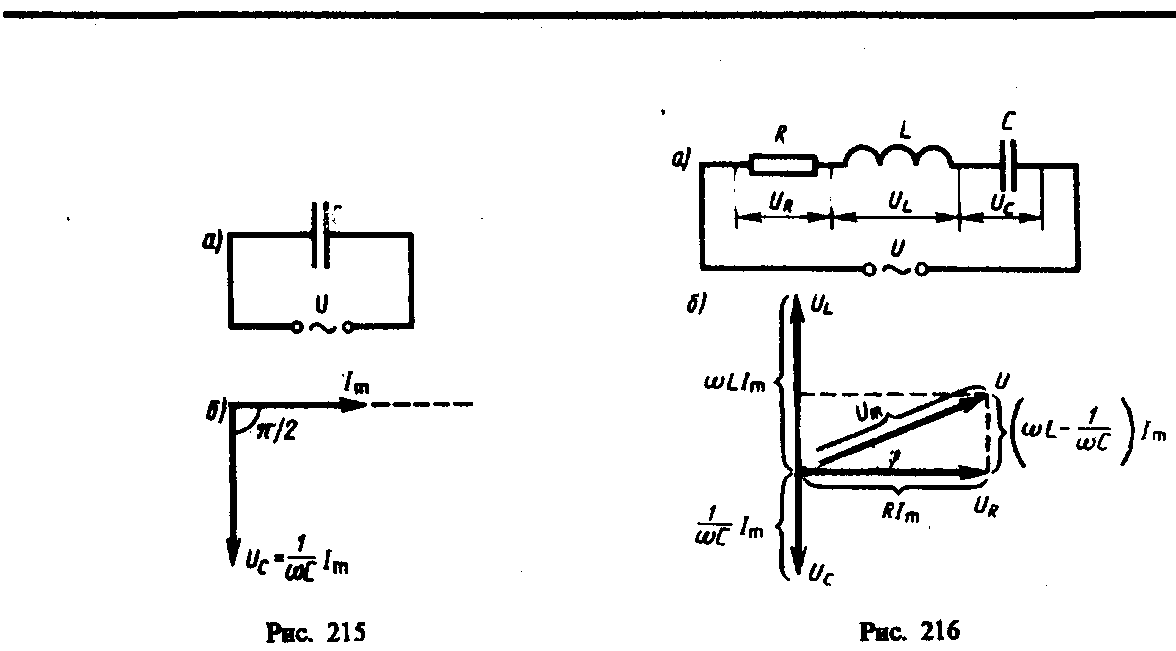
Цепь переменного тока, содержащая активное и реактивное сопротивления (нагрузки).

На рис. 216, а представлен участок цепи, содер­жащий резистор сопротивлением R, катушку индуктивностью L и конденсатор ем­костью С, к концам которого приложено переменное напряжение. В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения U_R, U_L и U_C. На рис. 216, б представлена векторная диаграмма амплитуд падений напряжений на резисторе (U_R), катушке (U_L) и конденсаторе (U_C). Амплитуда U_m приложенного напряжения должна быть равна векторной сумме амп­литуд этих падений напряжений. Как видно из рис. 216, б, угол  определяет разность фаз между напряжением и силой тока. Из рисунка следует, что

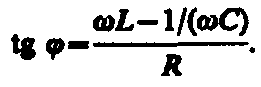
Из прямоугольного треугольника получаем откуда ам­плитуда силы тока имеет значение

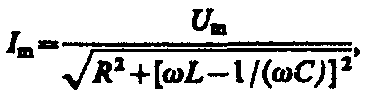
Следовательно, если напряжение в цепи изменяется по закону U = U_mcos  t, то в цепи течет ток

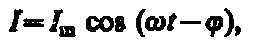
где  и I_m определяются соответственно формулами, представленными выше. Величина

называется полным сопротивлением цепи, а величина

– реактивным сопротивлением.

Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_R и U_L в сумме равны приложенному напряжению U. Векторная диаграмма для данного случая представлена на рисунке, из которого следует, что

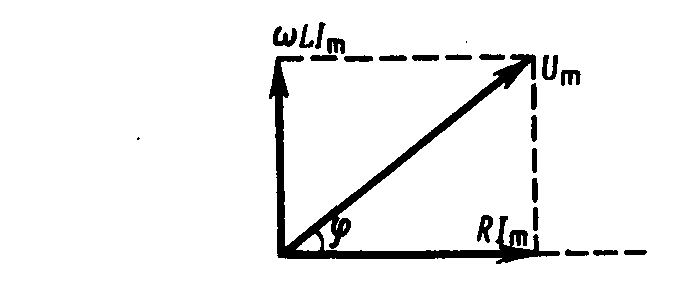
Выражения выше совпадают с данным, если в них 1/(C)=0, т.е. С=. Следовательно, отсутствие конденсатора в цепи означает С=, а не С=0. Данный вывод можно трактовать следующим образом: сближая обкладки конденсатора до их полного соприкосновения, получим цепь, в которой конденсатор отсутствует (расстоя­ние между обкладками стремится к нулю, а емкость — к бесконечности).

Мощность, выделяемая в цепи переменного тока. Действующие значения тока и напряжения.

Мгновенное значение мощности переменного тока равно произведению мгновенных значений напряжения и силы тока:

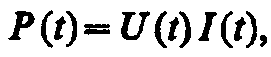
где U(t)=U_mcost, I(t)=I_mcos(t – ). Раскрыв cos(t – ), получим

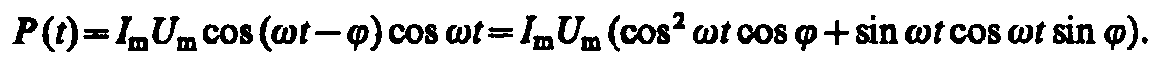
Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что cos² t= ¹/₂, sin  t cos  t = 0, получим

Как мы уже знаем, U_mсos  = RI_m. Поэтому

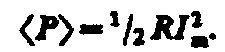
Такую же мощность развивает постоянный ток .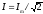

Величины

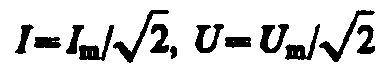
называются соответственно действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения.

Учитывая действующие значения тока и напряжения, выражение средней мощности можно записать в виде

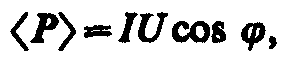
где множитель соs  называется коэффициентом мощности.

Формула показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cos =1 и P=IU. Если цепь содержит только реактивное сопротивление (R=0), то cos=0 и средняя мощ­ность равна нулю, какими бы большими ни были ток и напряжение. Если cos имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить соs, наименьшее допустимое значение которого для промышленных уста­новок составляет примерно 0,85.

Использованная литература

1. Трофимова Т.И. Курс физики – 12-е издание, Москва, 2006, п. 149-152.

2. Википедия свободная энциклопедия — http://ru.wikipedia.org/wiki/переменный_ток.