Первый закон Кирхгофа для электрической цепи

Электротехника это точная наука и, как любая наука, не может обойтись без формул. Они нашли отображение в нескольких фундаментальных законах или правилах, один из которых первый закон Кирхгофа. Он используется при расчётах силы тока в проводах и различных участках электропроводки.

Теория: что такое узел, ветвь, контур

Электрические цепи состоят из ветвей, узлов и контуров.

Ветвь электросхемы

Это основной элемент цепи, на всём протяжении которого протекает один и тот же ток. В простейшем случае это отрезок провода, ветвью так же является электроприбор, включённый в розетку и подходящий к этой розетке кабель.

 

Каждая из ветвей, в свою очередь, может разделяться в узлах на несколько новых ветвей. Ветви могут соединяться между собой параллельно, в узлах, и последовательно. В последнем случае они образуют новую ветвь бОльших размеров.

Узел цепи

Место соединения ветвей в электросхеме называются узлом. Закон Кирхгофа для электрической цепи описывает распределение тока в различных ветвях, подключённых к одному узлу.

Применительно к электропроводке узлом является подключение нескольких проводов к одному автомату или к одной клемме, а так же блок розеток или двойная розетка.

Что такое контур

Все электрические сети включают в себя источник тока. В электрическом фонарике это батарейка и весь контур прослеживаются визуально, а в системе электроснабжения жилого дома им является трансформаторная подстанция, которая может находиться за несколько километров.

В таких сетях мощность источника тока многократно превышает мощность квартирной проводки, поэтому при проектировании электропроводки параметры трансформатора не учитываются и расчёт производится только для цепи, включающей в себя несколько узлов. 

Определение

Первый закон Кирхгофа для электрической цепи основан на законе сохранения заряда или на законе сохранения энергии. Согласно этим законам количество «электричества», приходящее в узел, должно быть равно уходящему из него.

Поэтому у этого правила есть две формулировки:

1. №1. Алгебраическая сумма токов в узле равна нулю. Это алгебраическая сумма, в которой положительное значение «+» имеет ток направленный в точку узла, а отрицательное значение «-«, это ток отходящий от узла. Такая формула применяется при расчётах сложных схем.
2. №2. Сумма токов, втекающих в узле равна сумме токов вытекающих из узла. Это арифметическая сумма, без учёта знака величины.

Важно! В сетях переменного тока, особенно высокой частоты, имеются потери, связанные с ёмкостью линии. Величину этих потерь невозможно измерить прямыми методами, что приводит к кажущемуся нарушению первого правила Кирхгофа.

Формула первого правила Кирхгофа

Как и любой другой закон электротехники 1 закон Кирхгофа выражается формулой, имеющей два варианта написания. Для примера можно взять узел с двумя входящими проводами и токами в них I1 и I2 и тремя отходящими I3, I4 и I5:

• Алгебраическая сумма. Получается преобразованием предыдущей формулы Σk-Σm=0 или I1+I2-I3-I4-I5=0. Это выражение применяется при сложных расчётах электронных схем.
• Арифметическая сумма
  . Σk=Σm или I1+I2=I3+I4+I5. Здесь k — подходящие линии, а m — отходящие. Такая формула используется при определении сечения токопроводящих жил для однофазной электропроводки или однолинейной схемы систем электроснабжения, а так же необходимой мощности блоков питания.

Такие уравнения составляются для каждого узла сети, причём нижестоящий узел является ветвью для вышестоящего. Это видно при составлении однолинейной схемы.

Информация! Ток в подходящих проводах считается положительным, а в отходящих отрицательным.

Для трёхфазной сети

Чаще всего трёхфазные сети переменного тока выполняются по схеме с рабочей нейтралью. При этом место соединения фазных проводов с нолём является узлом и подчиняется первому правилу Кирхгофа, однако эта формула имеет более сложный вид.

Дело в том, что в сетях переменного тока кроме активного протекает реактивный, индуктивный или ёмкостной ток. В результате ток в проводах разных фаз сдвинут не на 120°, а на другую величину.

Для расчётов в таких сетях вычерчивается векторная диаграмма и при вычислении величины тока в нейтрали складывается не величина тока, а соответствующий вектор ↑In=↑Ia+↑Ib+↑Ic.

Из-за сложности такого расчета, как правило, он не выполняется, а вместо него производится максимально равномерное распределение нагрузки по фазам, а сечение нейтрального проводника не выбирается, а используется предлагаемое производителями кабельно-проводниковой продукции.

Расчеты электрической цепи с помощью первого закона Кирхгофа

Первый закон Кирхгофа используется для расчёта силы тока и сечения проводов электропроводки и мощности блоков питания.

Расчёт электропроводки

Электропроводка и линии электроснабжения имеют форму дерева — кабель с бОльшим сечением и силой тока делится в узле на несколько ветвей с меньшим сечением и силой тока. При этом Iвх=ΣIвых.

Например, при подключении к линии электроприборов с номинальным током 5 А, 4 А и 2 А ток в подходящем кабеле составит Iвх=5+4+2=11А.

Расчёт блока питания

Большинство электроприборов подключаются непосредственно к сети переменного тока 220 В, но есть аппараты, которым необходимо пониженное напряжение. Такие устройства присоединяются к блокам питания.

Например, имеются два источника постоянного напряжения 12 В с силой тока 1,5 А и 2,5 А. Необходимо узнать, какую светодиодную ленту можно подключить к этим устройствам, если их включить параллельно.

Этот расчёт производится по формуле Iвых=ΣIвх=1,5А+2,5А=4А. Следовательно, ток потребления этой ленты может быть не более 4 А или 48 Вт.

Вывод

Первый закон Кирхгофа определяет связь между силой тока в подходящих и отходящих проводах одного узла. Электрический ток это направленное движение заряженных частиц и, согласно закону сохранения массы и энергии, сколько этих элементов подходит, столько же и должно отходить.

Этот закон используется при расчёте сечения токопроводящих жил и мощности источника питания.

Похожие материалы на сайте:

• Формула для емкости конденсатора
• Электрическое (активное) сопротивление
• Индуктивное сопротивление

Закон Кирхгофа в элекротехнике

В расчетах электрических цепей переменного и постоянного тока кроме знаменитой формулы Ома также применяется закон Кирхгофа. Человек, работа которого связана с электротехникой, должен даже среди ночи без запинки дать определения для каждого из двух законов. Часто это необходимо не столько для выполнения расчетов, сколько для понимания происходящих процессов.

В далеком 1845 году германский физик Густав Кирхгоф на основании трудов Максвелла (сохранение заряда и свойства электростатического поля) сформулировал два Правила, позволяющие указать соотношение между током и напряжением в замкнутой электрической цепи. Благодаря этому стало возможно решать практически любые прикладные задачи, связанные с электричеством. Закон Кирхгофа, используемый для расчета линейной электрической цепи, дает возможность получить классическую систему линейных уравнений, учитывающих напряжения и токи, которые становятся известными после решения поставленной задачи.

Формулировка предполагает использование терминов электрических «контур, узел и ветвь». Ветвь – это любой двухсторонний участок цепи, произвольный ее отрезок. Контур – это система зацикленных ветвей, то есть, начав мысленное движение из произвольной точки по любой ветви, в итоге все равно попадешь в место, откуда движение началось. Более понятно ветви называть «закольцованными», хотя это не совсем корректно. Узел – это точка, в которой сходятся две или более ветвей.

1 закон Кирхгофа очень прост. Он основывается на фундаментальном законе сохранения заряда. Первый закон Кирхгофа гласит: сумма токов (алгебраическая), стекающихся по ветвям к единому узлу, равна нулю. То есть, I1+I2+I3=0. Для расчетов принято считать, что значение втекающих в узел токов имеет знак «+», а вытекающих «-». Поэтому расширенная формула приобретает вид I1 + I2 — I3 = 0. Другими словами: количество втекающего в узел тока равно количеству вытекающего. Этот закон Кирхгофа очень важен для понимания принципов работы электрооборудования. Например, он поясняет, почему при соединении обмоток электрического двигателя по схеме «звезда» или «треугольник» не происходит межфазного короткого замыкания.

2 закон Кирхгофа обычно используют для расчета замкнутого контура с определенным количеством ветвей. Он непосредственно взаимосвязан с третьим законом Максвелла (неизменное магнитное поле). Правило гласит, что алгебраическая сумма падений напряжений на каждой из веток контура приравнивается к сумме значений ЭДС для всех ветвей рассчитываемого контура. Очевидно, что при отсутствии в замкнутой цепи источников электрической энергии (ЭДС), итоговое падение напряжений также будет равняться нулю. Говоря более простым языком, энергия источника лишь преобразуется на потребителях, а при возвращении стремится к своему исходному значению. Использование данного закона имеет ряд особенностей, как и в случае с первым.

Составляя уравнение цепи, принято считать, что численное значение ЭДС имеет положительный знак, если изначально принятое направление обхода контура (обычно по часовой стрелке) совпадает с ее направлением, и отрицательное, если направления противоположны. То же самое касается резисторов: если направление движения тока такое же, как у выбранного обхода, то падению напряжения на нем приписывается знак «+». Например, E1 — E2 + E3 = I1R1 — I2R2 + I3R3 + I4R4…

В результате обхода всех ветвей, входящих в контур, составляется система линейных уравнений, решив которую, удается узнать все токи ветвей (и узлов). Решаются полученные соотношения с помощью метода контурных токов.

Сложно переоценить значение законов Кирхгофа для электротехники. Простота написания формул и их решение с помощью способов классической алгебры явились причиной для широкого их использования.

21.3 Правила Кирхгофа – Колледж физики, главы 1-17

21 Цепи и приборы постоянного тока

Резюме

• Проанализируйте сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных термов.

Многие сложные схемы, такие как схема на рис. 1, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в главе 21.1 Резисторы в последовательном и параллельном соединении и главе 21.2 Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Правила известны как

Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

Рисунок 1. Эту схему нельзя свести к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква E на рисунке обозначает электродвижущую силу, эдс.)

Правила Кирхгофа

• Первое правило Кирхгофа — правило пересечения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.

Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.

Первое правило Кирхгофа (правило соединения ) представляет собой применение закона сохранения заряда к соединению; это показано на рис. 2. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы [латекс]\boldsymbol{I_1 = I_2 + I_3}[/латекс] (см. рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.

Установление соединений: законы сохранения

Правила Кирхгофа для анализа цепей представляют собой применение законов сохранения к цепям. Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.

Рисунок 2. Правило соединения. На диаграмме показан пример первого правила Кирхгофа, в котором сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I ₁ = I ₂ + I ₃ . Здесь I ₁ должно быть 11 А, так как I ₂ равно 7 А, а I ₃ 4 равно 9 А.

Второе правило Кирхгофа ( петлевое правило ) является применением закона сохранения энергии. Правило цикла сформулировано с точки зрения потенциала, [латекс]\boldsymbol{V}[/латекс], а не потенциальной энергии, но они связаны, поскольку [латекс]\boldsymbol{\textbf{PE}_{\textbf{ elec}} = qV}[/latex].

Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рис. 3 показаны изменения потенциала в простой последовательной цепи.

Второе правило Кирхгофа требует [латекс]\жирныйсимвол{\текстбф{ЭДС} — Ir — IR_1 — IR_2 = 0}[/латекс]. В перестановке это [латекс]\boldsymbol{\textbf{ЭДС} = Ir + IR_1 + IR_2}[/latex], что означает, что ЭДС равна сумме [латекс]\boldsymbol{IR}[/латекс] (напряжение ) попадает в петлю.

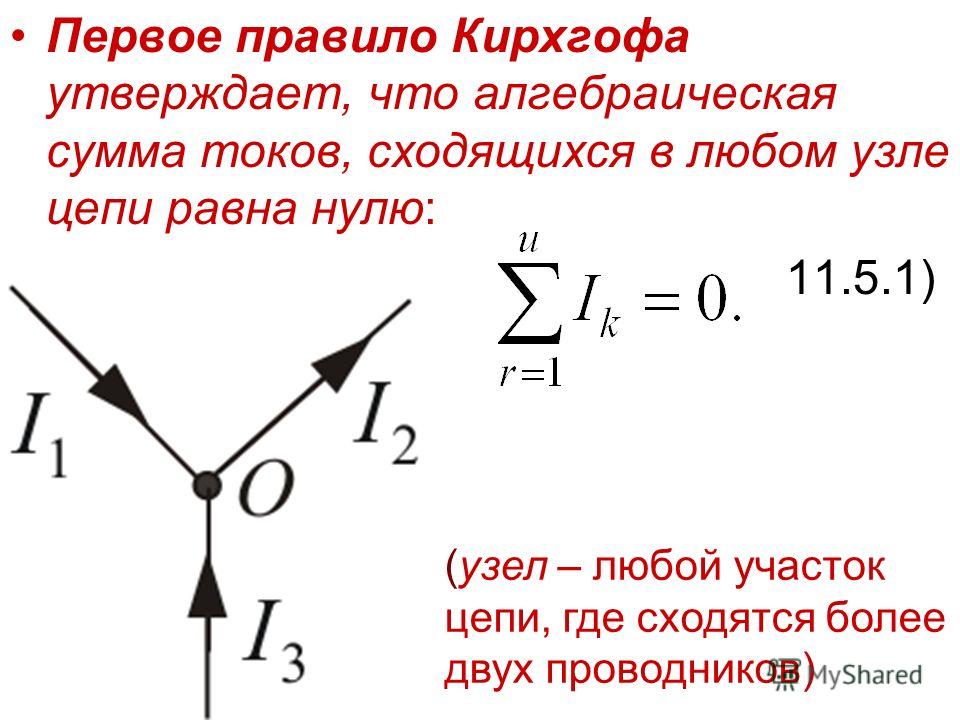Рисунок 3. Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает emf.)

Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.

1. Применяя первое правило Кирхгофа, правило соединения, вы должны пометить ток в каждой ветви и решить, в каком направлении он течет. Например, на рис. 1, рис. 2 и рис. 3 токи помечены [латекс]\boldsymbol{I_1}[/латекс], [латекс]\boldsymbol{I_2}[/латекс], [латекс]\boldsymbol{I_3 }[/latex] и [latex]\boldsymbol{I}[/latex], а стрелки указывают их направления.
   Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
2. Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рис. 3 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.

Рисунок 4 и следующие пункты помогут вам правильно расставить знаки «плюс» или «минус» при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 1.)

Рисунок 4. Каждый из этих резисторов и источников напряжения проходит от a до b.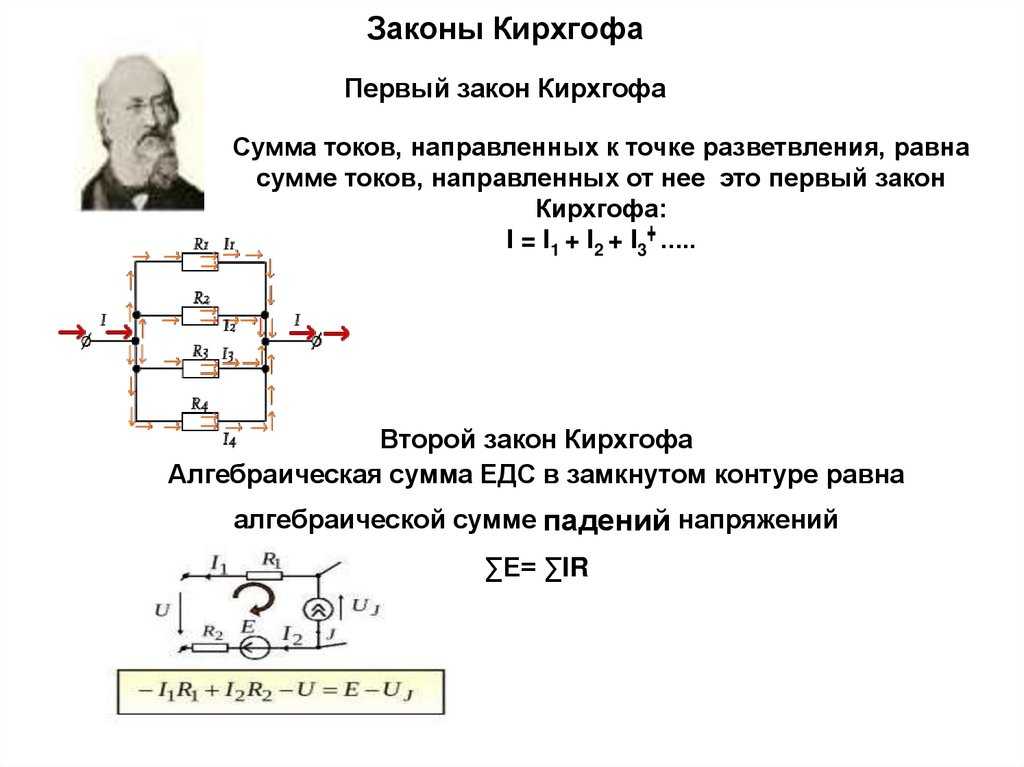 Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)

• Когда резистор перемещается в том же направлении, что и ток, изменение потенциала составляет [латекс]\жирный символ{-IR}[/латекс]. (См. рис. 4.)
• Когда резистор перемещается в направлении, противоположном току, изменение потенциала составляет [латекс]\boldsymbol{+IR}[/латекс]. (См. рис. 4.)
• Когда ЭДС перемещается от – к + (в том же направлении, что и положительный заряд), изменение потенциала составляет +ЭДС. (См. рис. 4.)
• Когда ЭДС перемещается от + к – (противоположно направлению движения положительного заряда), изменение потенциала равно −ЭДС. (См. рис. 4.)

Пример 1. Расчет тока: использование правил Кирхгофа

Найдите токи, протекающие в цепи на рисунке 5.

Рисунок 5. Эта цепь аналогична схеме на рисунке 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены как [латекс]\boldsymbol{I_1}[/latex], [латекс]\boldsymbol{I_2}[/latex] и [латекс]\boldsymbol{I_3}[/latex]. сделал о своих направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и контура, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.

Решение

Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает

[латекс]\boldsymbol{I_1 = I_2 + I_3} ,[/latex]

, так как [латекс]\boldsymbol{I_1}[/latex] впадает в соединение, а [латекс]\boldsymbol{I_2} [/latex] и [latex]\boldsymbol{I_3}[/latex] вытекают наружу. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.

Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем [латекс]\boldsymbol{R_2}[/латекс] в том же (предполагаемом) направлении, что и текущий [латекс]\boldsymbol{I_2}[/латекс], поэтому изменение потенциала равно [латекс]\boldsymbol{-I_2R_2}[/латекс]. Затем, переходя от b к c, мы переходим от – к +, так что изменение потенциала составляет [латекс]\boldsymbol{+ \textbf{emf}_1}[/латекс]. Перемещение внутреннего сопротивления [латекс]\boldsymbol{r_1}[/латекс] от c к d дает [латекс]\boldsymbol{-I_2r_1}[/латекс]. Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала [latex]\boldsymbol{-I_1R_1}[/latex].

Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,

[латекс]\boldsymbol{-I_2R_2 + \textbf{emf}_1 — I_2r_1 — I_1R_1 = -I_2(R_2 + r_1) + \textbf{emf}_1 — I_1R_1 = 0}. [/latex]

Подстановка значений сопротивления и ЭДС из принципиальной схемы и отмена единиц измерения ампер дает

[latex]\boldsymbol{-3I_2 + 18 -6I_1 = 0}.[/latex]

Теперь применим правило цикла к aefgha ( мы могли бы выбрать и abcdefgha) аналогично дает

[латекс]\boldsymbol{+I_1R_1 + I_3R_3 + I_3r_2 — \textbf{emf}_2 = +I_1R_1 + I_3(R_3+r_2) — \textbf{emf}_2 = 0} .[/latex]

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы проходятся в противоположном направлении. С введенными значениями это становится

[латекс]\boldsymbol{+6I_1 + 2I_3 — 45 = 0}.[/латекс]

Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решим второе уравнение для [латекс]\boldsymbol{I_2}[/латекс]:

[латекс]\boldsymbol{I_2 = 6 — 2I_1}.[/latex]

Теперь решите третье уравнение для [латекс]\boldsymbol{I_3}[/латекс]:

[латекс]\boldsymbol{I_3 = 22.5 — 3I_1}.[/latex]

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для [latex]\boldsymbol{I_1}[/latex]:

[latex]\boldsymbol{I_1 = I_2 + I_3 = (6 — 2I_1) + (22,5 — 3I_1) = 28,5 — 5I_1}. [/latex]

Объединение терминов дает

[latex]\boldsymbol{6I_1 = 28,5}[/latex] и

[латекс]\boldsymbol{I_1 = 4,75 \;\textbf{A}}.[/latex]

Подстановка этого значения вместо [латекс]\boldsymbol{I_1}[/латекс] обратно в четвертое уравнение дает

[латекс]\boldsymbol{I_2 = 6 — 2I_1 = 6 — 9,50}[/латекс]

[латекс]\boldsymbol{I_2 = -3,50 \;\textbf{A}}.[/latex]

Знак минус означает, что [латекс]\boldsymbol{I_2}[/латекс] течет в направлении, противоположном предполагаемому на рисунке 5.

Наконец, подстановка значения для [латекс]\жирныйсимвол{I_1}[/латекс] в пятое уравнение дает

[латекс]\boldsymbol{I_3 = 22,5 — 3I_1 = 22,5 — 14,25}[/latex]

[латекс]\boldsymbol{I_3 = 8,25 \;\textbf{A}}.[/latex]

Обсуждение

Просто для проверки отметим, что действительно [латекс]\boldsymbol{I_1 = I_2 + I_3}[/latex]. Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.

Стратегии решения задач по правилам Кирхгофа

1. Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
2. Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
3. Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.9.0010
4. Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
5. Проверьте, разумны ли и последовательны ли ответы. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.

Теоретически материал в этом разделе верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, являются прямым применением принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.

• Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
• Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
• Два правила основаны соответственно на законах сохранения заряда и энергии.
• При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
• Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.

Правила Кирхгофа

набор из двух правил, основанных на сохранении заряда и энергии, регулирующих ток и изменения потенциала в электрической цепи

соединительная линейка

первое правило Кирхгофа, применяющее закон сохранения заряда к соединению; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; правило может быть сформулировано [латекс]\boldsymbol{I_1 = I_2 + I_3}[/latex]

правило цикла

Второе правило Кирхгофа, которое гласит, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. Таким образом, ЭДС равна сумме [latex]\boldsymbol{IR}[/latex] (напряжения) падений в контуре и может быть сформулирована следующим образом: [latex]\boldsymbol{\textbf{ЭДС} = Ir + IR_1 + IR_2 }[/латекс]

законы сохранения

требуют сохранения энергии и заряда в системе

 

Законы Кирхгофа — Учебники по аналоговой электронике

Законы Кирхгофа — это два равенства, которые касаются сохранения заряда и энергии в электрических цепях. Впервые они были описаны в 1845 году Густавом Кирхгофом. Широко используемые в электротехнике, они также называются правилами Кирхгофа или просто законами Кирхгофа. 9{n}V_k = 0 \end{уравнение}

Этот закон также называют вторым законом Кирхгофа или правилом петли (или сетки) Кирхгофа. Другой способ сформулировать этот закон Сумма ЭДС в замкнутой цепи равна сумме падений потенциала

\begin{уравнение} v_4 = v_1 + v_2 + v_3 \end{уравнение}

Уравнения 3 и 4 эквивалентны, поскольку напряжение является величиной со знаком (положительной или отрицательной) в зависимости от того, является ли оно ЭДС и падением потенциала.

KVL и KCL Примеры

Делитель напряжения

Делитель напряжения является обычной конфигурацией в аналоговых схемах. Он также известен как потенциальный делитель. Это линейная схема, которая создает выходное напряжение (Vout), которое составляет часть его входного напряжения (Vin). Разделение напряжения относится к разделению напряжения между компонентами делителя.

Применяя KCL, можно убедиться, что ток i, протекающий через резисторы R1 и R2, должен быть равен. Применение КВЛ \begin{уравнение} v_{in} = я R_1 + я R_2 \end{уравнение} \begin{уравнение} я = {v_{in} \над {R_1 + R_2}} \end{уравнение} Напряжение на R2 определяется выражением \начать{выравнивать} v_{out} &= i R_2 \\ \метка{vd} &= {R_2 \over {R_1 + R_2}}v_{in} \end{выравнивание} Эта формула называется правилом делителя напряжения

Эффект нагрузки

Делитель напряжения с двумя резисторами часто используется для подачи напряжения, отличного от имеющегося аккумулятора или источника питания.