Меандр (радиотехника)
Вызов:
Википедия
Октябрь 28, 2021
У этого термина существуют и другие значения, см. Меандр (значения).
Меа́ндр (по названию геометрического орнамента в виде ломаной линии) — периодический сигнал прямоугольной формы, широко используемый в радиотехнике и электронике. Меандр может быть знакопеременным (двухполярным) или однополярным. Во втором случае длительность импульса и длительность паузы между импульсами равны, то есть в этом случае меандр — периодический сигнал прямоугольной формы, имеющий скважность 2 (или коэффициент заполнения 0,5).
Содержание
- 1Аналитическое описание
- 2Спектр меандра
- 3Прямоугольные сигналы в радиотехнике и электронике
- 4Примечания
- 5Ссылки
Математически меандр можно описать многими разными способами, например, через функцию сигнум:
- x(t)=sgn(sin(t)).
 {\infty }{\frac {\sin \left(2\pi (2k-1)ft\right)}{2k-1}}=\\&={\frac {4}{\pi }}\left(\sin(2\pi ft)+{\frac {1}{3}}\sin(6\pi ft)+{\frac {1}{5}}\sin(10\pi ft)+\dots \right).\end{aligned}}}
{\infty }{\frac {\sin \left(2\pi (2k-1)ft\right)}{2k-1}}=\\&={\frac {4}{\pi }}\left(\sin(2\pi ft)+{\frac {1}{3}}\sin(6\pi ft)+{\frac {1}{5}}\sin(10\pi ft)+\dots \right).\end{aligned}}}
Примечательно, что в спектре меандра отсутствуют чётные гармонические составляющие (гармоники). Амплитуда нечётных гармоник обратно пропорциональна их частоте с нулевым сдвигом фазы.
На практике форма прямоугольных импульсов, в том числе меандра, отличается от идеальной. Импульс искажается из-за паразитных параметров реальной электрической цепи. Поэтому в радиотехнике и электронике меандром обычно называют сигнал со скважностью 2 (или близкой к этому значению), с длительностью фронтов, много меньшей периода повторения сигнала, и без значительного спада (в общем случае — наклона) плоской вершины импульса.
Сигнал приближённо такого вида генерируется различными автогенераторами, например симметричным мультивибратором. Такой сигнал получается на выходе двоичного триггера со счётным входом, переключаемого периодическими импульсами.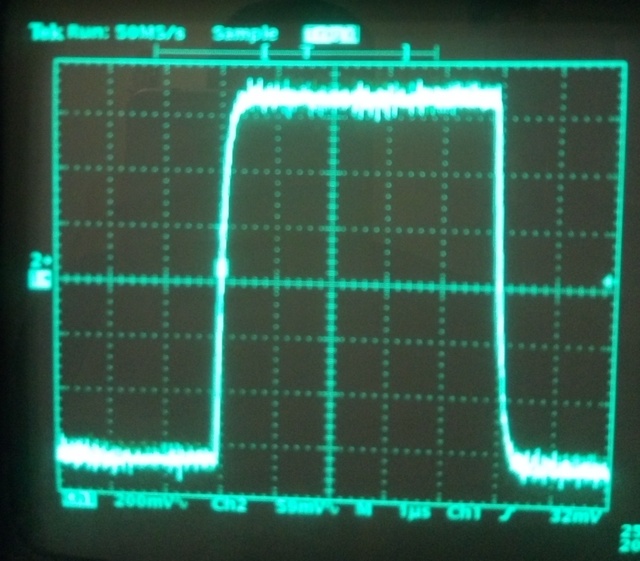
- .
Это заготовка статьи об электронике. Вы можете помочь проекту, дополнив её. |
Для улучшения этой статьи желательно:
Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником. |
Меандр, радиотехника, Язык, Следить, Править, этого, термина, существуют, другие, значения, см, Меандр, значения, Меа, ндр, по, названию, геометрического, орнамента, виде, ломаной, линии, периодический, сигнал, прямоугольной, формы, широко, используемый, радио. Meandr radiotehnika Yazyk Sledit Pravit U etogo termina sushestvuyut i drugie znacheniya sm Meandr znacheniya Mea ndr po nazvaniyu geometricheskogo ornamenta v vide lomanoj linii periodicheskij signal pryamougolnoj formy shiroko ispolzuemyj v radiotehnike i elektronike Meandr mozhet byt znakoperemennym dvuhpolyarnym ili odnopolyarnym Vo vtorom sluchae dlitelnost impulsa i dlitelnost pauzy mezhdu impulsami ravny to est v etom sluchae meandr periodicheskij signal pryamougolnoj formy imeyushij skvazhnost 2 ili koefficient zapolneniya 0 5 Soderzhanie 1 Analiticheskoe opisanie 2 Spektr meandra 3 Pryamougolnye signaly v radiotehnike i elektronike 4 Primechaniya 5 SsylkiAnaliticheskoe opisanie PravitMatematicheski meandr mozhno opisat mnogimi raznymi sposobami naprimer cherez funkciyu signum x t sgn sin t displaystyle x t operatorname sgn sin t Ili cherez funkcii Hevisajda h t displaystyle h t x t n h t n T 1 2 h t n T 1 2 displaystyle x t sum n infty infty left h left t nT 1 over 2 right h left t nT 1 over 2 right right Dlya togo chtoby skvazhnost ravnyalas 2 neobhodimo polozhit T 2 displaystyle T 2 I mnogimi drugimi sposobami Spektr meandra Pravit Sintez meandra iz nabora garmonik periodicheskogo signala Chem bolshe chislo garmonik tem blizhe k idealnoj forma signala Vybrosy na frontah obuslovleny neravnomernoj shodimostyu ryada Fure v tochkah razryva Razlozhenie meandra s narastayushim frontom pri t 0 displaystyle t 0 v ryad Fure daet x meandr t 4 p k 1 sin 2 p 2 k 1 f t 2 k 1 4 p sin 2 p f t 1 3 sin 6 p f t 1 5 sin 10 p f t displaystyle begin aligned x text meandr t amp frac 4 pi sum k 1 infty frac sin left 2 pi 2k 1 ft right 2k 1 amp frac 4 pi left sin 2 pi ft frac 1 3 sin 6 pi ft frac 1 5 sin 10 pi ft dots right end aligned Primechatelno chto v spektre meandra otsutstvuyut chyotnye garmonicheskie sostavlyayushie garmoniki Amplituda nechyotnyh garmonik obratno proporcionalna ih chastote s nulevym sdvigom fazy Pryamougolnye signaly v radiotehnike i elektronike PravitNa praktike forma pryamougolnyh impulsov v tom chisle meandra otlichaetsya ot idealnoj Impuls iskazhaetsya iz za parazitnyh parametrov realnoj elektricheskoj cepi 1 Poetomu v radiotehnike i elektronike meandrom obychno nazyvayut signal so skvazhnostyu 2 ili blizkoj k etomu znacheniyu s dlitelnostyu frontov mnogo menshej perioda povtoreniya signala i bez znachitelnogo spada v obshem sluchae naklona ploskoj vershiny impulsa Signal priblizhyonno takogo vida generiruetsya razlichnymi avtogeneratorami naprimer simmetrichnym multivibratorom Takoj signal poluchaetsya na vyhode dvoichnogo triggera so schyotnym vhodom pereklyuchaemogo periodicheskimi impulsami Primechaniya Pravit Grebennikov V V Teoriya elektricheskih cepej S 16 17 Ssylki PravitGOST 16465 70 Eto zagotovka stati ob elektronike Vy mozhete pomoch proektu dopolniv eyo Dlya uluchsheniya etoj stati zhelatelno Dopolnit statyu statya slishkom korotkaya libo soderzhit lish slovarnoe opredelenie Najti i oformit v vide snosok ssylki na nezavisimye avtoritetnye istochniki podtverzhdayushie napisannoe Pozhalujsta posle ispravleniya problemy isklyuchite eyo iz spiska parametrov Posle ustraneniya vseh nedostatkov etot shablon mozhet byt udalyon lyubym uchastnikom Istochnik https ru wikipedia org w index php title Meandr radiotehnika amp oldid 110811282, Википедия, чтение, книга, библиотека, поиск, нажмите,
истории
, книги, статьи, wikipedia, учить, информация, история, секс, порно, скачать, скачать, sex, seks, porn, porno, скачать, бесплатно, скачать бесплатно, mp3, видео, mp4, 3gp, jpg, jpeg, gif, png, картинка, музыка, песня, фильм, игра, игры Амплитуда генерируемого сигнала в таких генераторах очень стабильна и близка к напряжению питания. Основной и широко распространенный вид релаксационного генератора — симметричный мультивибратор на двух транзисторах, схема которого показана на рисунке ниже. В нем два стандартных усилительных каскада на транзисторах VT1 и VT2 соединены в последовательную цепочку, то есть выход одного каскада соединен со входом другого через разделительные конденсаторы С1 и С2. Они же определяют и частоту генерируемых колебаний F, точнее, их период Т. Напомню, что период и частота связаны простым соотношением Если схема симметрична и номиналы деталей в обоих каскадах одинаковы, то и выходное напряжение имеет форму меандра. Работает генератор так: сразу после включения, пока конденсаторы С1 и С2 не заряжены, транзисторы оказываются в «линейном» усилительном режиме, когда резисторами R1 и R2 задается некоторый малый ток базы, он определяет в Вст раз больший ток коллектора, и напряжение на коллекторах несколько меньше напряжения источника питания за счет падения напряжения на резисторах нагрузки R3 и R4. Предположим, что коллекторное напряжение VT1 чуть-чуть понизилось. Это изменение передается через конденсатор С2 в цепь базы VT2 и немного его запирает. Коллекторное напряжение VT2 возрастает, и это изменение передается конденсатором С1 на базу VT1, он отпирается, его коллекторный ток возрастает, а коллекторное напряжение понижается еще больше. Процесс происходит лавинообразно и очень быстро. В результате транзистор VT1 оказывается полностью открыт, его коллекторное напряжение будет не более 0,05. 0,1 В, a VT2 — полностью заперт, и его коллекторное напряжение равно напряжению питания. Теперь надо ждать, пока перезарядятся конденсаторы С1 и С2 и транзистор VT2 приоткроется током, текущим через резистор смещения R2. Лавинообразный процесс пойдет в обратном направлении и приведет к полному открыванию транзистора VT2 и полному запиранию VT1. Время перезарядки определяется напряжением питания, током через резисторы Rl, R2 и емкостью конденсаторов Cl, С2. При этом говорят о «постоянной времени» цепочек Rl, С1 и R2, С2, примерно соответствующей периоду колебаний. Действительно, произведение сопротивления в омах на емкость в фарадах дает время в секундах. Для номиналов, указанных на схеме рисунка 1 (360 кОм и 4700 пФ), постоянная времени получается около 1,7 миллисекунды, что говорит о том, что частота мультивибратора будет лежать в звуковом диапазоне порядка сотен герц. Частота повышается при увеличении напряжения питания и уменьшении номиналов Rl, С1 и R2, С2. Описанный генератор весьма неприхотлив: в нем можно использовать практически любые транзисторы и изменять номиналы элементов в широких пределах. К его выходам можно подключать высокоомные телефоны, чтобы услышать звуковые колебания, или даже громкоговоритель — динамическую головку с понижающим трансформатором, например абонентский трансляционный громкоговоритель. Поскольку два противофазных выхода мультивибратора в радиолюбительской практике нужны редко, автор задался целью сконструировать более простой и экономичный генератор, содержащий меньше элементов. То, что получилось, показано на следующем рисунке. Здесь использованы два транзистора с разными типами проводимости — п-р-п и р-n-р. Открываются они одновременно, коллекторный ток первого транзистора служит током базы второго. Вместе транзисторы образуют также двухкаскадный усилитель, охваченный ПОС через цепочку R2,C1. Когда транзисторы запираются, напряжение на коллекторе VT2 (выход 1 В) падает до нуля, это падение передается через цепочку ПОС на базу VT1 и полностью его запирает. Когда конденсатор С1 зарядится до примерно 0,5 В на левой обкладке, транзистор VT1 приоткроется, через него потечет ток, вызывая еще больший ток транзистора VT2; напряжение на выходе начнет расти. Скважность генерируемых импульсов, то есть соотношение длительностей импульса и паузы, регулируется подбором резисторов R1 и R2, а частота колебаний — подбором емкости С1. Устойчивой генерации при выбранном напряжении питания добиваются подбором резистора R5. Им же в некоторых пределах можно регулировать выходное напряжение. Так, например, при указанных на схеме номиналах и напряжении питания 2,5 В (два дисковых щелочных аккумулятора) частота генерации составила 1 кГц, а выходное напряжение — ровно 1 В. Потребляемый от батареи ток получился около 0,2 мА, что говорит об очень высокой экономичности генератора. Нагрузка генератора R3, R4 выполнена в виде делителя на 10, чтобы можно было снимать и меньшее напряжение сигнала, в данном случае 0,1 В. Еще меньшее напряжение (регулируемое) снимается с движка переменного резистора R4. Эта регулировка может оказаться полезной, если нужно определить или сравнить чувствительность телефонов, проверить высокочувствительный УНЧ, подав малый сигнал на его вход, и так далее. Если же таких задач не ставится, резистор R4 можно заменить постоянным или сделать еще одно звено делителя (0,01 В), добавив снизу еще резистор номиналом 27 Ом. Сигнал прямоугольной формы с крутыми фронтами содержит широкий спектр частот — кроме основной частоты F, еще и ее нечетные гармоники 3F, 5F, 7F и так далее, вплоть до радиочастотного диапазона. Поэтому генератором можно проверять не только звуковую аппаратуру, но и радиоприемники. Конечно, амплитуда гармоник убывает с ростом их частоты, но достаточно чувствительный приемник позволяет прослушивать их во всем диапазоне длинных и средних волн. |
Чистый синус или модифицированный меандр
09-03-2013
Графики чистого синуса и меандра на экране осциллографа
Что такое «чистый синус» электропитания, и зачем он нужен? Давайте разбираться.
Качество электроэнергии, поставляемой в наши дома, отвечает определенным требованиям. Один из важных показателей качества — вид графика напряжения. График напряжения электрического сигнала в сети должен иметь правильную синусоидальную форму. Для такого графика часто используют определение «чистый синус».
В случае отключения сетевого электропитания используются источники бесперебойного питания. Однако далеко не все ИБП обеспечивают электропитание правильной синусоидальной формы.
Вид графика напряжения выходного сигнала источника бесперебойного питания зависит от типа и конструкции данного устройства.
Большинство обычных компьютерных ИБП генерируют на выход сигнал, называемый «модифицированный синус» или «меандр».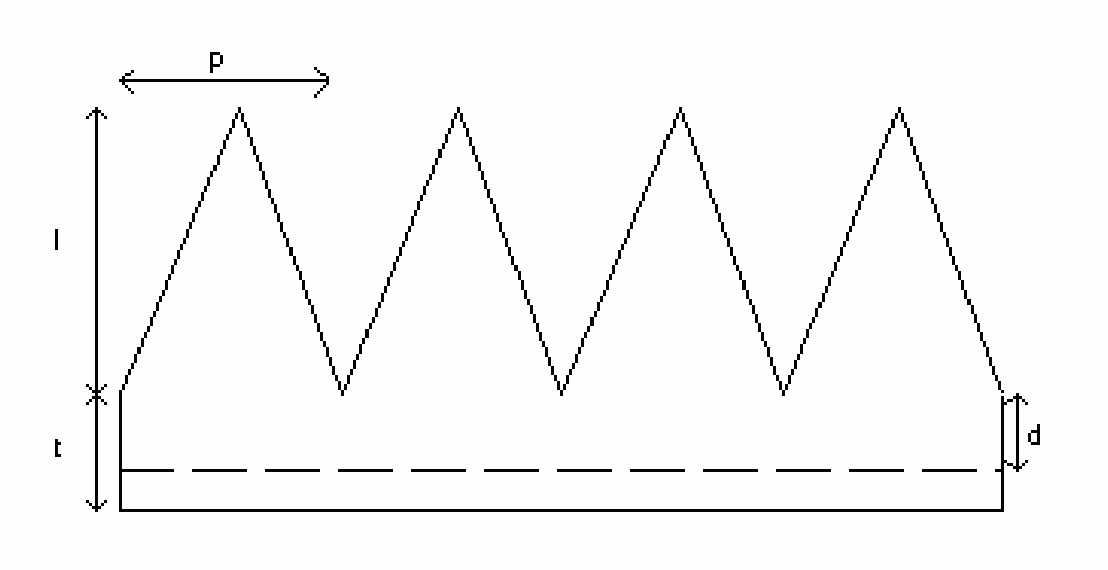
Различные типы графиков выходного сигнала, полученные с помощью осциллографа, представлены на следующем рисунке.
Методы аппроксимации графика чистого синуса
В этом разделе мы ознакомимся с различными методами аппроксимации графика чистого синуса, применяемыми на практике.
График напряжения в форме правильной синусоиды на следующих рисунках представлен красным цветом. Графики напряжения, имеющие приближенную к синусоиде форму, представлены другим цветом.
Самым простым приближением является график меандра. Меандр — простая ломаная линия, в данном случае имеющая форму прямоугольника в каждом полупериоде графика синуса. График простого меандра представлен на рисунке 1. На практике преобразователи такого типа не используются по причине резкого изменения значения напряжения в точках пересечения нулевого значения напряжения. Электрический сигнал такой формы создает большие электрические помехи и может вывести из строя подключенное оборудование.
Для снижения негативных эффектов применяется преобразование типа «меандр» с дополнительными «паузами» в точках смены полярности сигнала. График такого модифицированного меандра представлен на рисунке 2.
Более совершенные методы аппроксимации графика синусоиды напряжения позволяют получать график с большим количеством «ступенек». Такой подход позволяет снизить амплитуду перехода на следующую ступень и ближе подойти к графику «чистого синуса». Такой график носит название «модифицированный синус» и представлен на рисунке 3.
Когда нужен «чистый синус», а когда достаточно и «модифицированного»
Различные электроприборы и электрооборудование имеют разные требования к качеству электропитания. Ряд устройств корректно работает только с сигналом «чистый синус», другие приборы могут без проблем использовать электропитание в форме «модифицированного синуса». С другой стороны, источники бесперебойного питания с выходным сигналом в форме чистого синуса существенно дороже, чем ИБП с модифицированным синусом.
Не критичны к форме графика напряжения и могут использовать «модифицированный синус» следующие приборы:
- нагревательные приборы;
- компьютеры;
- бытовые приборы, имеющие импульсные источники питания.
Требуют использования питания форме чистого синуса следующие приборы:
- электродвигатели;
- котлы отопления;
- циркуляционные и погружные насосы;
- компрессоры;
- приборы и оборудование, имеющие трансформаторные источники питания;
- приборы и оборудование, чувствительные к электрическим помехам в сети.
Отклонения от правильной синусоидальной формы напряжения приводят к перегреву такого оборудования, повышенному трению и биению подвижных частей конструкции, к возможным авариям и поломкам. Использование источников питания с модифицированным синусом выходного сигнала приводит к существенному сокращению срока эксплуатации приборов, имеющих трансформаторные источники питания или электродвигатели.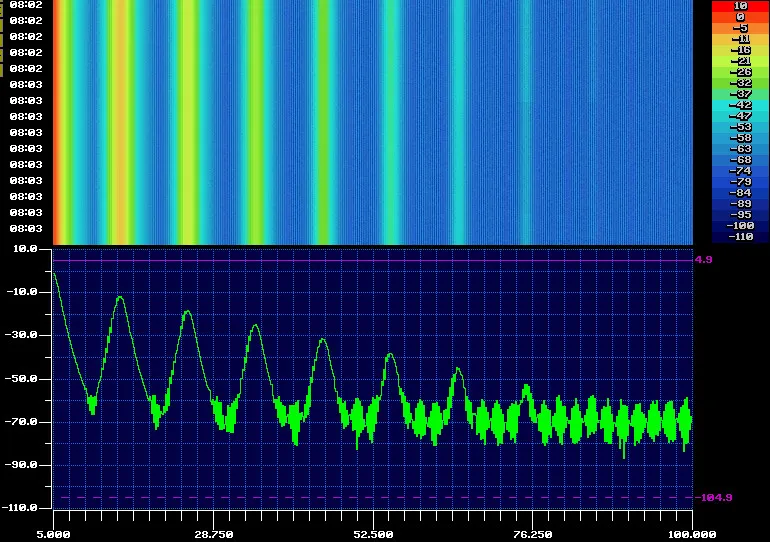
ИБП с чистым синусом для питания котлов отопления
Для правильного и безопасного электропитания газовых котлов отопления необходимо использовать только ИБП с синусоидальной формой сигнала.
В конструкцию современного котла отопления входят: электронный блок управления, циркуляционные насосы, насосы или компрессоры для обогащения воздухом горючей смеси. Все эти устройства требуют правильного синусоидального электропитания.
Использование источников бесперебойного питания с формой сигнала в виде модифицированного синуса приведет к сбоям в работе электронного блока и повышенному износу и перегреву насосов котла отопления.
Надёжные российские источники бесперебойного питания компании БАСТИОН представлены в разделе Бесперебойное питание.
Читайте также по теме:
- 12 причин появления скачков в сети
- Гальваническая развязка, принципы и задачи
- Регуляторы напряжения
Рекомендации для вас
Управляемая многозонная система отопления
«Бастион» — ТЕПЛО
Отдел сбыта
8-800-200-58-33
teplo@bast. ru
ru
Тех. поддержка
8-800-200-58-30
с 9 до 18 (Мск), звонок по России бесплатный
[email protected]
Бастион в соц. сетях
Канал Бастион на YouTube
Бастион Скат
YouTube Подписаться
ПрофКиП Г6-67М генератор сигналов специальной формы
ПрофКиП Г6-67М генератор сигналов специальной формы
▪ Диапазон частот: 0.03 Гц … 3 МГц
▪ Форма сигнала: синус, треугольник, меандр, импульс, пила, искаженный синусоидальный
▪ Точность измерения: 0.01%
▪ Режим качания частоты с внутренним и внешним управлением: 10:1 … 1000:1
▪ Частотная модуляция с помощью внешнего управления
▪ Плавный и ступенчатый (-20 дБ) аттенюаторы
▪ Встроенный частотомер
▪ Питание: 100 В /120 В /220 В /230 В ± 10%, 50 Гц /60 Гц, 13 Вт
▪ Габаритные размеры, вес: 220х85х300 мм, 2. 5 кг
5 кг
ПрофКиП Г6-66М генератор сигналов специальной формы
▪ Диапазон частот: 0.02 Гц … 2 МГц
▪ Форма сигнала: синус, треугольник, меандр, импульс, пила, искаженный синусоидальный
▪ Точность измерения: 0.01%
▪ Режим качания частоты с внутренним и внешним управлением: 10:1 … 1000:1
▪ Частотная модуляция с помощью внешнего управления
▪ Плавный и ступенчатый (-20 дБ) аттенюаторы
▪ Встроенный частотомер
▪ Питание: 100 В /120 В /220 В /230 В ± 10%, 50 Гц /60 Гц, 13 Вт
▪ Габаритные размеры, вес: 220х85х300 мм, 2.5 кг
подробнее…ПрофКиП Г6-37М генератор сигналов специальной формы
▪ Частотный диапазон: 20 МГц
▪ 2 Канала
▪ Технология прямого цифрового синтеза (DDS)
▪ Дискретизация 125 МВыб/с с разрешением 14 бит
▪ Встроенный частотомер до 200 МГц
▪ Разрешение 1 мкГц
▪ Интерактивное меню подсказок
▪ Питание: 100 В … 240 В, 45 Гц … 66 Гц
▪ Габаритные размеры, вес: 229х105х281 мм, 2.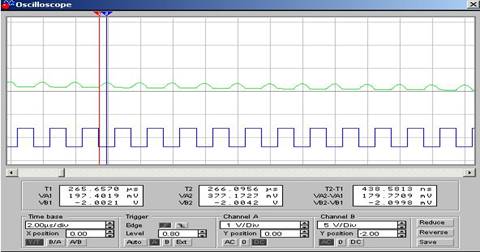 5 кг
5 кг
ПрофКиП Г6-36М генератор сигналов специальной формы
▪ Частотный диапазон: 50 МГц
▪ 2 Канала
▪ Технология прямого цифрового синтеза (DDS)
▪ Дискретизация 125 МВыб/с с разрешением 14 бит
▪ Встроенный частотомер до 200 МГц
▪ Разрешение 1 мкГц
▪ Интерактивное меню подсказок
▪ Питание: 100 В … 240 В, 45 Гц … 66 Гц
▪ Габаритные размеры, вес: 229х105х281 мм, 2.5 кг
подробнее…ПрофКиП Г6-34М генератор сигналов специальной формы
▪ Частотный диапазон: 10 МГц
▪ 2 Канала
▪ Технология прямого цифрового синтеза (DDS)
▪ Дискретизация 125 МВыб/с с разрешением 14 бит
▪ Встроенный частотомер до 200 МГц
▪ Разрешение 1 мкГц
▪ Интерактивное меню подсказок
▪ Питание: 100 В … 240 В, 45 Гц … 66 Гц
▪ Габаритные размеры, вес: 229х105х281 мм, 2.5 кг
подробнее…ПрофКиП Г6-33М генератор сигналов специальной формы
▪ Частотный диапазон: 25 МГц
▪ 2 Канала
▪ Технология прямого цифрового синтеза (DDS)
▪ Дискретизация 125 МВыб/с с разрешением 14 бит
▪ Встроенный частотомер до 200 МГц
▪ Разрешение 1 мкГц
▪ Интерактивное меню подсказок
▪ Питание: 100 В … 240 В, 45 Гц … 66 Гц
▪ Габаритные размеры, вес: 229х105х281 мм, 2.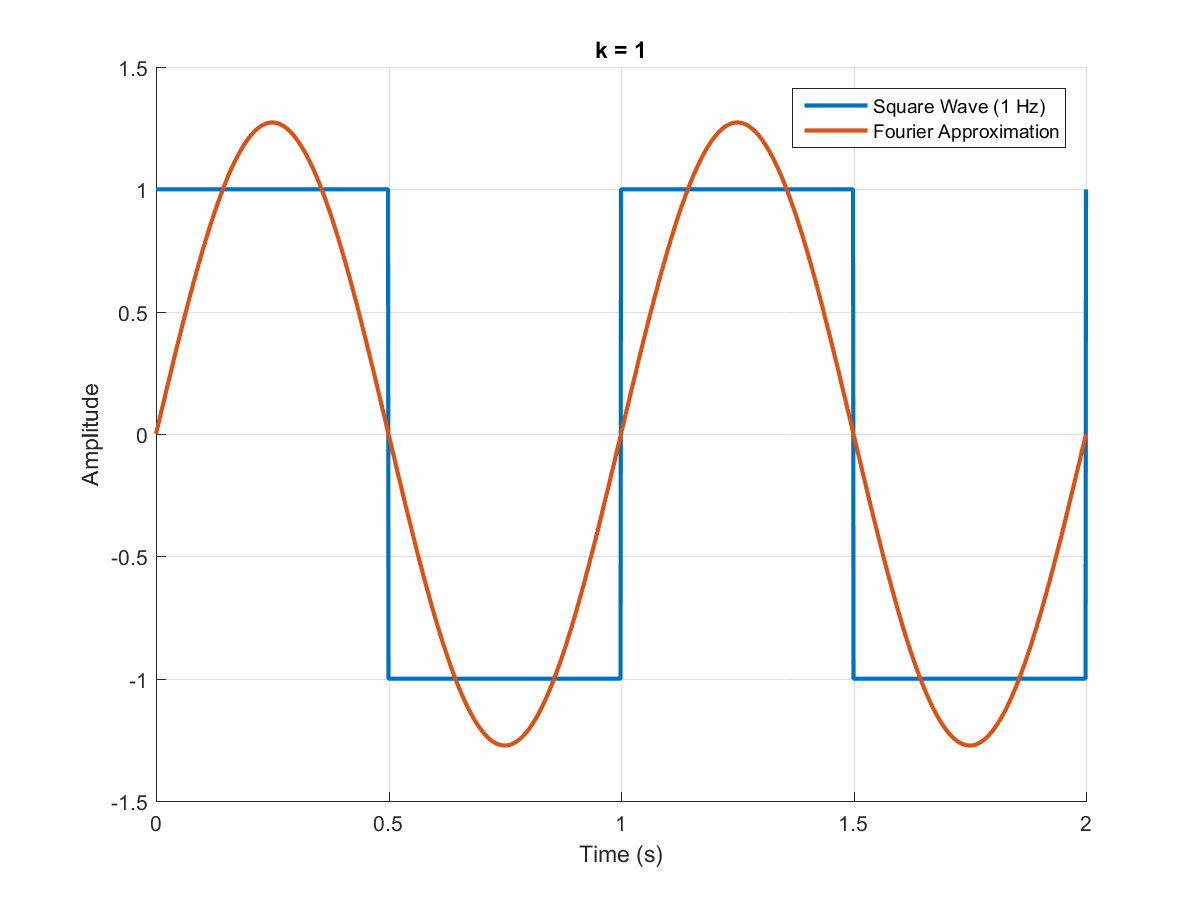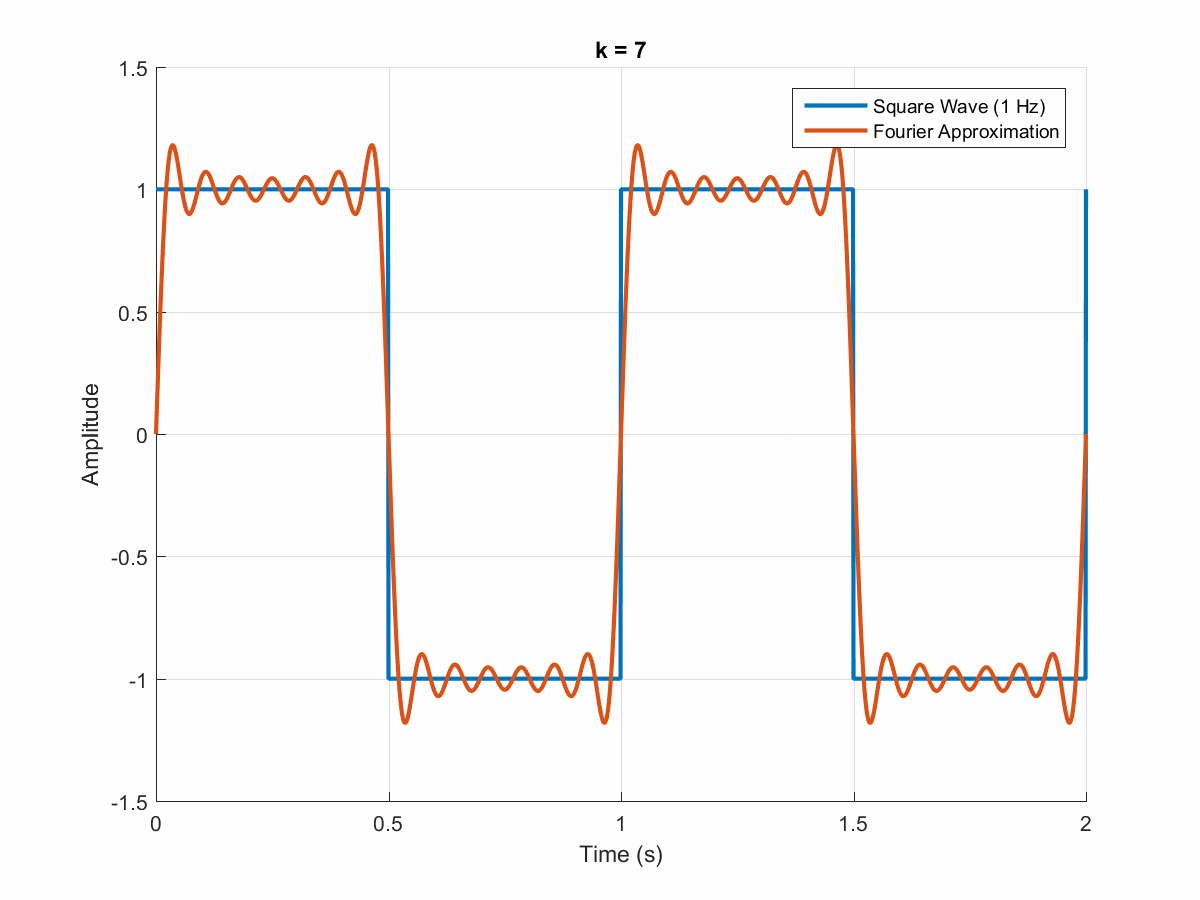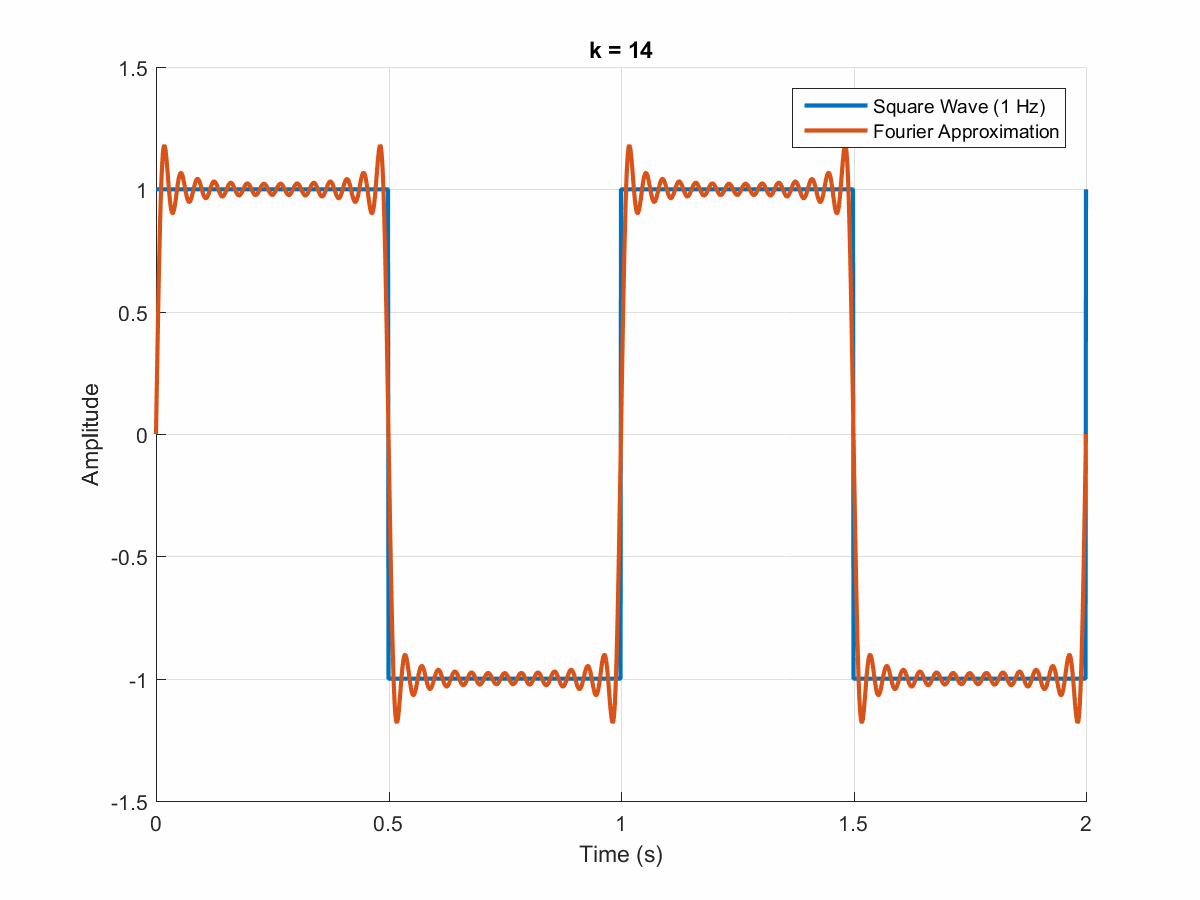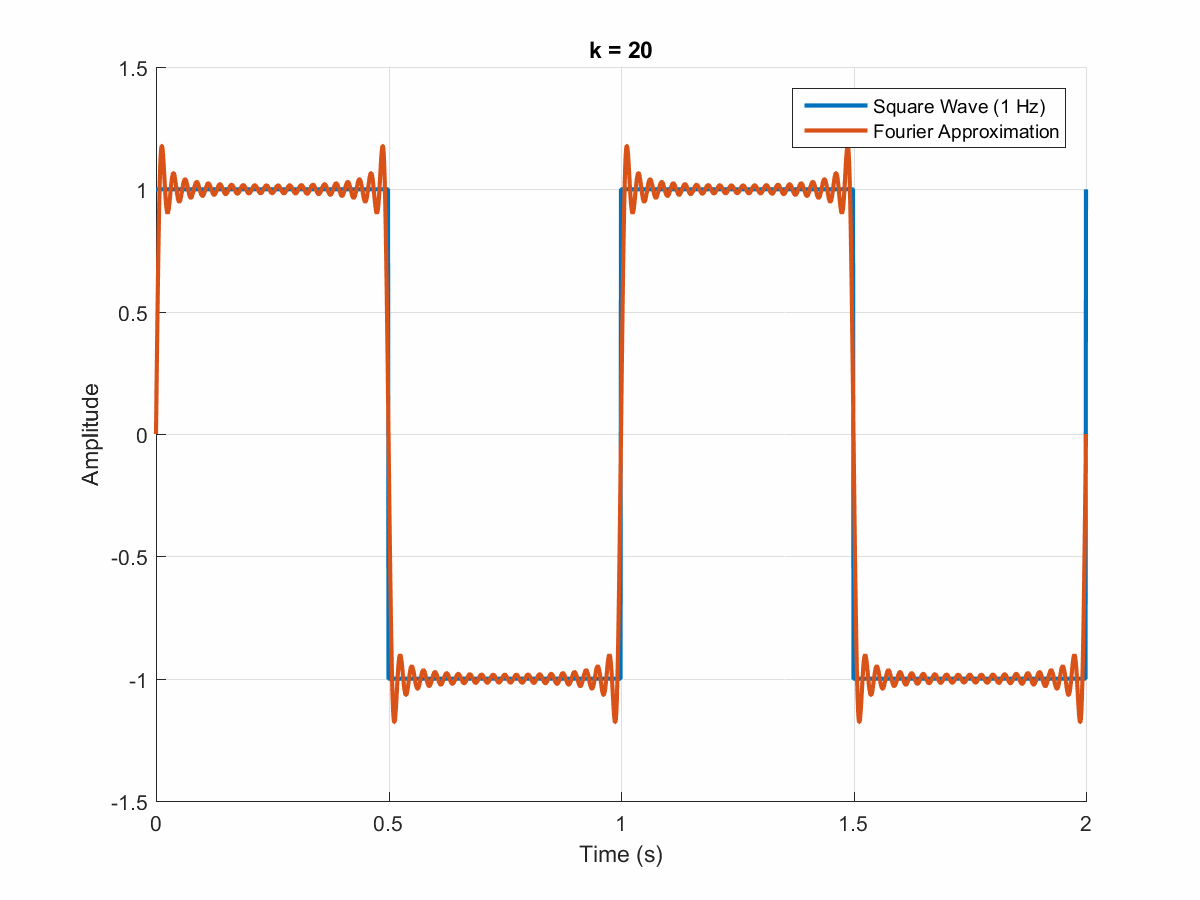 5 кг
5 кг
ПрофКиП Г6-27М генератор сигналов специальной формы
▪ Частотный диапазон: 5 МГц
▪ 2 Канала
▪ Технология прямого цифрового синтеза (DDS)
▪ Дискретизация 125 МВыб/с с разрешением 14 бит
▪ Встроенный частотомер до 200 МГц
▪ Разрешение 1 мкГц
▪ Интерактивное меню подсказок
▪ Питание: 100 В … 240 В, 45 Гц … 66 Гц
▪ Габаритные размеры, вес: 229х105х281 мм, 2.5 кг
подробнее…ПрофКиП Г4-222М генератор сигналов высокочастотный
▪ Частотный диапазон: 5 кГц … 1100 МГц
▪ Разрешение: 1 кГц
▪ Дисплей: 16 цифр, 2 строки
▪ Полный охват спектра УКВ
▪ Сохранение до 100 предустановок
▪ Компактный дизайн
▪ Защита выхода
▪ Питание: 110 В /220 В ±10%, 50 Гц /60 Гц
▪ Габаритные размеры, вес: 134х300х330 мм, 8.5 кг
подробнее…ПрофКиП Г4-176М генератор сигналов высокочастотный
▪ Частотный диапазон: 10 МГц … 3000 МГц
▪ Высокое разрешение выходной частоты (1 Гц)
▪ Прямой цифровой синтез сигналов
▪ Низкий уровень фазовых шумов
▪ Девиация частоты до 100 кГц с разрешением 0. 1 кГц
1 кГц
▪ Широкий диапазон установки выходного уровня (-120 … 0 дБм)
▪ Запись в память до 20 профилей
▪ Питание: 115 В /230 В, 50 Гц /60 Гц
▪ Габаритные размеры, вес: 130х430х435 мм, 18 кг
подробнее…ПрофКиП Г4-165М генератор сигналов высокочастотный
▪ Частотный диапазон: 100 кГц … 150 МГц
▪ Выходной уровень: -20 дБмкВ … 126 дБмкВ
▪ Микропроцессорное управление
▪ ЧМ стерео-модуляция
▪ Запись /считывание до 100 профилей
▪ Четыре цифровых дисплея (частота /уровень /глубина АМ /девиация ЧМ)
▪ Питание: 220 В /240 В ±10%, 50 Гц /60 Гц
▪ Габаритные размеры, вес: 115х430х310 мм, 7 кг
подробнее…ПрофКиП Г4-164М генератор сигналов высокочастотный
▪ Частотный диапазон: 200 кГц … 1000 МГц
▪ Погрешность установки частоты: ±2 х 10-7
▪ Нестабильность частоты: ±1 х 10-8
▪ Высокое разрешение выходной частоты (1 Гц)
▪ Девиация частоты до 100 кГц (разрешение 0.1 кГц)
▪ Коэффициент АМ до 100 % (разрешение 0. 1 %)
1 %)
▪ Интерфейсы: RS-232C
▪ Питание: 115 В /230 В, 50 Гц /60 Гц
▪ Габаритные размеры, вес: 115х430х410 мм, 14 кг
подробнее…ПрофКиП Г4-158М генератор сигналов высокочастотный
▪ Частотный диапазон: 100 кГц … 150 МГц
▪ Разрешение:1 Гц
▪ Точность частоты: ±25 ppm
▪ Стабильность частоты: ±5 ppm /день
▪ Технология прямого цифрового синтеза (DDS)
▪ FM, AM, FSK, свипирование, сохранения /восстановление, режим качания частоты
▪ Многообразие интерфейсов и функций хранения
▪ Питание: 110 В … 127 В ±10%, 50 Гц ±2 ГЦ, 220 В … 240 В ±10%, 60 Гц ±2 Гц
▪ Габариты, вес: 240х90х363 мм, 3 кг
подробнее…ПрофКиП Г4-151М генератор сигналов высокочастотный
▪ Частотный диапазон: 100 кГц … 150 МГц
▪ Точность (100 кГц … 3.5 МГц): 5%
▪ Точность (3.3 МГц … 35 МГц): 6%
▪ Точность (34 МГц … 150 МГц): 8%
▪ Внутренняя /внешняя амплитудная модуляция (0% … 30%)
▪ Частотная модуляция (0% … 10%)
▪ ЧМ-стереовещание
▪ Питание: 110 В … 127 В ±10% /220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 220х160х240 мм, 4 кг
подробнее. ..
..ПрофКиП Г4-129М генератор сигналов высокочастотный
▪ Двойной интервал частот
▪ Диапазоны частот: 700 МГц … 1200 МГц, 0.1 МГц … 99.9 МГц
▪ Плавная регулировка установки частоты
▪ Разрешение установки частоты: 0.1 МГц
▪ Высокая стабильность установки частоты: 2 х 106
▪ Микропроцессорное управление
▪ Удобный интерфейс и легкочитаемый светодиодный дисплей
▪ Питание: 220 В ±10%, 50 Гц … 60 Гц
▪ Габариты, вес: 330х210х100 мм, вес 2 кг
подробнее…ПрофКиП Г3-135М генератор сигналов низкочастотный
▪ Частотный диапазон: 0.2 Гц … 5 МГц
▪ Форма сигналов: синус, прямоугольник, треугольник, пила и т.д.
▪ Режимы входа: свип (внутр /внеш), АМ, ЧМ, ФМ и т.д.
▪ Плавная регулировка смещения, симметрии, амплитуды
▪ Встроенный частотомер до 100 МГц
▪ Полная защита выходной цепи
▪ Индикация амплитуды: среднеквадратичной уровень, пиковое значение
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 240х80х220 мм, 1. 75 кг
75 кг
ПрофКиП Г3-134М генератор сигналов низкочастотный
▪ Частотный диапазон: 0.1 Гц … 3 МГц
▪ Форма сигнала: синусоида, меандр, треугольник и д.т.
▪ Импульсная и частотная модуляция
▪ Плавно регулируемое смещение постоянной составляющей
▪ Встроенный частотомер: 0.1 Гц … 50 МГц
▪ Защита выхода
▪ Высокая надежность: наработка на отказ > 10000 часов
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 230х80х210 мм, 1.5 кг
подробнее…ПрофКиП Г3-133М генератор сигналов низкочастотный
▪ Диапазон частот: 0.06 Гц … 6 МГц
▪ Форма сигналов: синусоидальный, меандр, треугольник и т.д.
▪ Выходной аттенюатор: 0 дБ /20 дБ /40 дБ / 60 дБ
▪ Амплитуда выходного сигнала: ≥ 20 Впик-пик (без нагрузки)
▪ Сдвиг по постоянному току: 0 В … ±10В регулируемый
▪ Отдельный TTL, VCF выход
▪ Частотомер 5 знаков: 1 Гц … 15 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 310х80х230 мм, 1. 75 кг
75 кг
ПрофКиП Г3-132М генератор сигналов низкочастотный
▪ Диапазон частот: 0.03 Гц … 3 МГц
▪ Форма сигналов: синусоидальный, меандр, треугольник и т.д.
▪ Выходной аттенюатор: 0 дБ /20 дБ /40 дБ / 60 дБ
▪ Амплитуда выходного сигнала: ≥ 20 Впик-пик (без нагрузки)
▪ Сдвиг по постоянному току: 0 В … ±10В регулируемый
▪ Отдельный TTL, VCF выход
▪ Частотомер 5 знаков: 1 Гц … 15 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 310х80х230 мм, 1.75 кг
подробнее…ПрофКиП Г3-131М генератор сигналов низкочастотный
▪ Диапазон частот: 0.02 Гц … 2 МГц
▪ Форма сигнала: синус, треугольник, меандр, импульс, пила, искаженный синусоидальный
▪ Точность измерения: 0.01%
▪ Режим качания частоты с внутренним и внешним управлением: 10:1 … 1000:1
▪ Частотная модуляция с помощью внешнего управления
▪ Плавный и ступенчатый (-20 дБ) аттенюаторы
▪ Стабильность установленной частоты: ±0. 1% спустя 20 минут
1% спустя 20 минут
▪ Питание: 100 В /120 В /220 В /230 В ± 10%, 50 Гц /60 Гц, 13 Вт
▪ Габаритные размеры, вес: 220х80х300 мм, 2.5 кг
подробнее…ПрофКиП Г3-131/1М генератор сигналов низкочастотный
▪ Диапазон частот: 0.2 Гц … 2 МГц
▪ Форма сигнала: синус, меандр, треугольник, пилообразный, импульс и т.д.
▪ Отдельный TTL, 50 Гц синус и сигнальный выход
▪ Сдвиг по постоянному току: 0 В … 10 В
▪ Плавная регулировка симметрии: 10% … 90%
▪ Вход управления частотой напряжением (VCF)
▪ Встроенный 6-разрядный частотомер: 1 Гц … 15 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 250х105х280 мм, 2.5 кг
подробнее…ПрофКиП Г3-130М генератор сигналов низкочастотный
▪ Диапазон частот: 0 Гц … 3 МГц
▪ Форма сигнала: синус, меандр, треугольник и т.д.
▪ Импульсная и частотная модуляция
▪ Плавно регулируемое смещение постоянной составляющей
▪ Амплитуда выходного сигнала: до 20 Впик-пик
▪ Защита выхода
▪ Встроенный частотомер: 0.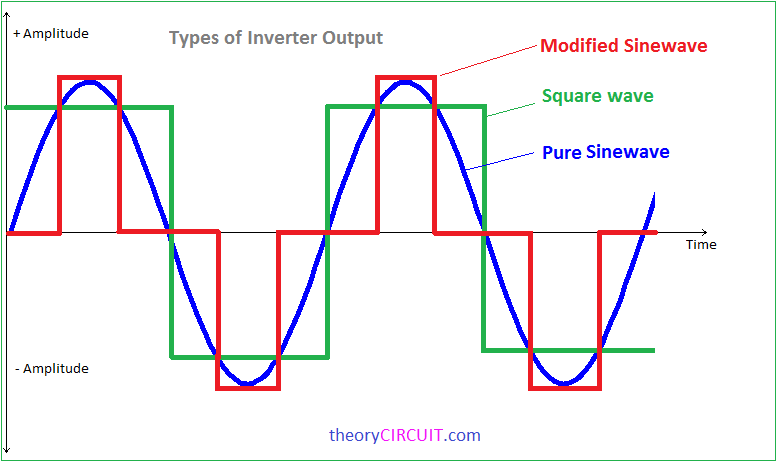 1 Гц … 50 кГц
1 Гц … 50 кГц
▪ Питание: 100 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 285х90х360 мм, 1.75 кг
подробнее…ПрофКиП Г3-129М генератор сигналов низкочастотный
▪ Диапазон частот: 0 Гц … 2 МГц
▪ Форма сигнала: синус, меандр, треугольник и т.д.
▪ Импульсная и частотная модуляция
▪ Плавно регулируемое смещение постоянной составляющей
▪ Амплитуда выходного сигнала: до 20 Впик-пик
▪ Защита выхода
▪ Встроенный частотомер: 20 Гц … 20 кГц
▪ Питание: 100 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 230х85х240 мм, 1.75 кг
подробнее…ПрофКиП Г3-128М генератор сигналов низкочастотный
▪ Диапазон частот: 1 мкГц … 5 МГц
▪ Форма сигнала: синус, прямоугольный, импульс, треугольник, пила, TTL, и произвольный
▪ Модуляция: одной частотой, частотой развертки, AM, FM, PM, FSK, ASK, PSK
▪ Разрешение по вертикали 10 бит
▪ Произвольная установка режима AM-модуляции: 1% … 120%
▪ Память формы сигнала: 4096 точек
▪ Встроенный частотомер до 100 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪Габариты, вес: 255х100х370 мм, 2. 5 кг
5 кг
ПрофКиП Г3-127М генератор сигналов низкочастотный
▪ Диапазон частот: 1 мкГц … 10 МГц
▪ Форма сигнала: синус, прямоугольный, импульс, треугольник, пила, TTL, и произвольный
▪ Модуляция: одной частотой, частотой развертки, AM, FM, PM, FSK, ASK, PSK
▪ Разрешение по вертикали 10 бит
▪ Произвольная установка режима AM-модуляции: 1% … 120%
▪ Память формы сигнала: 4096 точек
▪ Встроенный частотомер до 100 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪Габариты, вес: 255х100х370 мм, 2.5 кг
подробнее…ПрофКиП Г3-126М генератор сигналов низкочастотный
▪ Диапазон частот: 1 мкГц … 15 МГц
▪ Форма сигнала: синус, прямоугольный, импульс, треугольник, пила, TTL, и произвольный
▪ Модуляция: одной частотой, частотой развертки, AM, FM, PM, FSK, ASK, PSK
▪ Разрешение по вертикали 10 бит
▪ Произвольная установка режима AM-модуляции: 1% … 120%
▪ Память формы сигнала: 4096 точек
▪ Встроенный частотомер до 100 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪Габариты, вес: 255х100х370 мм, 2. 5 кг
5 кг
ПрофКиП Г3-125М генератор сигналов низкочастотный
▪ Диапазон частот: 10 Гц … 1 МГц
▪ Диапазон частот (меандр): 10 Гц … 10 кГц
▪ Точность: ±0.1%
▪ Встроенный 7-разрядный частотомер: 1 Гц … 100 МГц
▪ Индикатор частоты: 7-разрядный цифровой дисплей
▪ Формы сигнала: синусоида, меандр
▪ 6-ступенчатый выходной аттенюатор
▪ Функция внешней синхронизации
▪ Питание: 110 В … 127 В ±10% /220 В … 240 В ±10%, 50 Гц ±2Гц /60 Гц ±2 Гц
▪ Габариты, вес: 130х200х280 мм, 2.5 кг
подробнее…ПрофКиП Г3-124М генератор сигналов низкочастотный
▪ Диапазон частот: 0.01 мкГц … 31 МГц
▪ Количество каналов: 1 канал
▪ Форма сигнала: синус, меандр, треугольник, пила, шум и произвольная форма
▪ Дискретность установки частоты: 0.01 мкГц
▪ Время развертки до 1000 сек. амплитудной, частотной и фазовой модуляции
▪ Линейное, логарифмическое свипирование и непрерывная фаза
▪ Интерфейс RS-232C
▪ Питание: 100 В /120 В /220 В /240 В (±15%), 50 /60 Гц
▪ Габариты, вес: 363х109х386 мм, 8.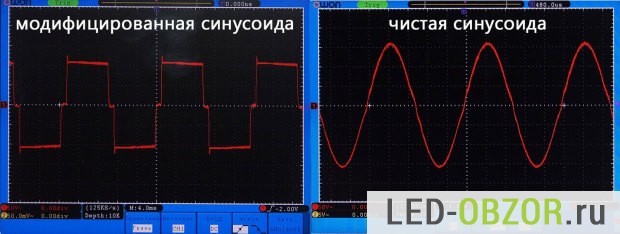 5 кг
5 кг
ПрофКиП Г3-123М генератор сигналов низкочастотный
▪ Диапазон частот: до 50 МГц
▪ Разрешение по частоте 1 мкГц
▪ Форма сигнала: синус, меандр, пила, треугольник, импульс, шум, произвольная форма
▪ Режимы АМ, ФМ, ЧМ, ИМ, ГКЧ, фазо-частотная манипуляция
▪ Частота дискретизации 125 МГц
▪ Память 256 тысяч точек
▪ Интерфейс USB, LAN
▪ Питание: 220 В (±15%), 50 /60 Гц
▪ Габариты, вес: 107х224х380 мм, 3.6 кг
подробнее…ПрофКиП Г3-122М генератор сигналов низкочастотный
▪ Диапазон частот: 0.01 мкГц … 31 МГц
▪ Количество каналов: 2 независимых канала
▪ Форма сигнала: синус, меандр, треугольник, пила, шум и произвольная форма
▪ Дискретность установки частоты: 0.01 мкГц
▪ Время развертки до 1000 сек. амплитудной, частотной и фазовой модуляции
▪ Линейное, логарифмическое свипирование и непрерывная фаза
▪ Интерфейс RS-232C
▪ Питание: 100 В /120 В /220 В /240 В (±15%), 50 /60 Гц
▪ Габариты, вес: 363х109х386 мм, 8. 5 кг
5 кг
ПрофКиП Г3-121М генератор сигналов низкочастотный
▪ Диапазон частот: 10 Гц … 1 МГц
▪ Диапазон частот (меандр): 10 Гц … 10 кГц
▪ Точность: ±0.1%
▪ Цифровая индикация напряжения: 3-разрядный дисплей
▪ Индикатор частоты: 5-разрядный цифровой дисплей
▪ Формы сигнала: синусоида, меандр
▪ 6-ступенчатый выходной аттенюатор
▪ Функция внешней синхронизации
▪ Питание: 110 В … 127 В ±10% /220 В … 240 В ±10%, 50 Гц ±2Гц /60 Гц ±2 Гц
▪ Габариты, вес: 130х200х280 мм, 2.5 кг
подробнее…ПрофКиП Г3-120М генератор сигналов низкочастотный
▪ Частотный диапазон: 10 Гц … 1 МГц
▪ Форма сигналов: синус, меандр
▪ 6-ступенчатый выходной аттенюатор
▪ Функция внешней синхронизации
▪ Точность: ±(3% + 1 Гц)
▪ Максимально допустимое входное напряжение: 10 В
▪ Встроенный частотомер (7 разрядов): 1 Гц … 1 МГц
▪ Питание: 110 В … 127 В ±10% /220 В … 240 В ±10%, 50 Гц ±2Гц /60 Гц ±2 Гц
▪ Габариты, вес: 142х197х233 мм, 3. 5 кг
5 кг
ПрофКиП Г3-119М генератор сигналов низкочастотный
▪ Диапазон частот: 1 мкГц … 20 МГц
▪ Форма сигнала: синус, прямоугольный, импульс, треугольник, пила, TTL, и произвольный
▪ Модуляция: одной частотой, частотой развертки, AM, FM, PM, FSK, ASK, PSK
▪ Разрешение по вертикали 10 бит
▪ Произвольная установка режима AM-модуляции: 1% … 120%
▪ Память формы сигнала: 4096 точек
▪ Встроенный частотомер до 100 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪Габариты, вес: 255х100х370 мм, 2.5 кг
подробнее…ПрофКиП Г3-118М генератор сигналов низкочастотный
▪ Диапазон частот: 10 Гц … 1 МГц
▪ Диапазон частот (меандр): 10 Гц … 10 кГц
▪ Точность: ±(3% + 1 Гц)
▪ Максимальное входное напряжение: 15 В
▪ Индикатор частоты: Лимб
▪ Формы сигнала: синусоида, меандр
▪ 6-ступенчатый выходной аттенюатор
▪ Функция внешней синхронизации
▪ Питание: 110 В … 127 В ±10% /220 В … 240 В ±10%, 50 Гц ±2Гц /60 Гц ±2 Гц
▪ Габариты, вес: 130х200х280 мм, 2.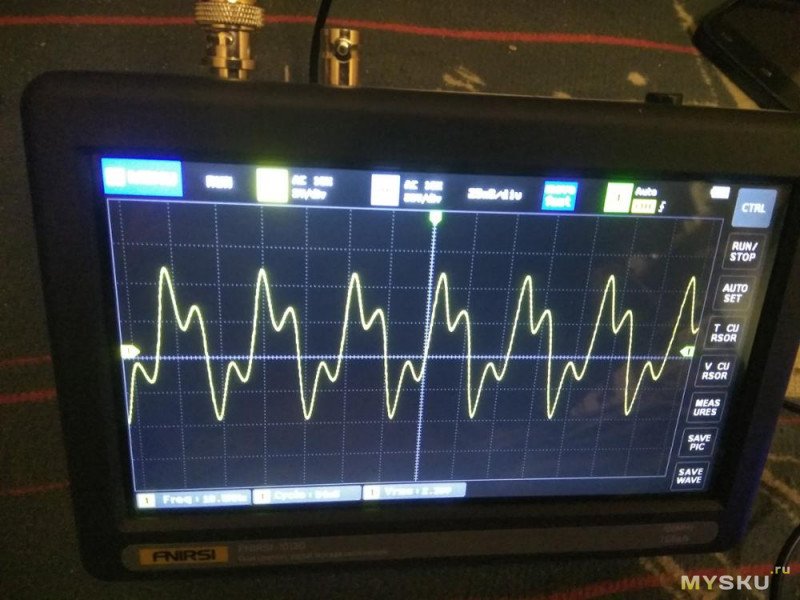 5 кг
5 кг
ПрофКиП Г3-117М генератор сигналов низкочастотный
▪ Диапазон частот: 1 мкГц … 25 МГц
▪ Форма сигнала: синус, прямоугольный, импульс, треугольник, пила, TTL, и произвольный
▪ Модуляция: одной частотой, частотой развертки, AM, FM, PM, FSK, ASK, PSK
▪ Разрешение по вертикали 10 бит
▪ Произвольная установка режима AM-модуляции: 1% … 120%
▪ Память формы сигнала: 4096 точек
▪ Встроенный частотомер до 100 МГц
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪Габариты, вес: 255х100х370 мм, 2.5 кг
подробнее…ПрофКиП Г3-113М генератор сигналов низкочастотный
▪ Диапазон частот: 0.2 Гц … 2 МГц
▪ Форма сигнала: синус, меандр, треугольник, пилообразный, импульс и т.д.
▪ Отдельный TTL, 50 Гц синус и сигнальный выход
▪ Сдвиг по постоянному току: 0 В … 10 В
▪ Плавная регулировка симметрии: 10% … 90%
▪ Вход управления частотой напряжением (VCF)
▪ Амплитуда входного сигнала: 20 Впик-пик
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 250х105х280 мм, 2.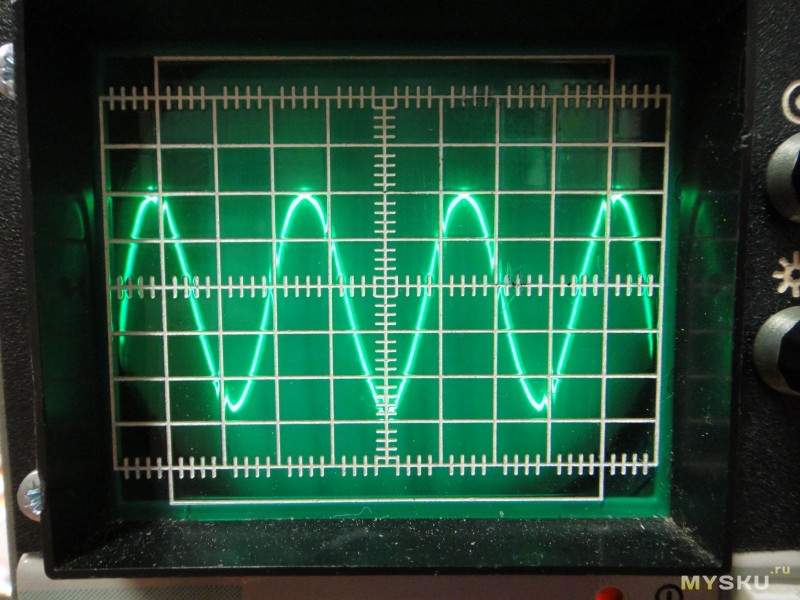 5 кг
5 кг
ПрофКиП Г3-112М генератор сигналов низкочастотный
▪ Диапазон частот: 10 Гц … 1 МГц
▪ Диапазон частот (меандр): 10 Гц … 10 кГц
▪ Точность: ±(3% + 1 Гц)
▪ Выходная мощность: 5 Вт
▪ Индикатор частоты: Лимб
▪ Формы сигнала: синусоида, меандр
▪ 6-ступенчатый выходной аттенюатор
▪ Функция внешней синхронизации
▪ Питание: 110 В … 127 В ±10% /220 В … 240 В ±10%, 50 Гц ±2Гц /60 Гц ±2 Гц
▪ Габариты, вес: 130х200х280 мм, 2.5 кг
подробнее…ПрофКиП Г3-112/1М генератор сигналов низкочастотный
▪ Частотный диапазон: 0.1 Гц … 10 МГц
▪ Форма сигнала: синусоида, меандр, треугольник и д.т.
▪ Импульсная и частотная модуляция
▪ Плавно регулируемое смещение постоянной составляющей
▪ Встроенный частотомер: 0.1 Гц … 50 МГц
▪ Защита выхода
▪ Высокая надежность: наработка на отказ > 10000 часов
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 230х80х210 мм, 1. 5 кг
5 кг
ПрофКиП Г3-111М генератор сигналов низкочастотный
▪ Частотный диапазон: 10 Гц … 1 МГц
▪ Форма сигналов: синус, меандр
▪ 6-ступенчатый выходной аттенюатор
▪ Функция внешней синхронизации
▪ Точность: ±(3% + 1 Гц)
▪ Максимально допустимое входное напряжение: 10 В
▪ Индикатор частоты: Лимб
▪ Питание: 110 В … 127 В ±10% /220 В … 240 В ±10%, 50 Гц ±2Гц /60 Гц ±2 Гц
▪ Габариты, вес: 142х197х233 мм, 3.5 кг
подробнее…ПрофКиП Г3-110М генератор сигналов низкочастотный
▪ Частотный диапазон: 0.2 Гц … 20 МГц
▪ Форма сигналов: синус, прямоугольник, треугольник, пила и т.д.
▪ Режимы входа: свип (внутр /внеш), АМ, ЧМ, ФМ и т.д.
▪ Плавная регулировка смещения, симметрии, амплитуды
▪ Встроенный частотомер до 100 МГц
▪ Полная защита выходной цепи
▪ Индикация амплитуды: среднеквадратичной уровень, пиковое значение
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 240х80х220 мм, 1.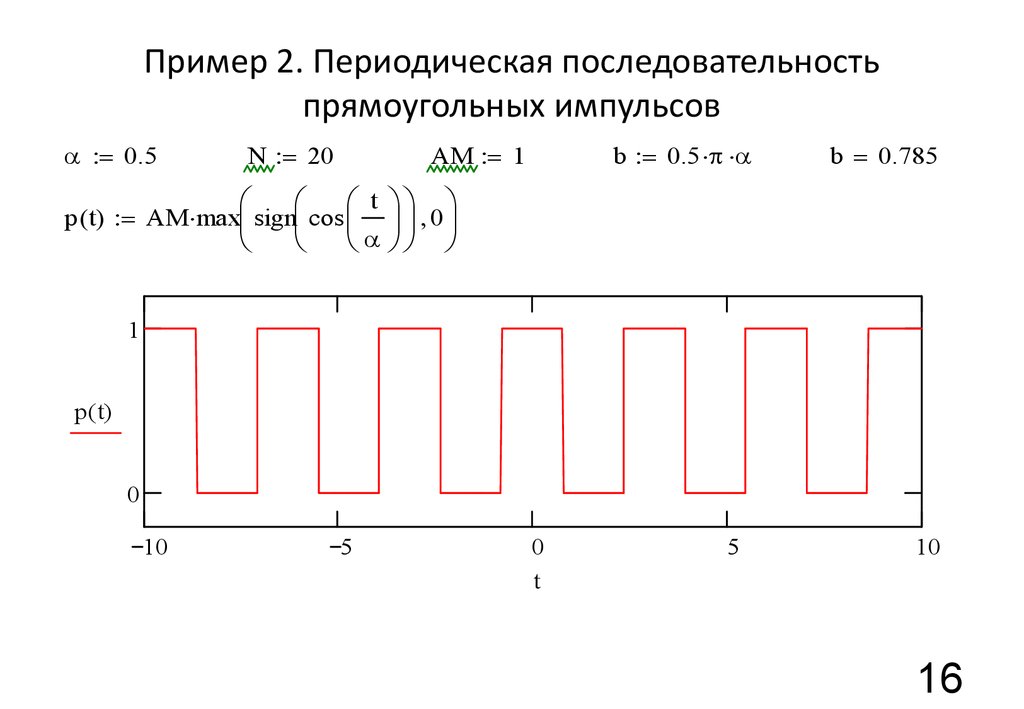 75 кг
75 кг
ПрофКиП Г3-109М генератор сигналов низкочастотный
▪ Частотный диапазон: 0.2 Гц … 10 МГц
▪ Форма сигналов: синус, прямоугольник, треугольник, пила и т.д.
▪ Режимы входа: свип (внутр /внеш), АМ, ЧМ, ФМ и т.д.
▪ Плавная регулировка смещения, симметрии, амплитуды
▪ Встроенный частотомер до 100 МГц
▪ Полная защита выходной цепи
▪ Индикация амплитуды: среднеквадратичной уровень, пиковое значение
▪ Питание: 110 В … 127 В ±10%, 220 В … 240 В ±10%, 50 Гц ±2 Гц /60 Гц ±2 Гц
▪ Габариты, вес: 240х80х220 мм, 1.75 кг
подробнее…Треугольный сигнал — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Треугольный сигнал подается на транзистор 77 ( BF256B), выполняющий функцию формирователя. Он работает как нелинейный резистор в области низких значений рабочего напряжения. При этом диод 1N4148 на затворе транзистора 77 из отрицательного полупериода треугольного сигнала формирует синусоиду, а сам транзистор — синусоидальный сигнал из положительного полупериода.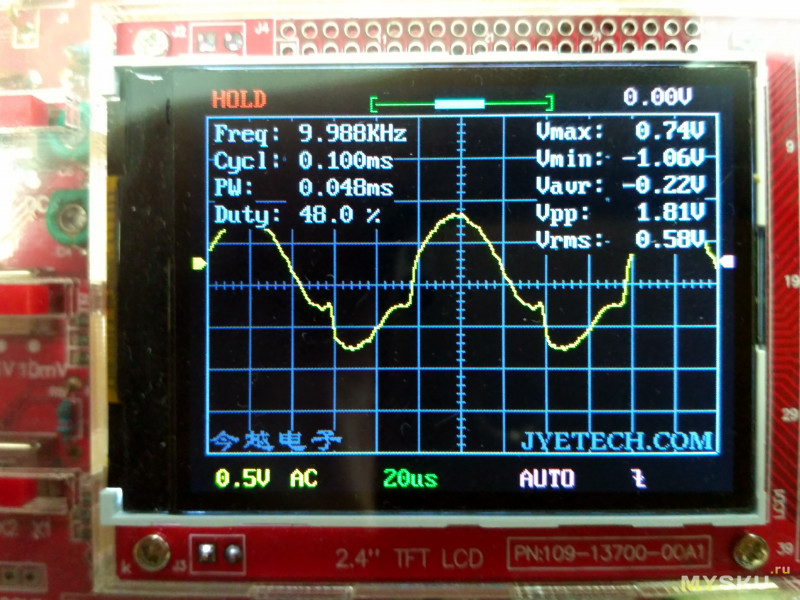 Посредством потенциометра РЗ регулируется качество синусоидального сигнала.
[1]
Посредством потенциометра РЗ регулируется качество синусоидального сигнала.
[1]
Отметим, что треугольный сигнал можно представить как автокорреляционную функцию прямоугольного сигнала с соответствующими коэффициентами, поэтому его спектр совпадает со спектром Ч ( о) для прямоугольного импульса. [2]
| Генератор, управляемый напряжением. ( Формулу для UBX следует читать так. 0 УВХ2 ( У — 1 5 В. — Прим. ред. [3] |
В приведенной схеме частота и амплитуда треугольного сигнала стабильны. [4]
Функция передачи звена с гистерезисом для треугольного сигнала также показана на рис. 13.21. Наклон треугольной волны меньше, чем ее основной составляющей; поэтому запаздывание по фазе заметно даже при больших сигналах. Эту функцию передачи в качестве упражнения предлагается получить читателю. Функция передачи звена с гистерезисом для случайного сигнала, подчиняющегося нормальному распределению, может быть приближенно выражена функцией передачи для треугольного сигнала, максимальная величина которого равна удвоенной среднеквадратичной величине случайного сигнала.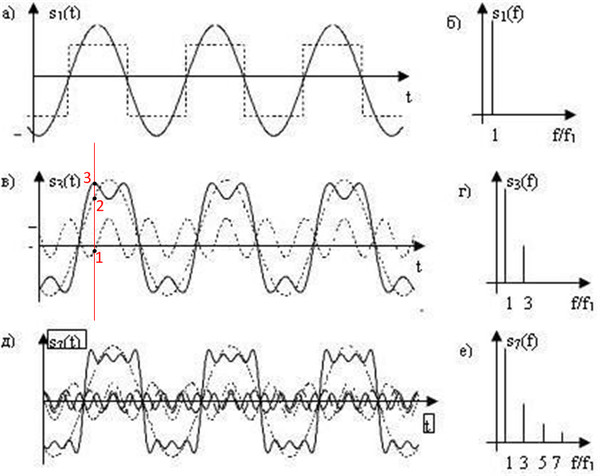 [5]
[5]
На выходе компаратора с петлей гистерезиса формируется меандр, который, как и треугольный сигнал интегратора, служит одним из выходных сигналов измерительного генератора. [6]
В разделе III, Б, 4 ( см. рис. 48) было показано, что при сканировании смешанного спектра спектрометром с одинаковой шириной входной и выходной щелей каждая монохроматическая линия испускания дает наложенный на непрерывный спектр треугольный сигнал с полушириной полосы, равной полуширине установленной щели монохроматора. [7]
| Генератор, управляемый напряжением. [8] |
Шмитта задаются точно и не имеют погрешности смещения, как это происходит при использовании в ОУ обычного выходного каскада, у которого пределы изменения выходного сигнала не заданы точно. В приведенной схеме частота и амплитуда треугольного сигнала стабильны. [9]
У многих измерительных генераторов специальной формы предусмотрена возможность образования выходного пилообразного сигнала, форма которого подобна форме развертывающего напряжения электронно-лучевого осциллографа. Для этого в схеме прибора предусматривается специальный формирователь, который формирует пилообразное напряжение из напряжений треугольного сигнала и меандра.
[10]
Для этого в схеме прибора предусматривается специальный формирователь, который формирует пилообразное напряжение из напряжений треугольного сигнала и меандра.
[10]
| Блок-схема перемножения напряже.| Формирование переменной скважности импульсов. [11] |
На рис. 11.37 приведена блок-схема временного разделения. Изменение скважности импульсов выполняется с — помощью компаратора, в котором входное напряжение С / 2 сравнивается с выходным напряжением генератора треугольного сигнала. [12]
Другая схема, рис. 11.3, б, используют нормальное включение транзисторов. В этих схемах происходит поочеред ное включение транзисторов. Высокая идентичность параметров транзисторов позволяет получить хорошую симметрию треугольного сигнала. [13]
Коэффициент усиления для случайного сигнала, подчиняющегося нормальному распределению, на входе звена с насыщением показан на рис. 13.6. Кривая этого коэффициента усиления является очень важной, так как она определяет фактический коэффициент усиления, от которого зависит точность вычислений при фактических рабочих условиях, когда сигналы являются непериодическими функциями. Коэффициент усиления для случайных сигналов значительно меньше, чем для периодических сигналов, имеющих ту же эффективную или среднеквадратичную величину. При сильном ограничении коэффициенты усиления для случайного сигнала и треугольного сигнала равны, если максимальная величина треугольного сигнала равна удвоенному среднеквадратичному значению случайного сигнала. В функции передачи для случайного сигнала фазовый сдвиг отсутствует.
[14]
13.6. Кривая этого коэффициента усиления является очень важной, так как она определяет фактический коэффициент усиления, от которого зависит точность вычислений при фактических рабочих условиях, когда сигналы являются непериодическими функциями. Коэффициент усиления для случайных сигналов значительно меньше, чем для периодических сигналов, имеющих ту же эффективную или среднеквадратичную величину. При сильном ограничении коэффициенты усиления для случайного сигнала и треугольного сигнала равны, если максимальная величина треугольного сигнала равна удвоенному среднеквадратичному значению случайного сигнала. В функции передачи для случайного сигнала фазовый сдвиг отсутствует.
[14]
Треугольный сигнал подается на транзистор 77 ( BF256B), выполняющий функцию формирователя. Он работает как нелинейный резистор в области низких значений рабочего напряжения. При этом диод 1N4148 на затворе транзистора 77 из отрицательного полупериода треугольного сигнала формирует синусоиду, а сам транзистор — синусоидальный сигнал из положительного полупериода. Посредством потенциометра РЗ регулируется качество синусоидального сигнала.
[15]
Посредством потенциометра РЗ регулируется качество синусоидального сигнала.
[15]
Страницы: 1 2
Что такое квадратная волна и прямоугольная форма волны » Electronics Notes
Квадратные волны, прямоугольные волны и импульсные сигналы — это все формы сигналов, которые имеют два состояния; высокий и низкий, и они широко используются с цифровыми схемами.
Электронные и электрические сигналы Включает:
Типы сигналов и основные сведения
Синусоидальная волна
Квадратные и прямоугольные волны
Треугольная волна
Прямоугольные волны — это форма периодической формы волны, которая чередуется между двумя состояниями и не является синусоидальной.
В идеальной прямоугольной волне переходы между двумя состояниями мгновенны, но в реальном мире это, очевидно, не так, и время нарастания и спада представляет большой интерес.
Хотя термин прямоугольная волна используется для многих форм сигнала с двумя состояниями, строго говоря, прямоугольная волна является прямоугольной и имеет одинаковое время в любом состоянии, т. е. имеет отношение метки к пространству 1:1. Прямоугольный сигнал представляет собой периодический сигнал с двумя состояниями, который имеет неравное отношение метки к пространству.
е. имеет отношение метки к пространству 1:1. Прямоугольный сигнал представляет собой периодический сигнал с двумя состояниями, который имеет неравное отношение метки к пространству.
Импульсный сигнал может не быть повторяющимся или периодическим. Это может быть вызвано генерацией импульса при достижении определенного аналогового порога, передачей данных или многими другими причинами.
Как звучит прямоугольная волна
Прямоугольная волна звучит гораздо более пронзительно, чем синусоида. Это происходит из-за того, что он имеет острые края из-за быстрых возведенных в квадрат краев формы волны.
Прямоугольная волна богата гармониками, что придает ей довольно интересный тон с музыкальной точки зрения.
Звук прямоугольного сигнала
Основные аспекты прямоугольных волн
Прямоугольные волны появляются в различных электронных схемах и других областях электроники. Они особенно распространены в цифровых или логических схемах, где система имеет дело с цифровыми данными и сигналами.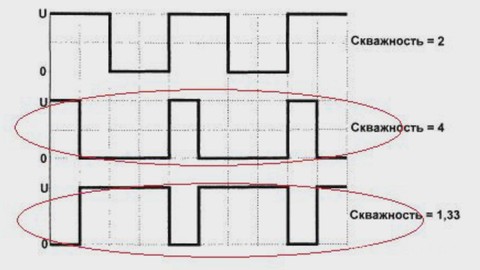
При использовании в логической или цифровой схеме два состояния часто обозначаются как «1» и «0», соответствующие двоичным разрядам. Их также можно обозначить как «ВЫСОКИЙ» и «НИЗКИЙ», указывая на напряжение.
Состояние логической «1» совпадает с состоянием «ВЫСОКИЙ», а состояние «0» соответствует состоянию «НИЗКИЙ».
Эта терминология принята, поскольку логическая схема обычно связана с двоичными числами и сигналами. Существует множество схем, использующих логические схемы, некоторые из них могут быть относительно простыми с использованием небольших логических микросхем, тогда как другие могут использовать микропроцессоры или микроконтроллеры и т. д.
Поскольку не всегда возможно определить точное напряжение, в электронных схемах обычно дается окно для высокого и низкого состояний.
Существует множество аспектов прямоугольной волны, которые часто необходимо указывать.
Период времени: Период времени прямоугольной волны является одним из ключевых параметров, описывающих форму волны.
 Поскольку основными характеристиками прямоугольной волны являются нарастающие и спадающие фронты, они являются ключевыми областями, которые используются для маркеров для определения периода времени. Либо измерение может быть выполнено от одного нарастающего фронта к другому, либо от одного спадающего фронта к следующему.
Поскольку основными характеристиками прямоугольной волны являются нарастающие и спадающие фронты, они являются ключевыми областями, которые используются для маркеров для определения периода времени. Либо измерение может быть выполнено от одного нарастающего фронта к другому, либо от одного спадающего фронта к следующему.Одно и то же напряжение запуска используется от цикла к циклу в случае наличия наклона нарастающего или спадающего фронта. Однако для любого измерительного прибора точка срабатывания будет одной и той же от одного измерения к другому, так что это не проблема.
Частота: Как и частота синусоидального сигнала, частота прямоугольного сигнала – это количество смен сигнала в секунду. Частота раньше измерялась в циклах в секунду, но теперь используется единица Герц, где один Герц равен одному циклу в секунду.
Если известна частота прямоугольной волны, то можно рассчитать период времени и наоборот.
Аналогичным образом, изменяя уравнение, мы видим, что:
Где:
f = частота в Гц
T = период времени одного цикла в секундахАмплитуда: Амплитуда прямоугольной волны может быть указана одним из нескольких способов.

Очевидно, что можно измерить и указать напряжение сигнала как пиковое напряжение или размах. Это может быть использовано, если прямоугольная волна использовалась с аналоговой системой наряду с другими формами волны, такими как синусоидальная волна или другие формы волны.
Однако прямоугольные сигналы наиболее широко используются в цифровых схемах для электронных систем или других логических систем. В цифровых схемах представляют интерес значения для низкого и высокого состояний.
Обычно низкое состояние находится между 0 В и 0,4 В, а высокое состояние — между 2 В и шиной питания, что обычно составляет 5,0 В для стандартного TTL. В более современных логических семействах используются гораздо более низкие напряжения, но сохраняются те же принципы, хотя напряжения будут немного отличаться.
Время нарастания и спада прямоугольной волны
Одним из важных аспектов прямоугольных волн является время, которое требуется форме волны, чтобы подняться, а затем спасть.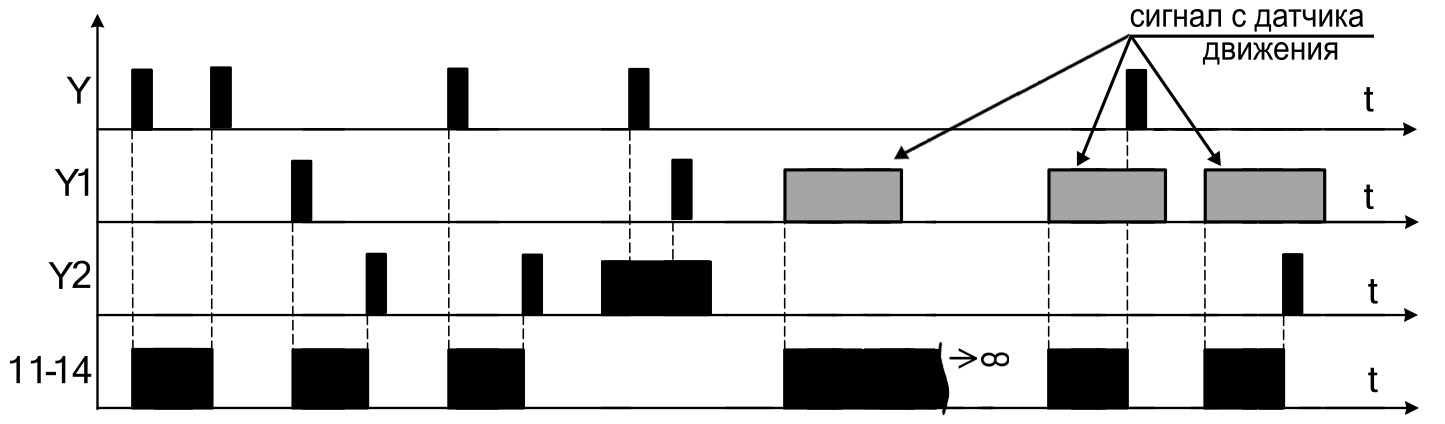
Часто указывается время нарастания и спада прямоугольной волны. Например, прямоугольная волна от генератора сигналов может иметь характеристики времени нарастания и спада.
Иногда необходимо измерить время нарастания и спада сигнала, поскольку это может повлиять на работу некоторых электронных схем, особенно использующих цифровые технологии.
Обычно время нарастания измеряется как время, за которое нарастающий фронт переходит от 10 % от конечного значения до 90 %. Точно так же задний фронт использует те же точки.
Обычно используются точки 10% и 90%, хотя в некоторых случаях могут использоваться 5% и 95%, но это менее распространено.
Время нарастания и спада для прямоугольной волныНа диаграмме даны значения 10 % и 90 %, а времена t нарастания и t спада относятся к временам нарастания и спада соответственно.
Для большинства логических семейств, использующих цифровые и прямоугольные сигналы, время нарастания и спада, скорее всего, будет указано в наносекундах.
Спектр прямоугольных волн и анализ Фурье
Если проанализировать спектр прямоугольной волны, то окажется, что он состоит из ряда гармонически связанных синусоидальных волн.
Фактически любой периодический сигнал может быть проанализирован таким образом, и могут быть определены составляющие частоты или синусоидальные волны.
Если проанализировать спектр прямоугольной волны, то будет видно, что форма волны состоит из синусоидальной волны на основной частоте, одна из которых в три раза больше основной, но с одной третью амплитуды, одна из которых является пятой гармоникой, а у квинты амплитуда и так далее. Другими словами, он состоит из ряда нечетно-целых гармонических частот.
Синусоидальные составляющие прямоугольной волны Чем больше количество присутствующих гармоник, тем точнее представление. Это означает, что если прямоугольный сигнал пропустить через фильтр нижних частот, он будет искажен, а фронты, время нарастания и т.п. будут хуже, чем у прямоугольного сигнала с бесконечной полосой пропускания.
В математическом выражении прямоугольная волна может быть представлена следующим уравнением:
x(t)=A(sin(ωt)+13sin(3ωt)+15sin(5ωt) …)
Фактический спектр прямоугольной волны можно увидеть на этом графике спектра прямоугольной волны, снятом с тестового прибора.
Спектр прямоугольной волныНа диаграмме основная частота будет видна слева от развертки — обратите внимание, что линия нулевой частоты находится справа слева от развертки. Затем гармоники можно увидеть в нечетных кратных основной гармонике.
Следует помнить, что шкала амплитуд является логарифмической, но видно, что гармоники находятся на уровне 3, 5, 7 и далее нечетных кратных основной гармонике и что их амплитуда уменьшается с увеличением частоты.
Также видно, что четные кратные отсутствуют, поскольку прямоугольная волна состоит только из нечетных целых гармоник.
Прямоугольные, прямоугольные и импульсные волны встречаются в огромном количестве электронных схем, систем и т.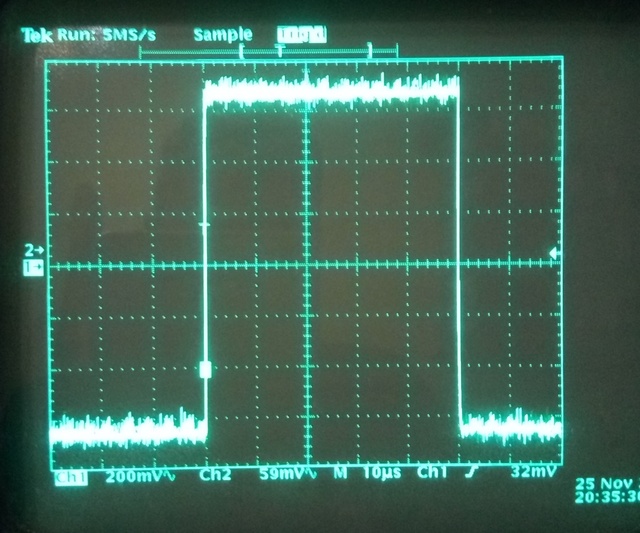 п. Они особенно распространены в схемах, основанных на цифровых или логических схемах, поскольку эта технология основана на формах сигналов, которые имеют два состояния.
п. Они особенно распространены в схемах, основанных на цифровых или логических схемах, поскольку эта технология основана на формах сигналов, которые имеют два состояния.
Дополнительные основные понятия и руководства по электронике:
Напряжение
Текущий
Сила
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ-шум
Сигналы
Вернуться в меню основных понятий электроники . . .
Square Waveform — прямоугольная волна FFT, гармоники и спектр
- Задачи проектирования
Войти
Добро пожаловать! Войдите в свою учетную запись
ваше имя пользователя
ваш пароль
Забыли пароль?
Создать учетную запись
Политика конфиденциальности
Зарегистрироваться
Добро пожаловать!Зарегистрируйте аккаунт
ваш адрес электронной почты
ваше имя пользователя
Пароль будет отправлен вам по электронной почте.
Политика конфиденциальности
Восстановление пароля
Восстановление пароля
ваш адрес электронной почты
Поиск
Изменено:
Статьи категорий
Содержание
Сигнал прямоугольной формы — это сигнал, который имеет два значения: -A и. Классический прямоугольный сигнал, который следует правильно называть прямоугольным, имеет те же полупериоды. Сигнал может быть создан с использованием пилообразного сигнала посредством пороговой обработки. Положительные амплитуды преобразуются в значения +A, а отрицательные усиленные значения преобразуются в -A. Для порога мы можем использовать логическое условие y>0, возвращающее логические значения True или False. Возможно преобразование логических чисел в числовые значения (numpy.astype) 1, 1 и 0 соответственно. Чтобы преобразовать их в числа +1 и -1, вам нужно умножить два значения на 2. Затем вычесть 1.
квадрат = (пила >= 0).astype(np.int) * 2 - 1 plt.plot(n, квадрат) plt.xlabel('номер образца') plt.ylabel('амплитуда') plt.title('Квадратный сигнал) plt.show()
Сигнал выше прямоугольной волны характеризуется соотношением сторон, обычно называемым скоростью заполнения, которое равно 0,5, т. е. половина сигнала занимает положительную сторону. Возможно, что прямоугольная форма сигнала также может иметь дополнительный форм-фактор. Это можно учесть, скорректировав любое смещение в сигнале. Ниже приведен пример соотношения сторон 0,8.
б = 0,8
фаза = ((n * 2 * f / fs + 1) % 2) + (b - 1)
Square08 = (фаза >= 0).astype(np.int) * 2 - 1
plt.plot(n, Square08)
plt.xlabel('номер образца')
plt.ylabel('амплитуда')
plt.title('Квадратный сигнал, коэффициент формы 0,8')
plt.show() Прямоугольная волна БПФ
Быстрое преобразование Фурье (БПФ) это алгоритм, который упрощает и уменьшает объем вычислений, необходимых для определения ДПФ. Алгоритм основан на использовании матричных примечаний для описания преобразования ДПФ с последующим равномерным распределением точек, которые аппроксимируют форму волны. Матрица, используемая в расчете, затем может быть разделена на несколько разреженных матриц (с большим количеством нулей), что значительно упрощает процесс.
Матрица, используемая в расчете, затем может быть разделена на несколько разреженных матриц (с большим количеством нулей), что значительно упрощает процесс.
Генерация периодических сигналов с помощью БПФ
Частота гармоник, а также других регулярных сигналов может быть получена путем создания желаемого спектра путем вычисления обратного преобразования Фурье. Главный недостаток этого метода в том, что невозможно определить какую-либо частоту сигнала. Частоты определяются размерами преобразования, а также частотой дискретизации. Для получения любой частоты сигнала требуется интерполяция. Преимущество этого метода в том, что он более эффективен, чем для аддитивного метода (особенно когда необходимо определить большое количество элементов), кроме возможности создания сигналов, имеющих любой спектр.
Для начала рассмотрим синусоидальный сигнал. Мы ищем, чтобы создать N выборок этого сигнала, и поэтому нам нужно N значений из спектра. Поскольку мы создаем реальный сигнал, который является реальным, нам нужно определить только половину спектра и использовать numpy.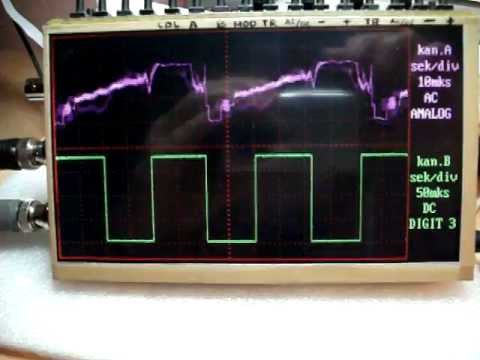 fft.irfft. функция numpy.fft.irfft. В частности, нам требуется N/2+1 значений в спектре, а именно: первое значение указывает на то, что известно как составляющая постоянного тока, а последнее значение — на то, что известно как значение Найквиста (для простоты мы предполагаем, что N равно равны), а другие значения определяют амплитуду (и фазу) и фазу компонентов сигнала. Значение спектра с индексом K представляет компонент сигнала, имеющий частоту kfs/N.
fft.irfft. функция numpy.fft.irfft. В частности, нам требуется N/2+1 значений в спектре, а именно: первое значение указывает на то, что известно как составляющая постоянного тока, а последнее значение — на то, что известно как значение Найквиста (для простоты мы предполагаем, что N равно равны), а другие значения определяют амплитуду (и фазу) и фазу компонентов сигнала. Значение спектра с индексом K представляет компонент сигнала, имеющий частоту kfs/N.
Создайте буфер N/2+1, заполненный нулями, гарантируя, что мы будем использовать комплексные числа. Величина сигнала должна быть не менее 1. Поскольку это правда, что синусоидальные компоненты сигнала должны быть видны дважды в спектре, поэтому мы должны разделить амплитуду на два. Эта составляющая, называемая синусоидальной, является частью импульса сложного спектра, следовательно, спектральная составляющая должна быть не менее -0,5j. Вставка этого значения в нижний индекс k=1 дает одну фазу сигнала, а нижний индекс nk дает частоту n раз. После расчета IFFT и удаления мнимой части, которая является остатком, все еще необходимо увеличить величину сигнала, используя уравнение N (функция irfft разделяет результат на величину преобразования).
После расчета IFFT и удаления мнимой части, которая является остатком, все еще необходимо увеличить величину сигнала, используя уравнение N (функция irfft разделяет результат на величину преобразования).
Обычный квадратный сигнал (соотношение сторон 0,5).
Для расчета прямоугольного сигнала с коэффициентом формы B важно помнить, что компоненты ряда Фурье изображаются косинусами. Поэтому мы должны определить действительные амплитуды составляющих спектрального спектра. Кроме того, необходимо изменить результаты по шкале амплитуд, что достигается заменой постоянной составляющей на 2b-1.
Спектр прямоугольных волн
Чтобы получить подробную информацию о различных элементах сложной формы волны, необходимо провести исследование спектра (частоты) частотного сигнала, полученного при измерении. Анализ сигналов может осуществляться цифровым, аналоговым или смешанным способами. Обработка аналоговых сигналов осуществляется с помощью анализаторов спектра. Это может быть набор фильтров с различными частотами пропускания, а также настраиваемые узкополосные фильтры. Цифровая обработка с использованием быстрого преобразования Фурье (БПФ) является наиболее часто используемым. Представление периодической функции в виде ряда Фурье эквивалентно разложению ее на составляющие функции, включающие в себя постоянную часть a0, а также гармонические составляющие, имеющие две пульсации: ω1, 2ω1, 3ω1, …, nω1, где ω1 — основная пульсация, nω1 — гармонические пульсации, n — натуральное число. Основная пульсация определяется по формуле.
Цифровая обработка с использованием быстрого преобразования Фурье (БПФ) является наиболее часто используемым. Представление периодической функции в виде ряда Фурье эквивалентно разложению ее на составляющие функции, включающие в себя постоянную часть a0, а также гармонические составляющие, имеющие две пульсации: ω1, 2ω1, 3ω1, …, nω1, где ω1 — основная пульсация, nω1 — гармонические пульсации, n — натуральное число. Основная пульсация определяется по формуле.
где: T – период функции
Уравнение, описывающее периодическую форму сигнала x(t) с помощью ряда Фурье, имеет вид.
Эффективность рядов Фурье а0, bn определяют путем анализа уравнения формы сигнала или по результатам измерений, выполненных с помощью гармонического анализатора. Например, периодический сигнал в форме прямоугольного сигнала может быть представлен как бесконечная тригонометрическая последовательность, включающая нечетные гармоники (1 3, 5, 7, …) с уменьшающимися амплитудами. Это иллюстрация сигнала во временной области.
Периодические сигналы также могут быть представлены графически в пределах частотного диапазона. По оси абсцисс отложена частота f (или пульсация 2pf). По оси координат величины или отношения величин. Ширина столбцов пропорциональна величине амплитуд соответствующих прямоугольных гармоник, присутствующих в исследуемом сигнале. График называется спектром амплитудного спектра, также известным как частотный спектр. Спектры, которые являются периодическими компонентами сигнала, имеют дискретность, однако спектры непериодического сигнала (например, стохастического или импульсного сигнала) являются непрерывными.
Амплитудный спектр сигнала прямоугольной формы
Гармоники прямоугольной формы
Прямоугольная волна представляет собой наложение нескольких синусоидальных волн с нечетными гармониками основной частоты. Интенсивность каждой гармоники обратно пропорциональна частоте. Подобно треугольным и пилообразным волнам, они также состоят из прямоугольных гармоник, частоты которых отличаются от основных частот. Импульс — это совокупность всех частот, которые можно представить в размере выборки, а также в количестве выборок. Частоты конусообразных сигналов являются дискретными и попадают в определенный интервал. Частота этих сигналов определяется размером выборки для начальной и конечной частот, а также количеством выборок.
Импульс — это совокупность всех частот, которые можно представить в размере выборки, а также в количестве выборок. Частоты конусообразных сигналов являются дискретными и попадают в определенный интервал. Частота этих сигналов определяется размером выборки для начальной и конечной частот, а также количеством выборок.
Наиболее часто используемые тестовые сигналы, за исключением синусоидального сигнала, не могут обеспечить полный контроль их спектральных свойств. Например, гармоники прямоугольной формы фиксированы по частоте, фазе и амплитуде по отношению к основной частоте. Напротив, многотональные сигналы могут создаваться с заданной частотой и амплитудой для каждой отдельной частоты компонента. Многотональный сигнал представляет собой комбинацию множества синусоид или тонов с четкой фазой, амплитудой и частотой. Многотональный сигнал обычно создается таким образом, что общее количество циклов в каждом тоне записывается в сигнал. Если вычислить быстрое преобразование Фурье всего многотонального сигнала, то каждый тон точно отображается в определенную полосу частот. Это означает, что нет никакого спектрального разброса или утечки. Многотональные сигналы являются частью многочисленных тестовых спецификаций и позволяют системам быстро и эффективно запускаться на всех частотах. Многотональные тестовые сигналы можно использовать для измерения того, какой частотный диапазон подходит для устройств, если он правильно выбран. выбор, можно использовать для определения таких вещей, как кросс-модуляционные помехи.
Это означает, что нет никакого спектрального разброса или утечки. Многотональные сигналы являются частью многочисленных тестовых спецификаций и позволяют системам быстро и эффективно запускаться на всех частотах. Многотональные тестовые сигналы можно использовать для измерения того, какой частотный диапазон подходит для устройств, если он правильно выбран. выбор, можно использовать для определения таких вещей, как кросс-модуляционные помехи.
Ссылки:
https://sound.eti.pg.gda.pl/~greg/dsp/06-GenerowanieSygnalow.html
https://home.agh.edu.pl/~mgi/instrukcje/LAB_1_Transformacja_FFT_Filtracja_Moc_sygna %B3u-student.pdf
http://www.kdm.p.lodz.pl/wyklady/lab/Cwiczenie8.pdf
http://www.prz.rzeszow.pl/kpe/materialy/astadler/DAQWWW /LabVIEW/Dataprocessing/Sygna%B3ytestowe/index.html
Михал
Инженер по электронике и телекоммуникациям с дипломом магистра электроэнергетики. Светодизайнер опытный инженер. В настоящее время работает в сфере IT.
Английский
Подробнее об прямоугольных волнах и постоянном содержании
Чарли Хьюз В этой статье Чарли рассматривает прямоугольные волны на более глубоком уровне. Такие вопросы, как «Почему он имеет квадратную форму?» будет решаться. Недавняя ветка на сервере рассылки SAC «В поисках нового цифрового мультиметра» вызвала много хороших дискуссий о переходных процессах, отсечении, прямоугольных волнах и постоянном токе. Я подумал, что было бы полезно немного рассказать об этом. Сначала давайте посмотрим на прямоугольную волну и посмотрим, почему она имеет квадратную форму. Сложная форма волны может быть построена или разложена на синусоидальные (и косинусоидальные) волны с различными амплитудами и фазовыми соотношениями. На этом основан анализ Фурье. Прямоугольная волна состоит из основной синусоиды (той же частоты, что и прямоугольная волна) и нечетных гармоник основной гармоники.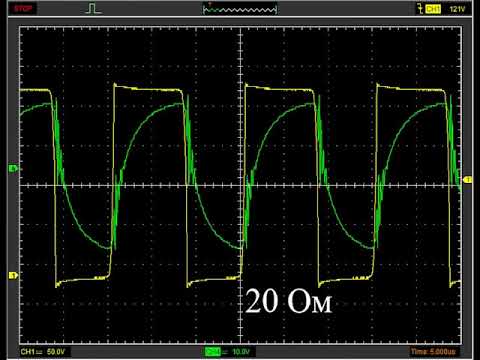 Амплитуда гармоник равна 1/N, где N — гармоника (1, 3, 5, 7…). Каждая гармоника имеет одинаковое фазовое отношение к основной частоте.
Амплитуда гармоник равна 1/N, где N — гармоника (1, 3, 5, 7…). Каждая гармоника имеет одинаковое фазовое отношение к основной частоте.
Если мы создадим прямоугольную волну только из первых двух гармонических составляющих, мы сможем увидеть, как возникает прямоугольная форма (рис. 1). Здесь мы видим, что красная кривая — это первая гармоника (основная), а зеленая — третья гармоника с правильной амплитудой. Когда первая гармоника имеет максимальное значение, третья гармоника имеет минимальное значение. Сложив эти два вместе, мы получим черный след, который начинает напоминать прямоугольную волну.
Если мы теперь используем 5 гармонических составляющих (1, 3, 5, 7 и 9) для построения прямоугольной волны мы видим, что она действительно начинает обретать форму (рис. 2). В конце каждого полупериода прямоугольной волны все гармонические компоненты движутся в одном направлении (либо в положительном, либо в отрицательном направлении). Этим и объясняется резкий рост. К середине каждого полупериода гармоники чередуются между минимальной и максимальной амплитудой, как мы видели на рисунке 1.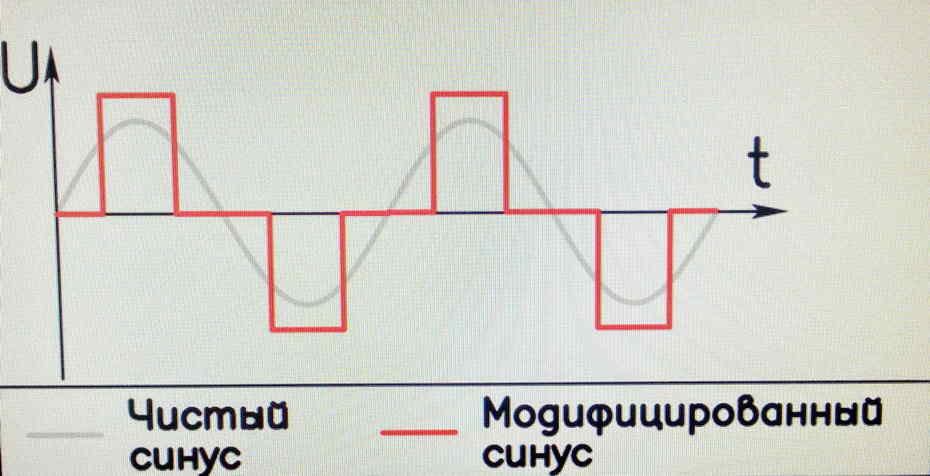 Это то, что объясняет плоскую часть прямоугольной волны.
Это то, что объясняет плоскую часть прямоугольной волны.
Увеличение до 10 гармонических составляющих приводит к рисунку 3. Обратите внимание, что только первые 6 гармоник показаны отдельно, но 10 гармоник используются для генерации прямоугольной волны.
Дальнейшее увеличение до 100 и 1000 гармонических составляющих показано на Рисунке 4 и Рисунке 5 соответственно. Из этих графиков должно быть хорошо понятно, что содержание высокочастотных гармоник, а не постоянная составляющая (0 Гц), отвечает за форму прямоугольной волны. На самом деле постоянный ток по своему определению не может вызывать какую-либо форму волны, зависящую от частоты. Постоянная составляющая сигнала — это просто среднее значение этого сигнала.
Сигналы, симметричные относительно временной оси, будут иметь нулевое значение DC. Сигналы, асимметричные относительно оси времени, могут иметь или не иметь значение DC, равное нулю. Если площадь между положительной половиной сигнала и осью времени равна площади между отрицательной половиной сигнала и осью времени, компонент постоянного тока не будет присутствовать.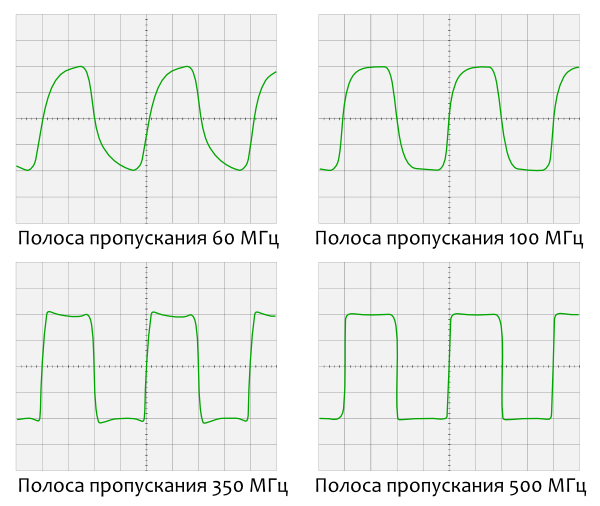 Если эти области не равны, в сигнале будет постоянный ток. Другими словами, среднее значение сигнала должно быть ненулевым, если в сигнале присутствует постоянный ток.
Если эти области не равны, в сигнале будет постоянный ток. Другими словами, среднее значение сигнала должно быть ненулевым, если в сигнале присутствует постоянный ток.
Чтобы проверить это для нашей прямоугольной волны, мы применим фильтр верхних частот ниже основной частоты прямоугольной волны. Наша прямоугольная волна имеет частоту 200 Гц, поэтому давайте воспользуемся фильтром верхних частот второго порядка (12 дБ/октава) с частотой 50 Гц. Результат показан на рисунке 6.
Здесь мы видим, что конец каждого полупериода прямоугольной волны спадает (или наклоняется) обратно к нулю. Некоторые могут подумать, что это связано с устранением постоянного тока фильтром верхних частот. Это не тот случай. Настоящая причина наклона заключается в фазовом сдвиге гармонических составляющих, составляющих прямоугольную волну. Обратите внимание, что в середине каждого полупериода максимум первой гармоники (красный) больше не совпадает с максимумом/минимумом других гармоник. Это также можно увидеть, возможно, более отчетливо, взглянув на пересечение нуля.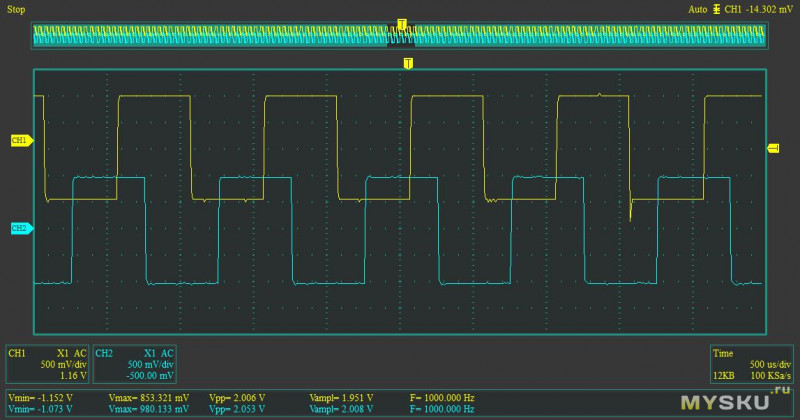 На предыдущих графиках всякий раз, когда основная гармоника пересекала нуль, все остальные гармоники также пересекали нуль. Это не относится к рисунку 6 с примененным фильтром верхних частот.
На предыдущих графиках всякий раз, когда основная гармоника пересекала нуль, все остальные гармоники также пересекали нуль. Это не относится к рисунку 6 с примененным фильтром верхних частот.
Если мы посмотрим на отклик фильтра верхних частот 50 Гц в частотной области (рис. 7), то увидим, как происходит фазовый сдвиг гармонических составляющих. Фазовый сдвиг на частоте 200 Гц составляет примерно 21° по сравнению с верхним частотным пределом 0° (без фазового сдвига), что приводит к временному сдвигу основной частоты на 292 мкс. Фазовый сдвиг следующей составляющей (3-я гармоника, 600 Гц) составляет примерно 7°. Это приводит к временному сдвигу этого компонента на 32 мкс. Все высшие гармоники подвержены меньшему фазовому сдвигу (находятся ближе по фазе) и, таким образом, возникают примерно в одно и то же время. Таким образом, рисунок 7 точно предсказывает то, что мы видим на рисунке 6.
Чтобы еще раз проверить наше утверждение о том, что фазовая характеристика фильтра верхних частот с частотой 50 Гц является причиной наклона прямоугольной волны, а не устранением какой-либо постоянной составляющей, давайте пропустим прямоугольную волну через всепропускающий фильтр с частотой 50 Гц вместо фильтр верхних частот. Это будет поддерживать примерно такой же фазовый сдвиг, как фильтр верхних частот, но низкочастотное содержание сигнала не будет ослаблено. Если есть какая-либо составляющая постоянного тока, вносящая вклад в прямоугольную волну, мы должны увидеть разницу (т.е. наклон больше не должен присутствовать). Беглый взгляд на рис. 8 должен подтвердить, что он практически идентичен рис. 6. Это должно однозначно подтвердить, что структура с плоской вершиной определенной формы волны не связана с постоянным током. Вместо этого это связано с гармоническим составом сигнала и фазовым отношением этих гармоник к основной частоте.
Это будет поддерживать примерно такой же фазовый сдвиг, как фильтр верхних частот, но низкочастотное содержание сигнала не будет ослаблено. Если есть какая-либо составляющая постоянного тока, вносящая вклад в прямоугольную волну, мы должны увидеть разницу (т.е. наклон больше не должен присутствовать). Беглый взгляд на рис. 8 должен подтвердить, что он практически идентичен рис. 6. Это должно однозначно подтвердить, что структура с плоской вершиной определенной формы волны не связана с постоянным током. Вместо этого это связано с гармоническим составом сигнала и фазовым отношением этих гармоник к основной частоте.
Надеюсь, некоторые читатели заметили что-то интересное в форме сигнала после того, как он был подвергнут фильтру высоких частот (или фильтру всех частот). Фазовый сдвиг компонентов привел к увеличению пиковой амплитуды на переднем фронте прямоугольной волны! Амплитуда необработанной прямоугольной волны (без фильтрации) составляет приблизительно 0,79. После прохождения фильтра высоких частот пиковая амплитуда составляет примерно 1,25.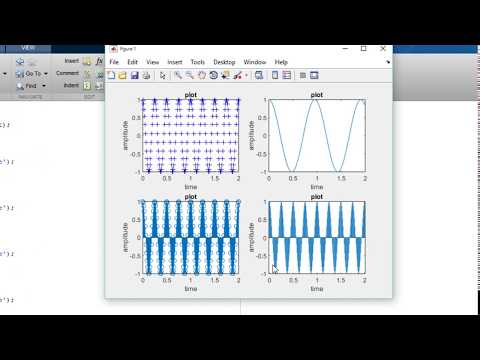 Увеличение порядка фильтра или увеличение частоты (до предела, связанного с основной волной прямоугольной формы) увеличит пиковую амплитуду. Как видно на рисунке 9, с фильтром верхних частот Баттерворта четвертого порядка на частоте 125 Гц пиковая амплитуда превышает 2,2. Это увеличение пиковой амплитуды почти на 280% по сравнению с амплитудой исходной прямоугольной волны!
Увеличение порядка фильтра или увеличение частоты (до предела, связанного с основной волной прямоугольной формы) увеличит пиковую амплитуду. Как видно на рисунке 9, с фильтром верхних частот Баттерворта четвертого порядка на частоте 125 Гц пиковая амплитуда превышает 2,2. Это увеличение пиковой амплитуды почти на 280% по сравнению с амплитудой исходной прямоугольной волны!
Этот сигнал с высоким пиком (больше не прямоугольный) возникает, когда основная гармоника и некоторые из более низких гармоник смещаются таким образом, что их положительные пики возникают в то же время или очень близко к тому же времени, что и положительные пики других гармоник. гармоники. Это также происходит для отрицательных пиков основной гармоники и отрицательных пиков гармоник. Тщательный осмотр рисунка 9покажет, что это так.
Когда сигналы обрезаются устройствами, которые не имеют достаточного запаса для их прохождения, верхние (и нижние) границы сигнала становятся сглаженными. Независимо от того, является ли сигнал периодическим, симметричным или асимметричным, сглаживание формы волны (по дизайну или путем ограничения) может быть достигнуто только путем добавления синфазных гармоник; как и в случае прямоугольной волны.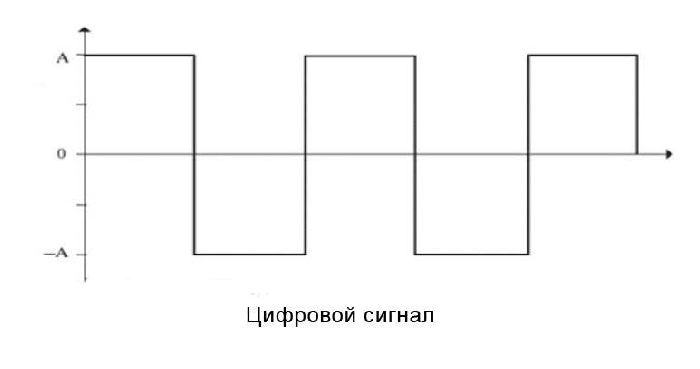 Если отсечение сигнала также приводит к тому, что области, ограниченные формой волны выше оси времени и ниже оси времени, больше не равны, то в сигнал также была введена постоянная составляющая. Это, однако, не влияет на общую форму волны. Если бы постоянная составляющая была каким-то образом удалена без какого-либо другого воздействия на сигнал, форма волны просто испытала бы вертикальный сдвиг вверх или вниз, в зависимости от того, была ли удаленная составляющая постоянной составляющей больше или меньше нуля.
Если отсечение сигнала также приводит к тому, что области, ограниченные формой волны выше оси времени и ниже оси времени, больше не равны, то в сигнал также была введена постоянная составляющая. Это, однако, не влияет на общую форму волны. Если бы постоянная составляющая была каким-то образом удалена без какого-либо другого воздействия на сигнал, форма волны просто испытала бы вертикальный сдвиг вверх или вниз, в зависимости от того, была ли удаленная составляющая постоянной составляющей больше или меньше нуля.
Я надеюсь, что это помогло проиллюстрировать, что именно гармоническая структура (содержание и соотношение фаз) сигнала отвечает за форму волны с плоской вершиной. Прямоугольные волны являются лишь одним из примеров этих типов сигналов.
Спасибо Дейлу Ширку за переписку в автономном режиме во время ветки DMM на сервере рассылки и за предложение этой статьи. ch
Синус, Пила, Квадрат, Треугольник, Импульс: основные формы сигналов при синтезе и их свойства
Прочтите это, чтобы использовать весь их потенциал и избежать каких-либо предостережений!
youtube.com/embed/7E8Ou6DYsJQ» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Форма волны — это графическое представление волны.
Синтез звука основан на 5 волновых формах: синусоида, треугольник, пилообразный (пила), импульс и квадрат (частный случай импульса).
Чтобы эффективно использовать их в композициях синтеза звука или звуковых программах, вам необходимо знать их основные свойства:
- математическую формулу для ее создания,
- визуализация во временной области, Амплитудный спектр
- : какие гармоники присутствуют и как затухают их амплитуды, и
- как это звучит!
В этой статье вы узнаете обо всех этих свойствах пяти основных сигналов.
Примечание: в этой статье сигналы показаны в их непрерывной (аналоговой) форме, что означает, что такие проблемы, как наложение спектров или эффективная генерация, не рассматриваются. Имейте в виду, что все эти формы волны (кроме синуса) имеют бесконечный спектр амплитуд.
Имейте в виду, что все эти формы волны (кроме синуса) имеют бесконечный спектр амплитуд.
Зачем изучать основные формы сигналов?
Изучение основных волновых форм в синтезе звука поможет вам
- использовать возможности современных синтезаторов,
- добиться желаемого тембра даже во время живых выступлений,
- понять поведение генераторов (часто обозначаемых как VCO, генератор, управляемый напряжением) и модуляторов (часто обозначаемых как LFO, низкочастотный генератор),
- используют эти формы волны в математических выводах анализа, синтеза и звуковых эффектов,
- написать эффективный код для генерации этих сигналов для алгоритмов синтеза звука и звуковых эффектов,
- обнаружить любые несоответствия в этих сигналах в системе,
- избежать потенциальных проблем с алиасингом и
- выяснить, откуда может возникнуть наложение (например, из-за неограниченного спектра).
Сигналы
Переход к выбранному сигналу
- Синусоида
- Треугольник
- Квадрат
- Пилообразный (пила)
- Импульс
Синусоида
Синусоида является самой простой волновой формой звукового синтеза.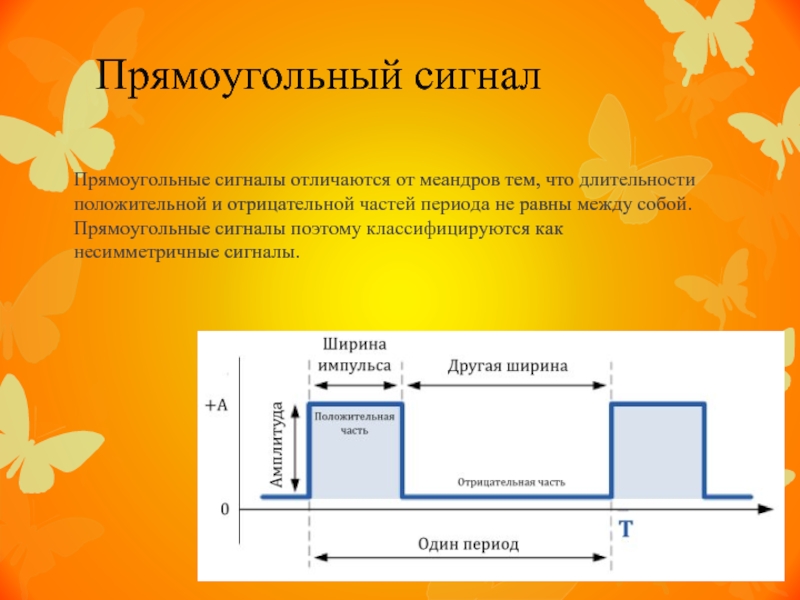
Формула синуса проста
s(t)=sin(2πft),(1)s(t) = \sin (2 \pi f t), \quad (1)s(t)=sin(2πft ),(1)
, где fff — частота синуса в Гц, а ttt — время в секундах.
Синус на частоте 220 Гц звучит так:
Ваш браузер не поддерживает тег audio.
Представление синуса во временной области выглядит следующим образом:
Рис. 1. Форма синусоидального сигнала: представление синусоидального сигнала во временной области.
Амплитудный спектр синуса очень скучен, потому что он состоит только из одной части: основной частоты.
Рис. 2. Амплитудный спектр синуса.
Как видите, гармоника всего одна. Это имеет смысл, поскольку расчет спектра предполагает, что анализируемый сигнал представляет собой суперпозицию (сумму) синусов. А один синус состоит всего из… одного синуса 🙃
Треугольник
Треугольник немного сложнее синуса.
Формула треугольника [Википедия]
s(t)=4∣ft−⌊ft+12⌋∣−1,(2)s(t) = 4 \left| ft — \left\lfloor ft + \frac{1}{2} \right\rfloor \right| — 1, \quad (2)s(t)=4∣∣∣∣∣ft−⌊ft+21⌋∣∣∣∣∣−1,(2)
, где fff — частота треугольника в Гц и ttt — время в секундах.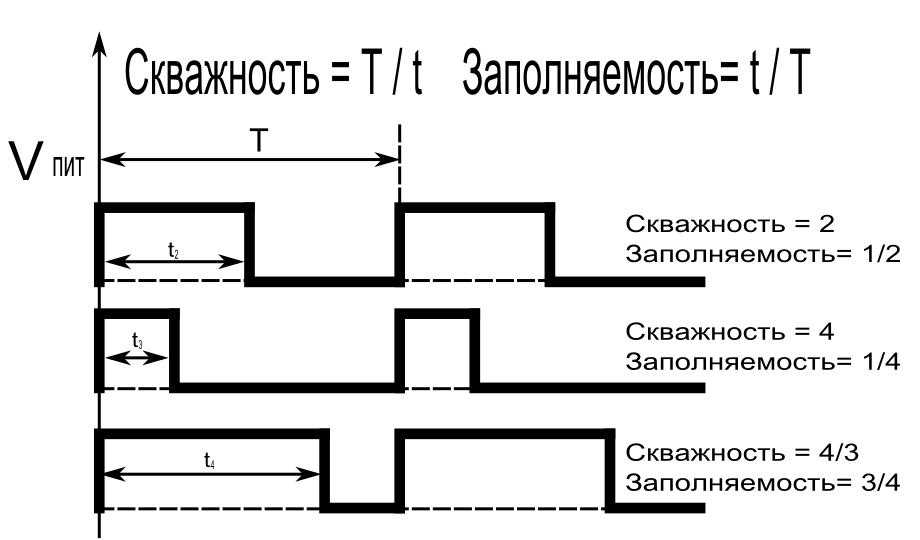
Треугольная волна на частоте 220 Гц звучит так:
Ваш браузер не поддерживает тег audio.
Как вы слышите, немного ярче синуса.
Треугольная форма сигнала во временной области выглядит следующим образом.
Рис. 3. Треугольная волна: представление треугольной волны во временной области.
График на рисунке 3 действительно выглядит как треугольник.
Это делает формулу из уравнения 2 более интуитивно понятной: треугольная форма сигнала, по сути, представляет собой разницу между линейной функцией и сдвинутой ступенчатой функцией. Эта разность возрастает и убывает кусочно-линейно, и мы получаем треугольник. 92}n21, где nnn — номер гармоники (основной тон имеет n=1n=1n=1, первый обертон имеет n=2n=2n=2 и т. д.).
Square
Прямоугольная волна более интересна, чем синусоида или треугольник, из-за своего характерного «пустого» тембра.
Прямоугольная волна на частоте 220 Гц звучит так:
Ваш браузер не поддерживает тег audio.
Для меня самой простой формулой для прямоугольной формы сигнала является взятие знака синуса:
s(t)=sign(sin(2πft)),(3)s(t) = \text{sign} (\sin (2 \pi f t)), \quad (3)s(t)= sgn(sin(2πft)),(3)
, где fff — частота квадрата в Гц, а ttt — время в секундах.
Конечно, возможны альтернативные формулы, например, использующие операцию по модулю.
Прямоугольная форма сигнала во временной области имеет прямоугольную форму (рис. 5).
Рис. 5. Прямоугольная форма сигнала: представление прямоугольной волны во временной области.
Амплитудный спектр прямоугольной волны состоит только из нечетных гармоник, точно так же, как и в случае треугольника (рис. 6).
Рис. 6. Амплитудный спектр квадрата.
Амплитуды гармоник квадрата затухают медленнее, чем в случае треугольника: они затухают как 1n\frac{1}{n}n1, где nnn – номер гармоники (n=1n=1n=1 соответствует фундаментальный).
Sawtooth (Пила)
Пилообразный сигнал (или просто «пила» ) — мой любимый сигнал, благодаря его богатому, «жирному» звуку, который невероятно хорошо воспроизводится с хорошим фильтром нижних частот.
Пилообразная волна на частоте 220 Гц звучит так:
Ваш браузер не поддерживает тег audio.
Ах, это так красиво ❤️
Простейшая формула пилообразной волны — это приближение по модулю:
s(t)=2(ft%1f)f−1,(0)s(t) = 2 \left ( ft \% \frac{1}{f} \right) f — 1, \quad (0)s(t)=2(ft%f1)f−1,(0)
, где fff — пилообразное частота в Гц, ttt — время в секундах, а %\%% — оператор по модулю, применяемый к действительным значениям.
Формула гласит: «Увеличивайте значение линейно (ftftft), возвращайтесь к 0 каждый период (%1f\% \frac{1}{f}%f1), масштабируйте до [0,1][0, 1][0,1] диапазон (умножение на fff), а затем расширить диапазон от [0,1][0, 1][0,1] до [−1,1][-1, 1][− 1,1] (умножение на 222 и вычитание 111)».
Пилообразный сигнал во временной области показан на рисунке 7.
Рисунок 7. Пилообразный сигнал: представление пилообразного сигнала во временной области.
Это так называемая пилообразная форма линейного нарастания , поскольку ее наклон увеличивается в каждом периоде.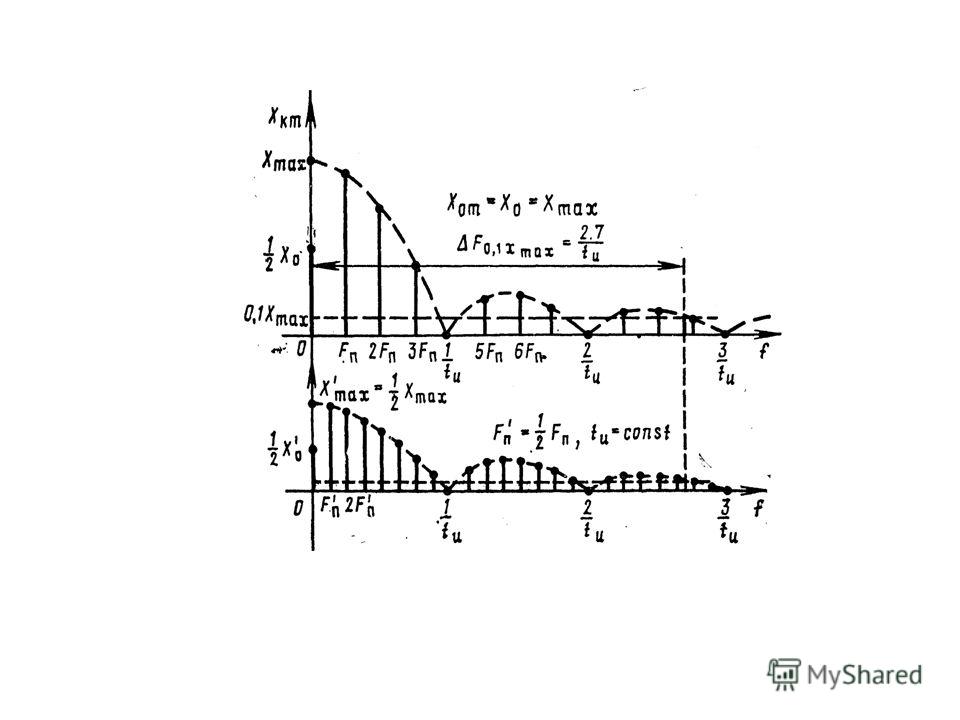 Если бы он падал, то назывался бы линейно снижающимся пилообразным. Поскольку речь идет всего лишь об инверсии фазы, варианты линейного нарастания и замедления имеют одинаковые свойства. Наклон имеет наибольшее значение, когда мы используем пилообразный сигнал для модуляции какого-либо другого параметра, например, когда мы используем пилообразный сигнал в низкочастотном генераторе (LFO). Затем мы можем создать периодически возрастающее ощущение (нарастание) или периодическое падение (нарастание).
Если бы он падал, то назывался бы линейно снижающимся пилообразным. Поскольку речь идет всего лишь об инверсии фазы, варианты линейного нарастания и замедления имеют одинаковые свойства. Наклон имеет наибольшее значение, когда мы используем пилообразный сигнал для модуляции какого-либо другого параметра, например, когда мы используем пилообразный сигнал в низкочастотном генераторе (LFO). Затем мы можем создать периодически возрастающее ощущение (нарастание) или периодическое падение (нарастание).
Название «пила» происходит от зубчатой формы волны.
Амплитудный спектр пилообразной формы можно увидеть на рисунке 8.
Рисунок 8. Амплитудный спектр пилообразной формы.
Спектр пилообразного сигнала содержит четные и нечетные гармоники. Амплитуды пилообразной гармоники затухают как 1n\frac{1}{n}n1, где nnn — номер гармоники (n=1n=1n=1 соответствует основной частоте).
Импульс
Форма импульса (также называемый последовательностью импульсов ) является обобщением прямоугольной формы сигнала.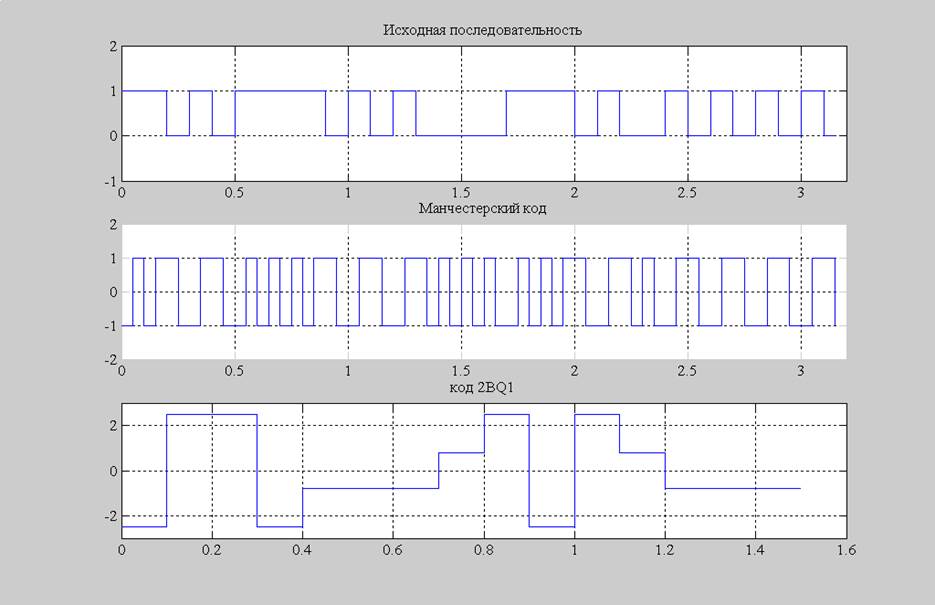
Пример формы пульсовой волны во временной области показан на рис. 9.
Рис. 9. Форма импульсной волны: представление пульсовой волны во временной области с коэффициентом заполнения 20 %.
Коэффициент заполнения этого сигнала составляет 20 %. Это означает, что для 20% его периода значение равно 1. Для оставшихся 80% значение равно -1.
Рабочий цикл определяет, для какой части периода значение сигнала равно 1. 9{\infty} \frac{4}{k\pi} \sin (\pi k D) \cos (2 \pi k f_0 t — \pi k D), 10s(t)=(2D−1)+k =1∑∞kπ4sin(πkD)cos(2πkf0t−πkD),10
, где DDD — коэффициент заполнения, kkk — индекс гармоники, f0f_0f0 — основная частота в Гц, ttt — время в секунды.
Амплитудный спектр пульсовой волны для случая D=0,2D=0,2D=0,2 показан на рисунке 10.
Рисунок 11. Амплитудный спектр пульсовой волны со скважностью 20%.
Однако спектр амплитуд динамически меняется в зависимости от рабочего цикла. Я изобразил это на рисунке 11.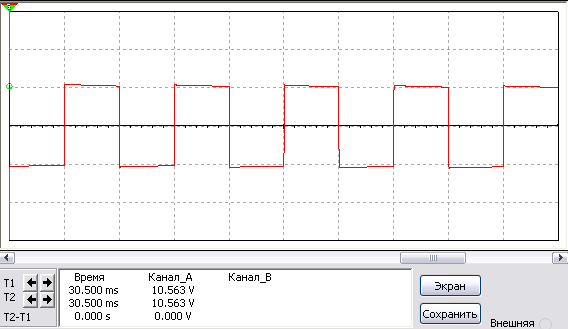 9.{-1} = 2(21)−1=2-я гармоника.
9.{-1} = 2(21)−1=2-я гармоника.
На рисунке вы также можете увидеть небольшой сбой вокруг частоты постоянного тока (0 Гц). Это связано с тем, что для очень высоких или очень низких значений коэффициента заполнения постоянная составляющая довольно значительна (среднее значение формы сигнала существенно отличается от нуля). Я намеренно скрыл постоянную составляющую от графиков для ясности, но часть ее все еще присутствует из-за спектральной утечки.
В музыкальных приложениях следует помнить о компоненте постоянного тока, поскольку он не добавляет музыкальной информации (мы ее не слышим), но может повредить оборудование, через которое он проходит.
Резюме
В этой статье вы узнали все об основных волновых формах (синус, треугольник, квадрат, пила, импульс), которые вам нужны для синтеза звука. Знакомство с этими волновыми формами поможет вам использовать возможности синтезаторов и программировать свои собственные.
Эти волновые формы являются частью головоломки, когда дело доходит до разработки собственных программных звуковых синтезаторов. Если вы хотите узнать, какая еще информация необходима для разработки аудио-плагинов, загрузите мой бесплатный Контрольный список для разработчиков Ultimate-аудио-плагинов.
Если вы хотите узнать, какая еще информация необходима для разработки аудио-плагинов, загрузите мой бесплатный Контрольный список для разработчиков Ultimate-аудио-плагинов.
Bibliography
[Pluta2019] Marek Pluta, Sound Synthesis for Music Reproduction and Performance , monograph, AGH University of Science and Technology Press, Kraków 2019.
[VälimäkiHuovilainen2006] Vesa Välimäki and Antti Huovilainen, Oscillator and Filter Algorithms для виртуального аналогового синтеза , Computer Music Journal, 30: 2, стр. 19–31, лето 2006 г. PDF
[Википедия] Треугольная волна в Википедии. Доступ: 28.06.2022.
Квадратная волна | Завораживающий кинетический спиннер
Что такое квадратная волна?
Квадратная волна — элегантная мобильная скульптура, разработанная удостоенным наград британским художником Иваном Блэком. Он сделан вручную в Италии опытными мастерами. Это красивое, вневременное произведение искусства, которое сделает любую обстановку более похожей на дом.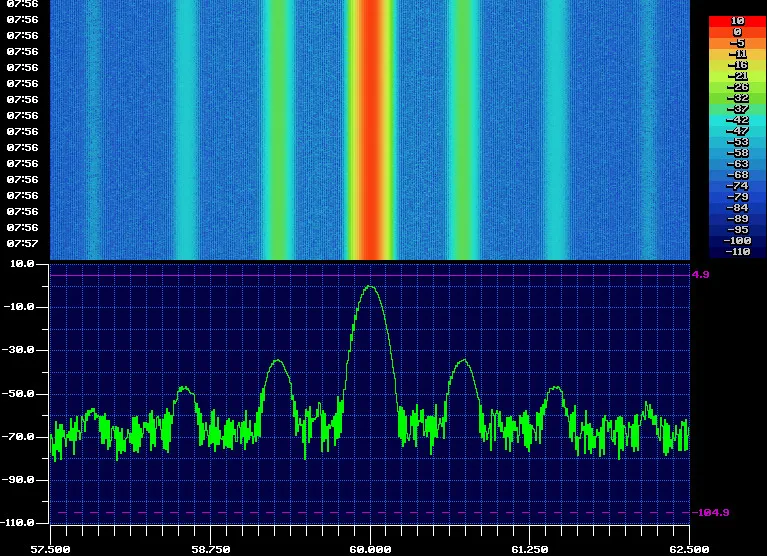 Square Wave может принести вам расслабление и улучшить ваше внимание, взаимодействуя с ним. Это этично, качественно и доступно.
Square Wave может принести вам расслабление и улучшить ваше внимание, взаимодействуя с ним. Это этично, качественно и доступно.
SQUARE WAVE BY IVAN BLACK
Handmade Kinetic Art
Square Wave — это уникальное произведение кинетического искусства, вдохновленное последовательностью Фибоначчи, базовой структурой, из которой состоит все живое. Просто поверните его, чтобы удивиться серии умопомрачительных оптических иллюзий и неожиданных гипнотизирующих революций. Каждая модель Square Wave, разработанная в Великобритании, изготавливается вручную и сочетает в себе знаковые природные формы с математическими формулами. Каждый изгиб и завиток материала точно откалиброван для создания бесшовно интегрированного механизма. Это и потрясающая скульптура, и успокаивающий, расслабляющий спиннер, идеально подходящий для борьбы со стрессом или даже для повышения вашего творчества.
ВНЕВРЕМЕННОЕ КИНЕТИЧЕСКОЕ ИСКУССТВО
Как родилась Square Wave?
Square Wave — результат тщательного прототипирования и итераций.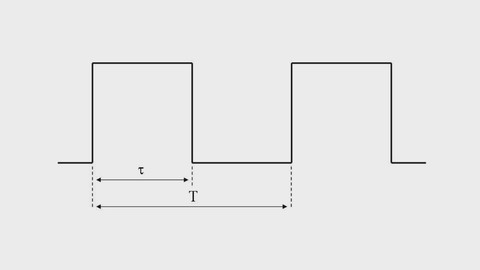 Были сделаны крошечные ручные настройки и корректировки, чтобы найти наиболее плавный баланс между весом и длиной каждого металлического стержня. Вторым шагом было преобразование этого кустарного метода в воспроизводимый процесс. Для этого мы полагались на мастеров мирового класса с многолетним опытом. Square Wave собирается вручную, что делает каждую из них уникальной. Каждая модель Square Wave производится в Италии с использованием исключительно высококачественных материалов и красок, сертифицированных ЕС.
Были сделаны крошечные ручные настройки и корректировки, чтобы найти наиболее плавный баланс между весом и длиной каждого металлического стержня. Вторым шагом было преобразование этого кустарного метода в воспроизводимый процесс. Для этого мы полагались на мастеров мирового класса с многолетним опытом. Square Wave собирается вручную, что делает каждую из них уникальной. Каждая модель Square Wave производится в Италии с использованием исключительно высококачественных материалов и красок, сертифицированных ЕС.
КУПИ СЕЙЧАС
СМОТРЕТЬ ВСЕ
О ХУДОЖНИКЕ
Иван Блэк
Иван Блэк (р. 1972) Лондон, британский скульптор, отмеченный наградами. Он начал делать скульптуры в раннем возрасте, движение быстро стало центральным в его работах, добавив еще одно измерение сложности и интереса к его экспериментам. В работах Ивана Блэка используется ряд уникальных механизмов для создания движущихся скульптур. Энергия направляется в работы Блэка через что угодно, от взаимодействия со зрителем до естественной силы дующего ветра и целенаправленного использования принципов гравитации. Когда предполагаемая форма энергии взаимодействует со скульптурой, она запускает цепную реакцию, создавая смену паттернов движения от случайных к высокоорганизованным движениям.0009
Энергия направляется в работы Блэка через что угодно, от взаимодействия со зрителем до естественной силы дующего ветра и целенаправленного использования принципов гравитации. Когда предполагаемая форма энергии взаимодействует со скульптурой, она запускает цепную реакцию, создавая смену паттернов движения от случайных к высокоорганизованным движениям.0009
КУПИТЕ ВАШУ КВАДРАТНУЮ ВОЛНУ
Различные способы использовать прямоугольную волнуВращайте его легким движением запястья и наблюдайте, как происходит волшебство
Вращайте его обеими руками, держа за края
Создавайте умопомрачительные формы и завораживающие геометрические узоры
Подвесьте его к потолку, используя стандартный комплект, поставляемый с каждой прямоугольной волной
Вы можете добавить дополнительную магнитную подставку, чтобы улучшить свои впечатления
Прямоугольная волна может отображаться в помещении и на улице
СОВЕРШЕННЫЙ ПОДАРОК ДЛЯ ВСЕХ
Завораживающие иллюзии
Квадратная волна состоит из 24 соединенных металлических стержней, которые неожиданно изгибаются и видоизменяются при подаче энергии.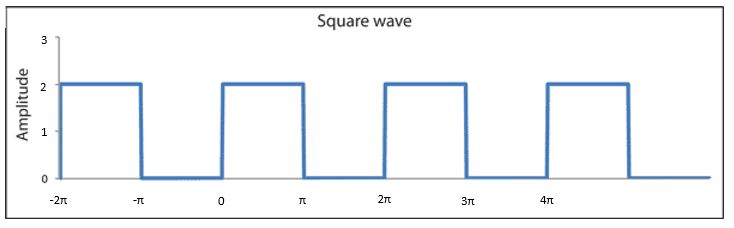 Повторение одинаковых элементов точно откалибровано для создания сложных плавных структур. Каждая квадратная волна изготавливается и собирается вручную, каждый металлический стержень соединяется со следующим вручную. Настоящее произведение искусства, которое терпеливо создает произведение искусства.
Повторение одинаковых элементов точно откалибровано для создания сложных плавных структур. Каждая квадратная волна изготавливается и собирается вручную, каждый металлический стержень соединяется со следующим вручную. Настоящее произведение искусства, которое терпеливо создает произведение искусства.
ЗАКАЗАТЬ КВАДРАТНУЮ ВОЛНУ
КИНЕТИЧЕСКОЕ ИСКУССТВО ДЛЯ СНЯТИЯ СТРЕССОВ
Расслабляющий и простой в использовании
Square Wave — прекрасно оформленное произведение искусства. Он по своей сути интуитивно понятен в использовании! Square Wave идеально подходит для того, чтобы помочь нам расслабиться, помедитировать или сконцентрироваться. Это отличное средство для снятия стресса именно благодаря своим завораживающим волнам и мягким поворотным движениям. Плавное и ритмичное движение Square Wave естественным образом увеличивает активность мозга, вырабатывая больше дофамина и серотонина, и поэтому оно может помочь при многих заболеваниях или просто улучшить ваше настроение и концентрацию.
Perfect для внутреннего и наружного применения
Square Wave изготовлен из стали и обработан как для внутреннего, так и для наружного применения. Да, вы можете повесить его в своем саду или на террасе, квадратная волна сделана на века. Размеры: 9,8 x 9,8 дюйма (25 x 25 см). Вы можете любоваться им в статном стоячем положении, или подвешивать его к потолку как прекрасную скульптуру, или играть с ним, так как он также становится расслабляющей кинетической игрушкой. В любом случае, Square Wave — это редкий пример оригинальности и идеальный подарок для людей, у которых уже есть все.
КОЛЛЕКЦИЯ
Они прекрасны! Весело и красиво! Продукт и компания — это настоящий «классный акт»! И НАСТОЛЬКО УМНО выступить с этой великолепной подставкой! Как весело! Нужен стильный подарок? Это оно!
ЛОРИ
Прекрасный дизайн и отличное обслуживание клиентов.
МЕЛАНИЯ заказал его с экспресс-доставкой, и когда он не был уверен, где моя посылка, они немедленно действовали, чтобы решить эту проблему, и доставили на следующий день. Действительно красивый и креативный дизайн.
Я заказал классическую коллекцию из 3 квадратных волн и был просто в восторге, когда открыл свою! Дизайн настолько элегантен в своей простоте; великолепный и завораживающий в своих движениях! Некоторые особенные люди получат удивительный рождественский подарок — и я собираюсь заказать 3 новых, уменьшенных версии (Horizon)!
РЕЙЧЕЛ
Я только что получил свою скульптуру «Квадратная волна», сразу же достал ее из коробки и начал с ней играть. Это настоящее визуальное удовольствие! Завораживающие узоры происходят так же, как видео в Интернете.
РЕНДИ
ПРОЧИТАТЬ ВСЕ ОТЗЫВЫ
Уэльский скульптор Иван Блэк
«Валлийский скульптор Иван Блэк использует металл, который он искусно сочетает с геометрией для создания плавных и довольно сложных скульптур. Повторение одинаковых форм является постоянной темой в работах Блэка. Иван строит увлекательные мобили, которые оживают простым движением запястья. Его работы выставлялись в галереях и парках по всему миру, в том числе в Музее Пегги Гуггенхайм и Фонде Касса, наряду с гигантскими скульптурами коллеги-кинетического художника Энтони Хоу».
КУПИТЬ СЕЙЧАС
Источник прямоугольных сигналов
Подсхема Источник прямоугольных сигналов моделирует повторяющееся напряжение источника прямоугольных сигналов
с нулевым временем нарастания и спада. В DVM этот источник не используется ни в каких задачах тестирования, но
вы можете установить источник для использования этой подсхемы с вызовом Squ() в
столбец «Источник» вашего плана тестирования.
Другие аналогичные импульсные источники напряжения включают:
- Пульс Источник — повторяющийся импульс — аналогичен источнику сигнала прямоугольной формы. но с настраиваемым временем нарастания, временем спада и рабочим циклом
- Пульс Источник — повторяющийся импульс с нулевым временем нарастания и спада — аналогично к источнику сигнала прямоугольной формы, но с конфигурируемым рабочим циклом
Аналогичные импульсные источники, дающие только один импульс, включают:
- Источник импульсного входа — Single Pulse – источник одиночного импульса напряжения с пусковым напряжение моделируется резистором.
В этой теме:
| ДВМ Информация | Источник питания (не DVM) Информация | |
| Модель Имя | Источник сигнала прямоугольной формы | |
| Симулятор | Это устройство совместимо как с SIMetrix, так и с SIMPLIS.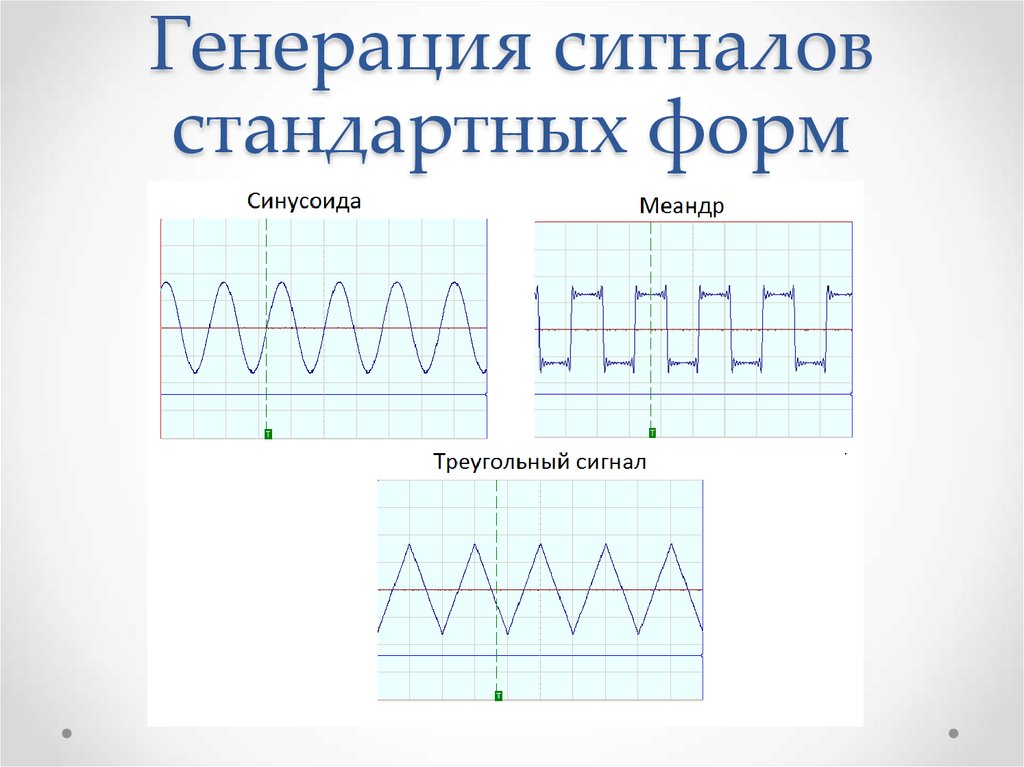 тренажеры. тренажеры. | |
| Части
Селектор Расположение меню | ДВМ > Источники > Источник входного сигнала DVM | Источники питания > Источник питания (напряжение постоянного тока, импульс, линейное изменение, Zin…) |
| Символ Библиотека | SIMPLIS_DVM_ADVANCED.sxslb | power_supply_source_and_loads. sxslb sxslb |
| Модель Файл | SIMPLIS_DVM_ADVANCED.lb | power_supply_source_and_loads.lb |
| Подсхема Имя | SIMPLIS_DVM_ADVANCED_SOURCE_SQU | POWER_SUPPLY_SOURCE_SQU |
| Символы | ||
| Схема | Примечание. | |
Параметры
В следующей таблице поясняются соответствующие параметры.
| Имя параметра | По умолчанию | Тип данных | Ассортимент | Единицы | Параметр Описание |
| КОНЕЧНОЕ_НАПРЯЖЕНИЕ | 750м | Реальный | В | Пиковое или конечное напряжение импульса источника. Это может быть числовое значение или символ
значение, например процент от номинального входного напряжения. Это может быть числовое значение или символ
значение, например процент от номинального входного напряжения. | |
| ЧАСТОТА | 10к | Реальный | мин: > 0 | Гц | Частота исходного импульса |
| IDLE_IN_POP | 0 | Реальный | 0 или 1 | Если установлено в 0, напряжение источника во время POP
анализ установлен на START_VOLTAGE ; иначе источник
будет активен во время анализа POP.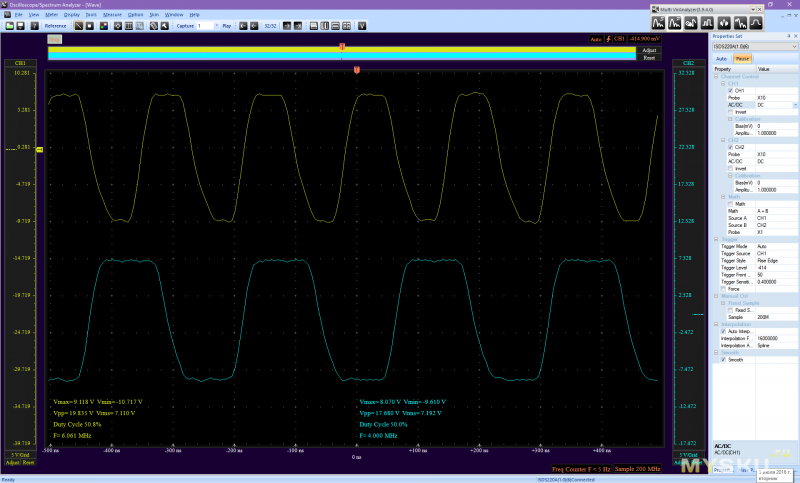 | |
| ИМЯ ИСТОЧНИКА | СРЦ | Строка | н/д | н/д | Имя источника DVM. Это имя не может содержать пространства. |
| ИСТОЧНИК_СОПРОТИВЛЕНИЕ | 0,4 | Реальный | мин:0 | Ом | Устанавливает исходное сопротивление источника |
| OFF_UNTIL_DELAY | 0 | Реальный | 0 или 1 | Если установлено значение 1, напряжение источника будет равно START_VOLTAGE до момента
указано TIME_DELAY . Если установлено 0, значение TIME_DELAY интерпретируется как
фазовая задержка. Если установлено 0, значение TIME_DELAY интерпретируется как
фазовая задержка. | |
| ФАЗА_УГОЛ | 90 | Реальный | ° | Фазовый угол импульса напряжения, используется только если USE_PHASE параметр 1. | |
| START_VOLTAGE | 0 | Реальный | В | Нижнее или начальное напряжение для источника напряжения
пульс. Это может быть числовое значение или символ
значение, например процент от номинального входного напряжения. Это может быть числовое значение или символ
значение, например процент от номинального входного напряжения. | |
| TIME_DELAY | 10у | Реальный | мин: 0 | с | Задержка перед началом импульса напряжения источника. Исходное поведение до TIME_DELAY определяется OFF_UNTIL_DELAY параметр. |
| USE_PHASE | 0 | Реальный | 0 или 1 | Если установлено значение 1, источник настроен на использование
фазовый угол, предоставленный PHASE_ANGLE параметр.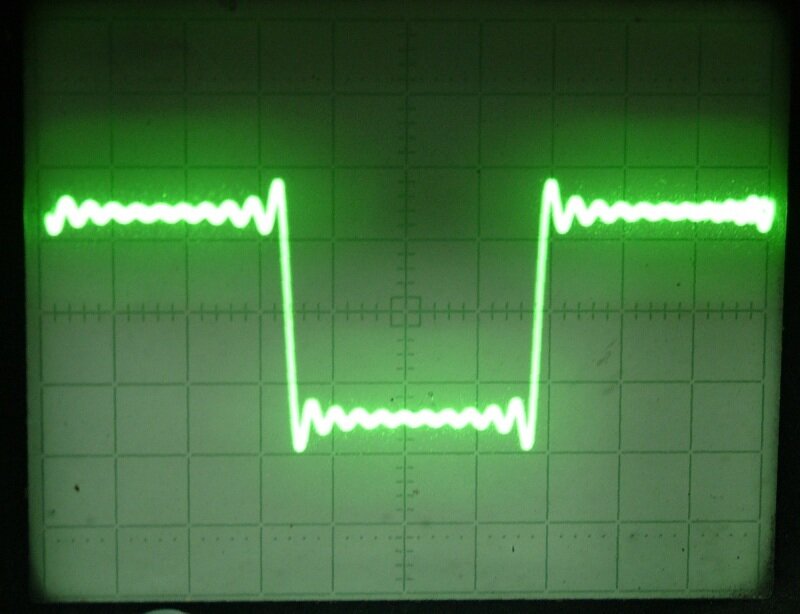 |
Запись плана тестирования DVM для источника прямоугольного сигнала
Чтобы настроить любой управляемый источник DVM на подсхему источника прямоугольного сигнала, поместите запись плана тестирования Squ() в столбец Источник.
Запись плана тестирования Squ() имеет следующий синтаксис с аргументами взяты из списка параметров выше.
Squ(REF, START_VOLTAGE, FINAL_VOLTAGE, FREQUENCY) Squ(REF, START_VOLTAGE, FINAL_VOLTAGE, FREQUENCY, OPTIONAL_PARAMETER_STRING)
| Аргумент | Ассортимент | Описание |
| № | н/д | Фактическое условное обозначение DVM
источник или более общий синтаксис INPUT: n , где n – целое число, указывающее позицию в списке. источников DVM. источников DVM. |
| START_VOLTAGE | н/д | Нижнее или начальное напряжение для прямоугольного источник. Это может быть числовое значение или символ значение, например процент от номинального входного напряжения. |
| КОНЕЧНОЕ_НАПРЯЖЕНИЕ | н/д | Пиковое или максимальное напряжение прямоугольного источник. Это может быть числовое значение или символ значение, например процент от номинального входного напряжения. |
| ЧАСТОТА | мин: > 0 | Частота источника прямоугольных импульсов |
| НЕОБЯЗАТЕЛЬНЫЙ_ПАРАМЕТР_СТРОКА | н/д | Строка параметров с любыми другими параметрами из таблицы параметров выше* |
* Если указано несколько параметров, присоедините параметр
пары ключ-значение с пробелом, как показано в примерах
ниже.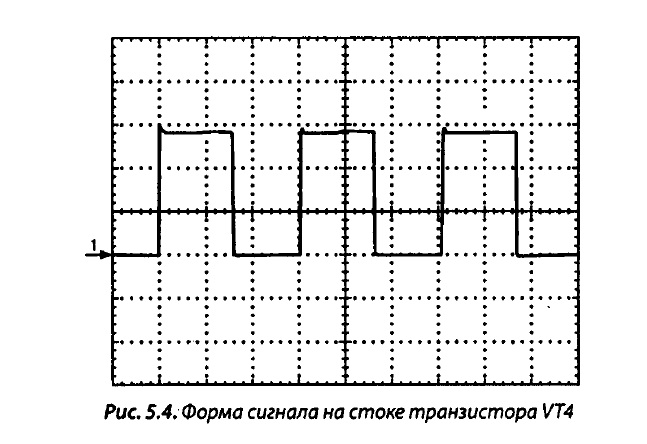 Порядок имен параметров не имеет значения.
Порядок имен параметров не имеет значения.
Примеры DVM
В следующих примерах для первого управляемого источника DVM задан источник прямоугольного сигнала с начальное напряжение 1В и конечное напряжение 5В. Временные параметры и необязательный строки параметров различны для каждого примера.
Примечание. В следующих планах тестирования перед столбцом «Источник» стоит с символами *?@ , потому что это первый столбец в план испытаний.
Нулевая временная задержка Пример
Поскольку Параметр TIME_DELAY установлен в ноль, осциллограмма начинается с FINAL_VOLTAGE значение 5 при t=0.
| *?@ Источник |
|---|
| Squ(ВХОД: 1, 1, 5, 10k, TIME_DELAY=0) |
Результаты этой записи плана тестирования показаны ниже:
Пример задержки
В этом примере Параметр TIME_DELAY установлен на 75 мкс.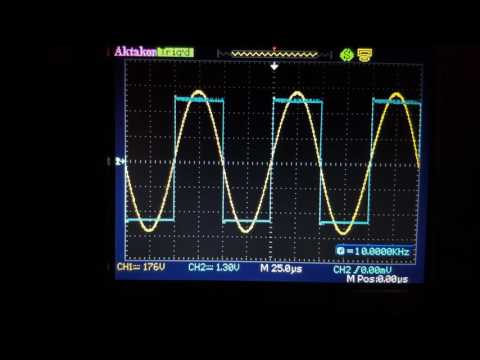 Начиная с OFF_UNTIL_DELAY параметр не указан, TIME_DELAY интерпретируется как фазовая задержка,
это означает, что сигнал активен с момента времени = 0.
Начиная с OFF_UNTIL_DELAY параметр не указан, TIME_DELAY интерпретируется как фазовая задержка,
это означает, что сигнал активен с момента времени = 0.
| *?@ Источник |
|---|
| Squ(ВХОД: 1, 1, 5, 10k, TIME_DELAY=75u) |
Результаты этой записи плана тестирования показаны ниже:
Пример временной задержки с OFF_UNTIL_DELAY=1
In
В этом примере параметр TIME_DELAY установлен на 75 мкс, а OFF_UNTIL_DELAY устанавливается в 1; следовательно, для времени моделирования меньше, чем Параметр TIME_DELAY , напряжение источника составляет 1 В, что является значением START_VOLTAGE аргумент.
| *?@ Источник |
|---|
| Squ(ВХОД: 1, 1, 5, 10k, TIME_DELAY=75u OFF_UNTIL_DELAY=1) |
Результаты этой записи плана тестирования показаны ниже:
Пример задержки фазы
В этом примере Параметр USE_PHASE установлен на 1, а параметр PHASE_ANGLE установлено значение 190. Установка USE_PHASE на 1 настраивает источник для использования Параметр PHASE_ANGLE для определения эффективной временной задержки. Задержка времени вычисляется по формуле:
\[ \text{TIME_DELAY} = \frac{\text{PHASE_ANGLE}}{\text{360*ЧАСТОТА}} \]
| *?@ Источник |
|---|
кв.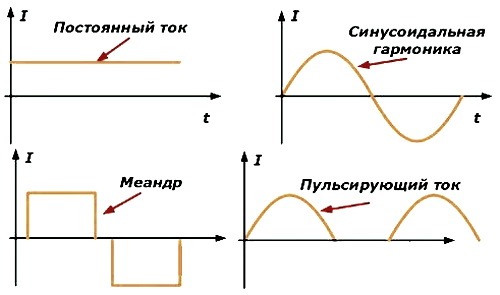 |


 {\infty }{\frac {\sin \left(2\pi (2k-1)ft\right)}{2k-1}}=\\&={\frac {4}{\pi }}\left(\sin(2\pi ft)+{\frac {1}{3}}\sin(6\pi ft)+{\frac {1}{5}}\sin(10\pi ft)+\dots \right).\end{aligned}}}
{\infty }{\frac {\sin \left(2\pi (2k-1)ft\right)}{2k-1}}=\\&={\frac {4}{\pi }}\left(\sin(2\pi ft)+{\frac {1}{3}}\sin(6\pi ft)+{\frac {1}{5}}\sin(10\pi ft)+\dots \right).\end{aligned}}}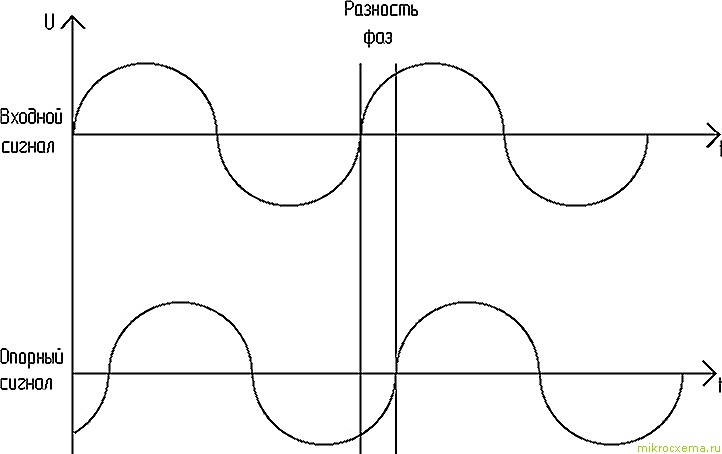 Но форма колебаний весьма далека от синусоидальной — сигнал получается импульсным, причем длительность импульсов и пауз между ними легко регулируется. Импульсам легко придать вид меандра, когда длительность импульса равна длительности паузы между ними.
Но форма колебаний весьма далека от синусоидальной — сигнал получается импульсным, причем длительность импульсов и пауз между ними легко регулируется. Импульсам легко придать вид меандра, когда длительность импульса равна длительности паузы между ними.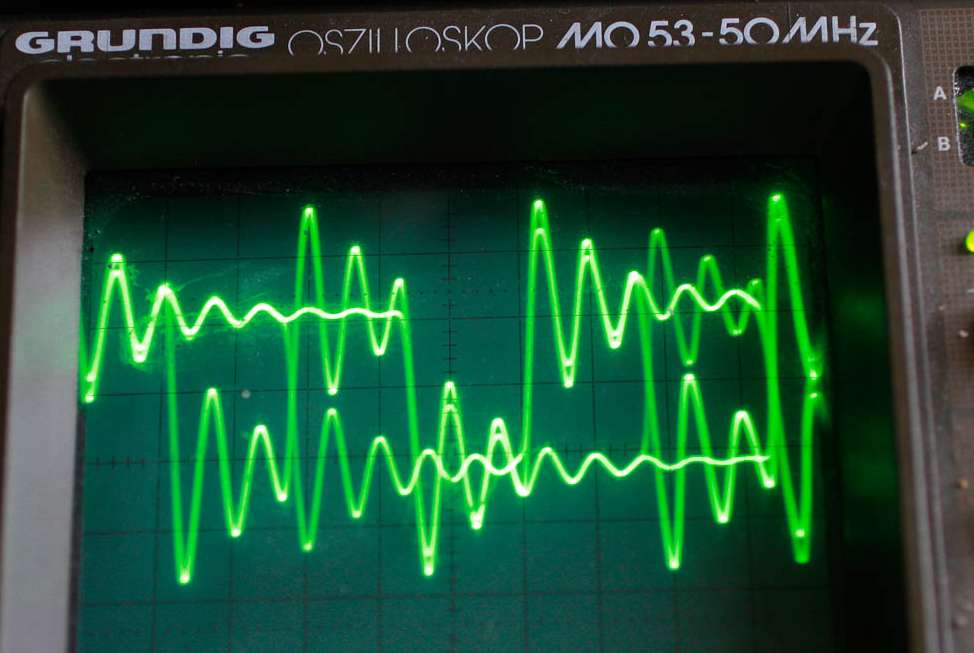 При этом малейшие изменения коллекторного напряжения (хотя бы из-за тепловых флуктуаций) одного транзистора передаются через конденсаторы С1 и С2 в цепь базы другого.
При этом малейшие изменения коллекторного напряжения (хотя бы из-за тепловых флуктуаций) одного транзистора передаются через конденсаторы С1 и С2 в цепь базы другого.
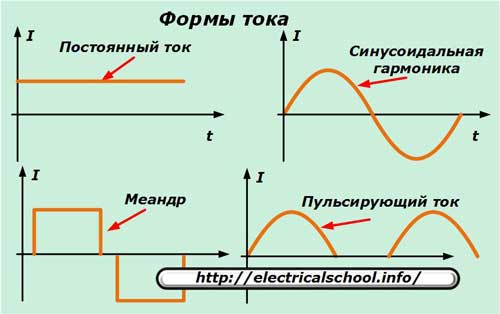
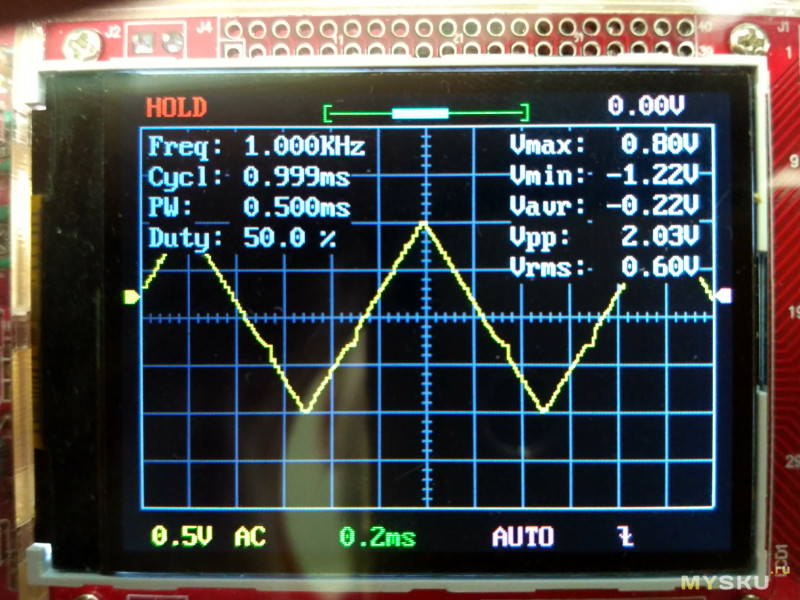
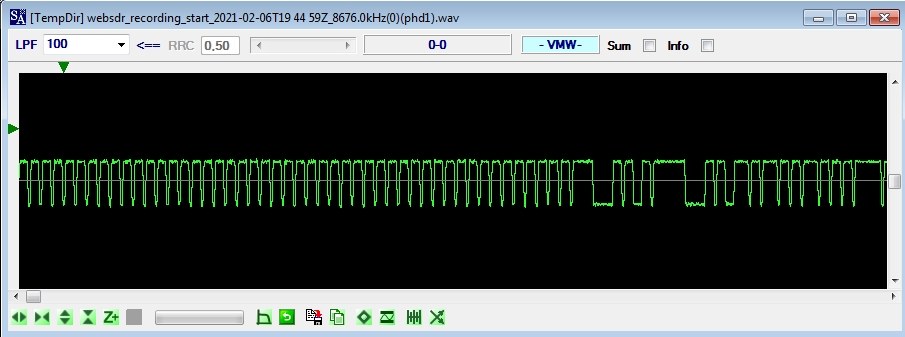
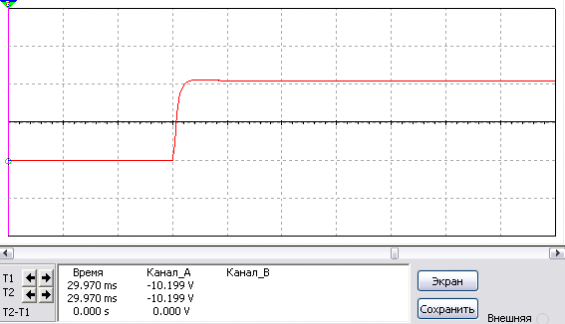
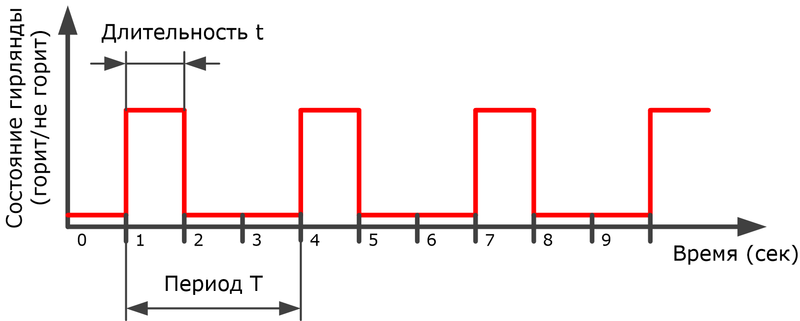 Поскольку основными характеристиками прямоугольной волны являются нарастающие и спадающие фронты, они являются ключевыми областями, которые используются для маркеров для определения периода времени. Либо измерение может быть выполнено от одного нарастающего фронта к другому, либо от одного спадающего фронта к следующему.
Поскольку основными характеристиками прямоугольной волны являются нарастающие и спадающие фронты, они являются ключевыми областями, которые используются для маркеров для определения периода времени. Либо измерение может быть выполнено от одного нарастающего фронта к другому, либо от одного спадающего фронта к следующему.
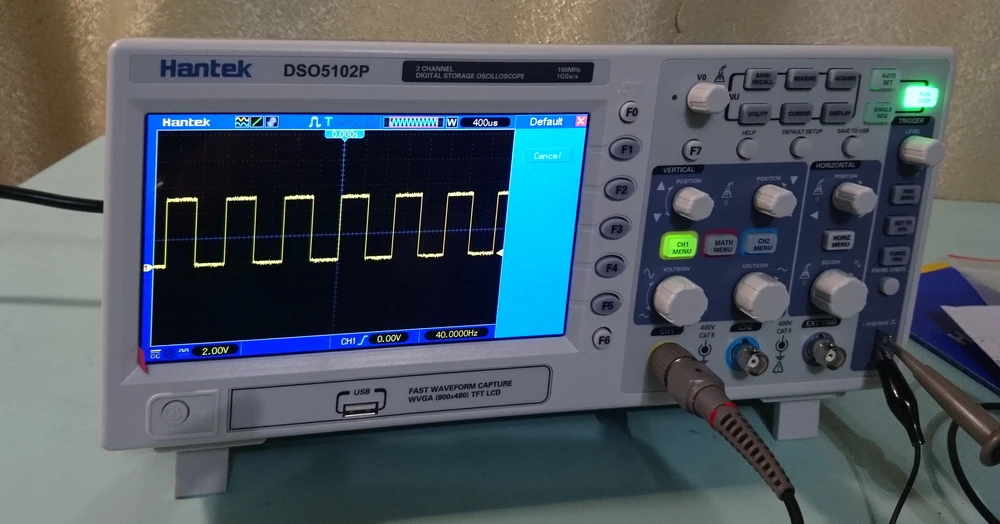 astype(np.int) * 2 - 1
plt.plot(n, квадрат)
plt.xlabel('номер образца')
plt.ylabel('амплитуда')
plt.title('Квадратный сигнал)
plt.show()
astype(np.int) * 2 - 1
plt.plot(n, квадрат)
plt.xlabel('номер образца')
plt.ylabel('амплитуда')
plt.title('Квадратный сигнал)
plt.show()  Я заказал его с экспресс-доставкой, и когда он не был уверен, где моя посылка, они немедленно действовали, чтобы решить эту проблему, и доставили на следующий день. Действительно красивый и креативный дизайн.
Я заказал его с экспресс-доставкой, и когда он не был уверен, где моя посылка, они немедленно действовали, чтобы решить эту проблему, и доставили на следующий день. Действительно красивый и креативный дизайн.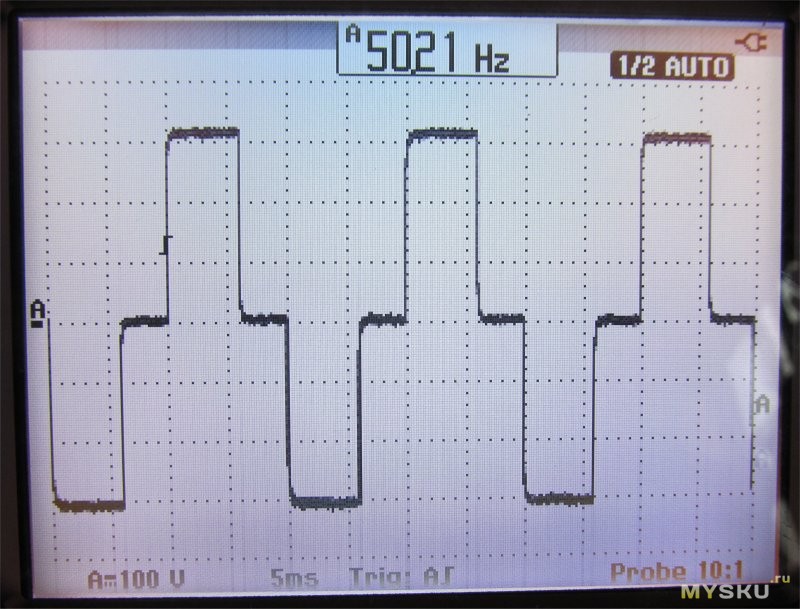
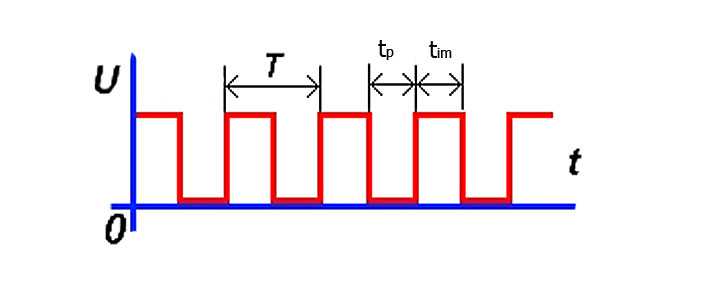 Датчики источника питания не имеют префикса «DVM».
Датчики источника питания не имеют префикса «DVM».