Все страницы — Юнионпедия

Все страницы — Юнионпедия

Новый! Скачать Юнионпедия на вашем Android™ устройстве!

Свободно

Более быстрый доступ, чем браузер!

Все страницы · Предыдущая (Меретка) · Следующий (Мега Шымкент)

Из:

Меандр (радиотехника)	Меандр (река)	Меандр (значения)
Меандр (математика)	Меандр (орнамент)	Меандр речной
Меандр Большой	Меандрирование	Меандрий
Меандрий Самосский	Меандрий Милетский	Меандров
Меандров М.	Меандров М. А.	Меандров Михаил Алексеевич
Меандров, Михаил	Меандров, Михаил Алексеевич	Меандровое число
Меандер	Меандер (река, Тасмания)	Меано
Меано Витторио	Меано, Витторио	Меано, Виктор
Меб Кефлезигхи	Мебус	Мебус Пауль
Мебус, Пауль	Мебш	Мебш Михаил Павлович
Мебш, Михаил Павлович	Мебруме	Мебрахтом Кефлезигхи
Мебрекур-Ришкур	Мебартсо	Мебартшо
Мебартцо	Мебарцо	Мебарки
Мебарки, Али	Мебарек Солтани	Мебагишвили
Мебагишвили Карл Александрович	Мебагишвили, Карл Александрович	Мебаза
Мебаза, Фуад	Мебгидролин	Меби
Мебиса	Мебиус	Мебиус (фильм)
Мебиус (лунный кратер)	Мебиус К.	Мебиус К. А.
Мебиус Карл Август	Мебиус А.	Мебиус А. Ф.
Мебиус Август Фердинанд	Мебиус Дитер	Мебиус, Карл
Мебиус, Карл Август	Мебиус, Карл-Август	Мебиус, Август
Мебиус, Август Фердинанд	Мебиус, Август-Фердинанд	Мебиус, Ральф Христиан
Мебиус, Штефан	Мебиус, Юстин	Мебиус, Дитер
Мебиам	Мебиам Леон	Мебиам, Леон
Мебибайт	Мебикс	Мебикар
Меблировка	Меблировочная музыка	Мебес
Мебес Григорий Оттонович	Мебес, Григорий Оттонович	Мебеверин
Мебель	Мебель для кухни	Мебель для офиса
Мебель из дерева	Мебель Москва (компания)	Мебельный
Мебельный (значения)	Мебельный (Башкортостан)	Мебельный стиль
Мебельный стиль Кабриоль	Мебельный точильщик	Мебельный холдинг Ангстрем
Мебельный щит	Мебельный гарнитур	Мебельный лифт
Мебельный проезд	Мебельный проезд (Санкт-Петербург)	Мебельные петли
Мебельная улица	Мебельная улица (Санкт-Петербург)	Мебельная фабрика Мария
Мебельная промышленность	Мебельная петля	Мебельное дело
Мебельное производство	Мебендазол	Мевтыёхан
Мевтынглемынг	Мевтыехан	Мевасерет-Цион
Меват (округ)	Мевати	Мевар
Мевари	Мевазар	Мевалонат
Мевалоновая кислота	Мевданчи (футбольный клуб, Бекабад)	Мевис
Мевис, Карл	Мевис, Мориц	Мевис, Йозеф
Мевиус	Мевиус Аполлон Фёдорович	Мевиус Аполлон Федорович
Мевиус, Аполлон Фёдорович	Мевиус, Аполлон Федорович	Мевлют Чавушоглу
Мевлют Эрдинч	Мевлют Мерт Алтынташ	Мевля
Мевля, Нейц	Мевля, Нейч	Мевля, Миха
Мевляна	Мевлан Дживелек, Нурие Улвие	Мевлис-Юган
Мевлисъюган	Мевлеви	Мево Модиин
Мево-Модиим	Меволи Абдон	Меволи, Абдон
Меве	Мевес	Мевес (дворянский род)
Мевес Ричард Троянович	Мевес Михаил Троянович	Мевес, фон
Мевес, фон, Ричард Троянович	Мевес, Ричард	Мевес, Ричард Троянович
Мевес, Михаил Троянович	Мевезер, Флойд	Мевен
Мевенн	Мевенн Бретонский	Мег
Мег Райан	Мег Розофф	Мег Стюарт
Мег Тилли	Мег Уайт	Мег Уитман
Мег Уитмен	Мег Фалкен	Мег Фостер
Мег Марта Уайт	Мег Вайт	Мег Гриффин
Мег-Тыг-Игол	Мег-Тыг-Еган	Мег-Хон-Юган
Мег.	Мег: Монстр глубины	Мегюрёнский наслег
Мегюренский наслег	Мегюль	Мегюль Этьенн, Никола
Мегюль, Этьен	Мегюль, Этьенн	Мегюль, Этьенн Николя
Мегс	Мегс (значения)	Мегс (округ)
Мегс (округ, Огайо)	Мегс (округ, Теннесси)	Мегсон
Мегсон Гари	Мегсон, Гари	Мегсон, Джанет
Мегуми Курихара	Мегуми Ёкота	Мегуми Хаясибара
Мегуер	Мегтыг-Еган	Мегтыг-Еган (река)
Мегтыг-Еган (приток Синтиг-Егана)	Мегтыгъёган	Мегтыгъёган (приток Сыхтингъёгана)
Мегтыгъёган (приток Синтигъёгана)	Мегтыгъёган (приток Глубокого Сабуна)	Мегтыгъеган
Мегтыгигол	Мегхадута	Мегхалая
Мегханада	Мегхна	Мегхна (река)
Мегхнад Десаи	Мегрское озеро	Мегрэ
Мегрэ (телесериал)	Мегрэ (телесериал, Франция)	Мегрэ (телесериал, Великобритания)
Мегрэ (английский телесериал)	Мегрэ расставляет силки	Мегрэ расставляет силки (фильм)
Мегрэ и дело Сен-Фиакр	Мегрэ и дело Сен-Фиакр (фильм)	Мегрян
Мегрян, Шаген	Мегра	Мегра (река)
Мегра (река, впадает в Онежское озеро)	Мегра (река, впадает в Белое море)	Мегра (Вологодская область)
Меграб	Меграбян, Андраник Амбарцумович	Меградзорский тоннель
Меградзорское золоторудное месторождение	Меградзорское месторождение	Меградзорское месторождение золота
Мегри	Мегри (река)	Мегри (значения)
Мегри (крепость)	Мегри (коммуна)	Мегринская ГЭС
Мегринский	Мегринский (Вологодская область)	Мегринский хребет
Мегринский район	Мегринское сельское поселение	Мегриньи
Мегрино	Мегрино (Вологодская область)	Мегрово
Мегрозеро	Мегре	Мегре В.
Мегре В. Н.	Мегре Владимир Николаевич	Мегре, Владимир
Мегре, Владимир Николаевич	Мегрец	Мегрецоц
Мегрегское сельское поселение	Мегрега	Мегрега (река)
Мегрега (деревня)	Мегрега (приток Олонки)	Мегрел
Мегрельская кухня	Мегрельский	Мегрельский язык
Мегрельский хребет	Мегрельское княжество	Мегрелы
Мегреладзе	Мегреладзе Георгий Мерабович	Мегреладзе, Мераб
Мегреладзе, Мераб Надарьевич	Мегреладзе, Георгий	Мегреладзе, Георгий Мерабович
Мегрелия	Мегрелишвили	Мегрелишвили Леван Иванович
Мегрелишвили, Джемал Карлович	Мегрелишвили, Леван Иванович	Мегрелидзе Иона
Мегрелидзе Иона Лукич	Мегрелидзе, Иона	Мегрелидзе, Иона Лукич
Мега	Мега (сеть торговых центров)	Мега (телеканал)
Мега (число)	Мега (баскетбольный клуб)	Мега (протока Оби)
Мега Парк	Мега Астана	Мега Актобе
Мега Алма-Ата	Мега Алма-Ата 2	Мега Спилео
Мега Тёплый Стан	Мега Теплый Стан	Мега Химки

Схема формирователя меандра | RigExpert™

09 Dec. 2016

Для формирования сигнала с ТТЛ-уровнями из высокочастотного сигнала синусоидальной формы часто используют простые схемы на логических элементах.
Автор приведенной ниже схемы предположил, что микросхема переключается при определенном и неизменном напряжении на ее входе (например, 2.5 вольта):

Плохо:

На самом деле это напряжение зависит даже от фазы Луны. Поэтому для нормальной работы такой схемы на ее вход нужно подать сигнал достаточно большой амплитуды (в противном случае фронты выходного сигнала заметно дрожат). Кроме того, на выходе невозможно получить меандр (который нужен для работы некоторых схем).
Недостатки первой схемы частично устраняются при помощи отрицательной обратной связи:

Лучше:

Но вот незадача: при искаженном входном сигнале получить на выходе меандр по-прежнему не удается. Этот же недостаток имеют и простые формирователи на основе компаратора.
В статье 4.5ns Dual-Comparator-Based Crystal Oscillator has 50% Duty Cycle and Complementary Outputs описывается кварцевый генератор, выходной сигнал которого представляет собой меандр. Идея отлично подходит для схемы формирователя меандра из искаженного сигнала с меняющейся амплитудой:

Хорошо:

Схема на операционном усилителе регулирует напряжение на одном из входов компаратора таким образом, что сигналы на обоих его выходах имеют 50-процентное заполнение. При этом качество работы схемы не зависит от разброса параметров элементов в цепи регулировки напряжения. Важно лишь, чтобы выходы компаратора были одинаково нагружены (например, одинаковыми входами логических элементов).

На практике (испытания проводились на частотах от 1 до 10 МГц) коэффициент заполнения на выходе этой схемы составлял 50±1% для входного сигнала  с амплитудой 200 мВ (при этом входной сигнал был настолько искажен, что на экране осциллографа был больше похож на «пилу», чем на синусоиду).

Денис Нечитайлов, UU9JDR
24. 12.2009

P.S. Это статья не о формирователях прямоугольного сигнала на логических элементах.

Календар

March 2023

M	T	W	T	F	S	S
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

Что такое квадратная волна и прямоугольная форма волны » Electronics Notes

Квадратные волны, прямоугольные волны и импульсные сигналы — это все формы сигналов, которые имеют два состояния; высокий и низкий, и они широко используются с цифровыми схемами.

---

Электронные и электрические сигналы Включает:
Типы сигналов и основные сведения Синусоидальная волна Квадратные и прямоугольные волны Треугольная волна

---

Прямоугольные волны — это форма периодической формы волны, которая чередуется между двумя состояниями и не является синусоидальной.

В идеальной прямоугольной волне переходы между двумя состояниями мгновенны, но в реальном мире это, очевидно, не так, и время нарастания и спада представляет большой интерес.

Хотя термин прямоугольная волна используется для многих форм сигнала с двумя состояниями, строго говоря, прямоугольная волна является прямоугольной и имеет одинаковое время в любом состоянии, т. е. имеет отношение метки к пространству 1:1. Прямоугольный сигнал представляет собой периодический сигнал с двумя состояниями, который имеет неравное отношение метки к пространству.

Импульсный сигнал может не быть повторяющимся или периодическим. Это может быть вызвано генерацией импульса при достижении определенного аналогового порога, передачей данных или многими другими причинами.

Как звучит прямоугольная волна

Прямоугольная волна звучит гораздо более пронзительно, чем синусоида. Это происходит из-за того, что он имеет острые края из-за быстрых возведенных в квадрат краев формы волны.

Прямоугольная волна богата гармониками, что придает ей довольно интересный тон с музыкальной точки зрения.

Звук прямоугольного сигнала

Основные аспекты прямоугольных волн

Прямоугольные волны появляются в различных электронных схемах и других областях электроники. Они особенно распространены в цифровых или логических схемах, где система имеет дело с цифровыми данными и сигналами.

При использовании в логической или цифровой схеме два состояния часто обозначаются как «1» и «0», соответствующие двоичным разрядам. Их также можно обозначить как «ВЫСОКИЙ» и «НИЗКИЙ», указывая на напряжение.

Состояние логической «1» совпадает с состоянием «ВЫСОКИЙ», а состояние «0» соответствует состоянию «НИЗКИЙ».

Эта терминология принята, поскольку логическая схема обычно связана с двоичными числами и сигналами. Существует множество схем, использующих логические схемы, некоторые из них могут быть относительно простыми с использованием небольших логических микросхем, тогда как другие могут использовать микропроцессоры или микроконтроллеры и т. д.

Поскольку не всегда возможно определить точное напряжение, в электронных схемах обычно дается окно для высокого и низкого состояний.

Существует много аспектов прямоугольной волны, которые часто необходимо указывать.

• Период времени:   Период времени прямоугольной волны является одним из ключевых параметров, описывающих форму волны. Поскольку основными характеристиками прямоугольной волны являются нарастающие и спадающие фронты, они являются ключевыми областями, которые используются для маркеров для определения периода времени. Либо измерение может быть выполнено от одного нарастающего фронта к другому, либо от одного спадающего фронта к следующему.

  Одно и то же напряжение запуска используется от цикла к циклу в случае наличия наклона нарастающего или спадающего фронта. Однако для любого измерительного прибора точка срабатывания будет одной и той же от одного измерения к другому, так что это не проблема.

• Частота:   Как и частота синусоидального сигнала, частота прямоугольного сигнала – это количество смен сигнала в секунду. Частота раньше измерялась в циклах в секунду, но теперь используется единица Герц, где один Герц равен одному циклу в секунду.

  Если известна частота прямоугольной волны, то можно рассчитать период времени и наоборот.

  Аналогичным образом, изменяя уравнение, мы видим, что:

  Где:
      f = частота в Гц
      T = период времени одного цикла в секундах

• Амплитуда:   Амплитуда прямоугольной волны может быть указана одним из нескольких способов.

  Очевидно, что можно измерить и указать напряжение сигнала как пиковое напряжение или размах. Это может быть использовано, если прямоугольная волна использовалась с аналоговой системой наряду с другими формами волны, такими как синусоидальная волна или другие формы волны.

  Однако прямоугольные сигналы наиболее широко используются в цифровых схемах для электронных систем или других логических систем. В цифровых схемах представляют интерес значения для низкого и высокого состояний.

  Обычно низкое состояние находится между 0 В и 0,4 В, а высокое состояние находится между 2 В и шиной питания, что обычно составляет 5,0 В для стандартного TTL. В более современных логических семействах используются гораздо более низкие напряжения, но сохраняются те же принципы, хотя напряжения будут немного отличаться.

Время нарастания и спада прямоугольной волны

Одним из важных аспектов прямоугольных волн является время, которое требуется форме волны, чтобы подняться, а затем спасть.

Часто указывается время нарастания и спада прямоугольной волны. Например, прямоугольная волна от генератора сигналов может иметь характеристики времени нарастания и спада.

Иногда необходимо измерить время нарастания и спада сигнала, поскольку это может повлиять на работу некоторых электронных схем, особенно использующих цифровые технологии.

Обычно время нарастания измеряется как время, за которое нарастающий фронт переходит от 10 % от конечного значения до 90 %. Точно так же задний фронт использует те же точки.

Обычно используются точки 10% и 90%, хотя в некоторых случаях могут использоваться 5% и 95%, но это менее распространено.

Время нарастания и спада для прямоугольной волны

На диаграмме даны значения 10 % и 90 %, а времена t _{нарастания} и t _спада относятся к временам нарастания и спада соответственно.

Для большинства логических семейств, использующих цифровые и прямоугольные сигналы, время нарастания и спада, скорее всего, будет указано в наносекундах.

Спектр прямоугольных волн и анализ Фурье

Если проанализировать спектр прямоугольной волны, то окажется, что он состоит из ряда гармонически связанных синусоидальных волн.

Фактически любой периодический сигнал может быть проанализирован таким образом, и могут быть определены составляющие частоты или синусоидальные волны.

Если проанализировать спектр прямоугольной волны, то будет видно, что форма волны состоит из синусоидальной волны на основной частоте, одна из которых в три раза больше основной, но с одной третью амплитуды, одна из которых является пятой гармоникой, а у квинты амплитуда и так далее. Другими словами, он состоит из ряда нечетно-целых гармонических частот.

Синусоидальные составляющие прямоугольной волны

Чем больше количество присутствующих гармоник, тем точнее представление. Это означает, что если прямоугольный сигнал пропустить через фильтр нижних частот, он будет искажен, а фронты, время нарастания и т.п. будут хуже, чем у прямоугольного сигнала с бесконечной полосой пропускания.

В математическом выражении прямоугольная волна может быть представлена ​​следующим уравнением:

x(t)=A(sin(ωt)+13sin(3ωt)+15sin(5ωt)  . ..)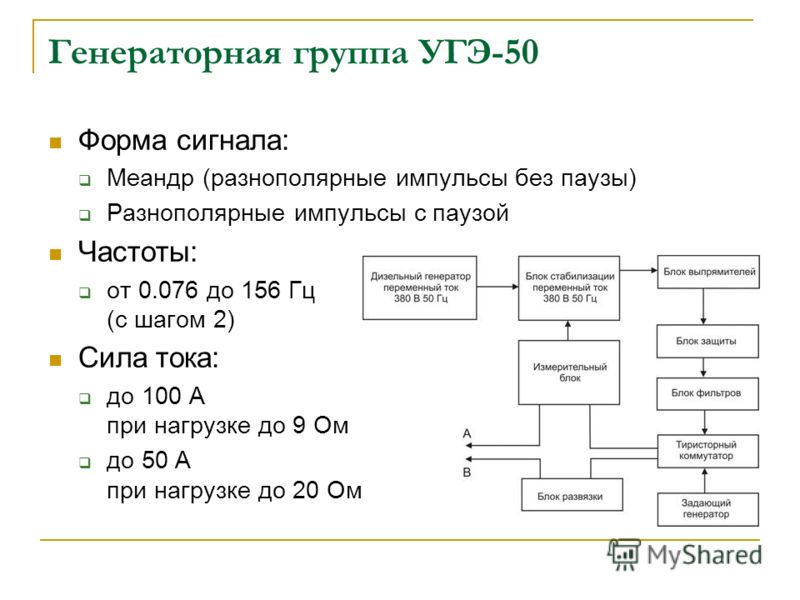

Фактический спектр прямоугольной волны можно увидеть на этом графике спектра прямоугольной волны, снятом с тестового прибора.

Спектр прямоугольной волны

На диаграмме основная частота будет видна слева от развертки — обратите внимание, что линия нулевой частоты находится справа слева от развертки. Затем гармоники можно увидеть в нечетных кратных основной гармонике.

Следует помнить, что шкала амплитуд является логарифмической, но видно, что гармоники находятся на уровне 3, 5, 7 и далее нечетных кратных основной гармонике и что их амплитуда уменьшается с увеличением частоты.

Также видно, что четные кратные отсутствуют, поскольку прямоугольная волна состоит только из нечетных целых гармоник.

Квадратные волны, прямоугольные волны и импульсные формы сигналов встречаются в огромном количестве электронных схем, систем и т.п. Они особенно распространены в схемах, основанных на цифровых или логических схемах, поскольку эта технология основана на формах сигналов, которые имеют два состояния.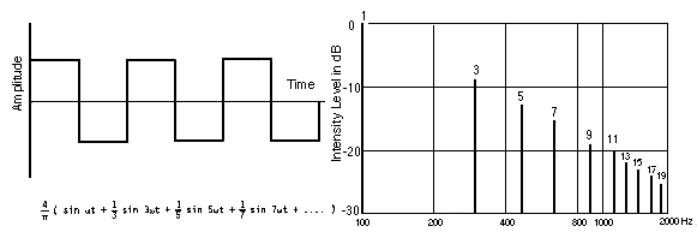

Дополнительные основные понятия и руководства по электронике:
Напряжение Текущий Власть Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность РЧ-шум Сигналы
    Вернуться в меню основных понятий электроники . . .

Определение прямоугольной волны | ПКМаг

Волна, которая быстро нарастает до определенной амплитуды, остается постоянной в течение определенного периода времени и быстро спадает в конце. В цифровых системах прямоугольные сигналы являются нормой, поскольку они представляют собой двоичную цифру (0 или 1). Квадратные волны также могут генерироваться в музыкальных синтезаторах и иметь хриплый звук.

Прямоугольные волны Это выход прямоугольной волны 1 кГц на осциллографе. Отображаются только вершины и основания волн, потому что рост и падение происходит быстрее, чем установлено в области видимости.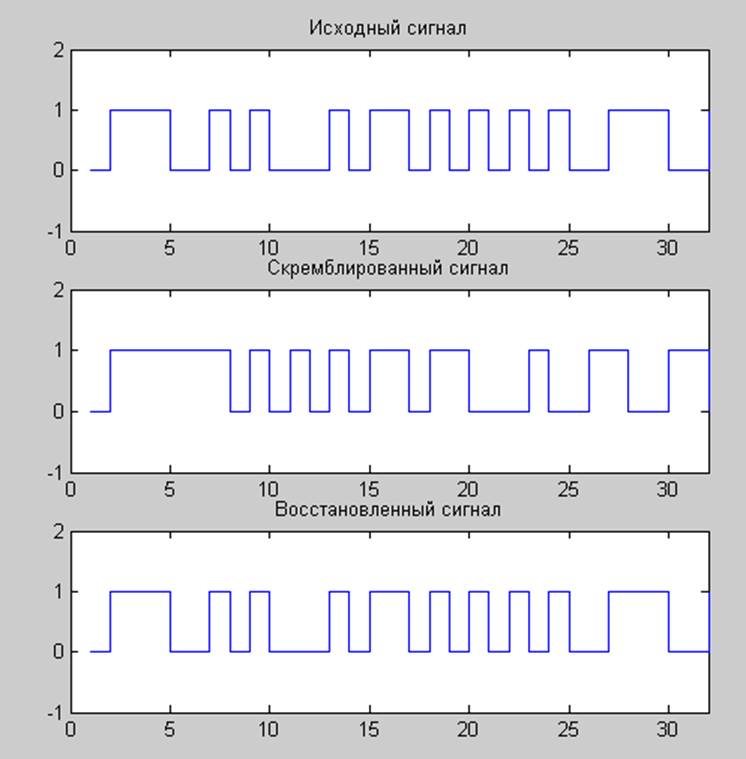

Реклама

Истории PCMag, которые вам понравятся

{X-html заменен}

Выбор редакции

ЭТО ОПРЕДЕЛЕНИЕ ПРЕДНАЗНАЧЕНО ТОЛЬКО ДЛЯ ЛИЧНОГО ИСПОЛЬЗОВАНИЯ. Любое другое воспроизведение требует разрешения.
Copyright © 1981-2023. The Computer Language(Opens in a new window) Co Inc. Все права защищены.

Информационные бюллетени PCMag

Информационные бюллетени PCMag

Наши лучшие истории в вашем почтовом ящике

Следите за новостями PCMag

• Фейсбук (Открывается в новом окне)
• Твиттер (Откроется в новом окне)
• Флипборд (Открывается в новом окне)
• Гугл (откроется в новом окне)
• Инстаграм (откроется в новом окне)
• Pinterest (Открывается в новом окне)

PCMag.com является ведущим авторитетом в области технологий, предоставляющим независимые лабораторные обзоры новейших продуктов и услуг. Наш экспертный отраслевой анализ и практические решения помогут вам принимать более обоснованные решения о покупке и получать больше от технологий.

Как мы тестируем Редакционные принципы

• (Открывается в новом окне) Логотип Зиффмедиа
• (Открывается в новом окне) Логотип Аскмен
• (Открывается в новом окне) Логотип Экстримтек
• (Открывается в новом окне) Логотип ИНГ
• (Открывается в новом окне) Логотип Mashable
• (Открывается в новом окне) Предлагает логотип
• (Открывается в новом окне) Логотип RetailMeNot
• (Открывается в новом окне) Логотип Speedtest
• (Открывается в новом окне) Логотип Спайсворкс

(Открывается в новом окне)

PCMag поддерживает Group Black и ее миссию по увеличению разнообразия голосов в СМИ и прав собственности на СМИ.

© 1996-2023 Ziff Davis, LLC.