Меандр — Википедия
Материал из Википедии — свободной энциклопедии
Меа́ндр (от греч. Μαίανδρος — древнее название извилистой реки Большой Мендерес в Малой Азии, сейчас в Турции) — плавный, но заметный изгиб русла (равнинной) реки.
Вогнутый (внешний) берег меандра обычно более крутой, а выпуклый (внутренний) — более пологий[1].
Иногда река спрямляет своё русло, и тогда на месте прежнего русла образуется старица.
Тип русловых процессов, заключающийся в закономерном развитии речного русла с меандрами, называется меандрирование.
- Чалов Р. С., Завадский А. С., Панин А. В. Речные излучины. — Изд-во МГУ, 2004. — 371 с.
Меандр (математика) — Википедия
Меандр или замкнутый меандр — это замкнутая кривая без самопересечений, которая пересекает прямую несколько раз. Интуитивно, меандр можно рассматривать как дорогу, пересекающую реку мостами в нескольких местах.
Если задана ориентированная прямая L на плоскости R2, меандр порядка n — это замкнутая кривая без самопересечений на R2, которая поперечно пересекает прямую в 2n точках для некоторого положительного n. Прямая и кривая вместе образуют меандровую систему. Говорят, что два меандра эквивалентны, если существует гомеоморфизм всей плоскости, которая переводит L
Пример[править | править код]
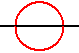
Меандр порядка 1 пересекает прямую дважды:
Меандровые числа[править | править код]
Число различных меандров порядка n называется меандровым числом Mn. Первые пятнадцать меандровых чисел (последовательность A005315 в OEIS).
- M1 = 1
- M2 = 2
- M3 = 8
- M4 = 42
- M5 = 262
- M6 = 1828
- M7 = 13820
- M8 = 110954
- M9 = 933458
- M10 = 8152860
- M11 = 73424650
- M12 = 678390116
- M13 = 6405031050
- M14 = 61606881612
- M15 = 602188541928
Меандровые перестановки[править | править код]
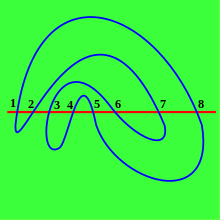Меандровая перестановка(1 8 5 4 3 6 7 2)
Меандровая перестановка порядка n задаётся на множестве {1, 2, …, 2n} и определяется меандровой системой следующим образом:
- Для прямой, ориентированной слева направо, каждое пересечение меандра последовательно помечаются целыми числами, начиная с 1.
- Кривая с точки пересечения, помеченной 1, ориентируется вверх.
- Циклическая перестановка без фиксированных точек получается проходом ориентированной кривой через помеченные точки.
На диаграмме справа меандрическая перестановка порядка 4 задаётся перестановкой (1 8 5 4 3 6 7 2). Это перестановка, записанная в циклической нотации и не следует путать с линейной нотацией.
Если π является меандровой перестановкой, то π2 состоит из двух циклов, одна содержит все чётные элементы, другая — все нечётные. Перестановки с такими свойствами называется чередующимися перестановками
Если задана фиксированная ориентированная прямая L на плоскости R2, открытый меандр порядка n — это ориентированная кривая без самопересечений на R2, которая пересекает прямую в n точках для некоторого положительного целого числа n. Говорят, что два открытых меандра эквивалентны, если они гомеоморфны на плоскости.
Примеры[править | править код]
Открытый меандр порядка 1 пересекает прямую один раз:
Открытый меандр порядка 2 пересекает прямую дважды:
Открытые меандровы числа[править | править код]
Число различных открытых меандров порядка n называется открытым меандровым числом mn. Первые пятнадцать открытых меандровых чисел (последовательность A005316 в OEIS).
- m1 = 1
- m2 = 1
- m
- m4 = 3
- m5 = 8
- m6 = 14
- m7 = 42
- m8 = 81
- m9 = 262
- m10 = 538
- m11 = 1828
- m12 = 3926
- m13 = 13820
- m14 = 30694
- m15 = 110954
Если дан ориентированный луч R на плоскости R2, полумеандр порядка n — — это непересекающаяся кривая в R2, которая пересекает луч в n точках для некоторого положительного n. Говорят, что два полумендра эквивалентны, если они гомеоморфны на плоскости.
Примеры[править | править код]
Полумеандр порядка два пересекает луч дважды:
Полумеандровые числа[править | править код]
Количество различных полумеандровых чисел порядка n называется полумеандровым числом Mn (обычно обозначается надчёркиванием, а не подчёркиванием). Первые пятнадцать полумеандровых чисел (последовательность A000682 в OEIS).
- M1 = 1
- M2 = 1
- M3 = 2
- M4 = 4
- M5 = 10
- M6 = 24
- M7 = 66
- M8 = 174
- M9 = 504
- M10 = 1406
- M11 = 4210
- M12 = 12198
- M13 = 37378
- M14 = 111278
- M15 = 346846
Существует инъекция из меандровых чисел в открытые меандровые числа:
- Mn = m2n−1
Любое меандровое число может быть ограничены полумеандровыми числами:
- Mn ≤ Mn ≤ M2n
Для n > 1 меандрические числа чётны:
- Mn ≡ 0 (mod 2)
Гармоники меандра — Дмитрий Бравиков
Меандр — это периодический сигнал вида:
На графике:
- t — время;
- f(t) — функция меандра;
- A — амплитуда меандра;
- T — период меандра;
- tPos — длительность положительного импульса;
- tNeg — длительность отрицательного импульса;
У меандра длительности импульсов равны:
Функцию меандра можно представить в виде ряда:
где:
- — номер гармоники;
- — частота меандра.
Меандр состоит из нечетных гармоник (h = 1, 3, 5 и т. д.), это учитывается выражением , которое принимает только нечетные значения.
Представим ряд в более простой форме:
где ω — это угловая частота:
Пример: если частота меандра равна 50 Гц, то меандр представляет из себя сумму синусоид (гармоник) с частотами 50 Гц, 150 Гц, 250 Гц и т. д.
Выделить из меандра синусоидальный сигнал можно с помощью полосового фильтра с резонансной частотой равной частоте нечетной гармоники.
Действующее (среднеквадратичное) значение меандра равно амплитуде меандра:
Амплитуда гармоники рассчитывается по формуле:
Действующее значение гармоники рассчитывается по формуле:
Таблица действующих значений гармоник для некоторых амплитуд меандра:
| Амплитуда меандра, A | Гармоника, h | ||
| 1 | 3 | 5 | |
| 1 | 0,90032 | 0,30011 | 0,18006 |
| 1,1 | 0,33012 | 0,19807 | |
| 1,2 | 1,08038 | 0,36013 | 0,21608 |
| 1,3 | 1,17041 | 0,39014 | 0,23408 |
| 1,4 | 1,26044 | 0,42015 | 0,25209 |
| 1,5 | 1,35047 | 0,45016 | 0,27009 |
| 1,6 | 1,44051 | 0,48017 | 0,28810 |
| 1,7 | 1,53054 | 0,51018 | 0,30611 |
| 1,8 | 1,62057 | 0,54019 | 0,32411 |
| 1,9 | 1,71060 | 0,57020 | 0,34212 |
| 2 | 1,80063 | 0,60021 | 0,36013 |
| 2,1 | 1,89066 | 0,63022 | 0,37813 |
| 2,2 | 1,98070 | 0,66023 | 0,39614 |
| 2,3 | 2,07073 | 0,69024 | 0,41415 |
| 2,4 | 2,16076 | 0,72025 | 0,43215 |
| 2,5 | 2,25079 | 0,75026 | 0,45016 |
| 2,6 | 2,34082 | 0,78027 | 0,46816 |
| 2,7 | 2,43085 | 0,81028 | 0,48617 |
| 2,8 | 2,52089 | 0,84030 | 0,50418 |
| 2,9 | 2,61092 | 0,87031 | 0,52218 |
| 3 | 2,70095 | 0,90032 | 0,54019 |
| 3,1 | 2,79098 | 0,93033 | 0,55820 |
| 3,2 | 2,88101 | 0,96034 | 0,57620 |
| 3,3 | 2,97104 | 0,99035 | 0,59421 |
| 3,4 | 3,06108 | 1,02036 | 0,61222 |
| 3,5 | 3,15111 | 1,05037 | 0,63022 |
| 3,6 | 3,24114 | 1,08038 | 0,64823 |
| 3,7 | 3,33117 | 1,11039 | 0,66623 |
| 3,8 | 3,42120 | 1,14040 | 0,68424 |
| 3,9 | 3,51123 | 1,17041 | 0,70225 |
| 4 | 3,60127 | 1,20042 | 0,72025 |
| 4,1 | 3,69130 | 1,23043 | 0,73826 |
| 4,2 | 3,78133 | 1,26044 | 0,75627 |
| 4,3 | 3,87136 | 1,29045 | 0,77427 |
| 4,4 | 3,96139 | 1,32046 | 0,79228 |
| 4,5 | 4,05142 | 1,35047 | 0,81028 |
| 4,6 | 4,14146 | 1,38049 | 0,82829 |
| 4,7 | 4,23149 | 1,41050 | 0,84630 |
| 4,8 | 4,32152 | 1,44051 | 0,86430 |
| 4,9 | 4,41155 | 1,47052 | 0,88231 |
| 5 | 4,50158 | 1,50053 | 0,90032 |
| 5,1 | 4,59161 | 1,53054 | 0,91832 |
| 5,2 | 4,68164 | 1,56055 | 0,93633 |
| 5,3 | 4,77168 | 1,59056 | 0,95434 |
| 5,4 | 4,86171 | 1,62057 | 0,97234 |
| 5,5 | 4,95174 | 1,65058 | 0,99035 |
| 5,6 | 5,04177 | 1,68059 | 1,00835 |
| 5,7 | 5,13180 | 1,71060 | 1,02636 |
| 5,8 | 5,22183 | 1,74061 | 1,04437 |
| 5,9 | 5,31187 | 1,77062 | 1,06237 |
| 6 | 5,40190 | 1,80063 | 1,08038 |
| 6,1 | 5,49193 | 1,83064 | 1,09839 |
| 6,2 | 5,58196 | 1,86065 | 1,11639 |
| 6,3 | 5,67199 | 1,89066 | 1,13440 |
| 6,4 | 5,76202 | 1,92067 | 1,15240 |
| 6,5 | 5,85206 | 1,95069 | 1,17041 |
| 6,6 | 5,94209 | 1,98070 | 1,18842 |
| 6,7 | 6,03212 | 2,01071 | 1,20642 |
| 6,8 | 6,12215 | 2,04072 | 1,22443 |
| 6,9 | 6,21218 | 2,07073 | 1,24244 |
| 7 | 6,30221 | 2,10074 | 1,26044 |
| 7,1 | 6,39225 | 2,13075 | 1,27845 |
| 7,2 | 6,48228 | 2,16076 | 1,29646 |
| 7,3 | 6,57231 | 2,19077 | 1,31446 |
| 7,4 | 6,66234 | 2,22078 | 1,33247 |
| 7,5 | 6,75237 | 2,25079 | 1,35047 |
| 7,6 | 6,84240 | 2,28080 | 1,36848 |
| 7,7 | 6,93244 | 2,31081 | 1,38649 |
| 7,8 | 7,02247 | 2,34082 | 1,40449 |
| 7,9 | 7,11250 | 2,37083 | 1,42250 |
| 8 | 7,20253 | 2,40084 | 1,44051 |
| 8,1 | 7,29256 | 2,43085 | 1,45851 |
| 8,2 | 7,38259 | 2,46086 | 1,47652 |
| 8,3 | 7,47263 | 2,49088 | 1,49453 |
| 8,4 | 7,56266 | 2,52089 | 1,51253 |
| 8,5 | 7,65269 | 2,55090 | 1,53054 |
| 8,6 | 7,74272 | 2,58091 | 1,54854 |
| 8,7 | 7,83275 | 2,61092 | 1,56655 |
| 8,8 | 7,92278 | 2,64093 | 1,58456 |
| 8,9 | 8,01282 | 2,67094 | 1,60256 |
| 9 | 8,10285 | 2,70095 | 1,62057 |
| 9,1 | 8,19288 | 2,73096 | 1,63858 |
| 9,2 | 8,28291 | 2,76097 | 1,65658 |
| 9,3 | 8,37294 | 2,79098 | 1,67459 |
| 9,4 | 8,46297 | 2,82099 | 1,69259 |
| 9,5 | 8,55301 | 2,85100 | 1,71060 |
| 9,6 | 8,64304 | 2,88101 | 1,72861 |
| 9,7 | 8,73307 | 2,91102 | 1,74661 |
| 9,8 | 8,82310 | 2,94103 | 1,76462 |
| 9,9 | 8,91313 | 2,97104 | 1,78263 |
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
Похожее
Меандр (радиотехника) — Карта знаний
- Меа́ндр (по названию геометрического орнамента в виде ломаной линии) — периодический сигнал прямоугольной формы, широко используемый в радиотехнике и электронике. Меандр может быть знакопеременным (двухполярным) или однополярным. Во втором случае длительность импульса и длительность паузы между импульсами равны, то есть в этом случае меандр — периодический сигнал прямоугольной формы, имеющий скважность 2 (или коэффициент заполнения 0,5).
Источник: Википедия
Связанные понятия
Электрический импульс — кратковременный всплеск электрического напряжения или силы тока в определённом, конечном временном промежутке. Различают видеоимпульсы — единичные колебания какой-либо формы и радиоимпульсы — всплески высокочастотных колебаний. Видеоимпульсы бывают однополярные (отклонение только в одну сторону от нулевого потенциала) и двухполярные. Гетеродини́рование — преобразование частоты сигнала в пару различных сигналов с разными частотами, эти сигналы принято называть сигналами промежуточных частот, причём исходная фаза сигнала сохраняется в порождённых сигналах. Цифровой вычислительный синтезатор (ЦВС), известный еще как схема прямого цифрового синтеза (DDS) — электронный прибор, предназначенный для синтеза сигналов произвольной формы и частоты из единственной опорной частоты, поставляемой генератором тактовых импульсов. Характерной особенностью ЦВС является то, что отсчеты синтезируемого сигнала вычисляются цифровыми методами, после чего передаются на цифро-аналоговый преобразователь (ЦАП), где и происходит их преобразование в аналоговую форму (напряжение… Спектрогра́мма (соногра́мма) — изображение, показывающее зависимость спектральной плотности мощности сигнала от времени. Спектрограммы применяются для идентификации речи, анализа звуков животных, в различных областях музыки, радио- и гидролокации, обработке речи, сейсмологии и в других областях.Упоминания в литературе
Кроме того, в поверхностном слое океана наблюдаются специфические физические явления, способствующие лучшему отображению на снимках РСА морских динамических структур, таких как, например, соленоиды вертикальной циркуляции Ленгмюра (Sole et al., 2000), образующих на поверхности моря линии дивергенции и конвергенции. На снимках РСА подобные области отображаются как совокупность параллельных светлых и тёмных полос или линий, трансформированных под действием внешних факторов и принимающих форму обуславливающих их динамических структур (океанические вихри, ринги, меандры поверхностных течений и др.). Таким образом, резюмируя, можно сказать, что снимки РСА отображают не сами природные явления, а их проявления (следы) на морской поверхности (рис. 6).Связанные понятия (продолжение)
Фильтр Чебышёва — один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад амплитудно-частотной характеристики (АЧХ) и существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания (фильтр Чебышёва I рода) и подавления (фильтр Чебышёва II рода), чем у фильтров других типов. Фильтр получил название в честь известного русского математика XIX века Пафнутия Львовича Чебышёва, так как характеристики этого фильтра… Морфинг (англ. morphing — трансформация) — звуковой эффект, заключающийся в наложении характеристик одного звука на другой. В качестве характеристик могут выступать огибающая, спектр или временная структура сигнала. Часто говорят о тембральном морфинге — процессе комбинирования двух или более звуков различного тембра для получения нового звука, тембр которого включает в себя отдельные характеристики обоих звуков. Фильтр Баттерво́рта — один из типов электронных фильтров. Фильтры этого класса отличаются от других методом проектирования. Фильтр Баттерворта проектируется так, чтобы его амплитудно-частотная характеристика была максимально гладкой на частотах полосы пропускания. Блочно-ориентированные модели — это представление нелинейных систем в виде различных комбинаций инерционных звеньев и нелинейных безынерционных математических элементов. Такое представление моделей позволяет связать в явном виде входные и выходные переменные объектов с различной структурой и степенью нелинейности. К таким системам относятся системы типа Гаммерштейна, Винера, Винера-Гаммерштейна, фильтра Заде, обобщенной модели Винера и Sm-системы. Синтезатор частот — устройство для генерации электрических гармонических колебаний с помощью линейных повторений (умножением, суммированием, разностью) на основе одного или нескольких опорных генераторов. Синтезаторы частот служат источниками стабильных (по частоте) колебаний в радиоприёмниках, радиопередатчиках, частотомерах, испытательных генераторах сигналов и других устройствах, в которых требуется настройка на разные частоты в широком диапазоне и высокая стабильность выбранной частоты. Стабильность… Частота́ — физическая величина, характеристика периодического процесса, равна количеству повторений или возникновения событий (процессов) в единицу времени. Рассчитывается, как отношение количества повторений или возникновения событий (процессов) к промежутку времени, за которое они совершены. Стандартные обозначения в формулах — ν, f или F. Це́лостность сигна́лов (англ. Signal Integrity) — наличие достаточных для безошибочной передачи качественных характеристик электрического сигнала. Фа́зовая манипуля́ция (ФМн, англ. phase-shift keying (PSK)) — один из видов фазовой модуляции, при которой фаза несущего колебания меняется скачкообразно в зависимости от информационного сообщения. Компле́ксная амплитуда — комплексная величина, модуль и аргумент которой равны соответственно амплитуде и начальной фазе гармонического сигнала. Реконструкционный фильтр (восстанавливающий фильтр, англ. reconstruction filter, anti-imaging filter) используется в смешанных аналогово-цифровых системах для вывода гладкого (smooth) аналогового сигнала c цифрового входа. В частности, он применяется в устройствах ЦАП. Яче́йка Блэ́кмера (англ. Blackmer cell) — схема электронного управляемого напряжением усилителя (УНУ, амплитудный модулятор) с экспоненциальной характеристикой управления, предложенная и доведённая до серийного выпуска Дэвидом Блэкмером в 1970—1973 годы. Четырёхтранзисторное ядро схемы образовано двумя встречно включёнными токовыми зеркалами на комплементарных биполярных транзисторах. Входной транзистор каждого из зеркал логарифмирует входной ток, а выходной транзистор антилогарифмирует сумму логарифма… Сигнальное созвездие (англ. constellation diagram) — представление всевозможных значений комплексной амплитуды манипулированных радиосигналов на комплексной плоскости. Фа́зовый дете́ктор, фазовый компара́тор (ФД) — электронное устройство, сравнивающее фазы двух входных сигналов равных или близких частот. Мультивибра́тор — релаксационный генератор электрических прямоугольных колебаний с короткими фронтами. Генератор ступенчатого тона (англ. stepped tone generator), также известный как «Atari Punk Console» (APC) — самодельное устройство, разработанное креационистом-радиолюбителем Форрестом М. Мимсом, описание которого было опубликовано в книгах «Engineer’s Notebook: Integrated Circuit Applications» (издательство сети магазинов «Radio Shack») 1980 года и «Engineer’s Mini-Notebook — 555 Circuits» (издательство «Siliconcepts») 1984 года. Цепь Чуа или схема Чуа — простейшая электрическая цепь, демонстрирующая режимы хаотических колебаний. Была предложена профессором Калифорнийского университета Леоном Чуа в 1983 году. Цепь состоит из двух конденсаторов, одной катушки индуктивности, линейного резистора и нелинейного резистора с отрицательным сопротивлением (обычно называемого диодом Чуа). Коэффициент стоячей волны (КСВ, от англ. standing wave ratio, SWR) — отношение наибольшего значения амплитуды напряжённости электрического или магнитного поля стоячей волны в линии передачи к наименьшему. Фильтр с конечной импульсной характеристикой (Нерекурсивный фильтр, КИХ-фильтр) или FIR-фильтр (FIR сокр. от finite impulse response — конечная импульсная характеристика) — один из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра… Фильтр в электронике — устройство для выделения желательных компонентов спектра электрического сигнала и/или подавления нежелательных. Амплиту́дно-часто́тная характери́стика (АЧХ) — зависимость амплитуды выходного сигнала некоторой системы от частоты её входного гармонического сигнала. Иногда эту характеристику называют «частотным откликом системы» (frequency response). Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы. Синхро́нный усили́тель — тип электронного усилителя, в котором применён принцип синхронного детектирования сигнала. Принцип транслинейности (англ. translinear principle, от англ. transconductance — крутизна передаточной характеристики) в анализе и проектировании аналоговых интегральных схем — правило (уравнение), определяющее соотношения токов, протекающих через активные элементы схемы (эмиттерные переходы биполярных транзисторов или каналы МДП-транзисторов). Сформулирован Барри Гилбертом в 1975 году. Принцип транслинейности — прямое следствие из второго закона Кирхгофа и формулы Шокли, описывающей вольт-амперную… Эксайтер (англ. exciter — возбудитель) — психоакустический процессор, используемый для фазовой манипуляции, гармонического синтеза (как правило) высокочастотных сигналов путём добавления небольших гармонических искажений. Динамическая обработка влечет за собой изменение характеристик эквалайзера во временной области в зависимости от входного сигнала, также уменьшается шум по сравнению с эффектом от работы статического эквалайзера. Эксайтеры также используются для синтеза гармоник низкочастотных сигналов… Электромехани́ческий фильтр (ЭМФ) — это фильтр, обычно используемый вместо электронного фильтра радиочастот, основное назначение которого: пропускать колебания в определенной полосе частот и подавлять остальные. В фильтре используются механические колебания, аналогичные подаваемому электрическому сигналу (это один из типов аналоговых фильтров). На входе и на выходе фильтра стоят электромеханические преобразователи, которые преобразуют электрические колебания сигнала в механические колебания рабочего… Длинная линия — модель линии передачи, продольный размер (длина) которой превышает длину волны, распространяющейся в ней (либо сравнима с длиной волны), а поперечные размеры (например, расстояние между проводниками, образующими линию) значительно меньше длины волны. Интегра́тор, блок интегри́рования — техническое устройство, выходной сигнал (выходная величина, выходной параметр) которого пропорционален интегралу, обычно по времени, от входного сигнала. Интермодуляция — это процесс взаимодействия нескольких различных сигналов в нелинейных каскадах радиоприёмного тракта. В результате возникают новые составляющие спектра, зашумляющие принимаемый сигнал (либо проявляющиеся в качестве зеркального сигнала). Согласованный фильтр — линейный оптимальный фильтр, построенный исходя из известных спектральных характеристик полезного сигнала и шума. Согласованные фильтры предназначены для выделения сигналов известной формы на фоне шумов. Под оптимальностью понимается максимальное отношение сигнал/шум на выходе фильтра, при этом форма сигнала при прохождении через фильтр изменяется. Кольцевой генератор — электронное устройство, состоящее из нечётного числа инвертирующих каскадов или цифровых инверторов и служащее для генерации последовательности прямоугольных импульсов. Генерация возникает за счёт того, что коэффициент усиления цепи элементов больше единицы, а фазовая задержка более 180 градусов. Замыкание входа и выхода одиночного каскада, как правило, не приводит к генерации, так как выполняется только первое условие. Один инвертирующий каскад с линией задержки (Фиг. 1) в… Классы электронных усилителей и режимы работы активных усилительных приборов (ламп или транзисторов) традиционно обозначаются буквами латинского алфавита. Буквенные обозначения классов усиления могут дополнительно уточняться суффиксом, указывающим на режим согласования мощного каскада с источником сигнала (AB1, AB2 и т. п.) и с нагрузкой (F1, F2, F3). Устройства, совмещающие свойства двух «однобуквенных» классов, могут выделяться в особые классы, обозначаемые сочетанием двух букв (AB, BD, DE и устаревший… Многолучево́е распростране́ние — это эффект, наблюдаемый при распространении сигналов. Возникает при условии существования в точке приема радиосигнала не только прямого, но и ещё одного или целого ряда отражённых или\и преломлённых лучей. Другими словами, на антенну приёмника приходят не только прямые лучи (непосредственно от самого источника), но и отражённые (от земной поверхности, зданий, строений и прочих объектов). Спектр сигнала — в радиотехнике это результат разложения сигнала на более простые в базисе ортогональных функций. В качестве разложения обычно используются преобразование Фурье, разложение по функциям Уолша, вейвлет-преобразование и др. Предусили́тель-корре́ктор, или усилитель-корректор (УК), или фо́нокорре́ктор — специализированный электронный усилитель тракта воспроизведения граммофонной записи, восстанавливающий исходный спектр записанного на пластинке звукового сигнала и усиливающий выходное напряжение головки звукоснимателя до типичного уровня линейного выхода — от 0,775 В (0 dBu) в бытовой аналоговой аппаратуре до 2 В (8 dBu) в цифровой и радиотрансляционной аппаратуре). Исторически звукозаписывающая промышленность использовала…Подробнее: Фонокорректор
Алгоритм Карплуса-Стронга для синтеза струны — способ синтеза звука, заключающийся в пропускании короткого сигнала через линию задержки с фильтром. В зависимости от параметров, полученный звук может быть похож на звук струны, извлекаемый медиатором или тэппингом, либо на звуки некоторых ударных инструментов. Фильтр Бесселя — в электронике и обработке сигналов один из наиболее распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной… Корреляционный фильтр — радиоэлектронное устройство, используемое для обнаружения сигнала заданной формы среди шума. Ква́рцевый резона́тор (жарг. «кварц») — электронный прибор, в котором пьезоэлектрический эффект и явление механического резонанса используются для построения высокодобротного резонансного элемента электронной схемы. Яче́йка Ги́лберта (англ. Gilbert cell) в электронике — схема четырёхквадрантного аналогового умножителя, предложенная Барри Гилбертом в 1968 году. Она представляет собой ядро умножителя на трёх дифференциальных каскадах, дополненное диодными преобразователями входных напряжений — в токи (V1, V2 на схемах). Ячейка Гилберта, в модифицированной бета-зависимой форме, выполняет функцию смесителя или балансного модулятора в большинстве современных радиоприёмников и сотовых телефонов. Бандга́п (англ. bandgap, запрещённая зона) — стабильный транзисторный источник опорного напряжения (ИОН), величина которого определяется шириной запрещённой зоны используемого полупроводника. Для легированного монокристаллического кремния, имеющего при Т=0 К ширину запрещённой зоны Eg=1,143 эВ, напряжение VREF на выходе бандгапа обычно составляет от 1,18 до 1,25 В или кратно этой величине, а его предельное отклонение от нормы во всём диапазоне рабочих температур и токов составляет не более 3 %. Бандгапы…Коэффициент формы — Википедия
Коэффициент формы — это отношение среднеквадратичного значения какой-то величины к среднему модулю (среднему абсолютному значению) той же величины. Если зависимость этой величины от другой переменной изобразить в виде графика, то коэффициент формы покажет, насколько форма этой линии отличается от горизонтальной прямой. Коэффициент формы постоянной функции равен единице.
Коэффициент формы нередко используется в электронике при описании зависимости тока или напряжения от времени. Он показывает, насколько сильно отличается форма сигнала переменного тока от постоянного тока той же средней мощности. Последний может быть также описан как ток, выделяющий на такой же нагрузке такое же тепло за одинаковый длительный промежуток времени.
Для функции x(t){\displaystyle x(t)}, конечной и непрерывной на интервале времени T, среднеквадратичное значение на этом отрезке времени может быть вычислено с помощью интеграла:
Xrms=1T∫t0t0+T[x(t)]2dt{\displaystyle X_{\mathrm {rms} }={\sqrt {{1 \over {T}}{\int _{t_{0}}^{t_{0}+T}{[x(t)]}^{2}\,dt}}}}
Средний модуль вычисляется с помощью интеграла от абсолютного значения на том же промежутке:
Xarv=1T∫t0t0+T|x(t)|dt{\displaystyle X_{\mathrm {arv} }={1 \over {T}}{\int _{t_{0}}^{t_{0}+T}{|x(t)|\,dt}}}
Отношение этих двух величин и есть коэффициент формы, обозначаемый обычно kf{\displaystyle k_{\mathrm {f} }}.
kf=XrmsXarv=1T∫t0t0+T[x(t)]2dt1T∫t0t0+T|x(t)|dt=T∫t0t0+T[x(t)]2dt∫t0t0+T|x(t)|dt{\displaystyle k_{\mathrm {f} }={X_{\mathrm {rms} } \over X_{\mathrm {arv} }}={\frac {\sqrt {{1 \over {T}}{\int _{t_{0}}^{t_{0}+T}{[x(t)]}^{2}\,dt}}}{{1 \over {T}}{\int _{t_{0}}^{t_{0}+T}{|x(t)|\,dt}}}}={\frac {\sqrt {T\int _{t_{0}}^{t_{0}+T}{{[x(t)]}^{2}\,dt}}}{\int _{t_{0}}^{t_{0}+T}{|x(t)|\,dt}}}}
Хотя оба средних значения (и Xrms{\displaystyle X_{\mathrm {rms} }}, и Xarv{\displaystyle X_{\mathrm {arv} }}) характеризуют расстояние кривой от нуля, среднеквадратичное значение Xrms{\displaystyle X_{\mathrm {rms} }} отражает также изменчивость этого расстояния, так как большие и маленькие отклонения от нуля вносят непропорциональные вклады в него.
Среднеквадратичное значение Xrms{\displaystyle X_{\mathrm {rms} }} всегда бывает больше или равно Xarv{\displaystyle X_{\mathrm {arv} }}. Поэтому коэффициент формы не может быть меньше 1 и не имеет теоретического верхнего предела.
Если сложный периодический сигнал можно представить как сумму N синусоидальных сигналов (гармоник) разной частоты, то среднеквадратичное значение сложного сигнала может быть вычислено так:
Xrms=Xrms12+Xrms22+…+XrmsN2{\displaystyle X_{\mathrm {rms} }={\sqrt {{{X_{\mathrm {rms1} }}^{2}}+{{X_{\mathrm {rms2} }}^{2}}+…+{{X_{\mathrm {rmsN} }}^{2}}}}}
В то же время средний модуль сложного сигнала просто равен сумме средних модулей гармоник: Xarv=Xarv1+Xarv2+…+XarvN{\displaystyle X_{\mathrm {arv} }=X_{\mathrm {arv1} }+X_{\mathrm {arv2} }+…+X_{\mathrm {arvN} }}.
Поэтому коэффициент формы сложного периодического сигнала можно вычислить по формуле:
kftot=XrmsXarv=Xrms12+Xrms22+…+XrmsN2Xarv1+Xarv2+…+XarvN{\displaystyle k_{\mathrm {f} _{\mathrm {tot} }}={X_{\mathrm {rms} } \over X_{\mathrm {arv} }}={\frac {\sqrt {{{X_{\mathrm {rms1} }}^{2}}+{{X_{\mathrm {rms2} }}^{2}}+…+{{X_{\mathrm {rmsN} }}^{2}}}}{X_{\mathrm {arv1} }+X_{\mathrm {arv2} }+…+X_{\mathrm {arvN} }}}}.
Цифровые инструменты для измерения переменного тока часто создаются с расчётом на определённую форму зависимости от времени. Например, многие цифровые мультиметры переменного тока, показывающие среднеквадратичное значение тока, на самом деле вычисляют средний модуль тока и умножают его на коэффициент формы для синусоидального тока. Хотя этот метод проще, он приводит к ошибкам для несинусоидальных токов.
И вычисление квадрата в Xrms{\displaystyle X_{\mathrm {rms} }}, и вычисление модуля в Xarv{\displaystyle X_{\mathrm {arv} }} приводят к независимости от знака функции. Поэтому, коэффициент формы тока переменного направления, если его среднее значение равно нулю, останется тем же после его полного выпрямления.
Коэффициент формы kf{\displaystyle k_{\mathrm {f} }} является наименьшим из трёх волновых коэффициентов, другие два — это ka=XmaxXrms{\displaystyle k_{\mathrm {a} }={\frac {X_{\mathrm {max} }}{X_{\mathrm {rms} }}}} и kav=XmaxXarv{\displaystyle k_{\mathrm {av} }={\frac {X_{\mathrm {max} }}{X_{\mathrm {arv} }}}}, где X_\mathrm{max} — наибольшее значение функции на том же интервале времени.
kav≥ka≥kf{\displaystyle k_{\mathrm {av} }\geq k_{\mathrm {a} }\geq k_{\mathrm {f} }}[1]
Эти три коэффициента связаны соотношением kav=kakf{\displaystyle k_{\mathrm {av} }=k_{\mathrm {a} }k_{\mathrm {f} }}, поэтому коэффициент формы может быть вычислен так: kf=kavka{\displaystyle k_{\mathrm {f} }={\frac {k_{\mathrm {av} }}{k_{\mathrm {a} }}}}.
Коэффициенты формы некоторых функций, важных в электронике[править | править код]
Обозначим буквой a{\displaystyle a} максимальное отклонение функции от нуля (для некоторых функций эта величина совпадает с амплитудой). Например, 8sin(t){\displaystyle 8\sin(t)} можно представить как f(t)=asin(t), a=8{\displaystyle f(t)=a\sin(t),\ a=8}. Так как и среднеквадратичное значение, и средний модуль пропорциональны этой величине, то она не влияет на коэффициент формы и может быть заменена на 1 при его вычислении.
Обозначим D=τT{\displaystyle D={\frac {\tau }{T}}} коэффициент заполнения, то есть отношение времени импульса τ{\displaystyle \tau } (когда функция не равна нулю) к периоду T{\displaystyle T}. Многие простейшие периодические функции достигают нуля лишь на бесконечно короткие мгновенья, и для них τ=T,D=1{\displaystyle \tau =T,D=1}.
- ↑ Ошибка в сносках?: Неверный тег
<ref>; для сносокDuszaне указан текст
Синус или меандр?
Cистемы автономного и бесперебойного питания, как правило, используются для обеспечения работы аппаратуры с питанием 220 В. В этом случае остро стоит вопрос обеспечения электропитания 220 В.
Как только речь заходит о мощности 220 В надо четко понимать, что существуют две единицы измерения мощности — ватты (Вт), и вольт-амперы (ВА).
1 Вт = 1.4 ВА или 1ВА = 0.7 Вт
Как правило, на блоках и инверторах указывают значения в вольт-амперах. Поэтому, чтобы получить значение максимальной мощности в Ваттах, эту величину надо поделить на 1,4. При этом мощность потребителя электроэнергии может быть указана в зависимости от типа прибора в любой из двух единиц. Скажем, обычная лампа накаливания имеет номинал в ваттах. Т.е. лампочку 100 Вт нельзя подключать к ББП или Инвертору с номиналом 100 ВА, а только не менее чем к 150 ВА.
Инверторы и Блоки бесперебойного питания (ББП) можно классифицировать по форме выходного напряжения — синус или модифицированный синус (меандр с паузами).Синус или меандр?
Большинство потребителей даже и не задумываются какова форма выходного напряжения данного прибора. А ведь большинство представленных на рынке приборов выдают не «чистый синус», а так называемый «модифицированный синус» (такие приборы гораздо дешевле «синусоидальных»).
Модифицированный синус — это приближения к синусоидальному сигналу с помощью сигналов «прямоугольной’» формы. Самое грубое, но простое приближение — это меандр — сигнал прямоугольной формы переменной полярности (рис. 1). Причем речь идет о передаче энергетики сигнала, т.е. о равенстве эффективного значения напряжения (площади под кривой напряжения). Как следствие, амплитуды двух сигналов — синуса и меандра отличаются. Чтобы получить Uэфф=220 В меандр должен иметь амплитуду 220 В, а синус имеет амплитуду 311 В.
На практике меандр не применяется, т.к. в момент резкой смены полярности возникают очень неприятные эффекты в аппаратуре. Применяют обычно меандр с паузой, или так называемый «модифицированный синус» (рис.2).
Более дорогие устройства используют более качественные приближения к синусу путем увеличения количества ступенек. На рис. 3 показан следующий уровень приближения. Увеличивая количество ступенек, мы постепенно получим сигнал, практически по своей форме мало отличающийся от синуса.
Чем синус лучше модифицированного синуса?
Существует аппаратура, для которой форма сигнала важна. Прежде всего, это аппаратура, чувствительная к помехам, аппаратура с трансформаторными источниками питания, электродвигатели, компрессоры и т.д. Есть потребители, которые нечувствительны к форме сигнала — это лампы накаливания, простые нагревательные приборы, приборы с бестрансформаторными импульсными источниками питания (компьютеры, современные телевизоры).
Что происходит, когда на трансформаторный источник питания подается модифицированный синус?
Резко снижается КПД трансформатора, в результате чего он начинает перегреваться и может выйти из строя. Кроме того, плохой (как правило, китайский подпольного производства) трансформатор начнет давать при работе посторонние звуки. Эта проблема не актуальна, когда мощность трансформатора заведомо существенно выше требуемой, но такие ситуации встречаются только в устройствах с очень малым потреблением (несколько ватт). Начиная с устройств, потребляющих 10 Вт трансформатор, как правило, оптимизирован, и использовать с такими потребителями прибор с модифицированным синусом не рекомендуется. Электродвигатели дают тот же эффект — снижение КПД, перегрев и посторонние звуки.
Не рекомендуют применять модифицированный синус для питания чувствительной аппаратуры (например, медицинской), т.к. модифицированный синус — верный источник помех.
Как определить форму выходного сигнала?
Конечно, прочитав паспорт. Если выходная форма синусоидальная, то производитель обязательно так и напишет. А фразы типа «квазисинус» или «модифицированный синус»указывают на несинусоидальную форму выходного сигнала. Иногда в паспорте указывается коэффициент гармоник. Если он меньше 8 %, то это почти идеальный синус.
Стоит заметить, что при одинаковой выходной мощности, цена преобразователя с синусом на выходе будет как минимум в 2 раза выше!
С покупкой обычного компьютерного UPS(источника бесперебойного питания) проблем нет — это проще сделать в любой компьютерной фирме. С хорошим мощным инвертором ситуация гораздо сложнее. Купить качественный прибор будет довольно непросто — очень мало фирм в России занимаются подобной техникой (одна из лучших — «Свободная Энергия»).
Хорошо налажено производство и поставки 220 В мощных инверторов, предназначенных для обеспечения питания систем связи, но удовлетворение очень высоких технических требований Минсвязи приводит к тому, что стоит подобная техника достаточно недешево.
| чистый синус | Квази-синус |
Автор: Яновский М.Г
Меандр (радиотехника) — Википедия
Материал из Википедии — свободной энциклопедии
Меа́ндр (по названию геометрического орнамента в виде ломаной линии) — периодический сигнал прямоугольной формы, широко используемый в радиотехнике и электронике. Меандр может быть знакопеременным (двухполярным) или однополярным. Во втором случае длительность импульса и длительность паузы между импульсами равны, то есть в этом случае меандр — периодический сигнал прямоугольной формы, имеющий скважность 2 (или коэффициент заполнения 0,5).
Аналитическое описание[ | ]
Математически меандр можно описать многими разными способами, например, через функцию сигнум:
- x(t)=sgn(sin(t)).{\displaystyle \ x(t)=\operatorname {sgn} (\sin(t)).}
Или через функции Хевисайда h(t){\displaystyle h(t)}:
- x(t)=∑n=−∞+∞(h[t−nT+12]−h[t−nT−12]).{\displaystyle \ x(t)=\sum _{n=-\infty }^{+\infty }\left(h\left[t-nT+{1 \over 2}\right]-h\left[t-nT-{1 \over 2}\right]\right).}
Для того, чтобы скважность равнялась 2 необходимо положить T=2.{\displaystyle T=2.}
И многими другими способами.
Спектр меандра[ | ]
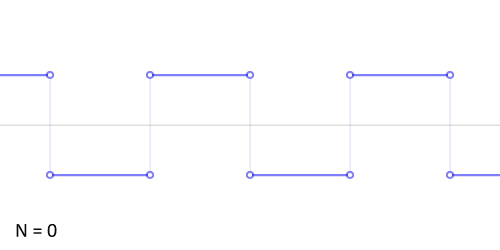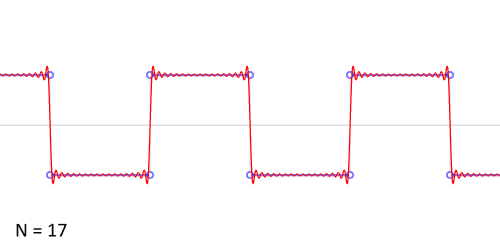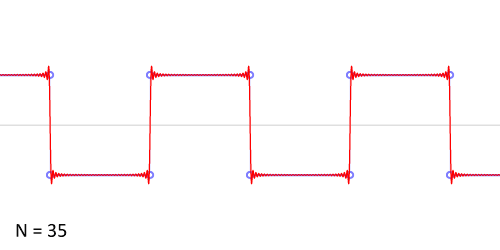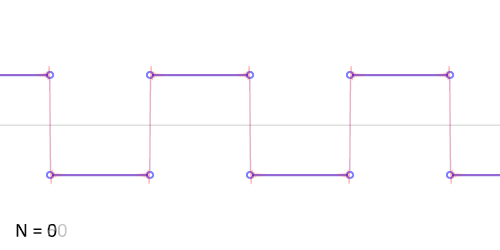Синтез меандра из набора гармоник периодического сигнала. Чем больше число гармоник, тем ближе к идеальной форма сигнала. Выбросы на фронтах обусловлены неравномерной сходимостью ряда Фурье в точках разрыва.Разложение меандра с нарастающим фронтом при t=0{\displaystyle t=0} в ряд Фурье дает:
- xмеандр(t)=4π∑k=1∞sin(2π(2k−1)ft)2k−1==4π(sin(2πft)+13sin(6πft)+15sin(10πft)+…).{\displaystyle {\begin{aligned}x_{\text{меандр}}(t)&={\frac {4}{\pi }}\sum _{k=1}^{
