Схема ФНЧ 2-го порядка по Баттерворду

Опубликовано: 28/10/2018Автор: Небесный Андрей

В радиотехнике регулярно возникает необходимость в использовании различных фильтров. Чаще других возникает необходимость в построении Фильтра Низких Частот (ФНЧ). Зачастую обходятся обычной RC-цепочкой. Но в некоторых случаях требуется более крутой спад частотной характеристики. Довольно универсальным можно назвать фильтр Баттерворда. Рассмотрим схему ФНЧ 2-го порядка.

Содержание статьи

1. Схема ФНЧ 2-го порядка
2. Формулы для расчета ФНЧ 2-го порядка
3. Расчет элементов ФНЧ 2-го порядка
4. Последний конденсатор
5. Вместо заключения

Схема ФНЧ 2-го порядка

В даташите на AD823 была найдена удобная для повторения схема ФНЧ второго порядка. С приведенными в даташите номиналами деталей R₁, R₂, C₁ и C₂ частота среза фильтра равна 200кГц.

АЧХ сигнала после фильтра приведена на следующей картинке:

Формулы для расчета ФНЧ 2-го порядка

Ребята из Analog Devices рекомендуют выбрать величину номинала резисторов, в пределах от 10 до 100кОм, а затем по приводимым формулам рассчитать емкости конденсаторов.

Стоящее в числителе число 1.414 это √2, а число 0.707, это 1/√2. Если поделить одно на второе получим, что емкость С₁ в два раза больше емкости С₂.

Это видно и из самих формул. Не знаю почему нельзя было привести формулу только для С₂ и написать что С₁=С₂*2. Выглядело бы это следующим образом.

В процессе углубления в тему фильтров было замечено, что большинство авторов начинают рассчет с того, что выбирают величину резистора, а затем рассчитывают величины емкостей.

Не знаю как у Вас, но у меня прецизионные конденсаторы не такое частое явление. По этой причине, на мой взгляд, проще взять за основу емкость имеющегося в наличии конденсатора и уже под него подобрать резисторы.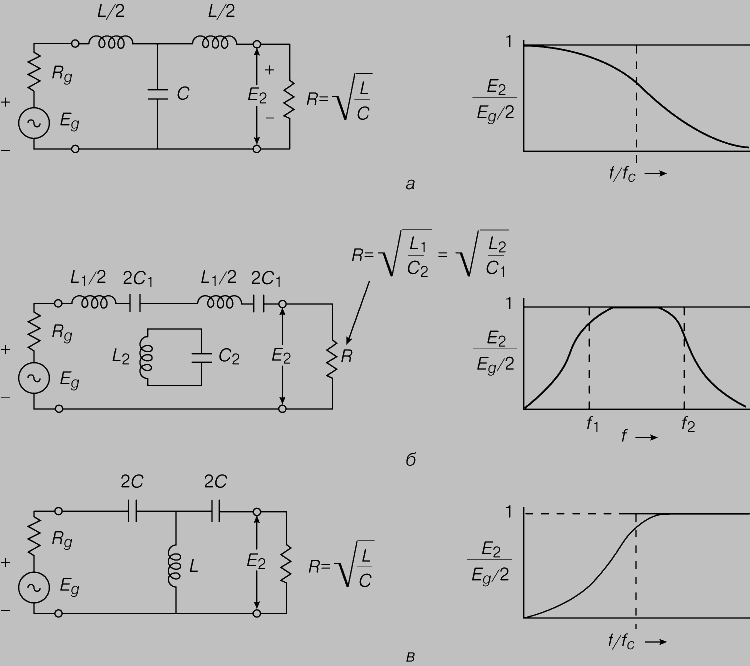

Для расчетов достаточно просто поменять местами R и C в формуле для C₂.

Расчет элементов ФНЧ 2-го порядка

В закромах родины были найдены конденсаторы на 82 пФ точностью 1%. Требовалась частота среза в 27 кГц. При расчетах величину конденсатора следует брать в фарадах, тогда величину резистора мы получим в Омах.

Подставляя нужные значения в переделанную формулу для С₂ находим нужную величину сопротивления.

Итак, получилось, что нужен резистор номиналом в 50849Ом. Отлично, это укладывается в рекомендуемый диапазон 10-100кОм. Самая близка величина резистора в стандартном ряду — 51кОм.

Теперь подсчитаем какой будет частота среза получившейся цепи с учетом выбора близкого резистора. Для подсчета f_cutoff наша формула будет выглядеть следующим образом:

Подставляем величины в формулу и проводим несложные расчеты.

Отлично! Думаю что ошибка в 0.3% и не ошибка вовсе. Тут точность номиналов элементов то +-1%.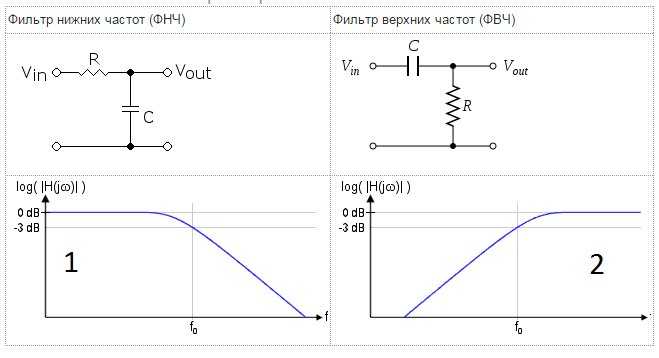

А что же делать с конденсатором C₁, где взять 162пФ? Для этого просто припаиваем два таких же конденсатора по 82 пФ параллельно.

Последний конденсатор

Обратите внимание, что на схеме так же присутствует конденсатор в 50пФ, включенный с выхода на землю. Можно считать, что этот конденсатор включен к инвертирующему входу усилителя и обеспечивает его привязку к  земле по переменке. Его я так же установил 82 пФ.

Отсутствие этого конденсатора может приводить к самовозбуждению ОУ. Особенно это актуально, если вы используете скоростные ОУ, например тот же AD823.

Вместо заключения

По хорошему, до и после фильтра желательно установить повторители, для развязки и согласованию по сопротивлениям. Это касается любого фильтра. Вопросу повторителей посвящена отдельная статья: Схема повторителя напряжение на ОУ. Мощный повторитель напряжения на TDA2030.

5.4 Расчёт фнч второго порядка с мос

На рис.  5.1 представлена схема фильтра нижних частот второго порядка с МОС. Для устранения шунтирования входа ОУ его полное входное сопротивление должно быть как минимум на порядок превосходить сопротивление R_экв, определяемое для данной схемы следующим образом:

.

Рис. 5.1. ФНЧ второго порядка с МОС

Частотная передаточная функция фильтра определяется выражением

,

где Y₁… Y₅ – проводимости соответствующих элементов фильтра (резисторов и конденсаторов). При этом .

Последняя формула является универсальной и может использоваться для расчета передаточной функции как ФНЧ, так и ФВЧ и ПФ.

После подстановки проводимостей Y₁,…,Y₅ и последующего преобразования выражения получаем

.

Используя приведенную формулу, можно проверить правильность расчета фильтра в любой программе, позволяющей выполнять математические расчеты, например, в Mathcad.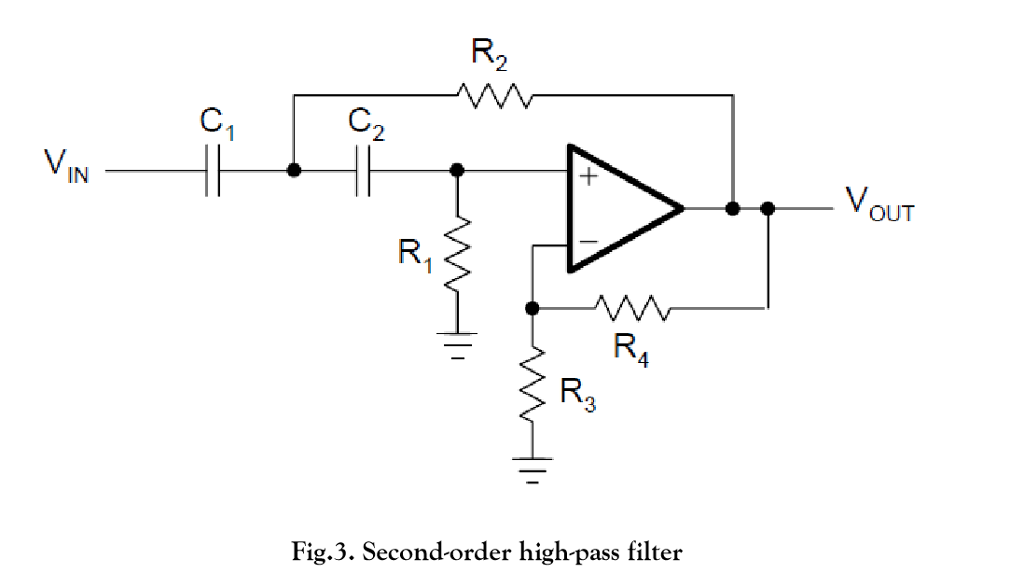

Для расчёта ФНЧ второго порядка или звена второго порядка фильтра Баттерворта или Чебышева более высокого порядка необходимо выполнить следующие действия.

1) Выбрать коэффициент усиления фильтра или звена K.

2) Из табл. 5.1…5.8 определить передаточную функцию фильтра или звена второго порядка, рассчитать пару комплексно-сопряжённых полюсов передаточной функции фильтра или звена и параметры, характеризующие пару полюсов: собственную нормированную частоту 

p, добротность Q_p и коэффициент затухания d_p.

3) Выбрать номинальное значение ёмкости С₁, близкое к значению

,

взятому в мкФ.

4) Выбрать номинальное значение ёмкости С₂, удовлетворяющее условию

.

Предпочтительным является наибольшее номинальное значение ёмкости.

5) Вычислить значения сопротивлений

,

,

.

6) Выбрать номинальные значения сопротивлений, наиболее близкие к вычисленным значениям и реализовать фильтр или звено второго порядка в соответствии с рис. 5.1.

На рис. 5.2 представлена схема ФНЧ на ИНУН второго порядка.

Рис. 5.2. ФНЧ на ИНУН второго порядка

Частотная передаточная функция фильтра определяется выражением

.

Для расчёта фильтра или звена второго порядка необходимо выполнить следующие действия.

1) Выбрать коэффициент усиления фильтра или звена K.

2) Из табл. 5.1…5.8 определить передаточную функцию фильтра или звена второго порядка, рассчитать пару комплексно-сопряжённых полюсов передаточной функции фильтра или звена и параметры, характеризующие пару полюсов: собственную нормированную частоту _p, добротность Q_p и коэффициент затухания d_p.

3) Выбрать номинальное значение ёмкости С

₂, близкое к значению

,

взятому в мкФ.

4) Выбрать номинальное значение ёмкости С₁, удовлетворяющее условию

.

Предпочтительным является наибольшее возможное номинальное значение.

5) Вычислить значения сопротивлений

а) Если K > 1

,

,

,

.

б) Если K = 1, то сопротивления R₁ и R₂ имеют значения, определённые в пункте а, сопротивление R₃ заменяется разомкнутой, а R₄

– короткозамкнутой цепью.

6) Выбрать номинальные значения сопротивлений как можно ближе к вычисленным значениям и реализовать фильтр или звено второго порядка в соответствии со схемой, показанной на рис.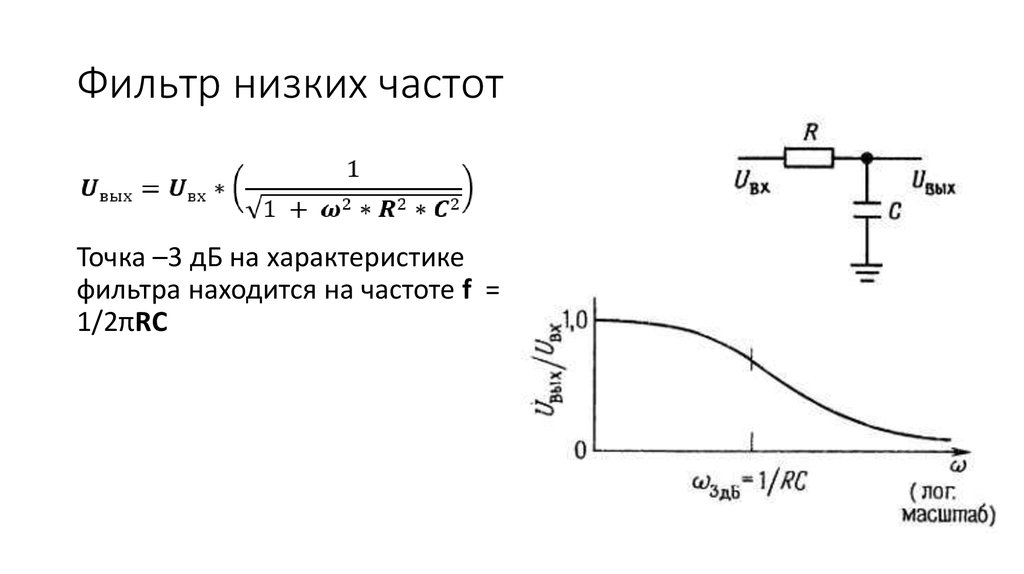 5.2.

Реализовать фильтр второго порядка — Simulink

Перейти к содержимому

Основное содержание

Реализовать фильтр второго порядка

Библиотека

Simscape / Electrical / Specialized Power Systems / Control / Filters

Описание

На основе выбранного в меню Тип фильтра Блок Second-Order Filter реализует следующую передачу функция:

ФНЧ:

H(s)=ωn2s2+2ζωns+ωn2

Фильтр верхних частот:

H(s)=s2s2+2ζωns+ωn2

Полосовой фильтр:

H(s)+ωn2+2ζωnss2

Полосовой режекторный фильтр:

H(s)=s2+ωn2s2+2ζωns+ωn2

s=оператор Лапласаωn=собственная частота; ωn=2πfnζ=коэффициент затухания (называется Zeta в меню блока)

Ключевые характеристики блока Second-Order Filter:

• N фильтров. Эта функция особенно полезна для разработки контроллеров. в трехфазных системах (N = 3).

• Состояния фильтра могут быть инициализированы для указанного DC и входы переменного тока.

• Позволяет вычислить и построить график отклика фильтра.

Параметры

Тип фильтра

Укажите тип фильтра: Lowpass , Highpass , Bandpass (по умолчанию 90), или Ленточная заглушка (выемка) .

Собственная частота fn (Гц)

Укажите собственную частоту фильтра в герцах. Этот значение должно быть скаляром или вектором. По умолчанию 120 .

Коэффициент демпфирования Zeta (Q = 1/(2*Zeta))

Укажите коэффициент демпфирования фильтра. Коэффициент демпфирования обычно значение от 0 до 1. По умолчанию

0,707 .

Коэффициент демпфирования связан с добротностью фильтра Q:

Q=12ζ

Для полосового или режекторного фильтра указана полоса пропускания 3 дБ по

BW=fnQ=2ζfn

Время выборки

Укажите время выборки блока в секундах. Установите от 0 до реализовать непрерывный блок. По умолчанию 0 .

Инициализировать состояния фильтра

Если этот флажок установлен, состояния фильтра инициализируются в соответствии с начальным входом

переменного тока и постоянного тока начальный ввод параметров. Выбрано значение по умолчанию.

Начальный вход переменного тока: [Mag, Phase (градусы), Частота (Гц) ]

Укажите величину начальной составляющей переменного тока на входе. сигнала, его фазы в градусах и частоты в герцах. По умолчанию [0, 0, 60] .

Когда входные данные векторизованы (N сигналов), задайте N-by-3 матрица, где каждая строка матрицы соответствует определенному входу.

Параметр AC начального ввода виден только когда фильтр Initialize указывает параметр выбран.

Начальный вход постоянного тока

Укажите значение начального постоянного компонента входного сигнала. Когда входной сигнал векторизован, задайте вектор 1 на N, где каждое значение соответствует определенному входу. По умолчанию 0 .

Параметр начального ввода постоянного тока виден только когда фильтр Initialize указывает параметр выбран.

График отклика фильтра

его диаграмма Боде (величина и фаза передаточной функции как функция частоты) нанесены на рисунок. Значение по умолчанию очищено.

Диапазон частот (Гц): [Start, End, Inc.]

Укажите диапазон частот для построения диаграммы Боде фильтра. Задайте вектор, содержащий начальную частоту, конечную частоту, и инкрементная частота в герцах. По умолчанию [0, 500, 1] .

Виден параметр Диапазон частот только когда параметр Plot filter response выбран.

Характеристики

Прямой ввод	Yes
Sample Time	Specified in the Sample Time parameter Continuous if Sample Time = 0
Scalar Expansion	Yes, of the parameters
States	Two states на фильтр
Размерный	Да

Примеры

Пример power_SecondOrderFilter показывает блок Second-Order Filter с использованием двух Тип фильтра параметр настройки ( Lowpass и Bandstop ).

Шаг расчета модели параметризуется переменной Ts (по умолчанию значение Тс = 50е-6). Чтобы симулировать непрерывные фильтры, задайте Ts = 0 в командном окне MATLAB ® перед запуском симуляции.

История версий

Представлено в R2013a

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .

Вы также можете выбрать веб-сайт из следующего списка:

Европа

Свяжитесь с местным офисом

• Пробная версия ПО
• Пробная версия ПО
• Обновления продукта
• Обновления продукта

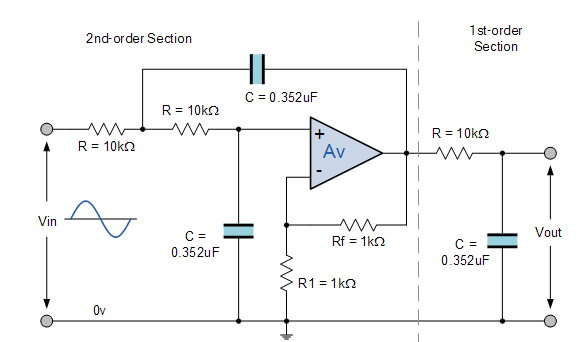
передаточная функция - Получение частоты среза пассивного фильтра нижних частот 2-го порядка

РЕДАКТИРОВАТЬ: Благодаря hryghr я вижу, что начальные предположения были неверными.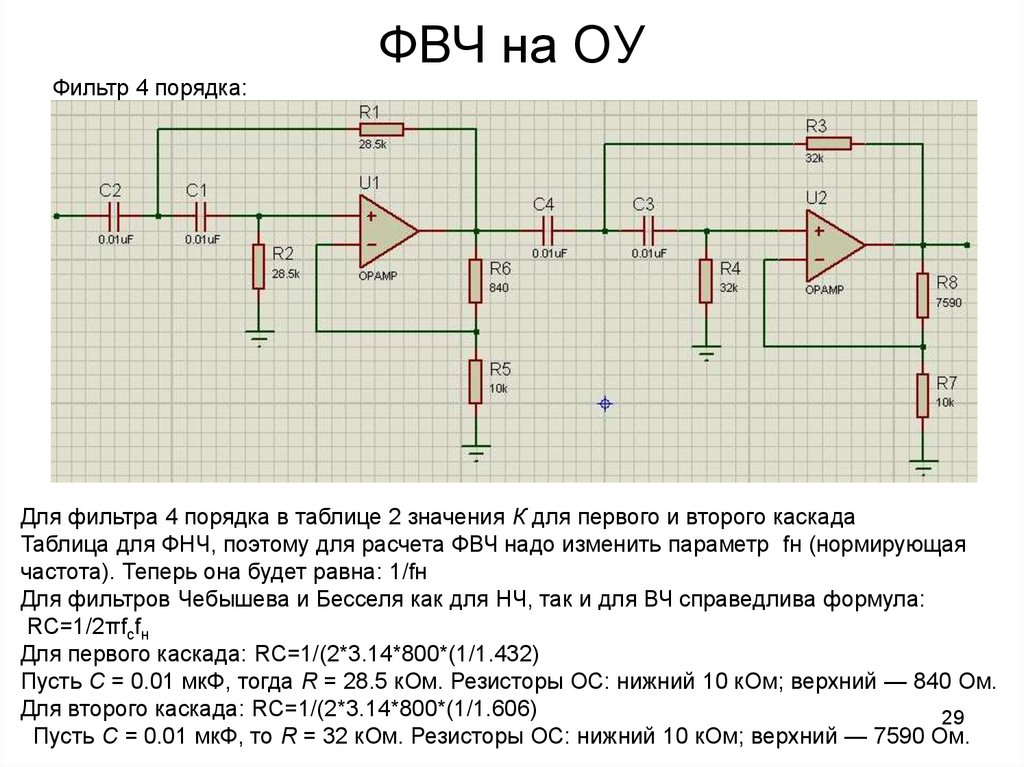 Величину передаточной функции нельзя найти так просто. Прошло более десяти лет с тех пор, как я считал свои навыки острыми в этом тема, а ножи в ящике не острее! Но я не могу что я разместил что-то формально неверное, так что вот попытка № 2:

Я получу передаточную функцию грязным способом .. используя Кирхгофа Текущее право (KCL) (очень общий метод). Я называю выходной узел \$V_{o}\$, а средний узел \$V_{x}\$. Для следующих уравнений я сократил запись на запись \$V_{o}\$ вместо более точного \$V_{o}(s)\$ :

I: KCL в \$V_{o}\$:

$$ \frac{V_{o}-V_{x}}{R_{2}}+sC_{2}V_{o}=0 $$

$$ V_{x}=V_{o}(1+sR_{2}C_{2}) $$ II: KCL в \$V_{x}\$:

$$ \frac{V_{x}-V_{i}}{R_{1}}+\frac{V_{x}-V_{o}}{R_{2}}+sC_{1}V_{x}=0 $$

Изменение условий:

$$ R_{2}(V_{x}-V_{i})+R_{1}(V_{x}-V_{o})+sR_{1}R_{2}C_{1}V_{x}=0 $$

Изменение условий:

$$ V_{x}(R_{1}+R_{2}+sR_{1}R_{2}C_{1})-R_{2}V_{i}-R_{1}V_{o}=0 $$

Замена \$V_{x}\$ на результат I: $$ V_{o}(1+sR_{2}C_{2})(R_{1}+R_{2}+sR_{1}R_{2}C_{1})-R_{2}V_{i}- R_{1}V_{o}+sR_{1}R_{2}C_{1}V_{o}=0 $$

Условия сбора для \$V_{o}\$

$$ V_{o}((1+sR_{2}C_{2})(R_{1}+R_{2}+sR_{1}R_{2}C_{1})-R_{1})=R_{ 2}В_{я} $$ 9{2}R_{1}R_{2}C_{1}C_{2}+s(R_{1}C_{1}+R_{1}C_{2}+R_{2}C_{2})+ 1} $$

Вероятно, это хорошее место для начала преобразования в стандартную форму, которая хигр упоминает.