Вектор, действия с векторами, сложение и вычитание

Тестирование онлайн

• Проекция вектора

• Сложение и вычитание векторов

Вектор

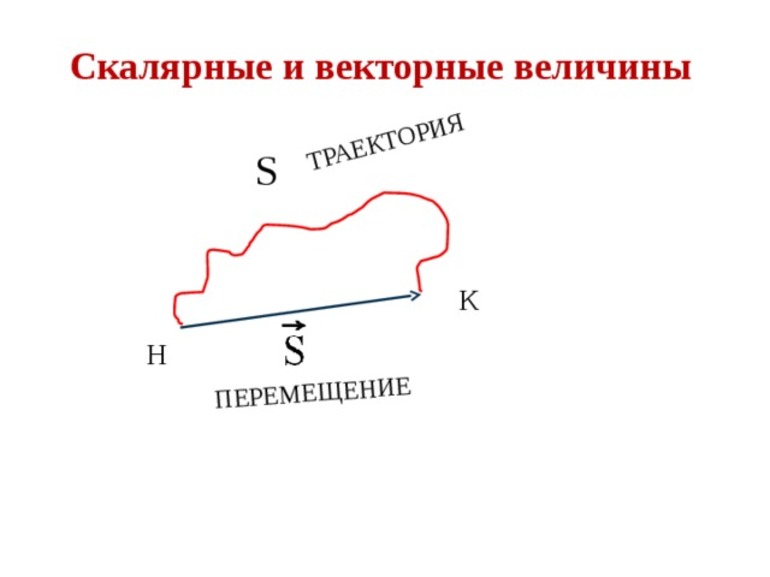
Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.

Если начало вектора совпадает с его концом, получим нулевой вектор.

Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.

На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону

Вектор -c — это вектор c, но противоположного направления. Тогда

Проекция вектора

Проекция вектора на ось имеет положительное значение в том случае, когда направление вектора совпадает с направлением оси. Отрицательное значение — в противоположном случае.

Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: s

x=x-x₀, на ось ОУ: s_y=y-y₀.

Рассмотрим примеры

Частные случаи, когда проекция на ось Ox или Oy нулевая.

Сумма составляющих вектора по осям равна данному вектору, т.е.

Сложение векторов

Правило параллелограмма: диагональ параллелограмма — сумма двух векторов с общим началом.

Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.

Рассмотрим правила на примерах.

Вычитание векторов

Вычитание векторов — это сумма положительного и отрицательного вектора.

Упражнения

Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?

Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?

Скалярные и векторные величины ☑️ определение, формулы, свойства и функции, обозначение, направление, действия над векторами, примеры применения в математике и физике

Особенности скалярных величин

Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:

• Чистые скаляры. Характеризуются числовым значением, не находящимся в зависимости от осей отсчета — линий пересечения плоских поверхностей в единой системе координат.
• Псевдоскаляры. Находятся при помощи расчета числа, знак которого зависит от положительного направления осей в системе координат.

В физике в список скалярных величин входят:

• Масса — определяет величину материи и ее гравитационные свойства. Измеряется в килограммах и обозначается буквой латинского алфавита m.
• Температура — средняя кинетическая энергия физического тела. Выражается в кельвинах или градусах Цельсия.
• Работа — мера действия силы на физическое тело или систему тел. Измеряется в Джоулях и обозначается латинской буквой A.
• Длина — величина, определяющая дистанцию между 2 концами тела в продольном направлении. Исчисляется в метрах. Особым видом длины является путь — скаляр, выражающий расстояние между начальным и конечным положением объекта, осуществляющего перемещение по заданной траектории.
• Время — продолжительность действия или события. Рассчитывается в секундах.
• Период — время совершения 1 полного колебания. Обозначается символом T и измеряется в секундах.
• Частота — величина, обратная периоду. Определяет количество полных колебаний в единицу времени. Рассчитывается в Герцах.
• Объем — скаляр, обозначающий размер пространства, ограниченного поверхностями со всех сторон. Измеряется в м³.
• Напряжение — измеряет изменение потенциальной энергии тела, приходящейся на единицу заряда. Обозначается буквой U и рассчитывается в Вольтах.
• Сила тока — скаляр, показывающий число электрических зарядов, проходящих через сечение проводника в единицу времени. Обозначается символом I и рассчитывается в Амперах.
• Энергия — обозначает способность тела осуществлять работу.

Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом.

Определение положительного скаляра и его измерения

Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.

Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).

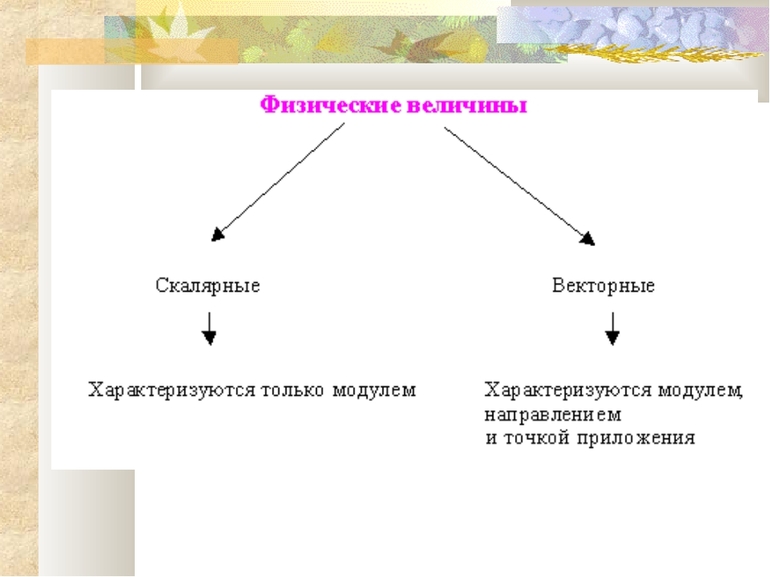
Особенности векторных величин

Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением». Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.

В физике и математике примерами векторных величин являются:

• Сила — мера взаимодействия физических веществ. Обозначается латинской буквой F и измеряется в Ньютонах. Три закона Исаака Ньютона составляют основу классической механики. С их помощью можно определить массу тела и его ускорение.
• Скорость — расстояние, пройденное материей за определенный временной промежуток. Маркируется символом V и рассчитывается в м/с. Скорость используется для определения пути и времени движения предмета при помощи формулы: S = V * t. Скорость, с которой тело движется по окружности, называется линейной.
• Ускорение — величина, показывающая изменение показателей скорости физического тела. Ускорение свободного падения действует на все тела, придавая им силу тяжести. Оно направлено к ядру Земли и равняется 9,8 м/с²
• Импульс — характеризует величину движения тела. Маркируется буквой латинского алфавита p и рассчитывается в кг*м/с. С помощью этой величины человек может определить массу физического тела и скорость ее передвижения.

На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе.

Свойства векторов

Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью.

Свойства проекции:

• Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
• Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
• Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.

Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными.

Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.

Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината. Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.

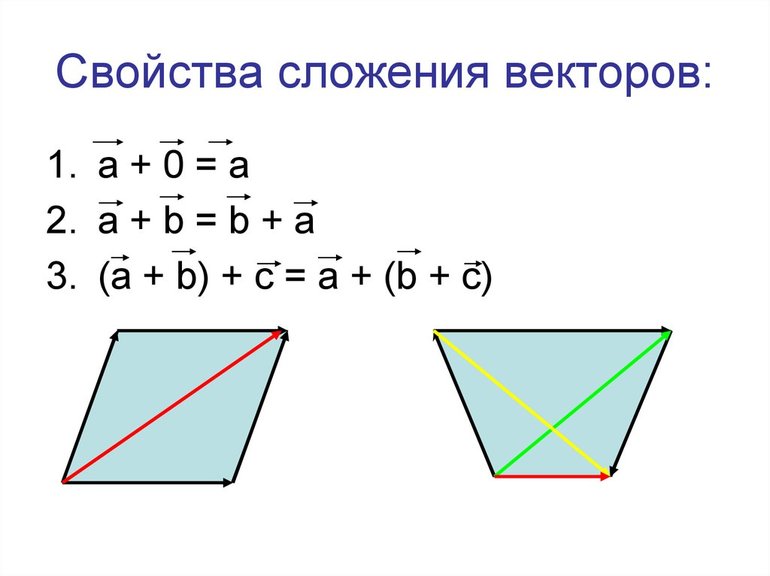
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.

Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.

Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.

С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.

Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.

Проектная работа. Вектор. 9 класс

МБОУ Одинцовская гимназия №13

Проектная работа по теме

‘’Векторы’’

Выполнили ученики 9А класса

Кононова Дарья,

Горбунова Полина,

Зотов Анатолий.

Руководитель учитель математики

Владимирова Л.М.

Одинцово

2018

Содержание

Введение

1. История возникновения.

2. Что такое вектор и действия над векторами.

3. Векторы в геометрии, в физике, в других науках.

4. Векторы в повседневной жизни.

5. Заключение.

6. Список литературы

Введение

С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор.

Далее, в процессе работы над данным проектом, Мы приведём ещё интересные примеры с векторами.

Вообще, мы считаем, что математика – это интереснейшая наука, в познании которой нет границ.

Мы выбрали тему о векторах не случайно, нас очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, мы думаем, что эта тема весьма актуальна. В физике, химии, психологии, биологии, экономике и многих других науках употребляют понятие «вектор».

Цель проекта – подготовить раздел школьной энциклопедии «Вектор».

Задачами данного проекта являются:

— познакомить с историей возникновения понятия «вектор»;

— дать понятие –вектор, продемонстрировать действий над векторами;

— показать применение векторов в решении задач по геометрии и физике;

— научить видеть необычное в обычном;

— выработать внимательное отношение к окружающему миру.

1. История возникновения понятия «вектор».

Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а также в технике.

Вектор относительно новое математическое понятие.

Интуитивно вектор понимается как объект, имеющий величину, направление и точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831).

Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа.

Гамильтону принадлежат и термин «скаляр», он определил в качестве операций над новыми объектами скалярное и векторное произведение.

Гибсс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.

Образ Гиббса запечатлён в «Галерее славы великих американцев». Его имя присвоено многим величинам и понятиям химической термодинамики: энергия Гиббса, парадокс Гиббса, правило фаз Гиббса, уравнения Гиббса — Гельмгольца, уравнения Гиббса — Дюгема, лемма Гиббса, треугольник Гиббса — Розебома и др.

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками.

2. Понятие вектор

Ве́ктор (от лат. vector, «несущий») — в простейшем случае математический объект, характеризующийся величиной и направлением. В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом^[1].

Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними. Другой распространённый способ записи: выделение символа вектора жирным шрифтом.

Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий).

Длина вектора –  это и есть длина этого отрезка. Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Виды векторов.

Единичным называется вектор, длина которого равна 1. Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором. У такого вектора конец и начало совпадают. Нулевой вектор обычно обозначается как 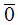. Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются сонаправленными векторами только тогда, когда их направления совпадают друг другу (направлены в одну сторону): a↑↑b

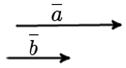
Противоположно направленные вектора – два коллинеарных вектора a и b называются противоположно направленными векторами, только когда они направлены в разные стороны: a↑↓b.

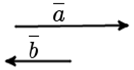
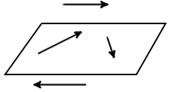
Компланарные вектора – это те вектора, которые параллельны одной плоскости или те, которые лежат на одной плоскости. С компланарными векторами мы встретимся в 10-11 классах.

Равные вектора. Вектора a и b будут равными, если они будут лежать на одной либо параллельных прямых и их направления и длины одинаковые. То есть, такой вектор можно перенести параллельно ему в каждое место плоскости. Таким образом, два вектора равны, если они коллинеарные, сонаправленые и имеют одинаковые длины:

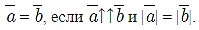
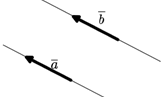
Действия над векторами.

Сумма векторов

Суммой векторов: , …называется вектор, получающийся после ряда последовательных сложений: к вектору прибавляется вектор , к полученному вектору прибавляется вектор и так далее.

= + + +

Это правило многоугольника или правило цепи, которое формулируется из правила треугольника. Из произвольного начала О откладываем вектор 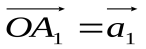, из точкиА₁, как из начала, откладываем вектор 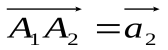, из точкиА₂ строим вектор 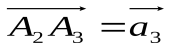и так далее. Вектор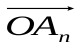есть сумма векторов.

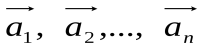Теорема. Для любых векторов , справедливы равенства:

1)  + = + (переместительный закон).

2)  ( + ) + = + ( + ) (сочетательный закон)

Эти законы сложения векторов позволяют нам находить сумму векторов в любом удобном порядке.

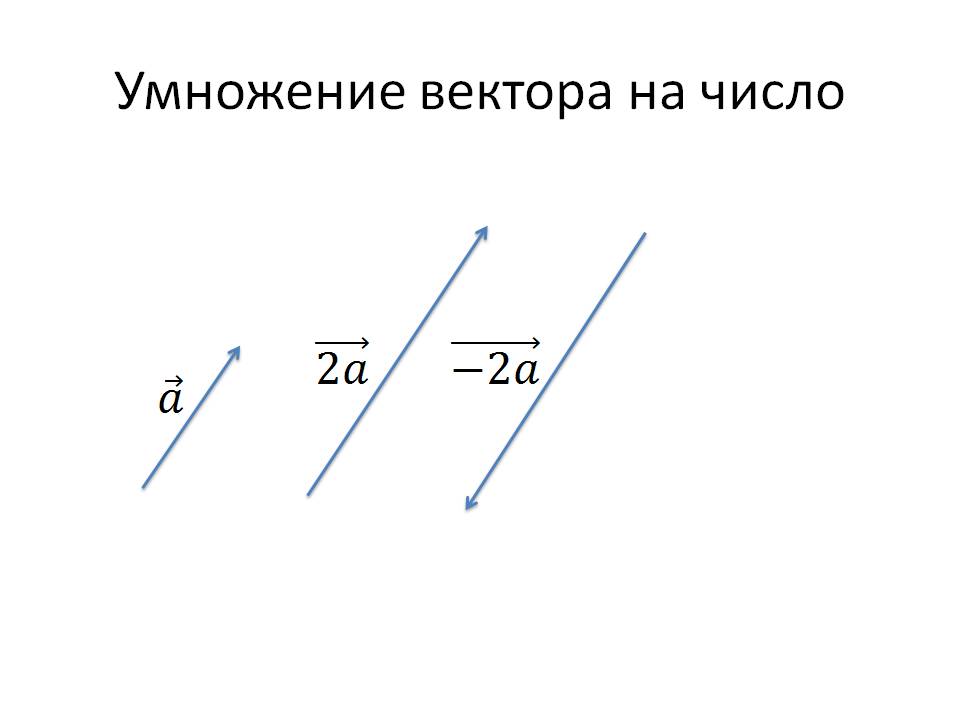
Умножение вектора на число

Для векторов существует три вида умножения векторов: скалярное и векторное произведение двух векторов и смешанное произведение трех векторов. Результатом первого и последнего есть число, а результатом векторного произведения – вектор.

Векторы в геометрии.

В геометрии под векторами понимают направленные отрезки. Эту
интерпретацию часто используют в компьютерной графике, строя карты освещения, с помощью нормалей к поверхностям. Так же с помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов, а также объёмы тел: тетраэдра и параллелепипеда. Иногда с вектором отождествляют направление.

Скалярным произведением  векторов и  называется число, равное произведению длин этих векторов на косинус угла между ними: · = ·cos . Если один из векторов нулевой, то скалярное произведение равно нулю.

Таким образом, длина (модуль) произведения векторов численно равна площади параллелограмма, построенного на векторах a и b

|= | | || sin ()

Смешанное произведение векторов называется скалярное произведение вектора на векторное произведение векторов и

Геометрический смысл смешанного произведения — модуль смешанного произведения численно равен объему параллелепипеда, образованного векторами ,.

Перечисленные выше свойства векторных операций во многом похожи на свойства сложения и умножения чисел. В этом состоит удобство векторных операций: вычисления с векторами выполняются по хорошо известным правилам. В то же время вектор – геометрический объект, и в определении векторных операций используются такие геометрические понятия, как длина и угол; этим и объясняется польза векторов в геометрии (и её приложений к физике и другим областям знания).

Однако для решения геометрических задач с помощью векторов необходимо прежде всего научиться «переводить» условие геометрической задачи на векторный «язык». После такого «перевода» осуществляются алгебраические вычисления с векторами, а затем полученное векторное решение снова «переводится» на геометрический «язык». В этом и состоит векторное решение геометрических задач.

C помощью векторов решаются задачи геометрии. Многие задачи не могли бы решаться иначе, либо решение их было очень затруднительным.

Приведём примеры некоторых из них:

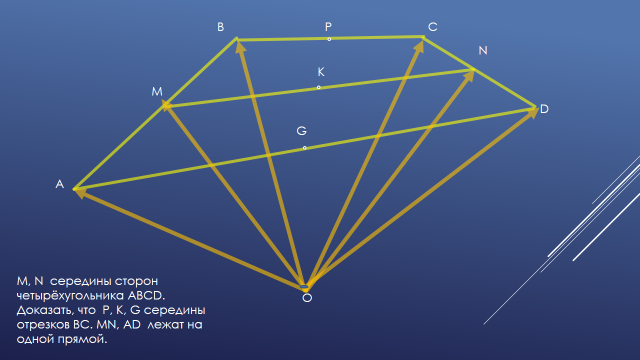
Задача №1 В четырёхугольнике ABCD точки M и N – середины сторон АВ и CD.

Доказать, что середины P, K, G – отрезков BC,MN, AD лежат на одной прямой.

Задача №2 Найти угол, лежащий против основания равнобедренного треугольника, если медианны, проведённые к боковым сторонам, взаимно перпендикулярны.

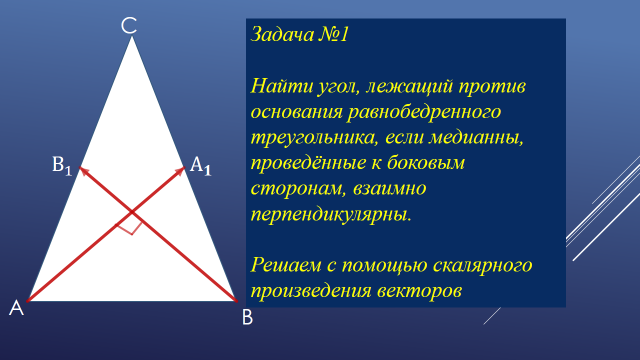
Задача №3 Дан равнобедренный треугольник МКN. Из вершины К проведена высота КР. Из вершин М и N проведены медианы MF и NE. КР =80, MN = 40. Найти MF и NE.

Маргарита Алигер, биография которой вызывает искренний интерес у поклонников ее творчества, – знаменитая советская поэтесса, удостоившаяся Сталинской премии второй степени за поэму «Зоя» о бесстрашном подвиге советской девушки Зои Космодемьянской. После семилетки училась в химическом техникуме. С детства писала стихи.

Векторы в физике.

О, физика, наука из наук!
Все впереди!
Как мало за плечами!
Пусть химия нам будет вместо рук,
Пусть станет математика очами.
Не разлучайте этих трех сестер,
Познания всего в подлунном мире.
Тогда лишь будет ум и глаз остер,
И знанье человеческое шире.

Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей.

Герман Грассман

Немецкий физик, математик и филолог. (1809-1877)

В области физики Грассману принадлежат работы по акустике и магнитному взаимодействию токов. Общие идеи Грассмана об абстрактных векторных пространствах привели его к открытию
важного положения – возможности рассматривать цветовые ощущения как трехмерные векторы, что лежит в основе современного учения о цвете. (Чёрный цвет имеет координаты (0,0,0), каждому цвету можно поставить в соответствие координаты точки трёхмерного пространства.
Интерпретация вектора, как параллельного переноса, позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного

применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число.

Джеймс Клерк Максвелл — английский физик, создатель классической электродинамики, один из
основоположников статистической физики, выдвинул идею электромагнитной природы света, установил первый статистический закон — закон распределения молекул по
скоростям, названный его именем. Альберт Эйнштейн однажды сказал, что » работа Джеймса клерка Максвелла изменила мир навсегда. «Действительно, Максвелл предоставил первую цветную фотографию и заложил основу для будущего развития телевизионных, радиолокационных, микроволновых и инфракрасных технологий.
Но в каждом учебном предмете вектор рассматривается так, как это удобно для изучаемого вопроса, но суть – одна.

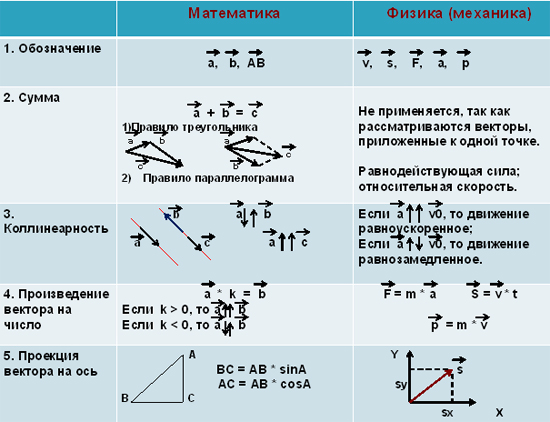
Проведём сравнительный анализ понятия “вектор” и действий над векторами в математике и физике.

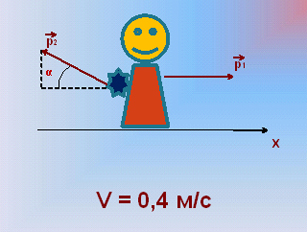
Задача №1

Мальчик массой 50 кг, стоя на гладком льду, бросает груз массой

8 кг под углом 60⁰ к горизонту со скоростью 5 м/с. Какую скорость приобретет мальчик?

Задача №2

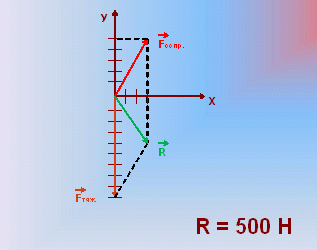
На парашютиста массой 90 кг в начале прыжка действует сила сопротивления воздуха, проекции которой на оси координат Х и Y равны 300 Н и 500 Н. Найти равнодействующую всех сил.

Заключение

Векторы всюду.

Вектор используются везде, даже там, где мы их не замечаем, например в литературе: вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу равна нулю. А сила, как известно, векторная величина.

В химии. Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца. Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее, основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».

Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы. Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

Векторы в экономике

Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора. Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.

Векторы в психологии

На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов. Системно-векторная психология позиционируется не как отрасль классической психологии или определенное течение, а как отдельная наука изучения типологии личности. 

Вектор – это симбиоз физиологических и психологических качеств человека. Это — характер, темперамент, здоровье, привычки индивида.

Векторы в повседневной жизни

Мы обратили внимание, что векторы, помимо точных наук, встречаются нам каждый день, т.е. повседневно. Векторы – указатели, которые помогают нам быстро найти тот или иной объект, отдел и сэкономить время, или стрелки дорожных знаков.

Базовое понятие «вектор», рассмотренное нами на уроках геометрии в 9 классе, является основой для изучения, а главное понимания других школьных предметов: физики, химии, биологи, экономики. Мы считаем, что этот раздел математики очень пригодится тем, кто планирует получать образование в любой профессии.

Выводы.

1. Векторы необходимы нам для изучения не только математики, но и других наук.

2. Каждый образованный человек должен знать, что такое вектор, потому что сталкивается с этим понятием не только во время учёбы, но и в повседневной жизни.

 Список литературы:

• Учебник Геометрия 7-9 авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев, Е.Г. Позняк, И.И. Юдина; издательство «Просвещение» 2016

• Геометрия: задачи на готовых чертежах для подготовки к ГИА и ЕГЭ: 7-9/Э.Н. Балаян. Изд. 7-е –Ростов н/Д; Феникс, 2015.

• Энциклопедический словарь юного математика для среднего и старшего школьного возраста.

Составитель А.П. Савин.- М.: Педагогика,, 1985.-352 с.,ил.

Физика 9 кл. Вектор. Проекция вектора на координатную ось

Физика 9 кл. Вектор. Проекция вектора на координатную ось

О векторных величинах

1. Какая величина называется векторной (или просто вектором)?

Физическая величина, которая характеризуется не только числовым значением (модулем), но и направлением, называется векторной величиной (или просто вектором).
Для векторной величины одинаково важны числовое значение (модуль) и направление.

Примеры векторных величин:

— скорость,
— перемещение,
— сила.

2. Какая величина называются скалярной (или просто скаляром)?

Величины, которые не имеют направления и задаются только числом, называются скалярными величинами или скалярами.

Примеры скалярных величин:

— число книг на полке,
— длина карандаша,
— высота комнаты.
Модуль вектора — тоже скаляр.

3. Как изображают векторную величину?

Векторную величину изображают в виде стрелки, которая начинается в некоторой точке и заканчивается острием, указывающим направление..
Такой отрезок-стрелка называется вектором.
Длина стрелки в выбранном масштабе выражает модуль векторной величины.

Векторы обозначают буквами со стрелкой над ними.
Такой же буквой, но без стрелки обозначают модуль вектора.

4. Если два вектора равны друг другу по модулю, но направления векторов различны, то можно ли сказать, что эти векторы равны друг другу?

Нет, нельзя.
Равными считаются векторы, у которых одинаковы и модули, и направления.

5. Чем отличается векториая величина от скалярной?

Векторная величина характеризуется модулем (величиной) и направлением, а скалярная величина — только модулем.
Вектор имеет направление, а скаляр не имеет направления.

 

Проекция вектора на координатную ось

1. Как построить проекцию вектора на координатную ось?

Есть вектор а.
Опустим из точки А (начало вектора) и точки В (конец вектора) перпендикуляры на ось ОX.
Получим на оси точки х_а и х_в — это проекции точек А и В на ось ОX.
Длину отрезка х_а-х_в между проекциями начала и конца вектора называют проекцией вектора а на ось ОX и обозначают, как а_х.
Проекцию вектора на ось обозначают той же буквой, что и вектор, но без стрелки и с индексом оси.
Проекция вектора — величина скалярная.

2. Если вектор перемещения параллелен координатной оси, то чему равен модуль проекции вектора на эту ось?

Если вектор параллелен оси координат, то модуль его проекции ( |a_x| ) равен модулю ( a ) самого вектора.

3. Что называют проекцией вектора на координатную ось?

Длину отрезка на координатной оси между проекциями начала и конца вектора, взятую со знаком « + » или « —», называют проекцией вектора а на координатную ось.

3. Когда проекция вектора на ось будет положительной, а когда — отрицательной?

Проекция вектора на координатную ось может быть, как положительной, так и отрицательной.

Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью.
Проекция вектора на ось считается отрицательной, если вектор направлен противоположно оси.

Если вектор перпендикулярен координатной оси, то при любом направлении вектора его проекция на ось равна нулю.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

9_физ_1(векторы)

2015-2016 уч. год, №1, 9 кл. Физика. Векторы в физике (вводное задание)

Одну из граничных точек вектора называют его началом, а другую – концом. Направление вектора задаётся от начала к концу, причём на чертеже конец вектора отмечают стрелкой. Начало вектора называют также точкой его приложения. Если точка A является началом вектора a ? то мы будем говорить, что вектор a приложен в точке A (рис. 2).

a
A
Рис. 2	Рис. 3	Рис. 4

Число, выражающее длину направленного отрезка, называют модулем вектора и обозначают той же буквой, что и сам вектор, но без стрелки наверху, например: модулем вектора v является число v. Ча-

сто для обозначения модуля вектора прибегают к помощи знака абсо-

лютной величины и пишут, например, v или F .

Вектор называется нулевым, если его начало и конец совпадают. Нулевой вектор не имеет определённого направления и его длина (модуль) равна нулю.

Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Так, например, на рис. 3 векто-

ры a, b и c коллинеарны.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

На рис. 4 слева изображены неравные векторы a и f , g и h, а справа – равные векторы p и q. Точка приложения геометрического

вектора a может быть выбрана произвольно. Мы не различаем двух равных векторов, имеющих разные точки приложения и получающихся один из другого параллельным переносом. В соответствии с этим векторы, изучаемые в геометрии, называют свободными (они определены

сточностью до точки приложения).

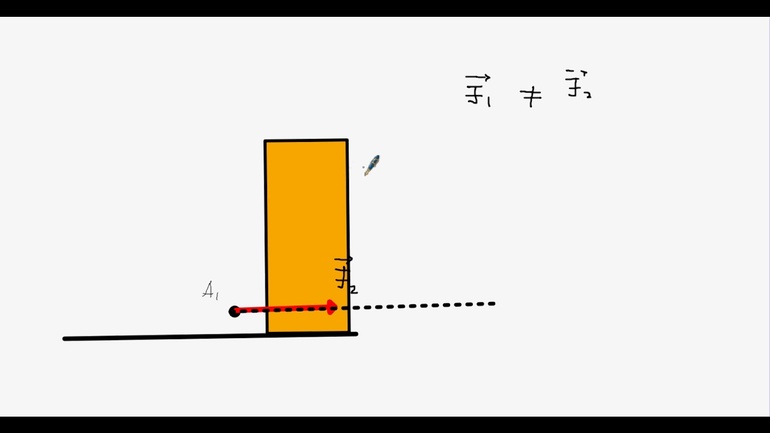
Вфизике точка приложения вектора иногда имеет принципиальное значение. Достаточно вспомнить рычаг: две равные по модулю силы, направленные в одну и ту же сторону, производят на рычаг разное действие, если плечи сил не равны друг другу. И всё же сами силы равны друг другу! Бывают и случаи, когда вектору трудно приписать конкретную точку приложения. Например, если одна система отсчёта дви-

жется относительно другой со скоростью v , то какой точке приписать эту скорость? – Всем точкам движущейся системы!

2015, ЗФТШ МФТИ, Чугунов Алексей Юрьевич Лукьянов Андрей Александрович

Вектор (математика и физика) — Vector (mathematics and physics)

В математике и физике , вектор является элементом векторного пространства .

Для многих конкретных векторных пространств, векторы получили конкретные имена, которые перечислены ниже.

Исторически сложилось, что векторы были введены в геометрии и физике ( как правило , в механике ) до формализации понятия векторного пространства. Поэтому, часто говорит о векторах без указания векторного пространства , к которому они принадлежат. В частности, в евклидовом пространстве , один рассмотреть пространственные векторы , также называемые евклидовы векторы , которые используются для представления величин , которые имеют как величину и направление, и могут быть добавлены и масштабированные (который умножается на действительное число ) для формирования векторного пространства.

Векторы в евклидовой геометрии

В классической евклидовой геометрии (т.е. в синтетической геометрии ), векторы были введены ( в течение 19 — го века) в качестве классов эквивалентности при равносильности , из упорядоченных пар точек; две пары ( А , В ) и ( С , D ) быть равносильна если точки , В , D , С , в таком порядке, образуют параллелограмм . Такой класс эквивалентности называется вектор , точнее, евклидовой вектор . Класс эквивалентности ( , Б ) часто обозначаетсяAВ→,{\ Displaystyle {\ overrightarrow {AB}}.}

Евклидово вектор , таким образом , субъект , наделенный величины (длина отрезка ( , Б ) ) и направление (направление от к B ). В физике, евклидовы векторы используются для представления физических величин , которые имеют как величину и направление, но они не расположены в определенном месте, в отличии от скаляров , которые не имеют направления. Так , например, скорость , сила и ускорения представлены векторами.

В современной геометрии, евклидовы пространства часто определяются из линейной алгебры . Точнее, евклидово пространство Е определяется как набор , к которому сопоставляется внутреннее пространство продукта конечной размерности над полем действительных чисел и действия группы в аддитивную группу из которой является свободным и транзитивным (см аффинное пространство для деталей этой конструкции) , Элементы называются переводы . Е→,{\ Displaystyle {\ overrightarrow {E}}}Е→,{\ Displaystyle {\ overrightarrow {E}}}Е→{\ Displaystyle {\ overrightarrow {E}}}

Было доказано, что эти два определения евклидовых пространств эквивалентно, и что классы эквивалентности под равносильностью может быть идентифицированы с переводами.

Иногда векторы евклидовых рассматриваются без ссылки на евклидово пространства. В этом случае евклидово вектор является элементом нормированного векторного пространства конечной размерности над полем действительных чисел, или, типично, элемент оснащены скалярным произведением . Это имеет смысл, так как добавление в таком векторном пространстве свободно и транзитивно действует на самом векторном пространстве. То есть, есть евклидово пространство, с собой в качестве ассоциированного векторного пространства, а скалярное произведение в качестве внутреннего продукта. рN{\ Displaystyle \ mathbb {R} ^ {п}}рN{\ Displaystyle \ mathbb {R} ^ {п}}

Eucidean пространство часто представляется как в евклидовом пространстве размерности п . Это вызвано тем , что каждый евклидово пространства размерности п является изоморфно к евклидову пространства Более точно, при таком евклидове пространства, можно выбрать любую точку O в качестве происхождения . По процессу Гр-Шмидт , можно также найти ортогональный базис ассоциированного векторного пространства (базис такого , что скалярное произведение двух базисных векторов равно 0 , если они различны , и 1 , если они равны). Это определяет декартовы координаты любой точки Р пространства, как координаты на этой основе вектора Эти выборы определяют изоморфизм данного евклидова пространства на , отображая любую точку в п -uple его декартовых координат, и каждый вектор в его координаты вектора . рN{\ Displaystyle \ mathbb {R} ^ {п}}рN,{\ Displaystyle \ mathbb {R} ^ {п}.}Оп→,{\ Displaystyle {\ overrightarrow {OP}}.}рN,{\ Displaystyle \ mathbb {R} ^ {п}}

Конкретные векторы в векторном пространстве

• Нулевой вектор (иногда называемый нулевой вектор ), то идентичность добавка в векторном пространстве. В нормированном векторном пространстве , это единственный вектор нулевой нормы. В евклидове векторного пространства , это единственный вектор нулевой длины.
• Базисный вектор , элемент данной основы векторного пространства.
• Единичный вектор , вектор в нормированном векторном пространстве, норма 1, или евклидовой вектор единичной длины.
• Изотропный вектор или нулевой вектор , в векторном пространстве с квадратичной форме , вектор ненулевой , для которого форма равна нулю. Если нулевой вектор существует, то квадратичная форма сказала изотропной квадратичной форма .

Векторы в конкретных векторных пространствах

• Вектор — столбец , матрица только с одной колонкой. Векторы столбцов с фиксированным числом строк образуют векторное пространство.
• Вектор — строка , матрица только с одной строкой. Векторы строк с фиксированным числом столбцов образуют векторное пространство.
• Координаты вектора , то п -uple из координат вектора на основе из п элементов. Для векторного пространства над полем Р , этот п -uples образует векторное пространство (где операция являются точечно сложение и умножение).FN{\ Displaystyle F ^ {п}}
• Смещение вектора , вектор , который определяет изменение положения точки относительно предыдущей позиции. Водоизмещение векторы принадлежат векторному пространству переводов .
• Позиция вектор точки, вектор смещения от опорной точки (называется происхождение ) до точки. Вектор положения представляет собой положение точки в евклидове пространства или аффинном пространстве .
• Скорость вектор , производная, в отношении времени, вектор положения. Это не зависит от выбора начала координат, и, таким образом , относится к векторному пространству переводов.
• Псевдовекторные , называемые также аксиальный вектор , элемент из двойных векторного пространства. В внутреннем пространстве продукта , скалярное произведение определяет изоморфизм между пространством и его сопряженным, что может сделать трудно отличить вектор псевда из вектора. Различие становится очевидным , когда один изменяет координату: матрица используется для изменения координат псевдовекторов является транспонированной из этого векторов.
• Касательный вектор , элемент касательного пространства в виде кривой , на поверхности или, более общо, дифференциальное многообразие в данной точке (эти касательные пространства естественным образом наделены структурой векторного пространства)
• Нормальный вектор или просто нормально , в евклидовом пространстве , или, в более общем случае , во внутреннем пространстве продукта, вектора, перпендикулярной к касательной в точке. Нормалей псевдовекторами , которые принадлежат к двойственной касательного пространства.
• Градиент , координаты вектор частных производных функции нескольких действительных переменных . В евклидовом пространстве градиент дает величину и направление максимального повышения скалярного поля . Градиент является псевдо вектор , который является нормальным к кривой уровня .
• Четыре-вектор , в теории относительности, вектор в четырехмерном вещественном векторном пространстве , называемом пространстве Минковского

Кортежи, которые на самом деле не векторы

Набор из кортежей из п действительных чисел имеет естественную структуру векторного пространства , определяемого покомпонентного сложения и скалярного умножения . Когда такие кортежи используются для представления некоторых данных, то их принято называть векторы , даже если сложение векторов ничего для этих данных, которые могут сделать терминологию в заблуждении не значит. Кроме того , некоторые физические явления связаны направление и величину. Они часто представлены векторами, даже если операции векторных пространств не применяются к ним. рN{\ Displaystyle \ mathbb {R} ^ {п}}

• Вращение вектора , А евклидова вектор , направление которого является то , что оси вращения и величины является угол поворота.
• Дарбоукс вектор , поверхностна вектор скорости Френе рамки пространственной кривой
• Вектор Бюргерса , вектор , который представляет собой величину и направление искажения решетки дислокаций в кристаллической решетке
• Лаплас-Рунг-Ленца вектор , вектор используется , главным образом , для описания формы и ориентации орбиты астрономического тела вокруг другого
• Интервальный вектор , в музыкальной теории множеств, массив , который выражает содержание интервального набора высоты тона класса
• Вектор Пойнтинга , в физике, вектор , представляющий плотность потока энергии в электромагнитном поле
• Вероятность вектор , в статистике, вектор с неотрицательными элементами , которые в сумме единицу.
• Случайный вектор или многомерная случайная величина , в статистике , множество реальных -значная случайных величин , которые могут быть соотнесены . Тем не менее, случайный вектор может также относиться к случайной переменной , которая принимает значения в векторном пространстве.
• Вектор отношение , бинарное отношение определяется логическим вектором.
• Волновой вектор , представление эволюции локальной фазы волны

Векторы в алгебрах

Каждая алгебра над полем является векторным пространством, а элементы алгебры , как правило , не называются векторами. Однако, в некоторых случаях они называются векторами , в основном по историческим причинам.

• Вектор кватернионы , кватернионы с нулевой действительной частью
• Поливектор или р -векторный , элемент внешней алгебры векторного пространства.
• Спиноры , называемые также спиновые векторы были введены для расширения понятия вектора вращения . В самом деле, векторы вращения представляют также вращение локально , но не во всем мире, так как замкнутый контур в пространстве векторов вращения может вызвать кривую в пространстве вращений, которое не является петлей. Кроме того , многообразие векторов севооборота ориентируема , в то время как многообразие вращений нет. Спиноры элементы векторного подпространства некоторой алгебры Клиффорда .
• Витт вектор , бесконечная последовательность элементов коммутативного кольца, которое принадлежит к алгебре над этим кольцом , и был введено для обработки переноса распространения в операциях на р-адических числа .

Смотрите также

Посмотрите вектор в Викисловарь, бесплатный словарь.

Векторные пространства с большей структурой

• Дифференцированное векторное пространство , типа векторного пространства , которое включает в себя дополнительную структуру градации
• Нормированное векторное пространство , векторное пространство , на котором определена норма
• гильбертово пространство
• Упорядоченное векторное пространство , векторное пространство , снабженное частичного порядка
• Супер векторное пространство , имя для Z ₂ -градуированного векторного пространства
• Симплекто векторное пространство , векторное пространство V оснащен невырожденным, кососимметрично, билинейная форма
• Топологическое векторное пространство , сочетание топологической структуры с алгебраическим понятием векторного пространства

векторные поля

Векторное поле является вектор-функция , которая, как правило , имеет домен одного и того же размера (как коллектор ) в качестве области значений,

Разнообразный

• Риччи исчисление
• Векторный анализ , учебник по векторному исчислению по Уилсон , впервые опубликованный в 1901 году, который сделал многочтобы стандартизировать обозначения и терминологию трехмерной линейной алгебры и векторное исчисления
• Векторное расслоение , топологическая конструкция , которая делает точную идею семейства векторных пространств , параметризованную другим пространство
• Вектор исчисление , раздел математики касается дифференциации и интеграции векторных полей
• Вектор дифференциал , или дель , вектор дифференциальный оператор , представленный набла∇{\ Displaystyle \ набла}
• Вектор Лаплас , вектор оператор Лапласа, обозначаемый , представляет собой дифференциальный оператор , определенный над векторным полем∇2{\ Displaystyle \ набла ^ {2}}
• Вектор обозначения , общие обозначения , используемые при работе с векторами
• Вектор оператор , тип дифференциального оператора используется в векторном исчислении
• Векторное произведение или векторное произведение, операция на двух векторов в трехмерном евклидовом пространстве, производя третье трехмерное евклидово вектор
• Вектор проекция , также известная как вектор решительный или компонента вектора , линейное отображение производящего вектора параллельно второй вектор
• Вектор-функция , функция , которая имеет векторное пространство в качестве области значений
• Векторизация (математика) , линейное преобразование , которое преобразует матрицу в вектор — столбец
• Вектор авторегрессия , эконометрическая модель , используемая для захвата эволюции и взаимозависимости между несколькими временными рядами
• Векторный бозон , бозон со спиновым квантовым числом равным 1
• Вектор мера , функция , определенная на семействе множеств и принимает значение векторов , удовлетворяющее определенные свойства
• Векторный мезон мезон с полным спином 1 и нечетностями
• Векторное квантование , метод квантования , используемый в обработке сигналов
• Вектор солитон , уединенная волна с несколькими компонентами , которые соединены друг с другом сохраняет свою форму при распространении
• Вектор синтез , тип звукового синтеза

Заметки

Векторы в физике и математике

Слайд 1

в физике Векторы и математике у х А О В n

Слайд 2

Объектом исследования являются Векторы и его свойства

Слайд 3

Предмет исследования Применение вектора и его свойств при решении задач школьного курса физики

Слайд 4

Цель работы -определить сущность, функции межпредметных связей и их классификацию, а так же повысить собственный уровень знаний и умений в применении свойств вектора при решении физических задач; -показать применение вектора и его свойств при решении физических задач школьного курса физики 7-11 классов, олимпиадных задач, а так же задач ЕГЭ;

Слайд 5

Задачи 3. Решить задачи разного уровня сложности, содержащиеся в учебниках физики, сборниках задач, олимпиадных задач и задач ЕГЭ по выбранным темам. 1. Сопоставить понятие вектор, которое дается в учебниках школьного курса физики и геометрии; 2. Проанализировать содержание курса физики 7-11 классов и отобрать темы, в которых при решении задач используется свойства вектора;

Слайд 6

Актуальность Необходимость формирования целостного представления о применении векторов в физике и математике и подготовки к ЕГЭ по этим предметам.

Слайд 7

Практическая значимость работы Заключается в том, что предложенные в работе задачи могут быть использованы на уроках математики, быть полезными учащимся при изучении курса физики и подготовке к ЕГЭ, решении практических задач. Данная работа может представлять интерес для учителей физики и математики при подготовке к урокам и организации повторения.

Слайд 8

Векторы в математике Впервые, понятие вектора дается на уроке геометрии в 8 классе учебника А. В. Погорелова. Вектором называют направленный отрезок, направление которого определяется указанием его начала и конца.

Слайд 9

Векторы в математике Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающая вектор. Если начало вектора совпадает с его концом, такой вектор называется нулевым вектором. Нулевой вектор обозначается .

Слайд 10

Векторы в математике Два вектора называются равными , если они совмещаются параллельным переносом. Равные векторы одинаково направлены и равны по абсолютной величине. Равные векторы имеют равные соответствующие координаты. m n

Слайд 11

Действия над векторами сложение векторов умножение вектора на число скалярное произведение векторов разложение вектора по координатным осям

Слайд 12

Сложение векторов Правило треугольника Правило параллелограмма

Слайд 13

Умножение вектора на число ( λ =

Слайд 14

Скалярное произведение векторов ( . ( = + Если скалярные векторы перпендикулярны, то их произведение равно нулю.

Слайд 15

Разложение вектора по координатным осям Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления координатных полуосей, называются координатными векторами. (1;0) (0;1) и ( λ + μ λ . μ

Слайд 16

Векторы в физике В школьном курсе физики учебника А.В. Пёрышкина 7 класса, впервые понятие векторной величины вводится на примере таких физических величин, как Сила и Скорость . Так же вводится понятие Вес тела , которое тоже является векторной величиной. Болеет углубленно понятие вектора и его свойств затрагивается при изучении физики 9 класса учебника А. В. Пёрышкина и Е. М. Гутник .

Слайд 17

Проекция вектора на ось Проекцией точки А на ось l называется число, соответствующее основанию перпендикуляра АВ, опущенного на ось l из точки А. Проекцией вектора на ось l называется разность проекций конца вектора и его начала.

Слайд 18

Решение физических задач векторным методом Задача . С какого расстояния S от центра полусферы радиуса R =1,35 м, с какой скоростью и под каким углом β нужно бросить маленькую шайбу (из положения 1), чтобы она, попав на полусферу, остановилась на её вершине (положение 2) рисунок (а)? Трением шайбы о полусферу и сопротивлением воздуха пренебречь. Ускорение свободного падения считать равным 10 м/с 2 . Сформулируем обратную задачу : На каком расстоянии S от центра полусферы, с какой скоростью U и под каким углом β упадёт шайба, скатывающаяся с вершины полусферы радиуса R рисунок (б)? Трением шайбы о поверхность полусферы и сопротивлением воздуха пренебречь.

Слайд 19

Решение физических задач векторным методом V 0 = . (1.1 ) Решение. mg cos α = m V 0 2 /R, откуда V 0 = . (1.2) h = R(1 – cos α) V 0 = . (1.3) cos α = 2/3 (1.4) V 0 = = = 3 м/с (1.5) Х = V ox t = ( V o cos α)t ( 1.6) Y = V oy t + gt 2 /2 = (V o sin α)t +gt 2 /2 ( 1.7) При t = t п – времени полёта шайбы до точки падения, X = X max , a Y = R cos α = 1,35 . 2/3 = 0,9 м sin α = = = = /3. ………………

Слайд 20

Решение физических задач векторным методом 0,9 = t п + 5t п 2 , (1.8) t п = ( + )/ 10 = 0,7 с. X max = ( V o cos α)t п = 3 . 2/3 . 0,7 = 1,4 м. S = X max + R sin α = 1,4 + 1,35 . /3 = 2,41 м. V = ( 1.9). V ox = V o cos α = 3 . 2/3 = 2 м; V y = V o sin α + gt п = 3 . /3 + 10 . 0,7 = 9,24 м/с , V = = 9,45 м/с. tg β = V y / V ox = 9,24/ 2 = 4,62 β = 77,8 o .

Слайд 21

Решение физических задач векторным метом Задача . Частица массы 2m налетает на неподвижную частицу массы m. После столкновения частицы разлетаются симметрично под углом 45 о к направлению начальной скорости, рисунок (а). Во сколько раз возросла суммарная кинетическая энергия после столкновения?

Слайд 22

Решение. = .(1.1 ) p = (1.2) Е к = р 2 /4m = 2р 1 2 / 4m = р 1 2 / 2m . (1.3 ) Е к1 + Е к2 = (р 1 2 / 2m) + (p 2 2 / 4m) = 3p 1 2 /4m. (1.4) (Е к1 + Е к2 )/ Е к = 3p 1 2 2m / p 1 2 4m = 3/2 = 1,5. (1.7 ) Решение физических задач векторным метом

Слайд 23

Решение физических задач векторным метом По двум длинным параллельным проводникам, расположенным на расстоянии r, текут токи I 1 и I 2 в направлениях, указанных на рисунке (а), на котором изображены сечения проводников плоскостью, перпендикулярной им. Определить индукцию магнитного поля в точке, находящейся на расстоянии r 1 от первого проводника и на расстоянии r 2 от второго. Задача . (а) (б)

Слайд 24

Решение физических задач векторным метом Решение. В= (1.1 ) а cos α по той же теореме, но только для треугольника rr 1 r 2 : cos α = (r 1 2 + r 2 2 – r)/ 2r 1 r 2 . (1.2 ) В = (1.3) (а) (б)

Слайд 25

Задачи из ЕГЭ по физике Через неподвижный блок переброшена нерастяжимая нить. На концах этой нити подвешены грузы равных масс М. На один из грузов поставили груз массой m . Определите ускорение движения грузов, силу натяжения нити, силу давления груза m на M , а также силу давления на ось блока. Массой блока и нити можно пренебречь. Задача .

Слайд 26

Задачи из ЕГЭ по физике Решение. для тела 1 для тела 2 для тела m Найдем mg = a ( 2 M + m ) a = g . Из уравнения (1) T = Mg + Ma = . Из уравнения (3) сила давления P = mg — ma = mg — m = .

Слайд 27

Задачи из ЕГЭ по физике = -2 T = 0 = 2 T

Слайд 28

Задачи из ЕГЭ по физике При скоростном спуске лыжник скользил вниз по склону с углом наклона , не отталкиваясь палками. Коэффициент трения лыж о снег 0.1. Сила сопротивления воздуха пропорциональна квадрату скорости: F = k , где k =0.7 кг/м. Какова максимальная скорость лыжника, если его масса 100 кг? Задача.

Слайд 29

Задачи из ЕГЭ по физике Решение. = k a = a ( t ) а= u ’( t )=0 =29,8 м/с

Слайд 30

Задачи из ЕГЭ по физике Два небольших упругих шарика подвешены на нити =10 см и =5 см так, что они соприкасаются, линия их центров горизонтальна, а нити вертикальны. Масса шариков Шарик массой отклоняют на угол от вертикали отпускают. На какие углы отклонятся нити после абсолютно упругого соударения шариков? Задача.

Слайд 31

Задачи из ЕГЭ по физике Решение. Из ∆ AOB OB = BD=OD-OB= cos α= (1) ; = / 2; ⟹ h = m /2⟹ = Рассмотрим систему, состоящую из двух шариков. = /2 = /2 + /2

Слайд 32

Задачи из ЕГЭ по физике = ⟹ = и = = /(2 g ) cos = 1- =1- =1-( ) =1- = = 1- (1- cos α )= =38, cos =1- =1 — = 1- =1- 2gh = = 1- 4(1- cos α) ( = ⟹ = arccos =8,

Слайд 33

в физике Векторы и математике у х А О В n