Тест: Векторы. Векторные величины — Физика 10 класс
Тест: Векторы. Векторные величины — Физика 10 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Физика »
- 10 класс »
- Векторы. Векторные величины
Векторы. Векторные величины
Проверка текущих знаний
Физика 10 класс | Автор: Чигринская И.Н. | ID: 9739 | Дата: 3.10.2017
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос № 1
Векторные величины — это
величины, которые характеризуются численным значением и направлением
величины, которые характеризуются только численным значением
Вопрос №
2
Температура, масса, время — это
векторные величины
скалярные величины
Вопрос №
3
Скорость, сила
скалярные величины
вектоорные величины
Вопрос №
4
длина пути
направленный отрезок, пара точек, взятых в определённом порядке.
Вопрос №
5
Действия над векторами:
сложение, вычитание, умножение на скаляр
умножение, деление, сложение, вычитание
возведение в степень, умножение, сложение, вычитание
Вопрос №
6
Сложение векторов методом треугольника
начало второго вектора присоединяют к концу первого, вектор соединяющий конец второго с началом первого вектора и есть сумма векторов
Вопрос №
7
Вычитание вектоора
начало вычитаемого вектора соединяют с концом уменьшаемого, вектор соединяющий конец вычитаемого вектора с началом уменьшаемого и есть разность вектооров
Конец вычитаемого вектора соединяют с началом уменьшаемого, вектор соединяющий начало уменьшаемого вектора с концом вычитаемого и есть разность векторов
Вопрос №
8
Проекцией вектора на какую-либо ось называется
длина траектории, выраженная в метрах, километрах
длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».
Вопрос №
9
Если вектор перпендикулярен оси ОХ, то его проекция на эту ось равна
0
модулю вектора
Вопрос №
10
Если вектор направлен под углом к оси ОХ, то его проекция на данную ось равна
0
модулю вектора умноженному на косинус угла наклона между вектором и осью
модулю вектора
Вопрос №
11
Если вектор направлен параллельно оси ОХ, то его проекция на данную ось равна
0
модулю вектора умноженному на косинус угла наклона между вектором и осью
модулю вектора
Вопрос №
12
Какие вы знаете способы описания движения
координатный
векторный
все выше перечисленные
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.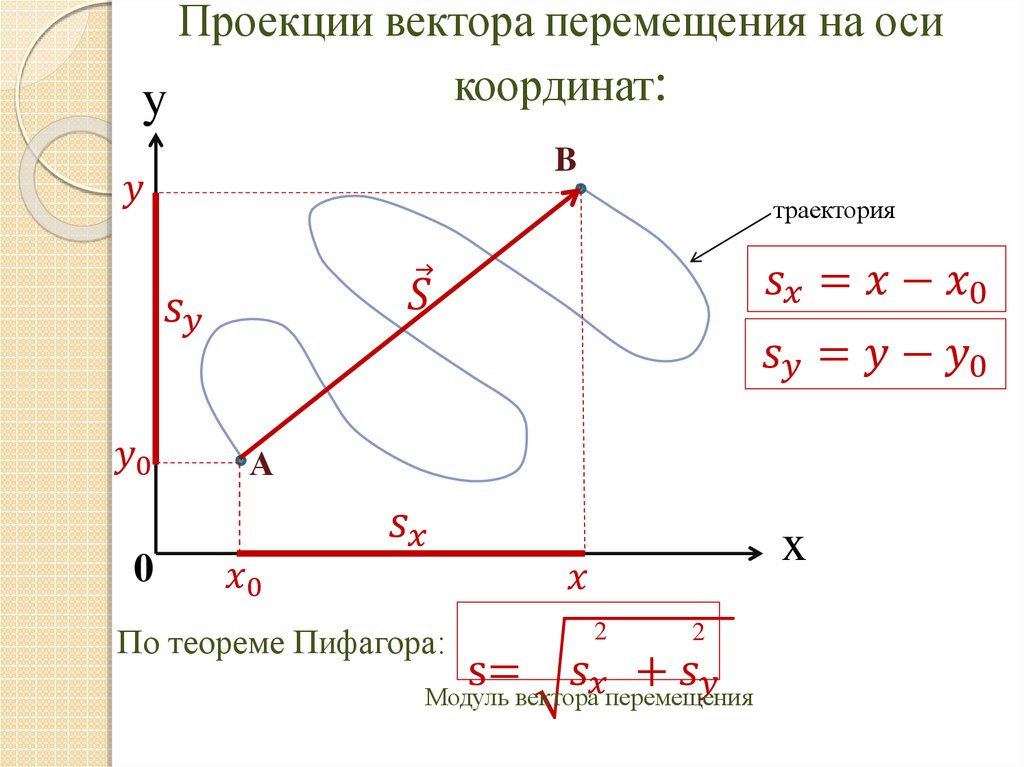 ru 2013-2022
ru 2013-2022
E-mail администратора: [email protected]
| Интегрированный урок по физике и математике «Векторы». 9 класс Повторение и закрепление основных понятий в математике и физике, связанных с векторами. Повторить и закрепить основные понятия, связанные с векторами, закрепить умение решать задачи, применяя теоретический материал геометрии и физики. Применение темы «Векторы» при решении задач практического содержания. Цель урока:
Задачи урока:
Ученик должен знать:
Ученик должен уметь:
Тип урока: Личностно-ориентированная, информационно-коммуникативная. КЭС: векторы, сумма, разность, умножение вектора на число, координаты вектора, скалярное произведение двух векторов, вычисление значений угла между векторами, радиус-вектор, практическая значимость понятия «вектор».
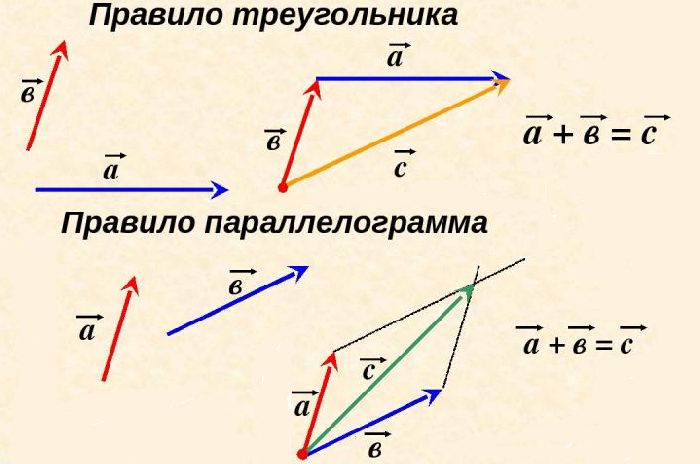
Сценарий урока: 1. Подготовка к восприятию материала: Вступительное слово учителя математики: «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И.Лобачевский -Мы изучаем векторы. А где это применяется? Векторная история это пограничная история, между математикой и физикой. Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию «направление», смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков. Прежде, чем говорить об использовании векторов при решении физических задач, вспомним действия, которые можно выполнять с векторами. (Задавая вопросы, учитель может использовать игровой компонент: бросая мячик, формулировать вопрос, принимая его, получать ответ). — Какие способы сложения векторов вам известны? (Правило треугольника и правило параллелограмма) — В чем принципиальное отличие этих правил? ( При сложении по правилу треугольника начало второго вектора совмещается с концом первого (слайд 2), а при сложении по правилу параллелограмма начала обоих векторов совпадают (слайд 3).) — Что будет вектором суммы при сложении векторов по правилу треугольника? (Вектор, берущий начало в начале первого и заканчивающийся в конце второго вектора.) — Что будет вектором суммы при сложении векторов по правилу параллелограмма? (Вектор, являющийся диагональю параллелограмма, построенного на исходных векторах, исходящий из общего начала слагаемых векторов. — Что будет вектором разности двух векторов? (Вектор, соединяющий концы векторов и идущий в направлении уменьшаемого (слайд 4)). — А если нужно выполнить действие с векторами, которые не выходят из одной точки? (Один из векторов параллельным переносом перенести так, чтобы начала их совпали.) — Что происходит при умножении вектора на положительное число? (Длина вектора изменяется во столько раз, на какое число выполняется умножение, а направление не изменяется). — А если выполняем умножение на отрицательное число? (Направление меняется на противоположное (слайд 5)). — Как называются получившиеся векторы? (Коллинеарные (сонаправленные и противоположно направленные)). Задача 1. Построить вектор , равный сумме трех заданных векторов (слайд 6). Решение (слайд 7): Задача 2. Построить вектор . (слайд 8). Решение (слайд 9). Задача 3 (слайд 10). Решение (слайд 11). Задача 4 (слайд 12). Решение (слайд 13). — Как найти координаты вектора, зная координаты его начала и его конца (слайд 14)? (Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала вектора (слайд 15)). — Как найти длину вектора, зная координаты его начала и его конца (слайд 16)? ( Длина вектора равна корню из суммы квадратов разностей соответствующих координат начала и конца вектора) . Задача 5(слайд 17). Решение (слайд 18). — Как найти координаты суммы двух векторов? (Найти сумму соответствующих координат (слайд 19)). — Как найти координаты разности двух векторов? (Найти разность соответствующих координат (слайд 20)). — Что называют «скаляром»? (Скаляр – это физический термин, обозначающий число). -Почему умножение векторов называется скалярным? (Потому что в результате умножения двух векторов получается число). — А что получается при умножении вектора на число (скаляр)? (Вектор). — Как найти в этой ситуации координаты нового вектора? (Координаты исходного вектора умножить на скаляр (слайд 21)). — Модуль вектора – это скаляр или вектор? (Скаляр, так как модуль – это длина вектора). — Чему равен модуль вектора? (Корню из квадрата этого вектора (слайд 22)). — Как найти модуль вектора, если нам известны его координаты? (Извлечь корень из суммы квадратов координат этого вектора (слайд 23)). — Как найти скалярное произведение векторов, зная их координаты? (Сложить произведения соответствующих координат этих векторов (слайд 24)). — Как найти скалярное произведение векторов другим способом? (Умножить произведение длин этих векторов на косинус угла между ними (слайд 25)). В физике дается определение радиус-вектора. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Если противоречие между двумя определениями, сформулированными в математике и физике? (В любом случае, сделать акцент на идею направления в обоих определениях) Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например: скорость, перемещение, импульс, напряженность электрического поля, сила и др. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора. Законы сложения и вычитания векторов мы будем использовать с вами на уроках физики неоднократно, изучая разные темы. Сейчас мы рассматриваем задачи по теме «Относительность механического движения, законы сложения скоростей и перемещений». Данные задачи обязательно встретятся вам на ГИА в этом году и при сдаче ЕГЭ по физике в 11 классе. Рассмотрим сегодня на уроке задачи практического содержания по этой теме. Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2км? Работа над задачей.
Задача 2. Штурман пытается провести судно в тумане через узкий проход между рифами. Представьте себе, что проход между рифами идет в северном направлении, Скорость океанского течения равна 5м/с, направлено оно на восток, а скорость, сообщаемая винтом судну 9 м/с. Идет аналогичная работа над задачей. (Слайды 30 – 32) Задача 3. Скорость лодки 4 м/с, скорость течения 2 м/с. Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж. (Слайды 33 – 35) В конце урока предлагается тест по материалам урока. Вопросы теста по карточкам, которые выдают каждому обучающемуся. Тест на тему «Векторы» ученика 9 класса гимназии №1799 «Экополис» _______________________________________________.
3. Лодка должна попасть на противоположный берег реки кратчайшим путем в системе отсчета, связанной с берегом. 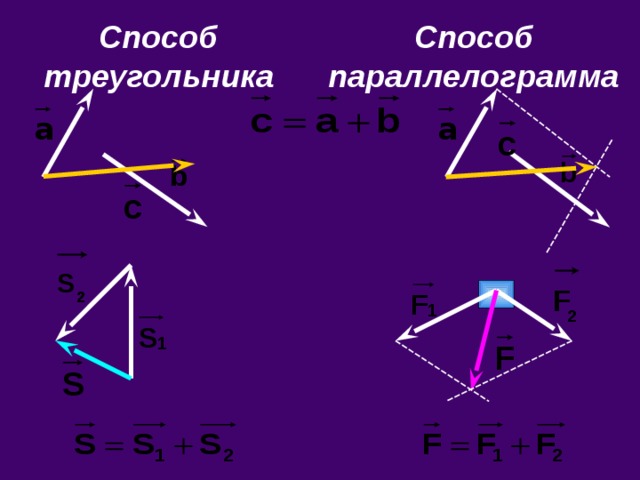 Скорость течения реки, а скорость лодки относительно воды . Модуль скорости лодки относительно берега должен быть равен Скорость течения реки, а скорость лодки относительно воды . Модуль скорости лодки относительно берега должен быть равен1) 2) 3) 4) Ответ: 4 4. Два автомобиля движутся по прямой дороге: один — со скоростью (–10 м/с), другой – со скоростью (–25 м/с). Скорость второго автомобиля относительно первого равна 1) –35 м/с 2) –15 м/с 3) –20 м/с 4) 35 м/с Ответ: 2 5. Пилот поднялся на воздушном шаре на высоту 800м, за это время шар был отнесен ветром в горизонтальном направлении на 600м. Найдите перемещение шара относительно земли? 1) 1400м 2)200м 3)1000м 4) 800м Ответ: 3 Заключительная часть урока. Подводится итог. Выставляются оценки за урок. Идет обобщение материала. Домашнее задание. 1. Лодка с туристами потерпела крушение в 40 м от берега, налетев на пороги. Туристы поплыли к берегу со скоростью 2 м/с, относительно воды перпендикулярно линии берега, но быстрое течение со скоростью 10 м/с сносило их в сторону. 2. Вертолет летел на юг со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует восточный ветер со скоростью 10 м/с? 3. Задачник Степановой Г.Н. №№ 61, 60,59. Интегрированные уроки имеют огромное значение для создания предметных, метапредметных и личностных компетенции обучающихся, являются мощным мотивом к интеллектуальному труду, способствуют более глубокому усвоению материала, расширению границ изученного материала, развитию творческих способностей учащихся, которые развиваются в рамках двух дисциплин, умению логично, научно и доступно излагать свои мысли, математически грамотно говорить. Литература:
|
Симметрия | Физика, определение и факты
- Ключевые люди:
- Пьер Кюри Юджин Вигнер
- Похожие темы:
- скрытая симметрия перевод асимметрия внутренняя симметрия инвариантность к обращению времени
См. весь связанный контент →
симметрия , в физике понятие о том, что свойства частиц, таких как атомы и молекулы, остаются неизменными после того, как они подвергаются различным преобразованиям симметрии или «операциям». С самых первых дней натурфилософии (Пифагор в VI веке до н. э.) симметрия давала понимание законов физики и природы космоса. Два выдающихся теоретических достижения 20-го века, теория относительности и квантовая механика, фундаментально связаны с понятиями симметрии.
Применение симметрии к физике приводит к важному выводу, что некоторые физические законы, особенно законы сохранения, управляющие поведением объектов и частиц, не затрагиваются, когда их геометрические координаты — включая время, когда оно рассматривается как четвертое измерение — преобразуется с помощью операций симметрии. Таким образом, физические законы остаются в силе в любом месте и во все времена во Вселенной. В физике элементарных частиц соображения симметрии могут быть использованы для вывода законов сохранения и определения того, какие взаимодействия частиц могут иметь место, а какие нет (последние называются запрещенными). Симметрия также находит применение во многих других областях физики и химии, например, в теории относительности и квантовой теории, кристаллографии и спектроскопии. Кристаллы и молекулы действительно могут быть описаны с точки зрения количества и типа операций симметрии, которые могут быть выполнены над ними. Количественное обсуждение симметрии называется теорией групп.
Допустимые операции симметрии — это операции, которые можно выполнять без изменения внешнего вида объекта. Количество и тип таких операций зависят от геометрии объекта, к которому применяются операции. Значение и разнообразие операций симметрии можно проиллюстрировать, рассмотрев квадрат, лежащий на столе. Для квадрата допустимы следующие операции: (1) вращение вокруг его центра на 90°, 180°, 270° или 360°, (2) отражение через зеркальные плоскости, перпендикулярные столу и проходящие либо через любые два противоположных угла квадрата или через середины любых двух противоположных сторон, и (3) отражение через зеркальную плоскость в плоскости стола. Следовательно, существует девять операций симметрии, которые дают результат, неотличимый от исходного квадрата. Можно сказать, что круг обладает более высокой симметрией, потому что, например, его можно повернуть на бесконечное число углов (не только кратных 9).0°), чтобы получить идентичный круг.
Субатомные частицы обладают различными свойствами и подвержены влиянию определенных сил, обладающих симметрией.
Элементарные частицы также обладают внутренней симметрией; эти симметрии полезны для классификации частиц и выведения правил отбора. Такой внутренней симметрией является барионное число, которое является свойством класса частиц, называемых адронами.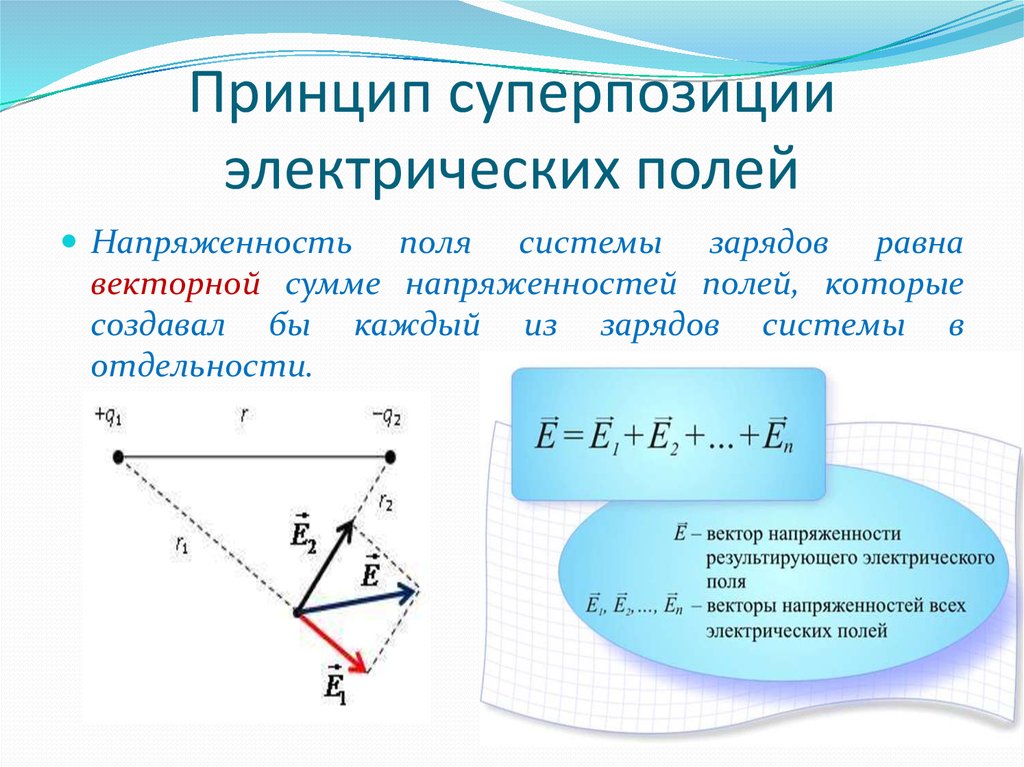 Адроны с барионным числом, равным нулю, называются мезонами, а с числом +1 — барионами. По симметрии должен существовать другой класс частиц с барионным числом -1; это аналоги барионов из антиматерии, называемые антибарионами. Барионное число сохраняется при ядерных взаимодействиях.
Адроны с барионным числом, равным нулю, называются мезонами, а с числом +1 — барионами. По симметрии должен существовать другой класс частиц с барионным числом -1; это аналоги барионов из антиматерии, называемые антибарионами. Барионное число сохраняется при ядерных взаимодействиях.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена Адамом Августином.
IB Physics Notes — 1.3 Векторы и скаляры
При выражении количества мы даем ему число и единицу измерения (например, 12 кг), это выражает величину количества. Некоторые величины также имеют направление, величина, которая имеет и величину, и направление, называется вектором. С другой стороны, величина, которая имеет только величину, называется скалярной величиной. Векторы представлены в печати жирным шрифтом и курсивом (например, F). Ниже приведена таблица, в которой перечислены некоторые векторные и скалярные величины:
| Скаляры | Векторы |
| Скорость | Скорость |
| Температура | Ускорение |
| Расстояние | Рабочий объем |
| Зона | Сила |
| Энтропия | Импульс |
| Том | Перетаскивание |
Таблица 1. 3.1 – Векторные и скалярные количественные показатели
3.1 – Векторные и скалярные количественные показатели
Обратите внимание, что некоторые величины, такие как скорость и скорость, кажутся одинаковыми, обе представляют расстояние во времени, разница в том, что скорость имеет направление, а скорость – нет.
Разница двух векторов
При сложении векторов необходимо учитывать как величину, так и направление. Часто у нас будут ситуации, когда два вектора имеют противоположные направления, в этом случае мы просто вычитаем наименьшую величину из наибольшей. Это показано на рисунке 1.3.1 ниже:
Рисунок 1.3.1 – Результирующая сила двух противоположных векторов
Сумма двух векторов
Иногда возникают ситуации, когда две силы действуют в одном направлении. В ситуациях мы просто складываем величины обоих векторов. Это показано на рисунке 1.3.2 ниже:
Рисунок 1.3.2 — Результирующая сила двух параллельных векторов
Соседние векторы
В определенных ситуациях нам нужно будет вычислить угол между двумя соседними векторами. Чтобы сделать это графически, мы рисуем масштабную диаграмму с хвостом одного вектора в голове другого, затем мы рисуем линию, соединяющую другую голову и хвост. Чтобы получить величину нового вектора, мы просто измеряем его. Это показано на диаграмме ниже:
Чтобы сделать это графически, мы рисуем масштабную диаграмму с хвостом одного вектора в голове другого, затем мы рисуем линию, соединяющую другую голову и хвост. Чтобы получить величину нового вектора, мы просто измеряем его. Это показано на диаграмме ниже:
Рисунок 1.3.3 – Графический метод решения смежных векторов
В качестве альтернативы мы можем использовать тригонометрию для получения более быстрого и точного результата. Это показано на рисунке 1.3.4 ниже:
Рисунок 1.3.4 – Тригонометрический метод решения смежных векторов
Скалярное умножение
Мы также можем умножать (и делить) векторы на скаляры. При этом мы следуем ряду правил:
- Умножение на 1 не меняет вектор 1 v = v
- Умножение на 0 дает нулевой вектор 0 v = 0
- Умножение на -1 дает обратную добавку -1 v = — v
- Левая дистрибутивность: ( c + d ) v = c v + d 18
- Правое распределение: c ( v + w ) = c v + c w
- Ассоциативность: ( cd ) v = c ( d v )
Скалярное умножение показано на рис.




 )
) 

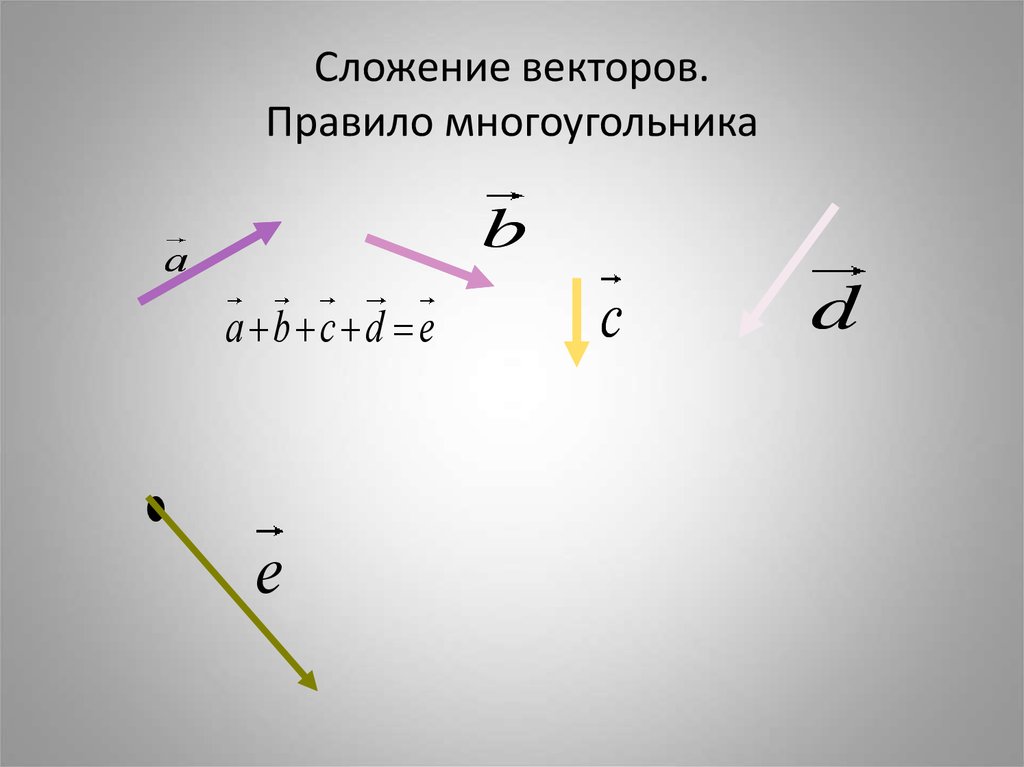
 Выполните построение и покажите в каком направлении штурман должен вести судно по компасу.
Выполните построение и покажите в каком направлении штурман должен вести судно по компасу. С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи.
С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи.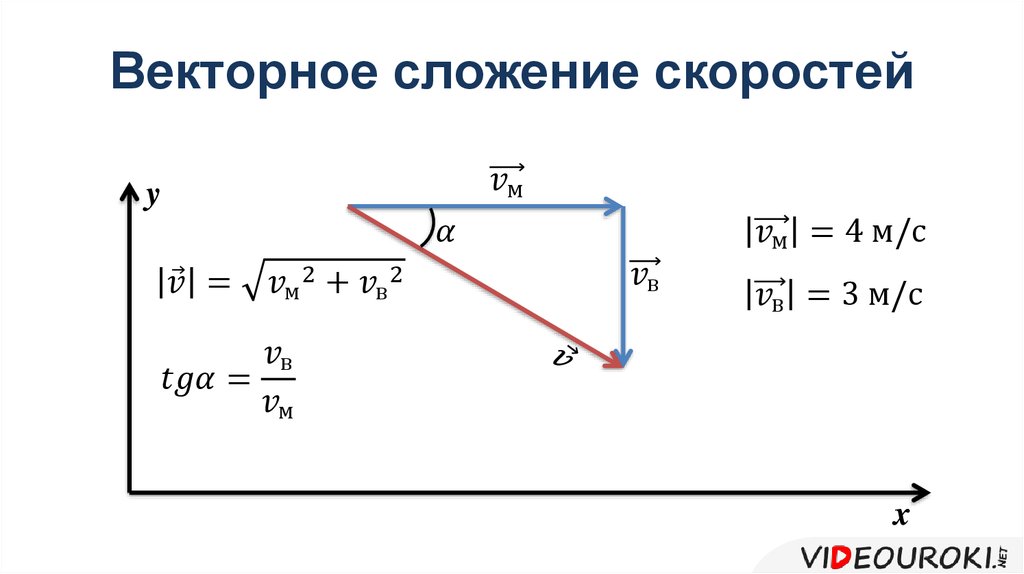 Дидактические материалы для 8 класса. Просвещение,2006
Дидактические материалы для 8 класса. Просвещение,2006