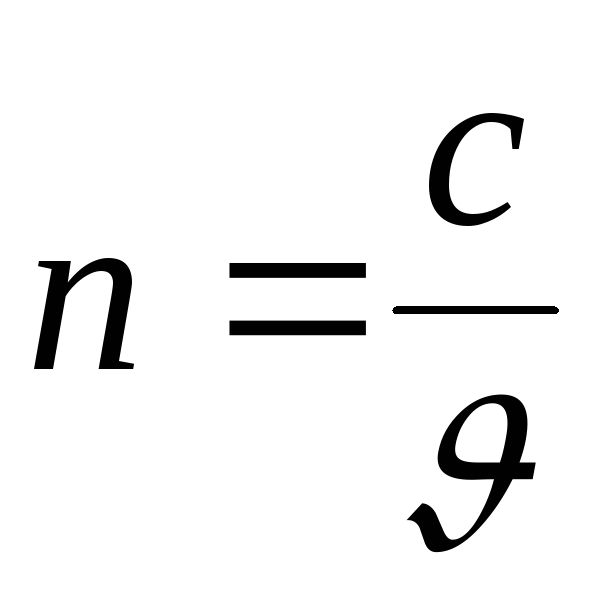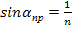Физика для чайников — Класс!ная физика
Физика для чайников
«Не так уж твёрд гранит науки» — телекурс для начинающих или наука для «чайников».
Не обижайтесь на «чайников»!
Здесь все будет на понятном языке, просто, доходчиво и увлекательно!
Годится для старшеклассников, абитуриентов, студентов, преподавателей и всех заинтересованных лиц….
Ведет занятия на первом образовательном канале Борис Сергеевич Бояршинов — доцент, кандидат физико-математических наук.
Итак, физика для чайников
1. Физика — наука о природе ………………………смотреть
2. Азы стихосложения: кинематика ………………………смотреть
3. Главное об ускорении ………………………смотреть
4. Наложение движений: принцип независимости движений ………………………смотреть
5. Куда кривая вывезет: криволинейное движение ………………………смотреть
6. Познание силы: механика ………………………смотреть
7. Движение по наклонной плоскости ………………………смотреть
8. Интегралы движения. Закон сохранения энергии ………………………смотреть
9. Закон сохранения импульса ………………………смотреть
10. Сложение сил ………………………смотреть
11. Моменты сил ………………………смотреть
12. «Потусторонние» силы. Силы инерции ………………………смотреть
13. Волчки. Гироскопы ………………………смотреть
14. Сила, что движет мирами. Всемирное тяготение ………………………смотреть
15. Изо всех сил. Сила, рычаг, путь ………………………смотреть
16. Новое о колебаниях ………………………смотреть
17. Затухающие колебания ………………………смотреть
18. Резонанс ………………………смотреть
19. Гидростатика ………………………смотреть
20. О течении жидкости. Гидродинамика ………………………смотреть
21. Почему ткань после стирки «садится»? Поверхностное натяжение ………………………смотреть
22. Аэродинамика ………………………смотреть
23. Волны. Волновые процессы ………………………смотреть
24. Упругое тело. Растяжение. Сжатие ………………………смотреть
26. Закон Бойля-Мариотта ………………………смотреть
27. Теплоемкость газов ………………………смотреть
28. Ближе к реальности. Реальные газы ………………………смотреть
29. Цикл инженера Карно. Идеальная паровая машина ………………………смотреть
30. Потрясающая вещь: число Авогадро ………………………смотреть
31. Вероятностный мир. Азы статистической физики ………………………смотреть
32. Энтропия ………………………смотреть
33. Электростатика ………………………смотреть
34. Напряженность и потенциал ………………………смотреть
35. Диполи, квадруполи, диэлектрики ………………………смотреть
36. Конденсаторы ………………………смотреть
37. Игры с конденсаторами ………………………смотреть
38. Пироэлектрики, сегнетоэлектрики и другие электрики ………………………смотреть
39. Закон Ома ………………………смотреть
40. Закон Джоуля-Ленца и правила Кирхгофа ………………………смотреть
41. Магнетизм ………………………смотреть
42. Молекулярные токи ………………………смотреть
43. Электромагнитная индукция ………………………смотреть
44. Движение заряда в магнитном поле ………………………смотреть
45. Переменный ток и напряжение ………………………смотреть
46. Электрические колебания ………………………смотреть
47. Классическая модель проводника ………………………смотреть
48. Подлинная история электронов. Квантомеханическое представление ………………………смотреть
49. Электроны в пустоте. Электровакуумные приборы ………………………смотреть
50. Явления в электрических контактах ………………………смотреть
51. Оптика. Принцип Ферма ………………………смотреть
52. Фокусы с линзами ………………………смотреть
53. Интерференция света ………………………смотреть
54. Волновая теория. Принцип Гюйгенса-Френеля ………………………смотреть
55. Дифракция ………………………смотреть
56. Поляризация света ………………………смотреть
57. Скорость света ………………………смотреть
58. Теория относительности ………………………смотреть
59. Абсолютно черное тело ………………………смотреть
60. Фотоны ………………………смотреть
61. Квантовая механика. Теория относительности ………………………смотреть
62. Волна-частица. Волна де Бройля ………………………смотреть
63. Проход сквозь стену. Туннельный эффект ………………………смотреть
64. Луч лазера. Вынужденное излучение ………………………смотреть
65. Ядро изнутри. Атомное ядро и его модели ………………………смотреть
66. Мы не люди и не птицы, нас в науке называют «виртуальные частицы» ………………………смотреть
67. Земные чудеса. Элементарные частицы ………………………смотреть
68. Творение. Рождение пространства, времени и материи ………………………смотреть
69. Чудеса небесные. Физика и астрономия ………………………смотреть
70. Прощание с физикой ……………………… смотреть
Геометрическая оптика
Основные законы геометрической оптики известны ещё с древних времен. Так, Платон (430 г. до н.э.) установил закон прямолинейного распространения света. В трактатах Евклида формулируется закон прямолинейного распространения света и закон равенства углов падения и отражения. Аристотель и Птолемей изучали преломление света. Но точных формулировок этих законов геометрической оптики греческим философам найти не удалось.Геометрическая оптика является предельным случаем волновой оптики, когда длина световой волны стремится к нулю.Простейшие оптические явления, например возникновение теней и получение изображений в оптических приборах, могут быть поняты в рамках геометрической оптики.
В основу формального построения геометрической оптики положено четыре закона, установленных опытным путем:· закон прямолинейного распространения света;· закон независимости световых лучей;· закон отражения;· закон преломления света.Для анализа этих законов Х. Гюйгенс предложил простой и наглядный метод, названный впоследствии принципом Гюйгенса.Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.
 | Гюйгенс Христиан (1629–1695), нидерландский ученый. В 1665–1681 гг. работал в Париже. Изобрел (1657) маятниковые часы со спусковым механизмом, дал их теорию, установил законы колебаний физического маятника. Опубликовал в 1690 г. созданную им в 1678 г. волновую теорию света, объяснил двойное лучепреломление. Усовершенствовал телескоп; сконструировал окуляр, названный его именем. Открыл кольцо у Сатурна и его спутник Титан. Автор одного из первых трудов по теории вероятностей (1657 г.). |
Основываясь на своем методе, Гюйгенс объяснил прямолинейность распространения света и вывел законы отражения и преломления.Закон прямолинейного распространения света:· свет в оптически однородной среде распространяется прямолинейно.Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их источниками малых размеров.Тщательные эксперименты показали, однако, что этот закон нарушается, если свет проходит через очень малые отверстия, причем отклонение от прямолинейности распространения тем больше, чем меньше отверстия.

Тень, отбрасываемая предметом, обусловлена прямолинейностью распространения световых лучей в оптически однородных средах.Рис 7.1Астрономической иллюстрацией прямолинейного распространения света и, в частности, образования тени и полутени может служить затенение одних планет другими, например затмение Луны, когда Луна попадает в тень Земли (рис. 7.1). Вследствие взаимного движения Луны и Земли тень Земли перемещается по поверхности Луны, и лунное затмение проходит через несколько частных фаз (рис. 7.2).

Рис. 7.2
Закон независимости световых пучков:· эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Разбивая световой поток на отдельные световые пучки (например, с помощью диафрагм), можно показать, что действие выделенных световых пучков независимо.Закон отражения (рис. 7.3):· отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;· угол падения α равен углу отражения γ: α = γ
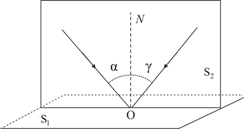
Рис. 7.3

Рис. 7.4
Для вывода закона отражения воспользуемся принципом Гюйгенса. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред (рис. 7.4). Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.· Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.Закон преломления (закон Снелиуса) (рис. 7.5):· луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; · отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.

Рис. 7.5

Рис. 7.6
Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна u (рис. 7.6).Пусть время, затрачиваемое волной для прохождения пути ВС, равно Dt. Тогда ВС = сDt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = uDt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. 7.6 видно, что , т.е.
, т.е.  .Отсюда следует закон Снелиуса:
.Отсюда следует закон Снелиуса: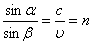 .Несколько иная формулировка закона распространения света была дана французским математиком и физиком П. Ферма.
.Несколько иная формулировка закона распространения света была дана французским математиком и физиком П. Ферма.
 | Ферма Пьер (1601–1665) – французский математик и физик. Родился в Бомон-де-Ломань. Получил юридическое образование. С 1631 г. был советником парламента в Тулузе. |
Физические исследования относятся большей частью к оптике, где он установил в 1662 г. основной принцип геометрической оптики (принцип Ферма). Аналогия между принципом Ферма и вариационными принципами механики сыграла значительную роль в развитии современной динамики и теории оптических инструментов.Согласно принципу Ферма, свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.Покажем применение этого принципа к решению той же задачи о преломлении света.Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела (рис. 7.7).
Рис. 7.7
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB: .Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:
.Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю: ,отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса:
,отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса: 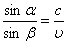 .Принцип Ферма сохранил свое значение до наших дней и послужил основой для общей формулировки законов механики (в том числе теории относительности и квантовой механики).Из принципа Ферма вытекает несколько следствий.Обратимость световых лучей: если обратить луч III (рис. 7.7), заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.Другой пример – мираж, который часто наблюдают путешественники на раскаленных солнцем дорогах. Они видят впереди оазис, но когда приходят туда, кругом оказывается песок. Сущность в том, что мы видим в этом случае свет, прошедший над песком. Воздух сильно раскален над самой дорогой, а в верхних слоях холоднее. Горячий воздух, расширяясь, становится более разреженным и скорость света в нем больше, чем в холодном. Поэтому свет проходит не по прямой, а по траектории с наименьшим временем, заворачивая в теплые слои воздуха.Если свет распространяется из среды с большим показателем преломления
.Принцип Ферма сохранил свое значение до наших дней и послужил основой для общей формулировки законов механики (в том числе теории относительности и квантовой механики).Из принципа Ферма вытекает несколько следствий.Обратимость световых лучей: если обратить луч III (рис. 7.7), заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.Другой пример – мираж, который часто наблюдают путешественники на раскаленных солнцем дорогах. Они видят впереди оазис, но когда приходят туда, кругом оказывается песок. Сущность в том, что мы видим в этом случае свет, прошедший над песком. Воздух сильно раскален над самой дорогой, а в верхних слоях холоднее. Горячий воздух, расширяясь, становится более разреженным и скорость света в нем больше, чем в холодном. Поэтому свет проходит не по прямой, а по траектории с наименьшим временем, заворачивая в теплые слои воздуха.Если свет распространяется из среды с большим показателем преломления  (оптически более плотной) в среду с меньшим показателем преломления
(оптически более плотной) в среду с меньшим показателем преломления  (оптически менее плотной) (
(оптически менее плотной) (  >
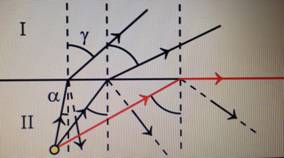
>  ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α (рис. 7.8 а).
), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α (рис. 7.8 а).
Рис.7.8
С увеличением угла падения увеличивается угол преломления (рис. 7.8 б, в), до тех пор, пока при некотором угле падения ( 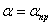 ) угол преломления не окажется равным π/2.Угол
) угол преломления не окажется равным π/2.Угол  называется предельным углом. При углах падения α >
называется предельным углом. При углах падения α >  весь падающий свет полностью отражается (рис. 7.8 г).· По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.· Если
весь падающий свет полностью отражается (рис. 7.8 г).· По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.· Если 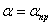 , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 7.8 г). · Таким образом, при углах падения в пределах от
, то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 7.8 г). · Таким образом, при углах падения в пределах от  до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.Предельный угол
до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.Предельный угол  определим из формулы:
определим из формулы: ;
; .Явление полного отражения используется в призмах полного отражения (Рис. 7.9).
.Явление полного отражения используется в призмах полного отражения (Рис. 7.9).
Рис. 7.9
Показатель преломления стекла равен n » 1,5, поэтому предельный угол для границы стекло – воздух  = arcsin (1/1,5) = 42°.При падении света на границу стекло – воздух при α > 42° всегда будет иметь место полное отражение.На рис. 7.9 показаны призмы полного отражения, позволяющие:а) повернуть луч на 90°;б) повернуть изображение;в) обернуть лучи.Призмы полного отражения применяются в оптических приборах (например, в биноклях, перископах), а также в рефрактометрах, позволяющих определять показатели преломления тел (по закону преломления, измеряя
= arcsin (1/1,5) = 42°.При падении света на границу стекло – воздух при α > 42° всегда будет иметь место полное отражение.На рис. 7.9 показаны призмы полного отражения, позволяющие:а) повернуть луч на 90°;б) повернуть изображение;в) обернуть лучи.Призмы полного отражения применяются в оптических приборах (например, в биноклях, перископах), а также в рефрактометрах, позволяющих определять показатели преломления тел (по закону преломления, измеряя  , определяем относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления второй среды известен).
, определяем относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления второй среды известен).

Явление полного отражения используется также в световодах, представляющих собой тонкие, произвольным образом изогнутые нити (волокна) из оптически прозрачного материала.Рис. 7.10В волоконных деталях применяют стеклянное волокно, световедущая жила (сердцевина) которого окружается стеклом – оболочкой из другого стекла с меньшим показателем преломления. Свет, падающий на торец световода под углам больше предельного, претерпевает на поверхности раздела сердцевины и оболочки полное отражение и распространяется только по световедущей жиле.Световоды используются при создании телеграфно-телефонных кабелей большой емкости. Кабель состоит из сотен и тысяч оптических волокон тонких, как человеческий волос. По такому кабелю, толщиной в обычный карандаш, можно одновременно передавать до восьмидесяти тысяч телефонных разговоров.Кроме того, световоды используются в оптоволоконных электронно-лучевых трубках, в электронно-счетных машинах, для кодирования информации, в медицине (например, диагностика желудка), для целей интегральной оптики.
Лекции по физике. Оптика.Геометрическая оптика
Оптика — раздел физики, который изучает природу света, световые явления и взаимодействие света с веществом.
Оптическое излучение представляет собой электромагнитные волны, и поэтому оптика является частью общего учения об электромагнитном поле.
В зависимости от круга рассматриваемых явлений оптику делят на геометрическую
1. Основные законы геометрической оптики.
Еще до установления природы света были известны следующие законы:
Закон прямолинейного распространения света — свет в оптически однородной среде распространяется прямолинейно.
Световой луч — линия, вдоль которой переносится световая энергия. В однородной среде лучи света представляют собой прямые линии.
 Закон
независимости световых пучков —
эффект, производимый отдельным
пучком, не зависит от того, действуют
ли одновременно остальные пучки
или они устранены.
Закон
независимости световых пучков —
эффект, производимый отдельным
пучком, не зависит от того, действуют
ли одновременно остальные пучки
или они устранены.
Закон
отражения — отраженный луч лежит
в одной плоскости с падающим лучом и
перпендикуляром,
проведенным к границе раздела
двух сред в точке падения; угол отражения  равен углу падения i1:
равен углу падения i1:

Закон преломления — луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела двух сред в точке падения, лежат в одной плоскости; отношение синуса угла
падения к синусу угла преломления есть величина постоянная для данных сред, | |
где | |
Следовательно, закон преломления будет иметь вид: Абсолютным показателем преломления среды называется величина и, равная отношению скорости электромагнитных волн в вакууме с к их фазовой скорости v в среде. | |
Поскольку  , то
, то 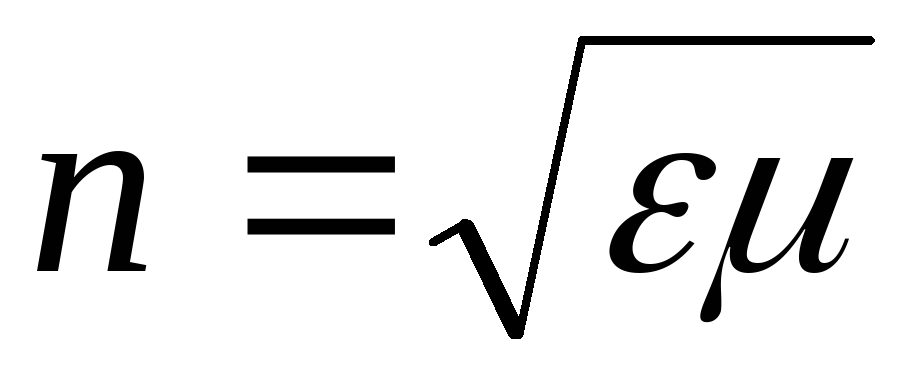
2. Полное отражение.
Если
свет распространяется из
среды с большим показателем
преломления  (оптически более плотной) в
среду с меньшим показателем
преломления n2 (оптически менее плотную) (n1 > п2) (например,
из стекла в воздух или из воды
в воздух),
то
(оптически более плотной) в
среду с меньшим показателем
преломления n2 (оптически менее плотную) (n1 > п2) (например,
из стекла в воздух или из воды
в воздух),
то



Следовательно, угол преломления i2 больше угла падения i1. Увеличивая угол падения, при некотором предельном угле iпр угол преломления окажется равным π/2. При углах падения i1 > iпр весь падающий свет полностью отражается.
При углах падения inp>i1> π/2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы.
Это явление называется полным внутренним отражением света.
Предельный угол определяется соотношением:

Явление полного отражения используется в призмах полного отражения и световодах
3. Линзы.
Л

1) двояковыпуклые;
2) плосковыпуклые;
3) двояковогнутые;
4) плосковогнутые;
5) выпукло-вогнутые.
Линза называется тонкой, если ее толщина значительно меньше, чем радиусы кривизны R1 и R2 обеих поверхностей. На оптических схемах линзы обычно обозначают двунаправленной стрелкой.
Радиус кривизны R > О для выпуклой поверхности; R < О для вогнутой.
П

Оптическим центром линзы (обычно обозначается О) называется точка, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь.
Побочными оптическими осями называются прямые, проходящие через оптический центр линзы и не совпадающие с главной оптической осью.
Фокусом линзы F называется точка, лежащая на главной оптической оси, в которой пересекаются лучи параксиального (приосевого) светового пучка, распространяющиеся параллельно главной оптической оси.
Фокальной плоскостью называется плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.
Фокусным расстоянием / называется расстояние между оптическим центром линзы О и ее фокусом F:


Формула тонкой линзы:

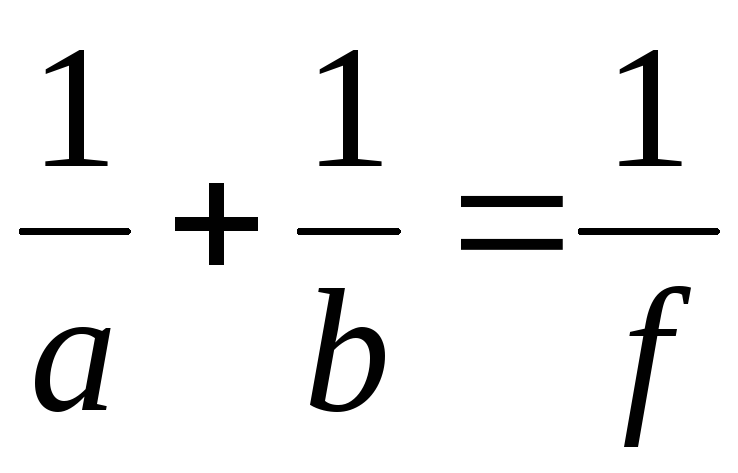
где а и b — расстояния от линзы до предмета и его изображения. Если а = ∞, т.е. лучи падают на линзу параллельным пучком (а), то b=f. Если b = ∞, т.е. изображение находится в бесконечности (б), и, следовательно, лучи выходят из линзы параллельным пучком, то a= f.
Фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны.
Величина Ф = 1/f называется оптической силой линзы. Ее единица — диоптрия (дптр) — оптическая сила линзы с фокусным расстоянием 1 м.
 Линзы
с положительной оптической
силой являются собирающими, с отрицательной — рассеивающими.
Линзы
с положительной оптической
силой являются собирающими, с отрицательной — рассеивающими.
В отличие от собирающей линзы, рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси.
Законы геометрической оптики. Видеоурок. Физика 11 Класс
Тема: Оптика
Урок: Законы геометрической оптики
Геометрическая оптика является самой древней частью оптики как науки.
Геометрическая оптика – это раздел оптики, в котором рассматривают вопросы распространения света в различных оптических системах (линзах, призмах и т. д.) без рассмотрения вопроса о природе света.
Одним из основных понятий в оптике и, в частности, в геометрической оптике, является понятие луча.
Световой луч – линия, вдоль которой распространяется световая энергия.
Световой луч – это пучок света, толщина которого много меньше расстояния, на которое он распространяется. Такое определение близко, например, к определению материальной точки, которое дается в кинематике.
Первый закон геометрической оптики (Закон о прямолинейном распространении света): в однородной прозрачной среде свет распространяется прямолинейно.
По теореме Ферма: свет распространяется по такому направлению, время распространения по которому будет минимально.
Второй закон геометрической оптики (Законы отражения):
1. Отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром к границе раздела двух сред.
2. Угол падения равен углу отражения (см. Рис. 1).
|
∟α = ∟β |
Рис. 1. Закон отражения
Третий закон геометрической оптики (Закон преломления) (см. Рис. 2)
1. Преломленный луч лежит в одной плоскости с падающим лучом и перпендикуляром, восстановленным в точку падения.
2. Отношение синуса угла падения к синусу угла преломления есть величина, постоянная для данных двух сред, которая называется показателем преломления (n).
Интенсивность отраженного и преломленного луча зависит от того, какова среда и что собой представляет граница раздела.
|
|
Рис. 2. Закон преломления
Физический смысл показателя преломления: 
Показатель преломления является относительным, так как измерения проводятся относительно двух сред.
В том случае, если одна из сред – это вакуум: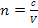
С – скорость света в вакууме,
n – абсолютный показатель преломления, характеризующий среду относительно вакуума.
Если свет переходит из оптически менее плотной среды в оптически более плотную среду, то скорость света уменьшается.
Оптически более плотная среда – среда, в которой скорость света меньше.
Оптически менее плотная среда – среда, в которой скорость света больше.
Закон полного внутреннего отражения
Существует предельный угол преломления – наибольший угол падения луча, при котором еще имеет место преломление при переходе луча в менее плотную среду. При углах падения больше предельного происходит полное внутреннее отражение (см. Рис. 3).
|
|
Рис. 3. Закон полного внутреннего отражения
Границы применимости геометрической оптики заключаются в том, что необходимо учитывать размер препятствий для света.
Свет характеризуется длиной волны, равной примерно 10-9 метра
Если препятствия больше длины волны, то можно использовать размеры геометрической оптики.
Список рекомендованной литературы
- Физика. 11 класс: Учебник для общеобразоват. учреждений и шк. с углубл. изучением физики: профильный уровень / А.Т. Глазунов, О.Ф. Кабардин, А.Н. Малинин и др. Под ред. А.А. Пинского, О.Ф. Кабардина. Рос. акад. наук, Рос. акад. образования. – М.: Просвещение, 2009.
- Касьянов В.А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Санкт-Петербургская Школа (Источник).
- AYP.ru (Источник).
- Техническая и учебно-методическая документація (Источник).
Рекомендованное домашнее задание
Рымкевич А.П. Физика. Задачник. 10–11 кл. – М.: Дрофа, 2010. – № 1023, 1024, 1042, 1054.
- Зная скорость света в вакууме, найдите скорость света в алмазе.
- Почему, сидя у костра, мы видим предметы, расположенные напротив, колеблющимися?
- Прокомментируйте опыт: положите монетку на стол и поставьте на нее пустую стеклянную банку (см. Рис. 4). Посмотрите на монетку сбоку сквозь стенку банки (или попросите кого-нибудь смотреть на монетку). Налейте воды полную банку и посмотрите вновь сбоку на дно банки. Куда исчезла монетка?

Рис. 4.
Основные законы геометрической оптики
Определение 1Оптика – один из разделов физики, который изучает свойства и физическую природу света, а также его взаимодействия с веществами.
Данный раздел делят на три, приведенные ниже, части:
- геометрическая или, как ее еще называют, лучевая оптика, которая базируется на понятии о световых лучах, откуда и исходит ее название;
- волновая оптика, исследует явления, в которых проявляются волновые свойства света;
- квантовая оптика, рассматривает такие взаимодействия света с веществами, при которых о себе дают знать корпускулярные свойства света.
В текущей главе нами будут рассмотрены два подраздела оптики. Корпускулярные свойства света будут рассматриваться в пятой главе.
Геометрическая оптика. Основные законы геометрической оптики
Задолго до возникновения понимания истинной физической природы света человечеству уже были известны основные законы геометрической оптики.
Закон прямолинейного распространения света
Определение 1Закон прямолинейного распространения света гласит, что в оптически однородной среде свет распространяется прямолинейно.
Подтверждением этому служат резкие тени, которые отбрасываются непрозрачными телами при освещении с помощью источника света сравнительно малых размеров, то есть так называемым «точечным источником».
Иное доказательство заключается в достаточно известном эксперименте по прохождению света далекого источника сквозь малое отверстие, с образующимся в результате узким световым пучком. Данный опыт подводит нас к представлению светового луча в виде геометрической линии, вдоль которой распространяется свет.
Определение 2Стоит отметить тот факт, что само понятие светового луча вместе с законом прямолинейного распространения света утрачивают весь свой смысл, в случае если свет проходит через отверстия, размеры которых аналогичны с длиной волны.
Исходя из этого, геометрическая оптика, которая опирается на определение световых лучей – это предельный случай волновой оптики при λ→0, рамки применения которой рассмотрим в разделе, посвященном дифракции света.
На грани раздела двух прозрачных сред свет может частично отразиться таким образом, что некоторая часть световой энергии будет рассеиваться после отражения по уже новому направлению, а другая пересечет границу и продолжит свое распространение во второй среде.
Закон отражения света
Определение 3Закон отражения света, основывается на том, что падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, находятся
Лекции по оптике — Кафедра общей физики
КУРС ЛЕКЦИЙ
ПО ОПТИКЕ:
Лекция №1 «Геометрическая оптика» от 9 февраля 2019 г.
Содержание лекции: Обзор литературы к курсу «Оптика». Энергия кванта света. Геометрическая оптика. Принцип Ферма. Закон преломления, закон отражения. Оптические Аберрации. Формула тонкой линзы. Условие синусов Аббе. Микроскоп.
Лекция №2 «Волновая оптика» от 16 февраля 2019 г.
Содержание лекции: Телескоп. Элементы фотометрии.
Волновая оптика. Волновое уравнение, монохроматические волны, комплексная амплитуда, уравнение Гельмгольца, плоские и сферические волны, показатель преломления, фазовая скорость распространения, комплексная диэлектрическая проницаемость и комплексный показатель преломления, связь мнимой части с поглощением света средой. Угол Брюстера.
Лекция №3 «Дисперсия» от 2 марта 2019 г.
Содержание лекции: Теория дисперсии. Коэффициент преломления. Коэффициент поглощения. Связь коэффициента преломления с поглощением среды. Аномальная дисперсия, нормальная дисперсия. Особенные случаи преломления. Поляризация в плотных средах. Формула Лоренца-Лоренца. Связь векторов E, H и k. Метаматериалы. Фазовая и групповая скорости. Волновой пакет. Формула Рэлея. Размытие волнового пакета. Эффект Доплера.
Лекция №4 «Интерференция» от 9 марта 2019 г.
Содержание лекции: Принцип суперпозиции. Интенсивность световой волны. Метод векторных диаграмм. Интерференция плоских монохроматических волн. Разность хода. Видность. Кольца Ньютона. Временная когерентность. Спектральный подход. Корреляционная функция.
Лекция №5 «Пространственная когерентность. Дифракция» от 16 марта 2019 г.
Содержание лекции: Временная когерентность (продолжение). Функция когерентности. Видность. Средняя интенсивность интерференционной картины.
Теорема Винера-Хинчина.
Пространственная когерентность. Радиус когерентности. Звездный интерферометр Майкельсона. Условие наблюдения интерференции.
Дифракция. Основная задача теории дифракции. Дифракция на тонком экране.
Лекция №6 «Дифракция Френеля» от 23 марта 2019 г.
Содержание лекции: Граничные условия Киргофа. Принцип Гюйгенса-Френеля. Дифракция Френеля. Задачи с осевой симметрией. Приближение Френеля. Зоны Френеля. Пятно Пуассона. Зонные пластинки. Линза Френеля. Дифракция Френеля на щели. Спираль Корню.
Лекция №7 «Дифракция Фраунгофера» от 30 марта 2019 г.
Содержание лекции: Дифракция Фраунгофера. Интеграл Френеля. Приближение Френеля. Дифракция на одной щели. Дифракция на круглом и квадратном отверстии. Разрешение оптического прибора. Волновой параметр. Демонстрация переходов между геометрической оптикой и дифракцией. Спектральные приборы.
Лекция №8 «Спектральные приборы» от 6 апреля 2019 г.
Содержание лекции: Спектральные приборы. Спектральные характеристики дифракционной решетки (дисперсия, дисперсионная область, разрешающая способность). Интерферометр Фабри-Перо. Спектральные характеристики интерферометра Фабри-Перо. Призма. Сравнение спектральных приборов. Лазеры. Дифракция Рентгеновских лучей. Условие Брегга-Вульфа.
Лекция №9 «Фурье-оптика» от 13 апреля 2019 г.
Содержание лекции: Элементы Фурье-оптики. Плоская волна. Дифракция на синусоидальной решетке. Теория Аббе формирования оптического изображения. Частотная характеристика свободного пространства. Голограммы.
Лекция №10 «Голограммы. Поляризация» от 20 апреля 2019 г.
Содержание лекции: Голограммы. Голограмма точечного источника (голограмма Габора). Объемная голограмма. Метод Денисюка. Поляризация. Эллиптическая, линейная, круговая поляризация. Монохроматическая волна. Естественный свет. Как получить поляризованный свет? Закон Малюса.
Лекция №11 «Поляризация. Оптика анизотропных сред» от 27 апреля 2019 г.
Содержание лекции: Поляризация. Линейная поляризация. Круговая поляризация. Эллиптическая поляризация. Поляризация естественного света. Поляроиды. Оптика анизотропных сред. Взаимная ориентация векторов k, E, D, B, направление вектора Пойнтинга. Модель осциллятора. Фазовые пластинки (λ/4, λ/2).
Лекция №12 «Анизотропия. Рассеяние света» от 4 мая 2019 г.
Содержание лекции: Двойное лучепреломление в одноосных кристаллах. Принцип Гюйгенса-Френеля для обыкновенной и необыкновенной волн. Явление Керра. Эффект Поккельса. Ячейка Поккельса. Эффект Фарадея. Рассеяние света. Рассеяние Рэлея. Поляризация рассеянного света. Рассеяние Ми. Закон Бугера-Ламберта-Бера.
Лекция №13 «Нелинейные эффекты» от 11 мая 2019 г.
Содержание лекции: Элементы нелинейной оптики. Нелинейная поляризация среды. Метод последовательных приближений. Генерация второй гармоники. Инверсия координат. Учет кубической поправки к поляризации. Самофокусировка. Гауссовы пучки. Радиус кривизны луча. Световоды. Градиентные оптоволокна. Одномодовое волокно.
Волновая оптика. Интерференция света . Видеоурок. Физика 11 Класс
На этом уроке мы узнаем, что свет имеет волновую природу, рассмотрим явление интерференции света. Узнаем, для чего применяется интерференция, а также поговорим о трех методах экспериментального получения когерентных волн. В конце урока решим задачу на нахождение разности путей, пройденных лучами.
Благодаря прошлым урокам нам известно, что свет является совокупностью прямолинейных лучей, определенным образом распространяющихся в пространстве. Однако для объяснения свойств некоторых явлений мы не можем пользоваться представлениями геометрической оптики, то есть не можем игнорировать волновые свойства света. Например, при прохождении солнечного света через стеклянную призму на экране возникает картина чередующихся цветных полос (рис. 1), которые называют спектром; при внимательном рассмотрении мыльного пузыря видна его причудливая окраска (рис. 2), постоянно меняющаяся с течением времени. Для объяснения этих и других подобных примеров мы будем использовать теорию, которая опирается на волновые свойства света, то есть волновую оптику.

Рис. 1. Разложение света в спектр

Рис. 2. Мыльный пузырь
На этом уроке мы рассмотрим явление, которое называется интерференцией света. С помощью этого явления ученые в XIX веке доказали, что свет имеет волновую природу, а не корпускулярную.
Явление интерференции заключается в следующем: при наложении друг на друга в пространстве двух или более волн возникает устойчивая картина распределения амплитуд, при этом в некоторых точках пространства результирующая амплитуда является суммой амплитуд исходных волн, в других точках пространства результирующая амплитуда становится равной нулю. При этом на частоты и фазы исходно складывающихся волн должны быть наложены определенные ограничения.
Пример сложения двух световых волн
Увеличение или уменьшение амплитуды зависит от того, с какой разностью фаз две складывающиеся волны приходят в данную точку.
На рис. 3 показан случай сложения двух волн от точечных источников  и
и  , находящихся на расстоянии
, находящихся на расстоянии 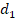 и
и  от точки M, в которой производят измерения амплитуды. Обе волны имеют в точке M в общем случае различные амплитуды, так как до попадания в эту точку они проходят разные пути и их фазы различаются.
от точки M, в которой производят измерения амплитуды. Обе волны имеют в точке M в общем случае различные амплитуды, так как до попадания в эту точку они проходят разные пути и их фазы различаются.

Рис. 3. Сложение двух волн
На рис. 4 показано, как зависит результирующая амплитуда колебания в точке M от того, в каких фазах приходят ее две синусоидальные волны. Когда гребни совпадают, то результирующая амплитуда максимально увеличивается. Когда гребень совпадает со впадиной, то результирующая амплитуда обнуляется. В промежуточных случаях результирующая амплитуда имеет значение между нулем и суммой амплитуд складывающихся волн (рис. 4).

Рис. 4. Сложение двух синусоидальных волн
Максимальное значение результирующей амплитуды будет наблюдаться в том случае, когда разность фаз между двумя складывающимися волнами равна нулю. То же самое должно наблюдаться, когда разность фаз равна  , так как
, так как  – это период функции синуса (рис. 5).
– это период функции синуса (рис. 5).
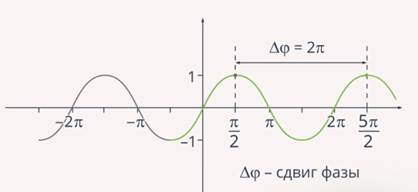
Рис. 5. Максимальное значение результирующей амплитуды
Амплитуда колебаний в данной точке максимальна, если разность хода двух волн, возбуждающих колебание в этой точке, равна целому числу длин волн или четному числу полуволн (рис. 6).
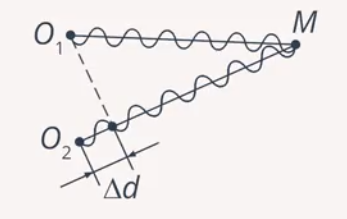
Рис. 6. Максимальная амплитуда колебаний в точке M
 , где
, где  .
.
Амплитуда колебаний в данной точке минимальна, если разность хода двух волн, возбуждающих колебание в этой точке, равна нечетному числу полуволн или полуцелому числу длин волн (рис. 7).

Рис. 7. Минимальная амплитуда колебаний в точке M
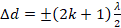 , где
, где  .
.
Интерференцию можно наблюдать только в случае сложения когерентных волн (рис. 8).
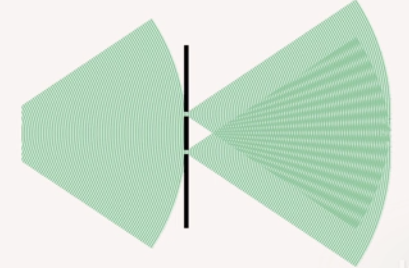
Рис. 8. Интерференция
Когерентные волны – это волны, которые имеют одинаковые частоты, постоянную во времени в данной точке разность фаз (рис. 9).
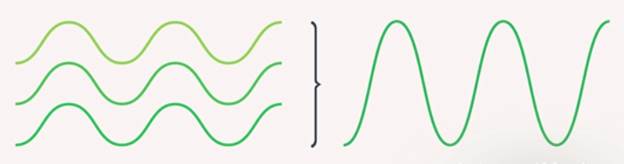
Рис. 9. Когерентные волны
Если волны не когерентны, то в любую точку наблюдения две волны приходят со случайной разностью фаз. Таким образом, амплитуда после сложения двух волн также будет случайной величиной, которая изменяется с течением времени, и эксперимент будет показывать отсутствие интерференционной картины.
Некогерентные волны – это волны, у которых разность фаз непрерывно меняется (рис. 10).

Рис. 10. Некогерентные волны
Существует много ситуаций, когда можно наблюдать интерференцию световых лучей. Например, бензиновое пятно в луже (рис. 11), мыльный пузырь (рис. 2).

Рис. 11. Бензиновое пятно в луже
Пример с мыльными пузырями относится к случаю так называемой интерференции в тонких пленках. Английский ученый Томас Юнг (рис. 12) первым пришел к мысли о возможности объяснения цветов тонких пленок сложением волн, одна из которых отражается от наружной поверхности пленки, а другая – от внутренней.

Рис. 12. Томас Юнг (1773-1829)
Результат интерференции зависит от угла падения света на пленку, ее толщины и длины волны света. Усиление произойдет в том случае, если преломленная волна отстанет от отраженной на целое число длин волн. Если же вторая волна отстанет на половину волны или на нечетное число полуволн, то произойдет ослабление света (рис. 13).

Рис. 13. Отражение световых волн от поверхностей пленки
Когерентность волн, отраженных от внешней и внутренней поверхности пленки, объясняется тем, что обе эти волны являются частями одной и той же падающей волны.
Различие в цветах соответствует тому, что свет может состоять из волн различной частоты (длины). Если свет состоит из волн с одинаковыми частотами, то он называется монохроматическим и наш глаз воспринимает его как один цвет.
Монохроматический свет (от др.-греч. μόνος – один, χρῶμα – цвет) – электромагнитная волна одной определенной и строго постоянной частоты из диапазона частот, непосредственно воспринимаемых человеческим глазом. Происхождение термина связано с тем, что различие в частоте световых волн воспринимается человеком как различие в цвете. Однако по своей физической природе электромагнитные волны видимого диапазона не отличаются от волн других диапазонов (инфракрасного, ультрафиолетового, рентгеновского и т. д.), и по отношению к ним также используют термин «монохроматический» («одноцветный»), хотя никакого ощущения цвета эти волны не дают. Свет, состоящий из волн с различными длинами, называется полихроматическим (свет от солнца).
Таким образом, если на тонкую пленку падает монохроматический свет, то интерференционная картина будет зависеть от угла падения (при некоторых углах волны будут усиливать друг друга, при других углах – гасить). При полихроматическом свете для наблюдения интерференционной картины удобно использовать пленку переменной толщины, при этом волны с разными длинами будут интерферировать в разных точках, и мы можем получить цветную картинку (как в мыльном пузыре).
Существуют специальные приборы – интерферометры (рис. 14, 15), с помощью которых можно измерять длины волн, показатели преломления различных веществ и другие характеристики.
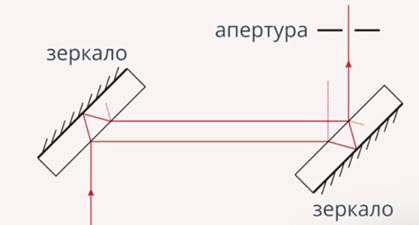
Рис. 14. Интерферометр Жамена

Рис. 15. Интерферометр Физо
К примеру, в 1887 году два американских физика, Майкельсон и Морли (рис. 16), сконструировали специальный интерферометр (рис. 17), с помощью которого они собирались доказать или опровергнуть существование эфира. Этот опыт является одним из самых знаменитых экспериментов в физике.

Рис. 16. А. Майкельсон и Э. Морли

Рис. 17. Звездный интерферометр Майкельсона
Интерференцию применяют и в других областях человеческой деятельности (для оценки качества обработки поверхности, для просветления оптики, для получения высокоотражающих покрытий).
Условие
Два полупрозрачных зеркала расположены параллельно друг другу. На них перпендикулярно плоскости зеркал падает световая волна частотой  (рис. 18). Чему должно быть равно минимальное расстояние между зеркалами, чтобы наблюдался минимум интерференции проходящих лучей первого порядка?
(рис. 18). Чему должно быть равно минимальное расстояние между зеркалами, чтобы наблюдался минимум интерференции проходящих лучей первого порядка?
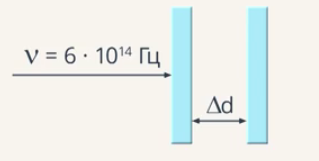
Рис. 18. Иллюстрация к задаче
Дано: 
Найти: 
Решение
Один луч пройдет сквозь оба зеркала. Другой пройдет сквозь первое зеркало, отразится от второго и первого и пройдет сквозь второе. Разность хода этих лучей составит удвоенное расстояние между зеркалами.

Номер минимума соответствует значению целого числа  .
.
Длина волны равна:
 ,
,
где 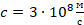 – скорость света.
– скорость света.

Подставим в формулу разности хода значение  и значение длины волны:
и значение длины волны:

Ответ:  .
.
Для получения когерентных световых волн при использовании обычных источников света применяют методы деления волнового фронта. При этом световая волна, испущенная каким-либо источником, делится на две или более частей, когерентных между собой.
1. Получение когерентных волн методом Юнга
Источником света служит ярко освещенная щель, от которой световая волна падает на две узкие щели  и
и 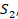 параллельные исходной щели S (рис. 19). Таким образом, щели
параллельные исходной щели S (рис. 19). Таким образом, щели  и
и  служат когерентными источниками. На экране в области BC наблюдается интерференционная картина в виде чередующихся светлых и темных полос.
служат когерентными источниками. На экране в области BC наблюдается интерференционная картина в виде чередующихся светлых и темных полос.

Рис. 19. Получение когерентных волн методом Юнга
2. Получение когерентных волн с помощью бипризмы Френеля
Данная бипризма состоит из двух одинаковых прямоугольных призм с очень малым преломляющим углом, сложенных своими основаниями. Свет от источника преломляется в обеих призмах, в результате этого за призмой распространяются лучи, как бы исходящие из мнимых источников  и
и  (рис. 20). Эти источники являются когерентными. Таким образом, на экране в области BC наблюдается интерференционная картина.
(рис. 20). Эти источники являются когерентными. Таким образом, на экране в области BC наблюдается интерференционная картина.

Рис. 20. Получение когерентных волн с помощью бипризмы Френеля
3. Получение когерентных волн с помощью разделения по оптической длине пути
Две когерентные волны создаются одним источником, но до экрана проходят разные геометрические пути длины  и
и  (рис. 21). При этом каждый луч идет в среде со своим абсолютным показателем преломления. Разность фаз между волнами, приходящими в точку на экране, равна следующей величине:
(рис. 21). При этом каждый луч идет в среде со своим абсолютным показателем преломления. Разность фаз между волнами, приходящими в точку на экране, равна следующей величине:
 ,
,
где и
и  – длины волн в средах, показатели преломления которых равны соответственно
– длины волн в средах, показатели преломления которых равны соответственно  и
и  .
.

Рис. 21. Получение когерентных волн с помощью разделения по оптической длине пути
Произведение геометрической длины пути на абсолютный показатель преломления среды называется оптической длиной пути.
 ,
,
 – оптическая разность хода интерферирующих волн.
– оптическая разность хода интерферирующих волн.
С помощью интерференции можно оценить качество обработки поверхности изделия с точностью до  длины волны. Для этого нужно создать тонкую клиновидную прослойку воздуха между поверхностью образца и очень гладкой эталонной пластиной. Тогда неровности поверхности до
длины волны. Для этого нужно создать тонкую клиновидную прослойку воздуха между поверхностью образца и очень гладкой эталонной пластиной. Тогда неровности поверхности до  см вызовут заметное искривление интерференционных полос, образующихся при отражении света от проверяемых поверхностей и нижней грани (рис. 22).
см вызовут заметное искривление интерференционных полос, образующихся при отражении света от проверяемых поверхностей и нижней грани (рис. 22).
Рис. 22. Проверка качества обработки поверхности
Множество современной фототехники использует большое количество оптических стекол (линзы, призмы и т. д.). Проходя через такие системы, световой поток испытывает многократное отражение, что пагубно влияет на качество изображения, поскольку при отражении теряется часть энергии. Чтобы избежать этого эффекта, необходимо применять специальные методы, одним из которых является метод просветления оптики.
Просветление оптики основано на явлении интерференции. На поверхность оптического стекла, например линзы, наносят тонкую пленку с показателем преломления, меньшим показателя преломления стекла.
На рис. 23 показан ход луча, падающего на поверхность раздела под небольшим углом. Для упрощения все вычисления делаем для угла, равного нулю.
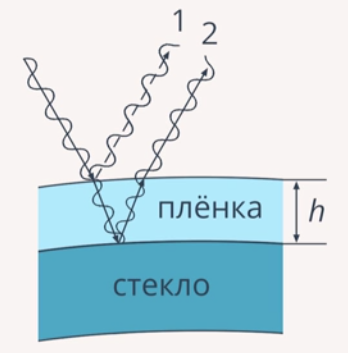
Рис. 23. Просветление оптики
Разность хода световых волн 1 и 2, отраженных от верхней и нижней поверхности пленки, равна удвоенной толщине пленки:

Длина волны в пленке меньше длины волны в вакууме в n раз (n – показатель преломления пленки):

Для того чтобы волны 1 и 2 ослабляли друг друга, разность хода должна быть равна половине длины волны, то есть:
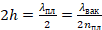

Если амплитуды обеих отраженных волн одинаковы или очень близки друг к другу, то гашение света будет полным. Чтобы добиться этого, подбирают соответствующим образом показатель преломления пленки, так как интенсивность отраженного света определяется отношением коэффициентов преломления двух сред.
Список литературы
- Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В.А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «Reprint1.narod.ru» (Источник).
- Интернет-портал «Eduspb.com» (Источник).
- Интернет-портал «Youtube.com» (Источник).
- Интернет-портал «Toehelp.ru» (Источник).
- Интернет-портал «Exir.ru» (Источник).
Домашнее задание
- Вопросы в конце параграфа 67 (стр. 202), вопросы в конце параграфа 68 (стр. 206) – Мякишев Г.Я. Физика 11 (см. список рекомендованной литературы)
- Где используется явление интерференции?
- Каково условие максимумов интерференции?
- В некоторую точку на экране приходит два когерентных излучения с оптической разностью хода 1,2 мкм. Длина волны этих лучей в вакууме – 600 нм. Определите, что произойдет в этой точке в результате интерференции в трех случаях: а) свет идет в воздухе; б) свет идет в воде; в) свет идет в стекле с показателем преломления 1,5.


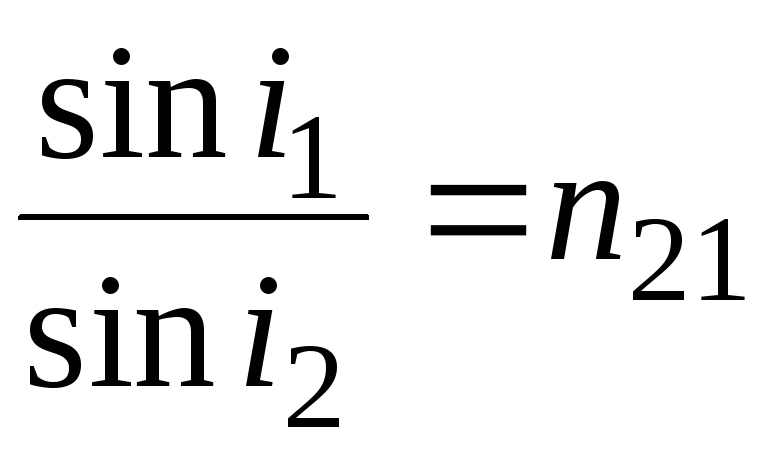
 — относительный
показатель преломления второй
среды относительно первой, который
равен отношению
абсолютных показателей преломления
двух сред.
— относительный
показатель преломления второй
среды относительно первой, который
равен отношению
абсолютных показателей преломления
двух сред.