Формулы по физике
Уравнение скорости при равноускоренном движении υ=υ0+a∙t
Ускорение a=(υ—υ 0)/t
Скорость при движении по окружности υ=2πR/Т
Центростремительное ускорение a=υ2/R
Связь периода с частотой ν=1/T=ω/2π
II закон Ньютона F=ma
Закон Гука Fy=-kx
Закон Всемирного тяготения F=G∙M∙m/R2
Вес тела, движущегося с ускорением а↑ Р=m(g+a)
Вес тела, движущегося с ускорением а↓ Р=m(g-a)
Сила трения Fтр=µN
Импульс тела p=mυ
Импульс силы Ft=∆p
Момент силы M=F∙ℓ
Потенциальная энергия тела, поднятого над землей Eп=mgh
Потенциальная энергия упруго деформированного тела Eп=kx2/2
Кинетическая энергия тела Ek=mυ2/2
Работа A=F∙S∙cosα
Мощность N=A/t=F∙υ
Коэффициент полезного действия η=Aп/Аз
Период колебаний математического маятника T=2π√ℓ/g
Период колебаний пружинного маятника T=2 π √m/k
Уравнение гармонических колебаний Х=Хmax∙cos ωt
Связь длины волны, ее скорости и периода λ= υТ
Количество вещества ν=N/ Na
Молярная масса М=m/ν
Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
Основное уравнение МКТ P=nkT=1/3nm0υ2
Закон Гей – Люссака (изобарный процесс) V/T =const
Закон Шарля (изохорный процесс) P/T =const
Относительная влажность φ=P/P0∙100%
Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
Работа газа A=P∙ΔV
Закон Бойля – Мариотта (изотермический процесс) PV=const
Количество теплоты
при нагревании Q=Cm(T
Количество теплоты при плавлении Q=λm
Количество теплоты при парообразовании Q=Lm
Количество теплоты при сгорании топлива Q=qm
Уравнение состояния идеального газа PV=m/M∙RT
Первый закон термодинамики ΔU=A+Q
КПД тепловых двигателей η= (Q1 — Q2)/ Q1
КПД идеал. двигателей (цикл Карно) η= (Т1 — Т2)/ Т1
Закон Кулона F=k∙q1∙q2/R2
Напряженность электрического поля E=F/q
Напряженность эл. поля точечного заряда E=k∙q/R2
Поверхностная плотность зарядов σ = q/S
Напряженность эл. поля бесконечной плоскости E=2πkσ
Диэлектрическая проницаемость ε=E0/E
Потенциальная энергия взаимод. зарядов W= k∙q1q2/R
Потенциал φ=W/q
Потенциал точечного заряда φ=k∙q/R
Напряжение U=A/q
Для однородного электрического поля U=E∙d
Электроемкость C=q/U
Электроемкость плоского конденсатора C=S∙ε∙ε0/d
Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
Сила тока I=q/t
Сопротивление проводника R=ρ∙ℓ/S
Закон Ома для участка цепи I=U/R
Законы послед. соединения I1=I2=I, U1+U2=U, R1+R2=R
Законы паралл. соед. U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R
Мощность электрического тока P=I∙U
Закон Джоуля-Ленца Q=I2
Закон Ома для полной цепи I=ε/(R+r)
Ток короткого замыкания (R=0) I=ε/r
Вектор магнитной индукции B=Fmax/ℓ∙I
Сила Ампера Fa=IBℓsin α
Сила Лоренца Fл=Bqυsin α
Магнитный поток Ф=BSсos α Ф=LI
Закон электромагнитной индукции Ei=ΔФ/Δt
ЭДС индукции в движ проводнике Ei=Вℓυsinα
ЭДС самоиндукции Esi=-L∙ΔI/Δt
Энергия магнитного поля катушки Wм=LI2/2
Период колебаний кол. контура T=2π ∙√LC
Индуктивное сопротивление XL=ωL=2πLν
Действующее значение силы тока Iд=Imax/√2,
Действующее значение напряжения Uд=Umax/√2
Полное сопротивление Z=√(Xc-XL)2+R2
Равномерное движение | Равноускоренное движение | Тело движется вертикально | Тело брошено горизонтально | Тело брошено под углом к горизонту |
|
| Движение вниз
Движение вверх
|
|
| Тело движется по окружности 1. 4. 6. а – центрострем. ускорение, — угловая скорость, — угол поворота, — угловое ускорение, — частота вращения, Т – период, R — радиус | Механические колебания и волны 1. смещение x = Asin(t + 0), 2. скорость v = Acos(t + 0), vmax = A 3. ускорение a = -A2sin(t + 0), amax = A2 4.
период пруж. маят. 6. А –амплитуда, t – время колебаний, N – число колебаний, v скорость, с – скорость света, λ – длина волны, ν – частота, l – длина маятника, Т — период |
Магнитная постоянная — Википедия
Материал из Википедии — свободной энциклопедии
Магнитная постоянная (μ0{\displaystyle \mu _{0}}) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма в виде коэффициента пропорциональности при записи их в форме, соответствующей Международной системе единиц (СИ)[1].
Иногда называют магнитной проницаемостью вакуума. Измеряется в генри на метр (или в ньютонах на ампер в квадрате).
В материальных уравнениях, в вакууме, через магнитную проницаемость связаны вектор напряжённости магнитного поля H и вектор магнитной индукции B:
- B=μ0 H.{\displaystyle \mathbf {B} =\mu _{0}\ \mathbf {H} .}
Через магнитную постоянную осуществляется связь между относительной и абсолютной магнитной проницаемостью.
В Международной системе единиц[править | править код]
До изменения СИ 2018—2019 годов[править | править код]
Численное значение магнитной постоянной вытекает из определения ампера, единицы силы электрического тока, являющегося одной из основных единиц СИ. Согласно определению, принятому IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году и действовавшему до 2019 года, «Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2⋅10−7ньютона»[2][3].
С другой стороны, сила взаимодействия двух расположенных на расстоянии r{\displaystyle r} друг от друга бесконечных параллельных проводников, по которым текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}, приходящаяся на единицу длины, выражается соотношением:
- F=μ04π2I1I2r.{\displaystyle F={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}.}
С учётом определения ампера из этого соотношения следует точное равенство:
- μ0 = 4π · 10−7 Гн/м.
Соответственно выполняется:
- μ0 ≈ 1,2566370614 · 10−6 Н/А2.
После изменений СИ 2018—2019 годов[править | править код]
С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение магнитной постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение, рекомендованное CODATA[4]:
- μ0 = 1,25663706212(19) · 10−6 Н·А−2, или Гн·м−1.
В системе СГС[править | править код]
В системе СГС магнитная постоянная как коэффициент, связывающий напряжённость и индукцию магнитного поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС магнитная постоянная имеет разную размерность и значение. В частности, Гауссова система единиц и система СГСМ построены так, что магнитная постоянная равна 1, а в системе СГСЭ она равна 1/c2{\displaystyle 1/c^{2}}.
Ответы@Mail.Ru: Что означает формула e=mc2
e = mc^2 — это самая знаменитая формула физики. Даже те, кто вообще ничего не знают про предмет, эту формулу видели хотя бы. Формулу ввёл в оборот Альберт Эйнштейн. В ней e — полная энергия тела, m — его масса, а c — скорость света в пустоте. Она иллюстрирует то, что масса и энергия, по сути, одно и то же свойство физической материи. Это очень в стиле нетривиального мышления Эйнштейна: объединить пространство и время в пространство-время, а энергию и массу в — энергию-массу. До него считалось, что в любом физическом процессе сохраняется масса и энергия по отдельности. Современная физика считает, что сохраняется «энергия-масса». Это, в частности, означает, что горячий чайник немного тяжелее холодного, а движущийся автомобиль — стоящего. Правда, это «немного» так мало, что заметить его можно только в крупном масштабе. Никакие весы не покажут изменение массы при нагревании чайника. Но вот Солнце ежесекундно теряет сотни миллионов тонн массы, которая превращается в энергию его излучения. При некоторых физических процессах материя может даже полностью перейти в излучение. В этом случае масса целиком пропадает, но её место занимает энергия разлетающихся частиц. И наоборот, из электромагнитного поля могут рождаться частицы конечной массы. В этом случае они «берут взаймы» свою массу у энергии излучения. Всем этим и «управляет» формула e = mc^2, и это обычное дело в квантовой механике. Кстати, сам Эйнштейн не признавал многие положения квантовой механики, но несмотря на это его знаменитая формула там всегда отлично работала и продолжает это делать и сейчас.
спроси у Альберта
«Исходя из специальной теории относительности, Эйнштейн в том же 1905 открыл закон взаимосвязи массы и энергии. Его математическим выражением является знаменитая формула E = mc2. Из нее следует, что любой перенос энергии связан с переносом массы. «
Отражает закон сохранения энергии — переход материи в энергию и наоборот и даёт количественную оценку из взаимосвязи
Из Советской армии. А расшифровывается она так — «Квадратное катают, а круглое носят».
Закон сохранения энергии
Из физики. Полная энергия тела равна произведению массы тела на квадрат скорости света в вакууме.
это взаимосвязь массы и энергии. E=mc2: e — полная энергия тела, m — его масса, а c — скорость света в пустоте.
Е-энергия, М-масса, С-скорость света в ваккуме. Вакуум-это свободное пространство. Я надеюсь.
e = mc^2 — это самая знаменитая формула физики. Даже те, кто вообще ничего не знают про предмет, эту формулу видели хотя бы. Формулу ввёл в оборот Альберт Эйнштейн. В ней e — полная энергия тела, m — его масса, а c — скорость света в пустоте. Она иллюстрирует то, что масса и энергия, по сути, одно и то же свойство физической материи. Это очень в стиле нетривиального мышления Эйнштейна: объединить пространство и время в пространство-время, а энергию и массу в — энергию-массу. До него считалось, что в любом физическом процессе сохраняется масса и энергия по отдельности. Современная физика считает, что сохраняется «энергия-масса». Это, в частности, означает, что горячий чайник немного тяжелее холодного, а движущийся автомобиль — стоящего. Правда, это «немного» так мало, что заметить его можно только в крупном масштабе. Никакие весы не покажут изменение массы при нагревании чайника. Но вот Солнце ежесекундно теряет сотни миллионов тонн массы, которая превращается в энергию его излучения. При некоторых физических процессах материя может даже полностью перейти в излучение. В этом случае масса целиком пропадает, но её место занимает энергия разлетающихся частиц. И наоборот, из электромагнитного поля могут рождаться частицы конечной массы. В этом случае они «берут взаймы» свою массу у энергии излучения. Всем этим и «управляет» формула e = mc^2, и это обычное дело в квантовой механике. Кстати, сам Эйнштейн не признавал многие положения квантовой механики, но несмотря на это его знаменитая формула там всегда отлично работала и продолжает это делать и сейчас.
е-энергия m-масса с2-скорость это из физики
Е- это енергия, М- масса, а С- скорость, и все это взято в квадрат.
Формула отражает суть устройства нашего мира. В частности, она показывает, что вещество и энергия могут превращаться друг в друга. Имея необходимое количество энергии, можно создать любое вещество/материю. При этом, в любом количестве материи потенциально присутствует энергия, в которую можно превратить это вещество/материю. При этом, глупо считать, что формула показывает, что горячий чайник тяжелее холодного. Нет, не тяжелее, т. к. в этом объекте присутствует отдельно материя (её масса) и энергия (накопленное тепло). Вот если каким-то образом энергию тепла преобразовать в вещество и присовокупить это вещество к чайнику, тогда да, он станет тяжелее, но просто горячий чайник не тяжелее и не легче (по крайней мере, в рамках рассматриваемой тематики). Можете поиграться и рассчитать, в какое количество чистой энергии превратится та или иная масса, удивитесь насколько это много. Самый «простой» способ превращения всей массы в чистую энергию — аннигиляция вещества с антивеществом (например, водорода с антиводородом и т. п.). Простой в касвычках потому, что антивещества в ближайшем доступном нам мире нет, а его синтез по энергозатратам, как раз, настолько колоссален, насколько показано в формуле. Возможно, механизм синтеза антивещества в будущем можно будет использовать как мегаэффективный (на самом деле, наверное, самый эффективный в рамках нашего мира) механизм накопления (аккумулирования) энергии.
E=mc2 Это формула объясняющая что энергия это тоже самое что и масса и скорость.
вы чатстично, но не правы. 1 в формуле не указан тип энергии, когда вы приводите формулу кинетической энергии, поэтому цитирую отрывок из википедии «Энергия тела пропорцианальна его массе. Вещество имеет массу и обладает энергией, поле имеет энергию и обладает массой» 2 формулу Е=мс в квадрате можно записать так : Е=kmc в квадрате, и вторую формулу ты тоже считаешь неверной???? Вообщем я все сказал, выводы делай сам
Энергия равна массе и скорости света в квадрате. Я десятилетний и я почему-то знаю это 😛
А Эйнштейн тебе на что?
Ни х. я себе, а я в 40 лет этого не знал!
Ответы@Mail.Ru: Формулы по Физике
Лови: http:// g o o . g l/V m2Cu Формулы по механике ДавлениеР=F/S Плотностьρ=m/V Давление на глубине жидкостиP=ρ∙g∙h Архимедова силаFa=ρж∙g∙Vт Скорость при движении по окружностиυ=2πR/Т I закон Ньютона II закон НьютонаF=ma III закон НьютонаF(1,2)=-F(2,1) Закон ГукаFy=-kx Закон Всемирного тяготенияF=G∙M∙m/R2 Вес тела, движущегося с ускорением а↑Р=m(g+a) Вес тела, движущегося с ускорением а↓Р=m(g-a) Сила тренияFтр=µN Импульс тела p=mυ Импульс силы Ft=∆p Момент силыM=F∙ℓ Потенциальная энергия телаEп=mgh Потенциальная энергия упруго деформированного телаEп=kx²/2 Кинетическая энергия телаEk=mυ²/2 РаботаA=F∙S∙cosα МощностьN=A/t=F∙υ Коэффициент полезного действияη=Aп/Аз Молекулярная физика и термодинамика Количество веществаν=N/ Na Молярная массаМ=m/ν Cр. кин. энергия молекул одноатомного газаEk=3kT/2 Основное уравнение МКТP=nkT=1/3nm0υ² Закон Гей – ЛюссакаV/T =const Закон ШарляP/T =const Закон Бойля – МариоттаPV=const Количество теплоты при нагреванииQ=Cm(T2-T1) Количество теплоты при плавленииQ=λm Количество теплоты при парообразованииQ=Lm Уравнение состояния идеального газаPV=m/M∙RT Первый закон термодинамикиΔU=A+Q КПД тепловых двигателейη= (Q1 — Q2)/ Q1 Электростатика и электродинамика Закон КулонаF=k∙q1∙q2/R2 Напряженность электрического поляE=F/q Напряженность эл. поля точечного зарядаE=k∙q/R2 Потенциальная энергия взаимод. зарядовW= k∙q1q2/R ЭлектроемкостьC=q/U Электроемкость плоского конденсатораC=S∙ε∙ε0/d Энергия заряженного конденсатораW=qU/2=q²/2С=CU²/2 Сила токаI=q/t Сопротивление проводникаR=ρ∙ℓ/S Закон Ома для участка цепиI=U/R Формулы по оптике Закон преломления светаn(2,1)=n2/n1= υ1/υ2 Показатель преломленияn21=sinα/sinγ Формула тонкой линзы1/F=1/d + 1/f Оптическая сила линзыD=1/F А также (это 9 — 10 класс) <img src=»//otvet.imgsmail.ru/download/761fc26b3a6d13f8c186cf7bd9bd96ff_i-33.jpg» >
Количество теплоты Q=cm(t2-t1 ) Теплота сгорания Q=qm Теплота парообразования Q=Lm КПД КПД=Qп/Qз100% Закон Ома I=U/R Электрическое сопротивление проводника R=pl/s Последовательное соединение проводников I=I1=I1 R=R1+R2 U=U1+U2 Параллельное соединение проводников U=U1=U2 I=I1+I2 1/R=1/R1+1/R2 Rобщ. =R1/n Работа тока A=IUt Мощность тока P=A/t P=UI Тепловое действие тока Q=I2Rt
Уравнение состояния идеального газа — Википедия
Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона или уравнение Клапейрона[1]) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
- p⋅VM=R⋅T{\displaystyle p\cdot V_{M}=R\cdot T}
или
- pV=νRT{\displaystyle pV=\nu RT},
где
Так как количество вещества ν=mM{\displaystyle \nu ={\frac {m}{M}}}, где m{\displaystyle m} — масса, M{\displaystyle M} — молярная масса, уравнение состояния идеального газа можно записать в виде:
- p⋅V=mMR⋅T{\displaystyle p\cdot V={\frac {m}{M}}R\cdot T}
или в виде
- p=nkT{\displaystyle p=nkT},
где n=N/V{\displaystyle n=N/V} — концентрация частиц (атомов или молекул), k=RNA{\displaystyle k={\frac {R}{N_{A}}}} — постоянная Больцмана.
Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную r,{\displaystyle r,} значение которой необходимо было измерять для каждого газа:
- p⋅V=r⋅T.{\displaystyle p\cdot V=r\cdot T.}
Менделеев же обнаружил, что r{\displaystyle r} прямо пропорциональна ν,{\displaystyle \nu ,} коэффициент пропорциональности R{\displaystyle R} он назвал универсальной газовой постоянной.[источник не указан 259 дней]
Связь с другими законами состояния идеального газа[править | править код]
В случае постоянной массы газа уравнение можно записать в виде:
- p⋅VT=ν⋅R,{\displaystyle {\frac {p\cdot V}{T}}=\nu \cdot R,}
- p⋅VT=const.{\displaystyle {\frac {p\cdot V}{T}}=\mathrm {const} .}
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
- T=const⇒p⋅V=const{\displaystyle T=\mathrm {const} \Rightarrow p\cdot V=\mathrm {const} } — закон Бойля — Мариотта.
- p=const⇒VT=const{\displaystyle p=\mathrm {const} \Rightarrow {\frac {V}{T}}=\mathrm {const} } — Закон Гей-Люссака.
- V=const⇒pT=const{\displaystyle V=\mathrm {const} \Rightarrow {\frac {p}{T}}=\mathrm {const} } — закон Шарля (второй закон Гей-Люссака, 1808 г.)
В форме пропорции p1⋅V1T1=p2⋅V2T2{\displaystyle {\frac {p_{1}\cdot V_{1}}{T_{1}}}={\frac {p_{2}\cdot V_{2}}{T_{2}}}} этот закон удобен для расчёта перевода газа из одного состояния в другое.
С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
- h3+Cl2⟶2HCl{\displaystyle {\ce {h3 + Cl2 -> 2HCl}}}.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
- N2+3h3⟶2Nh4{\displaystyle {\ce {N2 + 3h3 -> 2Nh4}}}.
- Закон Бойля — Мариотта
Закон Бойля — Мариотта
- T=const⇒p⋅V=const{\displaystyle T=\mathrm {const} \Rightarrow p\cdot V=\mathrm {const} }
назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
- p=(γ−1)ρε,{\displaystyle p=(\gamma -1)\rho \varepsilon ,}
где γ{\displaystyle \gamma } — показатель адиабаты, ε{\displaystyle \varepsilon } — внутренняя энергия единицы массы вещества.
Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение P⋅V{\displaystyle P\cdot V} немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение P⋅V{\displaystyle P\cdot V} увеличивается.
- Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.
Математическая физика — Википедия
Математи́ческая фи́зика — теория математических моделей физических явлений. Она относится к математическим наукам; критерий истины в ней — математическое доказательство. Однако, в отличие от чисто математических наук, в математической физике исследуются физические задачи на математическом уровне, а результаты представляются в виде теорем, графиков, таблиц и т. д. и получают физическую интерпретацию. При таком широком понимании математической физики к ней следует относить и такие разделы механики, как теоретическая механика, гидродинамика и теория упругости. Редакционная коллегия журнала Journal of Mathematical Physics определяет математическую физику как «применение математики к физическим задачам и разработка математических методов, подходящих для таких приложений и для формулировок физических теорий»[1].
Близким понятием является теоретическая физика, которая разрабатывает новые математические модели для явлений, удовлетворительных моделей которых пока не построено, и иногда жертвует математической строгостью методов и моделей, в то время как математическая физика обычно формулирует и глубоко исследует уже построенные модели на математическом уровне строгости.
Классическая математическая физика[править | править код]
Первоначально математическая физика сводилась к краевым задачам для дифференциальных уравнений. Это направление составляет предмет классической математической физики, которая сохраняет важное значение и в настоящее время.
Классическая математическая физика развивалась со времён Ньютона параллельно с развитием физики и математики. В конце XVII века было открыто дифференциальное и интегральное исчисление (И. Ньютон, Г. Лейбниц) и сформулированы основные законы классической механики и закон всемирного тяготения (И. Ньютон). В XVIII веке методы математической физики начали формироваться при изучении колебаний струн, стержней, маятников, а также задач, связанных с акустикой и гидродинамикой; закладываются основы аналитической механики (Ж. Даламбер, Л. Эйлер, Д. Бернулли, Ж. Лагранж, К. Гаусс, П. Лаплас). В XIX веке методы математической физики получили новое развитие в связи с задачами теплопроводности, диффузии, теории упругости, оптики, электродинамики, нелинейными волновыми процессами и т. д.; создаются теория потенциала, теория устойчивости движения (Ж. Фурье, С. Пуассон, Л. Больцман, О. Коши, М. В. Остроградский, П. Дирихле, Дж. К. Максвелл, Б. Риман, С. В. Ковалевская, Д. Стокс, Г. Р. Кирхгоф, А. Пуанкаре, А. М. Ляпунов, В. А. Стеклов, Д. Гильберт, Ж. Адамар, А. Н. Тихонов — некоторые из указанных здесь ученых творили и в XX веке или на рубеже XX и XIX веков). В XX веке возникают новые задачи газовой динамики, теории переноса частиц и физики плазмы.
Современная математическая физика[править | править код]
В XX в. появляются новые разделы физики: квантовая механика, квантовая теория поля, квантовая статистическая физика, теория относительности, гравитация, синергетика (А. Пуанкаре, Д. Гильберт, П. Дирак, А. Эйнштейн, Н. Н. Боголюбов, В. А. Фок, Э. Шрёдингер, Г. Вейль, Р. Фейнман, Дж. фон Нейман, В. Гейзенберг, И. Пригожин, С. Курдюмов). Достаточно особое место занимает математическая физика биологических объектов, изучающая действие физических законов на биологическом уровне организации вещества и энергии и в России развиваемая, в частности, на базе ИПМ РАН.
Для изучения этих явлений множество используемых математических средств значительно расширяется: наряду с традиционными областями математики стали широко применяться теория операторов, теория обобщённых функций, теория функций многих комплексных переменных, топологические и алгебраические методы, теория чисел, p-адический анализ, асимптотические и вычислительные методы. С появлением ЭВМ существенно расширился класс математических моделей, допускающих детальный анализ; появилась реальная возможность ставить вычислительные эксперименты, например моделировать взрыв атомной бомбы или работу атомного реактора в реальном масштабе времени[прояснить]. В этом интенсивном взаимодействии современной теоретической физики и современной математики оформилась новая область — современная математическая физика. Её модели не всегда сводятся к краевым задачам для дифференциальных уравнений, они часто формулируются в виде системы аксиом.
- Арнольд В. И. Математические методы классической механики. — М.: Наука, 1989. — 472 с.
- Арнольд В. И. Что такое математическая физика? // УФН. — 2004. — Т. 174, № 12. — С. 1381—1382.
- Владимиров В. С. Что такое математическая физика? — Препринт, Математический институт им. В. А. Стеклова РАН. — М.: МИАН, 2006. — 20 с.
- Владимиров В. С. Уравнения математической физики. — М.: Наука, 1981. — 512 с.
- Владимиров В. С., Волович И. В., Зеленов Е. И. Р-адический анализ и математическая физика. — М.: Физматлит, 1994. — 352 с.
- Джеффрис Г., Свирлс Б. Методы математической физики. — М.: Мир, 1969—1970. — 424+352+344 с.
- Курант Р., Гильберт Д. Методы математической физики. — М.: ГИТТЛ, 1951. — 476+544 с.
- Математическая физика. Энциклопедия / Гл. ред. Л. Д. Фаддеев. — М.: Большая Российская энциклопедия, 1998. — 691 с.
- Морс Ф. М., Фешбах Г. Методы теоретической физики. — М.: Издательство иностранной литературы, 1958—1960. — 930+886 с.
- Мэтьюз Дж., Уокер Р. Математические методы физики. — М.: Атомиздат, 1972. — 400 с.
- Петровский И. Г. Лекции об уравнениях с частными производными. — М.: Физматгиз, 1961. — 400 с.
- Полянин А. Д. Справочник по линейным уравнениям математической физики. — М.: Физматлит, 2001. — 576 с.
- Полянин А. Д., Зайцев В. Ф. Справочник по нелинейным уравнениям математической физики: Точные решения. — М.: Физматлит, 2002. — 432 с.
- Полянин А. Д., Зайцев В. Ф., Журов А. И. Методы решения нелинейных уравнений математической физики и механики. — М.: Физматлит, 2005. — 256 с.
- Рид М., Саймон Б. Методы современной математической физики. — М.: Мир, 1977—1982. — 356+396+444+432 с.
- Рихтмайер Р. Принципы современной математической физики. — М.: Мир, 1982—1984. — 488+384 с.
- Тирринг В. Курс математической и теоретической физики. — К.: TIMPANI, 2004. — 1040 с.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики. — М.: Наука, 1977. — 735 с.
- EqWorld — Мир математических уравнений. Содержит обширную информацию о линейных и нелинейных уравнениях математической физики (уравнениях с частными производными), интегральных уравнениях и других математических уравнениях
- John Baez, This week’s finds in mathematical physics — еженедельный обзор прогресса в математической физике



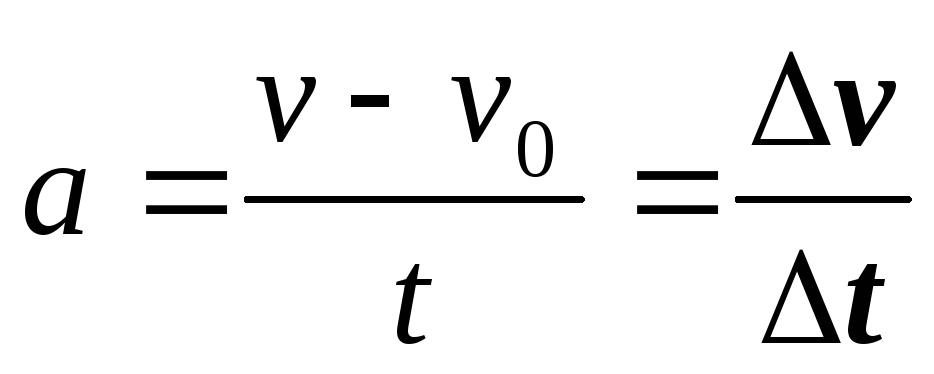
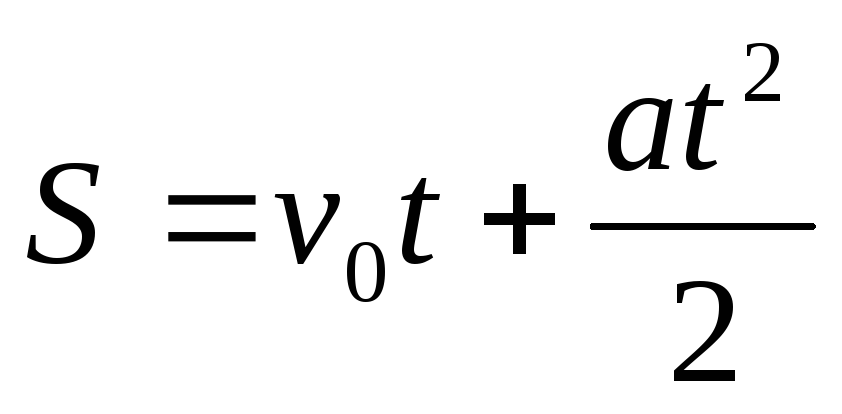 ,
, 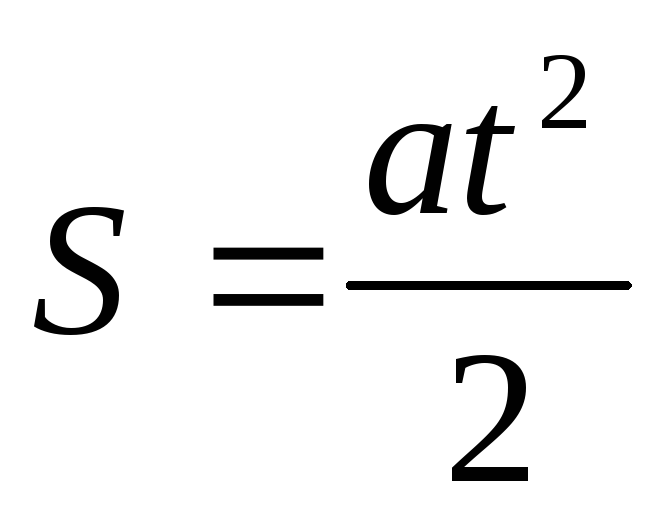
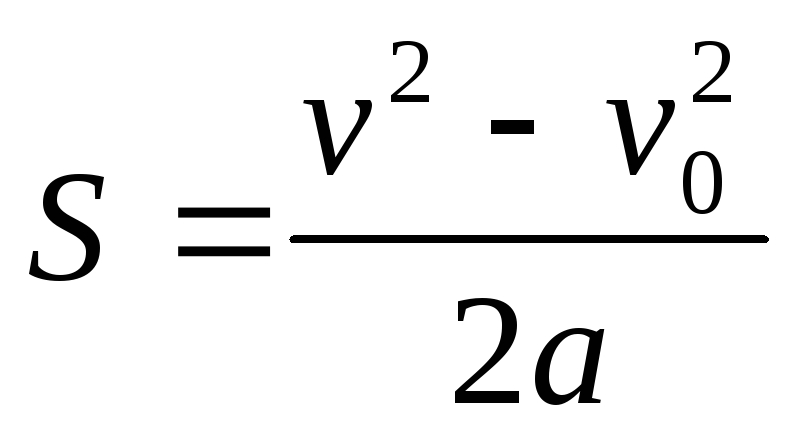 ,
, 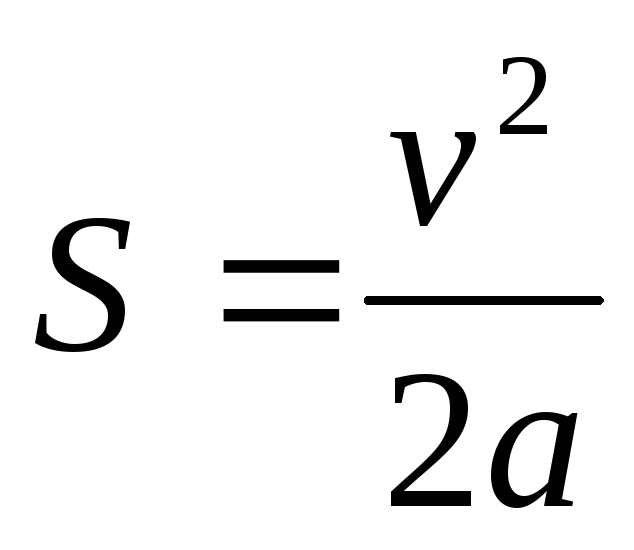
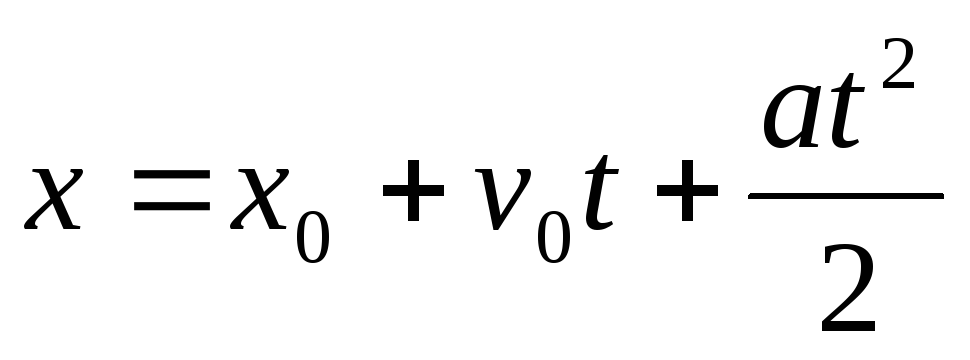 ,
, 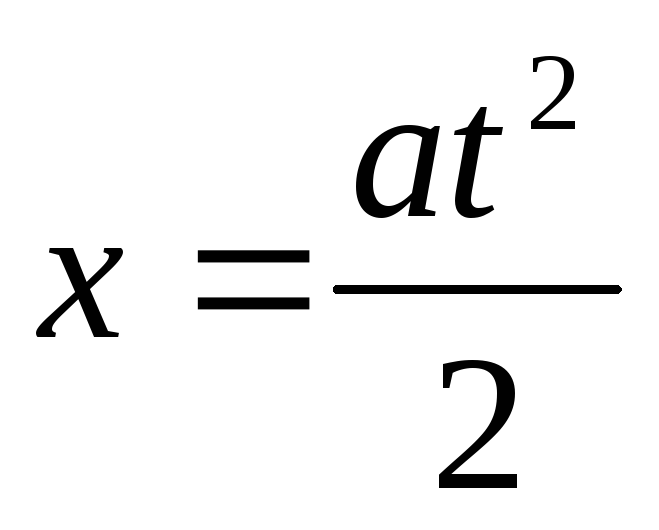

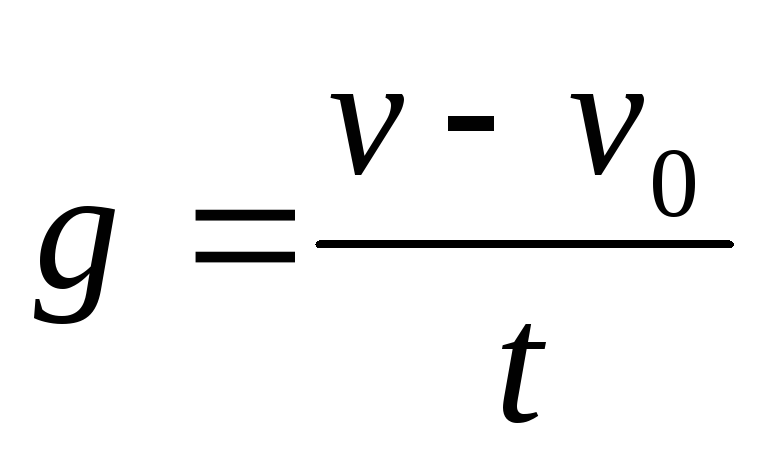
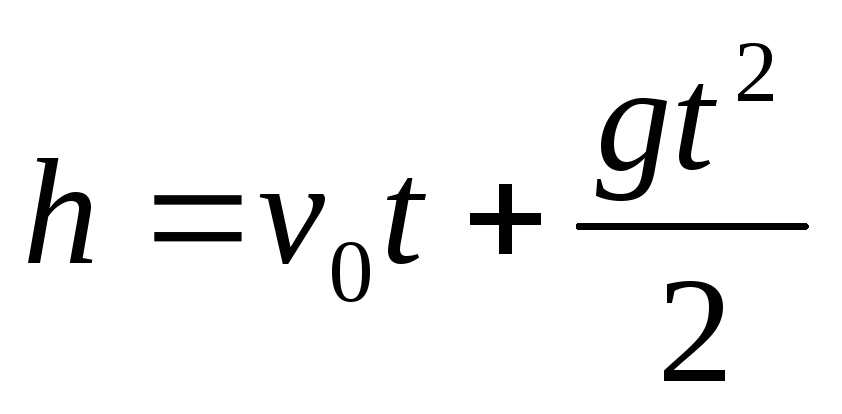 , если v0 = 0, то
, если v0 = 0, то 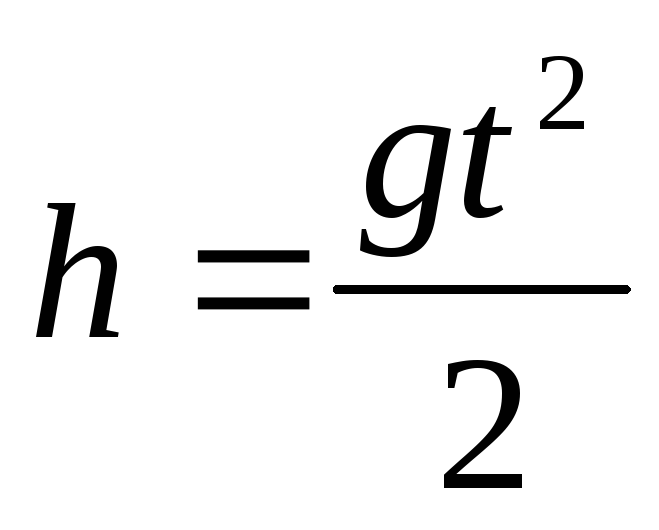
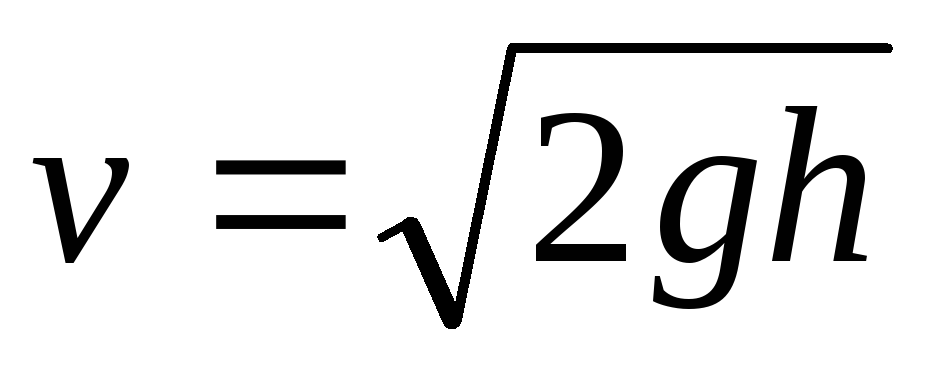 ,
,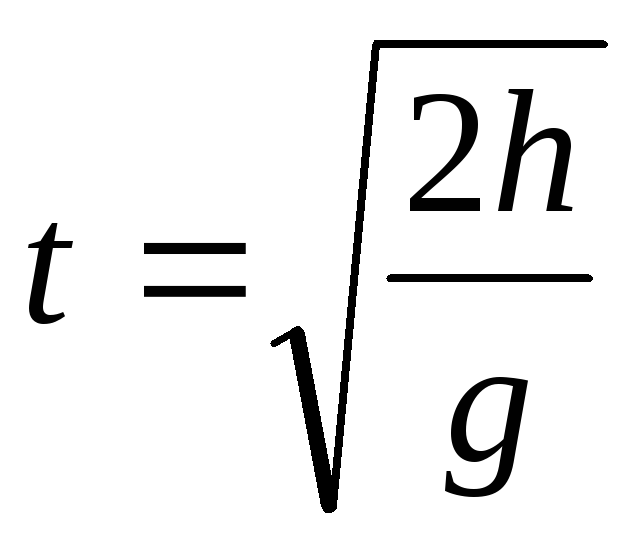 время падения
время падения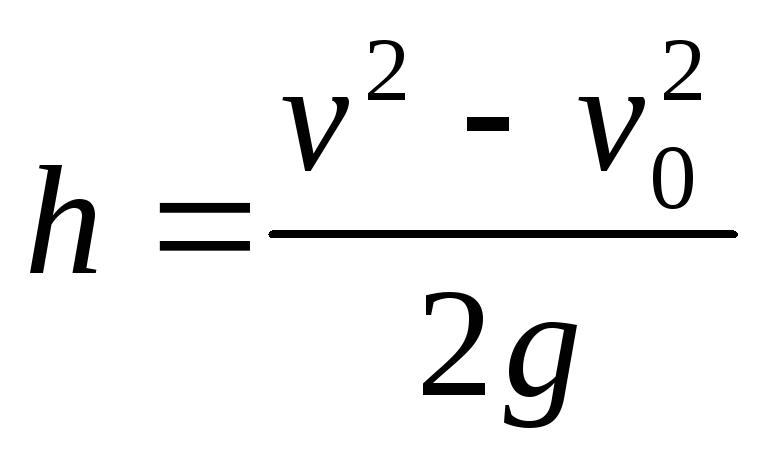 ,
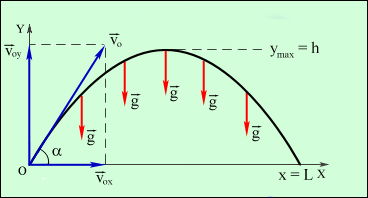
, 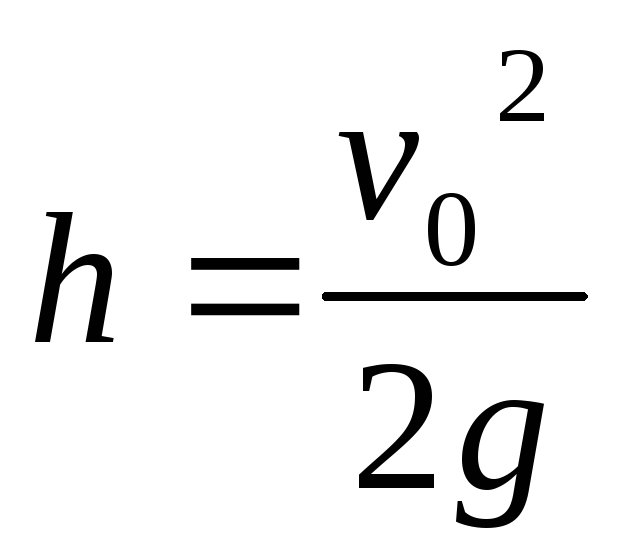 высота подъема
высота подъема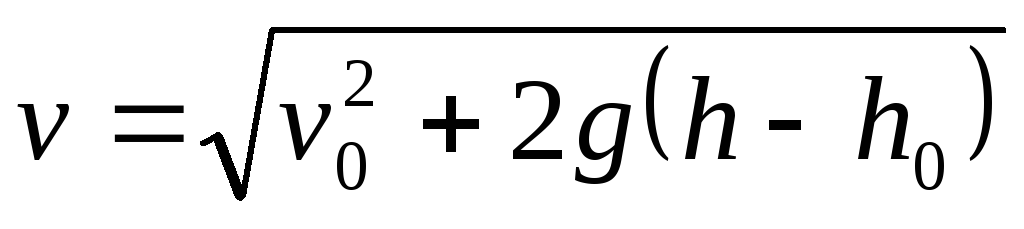 ,
скорость в момент времени t:
v = v0 — gt
,
скорость в момент времени t:
v = v0 — gt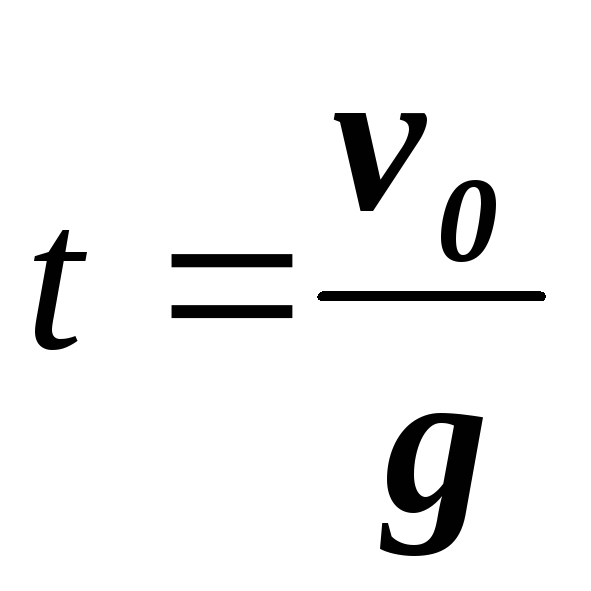 макс.
время подъема
макс.
время подъема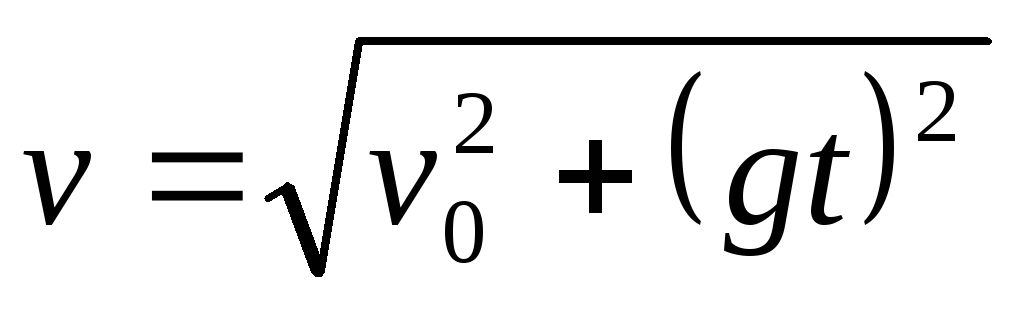
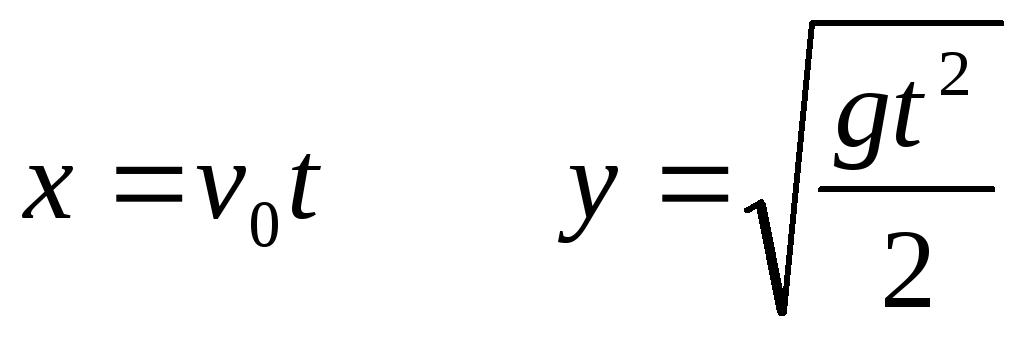
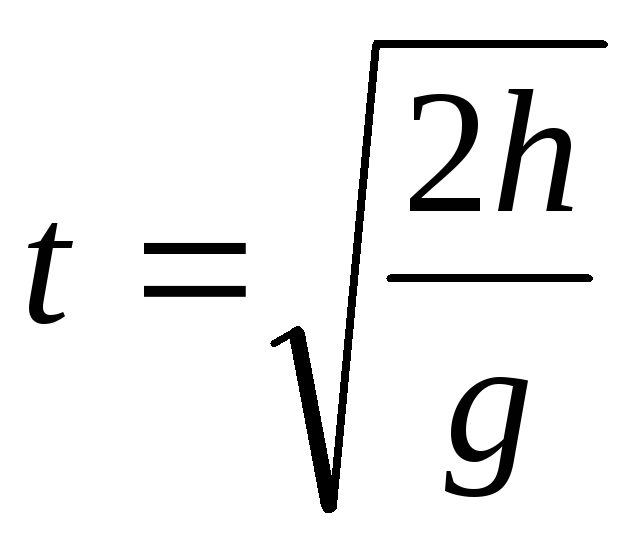
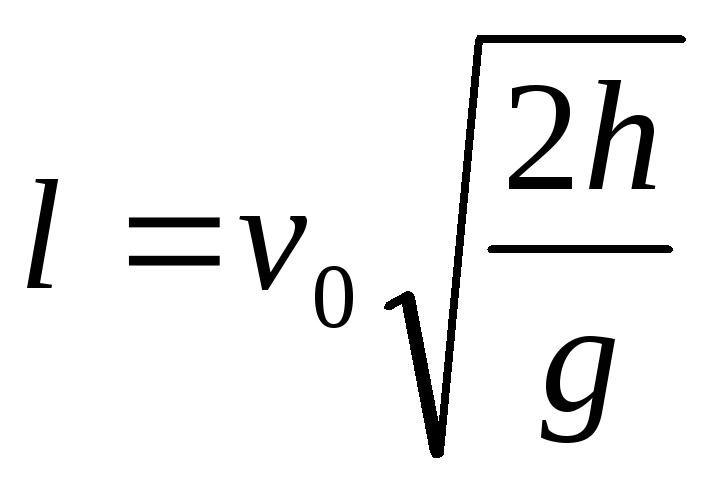
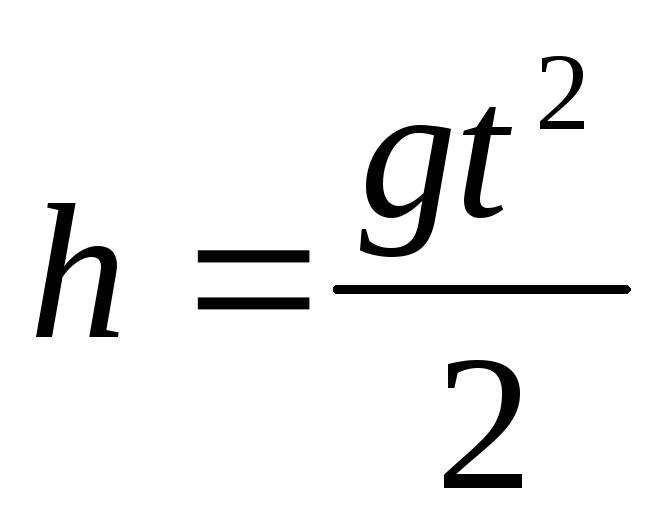
 os
os 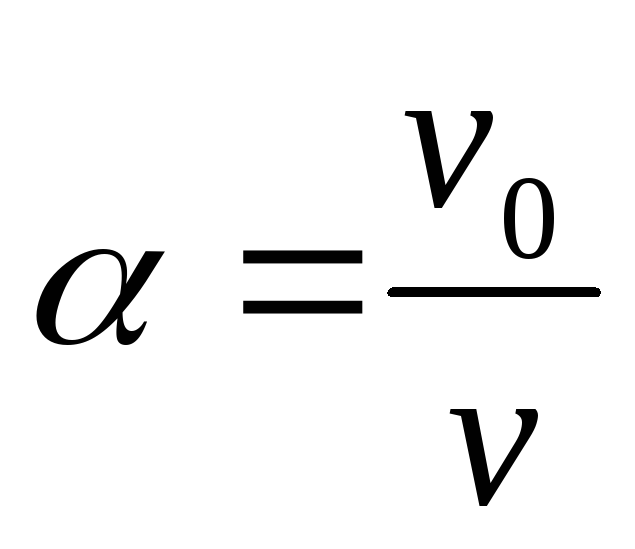 .
.
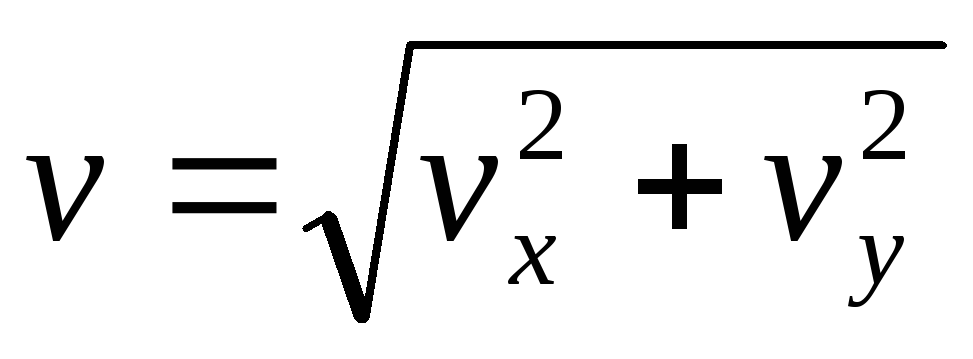
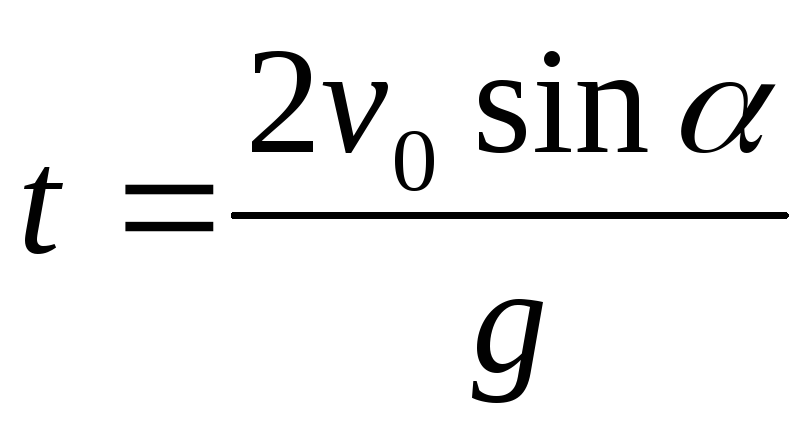 время
время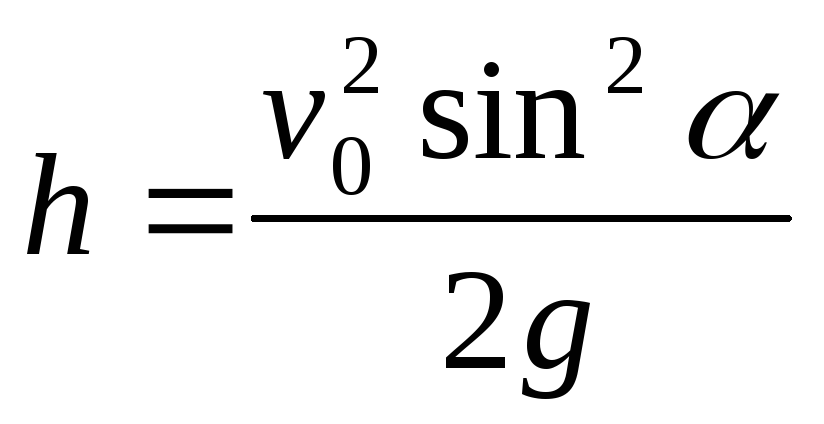 высота
высота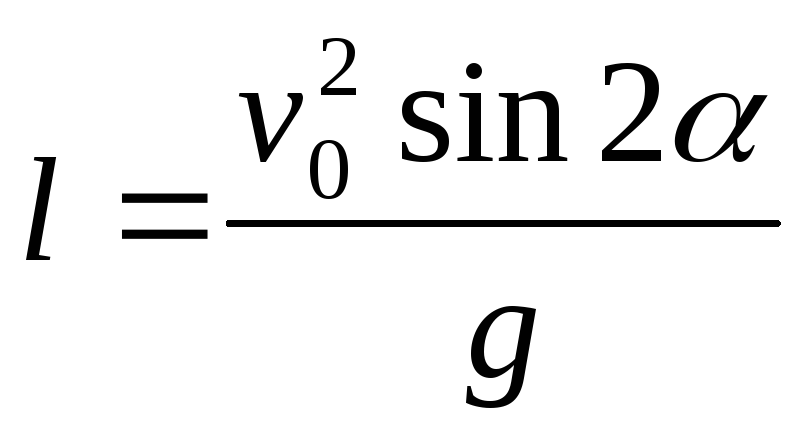 дальность
дальность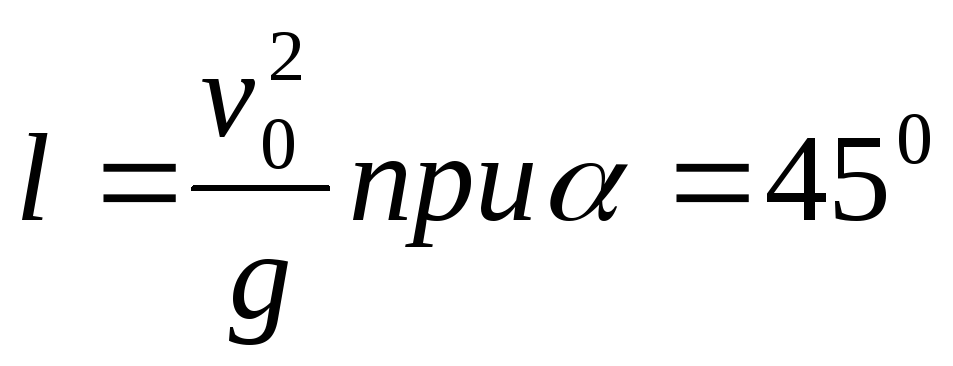 макс.
дальность полета
макс.
дальность полета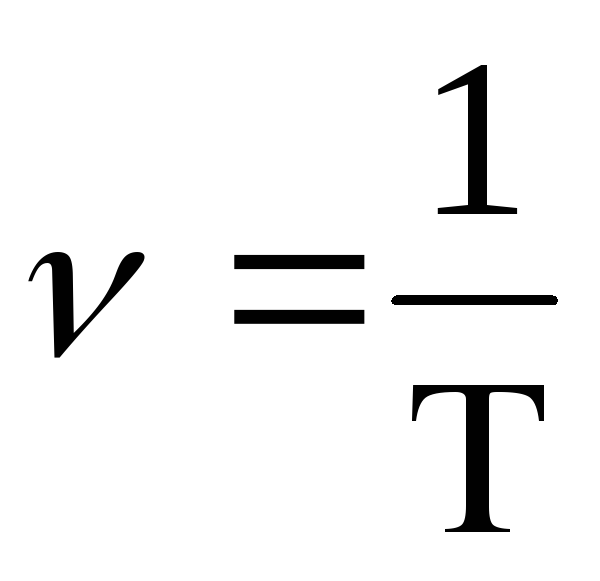 2.
2. 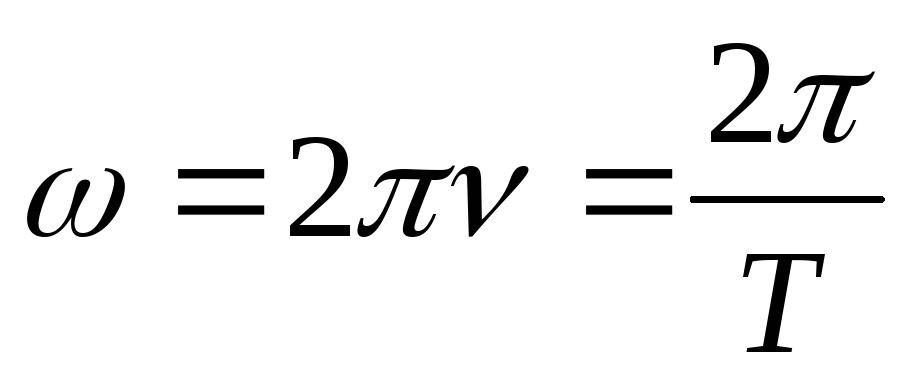 3. v
3. v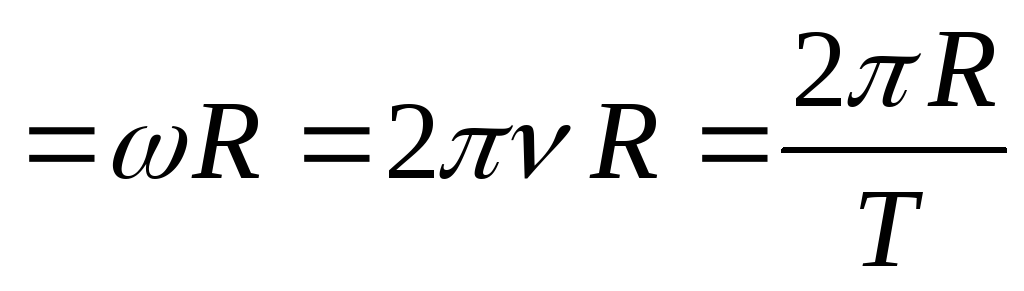
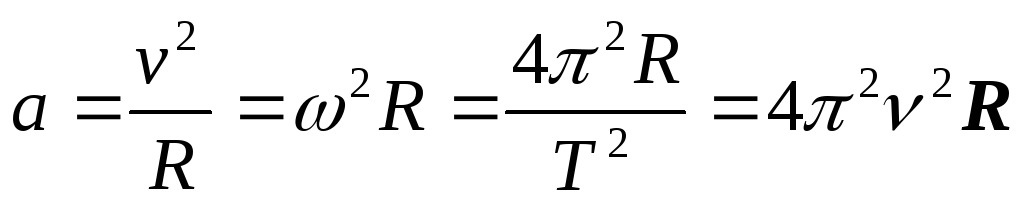 5.
5. 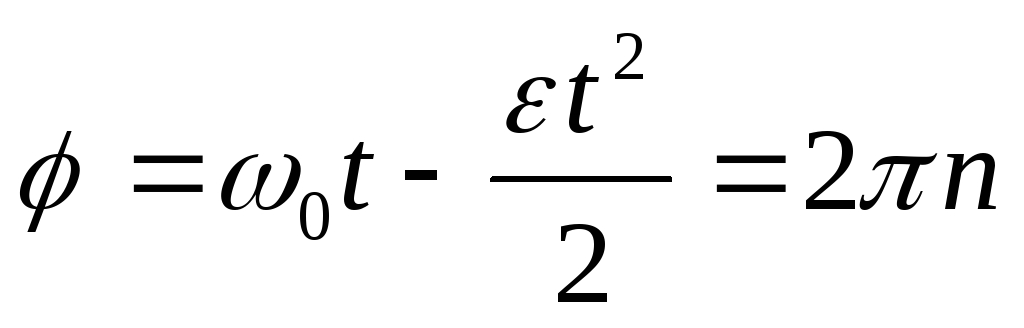
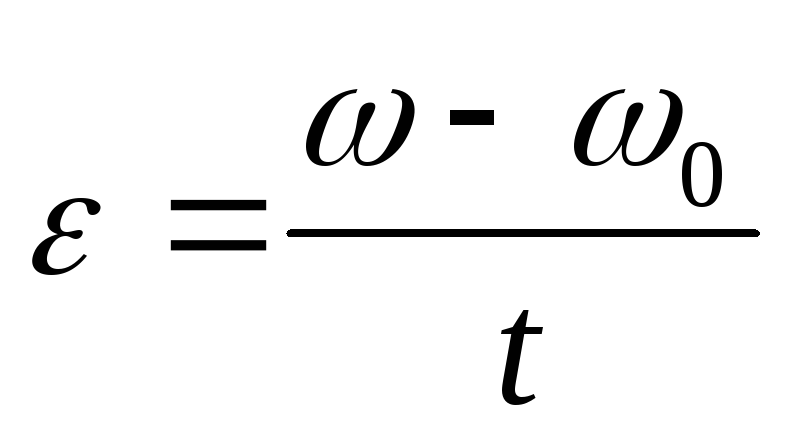
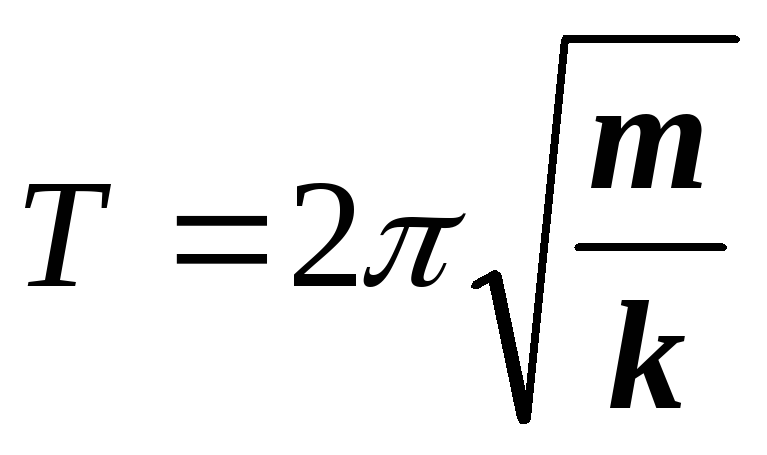 5. период мат. маят.
5. период мат. маят. 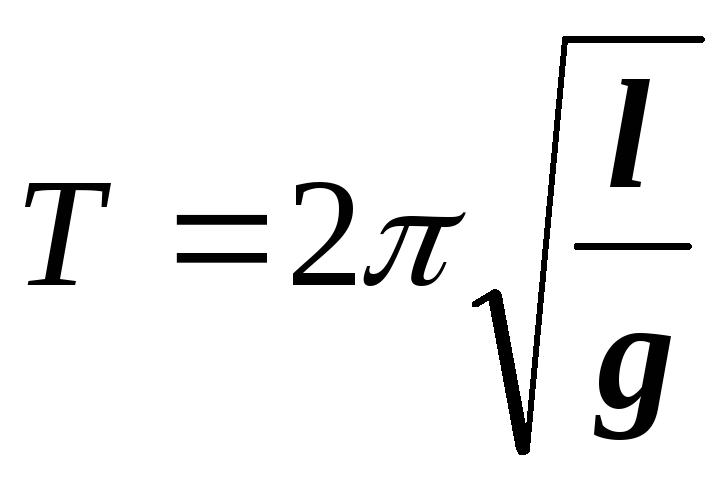
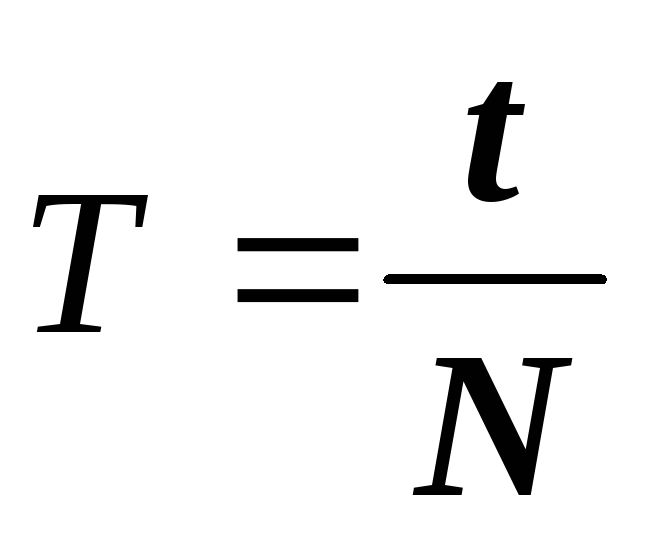 7.
7. 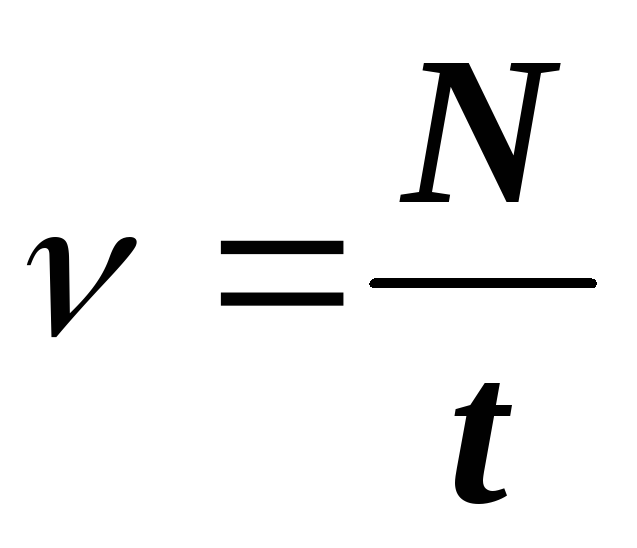 8.
8. 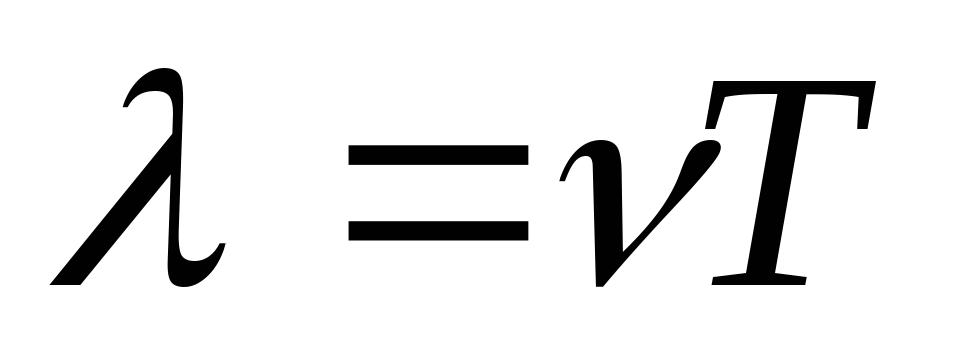 9.
9. 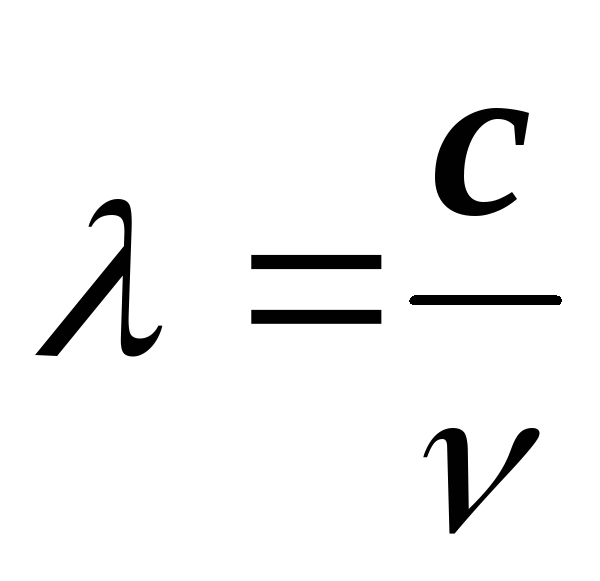 10. v =
10. v =